AN OPEN SOURCE TOOL FOR HEART RATE VARIABILITY

WAVELET-BASED SPECTRAL ANALYSIS

Constantino A. Garc´ıa

, Abraham Otero

, Xos´e Vila

and Mar´ıa J. Lado

Department of Software and Knowledge Engineering, University San Pablo CEU, 28668 Madrid, Spain

Department of Computer Science, University of Vigo, Campus As Lagoas s/n, 32004 Ourense, Spain

Keywords:

Heart Rate Variability, Wavelet Transform, RHRV.

Abstract:

Heart rate variability (HRV) power spectrum analysis is a well-known technique used to study the activity

of the autonomic nervous system. It is performed by calculating the spectral power of certain bands of the

RR time series. There are several tools that perform this type of analysis: Kubios HRV, PhysioNet’s HRV

toolkit for MatLab and aHRV, among others. All these tools use the Short Fourier Transform to estimate

spectral power. However, the RR time series is a non-stationary signal. The Wavelet transform is often a more

suitable tool for analyzing non-stationary signals than the Short Time Fourier Transform. Its usefulness in

HRV analysis has already been proven in the literature. However, the lack of HRV analysis tools that support

it has made this technique underutilized in HRV studies. In this paper we present an extension to the RHRV

opensource package that enables Wavelet-based HRV spectral analysis. Until now this package only supported

HRV spectral analysis based on the Fourier transform.

1 INTRODUCTION

Heart rate variability (HRV) analysis includes a set

of techniques to study the beat-to-beat variations in

the heart rate caused by the continuous modulation

of the autonomic nervous system (ANS). One of the

most powerful HRV techniques is based on the spec-

tral analysis of a time series obtained from the dis-

tances between each pair of consecutive heartbeats.

Relationships between the HRV spectral components

and the different components of the ANS were ex-

perimentally demonstrated by Akselrod et al. (Aksel-

rod et al., 1981), who described three relevant com-

ponents in the HRV power spectrum: the very low

frequency (VLF) component (frequencies below 0.03

Hz), which is modulated by the renina-angiotensin

system; the low frequency (LF) component (0.03-

0.15 Hz), which is thought to be of both sympathetic

and parasympathetic nature; and the high frequency

(HF) component (0.18-0.4 Hz), which is related to the

parasympathetic system. At present, although authors

agree on the existence of these three bands, there is

no absolute consensus on the precise location of their

boundaries.

The discrete Fourier transform is a common HRV

spectral technique. It is a simple and fast technique,

but its major disadvantage is its complete lack of tem-

poral resolution. This severely limits its capability

to analyze a non-stationary signal, such as the RR

time series. To alleviate this limitation the Short Time

Fourier Transform (STFT) is often used in the HRV

analysis. However, for solving this problem is often

preferable to use the Wavelet transform, which pro-

vides control over both temporal and spectral (scale)

resolution (Mallat, 1989).

The lack of tools for carrying out HRV analy-

sis using the Wavelet transform has made this po-

tentially superior analysis technique underutilized in

the literature. HRV analysis tools such as Kubios

HRV (Kubios, 2011), PhysioNet’s HRV toolkit for

MatLab (Matlab, 2011) or aHRV (Nevrokard-aHRV,

2011) only enable HRV spectral analysis based on the

Fourier transform. Therefore, until now, the only op-

tion for performing HRV spectral analysis based on

the Wavelet transform was to manually implement

the analysis algorithms. In this paper we present an

extension to the RHRV package (Rodr´ıguez-Li˜nares

et al., 2010) that enables Wavelet-based HRV spec-

tral analysis. RHRV is an open source package for

the R environment for statistical computing that com-

prises a complete set of tools for HRV analysis. Until

now this package only supported HRV spectral anal-

ysis based on the Fourier transform.

The structure of this paper is as follows: ﬁrst,

206

A. García C., Otero A., Vila X. and J. Lado M..

AN OPEN SOURCE TOOL FOR HEART RATE VARIABILITY WAVELET-BASED SPECTRAL ANALYSIS.

DOI: 10.5220/0003725002060211

In Proceedings of the International Conference on Bio-inspired Systems and Signal Processing (BIOSIGNALS-2012), pages 206-211

ISBN: 978-989-8425-89-8

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

we shall brieﬂy review the theory of Fast Orthogo-

nal Wavelet Transform and we shall introduce one of

its variants, the Maximum Overlap Discrete Wavelet

Packet Transform (MODWPT). Next, we shall ex-

plain the algorithm used to compute the spectral

power in the bands used in HRV analysis from the

MODWPT scalogram. Fourier and Wavelet based

analyses will be compared on simulated and real sig-

nals, and a discussion on the results of this paper will

be provided.

2 MATERIAL AND METHODS

2.1 Multiresolution Analysis

The wavelet transform is a powerful tool for analyz-

ing non-stationary signals, such as the RR time series.

The analysis is based on the mother wavelet, a well-

localized, oscillating, regular function ψ(t). Mother

wavelets functions, unlike the sinusoidal functions on

which Fourier transform is based, are localized in

space. This endows the Wavelet transform with both

temporal and spectral (scale) resolution, which makes

it preferable to the Fourier transform for the analysis

of non stationary signals.

ψ(t) can be considered as a band-pass ﬁlter that

can be translated and dilated in time, yielding a set of

wavelet functions:

u,s

(t) =

√



t −u



(1)

where s >0 is a dilation factor, and u is a real number

representing the translations.

The analysis of a function f(t) using wavelets

consists in the extraction of the signal information,

and the synthesis permits the recovering of the orig-

inal function from the representation obtained in the

analysis. In both cases, the information is represented

by several wavelet coefﬁcients, which usually provide

a redundant description of the original signal. How-

ever, for certain speciﬁc values of both the dilation

and translation parameters, the wavelet functions con-

stitute an orthonormal basis of L

(R), and originate

the multiresolution analysis.

The multiresolutionanalysis transformsa function

in a successive set of decomposition levels in which

each level increases the temporal resolution of the de-

composition, at the expense of losing spectral reso-

lution. The approximation of a function at a resolu-

tion 2

−j

, j ∈ Z, is deﬁned as an orthogonal projection

on a space V

⊂ L

(R), where the space V

contains

all possible approximations at the resolution 2

−j

. Let

}

j∈Z

be a multiresolution approximation verify-

ing V

j+1

⊂ V

∀j ∈ Z and let W

be the orthogonal

complement of V

in V

j−1

: V

j−1

= V

⊕W

. Accord-

ing to (Mallat, 1999), the families

{φ

j,n

√



t −2



}

n∈Z

(2)

{ψ

j,n

√



t −2



}

n∈Z

(3)

are an orthonormal basis for V

and W

, respectively,

for all j ∈ Z. ψ

j,n

are the wavelet functions and φ

j,n

are the scale functions. Thus, we can approximate any

function f ⊂ L

(R) at the resolution 2

f =

∞

∑

n=−∞

hf,φ

j,n

iφ

j,n

∞

∑

n=−∞

[n]φ

j,n

(4)

and the orthogonal projection of f onto detail space

is:

f =

∞

∑

n=−∞

hf,ψ

j,n

iψ

j,n

∞

∑

n=−∞

[n]ψ

j,n

. (5)

where a

[n] and d

[n] are called the approximation

and detail coefﬁcients, respectively.

To compute approximation and detail coefﬁcients,

a ﬁlter bank can be used instead of the inner prod-

ucts. Let h[n] and g[n] be the FIR ﬁlters that will be

used to compute the approximation and detail coefﬁ-

cients, respectively. It has been proven (Mallat, 1999)

that h[n] = hφ

j+1,0

,φ

j,n

iand g[n] = hψ

j+1,0

,φ

j,n

i. g[n]

ﬁlters can be regarded as an approximation to a high-

pass ﬁlter, whereas h[n] can be regarded as an approx-

imation to a low-pass ﬁlter. Applying recursively over

the approximation coefﬁcients the same ﬁltering op-

eration followed by sub-sampling by two, we obtain

the multiresolution expression of f. This algorithm,

know as the pyramid algorithm, is the most efﬁcient

way of computing the Fast OrthogonalWavelet Trans-

form (FOWT).

Given that the FOWT can be reformulated in

terms of ﬁlters, it can be used to calculate the spec-

tral power in certain frequency bands. However, the

FOWT only provides information on a limited set of

frequency bands. To be able to calculate the spectral

power in any given frequency band a slightly differ-

ent transform needs to be used: the wavelet packet

decomposition (WPD). In a WPD both detail and ap-

proximation coefﬁcients (instead of only the approxi-

mation coefﬁcients) are decomposed successively by

applying high pass and low pass ﬁlters to each set of

coefﬁcients. Thus, the transform coefﬁcients form a

full binary tree.

Among the WPD transforms we have chosen the

Maximal Overlap Discrete Wavelet Packet Trans-

form (MODWPT) (Percival and Walden, 2006) be-

cause this transform avoids the sub-sampling step,

AN OPEN SOURCE TOOL FOR HEART RATE VARIABILITY WAVELET-BASED SPECTRAL ANALYSIS

207

and therefore it has the same number of Wavelet co-

efﬁcients in every decomposition level, and because it

is well deﬁned for non-dyadic sequences.

The j th level of the MODWPT decomposes the

frequency interval [0, f

/2], where f

is the sam-

pling frequency of the original signal f, into 2

equal

width intervals. Each frequency interval will have N

Wavelet coefﬁcients associated, N being the length of

the sampled signal f. The N-dimensional vector W

j,n

will denote the N Wavelet coefﬁcients associated with

nth node (beginning at zero) in the jth level of the de-

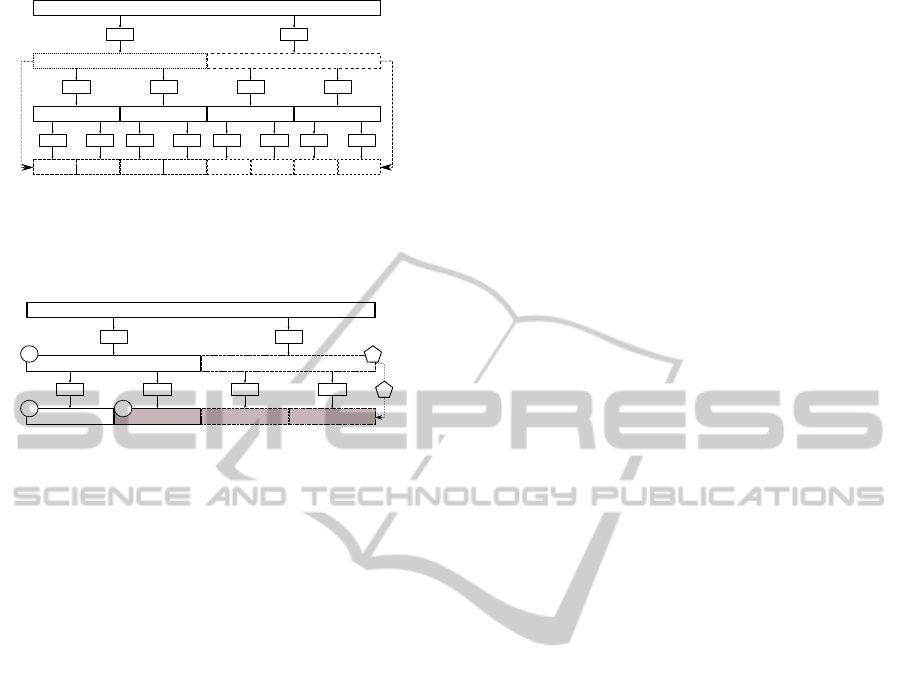
composition tree (see Figure 1). The nth node in the

jth level of the decomposition tree, the ( j,n) node, is

associated with the frequency interval:

j+1

[n,n+ 1] (6)

The MODWPT coefﬁcients fulﬁll that:

kfk

−1

∑

n=0

j,n

∀j (7)

Therefore, given a frequency band [ f

, f

] =

J+1

[k,k

′

], being f

the sampling frequency and k, k

′

and J integers, we can calculate the spectral power in

[ f

, f

], P([ f

, f

]), from the appropriate MODWPT

coefﬁcients. We just need to ﬁnd the nodes (J,k)

and (J,k

′

); then we compute the spectral power in the

band [ f

, f

] as:

P([ f

, f

]) =

′

∑

n=k

J,n

(8)

2.2 Finding a Proper Cover

Equation 8 can only be applied to bands that can be

written as

J+1

[k,k

′

], being f

the sampling frequency

and k, k

′

and J integers. In the general case, when

performing a HRV spectral analysis the user may be

interested in bands that cannot be written this way.

This forces us to permit a certain error when we try

to cover the bands speciﬁed by the user with coef-

ﬁcients obtained from the MODWPT decomposition

(see Figure 2).

Let [ f

, f

] be the band in which we want to cal-

culate the spectral power, and let ε

, ε

be the maxi-

mum errors allowed for the beginning and the ending

of the band, respectively (RHRV allows the user to

specify errors in absolute terms or relatively in % of

the band’s boundary value, but here we will work with

absolute errors for the sake of simplicity). We need to

ﬁnd a node ( j, n) whose lower frequency corresponds

roughly to f

with the tolerance allowed by ε

; that is:

∈

j+1

[n,n+ 1], (9)

−

j+1

n ≤ ε

. (10)

Equation 9 allows us to perform a quick search of

the adequate boundary node in the MODWPT de-

composition tree, while Equation 10 deﬁnes a cri-

terion of acceptability between the frequency values

delimited by a node and the frequencies speciﬁed by

the user. Analogously, we also need to ﬁnd a node

( j

′

) whose upper frequency corresponds roughly

to f

with the tolerance allowed by ε

∈

′



′

+ 1



, (11)

′

+ 1) − f

≤ ε

. (12)

The level j of the decomposition tree in which the

node ( j,n) that fulﬁlls Equations 9 and 10 is found

needs not be the same as the level j

′

in which the

node ( j

′

) that fulﬁlls Equations 11 and 12 is found.

However, Equation 8 requires that j = j

′

. To avoid

this problem, after the nodes ( j,n) and ( j

′

) have

been found, the node that is at the higher level is fur-

ther decomposed to the level of the other node (see

Figure 1). For example, let us suppose we have found

the nodes ( j, n) and ( j

′

), j < j

′

, which correspond

to the lower and upper limits of the frequency band,

respectively. The lower frequency node ( j,n) will be

further decomposed j

′

− j = m additional levels, ob-

taining as the new node corresponding to the lower

limit of the band the node given by:

( j + m,n·2

), (13)

This situation is exempliﬁed by the dotted nodes show

in Figure 1. If the nodes ( j, n) and ( j

′

), are such

that j > j

′

, the higher frequency node ( j

′

) will be

futher decomposed j − j

′

= m additional levels, ob-

taining a new node that corresponds to the upper limit

of the band. This node is given by:

( j + m,(n+ 1) ·2

−1), (14)

This situation is exempliﬁed by the dashed nodes

shown in Figure 1.

Figure 2 illustrates the complete search process

for the band [0.26,0.99] Hz with f

= 2 Hz and ε

= 0.01. We begin searching for the node whose

lower limit corresponds to the frequency f

= 0.26

Hz. The node (1,0) fulﬁlls Equation 9, but not Equa-

tion 10. The node (1, 1) neither fulﬁlls Equation 9

nor Equation 10. Therefore, we continue the search

decomposing the node (1,0) into the nodes (2,0) and

(2,1). The node (2, 0) does not verify Equation 9, but

(2,1) veriﬁes both Equation 9 and 10; i.e., (2,1) is the

node whose lower limit corresponds to f

= 0.26 Hz,

with the tolerance indicated by ε

. In Figure 2 the

BIOSIGNALS 2012 - International Conference on Bio-inspired Systems and Signal Processing

208

0,0

j=0

j=1

j=2

j=3

3,4

3,5

2,2

3,6

3,7

2,3

3,0

3,1

2,0

3,2

3,3

2,1

1/81/16 3/8

1/4

3/16 7/165/16 1/2

1,0

1,1

1/8 3/8

1/4

1/2

1/4

1/2

Figure 1: MODWPT decomposition tree showing an ex-

ample of node relocation for lower (f

) and upper ( f

) fre-

quency nodes. W

0,0

represents the original signal, f(t).

0,0

j=0

j=1

j=2

2,2

2,3

2,0

2,1

1,0

1,1

1/4 3/4

1/2

2 3

Figure 2: Search procedure for the nodes that cover the band

[0.26,0.99] Hz.

search path for this node is shown with circles. We

still have to ﬁnd the node corresponding to the upper

frequency f

= 0.99Hz. For this frequency, (1,1) ver-

iﬁes equations 11 and 12. Therefore our search ends.

In Figure 2 the search path for this node is represented

with the pentagon number 1.

However, the nodes corresponding with f

and f

are at different levels of the decomposition tree: lev-

els 2 and 1, respectively. Before we can apply Equa-

tion 14, the node corresponding with f

, (1,1), must

be further decomposed until it reaches level 2 of the

tree, where the node corresponding with f

, (2, 1), is

located. In Figure 2 the relocation is represented by

pentagon number 2. Finally, the power of the band

can be computed as P([0.26,0.99]) ≈

∑

n=1

2,n

3 SOFTWARE DESCRIPTION

A more detailed description on how the open source

RHRV package works can be found in (Rodr´ıguez-

Li˜nares et al., 2010). Here we will focus the descrip-

tion on the new functionality related to the extension

presented in this article.

Listing 4 shows a basic example of RHRV us-

ing Wavelet analysis. CreateHRVData() creates a

custom data structure to store all information re-

lated to the RR series and HRV analysis. Load-

BeatAscii() loads beat positions stored in the ASCII

ﬁle “BeatPosition.beats”. WFDB (Moody and Mark,

1990) data ﬁles can also be read with the function

LoadBeatWFDB(). Next, the function BuildNIHR()

computes the instantaneous heart rate (the inverse of

the time separation between two consecutive heart

beats). Outliers and points with unacceptable phys-

iological values can be removed using FilterNIHR().

An evenly spaced heart rate series is obtained with the

InterpolateNIHR() function.

The function CalculatePowerBand() calculates

the spectrogram and the power in the ULF, VLF,

LF and HF spectral bands. Although the package

provides default values for the boundaries of these

bands, they can be overridden by the user. Default

bands are ULF: [0,0.03] Hz, VLF: [0.03,0.05] Hz,

LF: [0.05,0.15] Hz, HF: [0.15,0.4] Hz. Until now,

this analysis could only be done using Shorth Time

Fourier Transform (size and shift of the analysis win-

dow can be modiﬁed by the user). The algorithms

presented in this paper were integrated into the Calcu-

latePowerBand() function, allowing both Fourier and

Wavelet analysis to be chosen by specifying an addi-

tional parameter. The default value for this parameter

is “fourier”. The function has been modiﬁed in such

a way that it is backwards compatible. Former code

using the RHRV package will keep exactly the same

behavior in the new version of the package.

When Wavelet analysis is selected in the Cal-

culatePowerBand() function, the mother wavelet to

be used in the analysis, the limits of the ULF,

VLF, LF and HF bands and the error for each of

the band boundaries can be speciﬁed by the user.

The most used mother wavelets are available: Haar

(“haar”), Daubechies (“d4”, “d6”, “d8” and “d16”)

and the least asymmetric(“la8”, “la16” and “la20”),

among others. The default mother wavelet is “d4”

(Daubechies, 2006).When Wavelet analysis is used in

the CalculatePowerBand() function, a tolerance for

the bands’ boundaries is requiered for the power spec-

trum calculations. This tolerance is is speciﬁed with

the parameter bandtolerance, which takes a default

value of 0.01.

4 RESULTS

In order to show how (at least in certain scenarios)

the HRV analysis based on the Wavelet transform pro-

vides more temporal resolution than the Fourier trans-

form, we will use a simulated RR series containing

a sharp transition in its spectral components. The

Integral Pulse Frequency Modulation (IPFM) model

(Hyndman and Mohn, 1973) has been suggested as a

functional description of the sino-atrial node. IPFM

models how the pacemaker heart cells collect electric

charge until the stored charge reaches a certain thresh-

AN OPEN SOURCE TOOL FOR HEART RATE VARIABILITY WAVELET-BASED SPECTRAL ANALYSIS

209

Listing 1: Wavelet-based analysis in RHRV.

CreateHRVData

( )

LoadBeatAscii

(

, ” B e a t P o s i t i o n s . beats ” )

BuildNIHR

(

)

FilterNIHR

(

)

InterpolateNIHR

(

freqhr

= 4)

CreateFreqAnalysis

(

)

CalculatePowerBand

(

indexFreqAnalysis

←֓

=1 ,

ULFmin

= 0 ,

ULFmax

=0.0 3 ,

VLFmin

= ←֓

0.03 ,

VLFmax

= 0.05 ,

LFmin

= 0.05 ,

LFmax

=←֓

0.15 ,

HFmin

= 0.15 ,

nHFmax

=0.4 ,

type

=”←֓

wavelet ” ,

wavelet

=”d4” ,

bandtolerance

←֓

=0.0 1)

PlotPowerBand

(

indexFreqAnalysis

=1)

old. Then the heartbeat is triggered.

Using the IPFM model we simulated an RR time

series such us it only has spectral power in 0.03125

Hz from t = 600 s to t = 1200 s; in 0.09375 Hz

from t = 1200 s to t = 2400 s; in 0.15625 Hz from

t = 2400 s to t = 3600 s. There it should present

sharp transitions in the spectral components. We an-

alyzed the spectrum of the resulting RR series with

RHRV using Fourier (see Figure 3) and Wavelet (see

Figure 4) transforms. Frequency bands for both anal-

ysis were VLF: [0,0.0625], .LF: [0.0625,0.125] HF:

[0.125, 0.5]. The mother Wavelet used in the analysis

was Daubechies 4. Fourier analysis used a 30-second

window with 12-second shift.

In Figures 3 and 4 red vertical lines delimit each

of the three zones with different spectral components

imposed by m(t). It can be seen that wavelet analy-

sis presents better time resolution than Fourier analy-

sis. For each of the three spectral bands, and for each

of the three zones with different spectral components,

we calculated the ratio of the power that the band

presents in each zone divided by the overall power

of the band in the three zones. Theoretically, all the

power in the VLF band should be in the ﬁrst zone,

all the power in the LF band should be in the second

zone, and all the power in the HF band should be in

the third zone. Therefore, the ideal ratios if perfect

frequency discrimination is obtained are (1, 0, 0), (0,

1, 0) and (0, 0, 1). Tables 1 and 2 show the real ra-

tios for Fourier and Wavelet analysis, respectively. It

can be appreciated how Fourier has better frequency

discrimination than Wavelets.

Finally, we analyzed the spectral components of

an ECG recording of an obese 54-year old male who

suffers from sleep apnea-hypopnea syndrome. The

ECG recording was performed during a sleep test.

The recording was analyzed using RHRV with the

mother Wavelet Haar and with a tolerance in the

band location of 0.01. Visual inspection of the re-

sults clearly shows that the spectral power in the band

normalized power

time(s)

Figure 3: Fourier HRV analysis of the simulated RR series.

normalized power

time(s)

Figure 4: Wavelet HRV analysis of the simulated RR series.

Table 1: Relative power for Fourier analysis.

[0,1200] [1200,2400] [2400,3600]

ULF 0,9785 0,0062 0,0153

VLF 0,0215 0,9317 0,0468

LF 0,0003 0,0030 0,9967

Table 2: Relative power for Wavelet analysis.

[0,1200] [1200,2400] [2400,3600]

ULF 0,9309 0,0456 0,0235

VLF 0,0674 0,7695 0,1631

LF 0,0087 0,3057 0,6856

[0.125, 0.250] is higher during episodes of apnea and

lower during normal breathing (see Figure 5). It

should be noted that the higher power regions are re-

marcably well localized in time. We tried to replicate

these results using Fourier, but we fail due to its lower

temporal resolution.

5 DISCUSSION AND

CONCLUSIONS

This paper presents what we believe to be the ﬁrst

HRV analysis toolkit that supports Wavelet-based

spectral analysis of the RR time series. To perform

such analysis the user only has to specify the spectral

bands to be analyzed and, optionally, a tolerance for

the position of the bands’ boundaries (default toler-

ance is 0.01) and a mother Wavelet to be used in the

analysis (by default is “db4”). This functionality has

BIOSIGNALS 2012 - International Conference on Bio-inspired Systems and Signal Processing

210

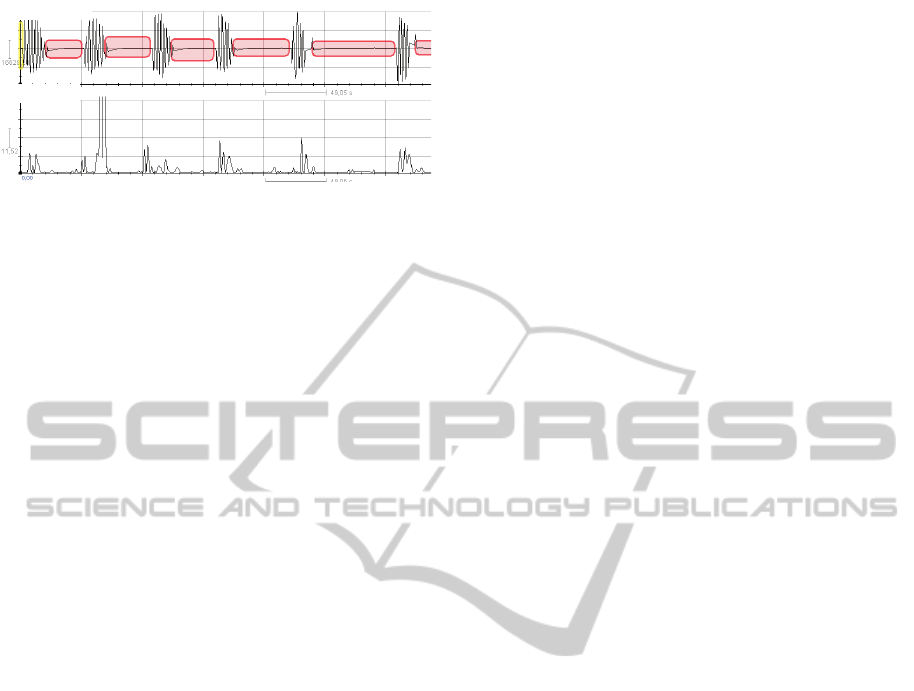
Spectralpower

Respiratoryairflow

Figure 5: Spectral power in the band [0.125, 0.250] is

higher during apnea episodes than during normal breathing.

been implemented as an extension to the open source

R package RHRV. The API of the new version of the

package is fully backwards compatible.

The results presented here suggest that Wavelet-

based analysis has a higher temporal resolution than

Fourier-based analysis. On the other hand, Fourier is

able to discriminate more precisely the spectral com-

ponents present in the signal. The results presented in

this paper are consistent with other similar tests con-

ducted by the authors.

However, it should be noted that as we descend

to lower levels in the frequency decomposition tree

when looking for a suitable node cover for a fre-

quency band, frequency resolution increases and tem-

poral resolution decreases because of the Gabor-

Heisenberg uncertainty principle for signals: (∆t∆f ≥

1/2) (Gabor, 1953). To obtain optimal temporal res-

olution, we should avoid descending to deep levels of

the tree. Our initial tests suggest that no more than

ﬁve or six levels of the frequency decomposition tree

should be expanded. In this sense, a careful selection

of the frequency bands to be analyzed provides some

control over the depth of the tree.

A corollary of the phenomenon described in the

previous paragraph is that in order to achieve optimal

temporal resolution the spectral bands used in HRV

analysis with Wavelets will probably have to differ

from those traditionally associated with ULF, VLF,

LF and HF. This opens the question of what may be

the pathophysiological signiﬁcance of spectral bands

different from those which have already been widely

studied in the literature.

The mother Wavelet used in analysis also in-

ﬂuences frequency-time resolution because it deter-

mines the ﬁlter shape. Further study on how the

mother Wavelet inﬂuences the results of the analysis

is required to understand more precisely the tradeoffs

of using Wavelets versus Fourier. For example, our

initial tests suggest that Haar Wavelet has greater time

resolution than Daubechies 4 Wavelet for HRV anal-

ysis, whereas the latter has a better ﬁltering behaviour

than the ﬁrst one.

ACKNOWLEDGEMENTS

This work was partially supported by the Spanish

MEC and the European FEDER under the grant

TIN2009-14372-C03-03, and by the Xunta de Gali-

cia under the grant PGIDIT06SIN30501PR.

REFERENCES

Akselrod, S., Gordon, D., Ubel, F., Shannon, D., Berger,

A., and Cohen, R. (1981). Power spectrum analysis of

heart rate ﬂuctuation: a quantitative probe of beat-to-

beat cardiovascular control. Science, 213(4504):220.

Daubechies, I. (2006). Ten lectures on wavelets. Society for

industrial and applied mathematics.

Gabor, D. (1953). Communication theory and physics.

Information Theory, IRE Professional Group on,

1(1):48–59.

Hyndman, B. and Mohn, R. (1973). A pulse modulator

model for pacemaker activity. In Digest of the 10th

Int. Conf. Med. & Biol. Eng, page 223.

Kubios (2011). http://kubios.uku.ﬁ.

Mallat, S. (1989). A theory for multiresolution signal de-

composition: The wavelet representation. Pattern

Analysis and Machine Intelligence, IEEE Transac-

tions on, 11(7):674–693.

Mallat, S. (1999). A wavelet tour of signal processing. Sec-

ond Edition. Academic Pr.

Matlab (2011). http://www.mathworks.com/index.html.

Moody, G. and Mark, R. (1990). The MIT-BIH arrhythmia

database on cd-rom and software for use with it. In

Computers in Cardiology, pages 185–188.

Nevrokard-aHRV (2011). http://www.nevrokard.eu.

Percival, D. and Walden, A. (2006). Wavelet methods for

time series analysis, volume 4. Cambridge Univ Pr.

Rodr´ıguez-Li˜nares, L., M´endez, A., Lado, M., Olivieri,

D., Vila, X., and G´omez-Conde, I. (2010). An open

source tool for heart rate variability spectral analysis.

Computer Methods and Programs in Biomedicine.

AN OPEN SOURCE TOOL FOR HEART RATE VARIABILITY WAVELET-BASED SPECTRAL ANALYSIS

211