SCALABLE CORPUS ANNOTATION BY GRAPH CONSTRUCTION

AND LABEL PROPAGATION

Thomas Lansdall-Welfare, Ilias Flaounas and Nello Cristianini

Intelligent Systems Laboratory, University of Bristol, Woodland Road, Bristol, U.K.

Keywords:

Text categorisation, Graph construction, Label propagation, Large scale.

Abstract:

The efﬁcient annotation of documents in vast corpora calls for scalable methods of text classiﬁcation. Rep-

resenting the documents in the form of graph vertices, rather than in the form of vectors in a bag of words

space, allows for the necessary information to be pre-computed and stored. It also fundamentally changes

the problem deﬁnition, from a content-based to a relation-based classiﬁcation problem. Efﬁciently creating

a graph where nearby documents are likely to have the same annotation is the central task of this paper. We

compare the effectiveness of various approaches to graph construction by building graphs of 800,000 vertices

based on the Reuters corpus, showing that relation-based classiﬁcation is competitive with Support Vector Ma-

chines, which can be considered as state of the art. We further show that the combination of our relation-based

approach and Support Vector Machines leads to an improvement over the methods individually.

1 INTRODUCTION

Efﬁciently annotating new documents coming from a

data stream is an important problem in modern data

management. Real world text mining and analysis

systems, such as news monitoring systems like ‘News

Outlets Analysis and Monitoring system’ (NOAM)

(Flaounas et al., 2011), Lydia (Lloyd et al., 2005)

and the ‘Europe Media Monitor’ (EMM) (Steinberger

et al., 2009) would beneﬁt from an approach that can

handle annotation on a large scale while being able

to adapt to changes in the data streams. A classical

approach is to develop content-based classiﬁers, e.g.

Support Vector Machines (SVMs), specialised in the

detection of speciﬁc topics (Joachims, 1998). One of

the key problems in this approach is that the classiﬁ-

cations are not affected by subsequent documents, un-

less the classiﬁers are retrained, and that entirely new

topics cannot be introduced unless a new classiﬁer is

developed. We are interested in the situation where

the annotation of a corpus improves with time, that

is with receiving new labelled data. We want the ac-

curacy of existing labels to improve with more data,

where old errors in classiﬁcation are possibly being

amended, and if entirely new topic labels start being

used in a data stream, the system will be able to ac-

commodate them automatically. The deployment of

such methods for real world textual streams, such as

news feeds coming from the Web where the feed is

constantly updated, requires an ability to track them

in real time, independent of the size of the corpus.

The na¨ıve approach to graph construction, comparing

all documents to all documents or building a complete

kernel matrix (Shawe-Taylor and Cristianini, 2004),

will not work in large scale systems due to high com-

putational complexity. The cost of label propagation

is also an important factor on the time needed to pro-

cess the incoming documents.

In this paper we focus on textual data and present

a method to propagate labels across documents by

creating a sparse graph representation of the data,

and then propagating labels along the edges of the

graph. There is a tendency for research to focus on the

method of propagating the labels, taking for granted

that the graph topology is given in advance (Herbster

et al., 2009; Cesa-Bianchi et al., 2010b). In reality,

unless working with webpages, textual corpora rarely

have a predeﬁned graph structure. Graph construc-

tion alone has a worst case cost of O (N

) when using

a na¨ıve method due to the calculation of the full N×N

pairwise similarity matrix. Our proposed method can

be performed efﬁciently by using an inverted index,

and in this way the overall cost of the method has a

time complexity of O (N logN) in the number of doc-

uments N.

We test our approach by creating a graph of

800,000 vertices using the Reuters RCV1 corpus

(Lewiset al., 2004), and we compare the quality of the

Lansdall-Welfare T., Flaounas I. and Cristianini N. (2012).

SCALABLE CORPUS ANNOTATION BY GRAPH CONSTRUCTION AND LABEL PROPAGATION.

In Proceedings of the 1st International Conference on Pattern Recognition Applications and Methods, pages 25-34

DOI: 10.5220/0003728700250034

 SciTePress

label annotations obtained by majority voting against

those obtained by using SVMs. We chose to com-

pare the graph-based methods to SVMs because they

are considered the state of the art for text categorisa-

tion (Sebastiani, 2002). We show that our approach

is competitive with SVMs, and that the combination

of our relation-based approach with SVMs leads to an

improvement in performance over either of the meth-

ods individually. Further to this, we show that the

combination of the approaches does not lead to a de-

crease in performance, relative to the weakest of the

approaches, i.e. the combination always gives an im-

provementover at least one of the methods on its own.

It is also important to notice that our methods can be

easily distributed to multiple machines.

This paper is organised as follows: Section 2 out-

lines graph construction, detailing methods of us-

ing an inverted index for graph construction, along

with various methods for maintaining sparsity of the

graph. Section 3 outlines the Label Propagation (LP)

method and Online Majority Voting (OMV), a natu-

ral adaption of LP for an online setting. Section 4

describes the implementation details concerning the

inverted index and edge lists, while Sect. 5 covers

our experimental comparison of our presented meth-

ods with Support Vector Machines on the Reuters cor-

pus before showing an improvement by combining

the methods. Finally, in Sect. 6 we discuss the ad-

vantages of a graph-based approach and summarise

our ﬁndings before posing some directions for future

work in the area.

1.1 Related Work

There is a growing interest in the problem of prop-

agating labels in graph structures. Previous work

by Angelova and Weikum (Angelova and Weikum,

2006) extensively studied the propagation of labels

in web graphs including a metric distance between

labels, and assigning weights to web links based

upon content similarity in the webpage documents.

Many alternative label propagation algorithms have

also been proposed over the years, with the survey

(Zhu, 2007) giving an overview of several different

approaches cast in a regularisation framework. A

common drawback of these approaches is the pro-

hibitively high cost associated with label propaga-

tion. A number of recent works on label propaga-

tion (Herbster et al., 2009; Cesa-Bianchi et al., 2010a;

Cesa-Bianchi et al., 2010b) concentrate on extracting

a tree from the graph, using a very small number of

the neighbours for each node.

While many graph-based methods do not address

the problem of the initial graph construction, assum-

ing a fully connected graph is given, or simply choos-

ing to work on data that inherently has a graph struc-

ture, there is a large number of papers dedicated to

calculating the nearest neighbours of a data point.

One such approximate method, NN-Descent (Dong

et al., 2011), shows promising results in terms of ac-

curacy and speed for constructing k-Nearest Neigh-

bour graphs, based upon the principle that ‘a neigh-

bour of a neighbour is also likely to be a neighbour’.

The All-Pairs algorithm (Bayardo et al., 2007) tack-

les the problem of computing the pairwise similar-

ity matrix often used as the input graph structure in

an efﬁcient and exact manner, showing speed im-

provementsover another inverted-list based approach,

ProbeOpt-sort (Sarawagi and Kirpal, 2004) and well-

known signature based methods such as Locality Sen-

sitive Hashing (LSH) (Gionis et al., 1999).

In this paper we take a broader overview, consid-

ering both the task of creating a graph from text docu-

ments, and then propagating labels for text categorisa-

tion simultaneously. We are interested in an approach

that can be applied to textual streams, with the previ-

ously mentioned additional beneﬁts offered by mov-

ing away from classical content-based classiﬁers.

2 GRAPH CONSTRUCTION

Graph construction X → G deals with taking a corpus

X = {x

, . . . , x

}, and creating a graph G = (V, E,W),

where V is the set of vertices with document x

being

represented by the vertex v

, E is the set of edges, and

W is the edge weight matrix. There are several ways

the construction can be adapted, namely the choice of

distance metric and the method for maintaining spar-

sity.

The distance metric is used to determine the edge

weight matrix W. The weight of an edge w

encodes

the similarity between the two vertices v

and v

. The

choice of metric used is mostly task-dependent, re-

lying on an appropriate selection being made based

upon the type of data in X . A common measure used

in text, such as cosine similarity (Tan et al., 2006),

may not be appropriate for other data types, such as

when dealing with histogram data where the χ

dis-

tance is more meaningful (Zhang et al., 2007).

Typically, a method for maintaining sparsity is re-

quired since it is not desirable to work with fully

connected graphs for reasons of efﬁciency, and sus-

ceptibility to noise in the data (Jebara et al., 2009).

This can be solved by working with sparse graphs,

which are easier to process. Two popular methods

for achieving sparsity include k-nearest neighbour

(kNN) and ε-neighbourhood, both utilizing the local

ICPRAM 2012 - International Conference on Pattern Recognition Applications and Methods

Figure 1: Illustration of an example where two graphs, G

and G

, are being constructed from graph G using the two

methods we investigate: ε-neighbourhood and k-nearest neighbour. In the example, the possible edges for vertex v

are being

considered. The ε-neighbourhood method adds all edges which connect v

to a vertex inside the grey circle which visualises

the radius ε. The k-nearest neighbour method ranks the closeness of the adjacent vertices with respect to a given similarity

measure, then adds edges to the closest k vertices. For this example, k = 2.

neighbourhood properties of each vertex in the graph

(Carreira-Perpinan and Zemel, 2004; Jebara et al.,

2009; Maier et al., 2009). Local neighbourhoodmeth-

ods are important for efﬁciencysince a data point only

relies on information about other points close by, with

respect to the distance metric, to determine the neigh-

bours of a vertex. This means that no global proper-

ties of the graph need to be calculated over the entire

graph each time a new vertex is added, a considera-

tion that has implications both for the scalability and,

more generally, for parallelisation.

The ﬁrst step of creating the graph usually in-

volves calculating the pairwise similarity score be-

tween all pairs of vertices in the graph using the ap-

propriately chosen distance metric. Many studies as-

sume that it is feasible to create a full N × N dis-

tance matrix (Jebara et al., 2009) or that a graph is al-

ready given (Herbster et al., 2009; Cesa-Bianchi et al.,

2010b). This assumption can severely limit the size

of data that is managable, limited by the O (N

) time

complexity for pairwise calculation. Construction of

a full graph Laplacian kernel, as required by standard

graph labelling methods (Belkin et al., 2004; Herbster

and Pontil, 2007; Zhu et al., 2003) is already compu-

tationally challenging for graphs with 10,000 vertices

(Herbster et al., 2009). Jebara et al. (Jebara et al.,

2009) introduce β-matching, an interesting method of

graph sparsiﬁcation where each vertex has a ﬁxed de-

gree β and show an improved performance over k-

nearest neighbour, but at a cost to the complexity of

the solution and the assumption that a fully connected

graph is given.

We can overcome the issue of O (N

) time com-

plexity for computing the similarity matrix by using

an alternative method, converting the corpus into an

inverted index where each term has a pointer to the

documents the term appears within. The advantage

of this approach is that the corpus is mapped into a

space based upon the number of terms, rather than

number of documents. This assumption relies on the

size of the vocabulary |t| being much smaller than the

size of the corpus. According to Heaps’ Law (Heaps,

1978), the number of terms |t| appearing in a corpus

grows as O (N

), where β is a constant between 0 and

1 dependent on the text. Some experiments (Araujo

et al., 1997; Baeza-Yates and Navarro, 2000) on En-

glish text show that β is between 0.4 and 0.6 in prac-

tice. The inverted index can be built in O (NL

) time

where L

is the average number of terms in a docu-

ment, with a space complexity of O (NL

) where L

is the average number of unique terms per document

(Yang et al., 2003).

Finding the neighbours of a document is also triv-

ial because of the inverted index structure. A classical

approach is to use the Term Frequency-Inverse Doc-

ument Frequency (TF-IDF) weighting (Salton, 1989)

to calculate the cosine similarity between two docu-

ments. This can be performed in O (L

log|t|) time for

each document by performing L

binary searches over

the inverted index. Assuming β from Heaps’ Law is

the average value of 0.5, the time complexity for ﬁnd-

ing the neighbours of a document can be rewritten as

SCALABLE CORPUS ANNOTATION BY GRAPH CONSTRUCTION AND LABEL PROPAGATION

O (

logN). Therefore, there is a total time complex-

ity O (N +

logN) for building the index and ﬁnd-

ing the neighbours of all vertices in the graph. This

is equivalent to O (N logN) under the assumption that

the average document length L

is constant.

A further advantage of this method is that the

number of edges per vertex is limited a priori, since

it is infeasible to return the similarity with all docu-

ments in the inverted index for every document. This

allows the construction of graphs that are already

sparse, rather than performing graph sparsiﬁcation to

obtain a sparse graph from the fully connected graph,

e.g. (Jebara et al., 2009).

We investigate two popular local neighbour-

hood methods, k-nearest neighbour (kNN) and ε-

neighbourhood, for keeping the graph sparse during

the initial construction phase and also when new ver-

tices are added to the graph (Carreira-Perpinan and

Zemel, 2004; Jebara et al., 2009; Maier et al., 2009).

Figure 1 shows intuitively how each of the methods

chooses the edges to add for a given vertex. The ﬁrst

method, kNN, connects each vertex to the k most sim-

ilar vertices in V, excluding itself. That is, for two

vertices v

and v

, an edge is added if and only if the

similarity between v

and v

is within the largest k re-

sults for vertex v

. The second method we investigate,

ε-neighbourhood, connects all vertices within a dis-

tance ε of each other, a similar approach to classical

Parzen windows in machine learning (Parzen, 1962).

This places a lower bound on the similarity between

any two neighbouring vertices, i.e. only edges with a

weight abovethe threshold ε are added to the graph. A

simple way of visualising this is by drawing a sphere

around each vertex with radius ε, where any vertex

falling within the sphere is a neighbour of the vertex.

While the ﬁrst method ﬁxes the degree distribution of

the network, the second does not, resulting in funda-

mentally different topologies. We will investigate the

effect of these topologies on labelling accuracy.

3 LABEL PROPAGATION

Label propagation aims to use a graph G = (V, E,W)

to propagate topic labels from labelled vertices to un-

labelled vertices. Each vertex v

can have multiple

topic labels, i.e. a document can belong to more

than one category, and each label is considered in-

dependently of the other labels assigned to a ver-

tex. The labels assigned to the set of labelled ver-

tices Y

= {y

, . . . , y

} are used to estimate the labels

= {y

l+1

, . . . , y

l+u

} on the unlabelled set.

Carreira-Perpinan et al. (Carreira-Perpinan and

Zemel, 2004) suggest constructing graphs from en-

sembles of minimum spanning trees (MST) as part

of their label propagation algorithm, with their two

methods Perturbed MSTs (PMSTs) and Disjoint

MSTs (DMSTs), having a complexity of approxi-

mately O (TN

logN) and O (N

(logN + t)) respec-

tively, where N is the number of vertices, T is the

number of MSTs ensembled in PMSTs, and t is the

number of MSTs used in DMSTs, typically t <<

However, to the best of the authors’ knowledge, no

studies have performed experiments on constructed

graphs with more than several thousand vertices, with

the exception of Herbster et al. (Herbster et al., 2009)

who build a shortest path tree (SPT) and MST for a

graph with 400,000 vertices from Web pages. Herb-

ster et al. (Herbster et al., 2009) also note that con-

structing their MST and SPT trees using Prim and Di-

jkstra algorithms (Cormen et al., 1990) respectively

takes O (NlogN+|E|) time, with the general case of a

non-sparse graph having a time complexity of Θ(N

In this paper we adopt Online Majority Voting

(OMV) (Cesa-Bianchi et al., 2010b), a natural adap-

tation of the Label Propagation (LP) algorithm (Zhu

et al., 2003), as our algorithm for the label propaga-

tion step due to its efﬁciency and simplicity. OMV is

based closely upon the locality assumption, that ver-

tices that are close to one another, with respect to a

distance or measure, should have similar labels. Each

vertex is sequentially labelled as the unweighted ma-

jority vote on all labels from the neighbouring ver-

tices. The time complexity for OMV is Θ(|E|), a no-

table reduction from the O (kN

) required for LP al-

gorithm, where k is the neighbours per vertex. The

complexity being dependent on the number of edges

in the graph further beneﬁts from the a priori limit we

impose upon the maximum edges per vertex, ensuring

that |E| = bN for some maximum edge limit b.

4 IMPLEMENTATION

The data structures for the implementation of the pro-

posed methods can be separated into two individual

parts. Firstly, an inverted index is built that is used for

the efﬁcient calculation of neighbours for a document,

and secondly, an edge list is maintained in a relational

database, allowing for queries to be executed on the

graph topology.

For the experiments in this paper, the inverted in-

dex is implemented using the open source Apache

Lucene

software. An inverted index is a data struc-

ture where, as previously described, a list of every

term in the corpus is maintained with a pointer (also

Open source implementation of an inverted index.

Available at: http://lucene.apache.org/

ICPRAM 2012 - International Conference on Pattern Recognition Applications and Methods

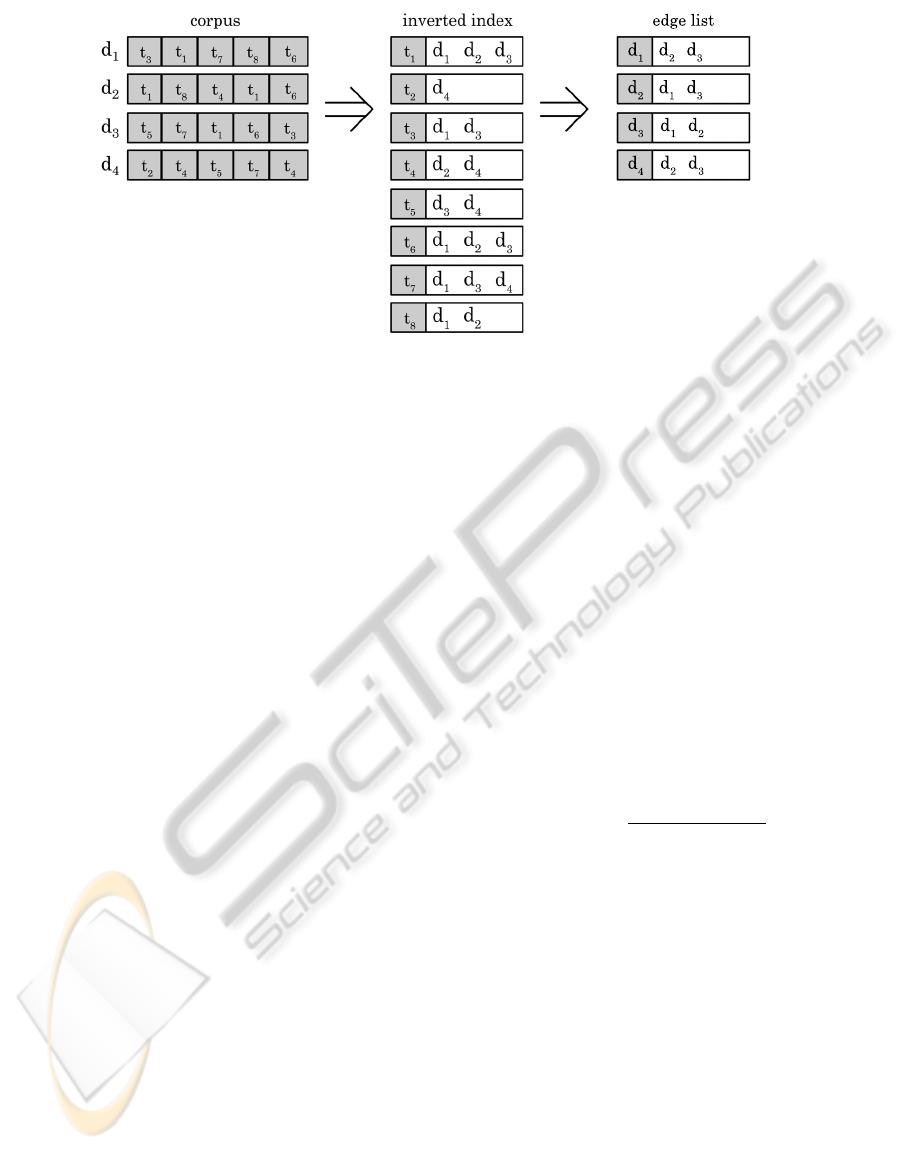
Figure 2: Illustration of the conceptual change in how the data is stored for the inverted index and edge list approach. This

example shows a corpus containing four documents (d

, d

) with terms t

, . . . ,t

being converted into an inverted

index with postings to each of the documents originally containing the term. From the inverted index, an edge list can then

be generated linking the documents (d

, d

) into a graph. In this example, the edge list depicts a k-Nearest Neighbour

graph where k = 2.

known as a posting) to each document that contains

that term. The inverted index can be stored in main

memory for small corpora, signiﬁcantly speeding up

the document search procedure, or on disk for larger

corpora.

The edge list generated from the inverted index is

stored in a relational database. For the experiments in

this paper MySQL is used allowing for neighbours of

a vertex to be retrieved quickly by querying the edge

list table for the relevant vertex identiﬁer. Figure 2

illustrates the structure of an inverted index and the

edge list generated from it.

We adapted the source code of Lucene to support

cosine similarity between documents, since it is ini-

tially optimised for document retrieval, rather than

document comparison. The SVMs were deployed us-

ing the LibSVM toolbox (Chang and Lin, 2001).

5 EXPERIMENTS AND

EVALUATION

We present an experimental study of the feasibility of

our approach on a large data set, the Reuters RCV1

corpus (Lewis et al., 2004). We split the corpus into

a training and test set, where the test set is the last

seven weeks of the corpus, and the training set covers

everything else. The test set is further subdivided into

seven test weeks.

For the graph-based methods, the hyperparam-

eters k and ε require careful selection in order to

achieve comparable performance with current meth-

ods. This is the most expensive step as it often

requires a search of the parameter space for the

best value. We use Leave-One-Out Cross Validation

(LOO-CV) on the training set to tune the parame-

ters. This involves constructing graphs for a range

of values of k and ε on the training set by iterating

over all vertices, predicting the labels of the vertex

based upon the majority vote of its neighbours. The

predictions are checked against the true labels, with

the highest performing parameter value being chosen.

The performance was evaluated using the F

Score,

which is the harmonic mean of the precision and re-

call, a widely used performance metric for classiﬁ-

cation tasks (Steinbach et al., 2000). Formally, it is

deﬁned as

= 2·

precision· recall

precision+ recall

. (1)

The precision and recall on the training set were cal-

culated by summing together the contingency matri-

ces for each topic, giving an F

Score for each pa-

rameter value across all topics. For the test sets, all

Scores reported are the individual topic F

Scores

averaged over the 50 most common topics. The

best parameters for each method were also recorded

for each topic individually, allowing for a multi-

parameter graph where each label has a different pa-

rameter value. This could be thought of as each la-

bel being able to travel a certain distance along each

edge. It was however found that the multi-parameter

approach only led to a small increase in performance

at additional cost to the complexity of the solution

since multiple graphs need to be constructed.

We trained one SVM per topic using the Cosine

kernel, which is a normalised version of the Lin-

ear kernel (Shawe-Taylor and Cristianini, 2004). For

SCALABLE CORPUS ANNOTATION BY GRAPH CONSTRUCTION AND LABEL PROPAGATION

0 0.2 0.4 0.6 0.8 1

100

ε−Neighbourhood Threshold

Score

Figure 3: This ﬁgure shows the F

performance averaged

across the 50 most common topics evaluated on the training

set using LOO-CV for ε = {0, 0.01, . . . , 1.00}. It can been

seen that there is a curve with a peak at ε = 0.4.

0 20 40 60 80 100

100

k−Nearest Neighbours

Score

Figure 4: This ﬁgure shows the F

performance for the

50 most common topics evaluated on the training set us-

ing LOO-CV for k = {1, 2, . . . , 100}. It can been seen that

the line peaks relatively quickly, at k = 5.

each topic, training used a randomly selected 10, 000

positive examples, and a randomly selected 10, 000

negative examples picked from the training set. The

examples were ﬁrst stemmed and stop words were re-

moved as for the graph-based methods. The last week

of the training corpus was used as a validation set to

empirically tune the regularisation parameter C out of

the set [0.01, 0.05, 0.1, 0.5, 1, 5, 10, 100]. For each

topic, C was tuned by setting it to the value achieving

the highest F

performance on that topic in the vali-

dation set. We report the performance on the test set.

5.1 Combining Graph-based and

Content-based Classiﬁcation

Further to the comparison of the graph-based meth-

ods with SVMs, an ensemble (Dietterich, 2000) of the

graph-based and content-based classiﬁcation methods

was evaluated. For each vertex, a majority vote for

each class label c is taken by counting the supporting

votes from k votes of the kNN method, supplemented

with s votes from the SVMs for a total of υ = k + s

votes. That is, each vertex has the k votes from the

kNN method, but also s votes assigned by the SVMs.

The number of votes from the SVM is chosen in the

interval s = [0, k + 1]. This moves the combination

method from purely graph-based at s = 0 (υ = k), to

purely content-based at s = k+ 1 (υ = 2k+ 1).

Given a set of p class labels C = {c

, c

, . . . , c

a set of n vertices V = {v

, v

, . . . , v

}, a graph ma-

trix A ∈ {0, 1}

n×n

where A

i, j

indicates whether v

a neighbour of v

, a label matrix Y ∈ {0, 1}

n×p

where

j,c

indicates if vertex v

has class label c, an SVM as-

signed label matrix S ∈ {0, 1}

n×p

where S

i,c

indicates

if class label c has been assigned to vertex v

by the

SVMs and a regularisation parameter λ = [0, 1],

i,c

the decision whether label c is to be assigned to vertex

. Formally, a linear combination of the methods was

created as

i,c

= θ(λ

∑

i, j

j,c

) + (1− λ)S

i,c

) (2)

θ(x) =



1 if x >

0 otherwise

(3)

Equation 2 can be reformulated so that it is easier

to interpret by setting µ =

1−λ

, giving

i,c

= θ(

∑

i, j

j,c

) + µS

i,c

) (4)

where µ represents the number of SVM votes s in the

interval [0, k + 1].

For our experiments, the value of µ for combining

the kNN and SVM methods was evaluated between 0

and 6 since the kNN method uses k = 5 neighbours.

5.2 Results

We evaluate the performance of each method on the

seven test weeks, where all previous weeks have al-

ready been added to the graph, to simulate an on-

line learning environment. The F

Scores reported are

the mean performance calculated over the seven test

weeks.

Figure 5 and Fig. 6 show a comparison of the

graph-based methods with SVMs. Out of the 50 most

common topics, SVM achieved a higher performance

than ε-Neighbourhood on 29 topics, but only beat

kNN on 19 of the topics, that is kNN performed bet-

ter than SVMs on 31 out of the 50 topics. This shows

that the graph-based methods are competitivewith the

performance of SVMs.

Figure 7 shows a comparison of the graph-based

methods. Out of the 50 most common topics, kNN has

a higher performance on 46 of the possible 50 topics.

Clearly, ε-Neighbourhood is the weaker of the graph-

based methods and so is not considered further.

ICPRAM 2012 - International Conference on Pattern Recognition Applications and Methods

0 20 40 60 80 100

100

ε−Neighbourhood F

Score

SVM F

Score

Figure 5: This ﬁgure shows a comparison of the mean

Score, averaged over all test set weeks, for ε-

Neighbourhood against SVMs on the 50 most common top-

ics. Points below the diagonal line indicate when SVMs

achieved a higher performance than ε-Neighbourhood,

with points above the diagonal line indicating that ε-

Neighbourhood achieved a higher performance than SVMs

on that topic.

0 20 40 60 80 100

100

SVM F

Score

kNN F

Score

Figure 6: This ﬁgure shows a comparison of the mean F

Score, averaged over all test set weeks, for k-NN against

SVMs on the 50 most common topics. Points below the di-

agonal line indicate when SVMs achieved a higher perfor-

mance than kNN, with points above the diagonal line indi-

cating that kNN achieved a higher performance than SVMs

on that topic.

Next, we consider the best value of µ for combin-

ing the kNN methods and SVMs in a linear combi-

nation. Figure 8 shows the performance of the com-

bined method averaged over the 50 most common top-

ics for each value of µ. Out of the 50 most common

topics, the combined method with µ = 4 provided an

improvement over the performance of both the SVM

and kNN methods for 36 of the topics. Using µ = 1

showed an improvement over both methods for the

0 20 40 60 80 100

100

ε−Neighbourhood F

Score

kNN F

Score

Figure 7: This ﬁgure shows a comparison of the mean F

Score, averaged over all test set weeks, for the graph-based

methods on the 50 most common topics. Points below the

diagonal line indicate when ε-Neighbourhood achieved a

higher performance than kNN, with points above the diago-

nal line indicating that kNN achieved a higher performance

than ε-Neighbourhood on that topic.

0 1 2 3 4 5 6

Score

Figure 8: This ﬁgure shows a comparison of the mean F

Score, averaged over all test set weeks, for the combined

method at different µ values on the 50 most common topics.

It can be seen that the combined method offers an improve-

ment over the kNN approach (µ= 0) and the SVM approach

(µ = 6).

greatest number of topics, with 38 of the 50 topics

seeing an improvement. The mean performance of

the combined method with µ = 1 is lower than for

µ = 4 however, indicating that when µ = 4 the im-

provements are greater on average, even if there are

slightly fewer of them.

When comparingthe combined method with SVM

and kNN as seen in Fig. 9 and Fig. 10 respectively,

the performance of the combined method was higher

than SVM on 45 of the 50 topics and higher than kNN

on 41 out of the 50 topics. This shows that the com-

SCALABLE CORPUS ANNOTATION BY GRAPH CONSTRUCTION AND LABEL PROPAGATION

0 20 40 60 80 100

100

Combined Method F

Score

SVM F

Score

Figure 9: This ﬁgure shows a comparison of the mean F

Score, averaged over all test set weeks, for the combined

method using µ = 4 against SVMs on the 50 most com-

mon topics. Points below the diagonal line indicate when

the combined method achieved a higher performance than

SVMs, with points above the diagonal line indicating that

SVMs achieved a higher performance than the combined

method on that topic.

0 20 40 60 80 100

100

Combined Method F

Score

kNN F

Score

Figure 10: This ﬁgure shows a comparison of the mean

Score, averaged over all test set weeks, for the com-

bined method using µ = 4 against kNN on the 50 most

common topics. Points below the diagonal line indicate

when the combined method achieved a higher performance

than kNN, with points above the diagonal line indicating

that kNN achieved a higher performance than the combined

method on that topic.

bined method does not only improve on SVM and

kNN on average, but provides an improvement for

90% and 82% of the 50 most common topics respec-

tively. It should be noted that in the cases where the

combined method does not provide an improvement

on one of the methods, it does still have a higher per-

formance than the lowest performing method for that

topic. That is, there were no cases where combining

0 20 40 60 80

SVM

εN

kNN

Combined

Method

Score

Figure 11: This ﬁgure shows a summary of the mean F

Score, averaged over all test set weeks, for the graph-based

methods and SVMs along with the best combined method

(µ = 4) on the 50 most common topics. It can be seen

that the graph-based methods are comparable with SVMs,

with the combined method showing a further improvement.

It should be noted that the performance of the combined

method is slightly bias due to selecting for the best µ. ε-

Neighbourhood has been abbreviated to εN.

the methods gives a performance below both of the

methods individually.

A summary of the overall performance of each

method can be seen in Fig. 11. The ε-Neighbourhood

method is the weaker of the two methods proposed

with a performance of 62.2%, while the kNN method

achieved a performance of 65.9%, beating the 64.5%

for SVMs. Combining the kNN and SVM meth-

ods reached the highest performance at 71.4% with

µ = 4, showing that combining the relation-based and

content-based approaches is an effective way to im-

prove performance.

6 CONCLUSIONS

There has been an increased interest in the effects

the method of graph construction plays in the overall

performance of any graph-based approach. Findings

suggest that the method of graph construction can-

not be studied independently of the subsequent algo-

rithms applied to the graph (Maier et al., 2009). Label

propagation has many advantages over the traditional

content-based approach such as SVMs. New labels

that are introduced into the system can be adopted

with relative ease, and will automatically begin to

be propagated through the graph. In contrast, a new

SVM classiﬁer would need to be completely trained

to classify documents with the new class label. A sec-

ond advantage of label propagation is that incorrectly

annotated documents can be reclassiﬁed based upon

new documents in a self-regulating way. That is, the

ICPRAM 2012 - International Conference on Pattern Recognition Applications and Methods

graph is continuously learning from new data and im-

proving its quality of annotation, while the SVM is

ﬁxed in its classiﬁcation after the initial training pe-

riod.

In this paper, we have investigated two different

local neighbourhood methods, ε-Neighbourhood and

k-Nearest Neighbour, for constructing graphs for text.

We have shown that sparse graphs can be constructed

from large text corpora in O (N logN) time, with the

cost of propagating labels on the graph linear in the

size of the graph, i.e. O (N). Our results show that the

graph-based methods are competitive with content-

based SVM methods. We have further shown that

combining the graph-based and content-based meth-

ods leads to an improvement in performance.

The proposed methods can easily be scaled out

into a distributed setting using currently available

open source software such as Apache Solr

, or Katta

allowing a user to handle millions of texts with simi-

larly effective performance.

Research into novel ways of combining the re-

lation and content based methods could lead to fur-

ther improvements in the categorisation performance

while keeping the cost of building and propagating la-

bels on the graph to a minimum.

ACKNOWLEDGEMENTS

I. Flaounas and N.Cristianini are supported by FP7

under grant agreement no. 231495. N. Cristianini is

supported by Royal Society Wolfson Research Merit

Award. All authors are supported by Pascal2 Network

of Excellence.

REFERENCES

Angelova, R. and Weikum, G. (2006). Graph-based text

classiﬁcation: learn from your neighbors. In Proceed-

ings of the 29th annual international ACM SIGIR con-

ference on Research and development in information

retrieval, pages 485–492. ACM.

Araujo, M., Navarro, G., and Ziviani, N. (1997). Large text

searching allowing errors.

Baeza-Yates, R. and Navarro, G. (2000). Block addressing

indices for approximate text retrieval. Journal of the

American Society for Information Science, 51(1):69–

82.

Bayardo, R., Ma, Y., and Srikant, R. (2007). Scaling up

all pairs similarity search. In Proceedings of the 16th

Open source implementation of a distributed inverted

index. Available at: http://lucene.apache.org/solr/

Open source implementation of a distributed inverted

index. Available at: http://katta.sourceforge.net/

international conference on World Wide Web, pages

131–140. ACM.

Belkin, M., Matveeva, I., and Niyogi, P. (2004). Regular-

ization and semi-supervised learning on large graphs.

Learning theory, pages 624–638.

Carreira-Perpinan, M. and Zemel, R. (2004). Proximity

graphs for clustering and manifold learning. In Ad-

vances in Neural Information Processing Systems 17,

NIPS-17.

Cesa-Bianchi, N., Gentile, C., Vitale, F., and Zappella, G.

(2010a). Active learning on graphs via spanning trees.

Cesa-Bianchi, N., Gentile, C., Vitale, F., and Zappella, G.

(2010b). Random spanning trees and the prediction of

weighted graphs. In Proc. of ICML, pages 175–182.

Citeseer.

Chang, C.-C. and Lin, C.-J. (2001). LIBSVM: a library

for support vector machines. Software available at

http://www.csie.ntu.edu.tw/ cjlin/libsvm.

Cormen, T., Leiserson, C., and Rivest, R. (1990). Introduc-

tion to Algorithms.

Dietterich, T. (2000). Ensemble methods in machine learn-

ing. Multiple classiﬁer systems, pages 1–15.

Dong, W., Moses, C., and Li, K. (2011). Efﬁcient k-

nearest neighbor graph construction for generic sim-

ilarity measures. In Proceedings of the 20th interna-

tional conference on World wide web, pages 577–586.

ACM.

Flaounas, I., Ali, O., Turchi, M., Snowsill, T., Nicart, F., De

Bie, T., and Cristianini, N. (2011). NOAM: News Out-

lets Analysis and Monitoring System. In Proceedings

of the 2011 ACM SIGMOD international conference

on Management of data, pages 1275–1278. ACM.

Gionis, A., Indyk, P., and Motwani, R. (1999). Similarity

search in high dimensions via hashing. In Proceedings

of the 25th International Conference on Very Large

Data Bases, pages 518–529. Morgan Kaufmann Pub-

lishers Inc.

Heaps, H. (1978). Information retrieval: Computational

and theoretical aspects. Academic Press, Inc. Or-

lando, FL, USA.

Herbster, M. and Pontil, M. (2007). Prediction on a graph

with a perceptron. Advances in neural information

processing systems, 19:577.

Herbster, M., Pontil, M., and Rojas-Galeano, S.(2009). Fast

prediction on a tree. Advances in Neural Information

Processing Systems, 21:657–664.

Jebara, T., Wang, J., and Chang, S. (2009). Graph construc-

tion and b-matching for semi-supervised learning. In

Proceedings of the 26th Annual International Confer-

ence on Machine Learning, pages 441–448. ACM.

Joachims, T. (1998). Text categorization with support vec-

tor machines: Learning with many relevant features.

Machine Learning: ECML-98, pages 137–142.

Lewis, D., Yang, Y., Rose, T., and Li, F. (2004). RCV1:

A new benchmark collection for text categorization

research. Journal of Machine Learning Research,

5:361–397.

Lloyd, L., Kechagias, D., and Skiena, S. (2005). Lydia: A

system for large-scale news analysis. In String Pro-

cessing and Information Retrieval, pages 161–166.

Springer.

SCALABLE CORPUS ANNOTATION BY GRAPH CONSTRUCTION AND LABEL PROPAGATION

Maier, M., Von Luxburg, U., and Hein, M. (2009). Inﬂu-

ence of graph construction on graph-based clustering

measures. Advances in neural information processing

systems, 22:1025–1032.

Parzen, E. (1962). On estimation of a probability density

function and mode. The annals of mathematical statis-

tics, 33(3):1065–1076.

Salton, G. (1989). Automatic text processing.

Sarawagi, S. and Kirpal, A. (2004). Efﬁcient set joins on

similarity predicates. In Proceedings of the 2004 ACM

SIGMOD international conference on Management of

data, pages 743–754. ACM.

Sebastiani, F. (2002). Machine learning in automated

text categorization. ACM computing surveys (CSUR),

34(1):1–47.

Shawe-Taylor, J. and Cristianini, N. (2004). Kernel methods

for pattern analysis. Cambridge University Press.

Steinbach, M., Karypis, G., and Kumar, V. (2000). A com-

parison of document clustering techniques. In KDD

workshop on text mining, volume 400, pages 525–526.

Citeseer.

Steinberger, R., Pouliquen, B., and van der Goot, E. (2009).

An Introduction to the Europe Media Monitor Family

of Applications. In Information Access in a Multilin-

gual World-Proceedings of the SIGIR 2009 Workshop,

pages 1–8.

Tan, P., Steinbach, M., Kumar, V., et al. (2006). Introduction

to data mining. Pearson Addison Wesley Boston.

Yang, Y., Zhang, J., and Kisiel, B. (2003). A scalability

analysis of classiﬁers in text categorization. In Pro-

ceedings of the 26th annual international ACM SI-

GIR conference on Research and development in in-

formaion retrieval, pages 96–103. ACM.

Zhang, J., Marszałek, M., Lazebnik, S., and Schmid, C.

(2007). Local Features and Kernels for Classiﬁca-

tion of Texture and Object Categories: A Comprehen-

sive Study. International Journal of Computer Vision,

73(2):213–238.

Zhu, X. (2007). Semi-supervised learning literature survey.

Computer Science, University of Wisconsin-Madison.

Zhu, X., Ghahramani, Z., and Lafferty, J. (2003). Semi-

supervised learning using gaussian ﬁelds and har-

monic functions. In International Conference of Ma-

chine Learning, volume 20, page 912.

ICPRAM 2012 - International Conference on Pattern Recognition Applications and Methods