
AN ALTERNATIVE METHOD
FOR MEASURING HUMAN RESPIRATORY IMPEDANCE
Robin De Keyser and Clara M. Ionescu
Ghent University, Faculty of Engineering and Architecture, Department of Electrical Energy, Systems and Automation,
Technologiepark 913, B9052, Gent-Zwijnaarde, Belgium
Keywords: Forced Oscillation Technique, Lung function test, Non-invasive measurement, Respiratory impedance.
Abstract: The Forced Oscillation Technique (FOT) denotes a non-invasive lung function test which serves as a
medical diagnostic tool to measure human respiratory impedance. The FOT principle is based on
superimposing air pressure oscillations onto the normal breathing waves of the subject, measuring both air
flow and air pressure at the mouth and analyzing the data with signal processing techniques which apply to
linear systems. The motivation to eliminate the need for flow measurement arises from i) economic reasons,
because measurement of air flow in this case requires the presence of an expensive component, the
pneumotachograph, in the FOT device and ii) innovative aspects. The present work assessed the possibility
that the requirement to measure flow could be eliminated if the transformation from excitation signal to
measured pressure in the FOT device (given by the internal impedances of the device) is known. This
conceptual solution was theoretically proven by analyzing the electrical circuit which models these
transformations. Measurements were conceived and performed in order to estimate these quantities.
1 INTRODUCTION
Non-invasive lung function tests are broadly used
for assessing respiratory mechanics (Northrop, 2002;
Oostveen et al., 2003). Contrary to the forced
manoeuvres from patient side and special training
for the technical medical staff necessary in
spirometry and in body plethysmography (Northrop,
2002), the technique of superimposing air pressure
oscillations is simple and requires minimal
cooperation from the patient, during tidal breathing.
Among the air pressure oscillation techniques for
lung function testing, the most popular one is that of
Forced Oscillation Technique (FOT) (Smith et al,
2005). FOT uses a multisine signal to excite the
respiratory mechanical properties over a wide range
of frequencies, usually between 4-48Hz (Oostveen et
al., 2003).
The FOT principle is based on superimposing air
pressure oscillations onto the normal breathing
waves of the subject, measuring both air flow and air
pressure at the mouth and analyzing the data with
signal processing techniques which apply to linear
systems. The attempt to eliminate the flow
measurement is justified from i) economic reasons,
because measurement of air flow in this case
requires the presence of an expensive component,
the pneumotachograph, in the FOT device and ii)
innovative aspects. The present work assessed the
possibility that the requirement to measure flow
could be eliminated if the transformation from
excitation signal to measured pressure in the FOT
device (given by the internal impedances of the
device) is known.
The paper is organized as follows: the traditional
measuring method and device is described in the
next section. The third section presents the
theoretical basis for eliminating the flow
measurement and the fourth section gives an
overview of the possible measurements, which can
be performed on such a commercially available FOT
device. The results of the proposed method are given
in the fifth section. A measurement on a healthy
subject is used to illustrate the usefulness of the
novel approach for measuring the respiratory
impedance. Finally, a conclusion section
summarizes the main outcome of this work.
119
De Keyser R. and M. Ionescu C..
AN ALTERNATIVE METHOD FOR MEASURING HUMAN RESPIRATORY IMPEDANCE.
DOI: 10.5220/0003729601190126
In Proceedings of the International Conference on Biomedical Electronics and Devices (BIODEVICES-2012), pages 119-126
ISBN: 978-989-8425-91-1
Copyright
c
2012 SCITEPRESS (Science and Technology Publications, Lda.)

2 STANDARD IMPEDANCE
MEASUREMENT
The impedance was measured using a modified FOT
setup, able to assess the respiratory mechanics from
4-50 Hz. The specifications of the device are: 11kg,
50x50x60 cm, 40 seconds measurement time,
European Directive 93/42 on Medical devices and
safety standards EN60601-1.
Typically for lung function testing purposes, the
subject is connected to the setup from figure 1 via a
mouthpiece, suitably designed to avoid flow leakage
at the mouth and dental resistance artefact. The
oscillatory pressure is generated by a loudspeaker
(LS), which is connected to a chamber. The LS is
driven by a power amplifier, which is fed with the
oscillatory signal generated by a computer (denoted
by U in figure 1-A and by U
g
in figure 1-B). The
movement of the LS cone generates a pressure
oscillation inside the chamber, which is applied to
the patient's respiratory system by means of a tube
connecting the LS chamber and the bacterial filter
(bf). A side opening of the main tubing (BT) allows
the patient to have fresh air circulation. Ideally, this
BT pipeline will have high impedance at the
excitation frequencies to avoid the loss of power
from the LS pressure chamber. It is advisable that
during the measurements, the patient wears a nose
clip and keeps the cheeks firmly supported. Before
starting the measurements, the frequency response of
the transducers (PT for pressure measurement) and
of the pneumotachograph (PN for flow
measurement) is calibrated.
Figure 1: A schematic overview (A) and an electrical
analogy of the FOT setup (B).
The measurements of air-pressure P and air-flow
Q during the FOT lung function test are done at the
mouth of the patient. The FOT excitation signal was
kept within a peak-to-peak range of 0.1-0.3 kPa, in
order to ensure optimality, patient comfort and
linearity (Oostveen et al., 2003). From these signals,
the non-parametric representation of the patient’s
lung impedance Z
r
is obtained assuming a linear
dependence between the breathing and
superimposed oscillations at the mouth of the patient
(Daroczy and Hantos, 1982; Ionescu and De Keyser,
2003).
Consider the equivalent circuit for the global
setup, denoted by figure 1-B, with the notations as:
U
g
= generator test signal – driving signal
(measured); U
r
= effect of spontaneous breathing
(respiratory system / unknown); Z
r
= impedance of
interest (to be estimated): the impedance of the total
respiratory system (including the airways, lung
tissues and chest wall); Z
1
= impedance (unknown)
describing the transformation of driving voltage (U
g
)
to chamber pressure; Z
2
= impedance (unknown) of
both bias tubes and loud-speaker chamber; Z
3
=
impedance (unknown) of tube segment between bias
tube and mouth piece (effect of pneumotachograph
essentially); P = (measured) pressure; Q =
(measured) flow. The corresponding equation is:
() () () ()
rr
P
sZsQsUs=+
(1)
where s denotes the Laplace operator. Since the
excitation signal is designed such that it is not
correlated with the breathing of the patient,
correlation analysis can be applied to the measured
signals. Therefore, one can estimate the respiratory
impedance as the ratio:
()
()
()
g
g
PU
r
QU
Sj
Zj
Sj
ω
ω
ω
=
(2)
where the P corresponds to pressure (its electrical
equivalent is voltage) and Q corresponds to air-flow
(its electrical equivalent is current), U
g
the excitation
signal,
()
ij
Sj
ω
the cross-correlation spectra
between the various input-output signals, ω is the
angular frequency and
1/2
(1)j =− , resulting in the
complex variable Z
r
. From the point of view of the
forced oscillatory experiment, the signal components
of respiratory origin (U
r
) have to be regarded as pure
noise for the identification task (Ljung, 1999).
3 THEORETICAL BASIS
The following input-output relationship can be
written based on figure 1-B (Ionescu and De Keyser,
2003):
LS
PT
bf
subject
P(t)Q(t)
LS
BT
PT
PN
bf
subject
DAQ board
Laptop / GUI
U(t)
P(t) Q(t)
LS
PT
bf
subject
P(t)Q(t)
LS
BT
PT
PN
bf
subject
DAQ board
Laptop / GUI
U(t)
P(t) Q(t)
A
B
Z
2
Z
1
Z
3
Z
r
P
Q
U
r
U
g
Z
2
Z
1
Z
3
Z
r
P
Q
U
r
U
g
Z
FOT
LS
PT
bf
subject
P(t)Q(t)
LS
BT
PT
PN
bf
subject
DAQ board
Laptop / GUI
U(t)
P(t) Q(t)
LS
PT
bf
subject
P(t)Q(t)
LS
BT
PT
PN
bf
subject
DAQ board
Laptop / GUI
U(t)
P(t) Q(t)
A
B
Z
2
Z
1
Z
3
Z
r
P
Q
U
r
U
g
Z
2
Z
1
Z
3
Z
r
P
Q
U
r
U
g
Z
FOT
Z
2
Z
1
Z
3
Z
r
P
Q
U
r
U
g
Z
2
Z
1
Z
3
Z
r
P
Q
U
r
U
g
Z
FOT
BIODEVICES 2012 - International Conference on Biomedical Electronics and Devices
120

=
(
)
(
)
(
)
∙
(3)
with
=
+
. In the classical approach
the two equations are divided and an expression for
the impedance of the subject, Z
r
, is obtained as in
(2). This requires knowing the flow. Now, suppose
that the flow measurement cannot be used, Z
r
can be
expressed from the first equation:
=
(
)
∙
(4)
The end result is:
=
(5)
The relation (5) is in agreement with Thévenin’s
theorem. We conclude therefore that if one needs to
measure the respiratory impedance by means of only
pressure signal, the internal impedances of the FOT
device need to be known. More precisely, two
combinations of these internal impedances:
+
and
.
4 PROPOSED METHOD
As shown in the previous section, one can estimate
the impedance of a load without measuring the air-
flow signal explicitly. However, a pre-requisite
condition is that the internal impedances of the lung
function testing device have to be known. The
content of this section will give a mathematical
background of the possible measurement protocols.
The measurements have to be made on each
FOT device on which the pressure-only estimation
technique is applied. This would mean that these
measurements will have to be done after a device is
built. This can be omitted in the case of mass-
production if the manufacturer can guarantee that the
parameters of the device which play a role in these
values are the same, with a certain tolerance, for
each of the devices produced. However, if these
parameters are found to be varying with time or with
other parameters (ageing, temperature, etc.) the
measurements will have to be renewed periodically.
The fact that the location of the sensors are fixed
reduces the freedom in measuring the internal
impedances of the device. The various parts of the
FOT device cannot be disassembled and measured
separately since measurement errors will
accumulate. Additionally, the behaviour of the
elements acting together cannot be captured. In
consequence, methods have to be developed which
allow measurement of these impedances using
available fixed instrumentation.
The final objective is that once the internal
impedances of the device are known, no flow
measurement is necessary to perform measurements
of the respiratory impedance in subjects.
Figure 2: Equivalent circuit for measurement M1.
Figure 3: Equivalent circuit for measurement M2.
4.1 M1: Measuring Pressure with a
Sealed Mouthpiece
The equivalent circuit in this setup is given in figure
2; notice that it ends in an open circuit. This implies
no flow going out from the device (through
mouthpiece)=0. The flow will only travel
through the bias tube =. In this
case
=
(6)
where
=
because Q is zero and in
consequence Z
3
does not play a role. Therefore:
=
= (7)
is the first set of measurement that we can apply.
4.2 M2: Measuring Flow with a Sealed
Bias Tube and Open Mouthpiece
The equivalent circuit in this measurement protocol
is given in figure 3. For this measurement the
pressure is theoretically zero, because the pressure
AN ALTERNATIVE METHOD FOR MEASURING HUMAN RESPIRATORY IMPEDANCE
121

sensor is directly connected to the atmosphere. In
order to perform this test, the bias tube has to be
sealed. Without disassembling the device, this is
only possible at the outer end. There is no flow
across the bias tube, so the associated impedance, Z
2
does not play a role. All the generated flow leaves
through the mouthpiece and is measured. This is a
simple series structure, which gives that flow is:
=
(8)
and the impedances of interest can be estimated as:
+
=
= (9)
4.3 M3: Measuring Flow, Both Bias
Tube and Mouthpiece Open
The equivalent circuit in this setup is given in figure
4. Here we also have pressure almost zero (pressure
sensor directly connected to atmosphere).
Figure 4: Equivalent circuit for measurement M3.
Flow is measured by
=
=
(
)
(10)
from where we extract the third relationship for
estimating internal impedances in the device:
=
(
)
= (11)
4.4 M4: Measuring Pressure with a
Known Load (Calibration Tube)
The equivalent circuit in this setup is given in figure
5, where Z
r
is in fact the known impedance of the
calibration tube.
Figure 5: Equivalent circuit for measurement M4.
The measured pressure is:
=
(12)
However, to have information only about the
internal impedances of the device, the effect of the
calibration tube has to be eliminated. Consider the
notation:
=
=
(13)
where Z
p
comes from the result of measurement M1,
namely
=
=
(14)
and, respectively
=
+
+
(15)
The new information is contained in Z
q
. It can be
expressed by:
=
(∙
)
(16)
Notice that Z
p
was measured in measurement M1
and Z
r
is known, hence (16) can be calculated.
4.5 M5: Measuring Pressure with a
Known Load and Closed Bias Tube
The equivalent circuit in this setup is given in figure
6, where Z
r
is in fact the known impedance of the
calibration tube. The measured pressure is:
=
(17)
from where we can extract that:
=
= (18)
The sum of the two unknown impedances can be
easily expressed as in
+
=
∙
=
(19)
Figure 6: Equivalent circuit for measurement M5.
BIODEVICES 2012 - International Conference on Biomedical Electronics and Devices
122

In consequence this is an alternative measurement,
along with measurement M2, to determine the sum
of the impedances Z
1
and Z
3
. The reliability of this
measurement is questionable because experiments
show that the result is not significantly different than
that of measurement M4. This may be explained by
a combination of two effects, as summarized below.
a) The bias tube does not play a significant role
in measurement M4, because it is designed to have
high impedance on the excited frequencies. This
effect is important in the case of the commercial
device, because it works on frequencies significantly
higher than the breathing (4-250Hz). It would be less
important in the case of a custom-built device which
works on lower frequencies, i.e. closer to the
breathing frequency, because on these frequencies
the bias tube does not have high impedance (<1Hz).
b) The bias tube is not entirely excluded in
measurement M5, because it is long and has elastic
walls, so it may have a capacitive role even if its
outer opening is closed. This effect is more
important in the case of the custom-built device,
because that, working on higher pressures at lower
frequencies, has the capability to push some air into
the elastic bias tube, exploiting its capacitive
properties.
4.6 Possible Combinations of
Measurements M1...M5
4.6.1 First Combination
The first set of measurements consists of
measurements M1, M2 and M3 (their results are
denoted by a, b and c, respectively). With these
parameters it results that the individual values of the
impedances can be determined from these equations:
=
(
)
(20)
=−
()
(
)
(21)
=
(
)
(22)
But, considering the equation (4), which gives the
impedance of the patient, the following two
equations become important:
==
(23)
+
=
=
=
(24)
where P
1
denotes the pressure measured during the
measurement M1, and Q
3
denotes the flow measured
during measurement M3. Relation (24) describes the
ratio between pressure measured with an infinite
load and flow measured with zero load in
concordance again with Thévenin’s theorem. Once
more, the formula by which the impedance of a
subject can be expressed from these results is:
=
∙
(25)
The conclusion is that only measurements M1
and M3 have to be performed to estimate the
subject’s impedance. If the individual values are
needed, measurement M2 needs to be added also. In
any case, there is a need to measure flow at least
once.
4.6.2 Second Combination
This set uses measurements M1, M4 and M5. None
of them involve flow measurement so they can be
done without the presence of a pneumotachograph in
the system. From the results of these measurements
it follows that the individual values of the
impedances can be determined from these equations:
=−
–
∙
–
(26)
=−
–
∙
(27)
=
–
–
(28)
where Z
p
comes from M1, namely
=
(29)
After performing a measurement with a patient,
his/her impedance can be calculated as:
=
+
−
=
=
∙
=
(30)
using pressure data collected during the FOT
experiment with the patient,
.
This is theoretically the same method as the one
from section 4.6.1, in the sense that it also contains
AN ALTERNATIVE METHOD FOR MEASURING HUMAN RESPIRATORY IMPEDANCE
123
the ratio between pressure measured with an infinite
load and flow measured with zero load. However, in
this case, flow measurement without load has been
replaced by pressure measurement with a known
load and further processing of that measurement.
Yet again, measurement M5 is only needed if the
individual values have to be known. To estimate a
subject’s impedance there is only need for the
results of measurements M1 and M4. Notice that
these two experiments require only the pressure
measurement.
5 RESULTS
5.1 Characterization of the Measuring
Device
We have applied the tests described in the previous
section in order to extract the transfer function of the
device using only the information coming from the
pressure signal. We have also applied these using
different types of excitation signals
. The
underlying rationale for this was to verify the
linearity of the system, since we suspected that the
voltage-to-pressure conversion holds a nonlinear
relationship. Indeed, the nonlinearity of the system is
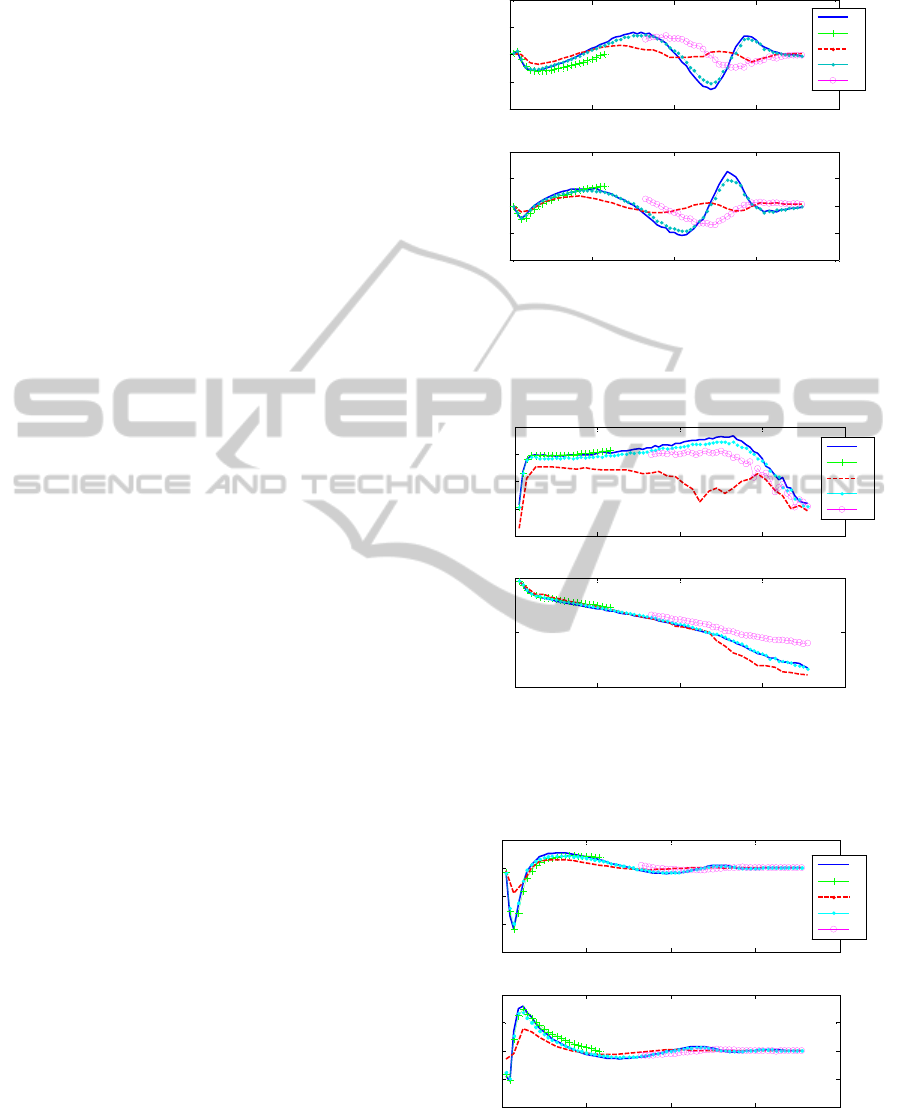
illustrated by the figures 7 and 8, respectively.
The lines depicted in figures 7, 8, 9, 10, 11 and
12 represent data collected with different
frequencies in the excitation signal, i.e. the
multisine:
A: 2.5:2.5:177.5 Hz, a total of 71 frequencies,
signal between -1 and 1 Volt
B: 2.5:2.5:57.5 Hz, a total of 23 frequencies,
signal between -1 and 1 Volt
C: 2.5:5:177.5 Hz, a total of 36 frequencies,
signal between -1 and 1 Volt
D: 2.5:2.5:177.5 Hz, a total of 71 frequencies,
signal between -0.5 and 0.5 Volt
E: 82.5:2.5:177.5 Hz, a total of 39 frequencies,
signal between -1 and 1 Volt
Figure 7 represents the impedance of the device
in terms of its complex representation (i.e. real and
imaginary parts), while Figure 8 is the equivalent
Bode plot (i.e. magnitude and phase). The data
presented in Figures 7 and 8 originates from the
measurement M4.
Figures 9 and 10 depict the same experiment
data when using flow as the information signal
(instead of pressure). Again, we observe that
different results are obtained for different input
signals, suggesting that the transformation from
Figure 7: Real and Imaginary parts of the impedance of
the lung function testing device extracted from
measurement M4 for various inputs (see text for legend).
Figure 8: Magnitude and Phase of the impedance of the
lung function testing device extracted from measurement
M4 for various inputs (see text for legend).
Figure 9: Real and imaginary parts of the impedance of the
device using only flow information extracted from
measurement M4 for various inputs (see text for legend).
0 50 100 150 200
-1
-0.5
0
0.5
1
Real Part [kPa s/l]
Sup/Suu
0 50 100 150 200
-1
-0.5
0
0.5
1
Imaginary Part [kPa s/l]
Frequency [Hz]
A
B
C
D
E
0 50 100 150 200
-40
-30
-20
-10
0
Magnitude [dB]
Sup/Suu
0 50 100 150 200
-1000
-500
0
Phase [degrees]
Frequency [Hz]
A
B
C
D
E
0 50 100 150 200
-6
-4
-2
0
2
Real Part [kPa s/l]
Suq/Suu
0 50 100 150 200
-4
-2
0
2
4
Imaginary Part [kPa s/l]
Frequency [Hz]
A
B
C
D
E
BIODEVICES 2012 - International Conference on Biomedical Electronics and Devices
124

voltage-to-flow is also nonlinear. Intuitively, one
expects that these nonlinearities cancel out if both
pressure and flow can be measured because pressure
and flow are all affected in the same way. This is
then illustrated by Figures 11 and 12 below, in terms
Figure 10: Bode plot of the impedance of the device using
only flow information extracted from measurement M4 for
various inputs (see text for legend).
Figure 11: Real and Imaginary parts of the impedance of
the device measured using both flow and pressure
knowledge (see text for legend).
Figure 12: Real and Imaginary parts of the impedance of
the device measured using both flow and pressure
knowledge (see text for legend).
of the complex representation and Bode plot of the
impedance. One may observe that in this case,
irrespective of the excitation signal we apply, we
always obtain the same frequency response.
A serious limitation, which arises from this
nonlinear behaviour, is that the data collected with
one range of excitation cannot be used to estimate
the impedance of the patient if the patient was not
measured with a signal which has the same spectral
composition.
5.2 Respiratory Impedance of a
Healthy Subject
In order to verify if the theoretical developments
under section 4 were correct, it was necessary to test
them on the respiratory impedance of a volunteer.
We performed the lung function test described in
section 2 on a healthy volunteer, non-caucasian
male, 23 years age, 182 cm height and 70 kg weight.
The protocol implied comparing the traditional
method using both flow and pressure signals in
relation (2) with the two combination sets described
in section 4.6. Figures 13 and 14 depict the obtained
results for the respiratory impedance by these three
methods, in terms of complex impedance and Bode
plot, respectively. One may conclude that the
traditional method and the second combination set
(i.e. M1 and M4) gave the same results, therefore the
proposed alternative estimation concept without
flow measurement may be useful in practice to
evaluate correctly the respiratory impedance.
Figure 13: Complex impedance data for human respiratory
impedance in a healthy volunteer.
0 50 100 150 200
-40
-20
0
20
Magnitude [dB]
Suq/Suu
0 50 100 150 200
-1000
-500
0
Phase [degrees]
Fre
q
uenc
y
[
Hz
]
A
B
C
D
E
0 50 100 150 200
-6
-4
-2
0
2
Real Part [kPa s/l]
Sup/Suq
0 50 100 150 200
-4
-2
0
2
4
Imaginary Part [kPa s/l]
Frequency [Hz]
A
B
C
D
E
0 50 100 150 200
-40
-20
0
20
Magnitude [dB]
Sup/Suq
0 50 100 150 200
50
100
150
200
250
Phase [degrees]
Frequency [Hz]
A
B
C
D
E
0 10 20 30 40 50 60
0
0.5
1
Real Part [kPa s/l]
Respiratory Impedance - Complex
0 10 20 30 40 50 60
-0.2
0
0.2
0.4
0.6
Frequency [Hz]
Imaginary Part [kPa s/l]
Traditional
Second Set
First Set
AN ALTERNATIVE METHOD FOR MEASURING HUMAN RESPIRATORY IMPEDANCE
125

Figure 14: Magnitude and Phase for human respiratory
impedance in a healthy volunteer.
6 CONCLUSIONS
The Forced Oscillations Technique (FOT) denotes a
non-invasive lung function test which serves as a
medical diagnostic tool to measure human
respiratory impedance. A justification to eliminate
the need for flow measurement arises from i)
economic reasons, because measurement of air flow
in this case requires the presence of an expensive
component, the pneumotachograph, in the FOT
device and ii) innovative aspects.
The present work assessed the possibility that the
requirement to measure flow could be eliminated if
the transformation from excitation signal to
measured pressure in the FOT device (given by the
internal impedances of the device) is known. This
conceptual solution was theoretically proven by
analyzing the equivalent electrical circuit, which
models these transformations. Measurements were
conceived and validated on a healthy volunteer,
showing good agreement between the traditional
method (using both flow and pressure signal
information) and the proposed alternative method
(using only pressure signal information).
ACKNOWLEDGEMENTS
The authors acknowledge the technical support
received from Mr Istvan Orban and Mr Matthias
Deneut in performing the necessary tests. C. M.
Ionescu is a postdoctoral fellow of the Flanders
Research Foundation, Belgium.
REFERENCES
Daróczi B., Hantos Z., 1982. “An improved forced
oscillatory estimation of respiratory impedance”, Int J
Bio-Medical Computing, 13, 221-235
Ionescu C., De Keyser R., 2003. “A novel parametric
model for the human respiratory system”, Proc. of the
IASTED Int. Conf. on Modelling and simulation., Palm
Springs, CA, USA, 246-251
Ljung, L., 1999, System Identification, NJ: Prentice Hall
Northrop R., 2002. Non-invasive measurements and
devices for diagnosis, CRC Press
Oostveen E., MacLeod D., Lorino H., Farré R., Hantos Z.,
Desager K., Marchal F., 2003. “The forced forced
oscillation technique in clinical practice: methodology,
recommendations and further developments”, Eur.
Respir. J., 22, 1026-1041
Smith H. J., Reinhold P., Goldman M.D., 2005. “Forced
oscillation technique and impulse oscillometry”, Eur
Resp Mon., 31, 72,105
0 10 20 30 40 50 60
-25
-20
-15
-10
-5
0
Magnitude [dB]
Respiratory Impedance - Bode Plot
0 10 20 30 40 50 60
-100
-50
0
50
100
Frequency [Hz]
Phase [degrees]
Traditional
Second Set
First Set
BIODEVICES 2012 - International Conference on Biomedical Electronics and Devices
126
