WHAT DO OBJECTS FEEL LIKE?

Active Perception for a Humanoid Robot

Jens Kleesiek

1,3

, Stephanie Badde

, Stefan Wermter

and Andreas K. Engel

Dept. of Neurophysiology and Pathophysiology, University Medical Center Hamburg-Eppendorf, Hamburg, Germany

Dept. of Biological Psychology and Neuropsychology, University of Hamburg, Hamburg, Germany

Department of Informatics, Knowledge Technology, University of Hamburg, Hamburg, Germany

Keywords:

Active perception, RNNPB, Humanoid robot.

Abstract:

We present a recurrent neural architecture with parametric bias for actively perceiving objects. A humanoid

robot learns to extract sensorimotor laws and based on those to classify eight objects by exploring their multi-

modal sensory characteristics. The network is either trained with prototype sequences for all objects or just two

objects. In both cases the network is able to self-organize the parametric bias space into clusters representing

individual objects and due to that, discriminates all eight categories with a very low error rate. We show that

the network is able to retrieve stored sensory sequences with a high accuracy. Furthermore, trained with only

two objects it is still able to generate fairly accurate sensory predictions for unseen objects. In addition, the

approach proves to be very robust against noise.

1 INTRODUCTION

The active nature of perception and the intimate re-

lation between action and cognition (Dewey, 1896;

Merleau-Ponty, 1963) has been emphasized in philos-

ophy and cognitive science for a long time. “Percep-

tion is something you do, not something that happens

to you” (Bridgeman and Tseng, 2011) has been postu-

lated in the neurosciences as well as in related ﬁelds.

Already in the 80’s of the last century it has been sug-

gested for machine perception and robotics that “[. . . ]

it should be axiomatic that perception is not passive,

but active. Perceptual activity is exploratory, prob-

ing, searching; percepts do not simply fall onto sen-

sors as rain falls onto ground. We do not just see, we

look” (Bajcsy, 1988). However, most of the current

approaches do not follow these insights.

In the computer vision and robotics literature ex-

pressions like ’active vision’ (Aloimonos et al., 1988),

’active perception’ (Bajcsy, 1988), ’smart sensing’

(Burt, 1988) and ’animate vision’ (Ballard, 1991) are

commonly used – sometimes even interchangeably,

despite varying intentions pursued by the original au-

thors. Usually, these terms refer to a sensor, which

can be moved actively, e. g. a scanning laser mounted

on an autonomous vehicle travelling offroad at high

speed (Patel et al., 2005) or a four-camera stereo head

using foveation for detection and ﬁxation of objects

(Rasolzadeh et al., 2009). The mobility of a sensor or

of a manipulator, e. g. robot arm, and especially the

knowledge about the movements in conjunction with

a changing sensory impression have been proven to be

of valuable assistance for object segmentation (Fitz-

patrick and Metta, 2003).

We take the notion of active perception a step fur-

ther and do not restrict it to the visual modality only.

Varela et al. suggested an enactive approach – mean-

ing that cognitive behavior results from interaction

of organisms with their environment (Varela et al.,

1991). A robot is embodied (Pfeifer et al., 2007) and

it has the ability to act and to perceive. In our opin-

ion it actually needs to act to perceive. The action-

triggered sensations are guided by the physical prop-

erties of its body, the world and the interplay of both.

Here we propose a model that can be seen as a ﬁrst

step towards this meaning of active perception. A hu-

manoid robot moves toy bricks up-and-down and ro-

tates them back-and-forth, while holding them in its

hand. The induced multi-modal sensory impressions

are used to train an improved version of a recurrent

neural network with parametric bias (RNNPB), origi-

nally developed by Tani et al. (Tani and Ito, 2003). As

a result, the robot is able to self-organize the contex-

tual information to sensorimotor laws, which in turn

can be used for object classiﬁcation. Due to the over-

whelming generalization capabilities of the recurrent

Kleesiek J., Badde S., Wermter S. and K. Engel A..

WHAT DO OBJECTS FEEL LIKE? - Active Perception for a Humanoid Robot.

DOI: 10.5220/0003729900640073

In Proceedings of the 4th International Conference on Agents and Artiﬁcial Intelligence (ICAART-2012), pages 64-73

ISBN: 978-989-8425-95-9

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

architecture, the robot is even able to correctly clas-

sify unknown objects. Furthermore, we show that the

proposed model is very robust against noise.

The paper is organized as follows. In section 2

we present the neural architecture, followed by a task,

scenario and data description in section 3. Then we

report on three experiments in section 4, concluding

with a discussion of the results, the architecture and

related literature in section 5.

2 RECURRENT NEURAL

NETWORK

Despite its intriguing properties the recurrent neural

network with parametric bias has hardly been used by

others than the original authors. Mostly, the archi-

tecture is utilized to model the mirror neuron system

(Tani et al., 2004; Cuijpers et al., 2009). Here we

apply the variant proposed by Cuijpers et al. using

an Elman-type structure at its core (Cuijpers et al.,

2009). Furthermore, we modify the training algo-

rithm to include adaptive learning rates for training

of the weights as well as the PB values. This results

in an improved architecture that is more stable and

converges faster. For instance, the storage of two 1-D

time series (t = 12) is sped up by a factor of 22 on

average (n = 1000, 5519 vs. 122.709 steps).

2.1 Storage of Time Series

The recurrent neural network with parametric bias

(an overview of the architecture unfolded in time can

be seen in Fig. 1) can be used for the storage, re-

trieval and recognition of sequences. For this pur-

pose, the parametric bias (PB) vector is learned si-

multaneously and unsupervised during normal train-

ing of the network. The prediction error with re-

spect to the desired output is determined and back-

propagated through time (BPTT) (Kolen and Kremer,

2001). However, the error is not only used to correct

all the synaptic weights present in an Elman-type net-

work. Additionally, the error with respect to the PB

nodes δ

is accumulated over time and used for up-

dating the PB values after an entire forward-backward

pass of a single time series, denoted as epoch e. In

contrast to the synaptic weights that are shared by all

training patterns, a unique PB vector is assigned to

each individual training sequence. The update equa-

tions for the i-th unit of the parametric bias pb for a

time series of length T is given as:

(e + 1) = ρ

(e) + γ

∑

t=1

i,t

, (1)

(e) = sigmoid(ρ

(e)) , (2)

where γ is the update rate for the PB values, which in

contrast to the original version is during training not

constant and not identical for every PB unit. Instead,

it is scaled proportional to the absolute mean value

of prediction errors being backpropagated to the i-th

node over time T :

∝



∑

t=1

i,t



. (3)

The other adjustable weights of the network are up-

dated via an adaptive mechanism, inspired by the re-

silient propagation algorithm (Riedmiller and Braun,

1993). However, there are decisive differences. First,

the learning rate of each neuron is adjusted after every

epoch. Second, not the sign of the partial derivative

of the corresponding weight is used for changing its

value, but instead the partial derivative itself is taken.

To determine if the partial derivative of weight w

i j

changes its sign we can compute:

i j

∂E

i j

∂w

i j

(t − 1) ·

∂E

i j

∂w

i j

(t) (4)

If ε

i j

< 0 the last update was too big and the local

minimum has been missed. Therefore, the learning

rate η

i j

has to be decreased by a factor ξ

−

< 1 . On

the other hand a positive derivative indicates that the

learning rate can be increased by a factor ξ

> 1 to

speed up convergence. This update of the learning

rate can be formalized as:

i j

(t) =







max(η

i j

(t − 1) · ξ

−

, η

min

) if ε

i j

< 0,

min(η

i j

(t − 1) · ξ

, η

max

) if ε

i j

> 0,

i j

(t − 1) else.

(5)

The succeeding weight update ∆w

i j

then obeys the

following rule:

∆w

i j

(t) =

(

−∆w

i j

(t − 1) if ε

i j

< 0,

i j

(t) ·

∂E

i j

∂w

i j

(t) else.

(6)

In addition to reverting the previous weight change in

the case of ε

i j

< 0 the partial derivative is also set to

zero (

∂E

i j

∂w

i j

(t) = 0). This prevents changing of the sign

of the derivative once again in the succeeding step and

thus a potential double punishment.

We use a nonlinear activation function with rec-

ommended parameters (LeCun et al., 1998) for all

neurons in the network as well as for the PB units

(Eq. 2):

sigmoid(x) = 1.7159 · tanh



· x



. (7)

WHAT DO OBJECTS FEEL LIKE? - Active Perception for a Humanoid Robot

Figure 1: Network architecture. The Elman-type Recurrent Neural Network with Parametric Bias (RNNPB) unfolded in

time. Dashed arrows indicate a verbatim copy of the activations (weight connections set equal to 1.0). All other adjacent

layers are fully connected. t is the current time step, T denotes the length of the time series.

2.2 Number of PB Units

The PB vector is usually low dimensional and resem-

bles bifurcation parameters of a nonlinear dynamical

system, i. e. it characterizes ﬁxed-point dynamics of

the RNN. To quantify the number of the principle

components (PCs) actually needed for (almost) loss-

less reconstruction of the PB space, we determined

how many are necessary to explain 99 % of the vari-

ance. Increasing the number of PB values, given a

bi-modal time series of length T = 14, resulted in a

constant number of two PCs. Hence, we use a 2-D

PB vector for our experiments.

2.3 Retrieval

During training the PB values are self-organized,

thereby encoding each time series and arranging it

in PB space according to the properties of the train-

ing pattern. This means that the values of similar

sequences are clustered together, whereas more dis-

tinguishable ones are located further apart. Once

learned, the PB values can be used for the genera-

tion of the time series previously stored. For this pur-

pose, the network is operated in closed-loop mode.

The PB values are ’clamped’ to a previously learned

value and the forward pass of the network is executed

from an initial input I(0). In the next time steps, the

output at time t serves as an input at time t + 1. This

leads to a reconstruction of the training sequence with

a very high accuracy, only limited by the convergence

threshold used during learning (e. g. shown in Fig. 5

on the left).

2.4 Recognition

A previously stored (time) sequence can also be rec-

ognized via its corresponding PB value. Therefore,

the observed sequence is fed into the network without

updating any connection weights. Only the PB values

are accumulated according to Eq. (1) and (2) using a

constant learning rate γ this time. Once a stable PB

vector is reached (as shown in Fig. 6), it can be com-

pared to the one obtained during training.

2.5 Generalized Recognition and

Generation

The network has substantial generalization potential.

Not only previously stored sequences can be recon-

structed and recognized. But, (time) sequences apart

from the stored patterns can be generated. Since only

the PB values but not the synaptic weights are updated

in recogniton mode, a stable PB value can also be as-

signed to an unknown sequence.

For instance, training the network with two sine

waves of different frequencies allows to generate

cyclic functions with intermediate frequencies sim-

ply by operating the network in generation mode and

varying the PB values within the interval of the PB

values obtained during training. Furthermore, the PB

values obtained during recognition of a previously

unseen sine function with an intermediate frequency,

w. r. t. the training sequences, will lie within the range

of the PB values acquired during learning. Hence, the

network is able to capture a reciprocal relationship be-

tween a time series and its associated PB value.

ICAART 2012 - International Conference on Agents and Artificial Intelligence

2.6 Network Parameters

Based on systematic empirical trials, the following

parameters have been determined for our experi-

ments. The network contained two input and two out-

put nodes, 24 hidden and 24 context neurons as well

as 2 PB units (cf. section 2.2). The convergence crite-

rion for BPTT was set to 10

−6

in the ﬁrst, and 10

−5

the second experiment. For recognition of a sequence

the update rate γ of the PB values was set to 0.1.

The values for all other individual adaptive learning

rates (Eq. 5) during training of the synaptic weights

were allowed to be in the range of η

min

= 10

−12

and

max

= 50; depending on the gradient they were ei-

ther increased with ξ

= 1.01 or decreased by a factor

−

= 0.9.

3 SCENARIO

The humanoid robot Nao from Aldebaran Robotics

(http://www.aldebaran-robotics.com/) is pro-

grammed to conduct the experiments (Fig. 2a). The

task for the robot is to identify what object (toy brick)

it holds in its hand. In total there are eight object cat-

egories that have to be distinguished by the robot: the

toy bricks have four different shapes (circular-, star-

, rectangular- and triangular-shaped), which exist in

two different weight versions (light and heavy) each.

Hence, for achieving a successful classiﬁcation multi-

modal sensory impressions are required. Addition-

ally, active perception is necessary to induce sensory

changes essential for discrimination of, depending on

the perspective, similar looking shapes, e. g. star- and

circular-shaped objects. For this purpose, the robot

performs a predeﬁned motor sequence and simultane-

ously acquires visual and proprioceptive sensor val-

ues.

3.1 Data Acquisition

The recorded time series comprises 14 sensor values

for each modality. In each single trial the robot turns

its wrist with the object between its ﬁngers by 45.8

◦

back-and-forth twice, followed by lifting the object

up-and-down three times (thereby altering the pitch

of the shoulder joint by 11.5

◦

) and ﬁnally, turning it

again twice.

After an action has been completed the raw im-

age of the lower camera of the Nao robot is cap-

tured, whereas the electric current of the shoulder

pitch servo motor is recorded constantly (sampling

frequency 10 hz) over the entire movement interval.

For each object category 10 single trial time series are

Figure 2: Scenario. a) Toy bricks in front of the humanoid

robot Nao. The toy bricks exist in four different shapes,

have an identical color and are either light-weight (15 g)

or heavy (50 g). This results in a total of eight categories

that have to be distinguished by the robot. b) Rotation

movement with the star-shaped object captured by the robot

camera. In the upper row the raw camera image is shown,

whereas the bottom row depicts the preprocessed image that

is used to compute the visual feature.

recorded in the described way and processed in real-

time. This yields 80 bi-modal time series in total.

3.2 Data Processing

For the proprioceptive measurements only the mean

values are computed for the time intervals lying in-

between movements. The visual processing, on the

other hand, involves several steps (Fig. 2b), which

are accomplished by using OpenCV (Bradski, 2000).

First, the raw color image is converted to a binary im-

age using a color threshold. Next, the convex hull is

computed and, based on that, the contour belonging

to the toy brick is extracted (Suzuki and Be, 1985).

For the identiﬁed contour the ﬁrst Hu moment h

calculated (Hu, 1962) by combining the normalized

central moments η

linearly.

p+q

, (8)

= η

+ η

. (9)

As a particular feature the Hu moments are scale,

translation and rotation invariant. Finally, the vi-

sual measurements are scaled to be in the interval

[−0.5, 0.5].

We are aware that more discriminative geometri-

cal features exist, e. g. orthogonal variant moments

(Mart

ın H. et al., 2010). However, we deliberately

posed the problem this way to make it a challenging

task and show the potential of the approach.

3.3 Training and Test Data

For testing, the data of single trials is used, i. e. 10

2-D time series per object category (one dimension

WHAT DO OBJECTS FEEL LIKE? - Active Perception for a Humanoid Robot

Figure 3: Training data. The mean values of the two

weight conditions (light and heavy, top) and the four vi-

sual conditions (matching symbols, bottom) are shown.

These mean time series are used as prototypes for training

of the RNNPB. Gray shaded area represents the up-and-

down movement, whereas back-and-forth movements are

unshaded. The red area surrounding the signals delineates

two standard deviations from the mean.

for each modality). However, for training a proto-

type for each object category and modality is deter-

mined (Fig. 3). To obtain this subclass representative,

the mean value of pooled single trials, with regard to

identical object properties, is computed. This means

that for instance all circular-shaped objects are com-

bined (n = 20) and used to compute the visual pro-

totype for circular-shaped objects. To ﬁnd the pro-

prioceptive prototype for e. g. all heavy objects, all

individual measurements with this property (n = 40)

are aggregated and used to calculate the mean value

at each time step. The subclass prototypes are then

combined to form a 2-D multi-modal time series that

serves as an input for the recurrent neural network

during training.

4 RESULTS

4.1 Experiment 1 – Classiﬁcation using

All Object Categories for Training

Three experiments have been conducted. In the ﬁrst

Figure 4: Experiment 1 – Classiﬁcation using all object

categories for training. PB values of the class prototypes

used for training are depicted in light and dark gray and

with a symbol matching the corresponding shape. Smaller

symbols depict PB values obtained during testing with bi-

modal single trial data. If the objects have been correctly

classiﬁed they are shown in light or dark blue, otherwise in

red. Light colors are used for light-weight, dark colors for

heavy-weight objects.

experiment the improved recurrent neural network

with parametric bias is trained with the bi-modal pro-

totype time series of all eight object categories (see

Fig. 3 and section 3.3). During training, the PB val-

ues for the respective categories emerge in an unsu-

pervised way. This means, the two-dimensional PB

space is self-organized based on the inherent proper-

ties of the sensory data that is presented to the net-

work. Hence, objects with similar dynamic sensory

properties are clustered together. This can be seen

in Fig. 4. For instance, the learned PB vectors repre-

senting star- and circular-shaped objects, either light-

weight (light gray) or heavy (dark gray), are located in

close proximity, whereas the PB values coding for the

triangular-shaped objects are positioned more distant.

This is due to the deviating visual sensory impression

they generate (Fig. 3). The experiment has been re-

peated several times with different random initializa-

tions of the network weights. However, the obtained

PB values of the different classes always demonstrate

a comparable geometric relation with respect to each

other.

To demonstrate the retrieval properties (section

2.3) of the fully trained architecture the PB values ac-

quired during training are ’clamped’ to the network.

Operating the network in closed-loop shows that the

input sequences used for training can be retrieved

with a very high accuracy. This is as an example

shown in Fig. 5 (left) for the heavy star-shaped object.

The steps needed until stable PB values are

reached, which in turn can be used for recognition, are

ICAART 2012 - International Conference on Agents and Artificial Intelligence

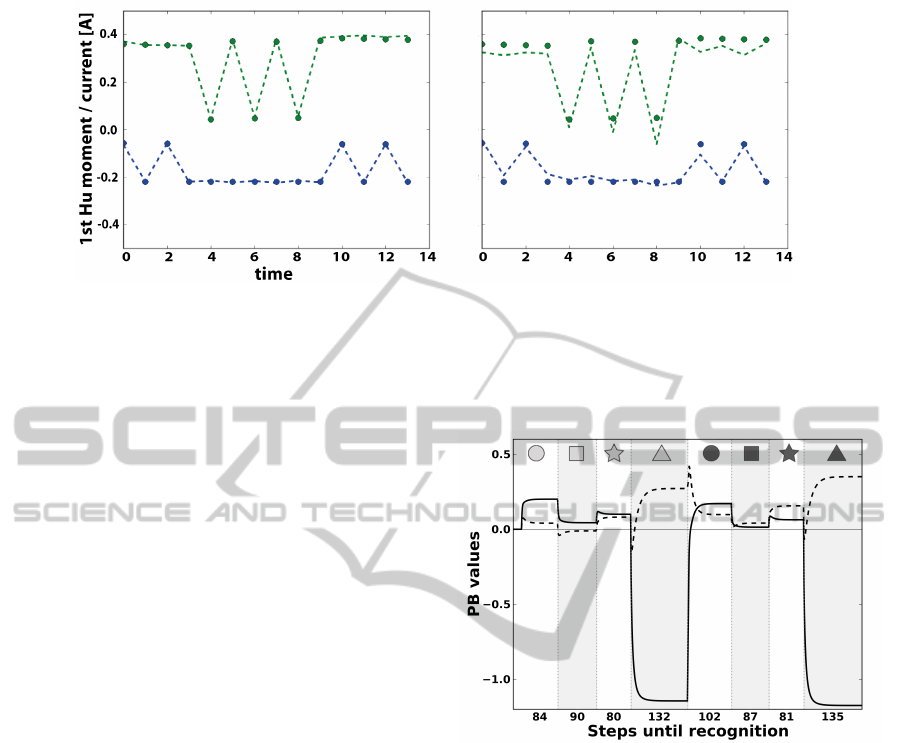
Figure 5: Retrieval and generation capabilities. Proprioceptive (green) and visual (blue) dots represent the sampling points

of the heavy star-shaped prototype time series (Fig. 3). Dashed lines are the time series generated by the network operated in

closed-loop with ’clamped’ PB values as the only input. The PB values have been acquired unsupervised either during full

training (left) or partial training (right). During partial training (right) the network has only been trained with the prototype

sequences for the light-weight circle and the heavy triangle. Still, the network is able to generate a fairly accurate sensory

prediction for the (untrained) heavy star-shaped object.

illustrated in Fig. 6. The bi-modal sensory sequences

for all light-weight and heavy objects are fed consec-

utively into the network. On average it takes less than

100 steps (about 200 ms) until the PB values have con-

verged. The convergence criterion is set to 20 consec-

utive iterations where the cumulative change of both

PB values is < 10

−5

. To assure that the PB values

reached a stable state, this number was successfully

increased to 100.000 consecutive steps in preliminary

experiments (not shown). Note, that the network and

PB values are not re-initialized when the next sensory

sequence is presented to the network. Thus, the robot

can continuously interact with the toy bricks and is

able to immediately recognize an object based on its

sensorimotor sequence.

For testing, the network is operated in general-

ized recognition mode (section 2.5). Single trial bi-

modal sensory sequences are presented to the network

that in turn provides an ’identifying’ PB value. The

class membership, i. e. which object the robot holds

in its hand and how heavy this object is, is then deter-

mined based on the minimal Euclidean distance to the

PB values of the class prototypes (gray symbols). In

Fig. 4 the PB values of all 80 single trial test patterns

are depicted.

Only 4 out of 80 objects are misclassiﬁed (shown

in red), yielding an error rate of 5 %. Interestingly,

only star- and circular-shaped objects are confused by

the network, which indeed generate very similar sen-

sory impressions (Fig. 3). To assess the meaning of

the error rate and estimate how challenging the posed

problem is, we evaluate the data with two other com-

monly used techniques in machine learning. First, we

train a multi-layer perceptron (28 input, 14 hidden and

one output unit) with the prototype sequences. Test-

ing with the single trial data results in an error rate

Figure 6: Steps until stable PB values are reached. Bi-

modal sensory sequences for all light-weight and heavy ob-

jects (represented by matching symbols in light and dark

gray, respectively) are consecutively fed into the network.

The time courses of PB value 1 (solid line) and PB value 2

(dashed line) during the recognition process are plotted.

of 46.8 %, reﬂecting weaker generalization capabili-

ties of the non-recurrent architecture. Next, we train

and evaluate our data with a support vector classi-

ﬁer (SVC) using default parameters (Chang and Lin,

2011). In contrast, this method is able to classify the

data perfectly.

4.2 Experiment 2 – Classiﬁcation using

Only the Light Circular-shaped and

the Heavy Triangular-shaped

Object for Training

In experiment 2 only the bi-modal prototypes for the

light circular- and heavy triangular-shaped objects are

used to train the RNNPB. Although, the absolute PB

WHAT DO OBJECTS FEEL LIKE? - Active Perception for a Humanoid Robot

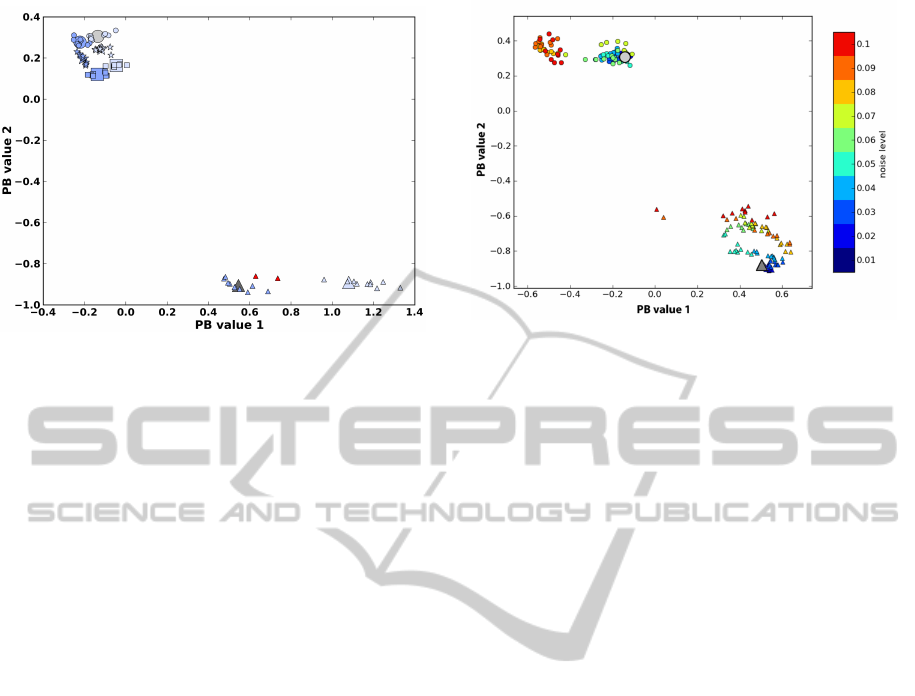
Figure 7: Experiment 2 – Classiﬁcation using only the

light circular-shaped and the heavy triangular-shaped

object for training. PB values of the class prototypes used

for training are depicted in light and dark gray and with a

symbol matching the corresponding shape. The a posteri-

ori computed cluster centers of the untrained object cate-

gories are depicted using larger symbols in either light or

dark blue. Smaller symbols are used for PB values of sen-

sory data of single trials. If the objects have been correctly

classiﬁed they are shown in light or dark blue, otherwise in

red. Light colors are used for light-weight, dark colors for

heavy-weight objects.

values obtained during training differ from the ones

being determined in the previous experiment, their

relative Euclidean distance in PB space is nearly the

same (1.39 vs. 1.35), stressing the data-driven self-

organization of the parametric bias space.

For testing, initially only the bi-modal sensory

time series matching the two training conditions are

fed into the network, thereby determining their PB

values. Using the Euclidean distance subsequently to

obtain the class membership results in a ﬂawless iden-

tiﬁcation of the two categories.

Further evaluation of the single trial test data is

performed in two stages. In a primary step the remain-

ing test data is presented to the network and the re-

spective PB values are computed (generalized recog-

nition, section 2.5). Despite not having been trained

with prototypes for these six object categories, the

network is able to clusters PB values stemming from

similar sensory situations, i. e. identical object cate-

gories. In a succeeding step we compute the centroid

for each class (mean PB value) and classify again

based on the Euclidean distance. This time only two

single trial time series are misclassiﬁed by the net-

work (error rate 2.5 %). The results are shown in

Fig. 7.

The generalization potential (section 2.5) of the

architecture is presented in Fig. 5 (right) for the heavy

star-shaped object. For this purpose, the mean PB val-

ues (centroid of the respective class) are clamped to

Figure 8: Uni-modal noise tolerance. Uniformly dis-

tributed noise of increasing levels (color coded) is only

added to the visual prototype time series for the light-weight

circle and the heavy triangle. The PB values are determined

and marked with a matching symbol.The light gray circle

and dark gray triangle show the PB values obtained during

training without noise.

the network, which is operated in closed-loop mode.

The network has only been trained with the light

circular- and the heavy triangular-shaped object. Still,

it is possible to generate sensory predictions for un-

seen objects, e. g. the heavy star-shaped toy brick, that

match fairly well the real sensory impressions.

4.3 Experiment 3 – Noise Tolerance

within and Across Modalities

Based on the network weights that have been ob-

tained in experiment 2 (training the RNNPB only

with the bi-modal prototypes for the light circular-

and heavy triangular-shaped objects), we evaluate the

noise tolerance of the recurrent neural architecture.

For this purpose, uniformly distributed noise of in-

creasing levels is either added to the visual prototype

time series only (Fig. 8) or to the time series of both

modalities (Fig. 9).

As it can be seen for both conditions, even high

levels of noise allow for a reliable linear discrimina-

tion of the two classes. Furthermore, the PB values

of increasing noise levels show commonalities and

are clustered together, again providing evidence for

a data-driven self-organization of the PB space. Thus,

determining the Euclidean distance of the PB values

obtained from the noisy signals to the class represen-

tatives enables not only to determine the class mem-

bership, it also allows to estimate the noise level with

respect to the prototypical sensory impression.

ICAART 2012 - International Conference on Agents and Artificial Intelligence

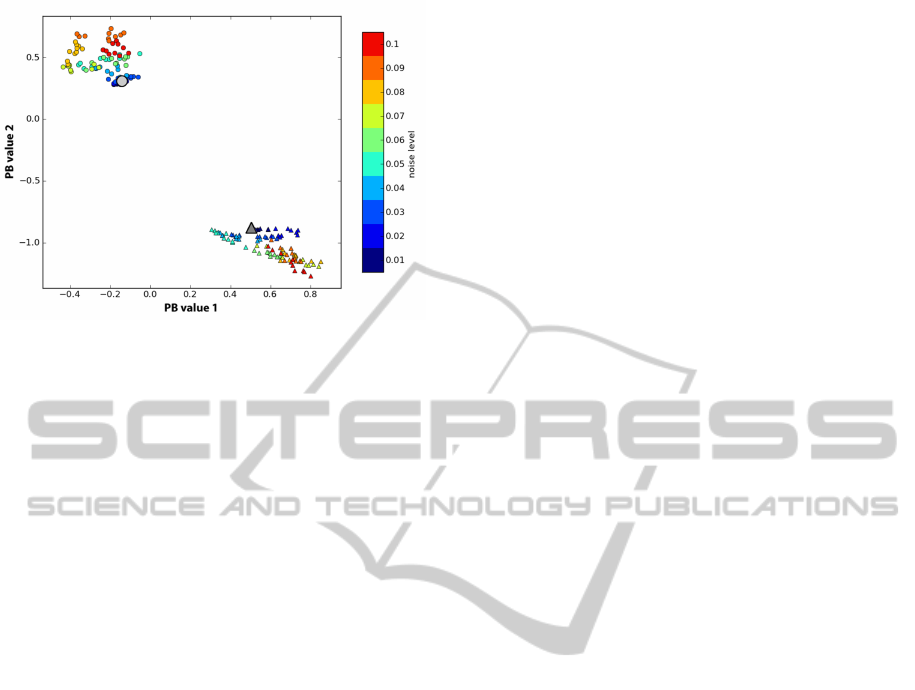
Figure 9: Bi-modal noise tolerance. Uniformly distributed

noise of increasing levels (color coded) is added to both (vi-

sual and proprioceptive) prototype time series for the light-

weight circle and the heavy triangle. The PB values are

determined and marked with a matching symbol. The light

gray circle and dark gray triangle show the PB values ob-

tained during training without noise.

5 DISCUSSION

We present a robust model with low error rates for

object classiﬁcation on a real humanoid robot. How-

ever, our primary goal is not to compete with other

approaches used for object classiﬁcation. Instead,

our intention is to provide a neuroscientiﬁcally and

philosophically inspired model for what do objects

feel like? For this purpose, we stress the active na-

ture of perception within and across modalities. Ac-

cording to the theory of sensorimotor contingencies

(SMCs), proposed by O’Regan and No

e, actions are

fundamental for perception and help to distinguish the

qualities of sensory experiences in different sensory

channels, e. g. ’seeing’ or ’touching’ (O’Regan and

e, 2001). It is suggested that “seeing is a way of

acting”. Exactly this is mimicked in our experiments.

A motor sequence induces multi-modal sensory

changes. During learning these high-dimensional per-

ceptions are ’engraved’ in the network. Simultane-

ously, low-dimensional PB values emerge unsuper-

vised, coding for a sensorimotor sequence character-

izing the interplay of the robot with an object. We

show that 2-D time series of length T = 14 can be reli-

ably represented by a 2-D PB vector and that this vec-

tor allows to recall learned sensory sequences with a

high accuracy (Fig. 5 left). Furthermore, the geomet-

rical relation of PB vectors of different objects can

be used to infer relations between the original high

dimensional time series, e. g. the sensation of a star-

shaped object ’feels’ more like a circular-shaped ob-

ject than a triangular-shaped one. Due to the exper-

imental noise of single trials, identical objects cause

varying sensory impressions. Still, the RNNPB can

be used to recognize those (Fig. 4). Additionally, sen-

sations belonging to unknown objects can be discrim-

inated from known (learned) ones. Moreover, sensa-

tions arising from different unknown objects can be

kept apart from each other reliably (Fig. 7).

Humans are able to immediately divide the per-

ceived world into different physical objects, seem-

ingly without effort, even when they are confronted

with previously unseen objects. Indeed, it makes per-

fect sense that the discrimination between different

sensory qualia is possible without training (section

4.2). However, actively generating (retrieving) sen-

sorimotor experiences does require training and gen-

eralization capabilities. Similar ﬁndings have been re-

ported recently for humans (Held et al., 2011). Pre-

viously blind subjects, regaining sight after a surgical

procedure, were able to visually discriminate different

objects right away. Cross-modal mappings between

seen and felt, however, had to be learned.

Comparing the classiﬁcation results of the fully

trained RNNPB with the SVC reveals a superior per-

formance of the support vector classiﬁer. Neverthe-

less, it has to be kept in mind that the maximum mar-

gin classiﬁer cannot be used to generate or retrieve

time series. Interestingly, the error rate is lower if the

recurrent network is only trained with two object cate-

gories (section 4.2). A potential explanation, besides

random ﬂuctuations, could be that during training a

common set of weights has to be found for all object

categories. This process presumably interferes, due to

the challenging input data, with the self-organization

of the PB space.

A drawback of the presented model is that it

currently operates on a ﬁxed motor sequence. It

would be desirable if the robot performs motor bab-

bling (Olsson et al., 2006) leading not only to a

self-organization of the sensory space, but to a self-

organization of the sensorimotor space. A simple so-

lution to this problem would be to train the network

additionally with the motor sequence most appropri-

ate for an object, i. e. reﬂecting its affordance (Gibson,

1977). This would lead to an even better classiﬁca-

tion result, because the motor sequences themselves

would help to distinguish the objects from each other

and thus the emerging PB values would be arranged

further apart in PB space. Conversely, this means cur-

rently it does not make sense to train the network with

the identical motor sequences in addition. However,

that does not address that the robot should identify the

object affordances, the movements characterizing an

object, by itself. Further lines of research will specif-

ically address this issue.

WHAT DO OBJECTS FEEL LIKE? - Active Perception for a Humanoid Robot

In related research, Ogata et al. also extract multi-

modal dynamic features of objects, while a humanoid

robot interacts with them (Ogata et al., 2005). How-

ever, there are distinct differences. Despite using

fewer objects in total, the problem posed in our ex-

periments is considerably harder. Our toy bricks have

approximately the same circumference and identical

color. Furthermore, they exist in two weight classes

with an identical in-class weight that can only be dis-

criminated via multi-modal sensory information. We

provide classiﬁcation results, compare the results to

other methods (MLP and SVC) and evaluate the noise

tolerance of the architecture. In addition, we only use

prototype time series for training (in contrast to using

all single trial time series) resulting in a reduced train-

ing time. Further, we demonstrate that, if the network

has already learned sensorimotor laws of certain ob-

jects, it is able to generalize and provide fairly accu-

rate sensory predictions for unseen ones (Fig. 5 right).

In conclusion, we present a promising framework

for object classiﬁcation based on active perception on

a humanoid robot, rooted in neuroscientiﬁc and philo-

sophical hypotheses.

5.1 Future Work

There are several potential applications of the pre-

sented model. As shown in Fig. 8 and 9 the network

tolerates noise very well. This fact can be used for

sensor de-noising. Despite receiving a noisy sensory

signal, the robot will still be able to determine the PB

values of the class representative based on the Eu-

clidean distance. In turn, these values can be used

to operate the RNNPB in retrieval mode (section 2.3)

generating the noise-free sensory signal previously

stored, which then can be processed further. It is also

conceivable, that the network is used for sensory (sen-

sorimotor) imagery. Due to the powerful generaliza-

tion capabilities of the network not only the trained

sensory perceptions can be recalled, but interpolated

’feelings’ can be generated (Fig. 5 right).

ACKNOWLEDGEMENTS

This work was supported by the Sino-German Re-

search Training Group CINACS, DFG GRK 1247/1

and 1247/2, and by the EU projects KSERA under

2010-248085. We thank R. Cuijpers and C. Weber

for inspiring and very helpful discussions, S. Hein-

rich, D. Jessen and N. Navarro for assistance with the

robot.

REFERENCES

Aloimonos, J., Weiss, I., and Bandyopadhyay, A. (1988).

Active vision. International Journal of Computer Vi-

sion, 1:333–356.

Bajcsy, R. (1988). Active perception. Proceedings of the

IEEE, 76(8):966 –1005.

Ballard, D. H. (1991). Animate vision. Artiﬁcial Intelli-

gence, 48(1):57–86.

Bradski, G. (2000). The OpenCV Library. Dr. Dobb’s Jour-

nal of Software Tools.

Bridgeman, B. and Tseng, P. (2011). Embodied cogni-

tion and the perception-action link. Phys Life Rev,

8(1):73–85.

Burt, P. (1988). Smart sensing within a pyramid vision ma-

chine. Proceedings of the IEEE, 76(8):1006 –1015.

Chang, C.-C. and Lin, C.-J. (2011). LIBSVM: A library

for support vector machines. ACM Transactions on

Intelligent Systems and Technology, 2:27:1–27:27.

Cuijpers, R. H., Stuijt, F., and Sprinkhuizen-Kuyper, I. G.

(2009). Generalisation of action sequences in RN-

NPB networks with mirror properties. In Proceedings

of the 17th European symposium on Artiﬁcal Neural

Networks (ESANN), pages 251–256.

Dewey, J. (1896). The reﬂex arc concept in psychology.

Psychological Review, 3:357–370.

Fitzpatrick, P. and Metta, G. (2003). Grounding vision

through experimental manipulation. Philosophical

Transactions of the Royal Society of London. Series

A: Mathematical, Physical and Engineering Sciences,

361(1811):2165–2185.

Gibson, J. J. (1977). The theory of affordances. In Shaw,

R. and Bransford, J., editors, Perceiving, acting, and

knowing: Toward an ecological psychology, pages

67–82. Hillsdale, NJ: Erlbaum.

Held, R., Ostrovsky, Y., Degelder, B., Gandhi, T., Ganesh,

S., Mathur, U., and Sinha, P. (2011). The newly

sighted fail to match seen with felt. Nat Neurosci,

14(5):551–3.

Hu, M.-K. (1962). Visual pattern recognition by moment

invariants. Information Theory, IRE Transactions on,

8(2):179 –187.

Kolen, J. F. and Kremer, S. C. (2001). A ﬁeld guide to dy-

namical recurrent networks. IEEE Press, New York.

LeCun, Y., Bottou, L., Orr, G., and M

uller, K. (1998). Ef-

ﬁcient backprop. Lecture Notes in Computer Science,

1524:5–50.

Mart

ın H., J. A., Santos, M., and de Lope, J. (2010). Or-

thogonal variant moments features in image analysis.

Inf. Sci., 180:846–860.

Merleau-Ponty, M. (1963). The structure of behavior. Bea-

con Press, Boston.

Ogata, T., Ohba, H., Tani, J., Komatani, K., and Okuno,

H. G. (2005). Extracting multi-modal dynamics of ob-

jects using RNNPB. Proc. IEEE/RSJ Int. Conf. on In-

telligent Robots and Systems, Edmonton, pages 160–

165.

Olsson, L. A., Nehaniv, C. L., and Polani, D. (2006). From

unknown sensors and actuators to actions grounded

in sensorimotor perceptions. Connection Science,

18(2):121–144.

ICAART 2012 - International Conference on Agents and Artificial Intelligence

O’Regan, J. K. and No

e, A. (2001). A sensorimotor account

of vision and visual consciousness. Behav Brain Sci,

24(5):939–73; discussion 973–1031.

Patel, K., Macklem, W., Thrun, S., and Montemerlo, M.

(2005). Active sensing for high-speed offroad driv-

ing. In Robotics and Automation, 2005. ICRA 2005.

Proceedings of the 2005 IEEE International Confer-

ence on, pages 3162 – 3168.

Pfeifer, R., Lungarella, M., and Iida, F. (2007). Self-

organization, embodiment, and biologically inspired

robotics. Science, 318(5853):1088–93.

Rasolzadeh, B., Bj

orkman, M., Huebner, K., and Kragic, D.

(2009). An active vision system for detecting, ﬁxating

and manipulating objects in real world. The Interna-

tional Journal of Robotics Research.

Riedmiller, M. and Braun, H. (1993). A direct adap-

tive method for faster backpropagation learning: the

RPROP algorithm. In Neural Networks, 1993., IEEE

International Conference on, pages 586 –591 vol.1.

Suzuki, S. and Be, K. (1985). Topological structural anal-

ysis of digitized binary images by border following.

Computer Vision, Graphics, and Image Processing,

30(1):32–46.

Tani, J. and Ito, M. (2003). Self-organization of behavioral

primitives as multiple attractor dynamics: A robot ex-

periment. Systems, Man and Cybernetics, Part A: Sys-

tems and Humans, IEEE Transactions on, 33(4):481 –

488.

Tani, J., Ito, M., and Sugita, Y. (2004). Self-organization of

distributedly represented multiple behavior schemata

in a mirror system: reviews of robot experiments using

rnnpb. Neural Netw, 17(8-9):1273–89.

Varela, F. J., Thompson, E., and Rosch, E. (1991). The

embodied mind: cognitive science and human experi-

ence. MIT Press, Cambridge, Mass.

WHAT DO OBJECTS FEEL LIKE? - Active Perception for a Humanoid Robot