EMOTION AS AN ENABLER OF CO-OPERATION

Martyn Lloyd-Kelly, Katie Atkinson and Trevor Bench-Capon

Department of Computer Science, The University of Liverpool, Ashton Street, Liverpool, U.K.

Keywords:

Emotion, Multi-agent systems, Agent models and architectures, Simulation.

Abstract:

We investigate the emergence of co-operation through emotions. We use agents playing an iterated Prisoner’s

Dilemma game, and show how the emotions of gratitude and anger enable co-operation to emerge as a re-

sponse to the emotional state of the agents without reference to payoffs or history. We investigate the effect of

different thresholds for these emotions to change behaviour on individual performance and system scores.

1 INTRODUCTION

The interplay and differences between rationality and

emotion has long been the subject of philosophi-

cal and psychological debates. Emotions appear

to be particularly signiﬁcant as determinants of be-

haviour in co-operative relationships (Fessler and Ha-

ley, 2003). We take the view that emotions play a

functional role, following (Frijda, 1987).

Our contribution therefore is to model emotions so

that they are able to play a functional and beneﬁcial

role in allowing agents to determine how to respond to

information received from the environment. We use

agents playing an iterated Prisoners’ Dilemma game

(Axelrod, 1984), and show how the emotions of grat-

itude and anger enable co-operation to emerge as a

response to the emotional state of the agents without

reference to payoffs or history. Please see (Lloyd-

Kelly et al., 2011) for an in-depth discussion of the

work that follows.

The concept of emotion is hotly contested and no

real consensual deﬁnition has been found. The idea

that an emotion is characterised by a collection of

physiological responses is noted as early as (James,

1884) but other psychologists such as (Baumeister

et al., 2009) take the view that emotions are functional

in that they provide motivations for future behaviour

and can act as evaluative tools to explain behaviour

that is exhibited in certain situations. We adopt the

functional view, and although we recognise that phys-

iological factors are important, we do not consider

this aspect here.

A logic of individual emotions for agents has been

developed by Steunebrink et al. (e.g (Steunebrink

et al., 2007)). They take small subsets of the 22 emo-

tions deﬁned in the Ortony, Clore and Collins model

(the OCC model (Ortony et al., 1988)) and adopt a

functional view of emotions by prescribing actions

that follow after an emotion has been elicited. We

adopt the idea of implementing small subsets of emo-

tions from this much larger set as it allows a concen-

tration of effort with respect to the emotions chosen,

faithful modelling of these emotions and recognition

that different emotions may have different functional

roles. The OCC is a framework of emotions that

serves as one of the standard psychological frame-

works that is well adapted for use in computer sci-

ence. The applicability of the OCC from a computer-

science standpoint and its extensive use by others is

the primary reason that we chose to use the model.

Our work furthers the functional use of emotions

as behavioural mediators and takes inspiration from

Axelrod’s Prisoner’s Dilemma tournament. One of

the general rules Axelrod suggested for constructing

a successful strategy i.e. one that maximises the indi-

vidual’s score and the total score of the system, states

that strategies should not be overly complex; in some

cases in his tournament, strategies were so elaborate

that they might as well have been acting randomly. It

is this rule that allows us to distinguish between our

emotional agent and a rational agent. Axelrod’s tour-

nament contains rational agents that determine their

behaviour on the basis of past, present and future pay-

offs; in contrast, our emotional agent has no concept

of payoffs, it is a simple reactive agent inspired by

the notions outlined in (Brooks, 1991). Essentially,

the emotional agent’s behaviour is a product of its

emotional character and its current emotional state

with the layer of rationality associated with consider-

ation of past and future payoffs stripped away. This

concept of a continuously updated current emotional

state is what motivates the design of a novel agent

164

Lloyd-Kelly M., Atkinson K. and Bench-Capon T..

EMOTION AS AN ENABLER OF CO-OPERATION.

DOI: 10.5220/0003730101640169

In Proceedings of the 4th International Conference on Agents and Artiﬁcial Intelligence (ICAART-2012), pages 164-169

ISBN: 978-989-8425-96-6

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

architecture since other architectures suggest actions

to perform in the present by consulting emotional re-

sponses to the outcomes of actions performed in the

past, when faced with the same situation again.

While rational, self-interested agents can enable

co-operation, (Frank, 1988) argues that such be-

haviour can be self-defeating and emotional individ-

uals are much more likely to establish and main-

tain co-operation. The importance of gratitude in co-

operation is explained by (Berg et al., 1995) who il-

lustrates that altruistic ﬁnancial loss to an individual

can be tolerated if the other party offers gratitude for

this action. Also, (Fehr and G

achter, 2002) shows that

altruistic punishment resulting from anger is essen-

tial in order for co-operation to ﬂourish. It is impor-

tant to note here that the rate at which anger/gratitude

is elicited may vary and so we introduce the idea of

emotional characters (described in detail in section

2) in order to take into account these various rates.

Consequently, we have chosen to focus our efforts on

implementing gratitude and anger and we investigate

how these emotions can inﬂuence the total score of

the system.

2 EXPERIMENTS

The experiments we ran were a set of iterated Pris-

oners’ Dilemma games played as a tournament as in

(Axelrod, 1984). This was realised in the Tileworld

environment (Pollack and Ringuette, 1990). Tile-

world was used because further experiments will ex-

ploit more features of the environment as we move to

consider populations of agents. Emotional agents are

initially defectors (liars) or co-operators (truth-tellers)

and were given two emotions: gratitude and anger. If

the other player co-operates, gratitude is experienced,

and if it defects, anger is experienced. Agents have

different characters corresponding to how intense an

emotion must be before it changes behaviour. Agents

can thus vary in tolerance (the number of defections

required to make anger sufﬁcient to move from co-

operation to defection) and responsiveness (the num-

ber of co-operations required to make gratitude suf-

ﬁcient to give rise to co-operation). Thus, there are

nine possible characters, as shown in table 1.

Payoffs were as standard for the Prisoner’s

Dilemma: dual co-operation rewards both players

with 3 points, dual defection earns 1 point for each

player and asymmetric co-operation/defection earns

the defector 5 points and the co-operator 0 points.

These payoffs are assigned to agents by a mediation

agent. Every round comprised 200 games, although

this was not known to the agents to avoid exploitation

Table 1: Emotional agent character (ch.#) descriptions.

If defecting,

#co-ops required to

co-op.

1 2 3

If co-op,

#defects

required

to defect.

1 Ch.1 Ch.2 Ch.3

2 Ch.4 Ch.5 Ch.6

3 Ch.7 Ch.8 Ch.9

of this information.

The agents used were: an emotional agent; a tit-

for-tat agent (which co-operates on the ﬁrst round

and then repeats the opponent’s previous move, the

most successful strategy in Axelrod’s tournament); a

mendacious agent, which always defects; a veracious

agent, which always co-operates; a random agent,

which co-operates or defects with equal probability;

a joss agent, which plays tit for tat, but with a 10%

probability of random defection; and a tester agent,

which defects on the ﬁrst round n, if the opponent co-

operated on round n then the agent co-operates up to

round n + 2 and defects on round n + 3. If, the oppo-

nent defects on round n, the agent plays tit-for-tat for

the rest of the game. The emotional agent began play

ﬁrst as a co-operator then as a defector for each of the

nine characters in turn.

We wished to explore which emotional characters

would replicate the behaviour of the tit-for-tat strat-

egy (to prove if emotional response can replicate ra-

tionality) and which emotional characters would be

most conducive to success. Success would be con-

sidered both from the perspective of individual agents

and from the perspective of the system as a whole.

3 RESULTS AND DISCUSSION

With respect to the question of whether the tit-for-

tat strategy can be replicated by emotional response,

the results obtained from the Tileworld Dilemma are

clear-cut. An initially co-operative emotional agent

with character 1 replicates the behaviour of the ratio-

nal tit-for-tat agent exactly. To demonstrate this, we

present tables 2 and 3, which contain the average in-

dividual scores of the initially co-operative emotional

agent with character 1 and the tit-for-tat agent ver-

sus the random and joss agents respectively. We have

chosen to only present the results from playing these

two agents as the behaviour of the random and joss

agents is non-deterministic whilst the behaviour of ev-

ery other agent in the simulation is completely deter-

ministic. Therefore, playing against these two agent

EMOTION AS AN ENABLER OF CO-OPERATION

165

types gives the greatest potential for disparateness to

exist between the scores of the emotional agent and

tit-for-tat agent. Consequently, by presenting these

two graphs as evidence we can assert that the be-

haviour of the tit-for-tat agent is exactly replicated by

the emotional agent with the set-up described.

Table 2: Individual scores of intially co-operative emotional

agent with character 1/tit-for-tat agent vs. random agent.

Game Number

Agent 1 2 3 4 5

Emotional 462 466 448 445 424

Tit-for-tat 462 466 448 445 424

Table 3: Individual scores of intially co-operative emotional

agent with character 1/tit-for-tat agent vs. joss agent.

Game Number

Agent 1 2 3 4 5

Emotional 219 213 213 255 242

Tit-for-tat 219 213 213 255 242

As can be seen in tables 2 and 3, the scores of

the emotional agent and tit-for-tat agent exactly over-

lap showing that their behaviour is undisputedly the

same. Explanation of these results is elementary:

whereas the tit-for-tat agent responds to its payoffs,

the emotional agent responds to information sent to

it (as detailed in section 1). Therefore, both agents

react in exactly the same way to inputs that are of dif-

ferent types but which will arise from the same sit-

uations. To clarify, if the tit-for-tat agent observes

that it has scored 0 in a round when it is currently co-

operating or 1 if is it defecting, then it can safely infer

that the opponent is defecting, therefore its behaviour

will switch to defection. Similarly, if the mediator

informs an emotional agent with character 1 that the

opponent has defected, then the emotional agent will

defect immediately in the next round.

We now address the question of whether any other

emotional character set-up is more successful with

respect to maximising the total system score when

playing against periodically defecting strategies than

the set-up previously discussed. To determine this,

we measure success in terms of total system pay-

off or, more speciﬁcally, the aggregated average to-

tal system score (the sum of all average total system

scores achieved by an emotional agent). As demon-

strated in table 4, we ﬁnd that an initially co-operative

agent with character 7 - the most tolerant and most re-

sponsive - offers the greatest aggregated total average

system score, so a more successful strategy does in-

deed exist. To explain this outcome we have iden-

tiﬁed three criteria, which must be considered and

Table 4: Intially co-operative emotional agent aggregated

average total system scores.

Character

Aggregated

Average Total

System Score

5230.80

5069.80

4979.80

5774.80

5241.80

5140.80

5895.60

5328.80

5235.80

discussed in turn: fairness, responsiveness and toler-

ance.

We deﬁne fairness as the extent to which all mem-

bers of a system are equal; in the context of the Tile-

world Dilemma, the fairest system possible is one

where each agent has an equal score at the end of each

game. Systems that are maximally fair are achieved

by agents who employ strategies that are quick to pun-

ish and reward (as noted by Axelrod). If such a strat-

egy is used by both players and a cycle of defection

is locked into on the ﬁrst round, then each player’s

score at the end of a game will be 200. Whilst this

is individually fair, the ﬁnal system score is relatively

low. For a player who wishes to achieve system fair-

ness and maximise the score of each player then the

best possible score that can be achieved is 600, which

is achieved by players immediately locking into a co-

operation cycle on the ﬁrst round and maintaining this

for a full game. We observe that the only agent pairs

to do this are those that co-operate initially, those that

are quick to punish/defect and those that always co-

operate, no matter what for example:

• Initially co-operative emotional agent with any

character and tit-for-tat agent.

• Initially co-operative emotional agent with any

character and veracious agent.

However, as mentioned above, such behaviour

does not maximise the system’s score when agents

that seek an advantage, such as the random, tester and

joss agents, are also present (see table 4); from the

system’s view, achievement of a good system score

requires two goals to be achieved:

• Co-operation must be established between the

members of the system.

• Co-operation must be maintained between the

members of the system.

ICAART 2012 - International Conference on Agents and Artificial Intelligence

166

Table 5: Comparison of the average total scores of an initially co-operative emotional agent of character 7 and an initially

defective emotional agent of character 7.

Opponent

Ini Dis. Mendacious Veracious Random Tit-for-tat Tester Joss

Co-op 409 1200 1002.8 1200 1111 972.8

Defect 400 1199 1001.8 1198 400 968.6

Table 6: Comparison of the average total scores for intially co-operative emotional agents with characters 7, 8 and 9.

Opponent

Character Mendacious Veracious Random Tit-for-tat Tester Joss

7 409 1200 1002.8 1200 1111 972.8

8 409 1200 942 1200 1089 488.8

9 409 1200 902 1200 1036 488.8

The score of a system is increased if agents lock

into cycles of co-operation quickly and break them

slowly. Therefore, readiness to co-operate (respon-

siveness) and being slow to defection (tolerance) are

both important factors. If we compare the average to-

tal scores for an initially co-operative emotional agent

of character 7 to an initially lying emotional agent of

character 7 (see table 5) then the effect of being re-

sponsive becomes clear.

If an agent initially defects, co-operation cycle es-

tablishment is delayed, resulting in lower total system

scores as it becomes more likely that the players will

establish cycles of defection. Conversely, the quicker

an agent is to co-operate and forgive its opponent, the

quicker a co-operation cycle is established. There-

fore, by co-operating initially an agent is more likely

to ﬁnd concurrent co-operation in a round and estab-

lish a co-operation cycle early in the game which is

important as the number of rounds in a game is ﬁnite;

table 6 clearly illustrates this point. The same pat-

tern also holds true for initially defective/co-operative

emotional agents with characters 1-3/4-6.

It is not enough to simply establish a cycle of co-

operation; in order to maximise the score of the sys-

tem then the established co-operation cycle must be

maintained, even when the other player temporarily

defects (as self interested agents will tend to do). If

we consider the scores of emotional agents with char-

acters 1, 4 and 7 displayed in table 4, we observe that

as an agent becomes more tolerant to defections, the

greater the aggregated average total system score be-

comes. If we then consider the individual scores that

are aggregated together for the initially co-operative

emotional agent of character 7 (see table 7) we can see

that character 7 sacriﬁces system fairness by taking a

reduced score in order to maximise the total system

score. This phenomenon of tolerance is the crucial

difference between character 7 and characters 1 and

4. Therefore, we can see that increased levels of toler-

ance are integral to maximising the total system score,

if playing against agents that periodically defect.

By being tolerant an agent enables the mainte-

nance of a co-operation cycle. Whilst the fairest sys-

tem possible entails the deployment of a strategy that

is quick to reward and quick to punish, such behaviour

breaks co-operation cycles quickly causing lower to-

tal system scores to be achieved. By one agent con-

tinuing to co-operate in the face of defection the sys-

tem scores ﬁve rather than two, so that when the de-

fector decides to co-operate again and it is met with

co-operation, a total system score of six is achieved.

A drawback to becoming more tolerant however, is

suffering a reduction in the tolerant agent’s individ-

ual score; table 8 illustrates the extent to which this

occurs.

Table 8 offers some interesting results, especially

if we consider those scores that pertain to the emo-

tional agent playing against the random agent. We ob-

serve that the average individual score of each agent

decreases as tolerance to defection increases, yet as

tolerance is increased the rate at which the average

individual score decreases slows; this can also be ob-

served in ﬁgure 1 and table 9. The salient point here

is: when the opponent is not a veracious or tit-for-

tat agent, there is a trade-off between fairness and to-

tal system score. From table 8 we can calculate this

trade-off exactly: for every point earned by the sys-

tem, the emotional agent must lose two points from its

individual score. This raises the question: how much

of a reduction in fairness is acceptable to achieve

these system gains?

It is worth mentioning that the situation is differ-

ent when the initially co-operative emotional agents

with characters 1, 4 and 7 play against a joss agent.

As the emotional agents become more tolerant, the

emotional agent’s average individual score increases

EMOTION AS AN ENABLER OF CO-OPERATION

167

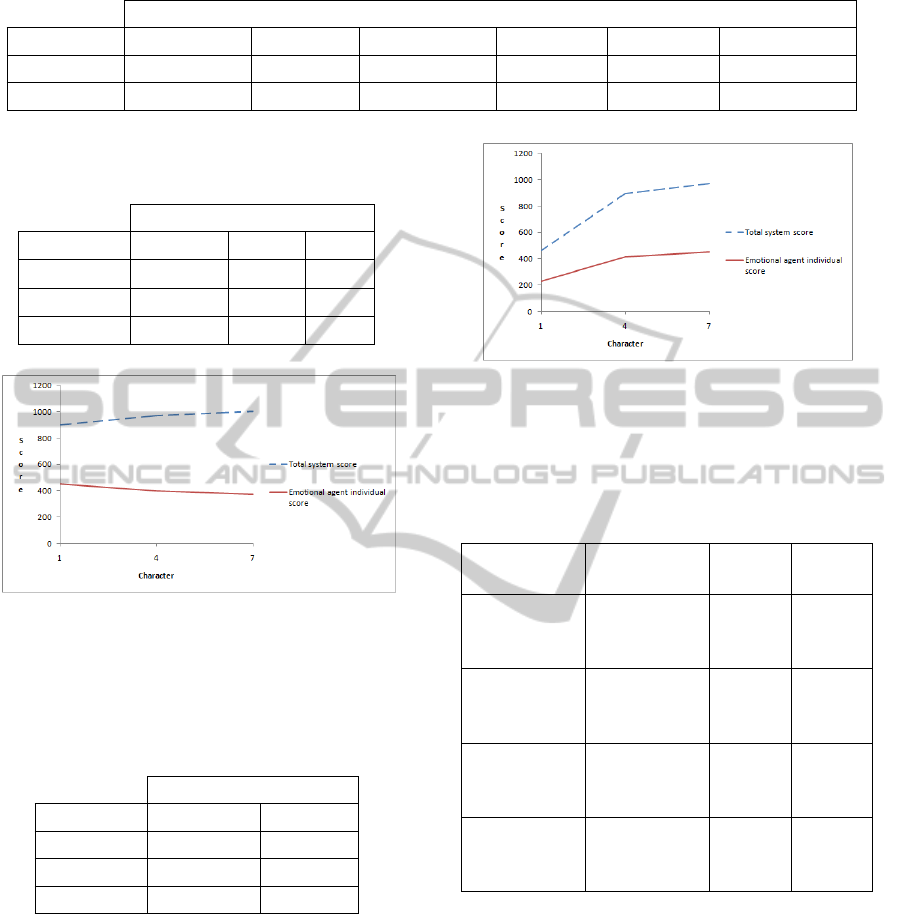
Table 7: Average individual scores of initially co-operative emotional agents with characters 1 and 7.

Opponent

Character

Mendacious Veracious Random Tit-for-tat Tester Joss

1 199

, 204

600

, 600

449

, 451

600

, 600

533

, 533

228.4

, 233.4

7 197

, 212

600

, 600

372.4

, 630.4

600

, 600

443

, 668

449.4

, 523.4

Table 8: Average individual score of initially co-operative

emotional agents with character 1, 4 and 7 when played

against random, tester and joss agents.

Opponent

Character Random Tester Joss

1 449 533 228.4

4 398.2 465 417.2

7 372.4 443 449.4

Figure 1: Total system score achieved when initially co-

operative emotional agents of characters 1, 4 and 7 play

against a random agent, plotted against the individual score

of the initially co-operative emotional agents.

Table 9: Percentage of total system score owned by the ini-

tially co-operative emotional agents of characters 1, 4 and 7

when playing aginst the random agent.

%Total Score Owned

Character Emotional Random

1 49.9 50.1

4 40.9 59.1

7 37.1 62.9

(see ﬁgure 2 and table 8). This is due to the joss

agent’s behaviour, which enables the maintenance of

co-operation cycles in the face of rare, one-off, peri-

odic defections.

In order to determine when the trade-off between

an individual’s score and the system’s score becomes

unacceptable we need to make note of a number

of thresholds. To do this we consider a number

of various maximal and minimal scores that can be

achieved/tolerated for/by each entity in the Tileworld

Dilemma; table 10 below illustrates these values:

The best possible score that an individual agent

can achieve is 1000 whilst the worst is 0, achieved

Figure 2: Total system score achieved when initially co-

operative emotional agents of characters 1, 4 and 7 play

against a joss agent, plotted against the individual score of

the initially co-operative emotional agents.

Table 10: The differing threshold values present in the Tile-

world Dilemma along with how they are derived and their

maximum/minimum values.

Threshold

Value

How

Derived

Max. Min.

Average

Agent 1

Score (A1)

Individual

Score

1000 0

Average

Agent 2

Score (A2)

Individual

Score

1000 0

Average

System

Score

A1 + A2 1200 400

Average

Fairness

Score

A1/A2 1 0

when a mendacious strategy is played against a vera-

cious strategy. An individual score of 0 is the worst

scenario possible; yet, the lowest acceptable score

that can be achieved by a single agent is 200, caused

by two players locking into a defection cycle for a

whole game. The best possible score from the sys-

tem’s perspective is 1200, achieved when two agents

co-operate initially and lock into a co-operation cycle

for a whole game and the worst score is achieved by

two agents locking into a defection cycle for a whole

game, leading to a total system score of 400. The rat-

ing of fairness ranges from 0 to 1, the closer to 1 the

more equal the two player’s scores are.

Therefore, if we take the above discussions into

ICAART 2012 - International Conference on Agents and Artificial Intelligence

168

consideration we can say that an initially co-operative

emotional agent with character 7 is more successful

than an initially co-operative emotional agent with

character 1 due to its ability to quickly establish

and maintain co-operation. Granted, the total sys-

tem scores produced are not fairly distributed: against

a random agent the system/fairness value for an ini-

tially co-operative emotional agent of character 7 is

0.59, whereas for an initially co-operative emotional

agent of character 1 the system/fairness value is 0.99.

Despite this, the system total achieved by an initially

co-operative emotional agent of character 7 is much

higher than that achieved by its less tolerant peers. It

is conceivable that more tolerant agents will produce

greater total system scores at the expense of fairness,

but only until a certain point i.e. when their individual

score passes below the threshold of 200; after this the

trade-off becomes deﬁnitely unacceptable since con-

sistent defection produces a better result and there are

no individual gains from co-operating.

4 CONCLUSIONS

Our experiments have demonstrated that the rational

behaviour exhibited by the tit-for-tat strategy present

in (Axelrod, 1984) can be replicated by an initially

co-operative emotional agent with character 1 i.e. an

agent with a low anger threshold resulting in imme-

diate punishment in response to defection and a low

gratitude threshold resulting in immediate reward in

response to co-operation. Furthermore, we have also

shown that when playing against strategies that inter-

sperse co-operation with periodic defection, a degree

of responsiveness and tolerance are key to maximis-

ing the total score of the system. However, by becom-

ing increasingly tolerant and remaining just as respon-

sive, one must expect to suffer a loss with respect to

one’s individual score. Consequently, such altruism is

only demonstrated if it is worthwhile to do so.

We have implemented and begun testing an ex-

tension to the Tileworld Dilemma entitled Emotional

Population. This test-bed consists of a population of

emotional agents who are capable of being initialised

with individual characters in exactly the same way as

described in this paper. The Emotional Population

adds admiration to the existing emotion set consist-

ing of anger and gratitude. Admiration has the poten-

tial to be elicited when an agent’s neighbour obtains

the highest individual score after n number of rounds,

but, as with anger and gratitude, agents have varying

degrees of sensitivity with respect to admiration. If

admiration is elicited then the evaluating agent will

change its emotional character to become more like

the successful agent. Through this new scenario we

aim to analyse which emotional characters become

prevalent in a population and if these emotional char-

acters are successful at maximising the total score of

the system.

REFERENCES

Axelrod, R. (1984). The Evolution Of Cooperation. Basic

Books, Inc.

Baumeister, R. F., DeWall, C. N., Vohs, K. D., and Alquist,

J. L. (2009). Does Emotion Cause Behavior (Apart

from Making People Do Stupid, Destructive Things)?,

chapter 7, pages 119–136. OUP.

Berg, J., Dickhaut, J., and McCabe, K. (1995). Trust, reci-

procity and social history. Games and Economic Be-

haviour, 10:122–142.

Brooks, R. A. (1991). Intelligence without representation.

Artiﬁcial Intelligence, 47:139–159.

Fehr, E. and G

achter, S. (2002). Altruistic punishment in

humans. Nature, 415:137–140.

Fessler, D. M. and Haley, K. J. (2003). Genetic and Cul-

tural Evolution of Cooperation. Cambridge, MA:

MIT Press.

Frank, R. H. (1988). Passions Within Reason: The Strategic

Role of the Emotions. W.W. Norton & Company.

Frijda, N. H. (1987). The Emotions. CUP.

James, W. (1884). What is an emotion? Mind, 9:188–205.

Lloyd-Kelly, M., Atkinson, K., and Bench-Capon, T.

(2011). Emotion as an enabler of co-operation. Tech-

nical Report ULCS-11-004, The University of Liver-

pool.

Ortony, A., Clore, G. L., and Collins, A. (1988). The Cog-

nitive Structure of Emotions. CUP.

Pollack, M. and Ringuette, M. (1990). Introducing the tile-

world: Experimentally evaluating agent architectures.

In Proc. of the 8th National Conference on Artiﬁcial

Intelligence, pages 183–189. AAAI Press.

Steunebrink, B. R., Dastani, M., and Meyer, J.-J. C. (2007).

A logic of emotions for intelligent agents. In Proc. of

the 22nd Conference on Artiﬁcial Intelligence, pages

142–147. AAAI Press.

EMOTION AS AN ENABLER OF CO-OPERATION

169