
DECISION TREE INDUCTION FROM COUNTEREXAMPLES
Nicolas Cebron, Fabian Richter and Rainer Lienhart
Multimedia Computing Lab, University of Augsburg, Universitaetsstr. 6a, Augsburg, Germany
Keywords:
Decision trees, Counterexamples, Machine learning, Data mining, Decision making.
Abstract:
While it is well accepted in human learning to learn from counterexamples or mistakes, classic machine
learning algorithms still focus only on correctly labeled training examples.We replace this rigid paradigm by
using complementary probabilities to describe the probability that a certain class does not occur. Based on
the complementary probabilities, we design a decision tree algorithm that learns from counterexamples. In
a classification problem with K classes, K − 1 counterexamples correspond to one correctly labeled training
example. We demonstrate that even when only a partial amount of counterexamples is available, we can still
obtain good performance.
1 INTRODUCTION
The goal of supervised classification is to deduce a
function from examples in a dataset that maps input
objects to desired outputs. By using a set of labeled
training examples, we can train a classifier that can be
used to predict the nominal target variable for unseen
test data. To achieve this, the learner has to generalize
from the presented data to unseen situations. While
a plethora of algorithms for supervised classification
has been developed, only a few works deviate from
this classical setting.
In this paper, we focus our attention on decision
trees. Especially in multi-class problems, they are a
reliable and effective technique. They usually per-
form well and offer a simple representation in form
of a tree or a set of rules that can be deduced from
it. They have been used a lot in situations where a
decision must be made effectively and reliably, e.g.
in medical decision making (Podgorelec et al., 2002).
However, like all inductive methods in machine learn-
ing, the performance of this classifier is based on cor-
rectly labeled training examples. Finding the correct
class label for an example when generating a train-
ing set for the classifier can be difficult – especially
when there is a large number of possible classes. In
the work of (Joshi et al., 2010), it has been shown that
the human error rate and the time needed to find the
correct label grows with the number of classes; at the
same time the user distress increases. In some situ-
ations, it might not even be possible for the human
expert to determine the correct class label out of ma-
ny possible class labels. In a normal classification set-
ting, we would have to ignore this example.
As an example, we stick to the domain of medical
decision making, where we have two common situa-
tions in which the human expert has problems provid-
ing the correct class label:
1. Ambiguous Information: different class labels
(e.g. diseases) may be possible, but there is a lack
of information to explicitly choose one of them.
For example, it is unclear whether a person with
headache symptoms is suffering from a cold or
has the flu (or another type of disease).
2. Rare Cases: the determination of the class label
may be difficult because of missing expertise in a
special field. For example, it may be difficult to
classify rare (so-called orphan) diseases.
In this work, we want to introduce a new paradigm
in supervised classification: we do not obtain the la-
bel information itself, but the labels of the classes that
this example does not belong to. We call these exam-
ples counterexamples. For the preceding examples in
medical decision making, it can be very easy to spec-
ify the diseases that are not likely (e.g. not typhlitis,
not heartburn, etc. for a headache symptom) in order
to narrow down the set of possible classes. We argue
that in many real world settings, it is much easier for
the human expert to provide a counterexample instead
of determining the correct class label. This does not
only apply to the domain of medical decision mak-
ing, it is also true for many other domains like image,
music or text classification.
525
Cebron N., Richter F. and Lienhart R. (2012).
DECISION TREE INDUCTION FROM COUNTEREXAMPLES.
In Proceedings of the 1st International Conference on Pattern Recognition Applications and Methods, pages 525-528
DOI: 10.5220/0003730405250528
Copyright
c
SciTePress

Within our new framework of classification with
counterexamples, we can gain information from al-
most every example in a dataset. However, we keep
our framework open and the information of examples
and counterexamples can be included seamlessly. In a
classification problem with K disjoint classes, there is
of course a loss of information induced from this set-
ting, as we can expect to observe less than K −1 labels
for each counterexample in practice
1
. The question
that we aim to answer in this paper is: How much
does this loss of information influence the resulting
classification model?
To the best of our knowledge, this is the first work
that considers feedback in the form of counterexam-
ples in a multiclass setting. Some works have inves-
tigated negative feedback in the image retrieval pro-
cess (Ashwin et al., 2001), (Mueller et al., 2000). As
the retrieval process corresponds to a two-class prob-
lem, these works only share the general idea of a dif-
ferent form of feedback with this work. At first sight,
our work seems to be related to the domain of mul-
tilabel classification (Tsoumakas and Katakis, 2007),
where a mapping from an example to a set of class
labels is sought. However, our goal is to predict one
class label from the set of counterexamples.
In order to quantify the information from coun-
terexamples, we introduce the probability theory for
counterexamples in section 2. In section 3, we will in-
troduce the decision tree learning algorithm for coun-
terexamples. We will present results on different
benchmark datasets in section 4 and finally draw con-
clusion in section 5.
2 COUNTEREXAMPLE
PROBABILITIES
We begin by recapitulating the basic laws of probabil-
ity theory: the probability of an event is the fraction of
times that the event occurs out of the total number of
trials, in the limit that the total number of trials goes
to infinity. In our case, the probabilities correspond to
the events that a certain class occurs in a set of exam-
ples. We denote the probability for class k by p(k).
By definition, the probabilities must lie in the inter-
val [0, 1], and if the events are mutually exclusive and
include all outcomes, their probabilities must sum to
one:
0 ≤ p(k) ≤ 1 (1)
1
If we would have K − 1 labels, we could deduce the
corresponding label directly.
K
∑
k=1
p(k) = 1 (2)
In order to work with counterexamples and to
quantify the amount of classes that are not contained
in a set of examples, we need to define complemen-
tary probabilities. A complementary probability for
event k, denoted by
p(k) describes the probability that
event k does not occur in a set of examples. By defini-
tion, the probability that event k does not occur is the
sum of the probabilities of all other events that have
occurred:
p(k) =
K
∑
j=1, j6=k
p( j)) (3)
The relation between p(k) and p(k) is defined as
p(k) = 1 − p(k).
Like normal probabilities, p(k) must lie in the in-
terval [0, 1]. However, as the set of events is not mutu-
ally exclusive (a counterexample may have more than
one class that it does not belong to), we need to adapt
the restriction from equation 2 taking into account the
definition of p(k):
K
∑
k=1
(p(k)) =
K
∑
k=1
"
K
∑
j=1, j6=k
p( j)
#
=
K
∑
k=1
[1 − p(k)]
= K −
K
∑
k=1
p(k)
= K − 1
(4)
Having established the basic laws for complementary
probabilities and rules to transform probabilities into
complementary probabilities and vice versa, we can
use them in the design of a decision tree that learns
from counterexamples in the next section.
3 DECISION TREE INDUCTION
We assume that instead of having one class label
for each example, we have a vector ~y = (y
1
,.. ., y
K
),
where each entry y
k
∈ {0, 1} indicates whether we
know that this example does not belong to class k (1)
or that we do not have any information concerning
class k for this example (0).
The main difference between learning a tree from
examples and learning a tree from counterexamples
is the notion of purity of a data partition. Figure 1
illustrates the situation of learning a decision tree
from counterexamples. Each partition can now con-
ICPRAM 2012 - International Conference on Pattern Recognition Applications and Methods
526

Figure 1: Decision tree with four partitions based on coun-
terexamples.
tain multiple class labels of the classes that the exam-
ples do not belong to. The goal is to find partitions
that have high complementary probabilities for K − 1
classes as they correspond to a ’pure’ distribution of
the class label.
We use our definition of mapping from comple-
mentary probabilities to probabilities in section 2 to
derive a new definition for the entropy (Shannon,
2001), which is commonly used to judge the quality
of a data partition X:
H(X) =
K
∑
k=1
(1 − p(k))ln(1 − p(k)). (5)
As can be seen in figure 1, the leaf nodes of our de-
cision tree contain a distribution of complementary
class probabilities. We can output this distribution or
transform it to normal class probabilities and use the
majority class as a decision.
4 RESULTS
The algorithms were implemented within the frame-
work of the weka (Hall et al., 2009) and mulan soft-
ware (Tsoumakas et al., 2011).
Each experiment has been been repeated 500
times. In each iteration, we split up the dataset ran-
domly and use 30% for training and 70% for test-
ing. We deduce the corresponding complementary
class probabilities from the original class probabili-
ties for each example. We then remove 0% (corre-
sponds to a fully labeled dataset) to 90% of informa-
tion from the ~y vectors in the training dataset (plotted
on the x-axis) and plot the accuracy as a boxplot on
the y-axis. As we remove information from the entries
in ~y, the counterexample probabilities p(k) become
smaller. However, this is not an issue as H(X) scales
monotonically with information removal as shown in
the Appendix.
4.1 Contact Lenses
The lenses dataset consists of 24 examples. The goal
is to predict whether a person should be fitted with
hard or soft contact lenses or no contact lenses based
on four attributes. Figure 2 shows the accuracy of
the decision tree that is induced from counterexam-
ples for a varying amount of information. We can ob-
Figure 2: Information vs. accuracy on lenses dataset.
serve a linear decline of accuracy with the amount of
information removed. As the dataset is very small, re-
moving information has a deep impact on the result-
ing decision tree. However, if we remove up to 30%
of information, we still get acceptable accuracy.
4.2 Balance Scale
In the balance scale dataset, each example is classi-
fied as having the balance scale tip to the right, tip to
the left, or be balanced. The four attributes are the
left weight, the left distance, the right weight, and the
right distance. Figure 3 shows the accuracy of the de-
cision tree that is induced from counterexamples for a
varying amount of information. The decline in accu-
racy is not as steep as for the contact lenses dataset,
which is due to the larger number of 187 examples in
the training set.
4.3 Nursery
The nursery dataset was derived from a hierarchical
decision model originally developed to rank applica-
tions for nursery schools in five different classes. It
contains 12960 examples. As the accuracy does al-
most not decline between 0% and 99%, we plot the
experiment with 99% to 99.9% information removed
in Figure 4. We can observe that the accuracy declines
very late.
DECISION TREE INDUCTION FROM COUNTEREXAMPLES
527
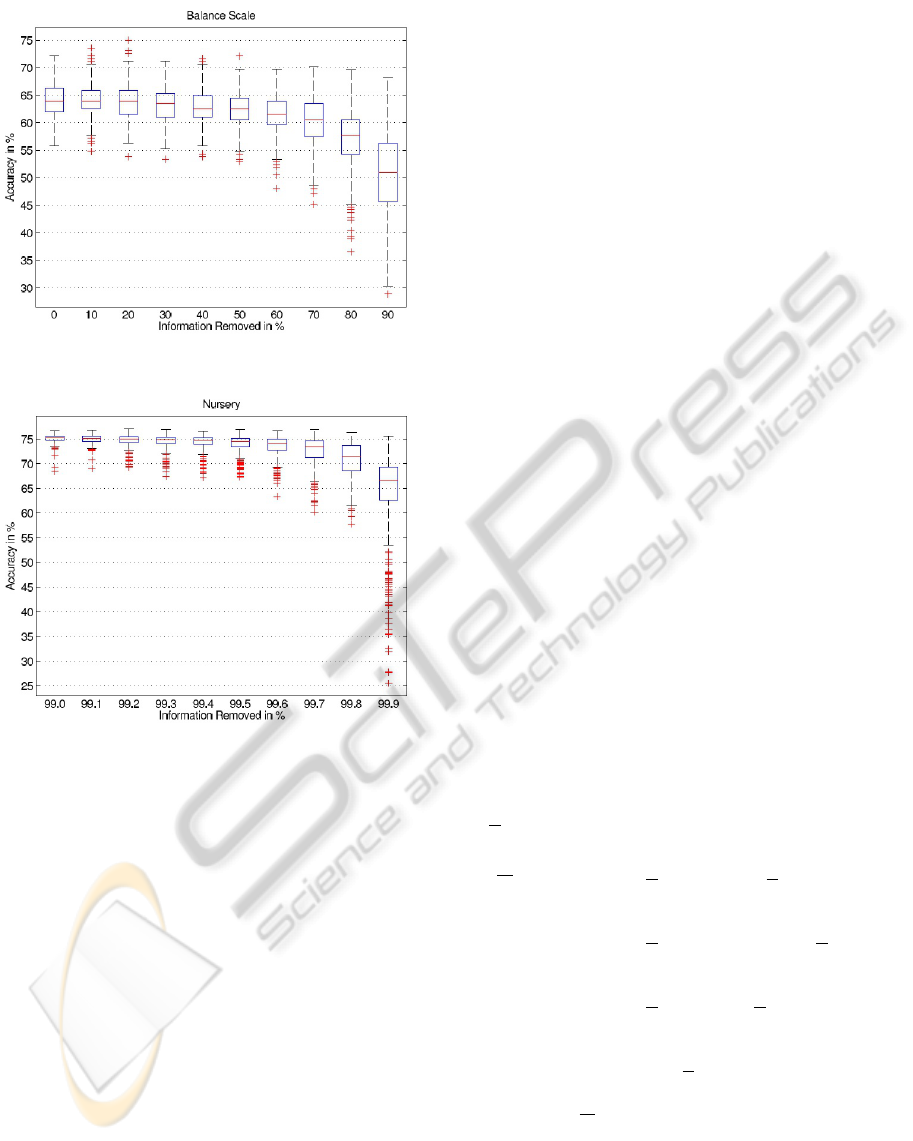
Figure 3: Information vs. accuracy on balance scale dataset.
Figure 4: Informations vs. accuracy on nurse dataset.
5 CONCLUSIONS
In this work, we have presented a new approach to
induce a decision tree classifier from counterexam-
ples. Based on complementary probabilities we have
adapted the entropy measure in order to work with
this new type of human feedback. Normal exam-
ples can also be integrated seamlessly by deducing
the complementary class probabilities from the given
class probabilities. We have observed that this ap-
proach works well even if we remove a significant
amount of information from the training examples.
This shows that we can learn from counterexamples in
a practical setting, where the user typically provides
less than K − 1 class labels. We hope that this work
does inspire future work in the community on differ-
ent forms of feedback in machine learning.
REFERENCES
Ashwin, T., Jain, N., and Ghosal, S. (2001). Improving
image retrieval performance with negative relevance
feedback. Acoustics, Speech, and Signal Processing,
IEEE International Conference on, 3:1637–1640.
Hall, M., Frank, E., Holmes, G., Pfahringer, B., Reutemann,
P., and Witten, I. H. (2009). The weka data mining
software: an update. SIGKDD Explor. Newsl., 11:10–
18.
Joshi, A. J., Porikli, F., and Papanikolopoulos, N. (2010).
Breaking the interactive bottleneck in multi-class clas-
sification with active selection and binary feedback. In
CVPR, pages 2995–3002. IEEE.
Mueller, H., Mueller, W., Squire, D. M., Marchand-Maillet,
S., and Pun, T. (2000). Strategies for positive and neg-
ative relevance feedback in image retrieval. In Pro-
ceedings of the International Conference on Pattern
Recognition - Volume 1, volume 1, pages 1043–1046,
Washington, DC, USA. IEEE Computer Society.
Podgorelec, V., Kokol, P., Stiglic, B., and Rozman, I.
(2002). Decision trees: An overview and their use
in medicine. J. Med. Syst., 26:445–463.
Shannon, C. E. (2001). A mathematical theory of commu-
nication. SIGMOBILE Mob. Comput. Commun. Rev.,
5(1):3–55.
Tsoumakas, G. and Katakis, I. (2007). Multi label classi-
fication: An overview. International Journal of Data
Warehouse and Mining, 3(3):1–13.
Tsoumakas, G., Spyromitros-Xioufis, E., Vilcek, J., and
Vlahavas, I. (2011). Mulan: A java library for multi-
label learning. Journal of Machine Learning Re-
search. (to appear).
APPENDIX
We use the scalar α ≥ 1 to compensate for the decline
in p(k) due to the information removal.
H(X) =
K
∑
k=1
α(1 − p(k))ln(α(1 − p(k)))
=
K
∑
k=1
α(1 − p(k))[ln(α) + ln(1 − p(k))]
= α
K
∑
k=1
(1 − p(k))ln((1 − p(k)))
+ α
K
∑
k=1
(1 − p(k))ln(α)
= αH(X) + α ln(α).
ICPRAM 2012 - International Conference on Pattern Recognition Applications and Methods
528
