TRACKING PLANAR-TEXTURED OBJECTS

On the Way to Transport Objects in Packaging Industry by Throwing and Catching

Naeem Akhter

Vienna University of Technology, Vienna, Austria

Keywords:

Efﬁcient, Flexible, Robust, Pose tracking, Planar-textured objects.

Abstract:

In manufacturing systems transportation of objects can be optimized by throwing and catching them mechan-

ically between work stations. There is a need to track thrown objects using visual sensors. Up to now only

ball-shaped objects were tracked under controlled environment, where no orientation had to be considered.

This work extends the task of object tracking to cuboid textured objects considering industrial environment.

Indeed, tracking objects with respect to the robotics tasks to be achieved in a not too restricted environment

remains an open issue. Thus, this work deals with efﬁcient, ﬂexible, and robust estimation of the object’s pose.

1 INTRODUCTION

Transporting objects within production systems by

throwing and catching is a new approach that aims

at future prospect. The basic advantages of the throw-

catch approach are: high speeds are possible, ﬂexibil-

ity can be achieved, and fewer resources are required

(Frank et al., 2008). Functionally the approach is di-

vided into four subtasks. A throwing machine throws

object towards a target where it needs to be grasped.

Since ﬂight of such an object is non-deterministic in

general, a catching mechanism has to be located be-

fore object reaches the target. This is achieved by

predicting current trajectory. Visual sensors are em-

ployed to ﬁnd trajectory. At each measurement inter-

ception is updated, consequently catching mechanism

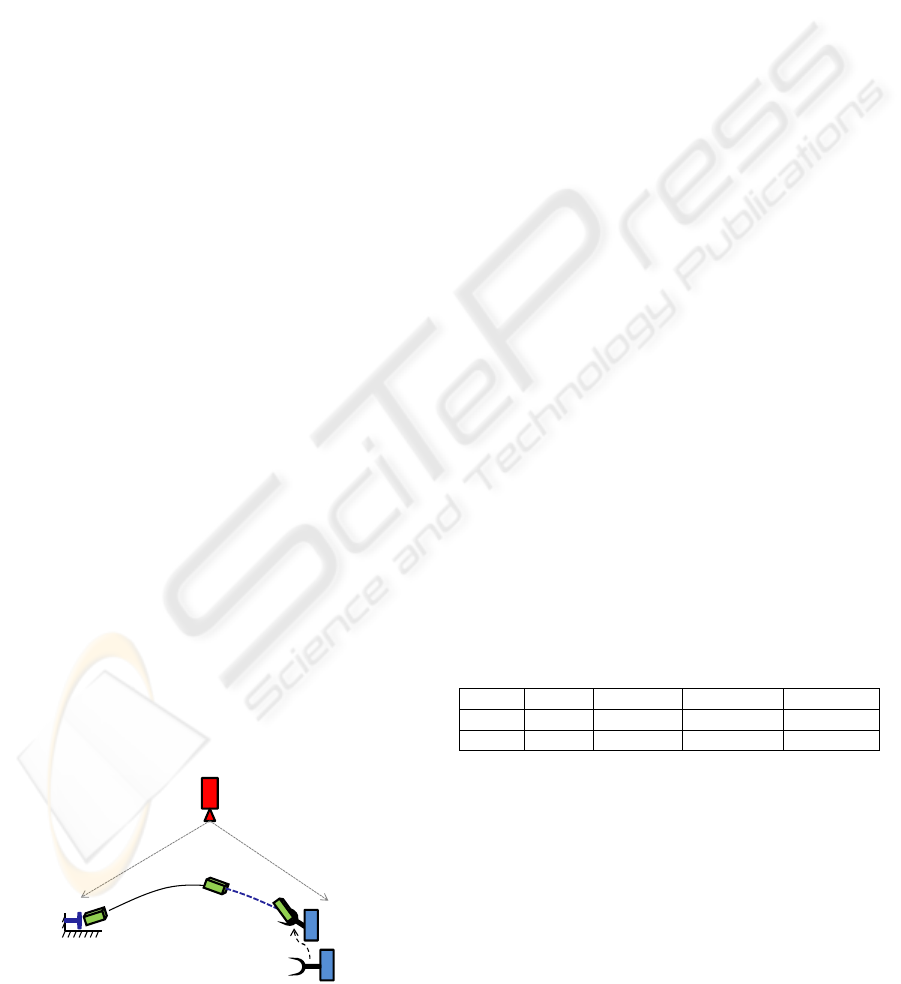
moves to the predicted interception. Figure 1 provides

schematic description of the approach. Scope of this

work is restricted to trajectory measurement.

There are four classes in logistic chains in which

trajectory measurement

trajectory prediction

gripper positioning

throwing

Figure 1: A schematic description of the throw-catch ap-

proach.

the throw-catch approach can be realized (Frank et al.,

2009). Table 1 summarizes these. So far feasibil-

ity of the approach is tested with spherical objects

in fact tennis ball (Barteit et al., 2009). Objects of

different nature behave aerodynamically differently.

Their appearance also varies. Among these spheri-

cal objects are least vulnerable to change their trajec-

tory, appearance, and grasping. Non-spherical objects

change their view and hence project differently on im-

age plane. A change in their view results into a change

in their area across airstream that changes its aero-

dynamic behavior. Moreover, grasping of the object

would also need its orientation information. There-

fore, task of trajectory measurements in that case be-

comes task of pose tracking.

Table 1: Classiﬁcation of throwing tasks and objects.

Object workpiece packaging assembly food

Shape ball cuboid axial symmetric irregular

Function sorting transportation separation commissioning

Work done so far in the throw-catch approach

is not only based on simpliﬁed nature of object but

also the environment. While trajectory measurement,

background is supposed to be static, a high contrast

between object and background is set, and diffused

lighting is assumed. This is contradiction to the

claim of ﬂexible transportation. In production envi-

ronments, pose tracking may present challenging sit-

uations. The ﬁrst is dynamic background. This is due

to a number of activities going on in parallel. These

include staff movement, motion of assembly units and

316

Akhter N. (2012).

TRACKING PLANAR-TEXTURED OBJECTS - On the Way to Transport Objects in Packaging Industry by Throwing and Catching.

In Proceedings of the 1st International Conference on Pattern Recognition Applications and Methods, pages 316-321

DOI: 10.5220/0003731503160321

 SciTePress

accessories, displacement of tools, chairs, tables etc.,

and objects of multirouting. The second is appearance

of object and background may change. A new ap-

pearance may be introduced. Maintaining high con-

trast and constraint of diffused light impose unneces-

sary conditions. The third is object can be partially

occluded. This could be due to moving entities of

the scene, on the way object may partially leave ﬁeld

of view, or illumination may blur part of the object.

Finally, interframe displacement may be large. This

could be due to high speed of object, low temporal

resolution of camera, or frame drop.

Indeed, ﬂexibility not only depends on overcom-

ing the challenging situations but also on adaptivity to

change in object and background nature. This can be

achieved by decoupling foreground from background.

An approach that provides 6-DoF pose without ofﬂine

learning and/or image segmentation becomes impor-

tant. Rather than independently performing object de-

tection and pose estimation, integration of these tasks

may reduce computational cost. A single camera and

exploiting minimum structural detail of object may

reduce information density. In brief, objective of this

research is not only to handle challenges of tracking

in industry, but also to make the throw-catch approach

ﬂexible in real sense. Scope of the work is restricted

to packaging industry. Packaging objects are labeled

with text and graphics such as product information,

brand name, brand logo etc. Therefore, it is reason-

able to assume they have sufﬁcient texture.

Rest of the paper is divided into four sections.

Section 2 reviews state of the art in pose tracking,

based on the outcome, a hybrid approach is presented

in Section 3. Evaluation of the approach is described

in Section 4. Finally, Section 5 concludes the paper.

2 POSE TRACKING

On a broad level, approaches of pose tracking

for textured-planar targets can be divided into two

groups: pose tracking by detection and pose track-

ing by modeling. The ﬁrst type of approaches (Bjork-

man and Kragic, 2004; Ekvall et al., 2005; Lepetit

et al., 2004) build 2D-3D mapping using training data

consisting of several views of the target. The con-

structed mapping is then used to ﬁnd pose of a given

2D target image, which makes them rigid to learned

scenarios. Scenes in which targets are easy to de-

tect are assumed (Azad, 2009). Although suitable for

large interframe displacement as strong prior on the

pose is not required, they are less accurate and more

computationally intensive than the second type of ap-

proaches (Lepetit and Fua, 2005).

The second type of approaches pre-assumes a 3D

model of target. They require a strong prior on the

pose to iteratively evolve to actual pose. Typically,

they recover pose by ﬁrst establishing 2-3D feature

correspondence and then solving for the pose using

a pose estimation technique. Based on the type of

feature, they are further divided into template based

and keypoint based approaches. Template based ap-

proaches (Mei et al., 2008; Baker and Matthews,

2004; Jurie and Dhome, 2002) estimate pose of a

reference template by minimizing an error measure

based on image brightness. In general, they work

under diffused lighting, no occlusion, and small in-

terframe displacement (Ladikos et al., 2009; Lepetit

and Fua, 2005). Keypoint based approaches (Ladikos

et al., 2009; Vacchetti et al., 2004b; Collet et al.,

2009) exploit local appearance of targets. They work

opposite to template based approaches but relatively

computationally expensive (Lepetit and Fua, 2005).

As they require sophisticated feature model of com-

plete object, they are less ﬂexible to adapt new ob-

ject. A common problem with the second type of ap-

proaches is pose drift due to error accumulation over

long sequences (Lepetit and Fua, 2005).

Approaches (Choi and Christensen, 2010;

Ladikos et al., 2009; Rosten and Drummond, 2005;

Vacchetti et al., 2004a) also exist that combine

more than one type of approaches with intention to

increase accuracy and/or achieve robustness. There is

none that simultaneously addresses large interframe

displacement and ﬂexibility to adapt change in scene.

Moreover, rather than fusing they work either by

feeding output of one approach to second approach

or by switching between the two approaches. The

proposed approach intrinsically assimilate template

based and keypoint based tracking due to their

complementary role in achieving the goal. In con-

trast to estimate pose from pre-learned samples,

deformation in the template is used. In place of

intensity, point based error measure is deﬁned to

ﬁnd the deformation. Tasks of detection and pose

estimation are performed simultaneously without

imposing constraints on background. The approach

intrinsically delays pose drift.

3 FUSING POINT AND

TEMPLATE INFORMATION

To fuse point information into template, template

based tracking introduced by Mei et al. (Mei et al.,

2008) is chosen. This is for its high accuracy and bet-

ter convergence. Pseudocode of the algorithm with

point information incorporated is given in ﬁgure 2.

TRACKING PLANAR-TEXTURED OBJECTS - On the Way to Transport Objects in Packaging Industry by Throwing

and Catching

317

Let I

be a reference image of a monocular se-

quence I

, k = 1...K, such that a region I

re f

(refer-

ence patch) of this contains projection of the planar

target. Given an approximate transformation

T con-

sisting of rigid motion (rotation

R, translation

t) in

terms of camera motion, features F

re f

extracted from

re f

, and a set of thresholds, the algorithm returns the

actual T . Theoretically, it is equivalent to map I

re f

desired region deﬁned by T in the current image I

that minimizes sum of square distance (SSD) over all

feature points.

Input:I1,Iref,Ik,Fref,,thresholds(maxIter,num,err)

Output:T

Iter = 0

While(iter < maxIter)

Compute ,

H = + nd

’

Icur = definePatch(Ik,Iref,H)

Fcur = extractFeatures(Icur)

matches = matchFeatures

(

ref

Fcur

)

removeOutliers(matches)

x = -2J

D(0)

if ||x|| < err

T =

break

else

= T(x)

end

Figure 2: Pseudocode of the ESM algorithm fused with

point information.

Algorithm starts by computing transformation of

the target in image plane using homography H asso-

ciated to

T . Such that

T =



0 1



(1)

H = (

R +

) (2)

p = π(w(H(

T )))π

−1

∗

) (3)

where n

is a vector deﬁned as

consisting of nor-

mal n and distance d of the target plane from cam-

era. w is a warping function that deﬁnes a coordinate

transformation between points on a unit plane (nor-

malized plane). π is a projection function that de-

ﬁnes projection of a point on the unit plane to im-

age plane. Practically, this is to ﬁnd the new position

p in the current image of a pixel p

∗

in the reference

image. With this a patch I

cur

(current patch) in the

current image is deﬁned. This leads to four beneﬁts.

One region to search the target in image is conﬁned.

Second explicit detection or segmentation of the tar-

get is avoided which saves computation on run time.

Third likelihood of correspondence with background

is reduced. Fourth background is intrinsically ignored

which in turn makes background dynamics irrelevant.

In the next step features F

cur

are extracted from the

deﬁned patch. The Scale Invariant Feature Transform

(SIFT) is an approach for extracting local features that

are reasonably invariant to scaling, translation, rota-

tion, illumination changes, image noise, afﬁne distor-

tion, occlusion, and viewpoint change (Sangle et al.,

2011). Further motivation comes from its use in real-

time tracking on mobile phones (Wagner et al., 2008).

Therefore, this work uses SIFT. Extracted features are

then matched with the F

re f

using K-d tree. False

correspondence is avoided by ﬁrst removing points

with multiple correspondences. Then further remov-

ing whose Euclidian distance and slope exceeds a spe-

ciﬁc range. Based on the number of features, empir-

ically determined two strategies are employed. If the

number exceeds 40, Gaussian distribution is assumed

and the range is deﬁned by equation 4. Otherwise, it

is deﬁned by equation 5.

Mean {slope, distance} ±1.5 × its Standard deviation (4)

Median {slope, distance} ±0.66 × Median {slope, distance} (5)

Once outliers are removed, cost of matching is

then computed between the corresponding points. Let

the corresponding points are {l

i, j

} and {m

i, j

} in the

reference and current patches respectively. Let D

the distance between q

pair of corresponding points,

the cost is deﬁned as:

∀i ∈ 1, 2, ..., q D

= l

− m

(6)

If the SSD value of vector D approaches to zero,

the estimated pose becomes equal to the actual pose.

Tracking jumps to the next image. Otherwise, there

is a need to update

T . Let the update is denoted by

T (x). Where x is a parameter vector that consists of

coefﬁcients of base elements: three for translation B

and three for rotation B

-B

such that

T (x) = exp(

∑

i=1

) (7)

0 0 0 1

0 0 0 0

0 0 −1 0

0 1 0 0

0 0 0 0

0 0 0 1

0 0 0 0

0 0 1 0

0 0 0 0

−1 0 0 0

0 0 0 0

(8)

0 0 0 0

0 0 0 1

0 0 0 0

0 −1 0 0

1 0 0 0

0 0 0 0

More precisely, the problem of pose estimation is

to minimize the cost of matching which in terms of

the parameter vector can be described as

∀i ∈ 1, 2, ..., q D

(x) = π(w(H(T (x)

T )))π

−1

) − m

(9)

ICPRAM 2012 - International Conference on Pattern Recognition Applications and Methods

318

Minimizing this expression is a nonlinear optimiza-

tion task. Let cost function D(x) be the vector

(x) D

(x) ... D

(x)]

that corresponds to the

distance over all points at the given parameter vec-

tor x. By the second order approximation of D(x)

about x = 0 using Taylor series and simpliﬁcation

(Mei et al., 2008)

D(x) ≈ D(0) +

Jx (10)

J = J

(11)

where J is jacobian of the D with respect to the x. In

contrast to the original Jacobian which is composed of

jacobians of each of image J

, image projection func-

tion J

, image warping function J

, homography J

and transformation J

. In this work, it is composed

of the other four except J

. This is to reduce non-

linearity in the cost function. In the former case there

are two factors that introduce non-linearity in the cost

function. First corresponds to non-linear projection

and second corresponds to intensity information. In

fact pixel values are essentially un-related to pixel co-

ordinates (Baker and Matthews, 2004), therefore, J

is ignored. This allows using fewer details, regions

in spite of the complete reference patch. Moreover,

impact of non-linearity should be reduced as the cost

function is better deﬁned. Outcome of testing with

simulated sequence conﬁrms this. Expression of each

of the jacobian for each feature point l

normalized to

the unit plane is

= ∇

π(P)|

P=l

(12)

= ∇

(w(H))(P)|

H=H(0)=I

(13)

= ∇

T )

−1

H(T

T )|

T =T(0)=I

(14)

= ∇

T (x)|

x=0

(15)

Solution to the problem lies in ﬁnding a param-

eter vector x

such that D(x

) = 0. This is obtained

by iteratively solving the cost function such that for a

vector x = x

∇D(x)|

x=x

= 0 (16)

At each iteration an updated x is calculated as follows

x = −2J

D(0) (17)

where D(0) is the cost at x = 0, and J

means

pseudo-inverse of J. Once convergence (kxk < err) is

achieved in the current image, the optimal transforma-

tion T

between the reference I

and the current image

is obtained. The algorithms ﬁnishes with this image

and restarts with the next image I

k+1

. Let T

) be

the relative transformation between the last two con-

secutive frames I

k−1

and I

. Pose estimation starts in

the next image with the following approximation

T (k +1) = T

(18)

Tracking continues till the last image I

is reached

and a total transformation T

without pose drift is

found.

4 RESULTS AND DISCUSSION

Evaluation of the proposed approach is made using

both the simulated and real sequences. In the ﬁrst

case, it is made with reference to the Mei et al. using

the same simulated sequence on which the referenced

approach was tested. Figure 3 shows three images of

the simulated sequence.

Figure 3: Images 1, 50, and 100 respectively in the simu-

lated sequence.

Figure 5 shows how do the two approaches be-

have on average bases, in terms of absolute transla-

tional error, absolute rotational error, and number of

iterations elapsed to converge, with the increase in in-

terframe displacement. The interframe displacement

is increased by skipping multiple images at regular

intervals from the original sequence. Started by skip-

ping alternate images and ending with two images in

the sequence. Figure 4 elaborates skipping procedure.

One can see by fusing point information into the pure

template based tracking both the errors remain more

than half below. The errors oscillate in the beginning

for the reason of small baseline effect while stabilizes

later. In the case of number of iterations, although

difference between the two is small in the beginning

but immediately that is after skipping just two images

raises dramatically. The proposed approach showed

consistent behavior. The most considerable fact is

that the referenced approach fails tracking beyond 10

number of images skipped. This is due to its reliance

on strong prior on the pose.

Figure 4: Three instances of skipping alternate images. N

corresponds to the number of images skipped. Arrow points

to the selected image.

In the second case, the approach is tested with real

sequences. These sequences consist of ﬂight of ten

cubical objects thrown horizontally across the princi-

pal axis of camera. For each object 50 sequences are

collected. They are thrown at a distance of 1.6

±0.45

m from camera with their largest plane exposed to the

TRACKING PLANAR-TEXTURED OBJECTS - On the Way to Transport Objects in Packaging Industry by Throwing

and Catching

319

0 5 10 15 20 25 30 35

0.5

1.5

2.5

number of images skipped

abs. translation error (mm)

← ~failed

proposed

referenced

0 5 10 15 20 25 30 35

0.5

1.5

2.5

number of images skipped

abs. rotational error (mrad)

← ~failed

proposed

referenced

0 5 10 15 20 25 30 35

number of images skipped

number of iterations

← ~failed

proposed

referenced

Figure 5: Comparison based on interframe displacement.

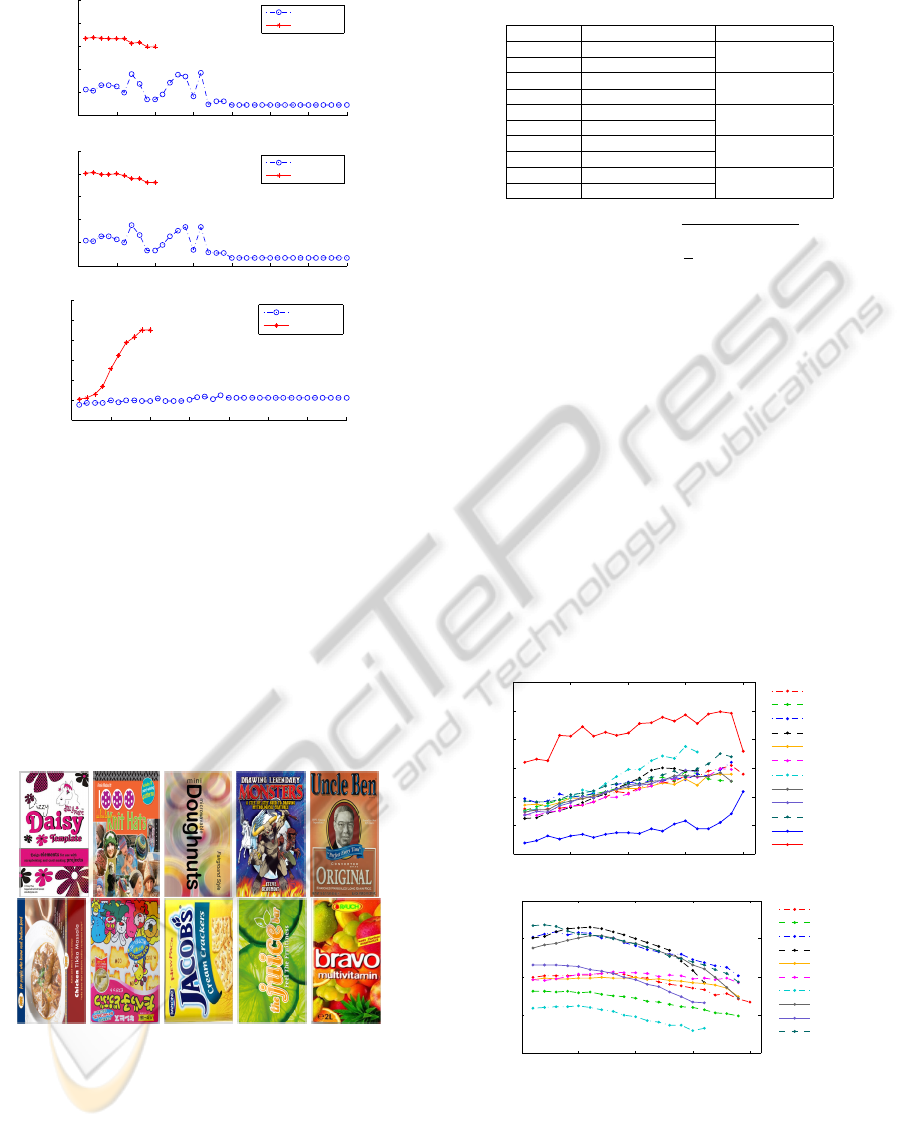
camera. Figure 6 shows the planes. Their sizes and

number of features extracted from each plane at this

distance are given in Table 2. Horizontal ﬁeld of view

at this distance is 1.2 m. Before leaving ﬁeld of view,

they lie at 1.44±0.45 and 0.07±0.21 m from camera

along Z and Y axis respectively. Another calibrated

camera is used to ﬁnd the distances and normal to the

plane using stereo vision. The range of estimated ro-

tation along each of the X, Y, and Z axis is -37.93 to

35.08, -30.50 to 50.90, and -15.50 to 44.68 degrees

respectively.

Figure 6: Planes of the objects and their assigned names.

Top to bottom followed by left to right: (a) Daisy, (b) Gar-

ment, (c) Donuts, (d) Monster, (e) Rice, (f) Chicken, (g)

China, (h) Biscuit, (i) Juice, (j) and Bravo.

Evaluation is made using the methodology intro-

duced in (Lieberknecht et al., 2010). Tracking error is

deﬁned as root mean square (RMS) distance between

estimated corner p of the plane and its ground truth

∗

which is generated manually. Such that

Table 2: Sizes and feature amount of the planes.

Plane Number of features Size (mm × mm)

Daisy 155 300 × 160

Garment 177

Donuts 99 285 × 120

Monster 130

Rice 185 250 × 160

Chicken 114

China 188 200 × 175

Biscuit 107

Juice 69 240 × 115

Bravo 102

tracking error =

∑

i=1

− p

∗

(19)

Figure 7(a) shows tracking error on average and

extreme bases. For each plane the average is taken

per image over all the 50 throws. One can see the

approach performs equally well in all the cases ex-

cept Juice. This is due its much lower amount of

texture (number of features) relative to the rest. A

common trend among all the planes is that the error

increases with the increase in image number. This is

partially due to error accumulation and partially due

to loss in features. The loss is due to throwing objects

in front of the camera. So in the subsequent frames

ﬁne texture loses. Figure 7(b) shows decrease in fea-

ture amount on average bases with the increase in im-

age number. The interframe displacement was large

enough that in no case the referenced approach is able

to track the plane.

0 5 10 15 20

tracking error (px)

image number

Bravo

Chicken

China

Daisy

Donuts

Biscuit

Juice

Garment

Monster

Rice

Minimum

Maximum

0 5 10 15 20

100

150

200

number of features

image number

Bravo

Chicken

China

Daisy

Donuts

Biscuit

Juice

Garment

Monster

Rice

Figure 7: Testing with real sequences: (a) tracking error, (b)

feature decay.

Sequences are acquired without diffused lighting.

Figure 8 conﬁrms this. Having success with this

shows robustness of the approach against illumination

changes. To further show robustness of the approach

ICPRAM 2012 - International Conference on Pattern Recognition Applications and Methods

320

against partial occlusion, Figure 9 presents two in-

stances of tracking under extreme occlusion for each

plane before it leaves ﬁeld of view.

seq/plane3D0001

seq/plane3D0006

Figure 8: Two images of a sequence in which appearance

of the plane changes due to non-diffused lighting.

Figure 9: Two instances of tracking each plane under ex-

treme occlusion. Top to bottom followed by left to right:

(a) Daisy, (b) Donuts, (c) Rice, (d) China, (e) Juice, (f) Gar-

ment, (g) Monster, (h) Chicken, (i) Biscuit, (j) and Bravo.

5 CONCLUSIONS

A hybrid approach by fusing point and template based

tracking to track planar-textured targets with large in-

terframe displacement is introduced. The approach is

ﬂexible to adapt change in scene. It makes an efﬁ-

cient use of object and scene detail. Its evaluation is

made using both the simulated and real sequences. In

the ﬁrst case, the approach performs better in terms

of accuracy, convergence, and interframe displace-

ment. In the second case, a consistent behavior is seen

with the change in target. Robustness of the approach

against partial occlusion and illumination changes is

also shown. One may argue the approach is compu-

tationally expensive in terms of feature employed. To

compensate this, a part of image is exploited. More-

over, faster convergence further weakens the argu-

ment, particularly, when the interframe displacement

is large. At the application level, scope of trajectory

measurement is extended to packaging industry con-

sidering industrial environment.

REFERENCES

Azad, P. (2009). State of the art in object recognition and

pose estimation. Cognitive Systems Monographs: Vi-

sual Perception for Manipulation and Imitation in Hu-

manoid Robots.

Baker, S. and Matthews, I. (2004). Lucas-kanade 20 years

on: A unifying framework. IJCV.

Barteit, D., Frank, H., Pongratz, M., and Kupzog, F. (2009).

Measuring the intersection of a thrown object with a

vertical plane. In IEEE INDIN.

Bjorkman, M. and Kragic, D. (2004). Combination of

foveal and peripheral vision for object recognition and

pose estimation. In IEEE ICRA.

Choi, C. and Christensen, H. I. (2010). Real-time 3d model-

based tracking using edge and keypoint features for

robotic manipulation. In IEEE ICRA.

Collet, A., Berenson, D., Srinivasa, S. S., and Ferguson, D.

(2009). Object recognition and full pose registration

from a single image for robotic manipulation. In IEEE

ICRA.

Ekvall, S., Kragic, D., and Hoffmann, F. (2005). Object

recognition and pose estimation using color cooccur-

rence histograms and geometric modeling. Image and

Vision Computing.

Frank, H., Barteit, D., and Kupzog, F. (2008). Throwing or

shooting - a new technology for logistic chains within

production systems. In IEEE TePRA.

Frank, H., Mittnacht, A., and Scheiermann, J. (2009).

Throwing of cylinder-shaped objects. In IEEE/ASME

AIM.

Jurie, F. and Dhome, M. (2002). Hyperplane approximation

for template matching. IEEE TPAMI.

Ladikos, A., Benhimane, S., and Navab, N. (2009). High

performance model-based object detection and track-

ing. incollection-Theory and Applications: Computer

Vision and Computer Graphics.

Lepetit, V. and Fua, P. (2005). Monocular model-based 3d

tracking of rigid objects. FTCGV.

Lepetit, V., Pilet, J., and Fua, P. (2004). Point matching as a

classiﬁcation problem for fast and robust object pose

estimation. In IEEE CVPR.

Lieberknecht, S., Benhimane, S., Meier, P., and Navab, N.

(2010). Benchmarking template-based tracking algo-

rithms. Virtual Reality.

Mei, C., Benhimane, S., Malis, E., and Rives, P. (2008).

Efﬁcient homography-based tracking and 3-d recon-

struction for single-viewpoint sensors. IEEE TRO.

Rosten, E. and Drummond, T. (2005). Fusing points and

lines for high performance tracking. In IEEE ICCV.

Sangle, P., Kutty, K., and Patil, A. (2011). A method for

generation of panoramic view based on images ac-

quired by a moving camera. IJCA.

Vacchetti, L., Lepetit, V., and Fua, P. (2004a). Combining

edge and texture information for real-time accurate 3d

camera tracking. In IEEE/ACM ISMAR.

Vacchetti, L., Lepetit, V., and Fua, P. (2004b). Stable real-

time 3d tracking using online and ofﬂine information.

IEEE TPAMI.

Wagner, D., Reitmayr, G., Mulloni, A., Drummond, T., and

Schmalstieg, D. (2008). Pose tracking from natural

features on mobile phones. In IEEE/ACM ISMAR.

TRACKING PLANAR-TEXTURED OBJECTS - On the Way to Transport Objects in Packaging Industry by Throwing

and Catching

321