DEAL EFFECT CURVE AND PROMOTIONAL MODELS

Using Machine Learning and Bootstrap Resampling Test

Cristina Soguero-Ruiz

, Francisco Javier Gimeno-Blanes

, Inmaculada Mora-Jiménez

María Pilar Martínez-Ruiz

and José Luis Rojo-Álvarez

Dep. of Signal Theory and Communications, University Rey Juan Carlos, Madrid, Spain

Dep. of Signal Theory and Communications, University Miguel Hernández, Elche, Spain

Dep. of Marketing, University Castilla La Mancha, Cuenca, Spain

Keywords:

Deal effect curve, Marketing, Multilayer perceptron, Bootstrap resampling, Promotional models.

Abstract:

Promotional sales have become in recent years a paramount issue in the marketing strategies of many compa-

nies, specially in the current economic situation. Empirical models of consumer promotional behavior, mostly

based on machine learning methods, are becoming more usual than theoretical models, given the complex-

ity of the promotional interactions and the availability of electronic recordings. However, the performance

description and comparison among promotion models are usually made in terms of absolute and empirical

values, which is a limited handling of the information. Here we ﬁrst propose to use a simple nonparametric

statistical tool, the paired bootstrap resampling, for establishing clear cut-off test based comparisons among

methods for machine learning based promotional models, by simply taking into account the estimated sta-

tistical distribution of the actual risk. The method is used to determine the existence of actual statistically

signiﬁcant differences in the performance of different machine design issues for multilayer perceptron based

marketing models, in a real database of everyday goods (milk products). Our results show that paired bootstrap

resampling is a simple and effective procedure for promotional modeling using machine learning techniques.

1 INTRODUCTION

In the present economic landscape, given by eco-

nomic instability and changes in the acquisition be-

havior of consumers, food retailers have turned to

the modiﬁcation of the conventional commercialdeci-

sions implemented in their shops (Haluk and Özgül,

2007). Therefore, sales promotion have become in

recent years a fundamental tool for retailers’ strate-

gies, and the investment in this setting has highly

increased in the marketing strategy, with percentage

even above 50% (Blattberg and Neslin, 1990). Bet-

ter understanding of the sales promotion dynamics

has receivedgrowing attention from machine learning

and data mining techniques, which are powerful tools

to extract information from examples in past quanti-

tative experience (Leeﬂang and Wittingk, 2000).

However, operational problems can arise in ma-

chine learning promotional modeling, when based

on nonlinear estimation techniques, for evaluating

and demonstrating working hypothesis (Heerde et al.,

2001; Liu et al., 2004; Martínez-Ruiz et al., 2006;

Martínez-Ruiz et al., 2006; Wang et al., 2008). First,

conventional parametric tests are often not appropri-

ate, because given the heavy tails and heteroscedas-

ticity for the prediction residuals, Gaussianity is no

longer a working property for them. Second, spe-

cial attention has to be paid in order to be sure to be

working with hypothesis tests in terms of actual risk

comparisons, and not of empirical risk comparisons,

to avoid as much as possible the unaware presence

of overﬁtting in the machine learning based models.

And third, as an indirect consequence of not having a

clear cut-off test, their results cannot always be easily

compared across studies, even when they have been

made on the same data set.

Therefore, the objective of this work was to pro-

pose an operative procedure for model diagnosis in

the context of using machine learning techniques for

promotional efﬁciency applications. We used an em-

pirical approach, based on machine learning tech-

niques for analyzing the sales dynamics in a speciﬁc

product, namely, milk, which is a everyday consumer

products, and we analyzed its response to promotional

537

Soguero-Ruiz C., Javier Gimeno-Blanes F., Mora-Jiménez I., Pilar Martínez-Ruiz M. and Luis Rojo-Álvarez J. (2012).

DEAL EFFECT CURVE AND PROMOTIONAL MODELS - Using Machine Learning and Bootstrap Resampling Test.

In Proceedings of the 1st International Conference on Pattern Recognition Applications and Methods, pages 537-540

DOI: 10.5220/0003732705370540

 SciTePress

discounts in a retailer environment by means of Multi

Layer Perceptron (MLP) neural networks.

2 TEST FOR ACTUAL RISK

Artiﬁcial Neural Networks (ANN) are multiparamet-

ric nonlinear models, and they are capable of learning

from samples and discovering complex relationships

among variables which can be hidden in the data vol-

ume available in the training set (Bishop, 1995). In

the MLP network, one of the mostly used ANN, there

is one input neuron for each variable in input pattern

x, and as many output neurons as output variables to

be estimated (i.e., y can be a multivariable output),

hence the number of hidden layers and the number of

neurons in each have to be chosen during the design

process.

Several merit ﬁgures can be used for benchmark-

ing estimation models with machine learning tech-

niques. On the one hand, absolute merit ﬁgures give

an idea of the actual magnitude of the averaged error,

being usual being the Mean Absolute Error (MAE),

given by MAE =

∑

i=1

| f(x

) − y

| whereas relative

merit ﬁgures can give a better idea of the amount of

variability in the data which has ben actually captured

by the model. In this work, a cross-validation tech-

nique is used for benchmarking and comparing sev-

eral model architectures (Haykin, 1999).

A bootstrap resample is a data subset is drawn

from the observation set according to their empirical

pdf ˆp

y,x

(x, y). Hence, the true pdf is approximated

by the empirical pdf estimated from the observations,

and the bootstrap resample can be seen as a sampling

with replacement process of the observed data, this

is, ˆp

y,x

(x, y) 7→ V

∗

= {(x

∗

, y

∗

);i = 1, ..., N}, where

superscript

∗

represents, in general, any observation,

functional, or estimator, that arises from the bootstrap

resampling process. A partition of V

∗

in terms of

resample V

∗

(b) is given by V = {V

∗

(b), V

∗

out

(b)},

where V

∗

(b) is the subset of observations that are in-

cluded in resample b, and V

∗

out

(b) is the subset of non

included observations. A bootstrap replication of an

estimator is given by its calculation constrained to the

observations included in the bootstrap resample. The

bootstrap replication of the empirical risk estimator

given by a calculation operator t and its weights w is

∗

emp

(b) = t ({w}, V

∗

(b)). The scaled histogram ob-

tained from B resamples is an approximation to the

true pfd of the empirical risk. However, further ad-

vantage can be obtained by calculating the bootstrap

replication of the risk estimator on the non included

observations. By doing so, rather than estimating the

empirical risk, we are in fact obtaining the replica-

tion of the actual risk, i.e.,

∗

act

(b) = t ({w}, V

∗

out

(b)).

The bootstrap replication of the averaged actual risk

can be obtained by just taking the average of

∗

act

(b)

for b = 1, . . . , B. Moreover, the replications of the pdf

of the model merit ﬁgures can provide conﬁdence in-

tervals (CI) for the performance. A typical range for

B in practical applications can be from 100 to 2000

bootstrap resamples.

For giving a clear cut-off test allowing us to

benchmark the signiﬁcance of the observed differ-

ences between the performance of two different ma-

chine learning based promotional models, we use

here the bootstrap nonparametric resampling proce-

dure. The use of bootstrap resampling is supported by

the previous observation of heavy tails in the resid-

ual distribution when using this kind of models, as

well as bimodalities, and other non-Gaussian effects

(Efron and Tibshirani, 1997). The procedure can

be readily adapted in order to benchmark the perfor-

mance of two different machine learning techniques

(or a given algorithm with different settings), by us-

ing a paired bootstrap resampling, in which the same

resamples are to be considered in the benchmarked

models. In this work, when resampling two different

models model

and model

, results have been com-

pared according to three different statistics, namely,

∆MAE = MAE(model

) − MAE(model

) (1)

∆CI = ∆CI(model

) − ∆CI(model

) (2)

∆CI

sup

= CI

sup

(model

) −CI

sup

(model

) (3)

where CI has been obtained for a 95% level, and

∆CI(model

) = CI

sup

(model

)−CI

inf

(model

). These

statistics provide a description in terms of the average

magnitude of the error, but also in terms of its scat-

ter. In general, given that it is complicated to obtain

closed forms for CI of scatter measurements, boot-

strap resampling represents a useful approximation

for making it possible.

3 EXPERIMENTAL RESULTS

We used a real database with a everyday consumer

products corresponding to the milk product category.

Speciﬁcally 6 products were analyzed corresponding

to 6 different promotional models, as indicated in Ta-

ble 1. The number of daily sold units were available

in the same retailer (supermarket) during one year, ex-

cluding the weekends. Up to 304 examples (patterns)

were available for each category, corresponding to the

days when transactions were recorded in the super-

market. They were aggregated into 43 weeks, in order

not to have a too strong effect of weekly seasonality

in this database. In all models, there are three kinds

ICPRAM 2012 - International Conference on Pattern Recognition Applications and Methods

538

of input variable: price indices x

, direct discount x

and baseline BL. Regarding the price indices variable

they are deﬁned as PI(i, t) =

prom

(i,t)

reg

(i,t)

, where P

reg

(i, t)

and P

prom

(i, t) are the regular and promotional price,

respectively, of product i at week t. Hence, the price

index gives the relative variation between the promo-

tional price and the regular price, and its value is 1

whenever both are equal.

The input pattern was given by concatenation of

the three kind of input variables, x = [x

, x

, BL].

The output of each model is given by the sold

units for that particular product. Hence, the

promotional model can be expressed as y(i, t) =

f(x

(i, t), x

(i, t), BL(t)), where y(i, t) is the num-

ber of sold units for the i − th product during week

t; x

(i, t) = [PI

(i, t), ..., PI

(i, t)] is a vector with

the price indices of product i during week t, with n

6; x

(i, t) is the direct discount dichotomous variable

for product i during week t; and BL(t) is the baseline

variable at week t. The input metric variables were

the same for all the models.

We considered the decision of two different de-

sign criteria for MLP-based promotional models. On

the one hand, the MLP for estimation problems can

give a multiple output, which in principle could ben-

eﬁt from the consideration of joint cross-information

among models. However, there is no warranty that

a multiple output architecture will work better than a

separate MLP single model for each product. On the

other hand, another design criterion is the use of dif-

ferent activation functions in the hidden layer nodes,

being two widely used forms the linear and the sig-

moid logistic activation. Given that there is no theo-

retical result, this function has to be chosen for each

data mining model.

For this purpose, free parameters were tuned in

the MLP for the single output set of models using

LOO. Then paired bootstrap test was used to check

which architecture can be pointed as more convenient,

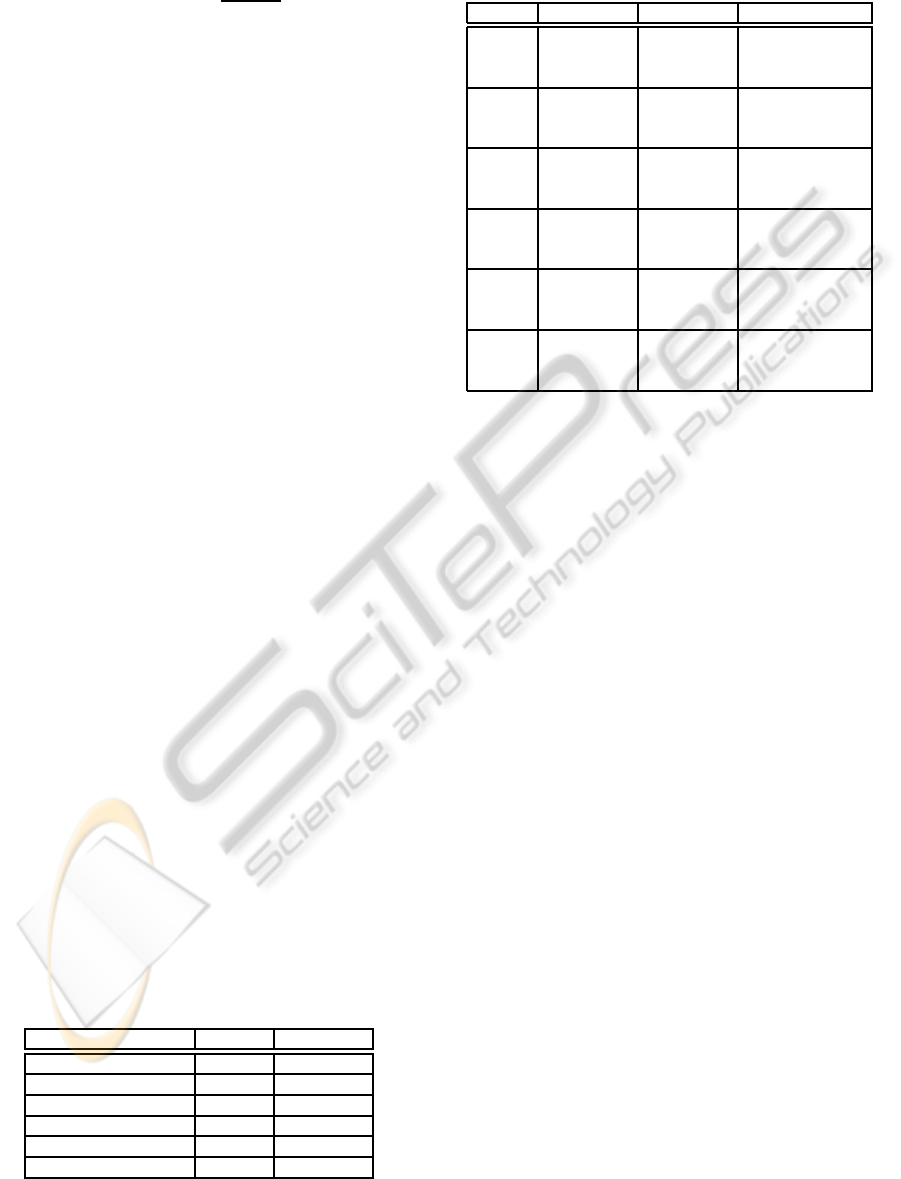
in terms of the previously used merit ﬁgures. Table 1

shows the comparison of the number of neurons in the

hidden layer (n

) for both architectures. Note that n

has a relevant variation in terms of different products

Table 1: Free parameter tuning in terms of n

for MLP with

multiple and with single output, for Milk Data Base.

(MLP) n

(MLP_ind)

Model 1 (Asturiana) 17 15

Model 2 (Ato) 17 8

Model 3 (House brand) 17 1

Model 4 (Pascual Calcio) 17 6

Model 5 (Pascual Clasica) 17 8

Model 6 (Puleva Calcio) 17 14

Table 2: Single vs multiple output MLP for Milk products,

using MAE merit ﬁgure. See text for details.

MLP

ind

MLP MLP

ind

vs MLP

Model 1 357.3 || 359.1 320.7 || 321.6 66.4 [-193.9,577.1]

[266.2,463.2] [248.5,401.5] 37.0 [-50.8,130.3]

65.4 [-192.1,569.9]

Model 2 222.6 || 222.3 199.6 || 200.4 26.2 [-114.1,192.1]

[180.8,267.2] [157.1,247.9] 28.6 [-17.9,72.9]

50.2 [-69.4,217.6]

Model 3 135.8 || 136.3 152.5 || 152.5 -66.9 [-144.6,49.3]

[105.5,167.3] [119.2,188.6] -14.4 [-36.0,7.8]

-57.5 [-124.6,62.0]

Model 4 59.6 || 59.7 72.3 || 72.4 -7.8 [-49.2,18.7]

[44.2,77.4] [58.5,88.3] -12.8 [-27.2,1.4]

-13.4 [-54.5,7.0]

Model 5 305.2 || 310.8 198.7 || 197.8 258.8 [63.9,528.1]

[227.9,397.5] [148.5,250.7] 103.3 [21.0,186.2]

267.3 [74.9,544.1]

Model 6 226.7 || 226.7 125.6 || 125.0 304.5 [98.2,447.1]

[167.3,293.2] [97.8,155.3] 100.7 [37.8,163.1]

304.5 [108.6,473.2]

with single output, and also, that n

is sensibly larger

for multiple output MLP architecture.

Table 2 shows the MAE and the comparison

among both schemes, with the sigmoid activation

function, for all the products in the data base. Indi-

vidual models for each product with single output is

denoted as MLP

ind

, whereas multiple output architec-

ture is denoted as MLP. Each cell in the second and

third columns contains the empirically estimated ac-

tual risk (i.e., averaged from LOO estimation of MAE

for each case), together with the bootstrap estimate

of the averaged MAE, namely, the mean (upper line,

right), and the 95% CI of this sample mean. The ap-

parently best model of both, in terms of empirical

LOO-MAE, is highlighted in bold. The comparison

between both models is represented in the last col-

umn, showing the average and the 95% CI for ∆MAE,

∆CI, and ∆CI

sup

, in the ﬁrst, second, and third line

of the cell, respectively. In this column, bold is used

for highlighting the CI which yield signiﬁcant differ-

ences with respect to the paired bootstrap test, i.e.,

those statistics for the differential merit ﬁgure whose

estimated difference does not overlap the zero level.

It can be observed that, for Models 3 and 4, the

performance is apparently better when using individ-

ual architectures, whereas Models 1, 2, 5, and 6 are

better when considering the joint architecture. How-

ever, only signiﬁcant differences are present in Mod-

els 5 and 6, both in terms of averaged and scatter

MAE, hence the most advantageous situation is to use

a multiple output architecture. No signiﬁcant differ-

ences are sustained by the paired bootstrap test for

Models 1, 2, 3 and 4. In general terms, we can con-

clude that, for this Milk Data Base, it is better to con-

DEAL EFFECT CURVE AND PROMOTIONAL MODELS - Using Machine Learning and Bootstrap Resampling Test

539

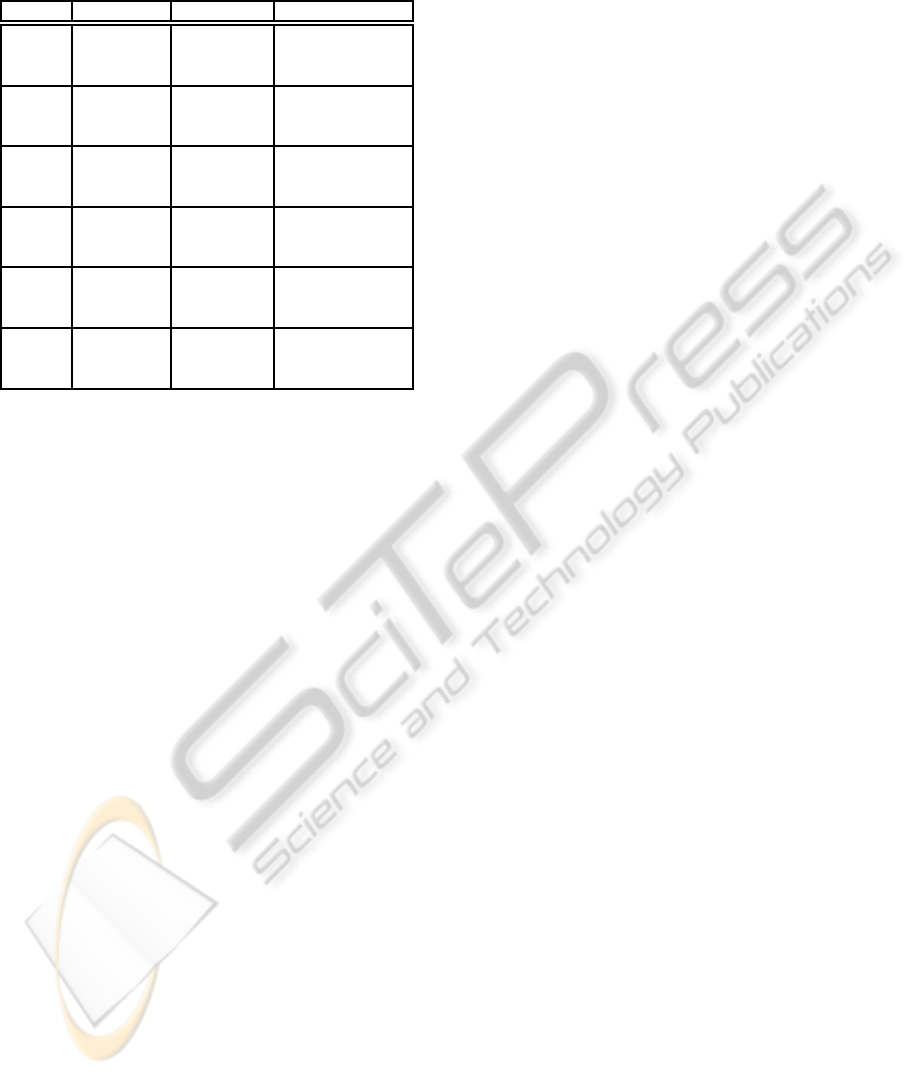
Table 3: Sigmoid vs linear MLP for Milk products, using

MAE merit ﬁgure. See text for details.

Sigmoid Linear Sigmoid vs Linear

Model 1 358.2 || 368.3 325.7 || 326.3 31.5 [-66.7,138.9]

[258.0,461.3] [252.4,414.2] 140.3 [-128.9,583.3]

141.0 [-118.1,584.0]

Model 2 235.1 || 235.5 203.8 || 205.6 32.0 [-4.6,67.5]

[195.2,281.7] [156.8,256.2] -36.56 [-219.9,85.8]

-25.6 [-185.5,91.3]

Model 3 143.3 || 148.6 137.7 || 140.7 6.1 [-14.1,29.1]

[111.9,174.9] [106.4,171.1] 2.24 [-50.5,84.3]

12.5 [-36.6,87.0]

Model 4 56.9 || 58.4 64.7 || 66.4 -8.9 [-18.8,2.0]

[40.36,78.2] [48.63,82.6] 0.79 [-28.6,56.7]

2.4 [-29.0,54.3]

Model 5 347.8 || 360.1 191.9 || 190.2 153.4 [68.1,242.2]

[271.9,426.3] [154.7,231.2] 372.8 [121.1,555.6]

377.8 [116.5,549.5]

Model 6 245.5 || 255.2 116.3 || 116.1 127.1 [69.2,187.4]

[190.7,302.3] [90.4,142.9] 335.5 [134.8,445.8]

346.8 [164.4,465.1]

sider multiple output MLP architecture in those prod-

ucts showing a more stable behavior, and hence, re-

sults can be strongly dependent on the speciﬁc prod-

uct.

For the case of MLP with single output, the in-

creased performance due to the use of linear or sig-

moid logistic activation function in the hidden layer

nodes, was further analyzed. Table 3 shows the same

information than in the previous analysis, for the

paired comparison of both models in each product,

after having ﬁxed the individual output architecture

design parameter, according to the previous result. In

this case, the empirical MAE is lower when using lin-

ear activation functions in all models except Model 4.

Signiﬁcant differences are supported by the bootstrap

test only in Models 5 and 6, but with strong con-

sistency for all the statistics evaluated for the merit

ﬁgure distribution. In general terms, it can be con-

cluded that using linear activation function in the hid-

den nodes yields better results consistently in the Milk

Data Base analyzed here.

4 CONCLUSIONS

In the present work, a method for giving a systematic

statistical comparison between two machine-learning

based models in promotional sales modeling has been

presented. The method has its bases on the princi-

ples of the estimation of statistical descriptors of ac-

tual risk and their pdf, by means of bootstrap resam-

pling, and on the use of the increment in the merit

ﬁgure. The consideration of paired differences gives

a suitable approach for controlling the standard error

of the statistical description of the merit ﬁgures, hence

allowing clear cut-off tests.

ACKNOWLEDGEMENTS

This work was supported by Research Project from

Fundación Ramón Areces.

REFERENCES

Bishop, C. (1995). Neural networks for pattern recognition.

Oxford University Press, Oxford.

Blattberg, R. and Neslin, A. (1990). Sales Promotion: Con-

cepts, Methods and Strategies. Prentice-Hall.

Efron, B. and Tibshirani, R. J. (1997). An introduction to

the bootstrap. Chapman & Hall, New York.

Haluk, M. and Özgül, E. (2007). The relationship between

marketing strategies and performance in a economic

crisis. Journal of Marketing Practice: Applied Mar-

keting Science, 25(4):326–342.

Haykin, S. (1999). Neural networks. A comprehensive foun-

dation. Presntice-Hall, New Jersey.

Heerde, H. J. V., Leeﬂang, P. S. H., and Wittink, D. R.

(2001). Semiparametric analysis to estimate the

deal effect curve. Journal of Marketing Research,

38(2):197–215.

Leeﬂang, P. S. H. and Wittingk, D. (2000). Building mod-

els for marketing decisions: past, present and future.

International Journal of Resarch in Marketing, 17(2-

3):178–185.

Liu, B. H., Kong, F. S., and Yang, B. (2004). PEPP: Proﬁts

Estimation in Prices Promotion. In Proc of 2004 In-

tern Conf Mach Learn Cybern, volume 2, pages 1146–

1151, Australia.

Martínez-Ruiz, M. P., Mollá-Descals, A., Gómez-Borja,

M. A., and Rojo-Álvarez, J. L. (2006). Evaluating

temporary retail price discounts using semiparametric

regression. Journal of Product & Brand Management,

15(1):73–80.

Martínez-Ruiz, M. P., Mollá-Descals, A., and Rojo-

Álvarez, J. L. (2006). Using daily store-level data to

understand price promotion effects in a semiparamet-

ric regression model. Retailing and Consumer Ser-

vices, 3(13):193–204.

Wang, T., Li, Y. Q., and Zhao, S. F. (2008). Application

of SVM Based on Rough Set in Real Estate Prices

Prediction. In 4th Int Conf on Networking, Comm and

Mob Comp, pages 1–4, Dalian.

ICPRAM 2012 - International Conference on Pattern Recognition Applications and Methods

540