
CLASSIFICATION OF 3D URBAN SCENES
A Voxel based Approach
Ahmad Kamal Aijazi
1,2
, Paul Checchin
1,2
and Laurent Trassoudaine
1,2
1
Clermont Universit´e, Universit´e Blaise Pascal, Institut Pascal, BP 10448, F-63000 Clermont-Ferrand, France
2
CNRS, UMR 6602, Institut Pascal, F-63171 Aubiere, France
Keywords:
3D point cloud segmentation, Hybrid data, Super-Voxels, Urban scene classification.
Abstract:
In this paper we present a method to classify urban scenes based on a super-voxel segmentation of sparse 3D
data. The 3D point cloud is first segmented into voxels, which are then joined together by using a link-chain
method rather than the usual region growing algorithm to create objects. These objects are then classified
using geometrical models and local descriptors. In order to evaluate our results a new metric is presented,
which combines both segmentation and classification results simultaneously. The effects of voxel size and
incorporation of RGB color and intensity on the classification results are also discussed.
1 INTRODUCTION
The automatic segmentation and classification of 3D
urban data have gained widespread interest and im-
portance in the scientific community due to the in-
creasing demand of urban landscape analysis and car-
tography for different popular applications, coupled
with the advances in 3D data acquisition technology.
The automatic extraction (or partially supervised) of
important urban scene structures such as roads, veg-
etation, lamp posts, and buildings from 3D data has
been found to be an attractive approach to urban scene
analysis because it can tremendously reduce the re-
sources required in analyzing the data for subsequent
use in 3D city modeling and other algorithms.
A common way to quickly collect 3D data of
urban environments is by using an airborne LiDAR
(Sithole and Vosselman, 2004), (Verma et al., 2006),
where the LiDAR scanner is mounted in the bottom of
an aircraft. Although this method generates a 3D scan
in a very short time period, there are a number of lim-
itations in 3D urban data collected from this method
such as a limited viewing angle.
These limitations are overcome by using a mobile
terrestrial or ground based LiDAR system in which
unlike the airborne LiDAR system, the 3D data ob-
tained is dense and the point of view of the images
is closer to the urban landscapes. However this of-
fers both advantages and disadvantages when pro-
cessing the data. The disadvantages include the de-
mand for more processing power required to handle
the increased volume of 3D data. On the other hand,
the advantage is the availability of a more detailed
sampling of the object’s lateral views, which provides
a more comprehensive model of the urban structures
including building facades, lamp posts, etc.
Our work revolves around the segmentation and
then classification of ground based 3D data of ur-
ban scenes. The aim is to provide an effective pre-
processing step for different subsequent algorithms or
as an add-on boost for more specific classification al-
gorithms.
2 RELATED WORK
In order to fully exploit3D point clouds, effective seg-
mentation has proved to be a necessary and critical
pre-processing step in a number of autonomous per-
ception tasks.
Earlier works including (Anguelov et al., 2005),
(Lim and Suter, 2007) and (Munoz et al., 2009) used
small sets of specialized features, such as local point
density or height from the ground, to discriminate
only few object categories in outdoor scenes, or to
separate foreground from background. Lately, seg-
mentation has been commonly formulated as graph
clustering. Instances of such approaches are Graph-
Cuts including Normalized-Cuts and Min-Cuts.
(Golovinskiy and Funkhouser, 2009) extended
Graph-Cuts segmentation to 3D point clouds by us-
61
Aijazi A., Checchin P. and Trassoudaine L. (2012).
CLASSIFICATION OF 3D URBAN SCENES - A Voxel based Approach.
In Proceedings of the 1st International Conference on Pattern Recognition Applications and Methods, pages 61-70
DOI: 10.5220/0003733100610070
Copyright
c
SciTePress

ing k-Nearest Neighbors (k-NN) to build a 3D graph.
In this work edge weights based on exponential decay
in length were used. But the limitation of this method
is that it requires prior knowledge of the location of
the objects to be segmented.
Another segmentation algorithm for natural im-
ages, recently introduced by Felzenszwalb and Hut-
tenlocher (FH) (Felzenszwalb and Huttenlocher,
2004), has gained popularity for several robotic ap-
plications due to its efficiency. (Zhu et al., 2010) pre-
sented a method in which a 3D graph is built with
k-NN while assuming the ground to be flat for re-
moval during pre-processing. 3D partitioning is then
obtained with the FH algorithm. We have used the
same assumption.
(Triebel et al., 2010) modified the FH algorithm
for range images to propose an unsupervised proba-
bilistic segmentation technique. In this approach, the
3D data is first over-segmentedduringpre-processing.
(Schoenberg et al., 2010) have applied the FH al-
gorithm to colored 3D data obtained from a co-
registered camera laser pair. The edge weights are
computed as a weighted combination of Euclidean
distances, pixel intensity differences and angles be-
tween surface normals estimated at each 3D point.
The FH algorithm is then run on the image graph to
provide the final 3D partitioning. The evaluation of
the algorithm is done on road segments only.
(Strom et al., 2010) proposed a similar approach
but modified the FH algorithm to incorporate angle
differences between surface normals in addition to the
differences in color values. Segmentation evaluation
was done visually without ground truth data. Our
approach differs from the above mentioned methods
as, instead of using the properties of each point for
segmentation resulting in over segmentation, we have
grouped the 3D points based on Euclidian distance
into voxels and then assigned normalized properties
to these voxels transforming them into super-voxels.
This not only prevents over segmentation but in fact
reduces the data set by many folds thus reducing post-
processing time.
A spanning tree approach to the segmentation
of 3D point clouds was proposed in (Pauling et al.,
2009). Graph nodes represent Gaussian ellipsoids as
geometric primitives.
These ellipsoids are then merged using a tree
growing algorithm. The resulting segmentation is
similar to a super-voxel type of partitioning with vox-
els of ellipsoidal shapes and various sizes. Unlike
this method, our approach uses cuboids of different
shapes and sizes as geometric primitives and a link-
chain method to group them together. In the litera-
ture survey we also find some segmentation methods
based on surface discontinuities such as (Moosmann
et al., 2009) who used surface convexity in a terrain
mesh as a separator between objects.
In the past, research related to 3D urban scene
classification and analysis had been mostly performed
using either 3D data collected by airborne LiDAR
for extracting bare-earth and building structures (Lu
et al., 2009) (Vosselman et al., 2005) or 3D data col-
lected from static terrestrial laser scanners for extrac-
tion of building features such as walls and windows
(Pu and Vosselman, 2009). In (Lam et al., 2010) the
authors extracted roads and objects just around the
roads like road signs. They used a least square fit
plane and RANSAC method to first extract a plane
from the points followed by a Kalman filter to ex-
tract roads in an urban environment. A method of
classification based on global features is presented in
(Halma et al., 2010) in which a single global spin
image for every object is used to detect cars in the
scene while in (Rusu et al., 2010) a Fast Point Fea-
ture Histogram (FPFH) local feature is modified into
global feature for simultaneous object identification
and view-point detection. Classification using local
features and descriptors such as Spin Image (John-
son, 1997), Spherical Harmonic Descriptors (Kazh-
dan et al., 2003), Heat Kernel Signatures (Sun et al.,
2009), Shape Distributions (Osada et al., 2002), 3D
SURF feature (Knopp et al., 2010) is also found in
the literature survey. There is also a third type of
Classification based on Bag Of Features (BOF) as dis-
cussed in (Liu et al., 2006). In (Lim and Suter, 2008)
a method of multi-scale Conditional Random Fields
is proposed to classify 3D outdoor terrestrial laser
scanned data by introducing regional edge potentials
in addition to the local edge and node potentials in
the multi-scale Conditional Random Fields. This is
followed by fitting plane patches onto the labeled ob-
jects such as building terrain and floor data using the
RANSAC algorithm as a post-processing step to ge-
ometrically model the scene. (Douillard et al., 2009)
presented a method in which 3D points are projected
on to the image to find regions of interest for classifi-
cation.
In our work we use geometrical models based on
local features and descriptors to successfully classify
different segmented objects represented by groups of
voxels in the urban scene. Ground is assumed to be
flat and is used as an object separator. Our segmen-
tation technique is discussed in Section 3. Section 4
deals with the classification of these segmented ob-
jects. In Section 5 a new evaluation metric is intro-
duced to evaluate both segmentation and classifica-
tion together while in Section 6 we present the results
of our work. Finally, we conclude in Section 7.
ICPRAM 2012 - International Conference on Pattern Recognition Applications and Methods
62

3 VOXEL SEGMENTATION
3.1 Voxelisation of Data
When dealing with large 3D data sets, the computa-
tional cost of processing all the individual points is
very high, making it unpractical for real time applica-
tions. It is therefore sought to reduce these points by
grouping or removing redundant or un-useful points
together. Similarly, in our work the individual 3D
points are clustered together to form a higher level
representation or voxel as shown in Figure 1.
Figure 1: A number of points is grouped together to form
cubical voxels of maximum size 2r. The actual voxel sizes
vary according to the maximum and minimum values of the
neighboring points found along each axis to ensure the pro-
file of the structure.
For p data points, a number of s voxels, where
s << p, are computed based on k-NN with w = 1/d
given as the weight to each neighbor (where d is the
distance to the neighbor). Let P and Q be two points
in the X, Y and Z coordinate system then d is given
as:
d =
q
(P
X
−Q
X
)
2
+ (P
Y
−Q
Y
)
2
+ (P
Z
−Q
Z
)
2
(1)
The maximum size of the voxel 2r, where r is ra-
dius of ellipsoid, depends upon the density of the 3D
point cloud. In (Lim and Suter, 2008) color values are
also added in this step but it is observed that for rel-
atively smaller voxel sizes, the variation in properties
such as color is not much and just increases computa-
tional cost. For these reasons we have only used dis-
tance as a parameter in this step and the other proper-
ties in the next step of clustering the voxels to form
objects. Also we have ensured that each 3D point
which belongs to a voxel is not considered for further
voxelisation. This not only prevents over segmenta-
tion but also reduces processing time.
For the voxels we use a cuboid because of its sym-
metry which avoids fitting problems while grouping
and also minimizes the effect of voxel shape during
feature extraction.
Although the maximum voxel size is predefined,
the actual voxel sizes vary according to the maximum
and minimum values of the neighboring points found
along each axis to ensure the profile of the structure.
Once these voxels are created we find the proper-
ties of each voxel. These properties include surface
normals, RGB-color, intensity, geometric primitives
such as barycenter, geometrical center, maximum and
minimum values along each axis, etc. Where some of
these properties are averaged and normalized values
of the constituting points, the surface normals are cal-
culated using PCA (Principal Component Analysis).
The PCA method has been proved to perform better
than the area averaging method (Klasing et al., 2009)
to estimate the surface normal.
Given a point cloud data set D = {x
i
}
n
i=1
, the PCA
surface normal approximation for a given data point
p ∈ D is typically computed by first determining the
k-Nearest Neighbors, x
k
∈ D , of p. Given the K
neighbors, the approximate surface normal is then the
eigenvector associated with the smallest eigenvalue of
the symmetric positive semi-definite matrix
P =
K
∑
k=1
(x
k
− p)
T
(x
k
− p) (2)
where p is the local data centroid: p =
1
K
∑
K
j=1
x
j
.
The estimated surface normal is ambiguous in
terms of sign; to account for this ambiguity the dot
product between estimated surface normals is re-
peated using the negative estimated surface normal
of one of the vectors and the minimum result of the
term is selected. Yet for us the sign of the normal
vector is not important as we are more interested in
the orientation. Using this method, a single surface
normal is estimated for all the points belonging to a
voxel and is then associated with that particular voxel
along with the other properties, transforming it into a
super-voxel.
All these properties would then be used in group-
ing these super-voxelsinto objects and then during the
classification of these objects. Instead of using thou-
sands of points in the data set, the advantage of this
approach is that we can now use the reduced number
of super-voxels to obtain similar results for classifica-
tion and other algorithms. In our case, the data sets
of 110, 392, 53,676 and 27,396 points were reduced
to 18,541, 6,928 and 7,924 super-voxels respectively
which were then used for subsequent processing.
3.2 Clustering by Link-chain Method
When the 3D data is converted into super-voxels, the
next step is to group these super-voxels to segment
into distinct objects.
CLASSIFICATION OF 3D URBAN SCENES - A Voxel based Approach
63
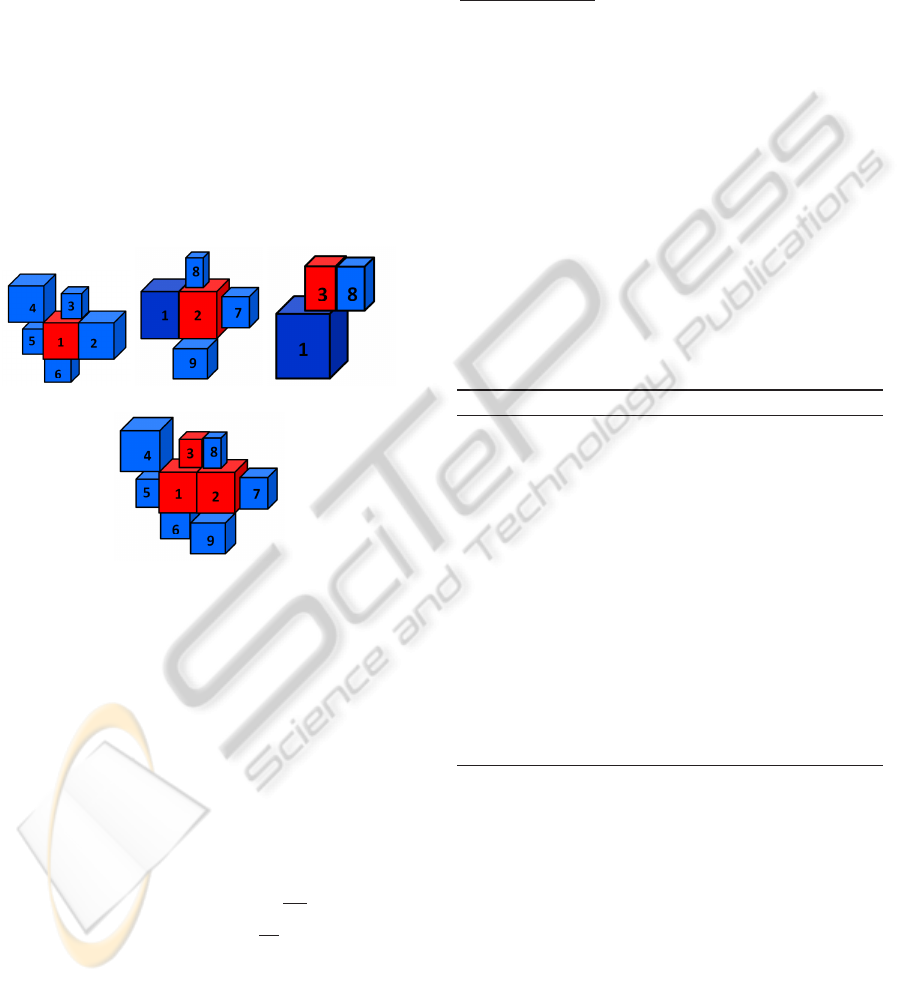
Usually for such tasks a region growing algorithm
(Vieira and Shimada, 2005) is used in which the prop-
erties of the whole growing region may influence
the boundary or edge conditions. This may some-
times lead to erroneous segmentation. Also com-
mon in such type of methods is a node based ap-
proach (Moosmann et al., 2009) in which at every
node, boundary conditions have to be checked in all
5 different possible directions. In our work we have
proposed a link-chain method instead to group these
super-voxels together into segmented objects.
In this method each super-voxel is considered as a
link of a chain. All secondary links attached to each
of these principal links are found. In the final step
all the principal links are linked together to form a
continuous chain removing redundantsecondary links
in the process as shown in Figure 2.
(a) (b) (c)
(d)
Figure 2: Clustering of super-voxels using a link-chain
method is demonstrated. (a) shows super-voxel 1 taken as
principal link in red and all secondary links attached to it
in blue. (b) and (c) shows the same for super-voxel 2 and
3 taken as principal links. (d) shows the linking of princi-
pal links (super-voxels 1, 2 & 3) to form a chain removing
redundant secondary links.
Let V
P
be a principal link and V
n
be the n number
of secondary links then each of the V
n
is linked to
V
P
if and only if the following three conditions are
fulfilled:
V
P
X,Y,Z
−V
n
X,Y,Z
≤ (w
D
+ c
D
) (3)
V
P
R,G,B
−V
n
R,G,B
≤ 3
√
w
C
(4)
|V
P
I
−V
n
I
| ≤ 3
√
w
I
(5)
where, for the principal and secondary link super-
voxels respectively:
• V
P
X,Y,Z
, V
n
X,Y,Z
are the geometrical centers;
• V
P
R,G,B
, V
n
R,G,B
are the mean RGB values;
• V
P
I
, V
n
I
are the mean intensity values;
• w
C
is the color weight equal to the maximum
value of the variances Var(R,G,B);
• w
I
is the intensity weight equal to the maximum
value of the variances Var(I).
w
D
is the distance weight given as
V
P
s
X,Y,Z
+V
n
s
X,Y,Z
2
. Here s
X,Y,Z
is the voxel size
along X, Y & Z axis respectively.
c
D
is the inter-distance constant (along the three
dimensions) added depending upon the density of
points and also to overcome measurement errors,
holes and occlusions, etc. The value of c
D
needs to
be carefully selected depending upon the data.
The orientation of normals is not considered in
this stage to allow the segmentation of complete ob-
jects as one entity instead of just planar faces.
This segmentation method ensures that only the
adjacent boundary conditions are considered for seg-
mentation with no influence of a distant neighbor’s
properties. This may prove to be more adapted to
sharp structural changes in the urban environment.
The segmentation algorithm is summarized in Algo-
rithm 1.
Algorithm 1: Segmentation.
1: repeat
2: Select a 3D point for voxelisation
3: Find all neighboring points to be included in
the voxel using k-NN within the maximum
voxel length specified
4: Find all properties of the super-voxel including
surface normal found by using PCA
5: until all 3D points are used in a voxel
6: repeat
7: Specify a super-voxel as a principal link
8: Find all secondary links attached to the princi-
pal link
9: until all super-voxels are used
10: Link all principal links to form a chain removing
redundant links in the process
With this method 18,541, 6,928 and 7,924 super-
voxels obtained from processing 3 different data sets
were successfully segmented into 237, 75 and 41 dis-
tinct objects respectively.
4 CLASSIFICATION OF
OBJECTS
In order to classify these objects, we assume the
ground to be flat and use it as separator between ob-
jects. For this purpose we first classify and segment
out the ground from the scene and then the rest of
ICPRAM 2012 - International Conference on Pattern Recognition Applications and Methods
64

the objects. This step leaves the remaining objects as
if suspended in space, i.e distinct and well separated,
making them easier to be classified as shown in Fi-
gure 3.
Figure 3: Segmented objects in a scene with prior ground
removal.
The ground or roads followed by these objects are
then classified using geometrical and local descrip-
tors. These mainly include:
a. Surface Normals. The orientation of the surface
normals is essential for classification of ground
and building faces. For ground object the surface
normals are along Z-axis (height axis) whereas for
building faces the surface normals are parallel to
the X-Y axis (ground plane), see Figure 4.
b. Geometrical Center and Barycenter. The height
difference between the geometrical center and the
barycenter along with other properties is very use-
ful in distinguishing objects like trees and vegeta-
tion, etc., where:
h(barycenter−geometrical center) > 0
with h being the height function.
c. Color and Intensity. Intensity and color are also
an important discriminating factor for several ob-
jects.
d. Geometrical Shape. Along with the above men-
tioned descriptors, geometrical shape plays an im-
portant role in classifying objects. In 3D space,
where pedestrians and pole are represented as
long and thin with poles being longer, cars and
vegetation are broad and short. Similarly, as roads
represent a low flat plane, the buildings are repre-
sented as large (both in width and height) vertical
blocks.
Using these descriptors we successfully classify
urban scenes into 5 different classes (mostly present
in our scenes) i.e. buildings, roads, cars, poles and
trees. The classification results and a new evaluation
metric are discussed in the following sections.
(a) Normals of building.
(b) Normals of road.
Figure 4: (a) shows surface normals of building super-
voxels are parallel to the ground plane. In (b) it can be
clearly seen that the surface normals of road surface super-
voxels are perpendicular to the ground plane.
5 EVALUATION METRICS
In previous works, different evaluation metrics are in-
troduced for both segmentation results and classifiers
independently. Thus in our work we present a new
evaluation metric which incorporates both segmenta-
tion and classification together.
The evaluation method is based on comparing the
total percentage of super-voxels successfully classi-
fied as a particular object. Let T
i
, i ∈ {1,··· ,N},
be the total number of super-voxels distributed into
objects belonging to N number of different classes,
i.e this serves as the ground truth, and let t
j
i
, i ∈
{1,··· ,N}, be the total number of super-voxelsclassi-
fied as a particular class of type-j and distributed into
objects belonging to N different classes (for example
a super-voxel classified as part of the building class
may actually belong to a tree) then the ratio S
jk
(j is
the class type as well as the row number of the matrix
and k ∈{1, ··· , N}) is given as:
S
jk
=
t
j
k
T
k
These values of S
jk
are calculated for each type of
CLASSIFICATION OF 3D URBAN SCENES - A Voxel based Approach
65
class and are used to fill up each element of the confu-
sion matrix, row by row (refer to Table 1 for instance).
Each row of the matrix represents a particular class.
Thus, for a class of type-1 (i.e. first row of the
matrix) the values of:
True Positive rate, TP = S
11
(i.e the diagonal of the
matrix represents the TPs)
False Positive rate, FP =
∑
N
m=2
S
1m
True Negative rate, TN = (1−FP)
False Negative rate, FN = (1−TP)
The diagonal of this matrix or TPs gives the Seg-
mentation ACCuracy SACC, similar to the voxel
scores recently introduced by (Douillard et al., 2011).
The effects of unclassified super-voxels are automati-
cally incorporated in the segmentation accuracy. Us-
ing the above values the Classification ACCuracy
CACC is given as:
CACC =
TP+ TN
TP+ TN+ FP+ FN
(6)
This value of CACC is calculated for all N types
of classes of objects present in the scene. Overall
Classification ACCuracy OCACC can then be calcu-
lated as
OCACC =
1
N
N
∑
i=1
CACC
i
(7)
where N is the total number of object classes present
in the scene. Similarly, the Overall Segmentation AC-
Curacy OSACC can also be calculated.
The values of T
i
and t
j
i
used above are laboriously
calculated by hand matching the voxeliseddata output
and the final classified super-voxels and points.
6 RESULTS
Our algorithm was validated on 3D data acquired
from different urban scenes on the Campus of Univer-
sity Blaise Pascal in Clermont-Ferrand, France. The
results of three such data sets are discussed here. The
data sets consisted of 27,396, 53, 676 and 110,392
3D points respectively. These 3D points were cou-
pled with corresponding RGB and intensity values.
The results are now summarized.
6.1 Data Set 1
The data set consisting of 27,396 data points was re-
duced to 7,924 super-voxels keeping maximum voxel
size 0.3 m and c
D
= 0.25 m. These super-voxels are
then segmented into 41 distinct objects. The classifi-
cation result of these objects is shown in Figure 5 and
in Table 1.
Table 1: Classification results of data set 1 in the new eval-
uation metrics.
Building Road Tree Pole Car CACC
Building 0.943 0.073 0 0 0 0.935
Road 0.007 0.858 0.015 0.008 0 0.914
Tree 0 0.025 0.984 0 0 0.979
Pole 0 0.049 0 0.937 0 0.944
Car – – – – – –
Overall segmentation accuracy: OSACC 0.930
Overall classification accuracy: OCACC 0.943
6.2 Data Set 2
The data set consisting of 53,676 data points was re-
duced to 6,928 super-voxels keeping maximum voxel
size 0.3 m and c
D
= 0.25 m. These super-voxels are
then segmented into 75 distinct objects. The classifi-
cation result of these objects is shown in Figure 6 and
in Table 2.
Table 2: Classification results of data set 2 in the new eval-
uation metrics.
Building Road Tree Pole Car CACC
Building 0.996 0.007 0 0 0 0.995
Road 0 0.906 0.028 0.023 0.012 0.921
Tree 0 0.045 0.922 0 0 0.938
Pole 0 0.012 0 0.964 0 0.976
Car 0 0.012 0 0 0.907 0.947
Overall segmentation accuracy: OSACC 0.939
Overall classification accuracy: OCACC 0.955
6.3 Data Set 3
The data set consisting of 110,392 data points was
reduced to 18, 541 super-voxels keeping maximum
voxel size 0.3 m and c
D
= 0.25 m. These super-
voxels are then segmented into 237 distinct objects.
The classification result of these objects is shown in
Figure 7 and in Table 3.
Table 3: Classification results of data set 3 in the new eval-
uation metrics.
Building Road Tree Pole Car CACC
Building 0.901 0.005 0.148 0 0 0.874
Road 0.003 0.887 0.011 0.016 0.026 0.916
Tree 0.042 0.005 0.780 0 0 0.867
Pole 0 0.002 0 0.966 0 0.982
Car 0 0.016 0.12 0 0.862 0.863
Overall segmentation accuracy: : OSACC 0.879
Overall classification accuracy: OCACC 0.901
6.4 Effect of Voxel Size on Classification
Accuracy
As the properties of super-voxels are constant mainly
over the whole voxel length and these properties
are then used for segmentation and then classifica-
tion, thus their size impacts the classification process.
However as the voxel size changes, the inter-distance
constant c
D
also needs to be adjusted accordingly.
ICPRAM 2012 - International Conference on Pattern Recognition Applications and Methods
66

(a) 3D data points.
(b) Voxelisation and segmentation into objects.
(c) Labeled points.
Figure 5: (a) Shows 3D data points of data set 1. (b) shows
segmentation of 3D points. (c) shows classification results
(labeled 3D points).
The effect of voxel size on the classification result
was studied. The maximum voxel size and the value
of c
D
was varied from 0.1 m to 1.0 m on data set-1
and corresponding classification accuracy was calcu-
lated. The results are shown in Figure 8(a). Then for
the same variation of maximum voxel size and c
D
the
variation in processing time was studied as shown in
Figure 8(b).
An arbitrary value of time T
a
is chosen for com-
parison purposes (along Z-axis time varies from 0 to
200T
a
). This makes the comparison results indepen-
dent of the processor used, even though the same pro-
(a) 3D data points.
(b) Voxelisation and segmentation into objects.
(c) Labeled points.
Figure 6: (a) Shows 3D data points of data set 2. (b) shows
segmentation of 3D points. (c) shows classification results
(labeled 3D points).
cessor was used for all computations.
The results show that with smaller voxel size the
segmentation and classification results improve (with
a suitable value of c
D
) but the computational cost in-
creases. It is also evident that variation in value of c
D
has no significant impact on time t. It is also observed
that after a certain reduction in voxel size the classi-
fication result does not improve much but the com-
putational cost continues to increase manifolds. As
CLASSIFICATION OF 3D URBAN SCENES - A Voxel based Approach
67

(a) 3D data points.
(b) Voxelisation and segmentation into objects.
(c) Labeled points.
Figure 7: (a) Shows 3D data points of data set 3. (b) shows
segmentation of 3D points. (c) shows classification results
(labeled 3D points).
both OCACC and time (both plotted along Z-axis)
are independent thus using and combining the results
of the two 3D plots in Figure 8 we can find the opti-
mal value (in terms of OCACC and t) of maximum
voxel size and c
D
depending upon the final applica-
tion requirements. For our work we have chosen a
maximum voxel size of 0.3 m and c
D
= 0.25 m.
6.5 RGB Color and Intensity
The effect of incorporating RGB Color and Intensity
on the segmentation and classification results was also
studied. The results are presented in Table 4.
(a) Influence of voxel size on OCACC.
(b) Influence of voxel size on processing time.
Figure 8: (a) is a 3D plot in which the effect of maximum
voxel size and variation on OCACC is shown. In (b) the
effect of maximum voxel size and variation on processing
time is shown. Using the two plots we can easily find the
optimal value for maximum voxel size and c
D
.
Table 4: Overall segmentation and classification accuracies
when using RGB-Color and intensity values.
Data Set
#
Only RGB-Color Intensity with RGB-Color
OSACC OCACC OSACC OCACC
#
1 0.660 0.772 0.930 0.943
#
2 0.701 0.830 0.939 0.955
#
3 0.658 0.766 0.879 0.901
It is observed that incorporating RGB color alone
is not sufficient in an urban environment due to the
fact that it is heavily affected by illumination variation
(part of an object may be under shade or reflect bright
sunlight) even in the same scene. This deteriorates
the segmentation process and hence the classification.
This is perhaps responsible for the lower classification
accuracy as seen in first part of Table 4. It is the rea-
son why intensity values are incorporated as they are
illumination invariant and found to be more consis-
tent. The improved classification results are presented
in second part of Table 4.
ICPRAM 2012 - International Conference on Pattern Recognition Applications and Methods
68

7 CONCLUSIONS
In this work we have presented a super-voxel based
segmentation and classification method for 3D urban
scenes. For segmentation a link-chain method is pro-
posed, which is followed by a classification of objects
using local descriptors and geometrical models. In
order to evaluate our work we have introduced a new
evaluation metric which incorporates both segmenta-
tion and classification results. The results show an
overall segmentation accuracy of 87% and a classifi-
cation accuracy of about 90%.
Our study shows that the classification accuracy
improves by reducing voxel size (with an appropriate
value of c
D
) but at the cost of processing time. Thus
a choice of an optimal value, as discussed, is recom-
mended.
The study also demonstrates the importance of us-
ing intensity values along with RGB colors in the seg-
mentation and classification of urban environment as
they are illumination invariant and more consistent.
The proposed method can also be used as an add-
on boost for other classification algorithms.
ACKNOWLEDGEMENTS
This work is supported by the Agence Nationale de
la Recherche (ANR - the French national research
agency) (ANR CONTINT iSpace&Time – ANR-10-
CONT-23) and by “le Conseil G´en´eral de l’Allier”.
The authors would like to thank Pierre Bonnet and all
the other members of Institut Pascal who contributed
to this project.
REFERENCES
Anguelov, D., Taskar, B., Chatalbashev, V., Koller, D.,
Gupta, D., Heitz, G., and Ng, A. (2005). Discrim-
inative Learning of Markov Random Fields for Seg-
mentation of 3D Scan Data. In Computer Vision and
Pattern Recognition, IEEE Computer Society Confer-
ence on, volume 2, pages 169–176, Los Alamitos, CA,
USA. IEEE Computer Society.
Douillard, B., Brooks, A., and Ramos, F. (2009). A 3D
Laser and Vision Based Classifier. In 5th Int. Conf. on
Intelligent Sensors, Sensor Networks and Information
Processing (ISSNIP), page 6, Melbourne, Australia.
Douillard, B., Underwood, J., Kuntz, N., Vlaskine, V.,
Quadros, A., Morton, P., and Frenkel, A. (2011). On
the Segmentation of 3D LIDAR Point Clouds. In
IEEE Int. Conf. on Robotics and Automation (ICRA),
page 8, Shanghai, China.
Felzenszwalb, P. and Huttenlocher, D. (2004). Ef-
ficient Graph-Based Image Segmentation. Inter-
national Journal of Computer Vision, 59:167–181.
10.1023/B:VISI.0000022288.19776.77.
Golovinskiy, A. and Funkhouser, T. (2009). Min-Cut Based
Segmentation of Point Clouds. In IEEE Workshop on
Search in 3D and Video (S3DV) at ICCV, pages 39 –
46.
Halma, A., ter Haar, F., Bovenkamp, E., Eendebak, P.,
and van Eekeren, A. (2010). Single spin image-ICP
matching for efficient 3D object recognition. In Pro-
ceedings of the ACM workshop on 3D object retrieval,
3DOR ’10, pages 21–26, New York, NY, USA.
Johnson, A. (1997). Spin-Images: A Representation for 3-
D Surface Matching. PhD thesis, Robotics Institute,
Carnegie Mellon University, Pittsburgh, PA.
Kazhdan, M., Funkhouser, T., and Rusinkiewicz, S. (2003).
Rotation Invariant Spherical Harmonic Representa-
tion of 3D Shape Descriptors. In Proceedings of the
2003 Eurographics/ACM SIGGRAPH symposium on
Geometry processing, SGP ’03, pages 156–164, Aire-
la-Ville, Switzerland, Switzerland. Eurographics As-
sociation.
Klasing, K., Althoff, D., Wollherr, D., and Buss, M. (2009).
Comparison of Surface Normal Estimation Methods
for Range Sensing Applications. In IEEE Int. Conf. on
Robotics and Automation, pages 3206 – 3211, Kobe,
Japan.
Knopp, J., Prasad, M., and Gool, L. V. (2010). Orien-
tation invariant 3D object classification using hough
transform based methods. In Proceedings of the ACM
workshop on 3D object retrieval, 3DOR ’10, pages
15–20, New York, NY, USA. ACM.
Lam, J., Kusevic, K., Mrstik, P., Harrap, R., and Greenspan,
M. (2010). Urban Scene Extraction from Mobile
Ground Based LiDAR Data. In International Sympo-
sium on 3D Data Processing Visualization and Trans-
mission, page 8, Paris, France.
Lim, E. and Suter, D. (2007). Conditional Random Field
for 3D Point Clouds with Adaptive Data Reduction.
In International Conference on Cyberworlds, pages
404–408, Hannover.
Lim, E. H. and Suter, D. (2008). Multi-scale Condi-
tional Random Fields for Over-Segmented Irregular
3D Point Clouds Classification. In Computer Vision
and Pattern Recognition Workshop, volume 0, pages
1–7, Anchorage, AK, USA. IEEE Computer Society.
Liu, Y., Zha, H., and Qin, H. (2006). Shape Topics-A Com-
pact Representation and New Algorithms for 3D Par-
tial Shape Retrieval. In IEEE Conf. on Computer Vi-
sion and Pattern Recognition, volume 2, pages 2025–
2032, New York, NY, USA. IEEE Computer Society.
Lu, W. L., Okuma, K., and Little, J. J. (2009). A Hy-
brid Conditional Random Field for Estimating the Un-
derlying Ground Surface from Airborne LiDAR Data.
IEEE Transactions on Geoscience and Remote Sens-
ing, 47(8):2913–2922.
Moosmann, F., Pink, O., and Stiller, C. (2009). Segmen-
tation of 3D Lidar Data in non-flat Urban Environ-
ments using a Local Convexity Criterion. In Proc. of
the IEEE Intelligent Vehicles Symposium (IV), pages
215–220, Nashville, Tennessee, USA.
CLASSIFICATION OF 3D URBAN SCENES - A Voxel based Approach
69

Munoz, D., Vandapel, N., and Hebert, M. (2009). On-
board contextual classification of 3-D point clouds
with learned high-order Markov Random Fields. In
IEEE Int. Conf. on Robotics and Automation (ICRA),
pages 2009 – 2016, Kobe, Japan.
Osada, R., Funkhouser, T., Chazelle, B., and Dobkin, D.
(2002). Shape distributions. ACM Trans. Graph.,
21:807–832.
Pauling, F., Bosse, M., and Zlot, R. (2009). Automatic
Segmentation of 3D Laser Point Clouds by Ellip-
soidal Region Growing. In Australasian Conference
on Robotics & Automation, page 10, Sydney, Aus-
tralia.
Pu, S. and Vosselman, G. (2009). Building Facade Recon-
struction by Fusing Terrestrial Laser Points and Im-
ages. Sensors, 9(6):4525–4542.
Rusu, R., Bradski, G., Thibaux, R., and Hsu, J. (2010).
Fast 3D Recognition and Pose Using the Viewpoint
Feature Histogram. In IEEE/RSJ Int. Conf. on Intel-
lig. Robots and Systems (IROS), pages 2155 – 2162,
Taipei, Taiwan.
Schoenberg, J., Nathan, A., and Campbell, M. (2010). Seg-
mentation of dense range information in complex ur-
ban scenes. In IEEE/RSJ Int. Conf. on Intellig. Robots
and Systems (IROS), pages 2033 – 2038, Taipei, Tai-
wan.
Sithole, G. and Vosselman, G. (2004). Experimental com-
parison of filter algorithms for bare-Earth extrac-
tion from airborne laser scanning point clouds. IS-
PRS Journal of Photogrammetry and Remote Sensing,
59(1-2):85 – 101. Advanced Techniques for Analysis
of Geo-spatial Data.
Strom, J., Richardson, A., and Olson, E. (2010). Graph-
based Segmentation for Colored 3D Laser Point
Clouds. In Proceedings of the IEEE/RSJ Int. Conf.
on Intellig. Robots and Systems (IROS), pages 2131 –
2136.
Sun, J., Ovsjanikov, M., and Guibas, L. (2009). A Con-
cise and Provably Informative Multi-Scale Signature
Based on Heat Diffusion. In Proceedings of the Sym-
posium on Geometry Processing, pages 1383–1392,
Aire-la-Ville, Switzerland. Eurographics Association.
Triebel, R., Shin, J., and Siegwart, R. (2010). Segmentation
and Unsupervised Part-based Discovery of Repetitive
Objects. In Proceedings of Robotics: Science and Sys-
tems, page 8, Zaragoza, Spain.
Verma, V., Kumar, R., and Hsu, S. (2006). 3D building de-
tection and modeling from aerial lidar data. In Com-
puter Vision and Pattern Recognition, IEEE Computer
Society Conference on, volume 2, pages 2213–2220,
New York, USA. IEEE Computer Society.
Vieira, M. and Shimada, K. (2005). Surface mesh seg-
mentation and smooth surface extraction through re-
gion growing. Computer Aided Geometric Design,
22(8):771 – 792.
Vosselman, G., Kessels, P., and Gorte, B. (2005). The util-
isation of airborne laser scanning for mapping. In-
ternational Journal of Applied Earth Observation and
Geoinformation, 6(3-4):177 – 186. Data Quality in
Earth Observation Techniques.
Zhu, X., Zhao, H., Liu, Y., Zhao, Y., and Zha, H.
(2010). Segmentation and classification of range im-
age from an intelligent vehicle in urban environment.
In IEEE/RSJ Int. Conf. on Intellig. Robots and Systems
(IROS), pages 1457 – 1462, Taipei, Taiwan.
ICPRAM 2012 - International Conference on Pattern Recognition Applications and Methods
70
