AN EFFICIENT NUMERICAL RESOLUTION FOR MRI RICIAN

DENOISING

A. Mart

ın

, J. F. Garamendi

and E. Schiavi

Fundaci

on CIEN-Fundaci

on Reina Sof

ıa, Madrid, Spain

Departamento de Tecnolog

ıa Electr

onica, Universidad Rey Juan Carlos, Madrid, Spain

Departamento de Matem

atica Aplicada, Universidad Rey Juan Carlos, Madrid, Spain

Keywords:

MRI Rician Denoising, Total Variation, Numerical Resolution, ROF Model.

Abstract:

We consider a variational Rician denoising model for Magnetic Resonance Images (MRI) that we solve by

a semi-implicit numerical scheme, which leads to the resolution of a sequence of Rudin, Osher and Fatemi

(ROF) models. This allows to implement efﬁcient numerical gradient descent schemes based on the dual

formulation of the ROF model which are compared with a direct semi-implicit approach for the primal problem

recently proposed for model validation. In this new framework the total variation operator is exactly solved as

opposed to the approximating problems which must be considered when the primal problem is dealt with. The

comparison among the above methods is performed using synthetic and real MR brain images and the results

show the effectiveness of the new method in both, the accuracy and the speeding up of the algorithm.

1 INTRODUCTION

Modelling MRI denoising, a fundamental step in

medical image processing, leads naturally to the as-

sumption that MR magnitud images are corrupted by

Rician noise which is a signal dependent noise (see

(Henkelman, 1985), (Gudbjartsson and Patz, 1995)

and (Sijbers et al., 1998)). In fact this noise is orig-

inated in the computation of the magnitude image

from the real and imaginary images, that are obtained

from the inverse Fourier Transform applied to the

original raw data. This process involves a non-linear

operation which maps the original Gaussian distribu-

tion of the noise to a Rician distribution, (Lysaker

et al., 2003).

Nevertheless it is usually argued that this bias do

not affect seriously the processing and subsequent

analysis of MR images and a gaussian noise, iden-

tically distribuited and not signal dependent, is mod-

eled. To go beyond the unlikely assumption of gaus-

sian noise, we consider, in a variational framework,

a denoising model for MR Rician noise contami-

nated images recently considered in (Mart

ın et al.,

2011), which combines the Total Variation semi-norm

with a data ﬁtting term (see also (Basu et al., 2006)

for an application to DT-MRI data denoising where

low SNR Diffusion Weighted Images (DWI) are ac-

quired). When the resulting functional is considered

for minimization, the variational approach leads to

the resolution of a nonlinear degenerate PDE ellip-

tic equation as the Euler Lagrange equation for op-

timization. This has a number of theoretical prob-

lems when the Total Variation operator is considered

as a smoother, because the energy functional is not

differentiable at the origin (i.e. ∇u =

0) and regu-

lar, approximating problems must be solved. In turn

this approach cause a over-smoothing effect in the nu-

merical solutions of the model and accuracy in ﬁne

scale details is lost because the edges diffuse. A di-

rect gradient descent method has been used in (Mart

ın

et al., 2011) in order to validate the model assumption

of rician noise but the method is found to be inher-

ently slow because a stabilization at the steady state is

needed. Also, that scheme is ﬁnally explicit and very

small time steps have to be used to avoid numerical

oscillations.

Our aim is to present a new framework to

solve numerically and efﬁciently the gradient descent

scheme (gradient ﬂow) associated to the Rician en-

ergy minimization problem introducing a new semi-

implicit formulation. Using a simple Euler discretiza-

tion of the time derivative, stationary problems of the

Rudin, Osher and Fatemi (ROF) type (Rudin et al.,

1992) are deduced. This allows to use the well

known dual formulation of the ROF model proposed

in (Chambolle, 2004) for a speed up of the computa-

Martín A., F. Garamendi J. and Schiavi E..

AN EFFICIENT NUMERICAL RESOLUTION FOR MRI RICIAN DENOISING.

DOI: 10.5220/0003734000150024

In Proceedings of the International Conference on Bio-inspired Systems and Signal Processing (BIOSIGNALS-2012), pages 15-24

ISBN: 978-989-8425-89-8

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

tions. As a by-product of this approach the exact Total

Variation operator can be computed and this provides

accuracy to the solution in so far truly (discontinuos)

bounded variation solutions are numerically approxi-

mated.

This paper is organized as follows: in section 2

and 3 we present the model equation and the numeri-

cal scheme recently proposed in (Mart

ın et al., 2011).

In section 4 we propose a new framework which leads

to a more efﬁcient and accurate numerical scheme.

The proposed method is tested in section 5, where

we consider synthetic MR brain images to compare it

with the method of (Mart

ın et al., 2011) and some pre-

liminary results of applying this algorithm to real Dif-

fusion Weighted Magnetic Resonance Images (DW-

MRI) are shown in subsection 5. Finally in section 6

we present our conclusions.

2 MODEL EQUATIONS

Let Ω be a bounded open subset of R

, d = 2,3

deﬁning the image domain and let f : Ω → R be a

given noisy image representing the data, with f ∈

∞

(Ω) ∩ [0,1] (otherwise we normalize). Let BV (Ω)

be the space of functions with bounded variation in Ω

equipped with the seminorm |u|

deﬁned as

|u|

= sup



Ω

u(x)div

ξ(x)dx :

ξ ∈ C

(Ω, R

), |

ξ(x)|

∞

≤ 1, x ∈ Ω

(1)

where |·|

∞

denotes the l

∞

norm in R

, |

ξ|

∞

= max

1≤i≤d

|ξ

(details on this space and the related geometric mea-

sure theory can be found in (Ambrosio et al., 2000)).

Following a Bayesian modelling approach we con-

sider the minimization problem

min

u∈BV (Ω)

{

J(u) + λH(u, f )

}

(2)

where J(u) is the convex nonnegative total variation

regularization functional

J(u) = |u|

= |Du|(Ω) (3)

being |Du|(Ω) the Total variation of u with Du its gen-

eralized gradient (a vector bounded Radon measure).

When u ∈ W

1,1

(Ω) we have |Du|(Ω) =

Ω

|∇u|dx.

The λ parameter in (2) is a scale parameter tuning the

model.

The data term H(u, f ) is a ﬁtting functional which

is nonnegative with respect to u for ﬁxed f . To model

rician noise the form of H(u, f ) has been deduced in

(Basu et al., 2006) in the context of weighed diffusion

tensor MR images. The Rician likelihood term is of

the form:

H(u, f ) =

Ω



+ f

2σ



− log I



u f



− log





(4)

where σ is the standard deviation of the rician noise

of the data and I

is the modiﬁed zeroth-order Bessel

function of the ﬁrst kind. Notice that the constant

terms (1/2σ

)k f k

and

Ω

log



f /σ



appearing in

(4) do not affect the minimization problem. Drop-

ping these terms (which do not allows to deﬁne the

energy H(u,0) corresponding to a black image f ≡ 0)

we have:

H(u, f ) =

2σ

Ω

dx −

Ω

logI



u f



dx (5)

with H(u,0) = (1/2σ

)kuk

and H(0, f ) = 0 for any

given f ≥ 0. Using (2), (3) and (5) the minimization

problem is formulated as:

Fixed λ and σ and given a noisy image f ∈

∞

(Ω) ∩ [0, 1] recover u ∈ BV (Ω) ∩ L

∞

(Ω) ∩ [0, 1]

minimizing the energy:

J(u) + λH(u, f ) = |Du|(Ω)+

2σ

Ω

dx − λ

Ω

logI



u f



dx (6)

Due to the fact that the functional in (3) (hence in (6))

is not differentiable at the origin we introduce the sub-

differential of J(u) at a point u by

∂J(u) = {p ∈ BV (Ω)

∗

|J(v) ≥ J(u)+ < p,v − u >}

for all v ∈ BV (Ω), to give a (weak and multivalued)

meaning to the Euler-Lagrange equation associated to

the minimization problem (6). In fact the ﬁrst order

optimality condition reads

∂J(u) + λ∂

H(u, f ) 3 0 (7)

with (G

ateaux) differential

∂

H(u, f ) =





−





u f





u f





where I

is the modiﬁed ﬁrst-order Bessel function

of the ﬁrst kind and veriﬁes ((Lassey, 1982)) 0 ≤

(ξ)/I

(ξ) < 1, ∀ξ > 0. This model, ﬁrst proposed

in (Mart

ın et al., 2011), differs from (Basu et al.,

2006) because of the geometric prior (the TV-based

regularization term) which substitutes their Gibb’s

prior model based on the Perona and Malik energy

functional (Perona and Malik, 1990) . Also it differs

from the classical gaussian noise model because of

the nonlinear dependence of the solution of the ratio

BIOSIGNALS 2012 - International Conference on Bio-inspired Systems and Signal Processing

3 THE PRIMAL DESCENT

GRADIENT NUMERICAL

SCHEME

A number of mathematical difﬁculties is associated

with the multivalued formulation (7) and a regular-

ization of the diffusion term div(∇u/|∇u|) in form

div(∇u/|∇u|

), with |∇u|

|∇u|

+ ε

and 0 <

ε  1 is implemented to avoid degeneration of the

equation where ∇u =

0. Using this approximation it

is possible to give a (weak) meaning to the following

formulation:

Fixed λ, σ and (small) ε and given f ∈ L

∞

(Ω) ∩

[0,1] ﬁnd u

∈ W

1,1

(Ω) ∩ [0,1] solving

−div



∇u

|∇u



− r

, f ) f ] = 0 (8)

complemented with Neumann homogeneous bound-

ary cond itions ∂u

/∂n = 0 and where, for nota-

tional simplicity, we introduced the nonlinear func-

tion r

, f ) = I

f /σ

)/I

f /σ

This is a nonlinear (in fact quasilinear) elliptic

problem that we solve with a gradient descent scheme

until stabilization (when t → +∞) of the evolutionaty

solution to steady state, i.e. a solution of the elliptic

problem (8) which is a minimum of the energy

) + λH(u

, f ) =

Ω

|∇u

+ ε

dx+

2σ

Ω

dx − λ

Ω

logI



u f



dx (9)

When ε → 0 we have u

→ u, J

) → J(u) and the

energies in (6) and (9) coincide.

This approach amounts to solve the associated

nonlinear parabolic problem:

∂u

∂t

= div



∇u

|∇u



−

− r

, f ) f ] (10)

complemented with Neumann homogeneous bound-

ary conditions ∂u

/∂n = 0 and initial condition

(0,x) = u

(x) whose (weak) solution stabilizes

(when t → +∞) to the steady state of (8), i.e. a min-

imum of (9) which approximates, for ε sufﬁciently

small, a minimum of the energy functional (6). Fol-

lowing (Mart

ın et al., 2011) and using forward ﬁnite

difference for the temporal derivative it is straightfor-

ward to deﬁne a semi-implicit iterative scheme which

simpliﬁes to the explicit one:



1 + ∆t



n+1

= u

+ ∆t



div



∇u

|∇u



r(u

, f ) f



(11)

where ∆t is the time step and spatial discretization

for the approximated TV-term is performed as in

(Nikolova et al., 2006) .

4 A SEMI-IMPLICIT

FORMULATION

In the previous section we considered the approxi-

mated Euler-Lagrange equation (8) associated to the

minimization of the energy (6). This is a modelling

approximation and we can get rid of it. In fact, con-

sidering the original Euler-Lagrange equation associ-

ated to the energy (6) we have (with abuse of notation

for the diffusive term)

−div



∇u

|∇u|



[u − r(u, f ) f ] = 0 (12)

with r(u, f ) = I

(u f /σ

)/I

(u f /σ

). A rigorous

treatment of equation (12) should follow the multi-

valued formalism of (7).

Using again a gradient descent scheme we have to

solve the parabolic problem:

∂u

∂t

= div



∇u

|∇u|



−

[u − r(u, f ) f ] (13)

together with Neumann homogeneous boundary con-

ditions ∂u/∂n = 0 and initial condition u(0,x) =

(x). For comparison purposes we used u

(x) =

(x) in all numerical tests.

Using forward ﬁnite difference for the temporal

derivative in (13) and a semi-implicit scheme where

only the term depending on the ratio of the Bessel’s

functions is delayed, results in the numerical scheme:



1 + ∆t



n+1

= u

+ ∆t



div



∇u

n+1

|∇u

n+1



r(u

, f ) f



(14)

where the diffusive term is (formaly) exact and im-

plicitly considered (compare with (11)). Defyining

α = (λ∆t + σ

)/(λ∆t) and



λ∆t



+ r(u

, f ) f

we can write:

−div



∇u

n+1

|∇u

n+1





αλ





n+1

−



= 0 (15)

AN EFFICIENT NUMERICAL RESOLUTION FOR MRI RICIAN DENOISING

(a) Original phantom (b) Noisy for σ = 0.025 (c) Noisy for σ = 0.05 (d) Noisy for σ = 0.1

(e) Original phantom (f) Denoised for σ = 0.025, λ =

0.025

(g) Denoised for σ = 0.05, λ =

0.075

(h) Denoised for σ = 0.1, λ =

0.125

Figure 1: The original free noise phantom is shown in images a) and e). In b), c) and d) the contaminated phantoms for

σ = 0.025, 0.05 and 0.1 respectively. Below, their respective denoised images e), f) and g) for λ = 0.025, 0.075 and 0.125.

which is the Euler-Lagrange equation of the ROF en-

ergy functional ((Rudin et al., 1992)):

E(u) = |Du|(Ω) +



2β



Ω

(u − g)

dx (16)

for β = σ

/(αλ) and g =

, for any positive integer

n > 0, with (artiﬁcial) time t

= n∆t. Hence, at each

gradient descent step ∆t, we can solve a ROF problem

associated to the minimization of the energy (16) in

the space BV (Ω) ∩ [0, 1]. This problem is mathemat-

ically well-posed and it can be numerically solved by

very efﬁcient methods, when formulated using well

known duality arguments (see (Chambolle, 2004) for

more details).

5 RESULTS AND DISCUSSION

The theoretical result presented in the previous sec-

tion have to be numerically conﬁrmed in order to

asses the well behaviour of the method and also the

advantages it presents when it is compared to the orig-

inal regularized method which computes the approxi-

mating u

solution. In order to assess the performance

of our algorithm we tested it with synthetic and real

brain images. The obtained results are presented and

discussed below.

Synthetic Brain Images

The synthetic brain images we used for our study

were obtained from the BrainWeb Simulated Brain

Database

at the Montreal Neurological Institute

(Aubert-Broche et al., 2006) . The original phantoms

were contaminated artiﬁcially with Rician noise con-

sidering the data as a complex image with zero imag-

inary part and adding random gaussian perturbations

to both the real and imaginary part, before comput-

ing the magnitude image. This process allows to con-

trol the amount and distribution of the Rician noise so

providing a gold standard for our study. For this we

used different values of the σ parameter which repre-

sents the variance of the noise (σ = 0.025, σ = 0.05

and σ = 0.1) and different values of the λ parame-

ter (λ = 0.05, λ = 0.1 and λ = 0.125). Notice that,

ﬁxed σ (which can be estimated for real images) the λ

parameter is the only one we have to choose for regu-

larization (as in the gaussian case).

We can observe in Figure 1 the performance of

the denoising method based on the semi-implicit for-

mulation for λ = 0.05, λ = 0.1 and λ = 0.125. This

implicit method solves exactly the total variation op-

erator in (6) due to its dual formulation and not

its approximate form as the explicit method which

solves the primal formulation, so the solution ob-

tained should be close to the ideal minimum of (6).

This behaviour can be in fact observed in Figure 2,

where using the same values for the algorithms (∆t =

−3

and λ = 0.1) the proposed method reach a solu-

tion whose energy is smaller than the obtained by the

solution of the ﬁrst method. This difference caused

by the fact that now we are using the true Total Vari-

available at http://www.bic.mni.mcgill.ca/brainweb

BIOSIGNALS 2012 - International Conference on Bio-inspired Systems and Signal Processing

Figure 2: Energy in functional 6 of the solution obtained at each step of the gradient descent by the approximated method

for λ = 0.1, σ = 0.05, dt = 0.001 and different values of ε = 10

−1

,10

−3

,10

−5

,10

−7

, and by the new method for λ = 0.1,

σ = 0.05, dt = 0.001.

ation can be also observed in the images of the ab-

solute difference between the original (free of noise)

image and the solutions found by the two methods.

We can see how the image difference corresponding

to the solution of the approximated method ( Figure

3 a ) presents more structural details than the image

corresponding to the implicit method ( Figure 3 b ),

which conﬁrms that this last method recovers more

structural details, that are eventually lost by the ex-

plicit method because of the ε approximation.

The other important characteristic of this new for-

mulation is that the diffusion term is implicitly con-

sidered and this provides numerical stability which

in turn allows to increase the value of ∆t compared

to those used in the explicit method, so less itera-

tions of the algorithm are necessary for time stabi-

lization. In fact if we increase the value of ∆t to

the value ∆t = 10

−1

the explicit method becomes un-

stable and it begins to oscillate without reaching the

minimum of the energy we obtained with ∆t = 10

−3

Also the implicit method takes less iterations to reach

the same minimum. The performance of the two al-

gorithms for ∆t = 10

−1

can be observed in Figure 4

where the energy computed along the iterates of the

implicit method is clearly less than the same energy

calculated along the approximated iterates.

This behaviour is crucial for the selection of the

algorithm in so far even if the new method has more

computational cost per iteration (because we solve a

ROF problem at each iteration), we can increase the

value of ∆t in order to reach the solution in less it-

erations than the ﬁrst method, ﬁnding a best solution

for our problem (in the sense of ﬁgure 4) and spend-

ing less time of computation. Finally, in the last ﬁg-

ure(ﬁgure 5) we show that this framework is robust

in the sense that the same solution is obtained when

completely different initial condition are used for ini-

tialization in the gradient ﬂow schemes we consid-

ered. This is suggestive of uniqueness for the non

trivial solution of the corresponding elliptic problems.

Real Brain Images

Apart from the modelling exercise and the imple-

mentation details of the algorithm presented above,

our main interest relies in the application of the pro-

posed algorithm to real brain images. In the following

we present some preliminary results we are obtaining

for Diffusion Weighted Magnetic Resonance Images

(DW-MRI) denoising. The DW-MR images are ac-

quired and used for Diffusion Tensor Image (DTI) re-

AN EFFICIENT NUMERICAL RESOLUTION FOR MRI RICIAN DENOISING

(a) Existing method (b) Proposed method

Figure 3: Absolute difference between the original image and the solution of the existing method and the proposed method

for the values λ = 0.1, σ = 0.05, dt = 0.001 in both methods and ε = 10

−

7 for the approximated method.

Figure 4: Energy in functional 6 of the solution obtained at each step of the gradient descent by the approximated method for

ε = 10

−7

, λ = 0.1, σ = 0.05, dt = 0.1 and by the new method for λ = 0.1, σ = 0.05, dt = 0.1.

construction, and the importance of the denoising step

is crucial in DW-MRI analysis because their charac-

teristic very low SNR (Basu et al., 2006). Diffusion

Tensor Imaging is a MRI technique that can mea-

sure the water diffusion which is restricted by the sur-

rounding structure, and this allows to infer the macro-

scopic axonal organization in nervous system tissues.

We show the results of the DTI reconstruction for

BIOSIGNALS 2012 - International Conference on Bio-inspired Systems and Signal Processing

Figure 5: Energy in functional 6 of the solution obtained at each step of the gradient descent by the new method for λ = 0.05,

σ = 0.05, dt = 0.1 and different initial data u

: black image (u

≡

0), white image (u

≡

1), the noisy image (u

≡ f ) and a

random image (u

≡ rand).

(a) Original (b) Denoised with λ = σ/2 (c) Denoised with λ = σ/4

Figure 6: A slice of the original Diffusion Weighted Image corresponding to the (1, 0, 0) gradient direction and the corre-

sponding denoised images.

the original DW-MRI data and the correspondent de-

noised data with different values of the parameter λ.

For this preliminary study we have used a

DW-MR brain volume provided by Fundaci

CIEN-Fundaci

on Reina Sof

ıa which was acquired

with a 3 Tesla General Electric scanner equipped

with an 8-channel coil. The DW images have

been obtained with a single-shot spin-eco EPI

sequence (FOV=24cm, TR=9100, TE=88.9, slice

thickness=3mm, spacing=0.3, matrix size=128x128,

AN EFFICIENT NUMERICAL RESOLUTION FOR MRI RICIAN DENOISING

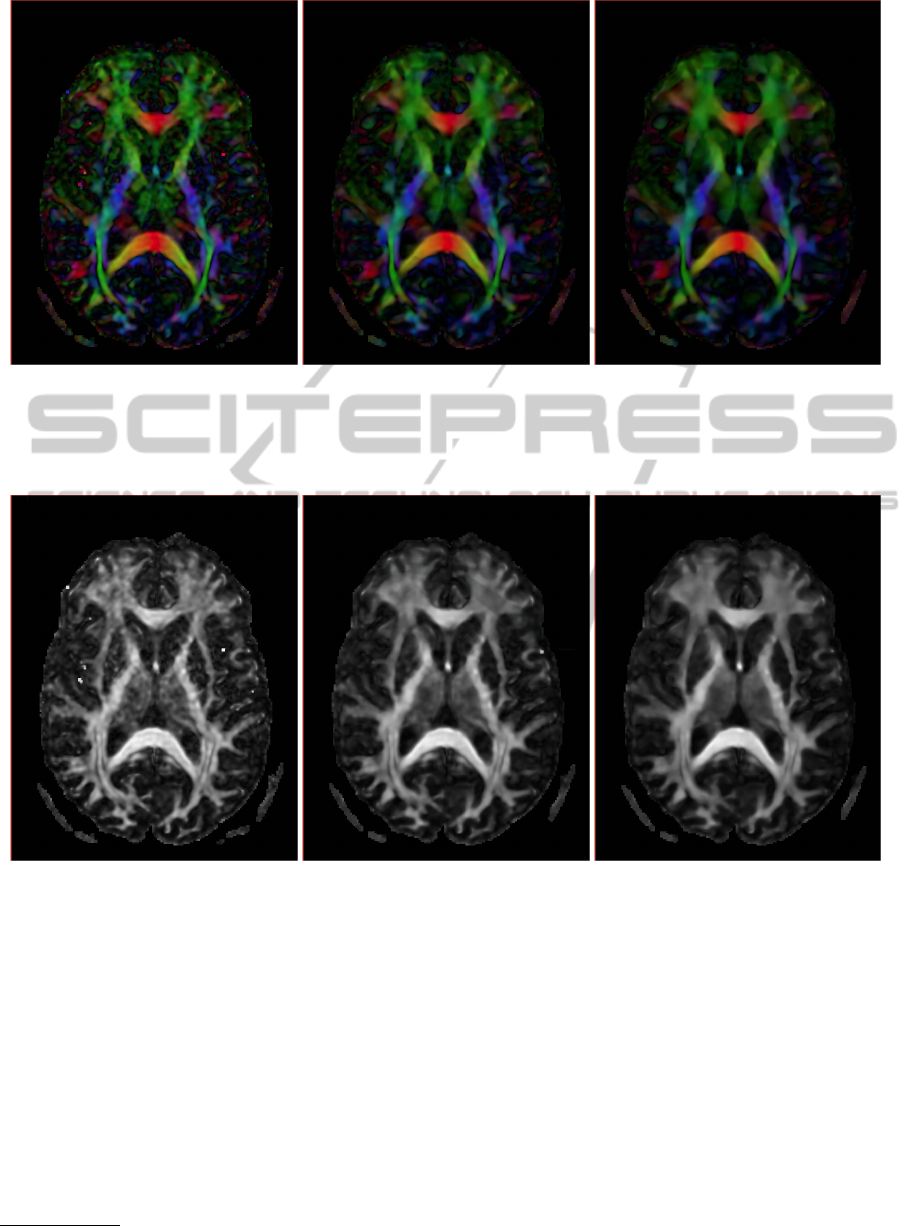
(a) From original DWI data (b) From denoised DWI data with λ = σ/2 (c) From denoised DWI data with λ = σ/4

Figure 7: A slice of the colormap orientation (of the main eigenvector) of the DTI data. red means right-left direction, green

anterior-posterior and blue inferior-superior. Fibers with an oblique angle have a color that is a mixture of the principal colors

and black color is used for the isotropic regions as the cerebrospinal ﬂuid.

(a) From original DWI data (b) From denoised DWI data with λ = σ/2 (c) From denoised DWI data with λ = σ/4

Figure 8: A slice of the Fractional Anisotropy estimated from the Tensor Image. Dark colour corresponds to values near zero

(isotropic regions) and bright color corresponds to values near one (anisotropic regions).

NEX=2 ). The DW-MRI data consists on a vol-

ume obtained with b=0/mm

and 15 volumes with

b=1000s/mm

corresponding with the gradient direc-

tions speciﬁed in (DK Jones, 1999). These DW-

MR images, which represent diffusion measurements

along multiples directions, are denoised with the pro-

posed method previously to the Diffusion Tensorial

Image reconstruction, which was done with the 3d

Slicer tools

In Figure 6(a) we show a slice of the original DWI

Free available in http://www.slicer.org/

data corresponding to the (1, 0, 0) gradient direction

where the affecting noise is clearly visible. The com-

plete DW-MRI data volume is denoised using the pro-

posed method where the Rician noise magnitude (σ)

has been estimated for each gradient direction follow-

ing (Sijbers et al., 1998), while we have used two

different values of λ for the denoising, λ = σ/2 and

λ = σ/4. The two slices resulting from the denoising

process are shown in Figures 6(b) and 6(c). It can be

observed that smaller values of λ provide stronger dif-

fusion (which is coherent with the model formulation

in 6) and how in the two denoised images the noise

BIOSIGNALS 2012 - International Conference on Bio-inspired Systems and Signal Processing

has been removed but the details and the edges have

been fully preserved, as we should expect when the

exact TV model is solved.

The effect of this denoising process over the re-

constructed tensor and their derived scalar measure-

ments (obtained with the 3d Slicer tools) is presented

in Figures 7 and 8. Figure 7 shows a color-coded

orientation map created from DTI data. In this im-

age, the principal colors (red, green, and blue) rep-

resent ﬁbers running along the spatial orientations

(x,y, z). Results in 7 shows that the structures are

better deﬁned if the DW-MRI volume is denoised

previously. As evidenced by Figure 8 this effect is

yet more visible in the measurements like the Frac-

tional Anisotropy where the structures and details are

clearly enhanced. When we use a lower value for λ

(Figures 7(c) and 8(c)) we obtain smoother tensorial

images but some details can be better distinguished

when the value of λ is higher (Figures 7(b) and 8(b)).

6 CONCLUSIONS

In this notes we address the problem of the numeri-

cal computation of the solution of the variational for-

mulation of the Rician denoising model proposed in

(Mart

ın et al., 2011). We deduce a semi-implicit for-

mulation for the gradient ﬂow which leads to the res-

olution of ROF like-problems at each step of the time

discretization. This is accomplished efﬁciently using

a gradient descent for the dual variable associated to

the primal ROF model. While our study is prelim-

inary it indicates how to obtain fast numerical solu-

tions for Rician denoising. This is specially inter-

esting when Diffusion Wheighted Images (DWI) are

considered for Diffusion Tensor Images reconstruc-

tion whereas they have poor resolution and low SNR

which makes Rician denoising necessary.

Challenging mathematical issues arise about the

existence, uniqueness and convergence, when ε → 0,

of weak bounded variation solutions of the quasilinear

elliptic equations considered in this paper (i.e. (8) and

(12)) and the gradient ﬂow analysis of their parabolic

counterpart ((10) and (13)) when t → +∞. A rigor-

ous justiﬁcation of the above arguments is desired.

Nevertheless this approach is the mostly used regu-

larization technique to approximate and compute the

minimizer of the total variation energy and its variants

(see (Casas et al., 1998)).

The semi-implicit method we propose is well

founded mathematically when the time-discretized

problems are dealt with and it represents a feasible al-

ternative to gaussian denoising for low SNR MR im-

ages. Further study is undoubtedly necessary in order

to make automatic the choice of the parameters in real

medical images. Other possibilities, such as Inverse

scaling, which makes the parameter estimation less

crucial and provide contrast enhanced images shall

also be explored.

ACKNOWLEDGEMENTS

This work was supported by project TEC2009-14587-

C03-03 of the Spanish Ministry of Science. Also we

thank to Mrs. Eva Alfayate, MR-scanner technician

of the Fundaci

on Reina Sof

ıa, for her professional and

kindly collaboration.

REFERENCES

Ambrosio, L., Fusco, N., and Pallara, D. (2000). Functions

of Bounded Variation and free discontinity problems.

The Clarendon Press, Oxford University.

Aubert-Broche, B., Grifﬁn, M., Pike, G., Evans, A., and

Collins, D. (2006). Twenty new digital brain phan-

toms for creation of validation image data bases. In

IEEE transactions on Medical Imaging, volume 25,

pages 1410–1416.

Basu, S., Fletcher, T., and Whitaker, R. (2006). Rician

noise removal in diffusion tensor mri. Medical Im-

age Computing and Computer-Assisted Intervention,

9(Pt 1):117–125.

Casas, E., Kunisch, K., and Pola, C. (1998). Some applica-

tions of bv functions in optimal control and calculus

of variations. In ESAIM: Proceedings. Control and

partial differential equations, volume 4, pages 83–96.

Chambolle, A. (2004). An algorithm for total variation

minimization and applications. Journal Mathematical

Imaging and Vision, 20:89–97.

DK Jones, MA Horsﬁeld, A. S. (1999). Optimal strate-

gies for measuring diffusion in anisotropic systems

by magnetic resonance imaging. Journal of Magnetic

Resonance in Medicine, 42 (3):515–525.

Gudbjartsson, H. and Patz, S. (1995). The rician distribution

of noisy mri data. Magnetic Resonance in Medicine,

34(6):910–914.

Henkelman, R. M. (1985). Measurement of signal intensi-

ties in the presence of noise in mr images. Medical

Physics, 12(2):232–233.

Lassey, K. R. (1982). On the computation of certain in-

tegrals containing the modiﬁed bessel function i

(ξ).

Mathematics of Computation, 39.

Lysaker, M., Lundervold, A., and cheng Tai, X. (2003).

Noise removal using fourth-order partial differential

equations with applications to medical magnetic res-

onance images in space and time. IEEE Trans. Imag.

Proc, 12:1579–1590.

Mart

ın, A., Garamendi, J., and Schiavi, E. (2011). Iterated

rician denoising. In IPCV’11 Proceedings, Las Vegas,

Nevada, USA. CSREA Press.

AN EFFICIENT NUMERICAL RESOLUTION FOR MRI RICIAN DENOISING

Nikolova, M., Esedoglu, S., and Chan, T. F. (2006). Al-

gorithms for ﬁnding global minimizers of image seg-

mentation and denoising models. SIAM Journal of Ap-

plied Mathematics, 66(5):1632–1648.

Perona, P. and Malik, J. (1990). Scale-space and edge de-

tection using anisotropic diffusion. Pattern Analy-

sis and Machine Intelligence, IEEE Transactions on,

12(7):629–639.

Rudin, L. I., Osher, S., and Fatemi, E. (1992). Nonlinear to-

tal variation based noise removal algorithms. Physica

D Nonlinear Phenomena, 60:259–268.

Sijbers, J., Dekker, A. D., Audekerke, J. V., Verhoye, M.,

and Dyck, D. V. (1998). Estimation of the noise in

magnitude mr images. Magnetic Resonance Imaging,

1(16):87–90.

BIOSIGNALS 2012 - International Conference on Bio-inspired Systems and Signal Processing