APPROACH TO ENABLE AN AUTOMATIC PRE-PROCESSING

OF qRT-PCR

Analysis

Marco Franke

, Klaus-Dieter Thoben

and Rainer Söller

BIBA - Bremer Institut für Produktion und Logistik GmbH, University Bremen

Hochschulring 20, 28359, Bremen, Germany

Qiagen Hamburg, Königstraße 4a, 22767, Hamburg, Germany

Keywords: Polymerase Chain Reaction, Automated Pre-processing of qRT-PCR Results, Noise Removal for Sigmoid

Curves.

Abstract: A fully automated analysis method for real-time PCR samples can be achieved through an automated noise

removal. This results in a guaranteed robustness against the factors that repeatedly impact the analysis of

real-time PCR data and usually lead to a manual analysis by skilled experts. The presented approach attains

a degree of robustness which allows an automated analysis for real-time PCR. This new automated pre-

processing method improves the real-time PCR data for the analysis in such a way that accepted qualitative

analysis methods can be used in an automated way. Furthermore, the article shows an evaluation of an

implemented demonstrator for an automated analysis which combines the developed pre-processing method

with the second derivation method for the qualitative analysis.

1 INTRODUCTION

The process of Real-time quantitative polymerase

chain reaction (qRT-PCR) has been widely used for

over ten years and has entered into the domain of

medicine, for example in Leukemia Research. The

determination of molecular targets by using

qualitative and quantitative qRT-PCR analysis has

become a common method. The qRT-PCR method

can also be used for the detection of microorganisms

or other organic media containing a genome.

The detection of microorganisms in industrial

environment is realized with the methods of

microbiology. Such methods are standardized and

accepted as solid proof. Its major disadvantage lies

in the considerable time it requires. A large

proportion of time is spent on the stage in which the

microorganisms grow on the medium. The duration

of this phase depends on the type of microorganisms

and environmental conditions and can be very long.

The quality check of a raw material, interstage

product or end product can take a few hours or a few

days. The needed time for a quality analysis is

longer than the time for producing the product. This

means that the quality check can not work in real

time and the usage of preventive methods for

reducing an occurrence of biological contamination

is needed. This issue is not resolved but improved by

the qRT-PCR method. The qRT-PCR method

requires a constant time for the detection of any

micro-organism, which takes less than 12 hours. In

the project ProDIAP(BIBA,2010) the qRT-PCR-

analysis required six hours.

Since the establishment of the qRT-PCR method,

different approaches have been developed in the

field of qualitative and quantitative analyses which

also include the fit points and second derivation as a

common method. For example, the softwares of

LightCycler (Roche Applied Science, 2010) and

RotorGene (Qiagen, 2010) use such methods. One of

the methods which are explored currently is the

maxRatio (Shain and Clemens, 2008) method. One

feature of the maxRatio method is to support a much

more aggressive noise filter without losing

significant signal information. All these developed

methods need an additional pre-processing to reduce

the wide range of noise within measurement data.

The currently used noise removal methods require

the experience of experts to estimate the parameter

values and to evaluate the result of noise removal.

The chosen parameter values describe e.g. the

281

Franke M., Thoben K. and Söller R..

APPROACH TO ENABLE AN AUTOMATIC PRE-PROCESSING OF qRT-PCR - Analysis.

DOI: 10.5220/0003734102810285

In Proceedings of the International Conference on Bioinformatics Models, Methods and Algorithms (BIOINFORMATICS-2012), pages 281-285

ISBN: 978-989-8425-90-4

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

specific characteristics of the used qRT-PCR-

analysis and the used qRT-PCR-KIT and have to

adapt to them each time. This adaption/calibration

can only be executed by a manual process. This fact

prevents the usage of the qRT-PCR-analysis in an

automated industrial environment or at the

customer`s side as an easy-to-use analysis product.

Therefore, the weakness of parameter based noise

removal methods and the research of the usage of

methods without parameters for noise removal are

the focus of this article.

This article presents a new approach for an

automatic pre-processing method for common qRT-

PCR-analysis. The objective is to achieve a pre-

processing method without the required intervention

of experts. If a pre-processing without parameters is

possible, it enables an automatic qRT-PCR-analysis

with common analysis methods. Such a solution has

been established under the project ProDiap (Bremer

Institut für Produktion und Logistik, 2010).The

solution is presented in chapter 4.

In this article, the problem and its solution,

which lies in an approach for the development of an

automated pre-processing method for a qRT-PCR-

analysis are presented. In the next section, the

common noise removal methods are discussed. After

this, the approach will be described and finally, the

evaluation by using the demonstrator will be shown.

2 STATE OF THE ART WITH

REGARD TO

PRE-PROCESSING

The influence of the noise within the analysis

process implies the need for pre-processing. As

minimal information, a qRT-PCR measurement

contains a set of tuples, which represent a time-

stamp and a measured fluorescence. The magnitude

of the fluorescence correlates with the concentration

of the qRT-PCR-analysis result product. The

influence on this correlation is declared in this

article as noise.

The interpretation of a measurement result is

based on the mapping of a measurement result in a

Cartesian coordinate system. The qualitative and the

quantitative analyses are grounded on such a curve.

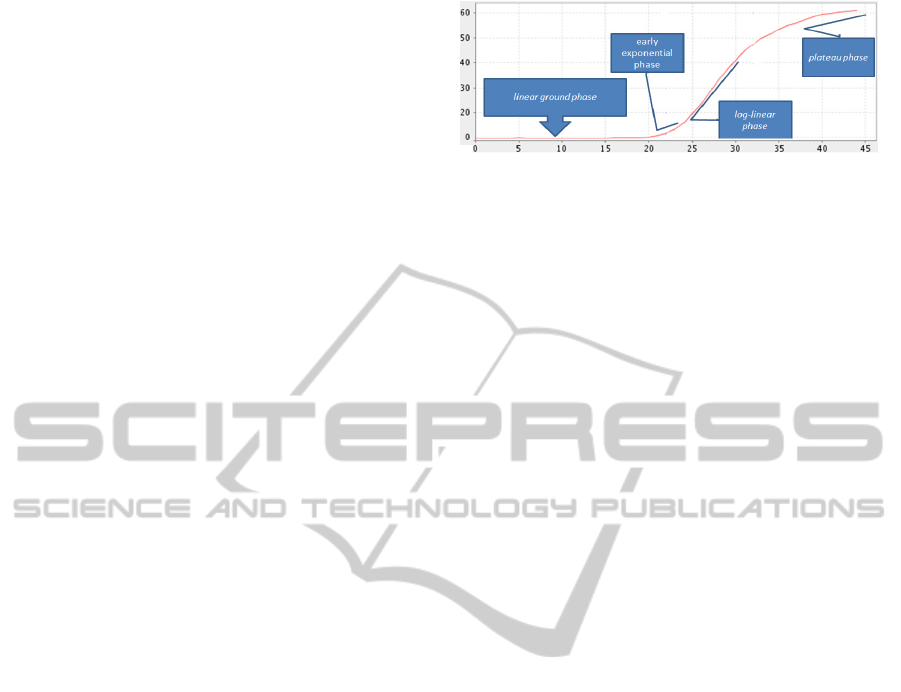
In figure 1, an example curve is shown, which

represents a positive result of a qRT-PCR-analysis.

It is characterized by four phases (Wong and

Medrano, 2005).

In such a case, a specific micro-organism would

be detected.

Figure 1: Four phases of qRT-PCR curve.

The quality of a curve decreases with the

decreasing quality of these four phases. In real

measurements, the noise changes the expression of

the four phases of the curve. This complicates the

classification of such curves compared to the

classification of noise-free curves significantly. The

effects on the curve are described below with regard

to different noise types.

2.1 Noise

Generally, in test results, two different types of noise

can occur (Wilhelm, 2003). As pointed out by

Wilhelm (2003) and Larinonov, Krause and Miller

(2005) a background noise is caused by properties of

materials and other external influences. Here,

Larinonov et al. (2005) a correlation between the

qRT-PCR systems and the occurrence of

background noise is mentioned. The expression of

noise ranges from a constant shift to a linear increase

of noise over cycles (Larinonov et al., 2005). The

second type of noise is defined as signal trend. The

possible causes of the occurrence of this are not yet

resolved. According to Wilhelm` s (2003) opinion,

the product accumulation is no reason for the signal

trend. The signal trend can influence the curve of a

test result in two ways. It can increase or decrease

the measured fluorescence of a test result. Without

additional information, an expert can not know the

resulting expression.

The effects of background noise and signal trend

for a repeated application of a sample analysis may

lead to varying results. In general, a background

noise always occurs, which leads to a measurable

fluorescence from the first cycle, although the

fluorescence in the linear ground phase would have

the value zero. The influence of noise is shown in

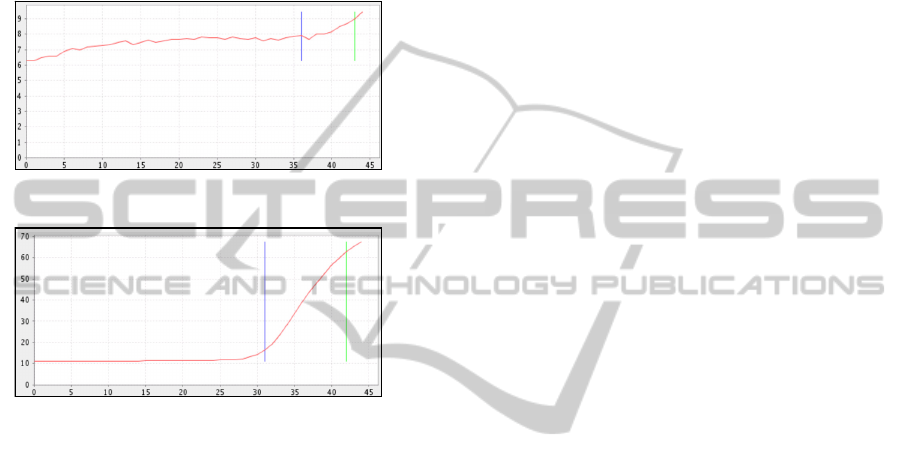
figure 2 and 3 by way of example.

The curve in figure 3 is representative for a test

result which would be classified as positive and

containing just a little noise. Figure 2 shows a

complement curve, which should be evaluated as

positive, although stronger effects of noise have

occurred.

BIOINFORMATICS 2012 - International Conference on Bioinformatics Models, Methods and Algorithms

282

In the following the influence of noise on the two

curves, as well as the possibilities of its detection

and elimination are presented.

2.2 Noise Removal

The curves in figure 2 and 3 include some noise of

the type background noise and noise of the type

signal trend.

Figure 2: Test result with intense noise.

Figure 3: Test result with some noise.

The background noise in figure 3 can be

described as a straight line with the gradient zero in

the linear ground phase. In contrast, the background

noise in figure 2 cannot be described as a straight

line in the linear ground phase. One possibility is to

use n-degree polynomial or cubic splines to define

such a background noise. The cross-over between

the linear ground phase and the early exponential

phase need to be defined for a downstream analysis.

This separation is not possible, which is shown in

figure 2. The signal trend has a similar influence on

the curve which is shown in figure 2.

The noise removal cannot generally detect and

mathematically formulate the background noise and

the signal trend of a curve. For that reason, the noise

cannot be eliminated without losing information of

the signal. Existing methods smooth the curves by

using parameters to control the intensity of noise

removal. If an expert chooses the wrong values for

parameters, the method removes the noise and the

underlying signal.

2.3 Noise Removal by Smoothing

In the following, the smoothing on the basis of

existing procedures will be presented shortly. Based

on the weaknesses of these procedures, the

requirements for the presented smoothing operator

will be presented. A smoothing is generally defined

for two areas of a curve, the so-called local and

global scope.

The local scope is defined by the range between

two points of a curve. There is no information from

the perspective qRT-PCR-analysis between them.

Thus, between two points, different courses of

curves could occur, such as a line, a polynomial or

something else. Polynomials are presumed as

possible curve progression to the technical base of

qRT-PCR systems. The intervals are interpolated in

accordance with polynomial smoothing in

corresponding software. For example, the software

Sofar (Wilhelm, 2003) uses splines (Gutenberg,

2004) for smoothing in local scope.

The global scope is defined as an interval of the

whole curve. Different smoothing operators are

currently used in the field of Simple Moving

Average (SMA) (Savitzky and Golay, 1964). The

methods smooth the course of curve by using an

averaging over fluorescence values. Thus, the

smoothing operator in the field of SMA needs two

parameters. The first parameter controls the choice

of a window function and the other one controls the

window size. The approximation to the original

curve progression, which contains no noise, can be

solved by an expert by adapting the two parameters.

This manual smoothing needs a lot of experience to

guarantee the success of the pre-processing. For an

automated pre-processing method, it would be

necessary that the used method contains no

parameters.

3 APPROACH OF AN

AUTOMATED

PRE-PROCESSING USING THE

BÉZIER CURVE

The presented approach uses no parameters for

smoothing. The objective is to restore a course of

curve which is similar to figure 1. This means that

the resulting curve progression contains the four

phases and the second derivation method can easily

detect them. In the following, the usage of the Bézier

curve for an automated pre-processing is described.

APPROACH TO ENABLE AN AUTOMATIC PRE-PROCESSING OF qRT-PCR - Analysis

283

3.1 Smoothing in Global Scope by the

Bézier Curve

A Bézier curve is a polynomial which represents a

smoothed curve of the test result and can have any

degree. The degree of Bézier curves corresponds to

the number of cycles in a test result.

The points of a curve will be defined as convex

hulle by the calculation of the Bézier curve. The

resulting curve only contains the first und the last

original point. The other points will be calculated by

the Bernstein polynomial. This method is

advantageous compared to the classical average

method because a set of original points of the test

result determines the coordinates of a calculated

point through the application of the Bernstein

polynomials.

An example of a calculation with a Bézier curve,

which is calculated with a java applet (Koegler,

2000), is given in figure 4 and in figure 5.

Figure 4: Calculation of a Bézier curve.

Figure 5: Smoothing with Bézier curve.

4 APPLICATION SCENARIO

As part of the project ProDIAP, the detection of

biological contamination in the manufacture of

emulsion paints was one task. The detection was

realised by the Real-Time qRT-PCR. The following

describes an evaluation about the quality of the

combination between the developed pre-processing

and the application of second derivation method for

qualitative analysis.

5 EVALUATION

The project ProDIAP used 640 samples for the

evaluation of a qualitative analysis. The automated

qualitative analysis was applied by the software,

which has been developed in this project. These

results were compared to a manual interpretation by

an expert from Qiagen Hamburg (Qiagen, 2010).

Figure 6 illustrates the results of the set of 640

samples.

Figure 6: Overview of the evaluation result.

6 SUMMARY

The evaluation has shown that an automated

qualitative analysis of qRT-PCR data is possible and

has reached a high quality. This quality could be

reached by the application of smoothing with Bézier

curves as a noise removal method.

The influence of smoothing with Bézier curves

on the results of a quantitative analysis is not

estimated.

ACKNOWLEDGEMENTS

This article was sponsored by the German

Bundesministerium für Bildung und Forschung

(BMBF), Ref# 01RI0709A-C.

REFERENCES

BIBA, (2010).

ProDIAP. Retrieved February 1, 2010, from

http://www.prodiap.de/

Gutenberg, J. (2004). Spline-Interpolation. Retrieved

February 1, 2010, from http://www.numerik.mathe

matik.uni-ainz.de/didaktikseminar/Gruppe3/html/kubi

sche_splines.html

Haftendorn, D. (1999). Lineare Algebra

BIOINFORMATICS 2012 - International Conference on Bioinformatics Models, Methods and Algorithms

284

Bernsteinpolynome. Retrieved February 1, 2010, from

http://haftendorn.uni-lueneburg.de/numerik/bezier/bezi

erkurve.pdf

Koegler, S. (2000). Java-Applet: Approximations

verfahren. Retrieved February 1, 2010, from

http://www.stefan-koegler.de/studienarbeit_online-tut

orium/java/approximation/ind

ex.html

Larinonov, A. and Krause, A. and Miller, W. (2005). A

standard curve based method for relative real time

PCR data processing. BMC Bioinformatics. 6, 62.

doi:10.1186/1471-2105-6-62

Qiagen.(2010). Sample & Assay Technologies. Retrieved

February 1, 2010, from http://www.qiagen.com/

Products/Rotor-GeneQ.aspx

Roche Applied Science. (2010). Roche Applied Science:

genome sequencing, microarray analysis, nucleic acid

purification, real-time PCR, transfe. Retrieved

February 1, 2010, from https://www.roche-applied-

science.com

Savitzky, A. and Golay, M. (1964). Smoothing and

Differentiation of Data by Simplified Least Squares

Procedures. Retrieved February 1, 2010, from

http://pubs.acs.org/doi/pdf/10.1021/ac60214a047

Shain, E. and Clemens, J. (2008). A new method for

robust quantitative and qualitative analysis of real-time

PCR. Nucleic Acids Research. doi:10.1093/nar/gkn408

WebProdiap. Retrieved February 1, 2010, from

http://gladiator.biba.uni-bremen.de:8080/WebProdiap

V3/index.zul

Wilhelm, J. (2003). Development of real-time PCR based

methods for modern DNA analytics, Retrieved

February 1, 2010, from http://geb.uni-giessen.de/

geb/volltexte/2003/1072/

Wong, M. and Medrano, J. (2005).Real-time PCR for

mRNA quantitation, BioTechniques 39, 75-85.

Retrieved from: http://www.biotechniques.com/

multimedia/archive/00011/BTN_A_05391RV01_O_1

1901a.pdf

APPROACH TO ENABLE AN AUTOMATIC PRE-PROCESSING OF qRT-PCR - Analysis

285