TISSUE TYPE DIFFERENTIATION FOR BRAIN

GLIOMA USING NON-NEGATIVE MATRIX FACTORIZATION

Yuqian Li

1,2,3

, Diana M. Sima

2,3

, Sofie Van Cauter

4,5

, Uwe Himmelreich

, Yiming Pi

and Sabine Van Huffel

2,3

School of Electronic Engineering, University of Electronic Science and Technology of China

Xiyuan Dadao 2006, Chengdu, China

Department of Electrical Engineering, ESAT-SCD, Katholieke Universiteit Leuven, Leuven, Belgium

IBBT-K.U.Leuven Future Health Department, Leuven, Belgium

Department of Radiology, University Hospitals of Leuven, Leuven, Belgium

Biomedical NMR Unit/Molecular Small Animal Imaging Center, Department of Medical Diagnostic Sciences

Katholieke Universiteit Leuven, Leuven, Belgium

Keywords: Non-negative Matrix Factorization (NMF), Blind Source Separation (BSS), Magnetic Resonance

Spectroscopic Imaging (MRSI), Brain Glioma, Glioblastoma Multiforme (GBM).

Abstract: The purpose of this paper is to introduce a hierarchical Non-negative Matrix Factorization (NMF) approach,

customized for the problem of blindly separating brain glioma tumor tissue types using short-echo time

proton magnetic resonance spectroscopic imaging (

H MRSI) signals. The proposed algorithm consists of

two levels of NMF, where two constituent spectra are computed in each level. The first level is able to

correctly detect the spectral profile corresponding to the most predominant tissue type, i.e., normal tissue,

while the second level is optimized in order to detect two ‘abnormal’ spectral profiles so that the 3

recovered spectral profiles are least correlated with each other. The two-level decomposition is followed by

the reestimation of the overall spatial distribution of each tissue type via standard Non-negative Least

Square (NNLS). This method is demonstrated on in vivo short-TE

H MRSI brain data of a glioblastoma

multiforme patient and a grade II-III glioma patient. The results show the possibility of differentiating

normal tissue, tumor tissue and necrotic tissue in the form of recovered tissue-specific spectra with accurate

spatial distributions.

1 INTRODUCTION

Glioblastoma multiforme (GBM), which is the

highest grade of glioma, is the most common and

aggressive type of brain tumor in adults. Accurate

diagnosis is of utmost importance in guiding therapy

and determining prognosis. Magnetic resonance

spectroscopic imaging (MRSI) (

Brown et al.,

1982

), which provides both spectral and spatial

information, is becoming increasingly popular as an

additional non-invasive tool for clinical diagnosis of

brain tumors. Since the concentration of metabolites

changes under disease conditions, the profile of the

measured signal in each MRSI voxel helps to

determine the location of abnormal tissue (Howe et

al., 2003).

Because of the heterogeneity of GBMs, the

tumoral region could consist of several tissue types

(Croitor Sava et al., 2011), which represent actively

growing tumor, necrosis or normal brain tissue.

Lower grade gliomas do not contain necrosis, but are

also heterogeneous, e.g., the tumor can present

infiltrations into the normal brain tissue. In MRSI,

the partial volume effect, i.e., the presence of several

tissue types within one voxel, may lead to increased

variability in the measured signals. The spectrum

corresponding to each voxel can be approximately

described as a linear combination of spectra from

different constituent tissue types (Su et al., 2008).

Using Non-negative matrix factorization (NMF)

to extract main tissue types from the mixed MRSI

data was firstly proposed by Sajda and his

colleagues (Sajda et al., 2003; Sajda et al., 2004; Du

Li Y., Sima D., Van Cauter S., Himmelreich U., Pi Y. and Van Huffel S..

TISSUE TYPE DIFFERENTIATION FOR BRAIN GLIOMA USING NON-NEGATIVE MATRIX FACTORIZATION.

DOI: 10.5220/0003734600250031

In Proceedings of the International Conference on Bio-inspired Systems and Signal Processing (BIOSIGNALS-2012), pages 25-31

ISBN: 978-989-8425-89-8

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

et al., 2008; Su et al., 2008). They developed a

constraint NMF (cNMF) algorithm, which enforces

positivity, and incorporate it into a hierarchical

decomposition framework to recover physically

meaningful spectra using long echo time (TE) MRSI

signals.

In this paper, we study the applicability of a

novel hierarchical NMF method for tissue type

differentiation on short-TE MRSI data, which is

potentially much more challenging than long-TE due

to more complex spectral profiles. The proposed

algorithm, as described in Section 3, consists of two

levels of NMF, where two constituent spectra are

computed in each level. Thus, we recover each

tissue type step by step using NMF, i.e., first

differentiate normal and abnormal tissue, and then,

only in the abnormal region, differentiate active

tumor and necrosis, or differentiate proliferation

level of active tumor if necrosis is not present. Since

the choice of the abnormal region has a high

influence on the estimated sources, we propose to

tune the threshold for selecting the abnormal region

by minimizing the correlations between all three

estimated tissue spectra, i.e., normal tissue spectral

profile from the first-level NMF, and the two

abnormal spectral profiles from the second-level

NMF. Afterwards, non-negative least squares

(NNLS) is applied on the original mixed signals

using the obtained spectra in order to reestimate the

spatial distribution of each tissue type over the

whole grid. In section 4, experimental results on two

typical patients show the capability of revealing

tissue-specific spectral profiles and their spatial

distribution, and are validated against expert

labelling.

2 IN VIVO 1H MRSI DATA

2.1 Data Acquisition Protocol and

Patients

The short-TE MRSI data were acquired at the

University Hospital of Leuven (UZ Leuven) on a 3T

MR scanner (Achieva, Philips, Best, The

Netherlands). Point-resolved spectroscopy (PRESS)

(Bottomley, 1987) was used as the volume selection

technique, TR/TE: 2000/35 ms, FOV: 16cm*16 cm,

volume of interest (VOI): 8cm*8cm, slice thickness:

1cm, acquisition voxel size: 1cm*1cm,

reconstruction voxel size: 0.5cm*0.5 cm, receiver

bandwidth: 2000Hz, samples: 2048.

Our algorithm was tested on two types of

patients:

 In vivo MRSI data of GBM patients containing

necrotic areas. Anatomic image of a typical

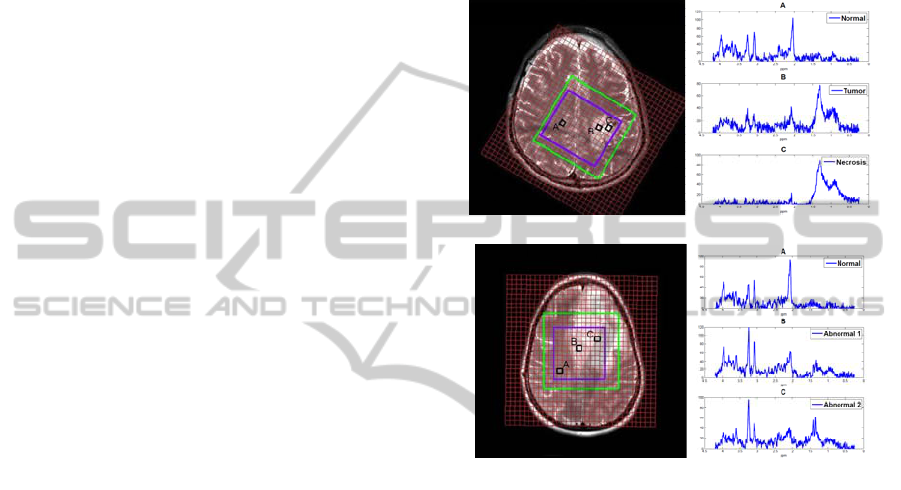
patient is shown in Figure. 1(a)

 In vivo MRSI data of glioma patients with no

apparent necrotic area. Figure 1 (b) shows the

anatomic image of a typical patient who has a

grade Ⅱ glioma with focal progression to a

grade Ⅲ glioma.

(a)

(b)

Figure 1: Left: Anatomic image. Right: tissue specific

spectra of patients. (a) Patient 1, a GBM patient with

necrosis. (b) Patient 2, a glioma patient with no apparent

necrosis areas. The outer green box is the PRESS box and

the inner blue box contains the selected voxels of interest.

2.2 Data Preprocessing

In-house software SPID (Poullet, 2008), which was

developed on the Matlab platform, was used for

standard spectroscopic signal preprocessing. The

applied steps were as follows:

 In the MRSI grid, signals of insufficient quality

(low signal-to-noise ratio (SNR), baseline

problems, chemical shift displacement effects,

etc.) usually exist, affecting mostly the voxels

close to the border of the PRESS box. Therefore,

these signals were excluded by selecting an inner

smaller box inside the PRESS box of the MRSI

grid (see Fig.1).

 Residual water components ware removed using

Hankel-Lanczos Singular Value Decomposition

with Partial Re-Orthogonalization (HLSVD-

PRO) (Laudadio et al., 2002). The model order

BIOSIGNALS 2012 - International Conference on Bio-inspired Systems and Signal Processing

was set to 30 and the passband from 0.25 to 4.2

ppm.

 A baseline offset correction was found

necessary. But this is not suppressing the

baseline due to macromolecules, which may be

relevant for tissue differentiation.

 The real parts of the preprocessed spectra were

truncated to the region 0.25 – 4.2 ppm before

analyzing them using the NMF algorithm.

3 METHODS

3.1 Basics of Non-negative Matrix

Factorization (NMF)

NMF (Paatero et al., 1994; Lee et al., 1999), as a

blind source separation (BSS) method, has attracted

much attention in performing the factorization:

XWHN=+

(1)

where

is a matrix of observed MRSI spectra

represented as column vectors, with one column per

voxel.

is a matrix of constituent tissue spectra,

with each column representing a typical spectrum

for each tissue type. Each row of the matrix

contains the linear combination weights (interpreted

here as abundances or concentrations) of all

constituent tissue spectra.

stands for additive

measurement noise. The mathematical formulation

of the basic NMF problem is

min ( , ) || ||

0, 0

fWH X WH

subject to W H

=−

≥≥

(2)

3.2 Hierarchical NMF-NNLS

In this section, a hierarchical NMF-NNLS algorithm,

which recovers the 3 most distinct tissue-specific

spectral profiles and their corresponding spatial

distributions step by step, is described.

 Step 1: First level NMF

. Apply NMF to the

preprocessed MRSI signals with the number of

components chosen to be 2. Two patterns of

spectra (W-normal and W-abnormal,

respectively) and their contribution to each

location in the brain image (H-normal and H-

abnormal) will be recovered. Then, label the

obtained 2 sources as normal and abnormal

tissue types according to typical metabolic

features of their spectral profiles (i.e., the NAA

peak at 2.01 ppm is higher in the source

corresponding to normal tissue).

 Step 2: Automatically find the optimal threshold

for the abnormal region. Perform intermediate

NMF decompositions with 2 sources on

gradually increasing sets of voxels, where these

sets are selected according to a variable threshold

on the magnitude of the H-abnormal map. A

reasonable trade-off for mutually least

correlation between recovered spectral profiles is

found by minimizing the sum: Corr(W-

normal,W-abnormal1) + Corr(W-normal,W-

abnormal2) + Corr(W- abnormal1+W-

abnormal2).

 Step 3: Second level NMF

. Apply NMF only to

the voxels of the abnormal region selected using

the optimal threshold in order to further separate

the abnormal tissue into two abnormal tumor

profiles, which reflect the aggressiveness level,

with their corresponding spatial distributions. If

one of the profiles contains predominantly lipids

(according to the peaks at 0.9 and 1.3 ppm) and

almost no other metabolites, then label that

profile as necrosis.

 Step 4: NNLS reestimation

. Since the second

level NMF was restricted to the selected

abnormal region, some border voxels containing

abnormal tissue may have been excluded due to

the thresholding. Applying non-negative least

squares approach (Lawson et al., 1974) to the

whole grid with the 3 recovered tissue spectra

(i.e., solving problem [2] for W fixed to a three-

column matrix [W-normal, W-abnormal1, W-

abnormal2]) will give a complete estimation of

the spatial information of these 3 tissue types

over the whole initially considered grid.

4 EXPERIMENTAL RESULTS

We studied the applicability of brain tumor tissue

type differentiation using the proposed hierarchical

NMF-NNLS algorithm. The results of two different

cases are shown in Figure 2 and Figure 3.

4.1 Results for Patient 1: GBM Patient

with Necrosis

Results of 2-level hierarchical NMF-NNLS to the

preprocessed brain signals of patient 1 are shown in

Figure 2. The corresponding anatomic picture of the

patient 1 (male, GBM) is shown in Figure 1 (a) with

the green box and the blue box representing the

TISSUE TYPE DIFFERENTIATION FOR BRAIN GLIOMA USING NON-NEGATIVE MATRIX FACTORIZATION

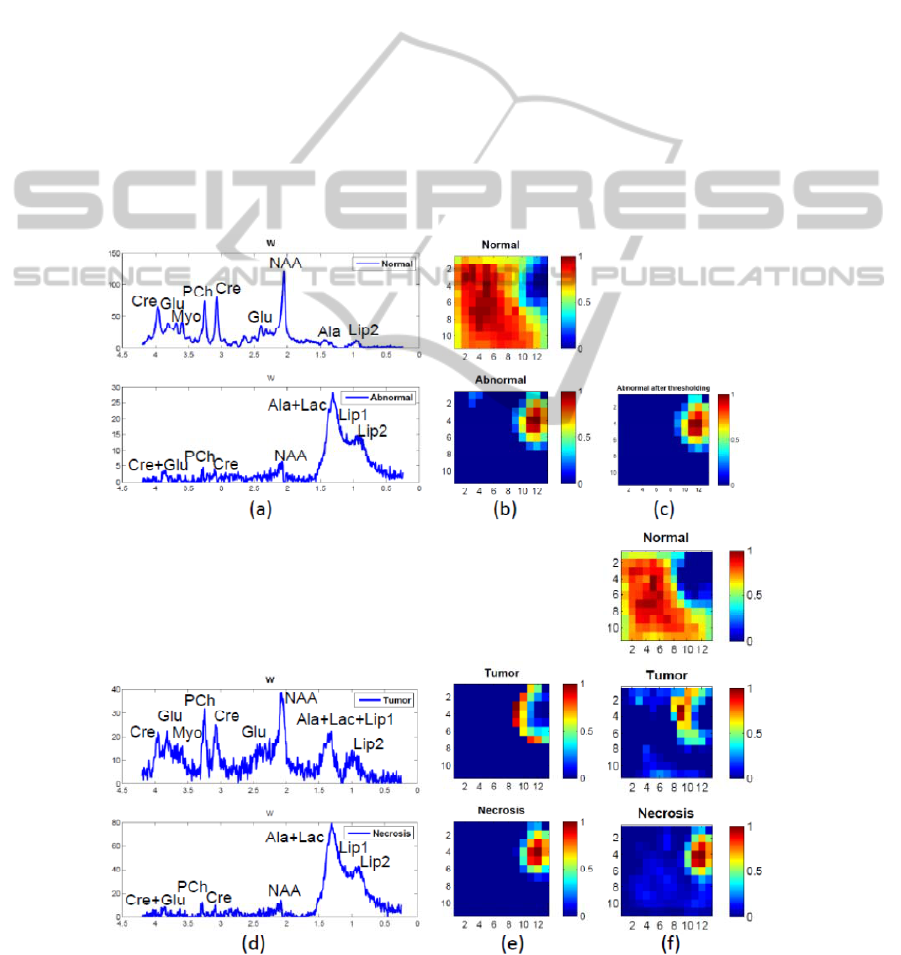
PRESS box and the selected voxels of reasonable

quality, respectively. Figure 2 (a) presents the

recovered normal and abnormal spectra of the first

level NMF. The spectrum that shows a decreased

NAA/Cho ratio, a decreased Cre and significant

levels of Lac-Lip, represents the tumor tissue. The

one with almost no metabolites other than lipids

(and potentially lactate), is the typical spectral

pattern of necrotic tissue. The H-maps in (b) give

their spatial distribution. (c) illustrates the selected

abnormal region. (d) and (e) are the results of the

second level NMF. (f) shows the reestimated spatial

information using NNLS. We can see tumor and

necrosis in (c) covering bigger regions than in (b)

and therefore being able to show more complete

information at the border region which contains

mixed tissues.

4.2 Results on Glioma Patients with no

Apparent Necrosis Area

To explore the applicability of the proposed method

(see Section 2.4), it was tested on another case,

which is a patient who has been diagnosed with

grade II-III glioma and, according to the expert

labeling, does not present macroscopic necrosis;

Anatomic picture is given in Figure 1 (b). Results

are shown in Figure 3. It is controversial if we still

try to search for 3 components with our method

when there is no necrosis. Still, this situation is

realistic, because in most cases we are not sure

beforehand if there is necrosis within the lesion.

Figure 3 (a) and (b) give the results of the first level

decomposition and thresholding. Panel (a) illustrates

the recovered spectra of normal tissue and abnormal

tissue; the H-maps in (b) show the spatial

distribution of the corresponding spectra after

Figure 2: Result of hierarchical NMF-NNLS on patient 1, a GBM patient with necrosis. (a) – (b): Step 1, first level NMF.

(c): Abnormal region after optimal thresholding. (d) – (e): Step 3, second level NMF. (f): Step 4, NNLS.

BIOSIGNALS 2012 - International Conference on Bio-inspired Systems and Signal Processing

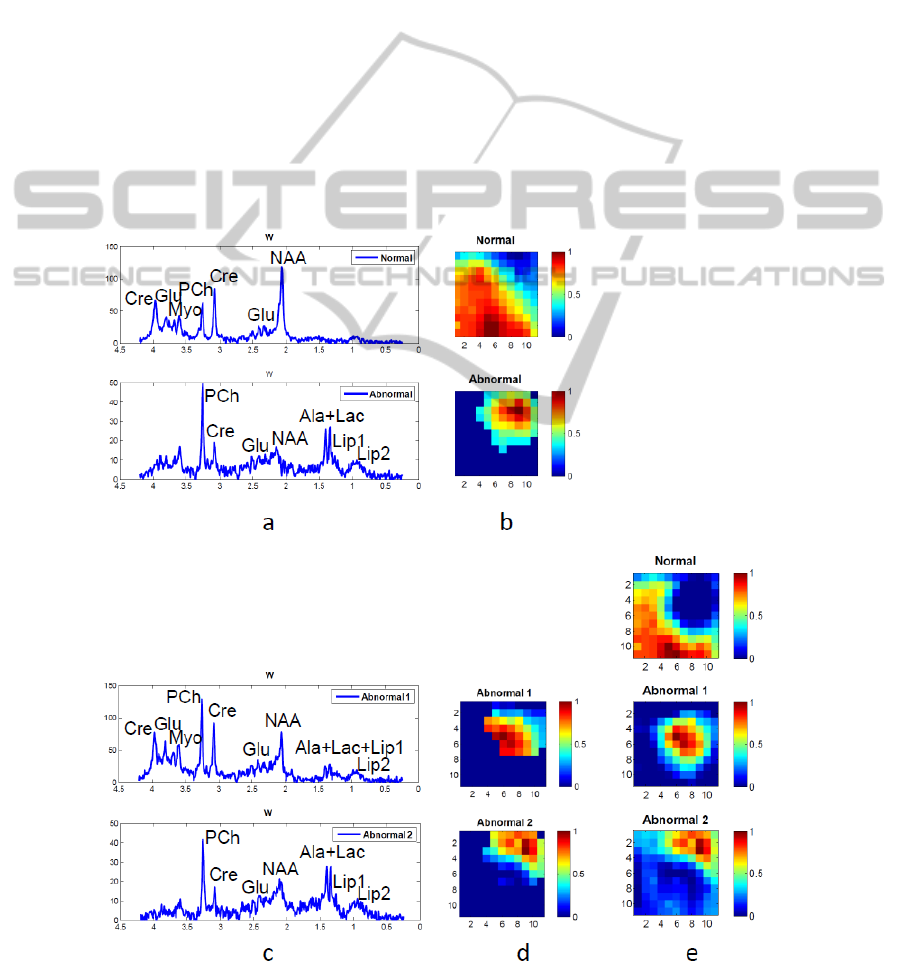
thresholding. We can see that the factorization is

effective in finding normal and abnormal tissue.

Then, in Step 3, the abnormal tissue was

separated into two parts that apparently do not

contain necrotic tissue (also confirmed by the

absence of lipids). The one near the normal region is

the border of the tumor, with its spectral pattern

(Abnormal 1 in Figure 3 (c)) still indicating

abnormality (low NAA/Cho). The recovered

spectrum from the other part of abnormal region

(Abnormal 2 in Figure 3 (c)) has a significant

increase of Cho and Lips, obvious peaks of Ala and

Lac, and a decrease of other metabolites. For this

case without necrosis, instead of separating tumor

and necrosis, our proposed method reveals the

regions in the tumor that correspond to different

levels of proliferating tumor cells. In the end, NNLS

estimation gives more complete spatial information

of each tissue type.

4.3 Results Validation

The distribution maps of the 3 tissue types were

overlapped onto the anatomical images; see Fig. 4.

The recovered location of our results corresponds

well to the one shown on the anatomic image.

As an additional validation for patient 1, we also

computed correlation coefficients between the

recovered spectra and the average of pure tissue-

specific spectra according to the labeling of an

expert (SVC). The result for normal tissue is 0.9933,

for tumor is 0.9618 and for necrosis is 0.9950, which

shows that all spectral sources are relatively highly

correlated with the validated spectra.

For patient 2, who has grade II-III glioma but

without macroscopic necrosis, the result of our

proposed method reflected the level of tumour

proliferation, which was validated by histopathology.

Figure 3: Result of hierarchical NMF-NNLS on patient 2, a glioma patient with no apparent necrosis area. (a) – (b): Step 1-

2, first level NMF and optimally selected abnormal region (c) – (d): Step 3, second level NMF. (e): Step 4, NNLS.

TISSUE TYPE DIFFERENTIATION FOR BRAIN GLIOMA USING NON-NEGATIVE MATRIX FACTORIZATION

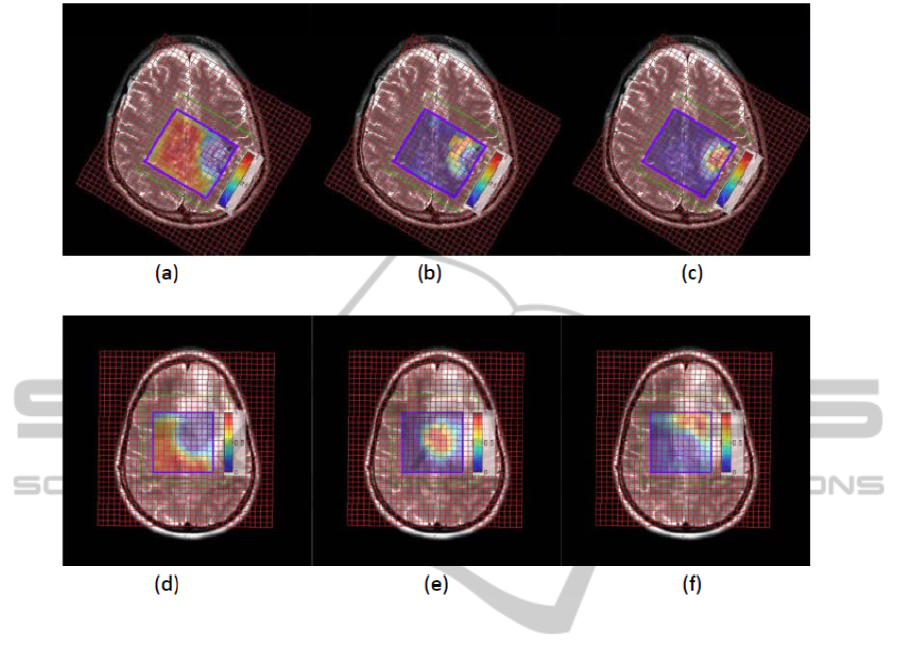
Figure 4: Overlap of the distribution results onto the anatomic images. The first row is the result of the GBM patient with

necrosis. (a): normal tissue distribution; (b): tumor tissue distribution; (c): necrosis tissue distribution. The second row is the

result of the glioma patient without necrosis. (a): normal tissue distribution; (b): abnormal 1 tissue distribution; (c):

abnormal 2 tissue distribution.

5 DISCUSSION & CONCLUSIONS

A novel tissue type differentiation approach,

hierarchical NMF-NNLS, and its clinical application

were explored in this study for GBM patients.

The data we used in this study is short-TE MRSI

signals because spectra of short-TE represent more

metabolites than long-TE spectra. But there is more

significant peak overlap and, usually, a higher noise

level. Therefore, using short-TE signals in solving

tissue type differentiation is more challenging but of

more significance.

The reason we need the hierarchical procedure is

based on the assumption in the considered data sets

that the MRSI grid encompasses mostly normal

tissue and a glioma tumor with heterogeneous tissue

content. Due to the unbalanced proportion of the

tumor tissue voxels inside the grid, the sources

corresponding to under-represented tissue types

would be difficult to be identified by simply using

NMF with more than 2 sources. Therefore, the

robustness of NMF for extracting meaningful

spectral patterns can be increased through a

hierarchical NMF approach.

The possibility of differentiating brain tumor

tissue types was demonstrated in two distinct cases.

Representative results from a GBM patient showed

the capability of the proposed algorithm to separate

short-TE MRSI data into normal tissue, tumor and

necrosis with accurate spatial information. For the

case of a glioma patient without necrosis, our

method is able to indicate the proliferation level of

the tumor. This result is useful because assessing

tumor proliferation level is important in brain tumor

diagnosis, as it gives information that is potentially

helpful in directing the patient’s clinical

management. Both cases show that the proposed

method is able to find meaningful sources and their

corresponding spatial distributions using short-TE

MRSI signals.

However, the data presented in this paper is

preliminary and a more appropriate data pool will be

BIOSIGNALS 2012 - International Conference on Bio-inspired Systems and Signal Processing

used in future work in order to actually fully assess

the performance of the proposed technique.

Another paper appearing in these proceedings

focuses on a “simulation study of tissue type

differentiation using non-negative matrix

factorization”. In that preliminary research, we

studied the performance of several NMF

implementations on simulated MRSI signals. The

‘(a)hals’ algorithm (Cichocki et al., 2007; Cichocki

et al., 2009; Gillis, 2011) had the best performance

in those simulations and has therefore been used for

all the NMF computations in this paper.

ACKNOWLEDGEMENTS

This research was supported by Research Council

KUL: GOA MaNet, CoE EF/05/006 Optimization in

Engineering (OPTEC), PFV/10/002 (OPTEC), IDO

08/013 Autism, several PhD/postdoc & fellow grants;

Flemish Government: FWO: PhD/postdoc grants,

projects: FWO G.0302.07 (SVM), G.0341.07 (Data

fusion), G.0427.10N (Integrated EEG-fMRI),

G.0108.11 (Compressed Sensing) research

communities (ICCoS, ANMMM); IWT:

TBM070713-Accelero, TBM070706-IOTA3,

TBM080658-MRI (EEG-fMRI), PhD Grants; IBBT

Belgian Federal Science Policy Office: IUAP P6/04

(DYSCO, `Dynamical systems, control and

optimization', 2007-2011); ESA AO-PGPF-

01, PRODEX (CardioControl) C4000103224;

EU: RECAP 209G within INTERREG IVB NWE

programme, EU HIP Trial FP7-HEALTH/ 2007-

2013 (n° 260777) (Neuromath (COST-BM0601):

BIR&D Smart Care. Li thank the China Scholarship

Council.

REFERENCES

Bottomley PA, 1987. Spatial localization in NMR-

spectroscopy in vivo. Ann N Y Acad Sci, 508:333–348.

Brown T, Kincaid B, Ugurbil K, 1982. NMR chemical

shift imaging in three dimensions. PNAS, 79(11):

3523-3526.

Croitor Sava A, Martinez-Bisbal MC, Van Huffel S, Cerda

JM, Sima DM, Celda B, 2011. Ex vivo high resolution

magic angle spinning metabolic profiles describe

intratumoral histopathological tissue properties in

adult human gliomas. Magn Reson Med, 65:320-328.

Cichocki A, Zdunek R, Amari S, 2007. Hierarchical ALS

algorithms for nonnegative matrix and 3D tensor

factorization. Lect Notes Comput Sci, 4666:169-176.

Cichocki A, Phan AH, 2009. Fast local algorithms for

large scale Nonegative Matrix and Tensor

Factorizations. IEICE Trans Fund Electron Comm

Comput Sci, 3:708-721.

Du S, Mao X, Sajda P and Shungu DC, 2008. Automated

tissue segmentation and blind recovery of 1H MRS

imaging spectral patterns of normal and diseased

human brain. NMR in Biomedicine, 21:33-41.

Gillis N, 2011. Nonnegative matrix factorization

complexity, algorithms and applications. PhD Thesis,

Louvan-La-Neuve, Belgium.

Howe FA, Barton SJ, Cudlip SA, Stubbs M, Saunders DE,

Murphy JR, Opstad KS, Doyle VL, McLean MA, Bell

BA, Griffiths JR, 2003. Metabolic profiles of human

brain tumours using quantitative in vivo 1H magnetic

resonance spectroscopy. Magn Res Med, 49:223-232.

Laudadio T, Mastronardi N, Vanhamme L, Van Hecke P,

Van Huffel S, 2002. Improved Lanczos algorithms for

blackbox MRS data quantitation. J Magn Reson, 157:

292-297.

Lawson C.L. and R.J. Hanson, 1974, Solving Least-

Squares Problems, Prentice-Hall, Chapter 23, p. 161,.

Lee DD, Seung HS, 1999. Learning the parts of objects by

non-negative matrix factorization. Nature, 401:788-

791.

Paatero P, Tapper U, 1994. Positive matrix factorization:

A non-negative factor model with optimal utilization

of error. Environmetrics, 5:111-126.

Poullet JB, 2008. Quantification and classification of

magnetic resonance spectroscopic data for brain

tumor diagnosis. PhD Thesis, Leuven, Belgium.

Sajda P, Du S, Brown TR, Parra LC, Stoyanova R, 2003.

Recovery of constituent spectra in 3D chemical shift

imagin using non-negative matrix factorization. In

Proc. 4th Int. Symp. ICA and BSS, 71-76.

Sajda P, Du S, Brown TR, Stoyanova R, Shungu DC, Mao

X, Parra LC, 2004. Nonnegative Matrix Factorization

for Rapid Recovery of Constituent Spectra in

Magnetic Resonance Chemical Shift Imaging of the

Brain. IEEE Trans Med Imaging, 23:1453-1465.

Su Y, Thakur SB., Karimi S, Du S, Sajda P, Huang W,

Parra LC, 2008. Spectrum separation resolves partial-

volume effect of MRSI as demonstrated on brain

tumor scans. NMR Biomed, 21:1030-1042.

TISSUE TYPE DIFFERENTIATION FOR BRAIN GLIOMA USING NON-NEGATIVE MATRIX FACTORIZATION