SIMULATION STUDY OF TISSUE TYPE DIFFERENTIATION

USING NON-NEGATIVE MATRIX FACTORIZATION

Yuqian Li

1,2,3

, Diana M. Sima

2,3

, Sofie Van Cauter

4,5

, Uwe Himmelreich

, Yiming Pi

and Sabine Van Huffel

2,3

School of Electronic Engineering, University of Electronic Science and Technology of China,

Xiyuan Dadao 2006, Chengdu, China

Department of Electrical Engineering, ESAT-SCD, Katholieke Universiteit Leuven, Leuven, Belgium

IBBT-K.U.Leuven Future Health Department, Leuven, Belgium

Department of Radiology, University Hospitals of Leuven, Leuven, Belgium.

Biomedical NMR Unit/Molecular Small Animal Imaging Center, Department of Medical Diagnostic Sciences,

Katholieke Universiteit Leuven, Leuven, Belgium

Keywords: Glioma, Magnetic Resonance Spectroscopic Imaging (MRSI), Non-negative Matrix Factorization (NMF),

Blind Source Separation (BSS).

Abstract: Finding the brain tumor tissue-specific magnetic resonance spectra and their corresponding spatial

distribution is a typical Blind Source Separation (BSS) problem. Non-negative Matrix Factorization (NMF),

which only requires non-negativity constraints, has become popular because of its advantages compared to

other BSS methods. A variety of algorithms based on traditional NMF have been recently proposed. This

study focuses on the performance comparison of several NMF implementations, including some newly

released methods, in brain glioma tissue differentiation using simulated magnetic resonance spectroscopic

imaging (MRSI) signals. Experimental results demonstrate the possibility of finding typical tissue types and

their distributions using NMF algorithms. The (accelerated) hierarchical alternating least squares algorithm

was found to be the most accurate.

1 INTRODUCTION

Automatic tissue type differentiation in brain tumor

patients is of utmost importance in guiding therapy

and determining prognosis. Magnetic resonance

spectroscopic imaging (MRSI) (Brown et al., 1982),

which produces localized spectra, is used as a non-

invasive tool for additional clinical diagnosis of

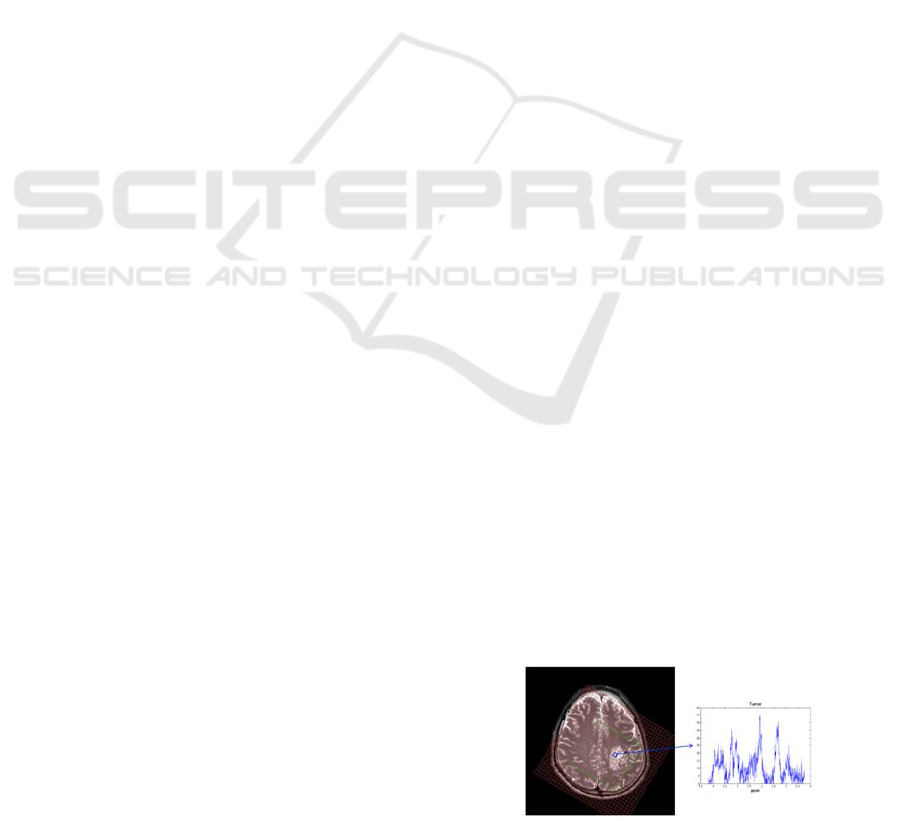
brain tumors; see Figure 1. Given an

mn×

matrix X

which represents the observed spectra from MRSI

data, each column containing a spectrum from one

voxel, previous studies (Su et al., 2008)

demonstrated that

can be approximately

described as a linear combination of constituent

specta of different tissue types. The model is

XWHN=+

(1)

W is a mr× matrix, with each column representing

a recovered spectrum for each tissue type. Each row

of the

matrix H contains the linear

combination weights (interpreted here as abundances

or concentrations) of all constituent tissue spectra. N

stands for additive measurement noise.

Figure 1: Left: anatomic image of a glioma patient’s brain

overlaid with the MRSI grid. Right: the spectral profile

from the blue voxel from the tumor area.

Blind Source Separation (BSS) is one of the

main approaches to perform such factorization. One

of the algorithms, non-negative matrix factorization

(NMF) (Lee et al., 1999), has attracted much

212

Li Y., Sima D., Van Cauter S., Himmelreich U., Pi Y. and Van Huffel S..

SIMULATION STUDY OF TISSUE TYPE DIFFERENTIATION USING NON-NEGATIVE MATRIX FACTORIZATION.

DOI: 10.5220/0003734702120217

In Proceedings of the International Conference on Bio-inspired Systems and Signal Processing (BIOSIGNALS-2012), pages 212-217

ISBN: 978-989-8425-89-8

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

attention in recent years because it does not require

the constituent spectra to be orthogonal or

independent. The mathematical formulation of the

basic NMF problem is

min ( , ) || ||

,, 0

ij ij

fWH X WH

subject to ij W H

=−

∀≥

(2)

In this paper, we designed a simulation study

aiming to evaluate the accuracy of several popular

NMF implementations in solving the brain glioma

tissue type differentiation problem. The algorithms’

performance was investigated specifically in terms

of their accuracy to estimate tissue-specific spectra

and their spatial distribution.

2 NMF ALGORITHMS

In this section we describe several NMF algorithms

that will be compared in Section 4.

 Multiplicative update method using Euclidean

distance measure (mu) (Lee et al., 2001):

This algorithm is used most commonly in

solving the NMF problem. It uses the Euclidean

distance as a measure to construct the cost

function

|| ||XWH−

. The cost function is

minimized using the update rule:

()

kj kj

ik ik

WWH

WHH

ijk

←

∀

(3)

 Alternating least squares (als) (Berry et al.,

2007): This algorithm alternately solves

unconstrained least squares subproblems for W

and H (see Eq. 4) and sets the negative elements

to zero.

argmin || ||

WXWH

HXWH

←−

(4)

 Alternating non-negative least squares using

projected gradients (cjlin) (Lin, 2007): In this

implementation, non-negatively constrained least

squares subproblems are solved alternatively for

W and H using the projected gradient method.

Consider the following standard form of bound-

constrained optimization problems:

min ( )

: , 1,...,

iii

ubject to l x u i n

∈

≤≤ =

(5)

Projected gradient methods are iterative and

update the current solution

to the following

by the rule:

[()]

kkkk

Px f x

=−∇

(6)

where

is the step size and

[]

i iii

ii ii

if l x u

Px u if x u

lifxl

⎧

⎪

=≥

⎨

⎪

≤

⎩

Hierarchical alternating least squares (hals)

(Cichocki et al., 2007; Cichocki et al., 2009):

hals

sequentially estimates one column of W and/or

one row of H while fixing all the other ones, that is

::0

||||minarg

FkkkkH

FHk

FkkkkW

FWk

HWHWX

WHXH

HWHWX

WHXW

−−

=−←

−−

=−←

−−≥

≥

−−≥

≥

(7)

where W

, W

-k

, H

-k

denote, respectively, the

kth column of W, the matrix W without the kth

column, the kth row of H, and the matrix H

without the kth row.

 Accelerated multiplicative update method

(amu) and Accelerated HALS (ahals) (Gillis,

2011): These two more efficient methods are

developed based on the mu and hals methods.

Computational cost is reduced by updating W

several times before updating H (and vice versa),

instead of updating W and H alternately. An

inner loop stopping criterion is utilized for each

()l

, defined as the iterate after l updates of W

using Eq. 3 for amu or Eq. 7 for ahals (while H

is being kept fixed):

(1) () (1) (0)

|| || || ||

WW WW

−≤ −

(8)

where

is a small constant, equal to 0.01 in the

implementation.

3 EXPERIMENT & RESULTS

3.1 Simulated Spatial Distribution

In order to construct a realistic MRSI grid

Containing spectra from normal tissue, as well as

SIMULATION STUDY OF TISSUE TYPE DIFFERENTIATION USING NON-NEGATIVE MATRIX

FACTORIZATION

213

tumor tissue and necrosis, we simulated an MRSI

grid in which these 3 tissue types are contained.

Table 1 shows the simulated distribution of brain

tissues. Each table cell represents a voxel. C, N, and

T denote respectively control tissue type (i.e.,

normal tissue), tumor tissue and necrotic tissue. In

the voxels at the interface between tissues, there is

usually a mixture of different tissue types.

Therefore, decimals are placed into the table to

represent concentration of mixed tissues. For

instance, 0.8C+0.2T denotes the tissue type in a

voxel composed of approximately 80% normal and

20% tumor tissue.

3.2 Simulated MRSI Signals

In our study, the simulated signals are linear

combinations of 9 metabolite profiles (two simulated

lipid profiles and seven metabolite profiles measured

in vitro), i.e., creatine (Cre), glutamate (Glu), myo-

inositol (Myo), phosphocholine (PCh), N-acetyl-

aspartate (NAA), alanine (Ala), lactate (Lac), lipid at

1.3ppm (Lip1), and lipid at 0.9ppm (Lip2). These

components are significant biomarkers for normal

brain tissue, tumor tissue, and necrosis tissue in

pathology (Howe et al., 2003). To choose proper

parameters for amplitude, damping, phase and

frequency for the simulated signals, we rely on a

parameter extraction procedure (Poullet et al., 2006).

In order to emulate the variability within an

MRSI grid, 4dB white Gaussian noise, which is in

agreement with our in vivo signals, is added to the

spectrum of each voxel.

The generated time domain signals, each having

2048 points, are Fourier transformed into the

frequency domain, then truncated to the frequency

range of interest, 0.25 – 4.2 ppm.

The simulated tissue-specific spectra with noise

are shown in the first row of Figure 2 (in blue) and

are compared with spectra from a clinical in vivo

case as shown in the second row of Figure 2. The

simulated pure spectra are in red.

3.3 Tissue Type Differentiation using

NMF Algorithms

Several NMF algorithms listed in section 2 are

applied to the simulated grid described in section 3.1;

see Table 1. The number of brain tissue types is set

to be 3, indicating normal tissue, tumor tissue and

necrotic tissue. The recovered constituent spectra

and their corresponding spatial distributions show

the variability of tissue type differentiation using

each of the described NMF algorithms; see Figure 3.

After scaling and normalization, we notice that

similar spectra with important peaks, which are

biomarkers for discrimination of different tissue

types (NAA, Cho, Lac/Lip), are obtained for each

tissue type with all methods. The corresponding

abundance maps clearly show the location of each

tissue type.

Table 1: Simulated tissue-specific spatial distribution. C denotes control tissue type, i.e., normal tissue. T denotes tumor

tissue. N denotes necrotic tissue.

C C C C C C C

0.8C

+0.2T

0.3C

+0.7T

T T

0.6T

+0.4N

C C C C C C C

0.8C

+0.2T

0.3C

+0.7T

T T

0.3T

+0.7N

0.5T

+0.5N

C C C C C C C

0.8C

+0.2T

0.3C

+0.7T

0.3T

+0.7N

0.2T

+0.8N

0.3T

+0.7N

C C C C C C C

0.8C

+0.2T

0.3C

+0.7T

0.1T

+0.9N

0.3T

+0.7N

C C C C C C C

0.8C

+0.2T

0.3C

+0.7T

0.1T

+0.9N

0.4T

+0.6N

C C C C C C C

0.8C

+0.2T

0.3C

+0.7T

0.5C

+0.5T

0.5T

+0.5N

0.5T

+0.5N

C C C C C C C C

0.8C

+0.2T

0.8C

+0.2T

0.5C

+0.5T

0.3C

+0.7T

0.5C

+0.5T

C C C C C C C C C C

0.8C

+0.2T

0.8C

+0.2T

0.8C

+0.2T

C C C C C C C C C C C C C

BIOSIGNALS 2012 - International Conference on Bio-inspired Systems and Signal Processing

214

Figure 2: Spectra with SNR of 4dB from different voxels. The first row shows simulated spectra from normal tissue, tumor

tissue and necrotic tissue, respectively. Simulated noiseless spectra are shown with thick red lines. For comparison, the last

row contains in vivo spectra from the three different tissue types.

(a) (b) (c)

(d) (e) (f)

Figure 3: Simulation results of normalized recovered spectra (left column) and their corresponding spatial distribution (right

column) averaged over successful runs among 500 runs with different initializations using several NMF algorithms: (a) mu;

(b) cjlin; (c) als; (d) hals; (e) amu; (f) ahals. The color bars show scales for the distribution of concentration.

3.4 Validation of Spectral Separation

and Abundance Estimates

In order to evaluate the accuracy of the algorithms

listed in section 2, averaged results from 500 runs

(results with convergence problems were excluded,

i.e. 8 out of 500 runs for mu, 9 out of 500 runs for

als) for each algorithm were calculated, with

different starting values. For every run, all the

methods take the same initial value. Specifically,

SIMULATION STUDY OF TISSUE TYPE DIFFERENTIATION USING NON-NEGATIVE MATRIX

FACTORIZATION

215

correlation coefficients R between constituent

spectra estimated by NMF and simulated spectra are

computed. The closer R to 1, the better the similarity

between spectra generated using NMF and the

simulated spectra, thus the better the performance.

Furthermore, we compute the error rate of the

corresponding spatial distribution for each tissue

type:

()

100%

ErrorRate

−

=⋅

∑

(9)

where

h is the estimated abundance map from

NMF and

is the original distribution (see Table 1)

When the value of the error is lower, the accuracy of

the estimated spatial distribution is higher.

Algorithms were adjusted to make sure they all

detect convergence according to the same stopping

criterion, namely the condition that

(1) ()

|| ||

−

(1) ()

|| ||

− (i.e., the difference of recovered

sources or the recovered abundance maps in

subsequent iterations) drops below a certain

tolerance level, set to

−

for all the methods.

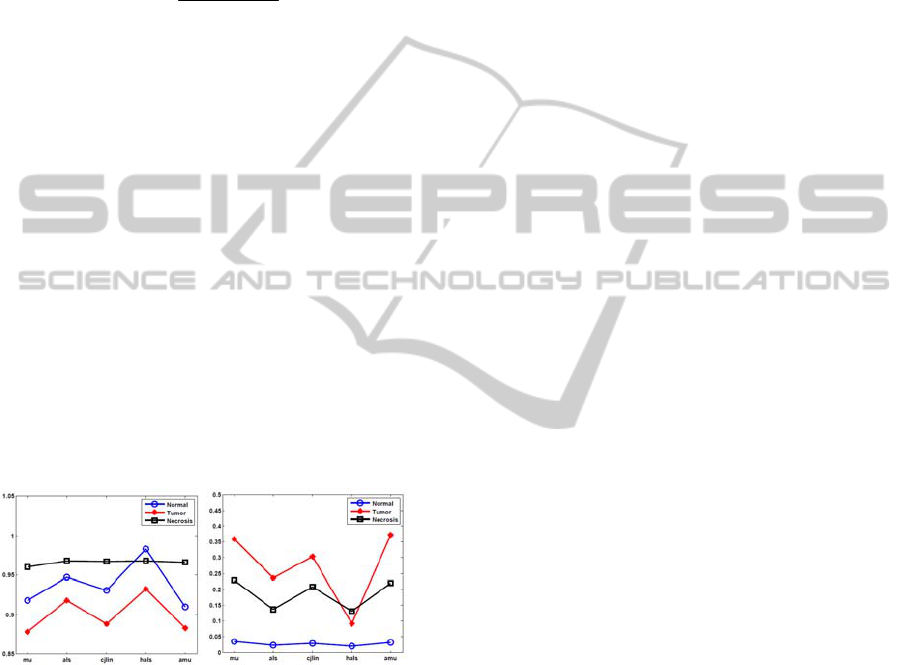
Results are shown in Figure 4. Overall, hals

gives the best result for all tissue types, especially

the error rate calculated by hals for tumor is

significantly lower than for other methods. Results

of ahals were also investigated but not shown here

since they are identical to hals.

(a) (b)

Figure 4: Accuracy evaluation. (a) correlation coefficient;

(b) error rate.

4 DISCUSSION & CONCLUSION

In this simulation study, we aimed at comparing the

performance of several NMF algorithms on spectra

with a high noise level. Spectral distortions due to,

e.g., magnetic field inhomogeneity and the chemical

shift displacement effect may lead to more signal

variability and to the violation of the model in Eq.1.

We chose not to include such non-linear factors of

variability in the simulations because those would

obscure the reasons for differences between

methods. Nevertheless, in vivo signals need to be

reprocessed and significantly distorted signals need

to be excluded before spectral separation using

NMF.

Among the tested NMF implementations, Lee

and Seung’s algorithm mu (Lee et al., 2001) was the

most commonly used one in the past. Comparisons

between various NMF algorithms have already been

presented in the literature (Kim et al., 2007). But

previous comparisons between algorithms were

mostly focused on evaluating computational

efficiency and divergence problems (Kim et al.,

2007; Cichocki et al., 2009), which are indicated by

the cost function

|| ||

XWH−

. However, the

accuracy of estimated tissue type profiles and the

corresponding spatial location is much more

important in the clinical diagnosis than

computational speed since the computing time of all

the methods is affordable for the dimensions of the

considered MRSI grids. Instead of evaluating the

results only visually, we follow (Croitor Sava et al.,

2010) who calculated correlation coefficients

between the obtained tissue sources and reference

tissue models. Our error rate is calculated between

the estimated spatial information and the simulated

spatial information. In this way, the accuracy of the

estimated spatial distribution of each tissue type can

be evaluated.

Overall, our results show that (a)hals gives the

best results in the simulation study, which confirms

the argumentation in (Gillis, 2011) that (a)hals has

remarkable performances. Especially the error for

tumor tissue shows a significant decrease compared

to all other methods. It demonstrates that the very

recent NMF algorithms hals and ahals can be

suitable for solving brain tissue type differentiation

problems using MRSI signals. In another study, we

further validate the feasibility of utilizing NMF

algorithms for brain tumor tissue differentiation

using in vivo MRSI signals.

ACKNOWLEDGEMENTS

This research was supported by Research Council

KUL: GOA MaNet, CoE EF/05/006 Optimization in

Engineering (OPTEC), PFV/10/002 (OPTEC), IDO

08/013 Autism, several PhD/postdoc & fellow grants;

Flemish Government: FWO: PhD/postdoc grants,

projects: FWO G.0302.07 (SVM), G.0341.07 (Data

fusion), G.0427.10N (Integrated EEG-fMRI),

G.0108.11 (Compressed Sensing) research

communities (ICCoS, ANMMM); IWT:

BIOSIGNALS 2012 - International Conference on Bio-inspired Systems and Signal Processing

216

TBM070713-Accelero, TBM070706-IOTA3,

TBM080658-MRI (EEG-fMRI), PhD Grants; IBBT

Belgian Federal Science Policy Office: IUAP P6/04

(DYSCO, `Dynamical systems, control and

optimization', 2007-2011); ESA AO-PGPF-

01, PRODEX (CardioControl) C4000103224;

EU: RECAP 209G within INTERREG IVB NWE

programme, EU HIP Trial FP7-HEALTH/ 2007-

2013 (n° 260777) (Neuromath (COST-BM0601):

BIR&D Smart Care. Li thank the China Scholarship

Council.

REFERENCES

Berry M, Browne M, Langville A, Pauca V, and

Plemmons R, 2007. Algorithms and applications for

approximate non-negative matrix factorization.

Comput Stat Data Anal,52:155-173.

Brown T, Kincaid B, Ugurbil K, 1982. NMR chemical

shift imaging in three dimensions. PNAS, 79(11):

3523-3526.

Cichocki A, Zdunek R, Amari S, 2007. Hierarchical ALS

algorithms for nonnegative matrix and 3D tensor

factorization. Lect Notes Comput Sci, 4666:169-176.

Cichocki A, Phan AH, 2009. Fast local algorithms for

large scale Nonegative Matrix and Tensor

Factorizations. IEICE Trans Fund Electron Comm

Comput Sci, 3:708-721.

Croitor Sava AR, Sima DM, Martinez-Bisbal MC, Celda

B, Van Huffel S, 2010. Non-negative Blind Source

Separation Techniques for Tumor Tissue Typing

Using HR-MAS signals. In Proceedings of the 32nd

Annual International Conference of the IEEE EMBS,

Buenos Aires, Argentina.

Gillis N, 2011. Nonnegative matrix factorization

complexity, algorithms and applications. PhD Thesis,

Louvan-La-Neuve, Belgium.

Gonzalez EF, Zhang Y, 2005. Accelerating the Lee-Seung

algorithm for non-negative matrix factorization. Tech

Report, Rice University.

Grippo L, Sciandrone M, 2000. On the convergence of the

block nonlinear Gauss-Seidel method under convex

constraints. Oper Res Letter, 26:127-136.

Howe FA, Barton SJ, Cudlip SA, Stubbs M, Saunders DE,

Murphy JR, Opstad KS, Doyle VL, McLean MA, Bell

BA, Griffiths JR, 2003. Metabolic profiles of human

brain tumours using quantitative in vivo 1H magnetic

resonance spectroscopy. Magn Res Med,49:223-232.

Jolliffe IT. Principal Component Analysis. Second edition,

New York: Springer-Verlag 2002. 487 p.

Kim D, Sra S., Dhillon IS, 2007. Fast Newton-type

Methods for the Least Squares Nonnegative Batrix

Approximation Problem. In Proceedings of the 2007

SIAM International Conference on Data Mining

(ICDM), Pisa, Italy.

Ladroue C, Howe FA, Griffiths JR, Tate AR, 2003.

Independent component analysis for automated

decomposition of in vivo magnetic resonance spectra.

Magn Reson Med, 50:697-703.

Lee DD, Seung HS, 1999. Learning the parts of objects by

non-negative matrix factorization. Nature, 401:788-

791.

Lee DD, Seung HS, 2001. Algorithms for Non-negative

Matrix Factorization, Advances in Neural Information

Processing Systems, 13:556-562.

Lin CJ, 2007. Projected Gradient Methods for

Nonnegative Matix Factorization, Neural Comput,

19:2756-2779.

Poullet JB, Sima DM, Simonetti AW, De Neuter B,

Vanhamme L, Lemmerling P, Van Huffel S, 2006. An

automated quantitation of short echo time MRS

spectra in an open source software environment:

AQSES. NMR Biomed, 20: 493-504.

Stoyanova R, Brown TR, 2001. NMR spectral quantitation

by principal component analysis. NMR Biomed,

14:260-264.

Su Y, Thakur SB., Karimi S, Du S, Sajda P, Huang W,

Parra LC, 2008. Spectrum separation resolves partial-

volume effect of MRSI as demonstrated on brain

tumor scans. NMR Biomed

, 21:1030-1042.

Szabo de Edelenyi F, Simonetti AW, Postma G, Huo R,

Buydens LMC, 2005. Application of independent

component analysis to 1H MR spectroscopic imaging

exams of brain tumours. Anal. Chim. Acta, 544:36-46.

SIMULATION STUDY OF TISSUE TYPE DIFFERENTIATION USING NON-NEGATIVE MATRIX

FACTORIZATION

217