SIFT-BASED CAMERA LOCALIZATION USING REFERENCE

OBJECTS FOR APPLICATION IN MULTI-CAMERA

ENVIRONMENTS AND ROBOTICS

Hanno Jaspers

, Boris Schauerte

and Gernot A. Fink

Department of Computer Science, TU Dortmund University, 44221 Dortmund, Germany

Institute of Anthropomatics, Karlsruhe Institute of Technology, 76131 Karlsruhe, Germany

Keywords:

Camera pose estimation, Relative pose, Camera calibration, Scale Ambiguity, Reference object, Local

features, SIFT, Multi-camera environment, Smart room, Robot localization.

Abstract:

In this contribution, we present a uniﬁed approach to improve the localization and the perception of a robot

in a new environment by using already installed cameras. Using our approach we are able to localize arbi-

trary cameras in multi-camera environments while automatically extending the camera network in an online,

unattended, real-time way. This way, all cameras can be used to improve the perception of the scene, and ad-

ditional cameras can be added in real-time, e.g., to remove blind spots. To this end, we use the Scale-invariant

feature transform (SIFT) and at least one arbitrary known-size reference object to enable camera localization.

Then we apply non-linear optimization of the relative pose estimate and we use it to iteratively calibrate the

camera network as well as to localize arbitrary cameras, e.g. of mobile phones or robots, inside a multi-camera

environment. We performed an evaluation on synthetic as well as real data to demonstrate the applicability of

the proposed approach.

1 INTRODUCTION

In recent years smart rooms have attracted an increas-

ing interest, e.g., to improve the productivity in of-

ﬁce environments and assist the personnel in crisis

response centers. For this purpose, the identities of

the persons in the room have to be determined (see

(Salah et al., 2008)) as well as the audio-visual focus

of attention has to be estimated (see (Voit and Stiefel-

hagen, 2010; Schauerte et al., 2009)), e.g. to present

personalized information on the display a person is

currently looking at. However, these applications rely

on the fusion of information that is provided by a set

of sensors, most importantly microphones and camera

arrays. In order to fuse the information from different

sensors in the environment it is necessary to deter-

mine their extrinsic parameters in a common coordi-

nate frame. In the following, we focus on cameras as

sensors and in this domain ofﬂine calibration meth-

ods are applied most commonly (see, e.g., (Br

uck-

ner and Denzler, 2010; Aslan et al., 2008; Xiong and

Quek, 2005; Rodehorst et al., 2008)). Unfortunately,

these methods usually require a time-consuming man-

ual procedure and need to be repeated if a new camera

is added or a camera is relocated.

In this contribution, we analyze how we can use

the views of the already calibrated cameras in an en-

vironment to localize a new camera and thus enable

subsequent sensor fusion. This, for example, can be

used to enable easily extensible camera networks, al-

low the seamless integration of the sensor information

of mobile robotic agents , and allow mobile robotic

agents to use the information of the sensors that are

installed in the environment to enhance their percep-

tion capabilities. With the proposed approach, we are

able to determine the absolute pose of a new cam-

era in the global coordinate system given only one

known camera and an arbitrary reference object. Al-

though our focus on a single known camera may limit

the achievable results in scenarios with a huge amount

of cameras with widely overlapping views, we chose

this focus, because it enables us to integrate cameras

that only view parts of the scene that are recorded by

only one other camera. This is especially important,

if the viewpoints of the cameras are very different or

only few cameras are used, which – according to our

experience – seems to be more realistic in most ap-

plication areas. However, our method can naturally

be extended to situations with multiple views. To this

end, we calculate the poses for all plausible camera

330

Jaspers H., Schauerte B. and Fink G. (2012).

SIFT-BASED CAMERA LOCALIZATION USING REFERENCE OBJECTS FOR APPLICATION IN MULTI-CAMERA ENVIRONMENTS AND ROBOTICS.

In Proceedings of the 1st International Conference on Pattern Recognition Applications and Methods, pages 330-336

DOI: 10.5220/0003735103300336

 SciTePress

pairs and subsequently aggregate the pairwise local-

ization results. In contrast to most previous work, we

do not rely on special calibration patterns or devices

and use arbitrary reference objects instead

. To this

end, only a very small amount of user interaction is re-

quired to build an appropriate database of known ob-

jects. The necessary information about the reference

objects might be automatically collected from the in-

ternet, or in the domain of cognitive robots, directly

obtained by actively exploring potential objects. Once

the information is available, cameras can be localized

completely automatic at any time.

2 RELATED WORK

The research area of camera calibration, of which

camera pose estimation is an important aspect, is

a well known and researched topic and accordingly

many different approaches have been proposed (see,

e.g., (Br

uckner and Denzler, 2010; Aslan et al., 2008;

Frank-Bolton et al., 2008; Xiong and Quek, 2005;

Rodehorst et al., 2008)).

In order to calculate the relative pose, the funda-

mental matrix has to be computed. The normalized

and the standard 8-point algorithm, variants of the

7-point algorithm (Hartley and Zisserman, 2004), as

well as a 6-point and 5-point algorithm were com-

pared (Stew

enius et al., 2006; Nist

er, 2004). The

normalized 8-point algorithm performed considerably

better than the non-normalized version and its use

was recommended when no prior knowledge about

the camera motion, i.e. sideways or forward mo-

tion, is available. The 5-point algorithm achieved bet-

ter results in most cases, as conﬁrmed in (Rodehorst

et al., 2008), but it had problems with forward motion,

where the results were worse. We used the 8-point al-

gorithm in our approach because of its overall good

results.

For ﬁnding point correspondences, we rely on

the matching of SIFT features, proposed by Lowe in

(Lowe, 1999; Lowe, 2004). In the context of relative

pose estimation and scene reconstruction, SIFT has

been used before in (Liu and Hubbold, 2006; Snavely

et al., 2008).

In previous work, (Xiong and Quek, 2005) de-

scribed a system to calibrate the intrinsic and extrin-

sic parameters of camera networks in meeting rooms.

They used a box with dots and other markers to cali-

brate the cameras. This resulted in a good accuracy of

less than 1cm for the camera positions of most cam-

eras. However, a lot of user interaction is required

However, we could – of course – use existing calibra-

tion patterns and objects as reference objects as well.

to perform the calibration: Camera pairs were chosen

manually and the calibration box had to be placed for

each camera pair speciﬁcally.

(Svoboda et al., 2005) proposed a technique with

less user interaction for the calibration of a multi-

camera environment. Instead of using dedicated cal-

ibration objects or markers, they used a bright spot

as the calibration feature, generated by a laser pointer

with a small diffusing piece of plastic attached to it.

Their algorithm can be used to fully calibrate the cam-

era network, the only user interaction is waving the

laser pointer through the working volume.

Aslan et al. pursued a similar approach to auto-

matically calibrate the extrinsic parameters of multi-

ple cameras (Aslan et al., 2008). Instead of a bright

spot, they detected people walking through the room

and used a point on top of every person’s head as cal-

ibration feature. The relative pose is estimated for ev-

ery camera pair, and with this, the complete camera

network is built up using a global error minimization

technique. The precision has been evaluated in differ-

ent indoor scenarios, arriving at a projection error of

less than 6px and a triangulation error of markers in

the scene of about 5cm. The positions of the camera

centers have not been compared to their ground truth.

Recently, Br

uckner and Denzler proposed an ac-

tive calibration technique for multi-camera systems

(Br

uckner and Denzler, 2010). They use the rotat-

ing and zooming capabilities of pan-tilt-zoom (PTZ)

cameras to optimize the relative poses between each

camera pair. The scaling factors in camera triangles

are estimated with two of the three relative poses. In

contrast to our approach no reference object is re-

quired, but the types of cameras that can be used are

limited to PTZ cameras. Our system does not put any

limitations on the types of cameras, allowing, for ex-

ample, a combination of ﬁxed PTZ cameras, cameras

mounted on robotic platforms and even smartphone

cameras. Furthermore, more than two cameras are

needed, whereas our approach allows to estimate the

absolute pose of only two cameras.

Similar techniques as those used for the calibra-

tion of multi-camera environments can be applied to

other applications, such as robot indoor localization.

In (Frank-Bolton et al., 2008), a system to localize

and track a robot based on a set of known views was

proposed. First, a set of views of the scene, an in-

door environment, was recorded with the robot for

speciﬁc positions and different orientations. The posi-

tions were chosen on a grid, roughly 90cm apart. The

environment was surrounded by project posters to fa-

cilitate the search for image correspondences. Frank-

Bolton et al. come to the conclusion, that epipolar

geometry in conjunction with the normalized 8-point

SIFT-BASED CAMERA LOCALIZATION USING REFERENCE OBJECTS FOR APPLICATION IN

MULTI-CAMERA ENVIRONMENTS AND ROBOTICS

331

Estimation of Relative Pose

using Epipolar Geometry

Relative Pose Optimization

of Reprojection Error

Computation of Scale

via Homography

Reference Object

Absolute Pose

Image 1 Image 2

Intrinsic

Parameters

Figure 1: This overview of our approach shows the three main steps to calculate the absolute pose of a camera. At ﬁrst the

relative pose is estimated using epipolar geometry. Afterwards, the relative pose is optimized and then scaled with a scaling

factor retrieved from a known reference object, giving the absolute pose of the second camera in relation to the ﬁrst camera.

algorithm is too sensitive to ensure a robust and ac-

curate pose estimation. Instead, they use a technique

called quality threshold clustering, which resulted in

an average position error of 46cm and a mean orienta-

tion error of 9

◦

. Our results (see section 4) lead to the

assumption, that a more precise localization can be

achieved with our approach, using the project posters

as reference objects.

3 POSE ESTIMATION

Our sytem that computes the global pose of a camera

in relation to a known camera consists of three main

steps (see Fig. 1). In the ﬁrst step, the relative pose of

the camera is calculated. This requires the detection

of point correspondences between the two considered

images. To this end, SIFT features (Lowe, 2004) are

computed and matched. This step may introduce out-

liers, i.e. correspondences of image points that are

not projections of the same scene point. If they are

not robustly eliminated, errors in the estimated pose

will occur. In the second step we optimize the esti-

mated relative pose in order to minimize the inﬂuence

of noise and achieve better results. Finally, the global

scaling of the relative pose is calculated in the third

step. This step is based on the detection of at least

one reference object of known size within the scene.

3.1 Relative Pose

The relative pose of the second camera is calculated

using epipolar geometry. For this, the fundamental

matrix F is calculated with the normalized 8-point al-

gorithm in conjunction with RANSAC, to eliminate

outliers from the point correspondences (Hartley and

Zisserman, 2004). Using the fundamental matrix the

scene can be reconstructed up to a projective ambigu-

ity. We assume calibrated cameras with the intrinsic

calibration matrices K

and K

. Accordingly, the re-

construction can be performed up to a scale ambigu-

ity, as illustrated in Fig. 2. As a result of the unknown

scale, the translation vector t is normalized to ktk = 1.

The essential matrix E, a special case of the fun-

damental matrix for normalized image coordinates, is

Figure 2: Visualization of the scale ambiguity. The second

camera can ”slide” along the baseline between the cameras

(i.e. different scaling of the relative position), without af-

fecting the point correspondences.

obtained as

E = K

F K

. (1)

The deﬁning property of the essential matrix is that

two of its singular values are equal and the third one

zero. Due to the presence of noise that is introduced

through small errors in the camera calibration pro-

cess and the estimation of the fundamental matrix,

this property has to be enforced. Thus, let

E = U diag(σ

, σ

) V

, with σ

≥ σ

(2)

be the SVD of E. The essential matrix

E, which min-

imizes the Frobenius norm kE −

Ek, is calculated as

E = U diag(σ, σ, 0) V

, with σ =

+ σ

. (3)

The essential matrix can be decomposed into four

possible solutions for the pose (t, R) of the second

camera, with translation t and rotation R. There’s

only one solution for which the reconstructed 3D-

points are in front of the image planes of both cam-

eras. This constraint is termed cheirality constraint.

In ideal circumstances it would sufﬁce to reconstruct

one point from a point correspondence pair and to test

whether it satisﬁes the cheirality constraint. But since

outliers can’t be ruled out a voting mechanism has to

be put in place to determine the correct solution: Each

reconstructed point ”votes” for the solution, that sat-

isﬁes its cheirality constraint. The solution with the

highest number of votes is chosen as the correct solu-

tion.

3.2 Pose Optimization

Figure 3(b) shows the reconstruction of a scene that

ICPRAM 2012 - International Conference on Pattern Recognition Applications and Methods

332

−150 −100 −50 0 50 100 150

100

150

200

250

300

x [cm]

y [cm]

(a)

−150 −100 −50 0 50 100 150

100

150

200

250

300

x [cm]

y [cm]

(b)

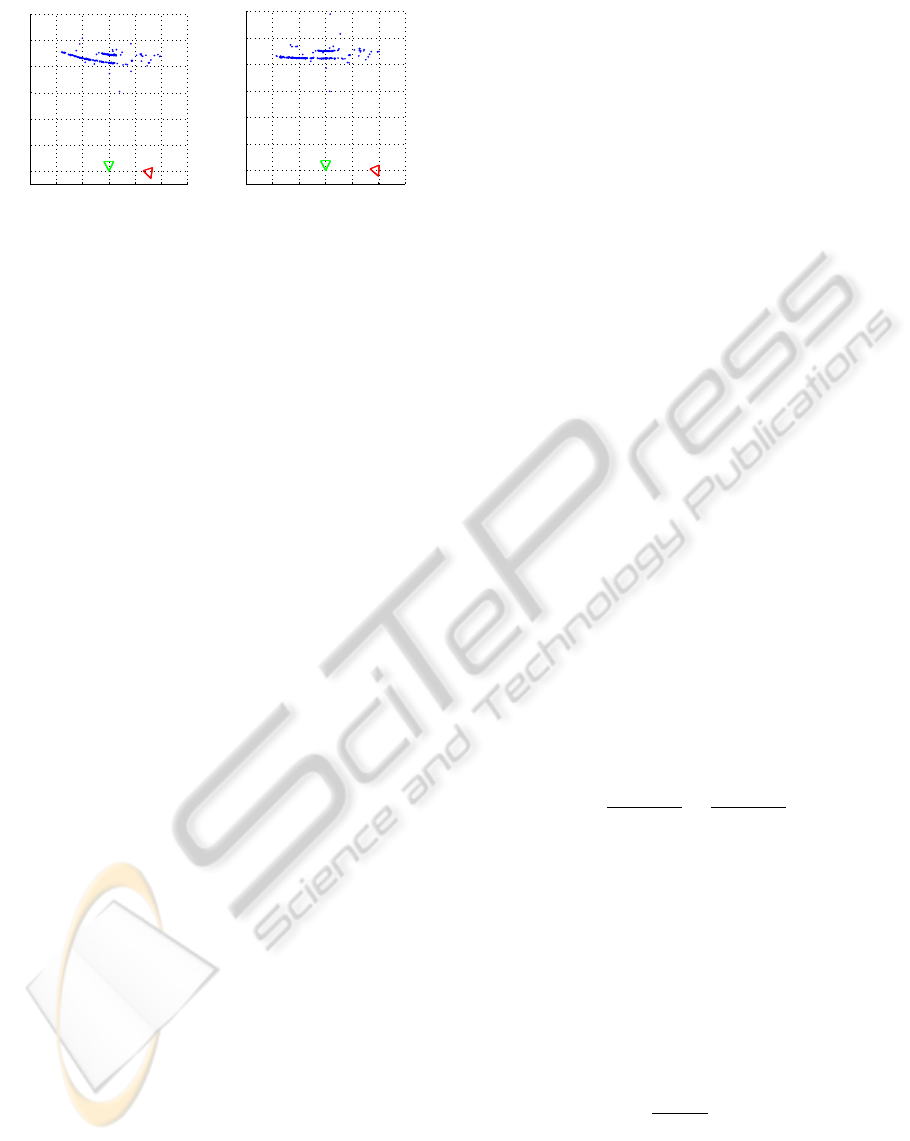
Figure 3: The relative pose of the red camera is estimated

(a) using only epipolar geometry, and (b) with additional

nonlinear optimization. With optimization, most of the re-

constructed points (blue) are parallel to the x-axis, which

complies with the ground truth.

was obtained using the relative pose as described

above. The camera was oriented towards a ﬂat wall.

However, the reconstructed points lay on a curved

surface. This indicates small errors in the obtained

pose. To improve the relative pose, a nonlinear,

Trust-Region-Reﬂective optimization step (Coleman

and Li, 1996) has been introduced that minimizes

the reprojection error. In contrast to Levenberg-

Marquardt optimization (Levenberg, 1944; Mar-

quardt, 1963), Trust-Region-Reﬂective optimization

can handle bound constraints on the optimization

space.

A pose normally has six degrees of freedom

(DOF), three for the translation and three for the rota-

tion. As a result of the scale ambiguity, this is reduced

to ﬁve DOF for the relative pose.

Because of the normalization ktk = 1, all possible

solutions for t are on the unit sphere around the ﬁrst

camera. Hence, t can be expressed in spherical coor-

dinates (θ, φ). Together with the rotation angles r

, r

and r

, the optimization space is (θ, φ, r

, r

). As

the optimization step only ﬁnds a local minimum of

the reprojection error, a good initial guess is impor-

tant in order to ﬁnd the global minimum. Thus, the

starting point for the optimization task is the relative

pose as computed before.

Depending on the application, further constraints

may exist, which reduce the dimension of the opti-

mization space. For example, in a room equipped

with PTZ cameras, r

(roll) can be ﬁxed to 0.

3.3 Solving the Scale Ambiguity

When given only two views of a scene, the solution

for the scale ambiguity problem requires more infor-

mation on the scene itself or the objects located in it.

Our approach uses the knowledge of reference objects

that have been detected, using SIFT, in both views.

The best results can be obtained with planar objects,

such as posters or pictures. Nevertheless, non-planar

objects are also possible as reference objects, but re-

quire certain restrictions or more complex processing

of the local features to achieve similar results.

The reference objects are detected by matching

an image of each reference object with both views

and calculating the projective transformations of the

objects. The matching is done with SIFT features.

This is an advantage since the SIFT features calcu-

lated for the estimation of the relative pose can be

reused. The projective transformations are homogra-

phies between the the reference objects and their oc-

curances in the two views. A homography is a pro-

jective transformation that maps points on one plane

to another plane (which is also the reason why pla-

nar reference objects yield the best results). It is for-

malized by a 3 × 3 matrix H, called the homography

matrix. An algorithm to compute the homography

is the direct-linear-transformation algorithm (Hartley

and Zisserman, 2004, p. 88), which can be combined

with RANSAC to ensure robustness against outliers.

Let H = [h

, h

] be the homography matrix be-

tween the image of the reference object and one of

the views and K the intrinsic calibration matrix of the

camera. According to (Zhang, 2000) the extrinsic pa-

rameters [R|t] of the camera image in relation to the

reference object can be computed as

= λK

−1

, (4)

= λK

−1

, (5)

= r

× r

, (6)

t = λK

−1

, (7)

with

λ =

−1

(8)

and the rotation matrix R = [r

, r

The distance of the reference object (more exactly

the origin of the reference object’s image) to the cam-

era center is given by ktk. If the size of the object

is known in the units of the world coordinate system

(e.g. mm, as used in the following), then t can also

be expressed in this unit. Let d

be the size vector

(width and height) of the reference object’s image in

pixels, and d

the size vector in millimeters. Thus,

the translation vector t scaled to millimeters is then

given as

t =

· t . (9)

Let x be the origin of the reference object’s image

in the scene. It can be reconstructed with the estimate

of the relative pose of the second camera as computed

previously. Thus, relating the translation vectors of

the reference object

and

to the distances between

SIFT-BASED CAMERA LOCALIZATION USING REFERENCE OBJECTS FOR APPLICATION IN

MULTI-CAMERA ENVIRONMENTS AND ROBOTICS

333

x and the camera centers c

and c

provides us with

two scaling factors:



x − c

and s



x − c

. (10)

These scaling factors are, in theory, equal, but usu-

ally differ slightly when estimated on real data. There

are two possibilities to use these factors to correctly

scale the yet unscaled position of the second camera:

+ s

) · c

, and (11)

= s

(x − c

) + s

(x − c

) . (12)

The ﬁrst possibility is straightforward and applies the

average scaling factor directly to the relative position

of the second camera. The second possibility applies

the scaling factors to the vectors between the camera

centers and the reference object. This has proven to

work better in scenes in which the reference object is

reliably and precisely detected, giving very accurate

scaling factors. In contrast, Eq. 11 achieves good

results for scenes in which the relative pose is very

precise, while the scaling factors are prone to noise,

which may occur with small reference objects.

4 EVALUATION

The evaluation of our system is divided into two parts,

synthetic and real benchmarks. The synthetic tests

evaluate the single components of our system, the es-

timation of the relative pose and the calculation of the

scale. To test our algorithm on real data, we used

the data sets presented in (Strecha et al., 2008) and

images recorded by ourselves in a smart room at our

university.

4.1 Synthetic Data

At ﬁrst, we evaluated the relative pose estimation al-

gorithm to determine the inﬂuence of the optimiza-

tion on the result. For this purpose, we generated

200 random 3D points in a box of side length 2, cen-

tered at (0 0 3)

. We then projected these points on

two virtual cameras with intrinsic calibration matri-

ces K = I. The second camera was positioned ran-

domly on the unit sphere. For each position, the pose

was estimated 1000 times. We set the threshold of

RANSAC to 1000 iterations. To test the inﬂuence of

noise, we introduced white Gaussian noise of a certain

signal-to-noise ratio to the projected points. More de-

scriptively, on a 640 × 480px picture, a noise level of

50dB would be equivalent to a standard deviation of

about 1.4px, 30dB to 14px and 20dB to 43px. Out-

liers were inserted by selecting a certain percentage

of points and assigning them to other points.

The performance for different percentages of out-

liers is unaffected by the optimization. This is due to

the fact, that outliers are removed by RANSAC when

calculating fundamental matrix. The optimization af-

terwards does not affect the point correspondences.

We obtain very robust results up to a outlier percent-

age of 60%, with a translation error of less than 3

◦

and a rotation error of less than 1

◦

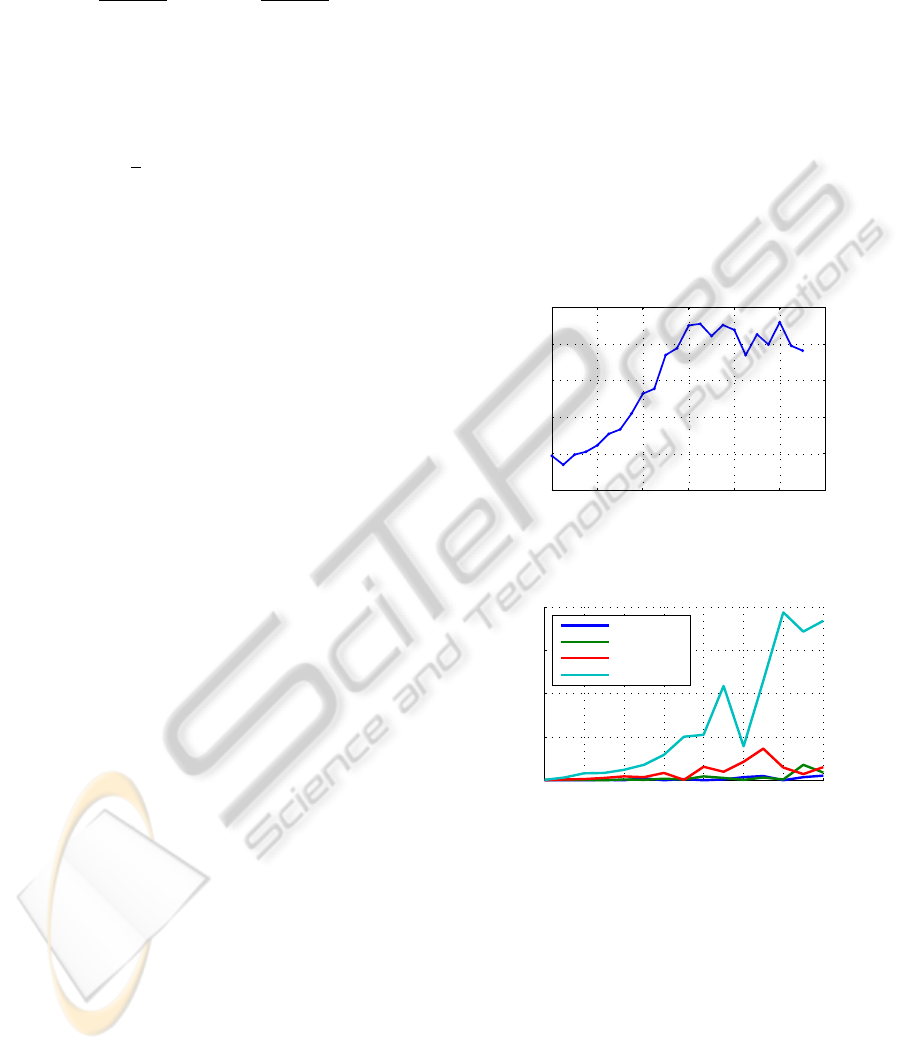
Figure 4 shows the improvement brought by the

optimization of the relative pose in the presence of

noise. The translation error is reduced by 31.6% for

noise levels starting at 25dB. The rotation error is

largely unaffected by the optimization.

0 10 20 30 40 50 60

−10

noise level [dB]

mean error improvement [%]

Figure 4: For noise levels starting at 25dB, the optimization

reduces the translation error by an average of 31%.

100 150 200 250 300 350 400 450

Distance to camera center [cm]

Error of computed distance [cm]

0° Rotation

15° Rotation

30° Rotation

45° Rotation

Figure 5: The graph shows the error of the calculated dis-

tance of a square reference object for different rotations.

To test, how accurate the distance of a reference

object can be estimated, a square reference object

with side lengths of 50cm was rotated around its y-

axis and positioned on different distances along the

z-axis. For every position and rotation an image was

created with a virtual camera with a focal length of

2000 and principal point [1000, 1000]

. The reference

object’s distance was retrieved as described in section

3.3, including its detection using SIFT and RANSAC-

based homography estimation. Each calculation was

repeated 100 times. The results, illustrated in Fig. 5,

show that the distance can be robustly computed for

ICPRAM 2012 - International Conference on Pattern Recognition Applications and Methods

334

all positions and rotations up to 30

◦

. The error is less

than 4cm and for most measurements less than 2cm.

Without rotation, the error is never above 1cm. For a

rotation of 45

◦

, the error increases to about 20cm at a

distance of 4m to 4.5m. This is still less than 5% of

the distance of the reference object.

4.2 Real Data

Furthermore, we evaluated our proposed approach

on different real data sets. The ﬁrst tests use the

Herz-Jesu-P8 and fountain-P11 data sets (see (Strecha

et al., 2008)). We chose these data sets, because they

contain images with a high resolution and are well

annotated. We generated reference objects for both

data sets by cropping parts of the images, that showed

walls which were visible in most pictures. We re-

duced the data sets to those images, in which the ref-

erence object could be detected. The camera poses

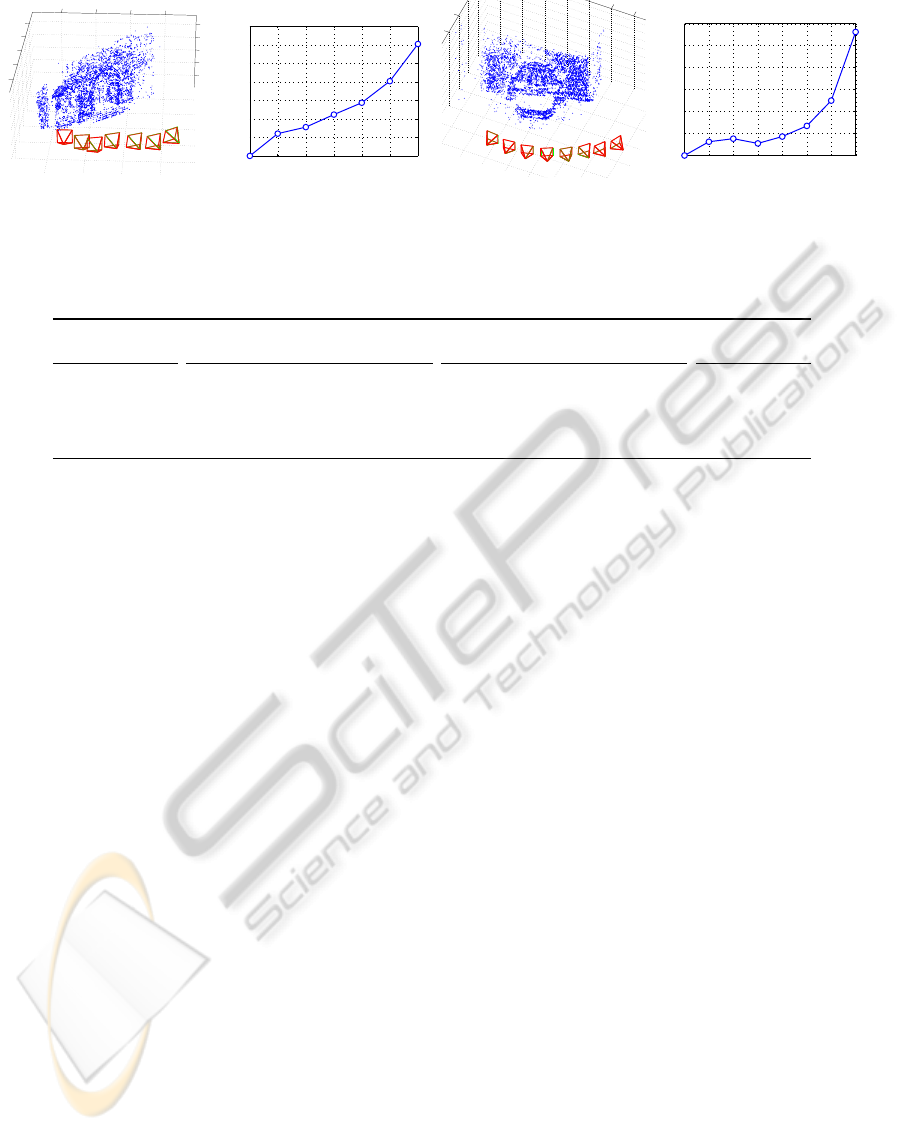
were calculated iteratively. Figure 6 shows the recon-

struction results and position errors for both data sets.

Since the camera poses are iteratively estimated,

small errors are propagated and increase in the pro-

cess of the computation. Still, the results are very

accurate and the errors are in the range of centime-

ters. Over a total distance of 15.5m in data set Herz-

Jesu-P8, the error of the last camera is only 12cm, or

0.77%. The distance between the ﬁrst and last camera

in fountain-P11 is 11m, yet the position error is a mere

6cm, or 0.55%. The data sets have certain character-

istics that help attaining such a high precision: high

resolution, small baselines between the cameras and

highly textured scenes that produce well distributed

point correspondences.

These characteristics are less present in the data

recorded in our smart environment, a room of roughly

25m

. It has several microphone arrays, computer

controlled lighting and, most importantly for our case,

four ceiling-mounted PTZ cameras with a resolution

of 752 × 596 pixels. The position and rotation of the

PTZ cameras are known. Pictures were taken with a

similar PTZ camera on a tripod at 23 different posi-

tions in the room. The positions were measured by

hand in the environment’s coordinate frame to obtain

a ground truth. For each position, the absolute cam-

era pose was calculated several times using one of the

known cameras. The results with the lowest repro-

jection error for every image were selected and aggre-

gated by using the mean and the median of the coor-

dinates and then compared to the ground truth. Three

posters, two of size 118.9 × 84.1cm and one of size

60 × 91cm, were chosen as reference objects. Table 1

shows the attained results.

We arrive at a mean position error of 41.30cm for

the mean position and 39.50cm for the median posi-

tion. Compared to the much lower median position er-

ror of 25.24cm, and 21.64cm respectively, we see that

the camera was very poorly localized for several mea-

surement points, with an error of over 2m for cam-

era position 3 and about 1m for positions 16 and 17.

The poses for other positions were very close to the

ground truth, often with an error of less than 16cm.

There are different reasons for the high errors in

the detected poses for the images in our smart room.

Most importantly, the cameras provide noisy images

without much detail and fail to record ﬁne structures.

Furthermore, the environment itself does not contain

much details, making it hard to ﬁnd reliable point cor-

respondences. This is made even more difﬁcult by the

the low number of cameras and big viewpoint changes

between the cameras. As a consequence, point cor-

respondences were often found mostly between the

projections of the reference objects and for this rea-

son only locally distributed in the images. Although

the error seems relatively large on the ﬁrst sight –

especially when compared to the results achieved on

Herz-Jesu-P8 and fountain-P11 –, we consider a me-

dian error of 21.64cm an acceptable result due to the

difﬁculty of the environment. Furthermore, we have

to consider the possible inﬂuence of minor ground

truth measurement errors that were, for example, in-

troduced by the unknown exact location of the focal

point within the PTZ camera casing.

5 CONCLUSIONS

We proposed a new approach to compute the global

scale between two views given a known reference ob-

ject. To this end, we ﬁrst calculate the relative pose

with established methods of epipolar geometry. We

then reduce the reprojection error of the pose with a

nonlinear optimization step, signiﬁcantly improving

the result. Afterwards, the overall scale of the scene

is reliably estimated by detecting a known reference

object in both camera views. Through different tests,

our system has proven to very precisely compute ab-

solute poses. In two data sets with small distances

between camera images, we achieved an absolute er-

ror for the iterative pose estimation of less than 1%.

The global localization of cameras in our conference

room was less accurate, hindered by low resolution

cameras, plain walls without much detail and wide

baselines. However, we still achieved an accuracy of

about 20cm for most camera pairs, making our system

a useful and convenient technique for the extrinisc

calibration of multiple cameras.

SIFT-BASED CAMERA LOCALIZATION USING REFERENCE OBJECTS FOR APPLICATION IN

MULTI-CAMERA ENVIRONMENTS AND ROBOTICS

335

−5

−15

−10

−5

−8

−6

−4

−2

(a)

1 2 3 4 5 6 7

Camera index

Error [cm]

Herz−Jesu−P8: Position error, iterative calculation

(b)

−14

−12

−10

−8

(c)

1 2 3 4 5 6 7 8

Camera index

Error [cm]

fountain−P11: Position error, iterative calculation

(d)

Figure 6: The scene reconstruction and position error of data sets Herz-Jesu-P8 (a-b) and fountain-P11 (c-d). Red cameras

show the iteratively calculated camera poses, green cameras the ground truth (might not be distinguishable from the calculated

poses in this scale). The scene reconstruction was achieved without further optimization, such as Bundle Adjustment.

Table 1: Errors for the estimated poses of 23 images taken in our smart room.

Error of mean position [cm] Error of median position [cm] mean reprojection

total x y z total x y z error [px]

mean 41,30 19,97 18,78 25,54 39,50 17,11 18,32 24,26 0,7914

median 25,24 8,27 8,65 11,29 21,63 6,64 7,77 12,11 0,6972

standard deviation 48,96 34,72 25,61 29,19 49,74 35,18 26,51 29,88 0,3897

min 8,06 0,20 0,02 0,10 5,31 0,97 0,10 0,10 0,3534

max 227,76 165,60 117,74 102,89 227,76 165,60 117,74 102,89 1,8259

ACKNOWLEDGEMENTS

This work is partly supported by the German Re-

search Foundation (DFG) within the Collaborative

Research Program SFB 588 ”Humanoide Roboter”.

The authors would like to thank Manel Martinez and

Jan Richarz for their helpful comments.

REFERENCES

Aslan, C. T., Bernardin, K., and Stiefelhagen, R. (2008).

Automatic calibration of camera networks based on

local motion features. ECCV-M2SFA2.

uckner, M. and Denzler, J. (2010). Active self-calibration

of multi-camera systems. Proc. DAGM.

Coleman, T. F. and Li, Y. (1996). An Interior Trust Re-

gion Approach for Nonlinear Minimization Subject to

Bounds. SIOPT, 6(2):418–445.

Frank-Bolton, P. et al. (2008). Vision-based localization for

mobile robots using a set of known views. Proc. ISVC,

pages 195–204.

Hartley, R. I. and Zisserman, A. (2004). Multiple View Ge-

ometry in Computer Vision. Cambridge University

Press, second edition.

Levenberg, K. (1944). A Method for the Solution of Certain

Problems in Least-Squares. Quart. Applied Math.,

2:164–168.

Liu, J. and Hubbold, R. (2006). Automatic camera cali-

bration and scene reconstruction with scale-invariant

features. Proc. ISVC, pages 558–568.

Lowe, D. G. (1999). Object recognition from local scale-

invariant features. Proc. IEEE ICCV, pages 1150–

1157.

Lowe, D. G. (2004). Distinctive image features from scale-

invariant keypoints. IJCV, 60(2):91–110.

Marquardt, D. W. (1963). An Algorithm for Least-

Squares Estimation of Nonlinear Parameters. SIAP,

11(2):431–441.

Nist

er, D. (2004). An efﬁcient solution to the ﬁve-point

relative pose problem. TPAMI, 26:756–777.

Rodehorst, V., Heinrichs, M., and Hellwich, O. (2008).

Evaluation of relative pose estimation methods for

multi-camera setups. Proc. Congress ISPRS.

Salah, A., Morros, R., Luque, J., Segura, C., Hernando, J.,

Ambekar, O., Schouten, B., and Pauwels, E. (2008).

Multimodal identiﬁcation and localization of users in

a smart environment. JMUI, 2(2):75–91.

Schauerte, B., Richarz, J., Pl

otz, T., Thurau, C., and Fink,

G. A. (2009). Multi-modal and multi-camera attention

in smart environments. Proc. ICMI.

Snavely, N., Seitz, S. M., and Szeliski, R. (2008). Model-

ing the world from internet photo collections. IJCV,

80(2):189–210.

Stew

enius, H., Engels, C., and Nist

er, D. (2006). Recent

developments on direct relative orientation. ISPRS,

60:284–294.

Strecha, C., von Hansen, W., Gool, L. V., Fua, P., and

Thoennessen, U. (2008). On benchmarking camera

calibration and multi-view stereo for high resolution

imagery. CVPR, 0:1–8.

Svoboda, T., Martinec, D., and Pajdla, T. (2005). A con-

venient multi-camera self-calibration for virtual envi-

ronments. PRESENCE: Teleoperators and Virtual En-

vironments, 14(4):407–422.

Voit, M. and Stiefelhagen, R. (2010). 3-D user-perspective,

voxel-based estimation of visual focus of attention in

dynamic meeting scenarios. ICMI-MLMI.

Xiong, Y. and Quek, F. (2005). Meeting room conﬁguration

and multiple camera calibration in meeting analysis.

Proc. ICMI.

Zhang, Z. (2000). A ﬂexible new technique for camera cal-

ibration. TPAMI, 22(11):1330–1334.

ICPRAM 2012 - International Conference on Pattern Recognition Applications and Methods

336