
CONSTRAINT-FREE TOPOLOGICAL MAPPING AND PATH
PLANNING BY MAXIMA DETECTION OF THE KERNEL SPATIAL
CLEARANCE DENSITY
Panagiotis Papadakis, Mario Gianni, Matia Pizzoli and Fiora Pirri
ALCOR Vision Perception and Cognitive Robotics Laboratory, Department of Computer and System Sciences
University of Rome “La Sapienza”, Rome, Italy
Keywords:
Topological mapping, Path planning, Mean shift, Distance transform.
Abstract:
Asserting the inherent topology of the environment perceived by a robot is a key prerequisite of high-level
decision making. This is achieved through the construction of a concise representation of the environment
that endows a robot with the ability to operate in a coarse-to-fine strategy. In this paper, we propose a novel
topological segmentation method of generic metric maps operating concurrently as a path-planning algorithm.
First, we apply a Gaussian Distance Transform on the map that weighs points belonging to free space according
to the proximity of the surrounding free area in a noise resilient mode. We define a region as the set of all the
points that locally converge to a common point of maximum space clearance and employ a weighed mean-
shift gradient ascent onto the kernel space clearance density in order to detect the maxima that characterize the
regions. The spatial intra-connectivity of each cluster is ensured by allowing only for linearly unobstructed
mean-shifts which in parallel serves as a path-planning algorithm by concatenating the consecutive mean-shift
vectors of the convergence paths. Experiments on structured and unstructured environments demonstrate the
effectiveness and potential of the proposed approach.
1 INTRODUCTION
In real-world robotic applications where environmen-
tal constraints are minimal, formulating the perceived
knowledge acquired from incoming sensory data into
meaningful, higher-level representations of the envi-
ronment, is a prerequisite of high-level decision mak-
ing (Murphy, 2004; Maxwell et al., 2004). Among the
various robotic sensors, mobile robots are commonly
equipped with range scanners that allow for mapping
of the environment and navigating within the created
map. By modelling a map as an occupancy grid map
(either 2D or 3D), a robot can be initially endowed
with a set of basic functionalities ranging from obsta-
cle avoidance and low-level path planning to frontier-
based exploration.
An important prerequisite for the development of
higher-level functionalities is a representation of the
environment that captures the topological structure of
the free area. This is the result of a topological seg-
mentation of the metric map, a process guided by the
morphological features that determine the distinction
between regions. By building a graph structure of
the environment where nodes correspond to topologi-
cal regions and edges determine the traversability be-
tween adjacent regions, a robot is able to operate in
a coarse-to-fine strategy (Kuipers et al., 2004), (Epp-
stein et al., 2006),(Gianni et al., 2011) using a hierar-
chical arrangement of the perceived knowledge about
the environment.
In this paper, we propose a novel method for topo-
logically segmenting metric maps acquired by mo-
bile robots in order to concisely capture the spatial
characteristics of the environment that are involved in
higher-level decision making. The input to the pro-
posed method is an occupancy grid wherein each grid
cell corresponds to space that is designated as free,
occupied or unknown. Merging the latter two cases,
we obtain a boolean occupancy grid that is provided
as input to a Gaussian Euclidean Distance Transfor-
mation (GEDT). By setting a threshold on the GEDT
of the map we classify the free areas into those that are
safely accessible by a robot in terms of distance from
surrounding obstacles. In the sequel, we cluster these
areas by detecting the local maxima of the GEDT via
a weighed mean-shift (Comaniciu and Meer, 2002;
Fukunaga and Hostetler, 1975) gradient ascent, where
cells are weighed by the corresponding GEDT value.
71
Papadakis P., Gianni M., Pizzoli M. and Pirri F. (2012).
CONSTRAINT-FREE TOPOLOGICAL MAPPING AND PATH PLANNING BY MAXIMA DETECTION OF THE KERNEL SPATIAL CLEARANCE
DENSITY.
In Proceedings of the 1st International Conference on Pattern Recognition Applications and Methods, pages 71-79
DOI: 10.5220/0003735300710079
Copyright
c
SciTePress

Each cluster is formed by all the points that locally
converge to the same point of maximum GEDT value,
i.e. maximum space clearance. To prevent from clus-
tering together cells that are spatially disjoint, we con-
strain the mean-shift vectors by allowing only for lin-
early unobstructed line segments. This ensures that
cells in the same cluster are actually reachable by the
robot by using the convergence paths of the mean-
shift clustering process that is in parallel functioning
as a path planning algorithm.
The proposed formulation resembles the intuitive
process for topological segmenting the free space in
the absence of prior knowledge about the environ-
ment, i.e. a topological region comprises of all the
points that locally converge to a common point of
maximum clearance-openness of free space where the
convergence path is composed of steps only within
free space.
The contributions of the present work are summa-
rized as follows:
• We propose a novel topological mapping method
concurrently operating as a path planning algo-
rithm.
• The proposed topological mapping method is ro-
bust to small topological changes, resilient to
noise and is applicable to structured as well as
unstructured-outdoor environments.
• The proposed path planning method, implicitly
derived from the proposed topological mapping
framework, yields the optimal paths for a robot
in terms of safety distance from surrounding ob-
stacles and maximum peripheral visibility.
The remainder of this paper is organized as fol-
lows: In Section 2, we briefly recall the state-of-the-
art in topological mapping methods identifying the
respective prominent streams of research. In Sec-
tion 3, we describe in detail the framework in which
we compute the GEDT of a map and employ an
adapted mean-shift gradient ascent for clustering the
free space and topologically segmenting the metri-
cal map. In Section 4, we evaluate the proposed
method through experiments in structured and semi-
structured environments that demonstrate its feasibil-
ity and effectiveness and finally, in Section 5, we sum-
marize the contributions of this paper.
2 RELATED WORK
Topological maps capture the structure of the per-
ceived environment in a concise representation that
allows high-level reasoning and planning together
with an easier human-robot interaction. In compar-
ison to metric maps, topological maps are more com-
pact and less sensitive to errors that are accumulated
due to noisy sensor readings.
Depending on the sensors that are used for per-
ceiving the environment, we could distinguish topo-
logical mapping methods into those that use visual
sensory data from cameras (appearance-based) and
those that use geometric sensory data from range
scanners (geometry-based).
Appearance-based methods employ scene under-
standing and object detection in order to derive the
semantics of regions within the explored environment
(Goedeme et al., 2007),(Goedeme et al., 2008),(Liu
et al., 2009),(Montijano and Sagues, 2011),(Murillo
et al., 2007),(Valgren and Lilienthal, 2008),(Murillo
et al., 2009),(Paul and Newman, 2010) and build a
topological graph wherein nodes are assigned to de-
tected landmarks. Creating a topological graph of
the environment is imperative in order to efficiently
process and maintain the huge amount of information
that is acquired from the cameras.
In this paper, we focus on the second category of
topological mapping methods that are based on the
morphological features of the shape of the environ-
ment as perceived by range sensors such as lasers.
In structured-indoor environments, the most common
feature that is used regards the distinction of free
space into large open spaces that are interconnected
through narrow passages or gateways. These pas-
sages determine the borders among distinct regions
that comprise the topological map.
Within this spirit, a number of relevant works
can be identified. In the pioneering work of Thrun
(Thrun, 1998) the borders of the topological regions
were determined by finding the critical points within
the Voronoi diagram of the free space that denote the
points where space clearance is locally minimized, a
concept that was also initially adopted by Beeson et
al. in (Beeson et al., 2003). In their following work
(Beeson et al., 2005), they proposed the Extended
Voronoi Graph defined as the subset of the General-
ized Voronoi Graph (GVG) that is closer than a fixed
threshold from any obstacle, added to the set of all
equidistant points from the closest obstacle. Myung
et al. (Myung et al., 2009) extract the GVG of an
eroded metric map in order to detect the position of
the narrowest passages while Joo et al. (Joo et al.,
2010) compute the curvature of the map border to de-
tect candidate cutting points. In the work of Fabrizi et
al. (Fabrizi and Saffiotti, 2000; Fabrizi and Saffiotti,
2002), concepts of digital topology are used as the ba-
sis of the closure and opening mathematical morpho-
logical operators that are applied in fuzzy gridmaps
ICPRAM 2012 - International Conference on Pattern Recognition Applications and Methods
72

producing constrained regions along with geometric
information using moments.
Spectral clustering has been widely used for topo-
logical segmentation of metric maps as an approxi-
mate solution to the normalized cut of a graph (Shi
and Malik, 2000). In the work of Brunskill et al.
(Brunskill et al., 2007), the initial set of graph nodes is
constructed by random sampling of the free space and
edges are created depending on the visibility between
the nodes while the method proposed by Choi et al.
(Choi et al., 2009) is initially driven by a quadtree cell
decomposition of free space. To support incremental
construction of the topological graph during explo-
ration the former detect discontinuities between the
eigenvalues of the similarity matrix, while the latter
measure the convexity of the regions. Zivkovic et al.
(Zivkovic et al., 2006) employed spectral clustering
at the finest level of resolution of the occupancy grid
and determine the optimal number of clusters by min-
imizing a cost function that relies on the structure of
the eigenvectors of the Laplacian. In recent work, Liu
et al. (Liu et al., 2011) highlighted limitations in spec-
tral clustering based topological segmentation related
to its instability under varying settings of parameters
and map examples. In their approach they compute
the mutual information graph of the occupancy grid
and segment it using Chow-Liu tree factorization.
While a study of the current approaches provides
a thorough understanding of the topological mapping
problem, it appears that the majority of methods is
formulated and evaluated in structured-indoor envi-
ronments where the segmentation process is driven
by the presence of rooms, corridors, doors, etc. On
the contrary, in applications of minimal environmen-
tal constraints, such as Urban Search and Rescue, an
explicit underlying structure of the explored environ-
ment is unlikely to exist. In addition, the noise in-
duced from the sensors becomes more pronounced as
a result of operating under a broader range of environ-
mental conditions such as the presence non-reflecting
surfaces, smoke or fire, etc. In the next section we
unfold the proposed topological segmentation method
that is accordingly formalized to be robust to noise
and relatively small changes of the environment.
3 TOPOLOGICAL MAPPING
In this Section we describe the method that we pro-
pose to segment a generic metrical map given in the
form of a boolean occupancy grid, into a set of topo-
logical regions. The proposed segmentation method
adheres to the following criteria:
i. A topological region is identified by a point of
maximum space clearance, i.e. whose distance
from surrounding obstacles is locally maximized.
ii. All points that locally converge to the same point
of maximum space clearance belong to the same
region.
iii. The convergence path of a point to the point of lo-
cally maximum clearance comprises only of steps
within free space.
3.1 Distance-based Classification of
Free Space
The first criterion formulates a space segmentation
approach that is beneficial for a mobile robot in terms
of safety and visibility. With respect to safety, a point
in space that has locally the furthest distance from sur-
rounding obstacles corresponds to a position that the
robot can efficiently reach by following a path with
reduced obstacle interference. In terms of visibility, a
point of maximum space clearance corresponds to the
position where occlusions are minimized and a robot
can have a broad overview of the surrounding area.
Furthermore, this criterion resembles the intuitive hu-
man process of space segmentation into rooms and
areas in general. Whenever we stand in a position
very close to occupied space where visibility is rela-
tively constrained we do not identify the center of a
region, rather, when we stand in the center of a region
we commonly have a relatively large distance from
obstacles and a broad, clear view of the surrounding
area.
To obtain a space classification of the metric map
according to the distance from surrounding obstacles,
the proposed approach adheres to the Distance Trans-
form.
More formally, we denote a boolean occupancy
grid of cells as a function C : p → {0, 1} where p =
{p
i
(x
i
, y
i
)|i = 1, 2, ..., n} is the set of cells and n is the
cardinality of the set. Letting F = {p|C(p) = 0} de-
note the set of free cells and O = {p|C(p) = 1} the set
of occupied cells, the Euclidean Distance Transform
D
f
(p) of the free area is given by:
D
f
(p) = min
p
k
∈O
kp − p
k
k (1)
where k.k denotes the Euclidean distance.
Ideally, the distance transform would be sufficient
to obtain a classification of the points in terms of
space clearance as shown in Figure. 1 (b) for the sim-
ulated environment shown in Figure. 1 (a). In practice
however, metric maps obtained from robotic sensors
are highly susceptible to noise as shown for a typical
example in Figure. 1 (c) together with the correspond-
ing EDT image in Figure. 1 (d). Due to noisy mea-
surements, individual grid cells that are designated as
CONSTRAINT-FREE TOPOLOGICAL MAPPING AND PATH PLANNING BY MAXIMA DETECTION OF THE
KERNEL SPATIAL CLEARANCE DENSITY
73
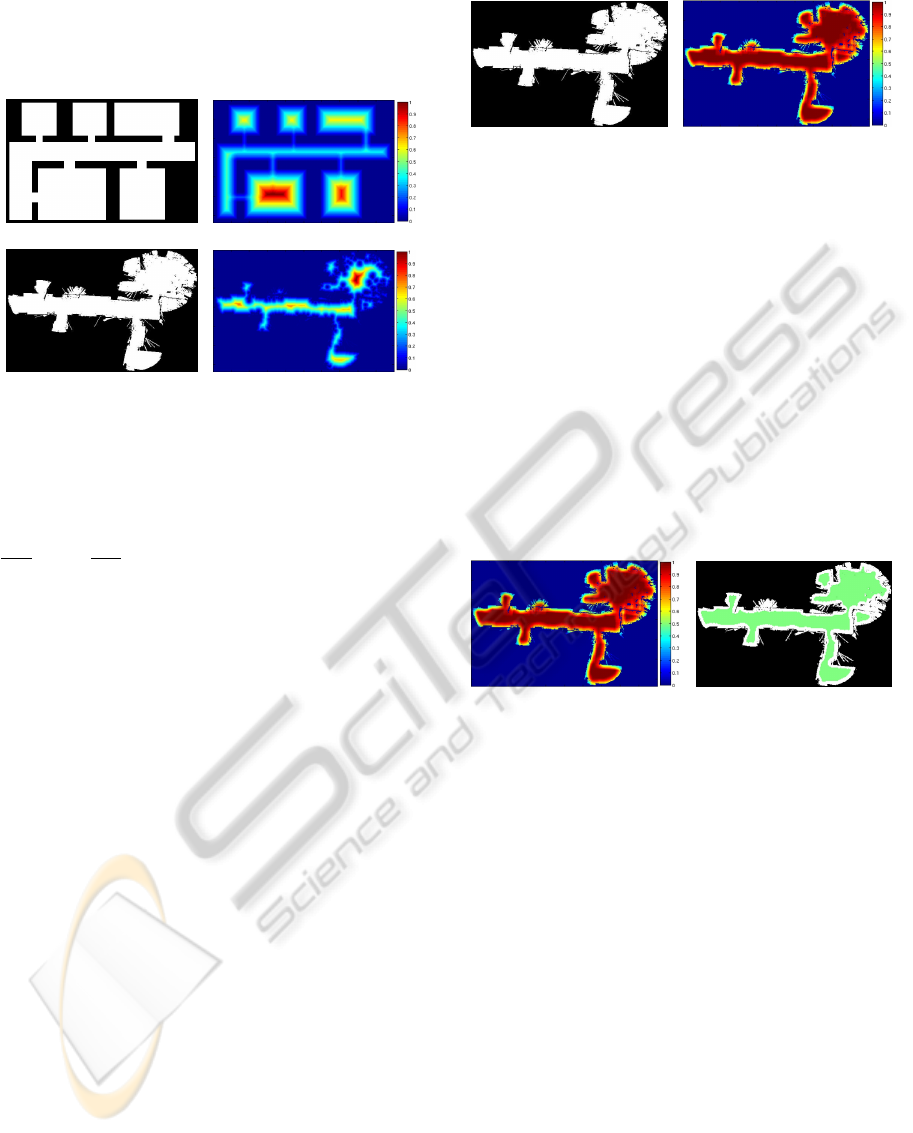
occupied may affect the EDT values of all the neigh-
bouring cells. This results in an undesirable reduction
of the estimated space clearance in relatively large
open areas.
(a) (b)
(c) (d)
Figure 1: Example occupancy grids (a),(c) and the corre-
sponding Euclidean Distance Transforms (b),(d).
To decrease the sensitivity to noise and to rela-
tively small obstacles, we compute the discrete con-
volution of C with the Gaussian kernel G(p) =
1
2πσ
2
exp(−
kpk
2
2σ
2
) given by:
∼
C(p) =
n
∑
i=1
C(p
i
)G(p − p
i
) (2)
According to this formulation we derive that
∼
C(p) ∈
[0, 1) hence for free cells lying close to occupied
space
∼
C(p) → 1 while for free cells lying away from
occupied space
∼
C(p) → 0. For the purpose of the im-
plementation that is followed in this paper (as detailed
in Section 3.2), we encode this information by setting
∼
D(p) = 1 −
∼
C(p) so that cells lying away from obsta-
cles will be characterized by a higher value than the
cells lying close to obstacles. The inversion is pur-
posely adopted after computing the convolution since
the computation of the latter is more efficient when
sparse matrices are used (in practise we compute the
convolution using a gaussian kernel of fixed size con-
taining 99% of the energy). In Figure 2 (a) we show
the initial grid map and in Figure 2 (b) the correspond-
ing
∼
D.
In comparison to the corresponding EDT shown
in Figure 1 (d) the convolved occupancy grid is more
robust to noise and relatively small obstacles which
results in an amended classification of free space with
respect to the distance from surrounding obstacles. In
the following, we apply a threshold t
s
in
∼
D to signify
the areas that are considered as safely accessible by a
mobile robot, in terms of distance from surrounding
(a) (b)
Figure 2: Example noisy occupancy grid (a) and the corre-
sponding Gaussian Euclidean Distance Transform (b).
obstacles. The value of the threshold depends on the
size of the footprint-radius of the mobile robot as well
as the confidence to its estimated localization within
the map. In Figure 3 we show the remaining free area
as a result of setting a threshold to
∼
D.
The magnitude of the σ of the kernel determines
the importance that is given to surrounding obstacles
in terms of their distance from a particular free cell.
By decreasing σ we give more confidence to the im-
mediate close neighbourhood of the free cell while by
increasing σ we can cover bigger areas around the cell
and consider obstacles that are more distant. The de-
termination of a fixed value is a balance between these
aspects and is related to the resolution of the grid map.
(a) (b)
Figure 3: Determination of safely accessible free area
(shown in green) (b) by setting a threshold on the distance
from surrounding obstacles (a).
3.2 Weighed Mean-shift Clustering of
Free Space
The next step is to detect the local maxima within
∼
D, i.e. the points of maximum space clearance that
will represent the centres of the topological regions,
together with all the points that belong to the same
region. Towards this goal, we employ a mean-shift
(Comaniciu and Meer, 2002) gradient ascent on the
∼
D
image of the occupancy grid, adapted to conform to
the criteria (as described in Section 3) on which the
proposed segmentation process is based . In practise,
depending on the size of the occupancy grid, a down-
sampled version of
∼
D may be preferred in order to
reduce the overall computational cost.
In the following, we give the preliminary techni-
cal details of mean-shift clustering (for the detailed
formulation see (Comaniciu and Meer, 2002)) needed
ICPRAM 2012 - International Conference on Pattern Recognition Applications and Methods
74

to make the paper self contained in accordance to the
notations already used.
Let u = {i|p
i
∈ F} then given a cell p that lies in
free space, its kernel density estimate f
k
is given by:
f
k
(p) =
1
nb
2
∑
u
k
kp − p
u
k
2
b
2
(3)
where b is the bandwidth of a radially symmetric ker-
nel and k the corresponding profile function.
By setting g(x) = −k
0
(x) and taking the gradient
∇ of eq. (3) we obtain:
m
s
(p) =
∑
u
p
u
g
kp−p
u
k
2
b
2
∑
u
g
kp−p
u
k
2
b
2
− p (4)
that denotes the mean-shift vector which points to-
wards the direction of maximum increase of the ker-
nel density. By repeatedly applying the mean-shift
operator, we can identify the points of locally maxi-
mum space clearance as the points where the gradient
of eq. (3) is minimized, according to a convergence
threshold ε.
For the computation of the kernel density we em-
ploy the Epanechnikov kernel which minimizes the
square error between the density and its estimate (Co-
maniciu and Meer, 2002). The profile k
E
of the
Epanechnikov kernel is given by:
k
E
(x) =
1 − x, if 0 ≤ x ≤ 1
0, if x > 1
(5)
We adapt the former formulation of mean-shift to
consider not only the spatial position of a data point in
the estimation of the kernel density, but also its con-
tribution as specified by a weight factor. This factor
is the corresponding
∼
D(p) value that determines the
space clearance of the point. Hence, we compute the
modified shift vector as:
m
s
(p) =
∑
u
p
u
g
k
∼
D(p)·p−
∼
D(p
u
)·p
u
k
2
b
2
∑
u
g
k
∼
D(p)·p−
∼
D(p
u
)·p
u
k
2
b
2
− p (6)
The convergence to the modes of the density pro-
duces slightly different locations due to the threshold
ε that determines the termination of the mean-shift it-
erations, as well as because the value of the gradient
is very close to zero within regions where the density
estimate is constant. These artifacts are eliminated by
fusing mode candidates at a distance less than the ker-
nel bandwidth b by choosing the one corresponding to
the highest density.
The magnitude of the bandwidth b of the kernel
sets the size of the window that is considered for the
computation of the mean-shift and therefore deter-
mines the surface area of the topological regions. The
bigger bandwidth we select, the bigger areas are de-
tected and vice versa.
3.3 Constraining of Mean-shifts to
Linearly Unobstructed Vectors
According to the former formulation of mean-shift,
there are no constrains in the computation of the m
s
vector. This may result in computing mean-shift vec-
tors that point to positions that do not belong to free
space or that comprise of cells lying within occupied
space. Hence, a cell may converge to a point of lo-
cally maximum space clearance although the two po-
sitions are spatially disjoint. In Figure 4 (a) we show
a typical example of this case.
In the case of topological map segmentation, we
require that every point that belongs to a topological
region is spatially accessible by a robot through a path
whenever the robot is located within this region. To
avoid the costly computation of paths within the met-
ric map, we introduce this condition into the conver-
gence path of the mean-shift clustering procedure. In
detail, for each cell we condition the mean-shift vec-
tors of the corresponding convergence path to allow
only linearly unobstructed vectors. In this way, we
prevent the mean-shift vector from jumping into or
crossing through occupied space and the convergence
path simulates a path that could be followed by the
robot in real.
In order to ensure the spatial intra-connectivity of
cells, we use Bresenham’s line algorithm (Theoharis
et al., 2008) through which we can recover the cells
that lie along each mean-shift vector. If for a par-
ticular mean-shift vector all the corresponding cells
belong to free space, then mean-shift proceeds nor-
mally to the next iteration. Otherwise, we decrease
the bandwidth to b
0
= b − 1 and recompute the mean-
shift vector. This is repeated until all cells along the
mean-shift vector lie on free space wherein conver-
gence advances or until b
0
= 1 where we identify an
isolated free cell that is discarded. The consistent
clustering of the example shown in Figure 4 (a) is
given in Figure 4 (b).
The advantage of the former formulation of mean-
shift relies on the usability of the convergence paths
of all cells to the corresponding centres of the topo-
logical regions for the purpose of low-level path plan-
ning. In particular, by concatenation of the consec-
utive mean-shift vectors for each cell we obtain the
set of convergence paths that a robot can readily fol-
low in order to navigate to the center of its topologi-
cal region. By repeated concatenation of the conver-
CONSTRAINT-FREE TOPOLOGICAL MAPPING AND PATH PLANNING BY MAXIMA DETECTION OF THE
KERNEL SPATIAL CLEARANCE DENSITY
75

(a) (b)
Figure 4: (a) Example of clustering together spatially disconnected areas. Topological regions are identified by the index of
their cluster and their corresponding color. The cells belonging to the areas highlighted in red are erroneously incorporated in
region #1 or #2 although they are spatially disjoint; (b) Example of consistent clustering by constraining mean-shifts to allow
only for linearly unobstructed vectors by using Bresenham’s line algorithm in order to ensure the intra-connectivity of cells.
gence paths of adjacent cells that belong to different
regions, longer paths can be constructed that endow
a robot to navigate to any position within the map by
following a path that passes through the centres of the
intermediate topological regions. These paths are op-
timal with respect to the safety of the robot in terms
of overall distance from surrounding obstacles as well
as visibility in terms of space clearance. In Figure 5
we show the convergence paths of cells to the points
of locally maximum space clearance.
Figure 5: Convergence paths of a subset of grid cells (shown
in red) to the corresponding points of locally maximum
space clearance (shown in black).
4 EXPERIMENTS
In this Section we present the experiments that
demonstrate the feasibility and effectiveness of the
proposed topological segmentation method.
We divide our experiments in two parts. First we anal-
yse the role of the parameters involved in the pro-
posed methodology and second we provide a quali-
tative evaluation of the proposed topological segmen-
tation in a variety of metric maps including structured,
semi-structured and totally unstructured maps.
The parameters of the proposed segmentation
method are set by taking into account the characteris-
tics of the robot and its sensors. The values that need
to be set concern the variance σ of the Gaussian func-
tion used for the convolution (eq. 2), the threshold
t
s
for the determination of the safely accessible areas
and the bandwidth parameter b for the estimation of
the kernel density (eq. 3, 4).
The σ parameter determines the importance of
surrounding obstacles according to their distance
from a particular free cell. By decreasing σ, i.e. the
uncertainty, we increase the confidence to the imme-
diate close neighbourhood of the free cell. This in-
creases the ratio of cells that are designated as hav-
ing maximum space clearance to all the other cells
that lie closer to occupied space. In other words, rela-
tively small free areas are characterized by high space
clearance. By increasing σ bigger areas around a cell
are covered by considering space that is more distant
which decreases the aforementioned ratio. Hence,
only wide open areas are characterized by having
high space clearance. The effect of various σ values
(σ = 15, 30, 45) in the estimation of space clearance
is demonstrated in Figure 6.
The threshold t
s
is set in proportion to the size
of the robot, since the bigger the robot the further
it should reside from occupied space and vice versa.
By increasing t
s
, the free area with sufficiently high
space clearance is decreased hence also decreasing
the area to be clustered. This may isolate portions
of free space if the access is through relatively nar-
row passages and hence not traversable by the robot.
In Figure 7 we show the effect of different thresholds
(t
s
= 0.8, 0.9, 0.99) in estimating the safely accessible
free space by a robot.
ICPRAM 2012 - International Conference on Pattern Recognition Applications and Methods
76

(a) (b)
(c) (d)
Figure 6: (a) Example metric map (499 × 319) and (b)-(d)
the estimated space clearance for varying σ.
(a) (b)
(c) (d)
Figure 7: (a) Space clearance estimation of metric map and
(b)-(d) determination of safely accessible areas for a robot
(in green) using different thresholds.
The bandwidth parameter b related to the estima-
tion of the kernel space clearance density determines
the surface area of the segmented regions. It defines
the radius of the kernel window, i.e. the neighbour-
hood around a cell in the estimation of the mean-shift
vector. By increasing the radius we allow for longer
mean-shift vectors and thus clustering together cells
that are more distant from one another which typi-
cally results in less number of clusters. Setting a par-
ticular value for the bandwidth depends on the desired
granularity of the segmentation process that can vary
in order to construct either coarse or fine topologi-
cal maps. In Figure 8 we show the effect of different
bandwidth values (b = 3, 5, 7) in the final clustering.
In Figure 9 we demonstrate the stability of the pro-
posed segmentation method in the presence of noise
or relatively small obstacles within a given map. It is
fairly evident that the effect of noise or very small ob-
stacles in the clustering result is minimal as relatively
small volumes do not naturally alter the topology of
space. However, when small volumes approach one
another or reside close to bigger volumes they have a
combined effect and space topology is altered (e.g. in
(a) (b)
(c) (d)
Figure 8: (a) Safely accessible area of metric map (in green)
and (b)-(d) topological segmentation for different values of
the bandwidth b in the kernel space clearance estimation.
(a) (b) (c)
(d) (e) (f)
Figure 9: Topological clustering of free area in the presence
of noise or relatively small obstacles; (a) initial clustering,
(b)-(f) clustering under various arrangements of small ob-
stacles or noise.
Figure 9 (d),(f) wherein the upper right region is con-
fined due to the presence of an obstacle close to the
wall).
A particular setting of the t
s
, σ and b parame-
ters depends on the size characteristics of the robot,
the desired granularity of the segmentation process as
well as the desired level of space clearance.
In Figure 10, we show the results of segmenta-
tion under a fixed setting of parameters (σ = 15,t
s
=
0.9, b = 5) in a variety of metric maps ranging from
structured to totally unstructured.
In the case of structured environments, the areas
corresponding to medium sized rooms are identified
as individual regions while larger constrained areas
such as corridors or halls, are segmented to more than
CONSTRAINT-FREE TOPOLOGICAL MAPPING AND PATH PLANNING BY MAXIMA DETECTION OF THE
KERNEL SPATIAL CLEARANCE DENSITY
77

(a) (b) (c)
(d) (e) (f)
Figure 10: Topological segmentation of generic metric maps; (a) parking lot, (b) tunnel car accident, (c) warehouse, (d) office
environment, (e) simulated indoor environment, (f) hallway.
one region. Hence, by adopting this approach elon-
gated areas are segmented. Alternatively, we could
decrease the granularity of segmentation by increas-
ing the b parameter as shown in Figure 8. Another
possibility would be to fuse distinct areas that belong
to an elongated area by comparing the convexity of
the fused regions against that of the resulting region.
In the case of unstructured maps where there is no
notion of rooms or corridors, the only meaningful seg-
mentation criterion corresponds to the identification
of regions where space clearance is locally high as
well as regions that are spatially disjoint-isolated and
hence unreachable by the robot. As can be seen from
the respective examples in Figure 8, these areas are
well defined by the proposed segmentation method
The connectivity among the regions, i.e. the
edges of the corresponding topological graph can
be straightforwardly obtained by checking the 6
th
-8
th
neighbourhood of each cell.
The average segmentation time for the maps
shown in Figure 10 using a Linux-based system
equipped with an Intel Core i7 CPU 860 was 0.41
secs. The overall computational cost of the proposed
algorithm is dominated by the mean-shift clustering
stage as the preceding stage involving the computa-
tion of the space clearance can be efficiently com-
puted by exploiting the separability property of the
gaussian kernel. Furthermore, if necessary, the effi-
ciency of the mapping process could be improved by
clustering different cells in parallel.
5 CONCLUSIONS AND FUTURE
WORK
We have presented a new topological mapping
method that is robust to noisy sensory data and does
not presume a particular structure of the environment.
By an initial parameterization that is imposed by the
characteristics of the robot, it can be readily applied to
generic metric maps of minimal environmental con-
straints, as demonstrated in a variety of real-world ex-
amples. As a result of its formulation, the proposed
approach can in parallel serve as a low level path-
planning algorithm by using the consecutive mean-
shift vectors of the convergence paths. This feature
together with the real-time performance of the topo-
logical segmentation increases the overall efficiency
of the robot by allowing for allocation of its compu-
tational resources to tasks other than path-planning.
As part of our future work, we are considering
the application of the proposed method for 3D topo-
logical mapping as well as segmentation of generic
3D volumes, since the notion of 2D space clearance
can be readily extended to 3D. In addition, it appears
that the proposed algorithm could be improved by in-
troducing appropriate criteria for fusing topological
regions that are part of constrained elongated areas,
whenever this is required.
ICPRAM 2012 - International Conference on Pattern Recognition Applications and Methods
78

ACKNOWLEDGEMENTS
This paper describes research done under the EU-FP7
ICT 247870 NIFTI project.
REFERENCES
Beeson, P., Jong, N., and Kuipers, B. (2005). Towards
autonomous topological place detection using the ex-
tended voronoi graph. In IEEE ICRA.
Beeson, P., MacMahon, M., Modayil, J., Provost, J., Savelli,
F., and Kuipers, B. (2003). Exploiting local perceptual
models for topological map-building. In IJCAI Work-
shop on Reasoning with Uncertainty in Robotics.
Brunskill, E., Kollar, T., and Roy, N. (2007). Topological
mapping using spectral clustering and classification.
In IEEE IRS.
Choi, J., Choi, M., and Chung, W. (2009). Incremental
topological modeling using sonar gridmap in home
environment. In IEEE IRS.
Comaniciu, D. and Meer, P. (2002). Mean shift: a robust
approach toward feature space analysis. IEEE Trans-
actions on Pattern Analysis and Machine Intelligence,
24(5):603–619.
Eppstein, E., Konolige, K., and Marthi, B. (2006). Hier-
archical map building and planning based on graph
partitioning. In IEEE ICRA.
Fabrizi, E. and Saffiotti, A. (2000). Extracting topology-
based maps from gridmaps. In IEEE ICRA.
Fabrizi, E. and Saffiotti, A. (2002). Augmenting topology-
based maps with geometric information. Robotics and
Autonomous Systems, 40(2-3):91–97.
Fukunaga, K. and Hostetler, L. (1975). The estimation of
the gradient of a density function, with applications in
pattern recognition. IEEE Transactions on Informa-
tion Theory, 21(1):32–40.
Gianni, M., Papadakis, P., Pirri, F., Liu, M., Pomerleau, F.,
Colas, F., Zimmermann, K., Svoboda, T., Petricek, T.,
Kruijff, G., Khambhaita, H., and Zender, H. (2011).
A unified framework for planning and execution-
monitoring of mobile robots. In AAAI Workshop on
Automated Action Planning for Autonomous Mobile
Robots.
Goedeme, T., Nuttin, M., Tuytelaars, T., and Gool, L.
(2007). Omnidirectional vision based topological nav-
igation. International Journal of Computer Vision,
74:219–236.
Goedeme, T., Tuytelaars, T., and Gool, L. . (2008). Visual
topological map building in self-similar environments.
In Informatics in Control Automation and Robotics,
volume 15, pages 195–205.
Joo, K., Lee, T., Baek, S., and Oh, S. (2010). Generat-
ing topological map from occupancy grid-map using
virtual door detection. In IEEE Congress on Evolu-
tionary Computation.
Kuipers, B., Modayil, J., Beeson, P., MacMahon, M., and
Savelli, F. (2004). Local metrical and global topolog-
ical maps in the hybrid spatial semantic hierarchy. In
IEEE ICRA.
Liu, M., Colas, F., and Siegwart, R. (2011). Regional
topological segmentation based on mutual informa-
tion graphs. In IEEE ICRA.
Liu, M., Scaramuzza, D., Pradalier, C., Siegwart, R., and
Qijun, C. (2009). Scene recognition with omnidi-
rectional vision for topological map using lightweight
adaptive descriptors. In IEEE IRS.
Maxwell, B., Smart, W., Jacoff, A., Casper, J., Weiss, B.,
Scholtz, J., Yanco, H., Micire, M., Stroupe, A., Stor-
mont, D., and Lauwers, T. (2004). 2003 aaai robot
competition and exhibition. AI Magazine, 25(2):68–
80.
Montijano, E. and Sagues, C. (2011). Distributed multi-
camera visual mapping using topological maps of pla-
nar regions. Pattern Recognition, 44(7):1528–1539.
Murillo, A., Abad, P., Guerrero, J., and Sagues, C. (2009).
Improving topological maps for safer and robust nav-
igation. In IEEE IRS.
Murillo, A., Sagues, C., Guerrero, J., Goedeme, T., Tuyte-
laars, T., and Gool, L. (2007). From omnidirectional
images to hierarchical localization. Robotics and Au-
tonomous Systems, 55(5):372–382.
Murphy, R. (2004). Human-robot interaction in res-
cue robotics. IEEE Transactions on Systems, Man,
and Cybernetics, Part C: Applications and Reviews,
34(2):138–153.
Myung, H., Jeon, H., Jeong, W., and Bang, S. (2009).
Virtual door-based coverage path planning for mobile
robot. In Advances in Robotics.
Paul, R. and Newman, P. (2010). Fab-map 3d: Topological
mapping with spatial and visual appearance. In IEEE
ICRA.
Shi, J. and Malik, J. (2000). Normalized cuts and image
segmentation. IEEE Transactions on Pattern Analysis
and Machine Intelligence, 22(8):888–905.
Theoharis, T., Papaioannou, G., Platis, N., and Patrikalakis,
N. (2008). Graphics & Visualization: Principles &
Algorithms. A K Peters.
Thrun, S. (1998). Learning metric-topological maps for in-
door mobile robot navigation. Artificial Intelligence,
99(1):21–71.
Valgren, C. and Lilienthal, A. (2008). Incremental spec-
tral clustering and seasons: Appearance-based local-
ization in outdoor environments. In IEEE ICRA.
Zivkovic, Z., Bakker, B., and Krose, B. (2006). Hierarchical
map building and planning based on graph partition-
ing. In IEEE ICRA.
CONSTRAINT-FREE TOPOLOGICAL MAPPING AND PATH PLANNING BY MAXIMA DETECTION OF THE
KERNEL SPATIAL CLEARANCE DENSITY
79
