A GENERALIZED HIDDEN MARKOV MODEL FOR

PREDICTION OF CIS-REGULATORY MODULES

IN EUKARYOTE GENOMES AND DESCRIPTION

OF THEIR INTERNAL STRUCTURE

Anna A. Nilulova

1,2

, Alexander V. Favorov

3,4

, Vsevolod Yu. Makeev

and Andrey A. Mironov

1,2

Department of Bioengineering and Bioinformatics, Moscow State University, Leninskie Gory, Moscow, Russia

Institute for Information Transmission Problems, Russian Academy of Sciences, Bolshoi Karetnyi per., Moscow, Russia

Department of Oncology, School of Medicine, Johns Hopkins University, N. Broadway, Baltimore, MD, U.S.A.

Engelhardt Institute of Molecular Biology, Russian Academy of Sciences, Vavilova str., Moscow, Russia

Keywords: Generalized hidden markov models, Regulation of transcription, Cis-regulatory modules, Binding sites,

Regulatory structure, Eukaryotes.

Abstract: Eukaryotic regulatory regions have been studied extensively due to their importance for gene regulation in

higher eukaryotes. However, the understanding of their organization is clearly incomplete. In particular, we

lack accurate in silico methods for their prediction. Here we present a new HMM-based method for the

prediction of regulatory regions in eukaryotic genomes using position weight matrices of the relevant

transcription factors. The method reveals and then utilizes the regulatory region structure (preferred binding

site arrangements) to increase the quality of the prediction, as well as to provide a new knowledge of the

regulatory region organization. We show that our method can be successfully used for the identification of

regulatory regions in eukaryotic genomes with a quality higher than that of other methods. We also

demonstrate the ability of our algorithm to reveal structural features of the regulatory regions, which could

be helpful for the deciphering of the transcriptional regulation mechanisms in higher eukaryotes.

1 INTRODUCTION

Transcription of genes is regulated mostly by special

proteins – transcription factors (TFs) – which bind

the DNA at specific binding sites (TFBSs) and thus

influence the transcription. In eukaryotes, stage- and

tissue-specific transcription of genes is achieved

through the interaction of different TFs with each

other and their co-factors, as well as through other

mechanisms, such as the chromatine remodelling.

Eukaryotic TFBSs are too short and degenerate to

detect them accurately in silico. On the other hand

eukaryotic TFBSs are often organized in groups, cis-

regulatory modules (CRMs). These modules seem to

coordinate protein-protein interactions for proper

regulation of gene expression. But despite a great

interest in the regulatory modules, their organization

is still not completely understood. Most researches

pay attention to the close situation of TFBSs and

their types. However, the structure of modules (the

order of sites and the distances between them) were

shown to be important in many cases (Makeev,

2003); (Hallikas, 2006); (Papatsenko, 2009).

One could suppose that if the structure of

regulatory modules was really crucial for the

transcriptional regulation, it would be conserved

during the evolution. In this case, despite a

considerable sequence divergence, regulatory

regions of orthologous genes should possess a

similar structure.

On the other hand, regulatory regions of co-

regulated genes also seem to be similar. Thus, the

analysis of the regulatory regions of orthologous

and/or co-regulated genes could reveal some rules or

preferences of site arrangements, which are common

for most of genes, and which therefore could be

important for a proper transciption regulation.

Here, we present a method called CORECLUST,

which uses a HMM-based technique to predict

regulatory modules for a set of known position

weight matrices (PWMs) for system-specific TFs.

The algorithm constructs a model of the regulatory

A. Nilulova A., V. Favorov A., Yu. Makeev V. and A. Mironov A..

A GENERALIZED HIDDEN MARKOV MODEL FOR PREDICTION OF CIS-REGULATORY MODULES IN EUKARYOTE GENOMES AND DESCRIP-

TION OF THEIR INTERNAL STRUCTURE.

DOI: 10.5220/0003735800340041

In Proceedings of the International Conference on Bioinformatics Models, Methods and Algorithms (BIOINFORMATICS-2012), pages 34-41

ISBN: 978-989-8425-90-4

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

regions that describes preferences of site

arrangements; the preferences can be revealed from

given regulatory sequences of co-regulated and/or

orthologous genes. The model then can be used for

searching for similar regulatory regions in the

sequences of interest or genome-wide.

2 ALGORITHM

The main idea of the algorithm is to scan genomic a

sequence and to search for segments that are much

more likely to be generated by a probabilistic

process that uses the model than by a random

background process. The model (hidden Markov

model) describes regulatory regions, the clusters of

binding sites, which can prefer some specific

relative arrangements (regulatory structure). We

describe the structure as a set of characteristics, such

as sites frequencies, sites order, and distance

distributions between adjacent sites. The preferences

of site arrangements, if any, can be obtained from

given regulatory sequences by training of the model

parameters.

2.1 The Hidden Markov Model

The hidden Markov model (HMM) presented here

describes the probabilistic process that is assumed to

generate a sequence with inclusions of cis-regulatory

module(s). The generated sequence consists of

segments (or subsequences) of three types:

 background sequence;

 TFBSs;

 inter-site regions (spacers), that is the regions

between two adjacent sites in one module.

Each CRM begins and ends with a site; CRMs are

surrounded by a background sequence.

Our HMM is of a generalized type (Rabiner,

1989), which means that each generative state emits

a string of nucleotides, rather than a single symbol.

This allows us to set any desirable distribution for

the length of strings generated from every emitting

state of the model.

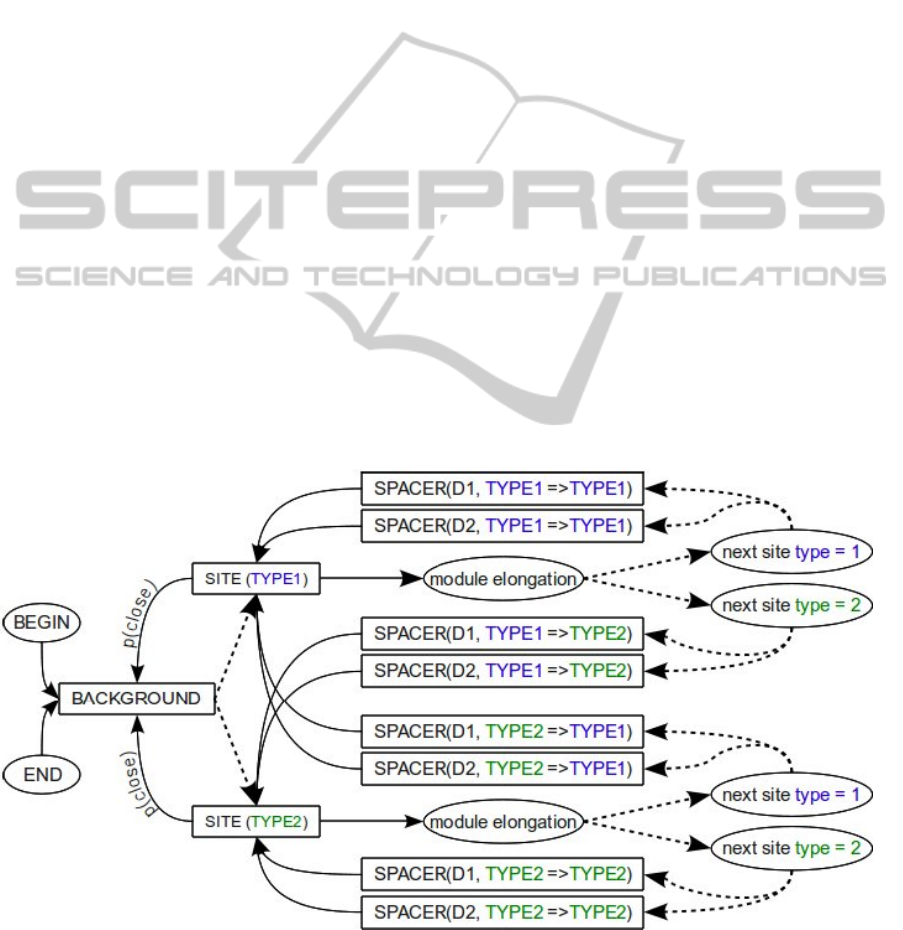
The HMM contains three main types of

generative states, which correspond to the types of

the sequence segments: inter-module background

sequence, sites and spacers (Figure 1). The

background sequence is generated according to the

first order local Markov model. The length of the

sequences emitted in the BACKGROUND state is

geometrically distributed with a mean 1/ p

open

. (p

open

is a probability to start a CRM).

Each SITE state emits a sequence according to

the corresponding position weigh matrix (PWM) in

one of the two orientations. In all SPACER states

nucleotides are generated according to the same

local Markov model as we use for the

Figure 1: The HMM scheme for two types of sites (TYPE1 and TYPE2) and two types of SPACER states, which vary in

their length distributions (D1 and D2). The emitting states are represented by rectangular boxes and the silent states are

shown by oval shapes. Arrows represent allowed transitions between states. Probabilities of the transitions marked by

dashed lines are updated during the Baum-Welch training.

A GENERALIZED HIDDEN MARKOV MODEL FOR PREDICTION OF CIS-REGULATORY MODULES IN

EUKARYOTE GENOMES AND DESCRIPTION OF THEIR INTERNAL STRUCTURE

BACKGROUND state. The length distribution

varies between the SPACER states of different

types, which will be described later.

The architecture of the model allows us to take

into account preferences in site arrangement

(regulatory structure), which include: 1) correlations

between binding sites of certain types and 2)

preferred distribution of the distance between

adjacent TFBSs of certain types (i.e. the length of

the spacer region). The correlation of TFBSs of

certain types could mean that the corresponding TFs

work together and their interaction is required for

the CRM activity. And if two TFs interact with each

other, the relative arrangement of their binding sites

should be non-random, with some preferences in

distance between the sites.

The structure of regulatory regions is taken into

account by introducing the set of SPACER states

with different length distribution and the set of silent

states that determine the choice of the next site type

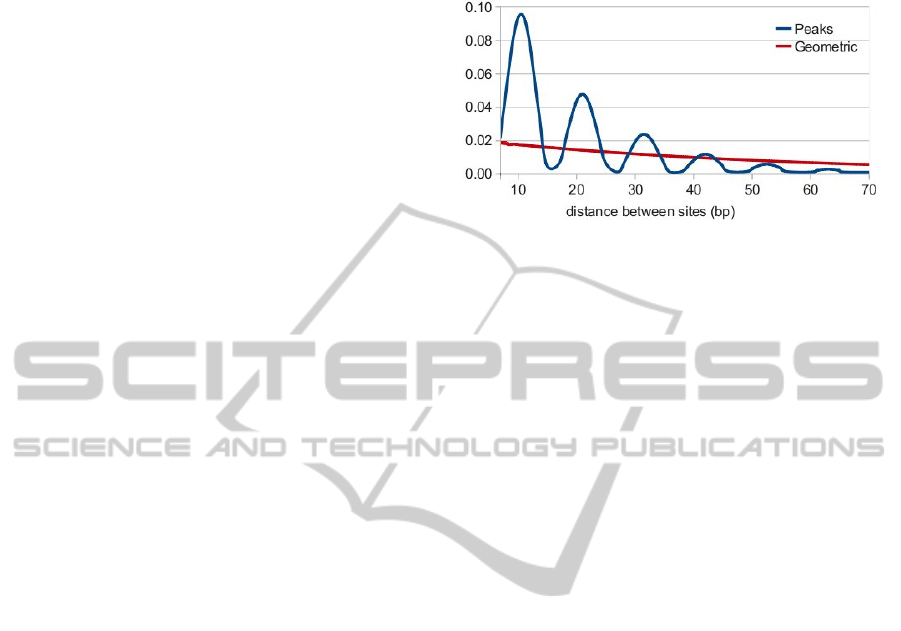
and the type of the spacer state. In this work, we use

two types of SPACER state with length distributed

according to either the geometric distribution, which

reflects sites clustering without any distance

specificity or the exponentially damped sinusoid

with a period of 10.5 bp, which corresponds to the

situation when interacting proteins are bound on the

same side of the DNA strand (Figure 2).

To reveal the regulatory structure from a given

set of sequences, we train the parameters that

determine the module structure (transitions marked

with dashed lines in Figure 1) by using the Baum–

Welch algorithm (Baum, 1972).

2.2 Search For Regulatory Modules

To find regulatory modules in a given sequence we

apply the trained model to the sequence and search

for the best way to segment it in the background and

CRM states (the latter are combinations of sites and

spacer regions). It corresponds to a path in the HMM

graph, which fits best our model. To find this path

we use the posterior Viterbi decoding algorithm,

described in (Fariselli, 2005), which was shown to

have a better performance than the standard Viterbi

or posterior decoding algorithms.

The algorithm identifies some CRMs in a

sequence, if any. To weight a module, we use the

log-likelihood ratio, which reflects how likely it is

that this sub-sequence was generated by the

regulatory region model, as compared to being

generated by the background model. It equals the

log-ratio of the probabilities of two sub-paths in the

HMM graph that emit the module and the

background sequence, respectively; both sub-paths

span from the beginning to the end of the module.

Figure 2: Distributions of distance between adjacent sites

in a module that are used in the model.

3 TESTING

3.1 Testing On The Vertebrate Muscle

Dataset

The muscle dataset, which initially was compiled by

Wasserman and Fickett (Wasserman, 1998), now is

widely used to assess the quality of the CRM

prediction programs. We used this dataset to test the

ability of CORECLUST to identify CRMs in a set of

upstream regions of co-regulated and orthologous

genes. The dataset consists of sequences with an

average length of 850 bp, which contain known

regulatory regions for 19 muscle genes from human,

mouse, cow and chicken. The set of PWMs includes

5 TFs, reported to be important in muscle regulation:

Mef2, Myf, Sp1, Srf and Tef. The dataset as well as

the assessment procedure were taken from (Klepper,

2008). These authors developed a benchmarking

framework for assessing programs' performance and

used it to evaluate the performance of eight

published module-discovery tools. We assessed the

performance of CORECLUST and compared the

results with other eight programs describer in the

paper (CMA (Kel, 2006), CisModule (Zhou, 2004),

ModuleSearcher (Aerts, 2003), Stubb (Sinha, 2003),

MSCAN (Johansson, 2003), MCAST (Bailey,

2003), Cister (Frith, 2001) and Cluster-Buster (Frith,

2003)).

To measure the prediction accuracy of the

method with respect to module location, we used six

measures described in (Klepper, 2008):

 correlation coefficient (CC);

 sensitivity (Sn);

 specificity (Sp);

 positive predictive value (PPV);

BIOINFORMATICS 2012 - International Conference on Bioinformatics Models, Methods and Algorithms

 performance coefficient (PC, phi-score);

 average site performance (ASP).

The sensitivity gives the fraction of nucleotides

known to be in a CRM that are correctly identified

as such. The specificity measures the proportion of

background nucleotides, which are correctly

identified. The positive predictive value gives the

fraction of nucleotides predicted to be in a CRM that

are known to be in one. The correlation coefficient,

performance coefficient and average site

performance are statistics that in some sense average

these quantities.

The results of the programs' performance

assessment (

Table 1) show that CORECLUST scored

better than other programs for almost all measures.

Losing a little in the sensitivity, the program scores

highest of all for the CC measure, which captures

the sensitivity and specificity values into a single

score.

3.2 Testing on the Drosophila Early

Developmental System

Genes of the Drosophila anterior-posterior axis

specification process (AP) have rather long

regulatory regions situated about 10-15 Kbp from

the respective transcription start sites (TSS).

Moreover there are twelve annotated genomes of the

Drosophila genus available in public databases. All

this allows us to use the upstream regions of genes

from only one orthologous group as a training set

without overfitting.

We assessed the performance of CORECLUST

using 17 AP genes from the D.melanogaster

genome, shown to possess experimentally verified

regulatory regions, bound by all or some of seven

TFs: Bcd, Hb, Cad, Kr, Kni, Tll and Gt. The model

training and CRM search were done for every gene

separately with the use of all available orthologous

sequences. As CRM predicting programs, used for

the prediction comparison, search for CRMs in the

same sequences they train the model on, we used the

same strategy for CORECLUST testing. The

predictions were made for 40Kb region ([-20Kb,

+20Kb] relative to TSS) of each gene. The modules

predicted in D. melanogester sequences were

compared with the known ones from the REDFly

database (Halfon, 2008).

As a performance measure we applied the

correlation coefficient (CC) as it combines all

aspects of the predictions quality. The results of the

performance analysis were compared with three

other publicly available programs: Stubb (Sinha,

2003), MOPAT (Hu, 2008) and Cluster-Buster

(Cbust) (Frith, 2003). The comparison shows (Table

2) that predictions made by CORECLUST have a

higher value of CC than Stubb (p-value = 0.05,

Wilcoxon signed-rank test), MOPAT (p-value =

0.00067, Wilcoxon signed-rank test) and Cluster-

Buster (p-value = 0.02, Wilcoxon signed-rank test).

The testing of the program on two distinct

systems shows that it is applicable to different

regulatory systems and eukaryotic clades and can be

successfully used for solving the standard problem

of identification cis-regulatory modules for a set of

system-specific TFs.

Table 1: Comparison of the programs' performance. The two maximum values in each column is set in bold. The maximum

value is marked by gray background. CC - correlation coefficient, Sn - sensitivity, Sp - specificity, PPV - positive predictive

value, PC - performance coefficient, ASP - average site performance.

Methods CC Sn Sp PPV PC ASP

CORECLUST 0.56 0.66 0.93 0.58 0.45 0.62

MSCAN 0.50 0.63 0.91 0.51 0.39 0.57

ModuleSearcher 0.46 0.48

0.95 0.57 0.35 0.53

CMA 0.46 0.56 0.92 0.51 0.36 0.53

Cluster-Buster 0.41 0.74 0.80 0.35 0.31 0.55

Cister 0.36 0.92 0.61 0.25 0.25 0.59

MCAST 0.30

0.96 0.48 0.21 0.21 0.58

CisModule 0.29 0.72 0.70 0.25 0.23 0.49

Stubb 0.24 0.65 0.70 0.24 0.21 0.44

A GENERALIZED HIDDEN MARKOV MODEL FOR PREDICTION OF CIS-REGULATORY MODULES IN

EUKARYOTE GENOMES AND DESCRIPTION OF THEIR INTERNAL STRUCTURE

Table 2: Comparison of the programs' performance. The

maximum value in each line is set in bold.

Gene CORECLUST MOPAT

bowl 0.20 0.10 -0.01 0.17

0.45 0.27 0.31 0.47

cad -0.03 0.17 -0.02 -0.04

ems -0.02 0.15 -0.01 -0.02

eve 0.73 0.56 0.54 0.58

0.31 0.28 0.27 -0.02

0.31 0.36 0.32 0.27

gt 0.41 0.48 0.27 0.40

h 0.69 0.17 0.26 0.49

0.32 0.33 0.17 0.22

0.43 0.22 0.27 0.45

Kr 0.45 0.24 0.29 0.64

0.26 0.14 0.13 0.17

run 0.08 0.17 0.07 0.11

0.23 0.07 -0.01 0.17

slp1 0.35 0.34 0.44 0.35

0.26 0.15 0.09 0.17

TOTAL 0.32 0.20 0.20 0.29

median 0.31 0.22 0.26 0.22

0.21 0.13 0.17 0.21

P-value 0.049 0.00067 0.0197

Stubb Cbust

btd

fkh

ftz

kni

prd

salm

tll

st.dev.

4 THE INTERNAL STRUCTURE

OF THE PREDICTED

REGULATORY MODULES

CORECLUST predicts regulatory modules that are

characterized by similar structure, which allows to

reveal and analyze the rules of site arrangement. The

structure of regulatory regions from training

sequences can be taken from the HMM parameters.

But it is even more interesting to study preferred site

arrangements in the predicted modules. As the

model describes preferences, but not strict rules, of

site arrangements, the regulatory regions that are

found in real genomic sequences can possess some

structural features not included in the model in

advance.

To reveal pairs of sites that are situated next to

each other more frequently than it is expected by

chance (in the case of site independence), we use the

Pearson correlation coefficient:

)1()1(

),(

jjii

jiji

pppp

ppp

jiCorr







where p

is the frequency of an occurrence of a site

of type i next to any other site, p

is the frequency of

an occurrence of a site of type j next to any other site

and p

i,j

is the frequency of an occurrence of a site of

type i next to a site of type j (the order and directions

of sites are taken into account).

4.1 Structural Analysis of CRMs

Found in the Drosophila Genomes

The method is applicable for genome-wide search.

That is, after training the model on regulatory

regions of some gene (“starting” gene) and its

orthologs it can be used for searching for similar

regulatory regions genome-wide.

We used each of the 17 Drosophila

developmental genes as a “starting” gene and then

searched all Drosophila genomes for regulatory

regions with the similar structure. After this we

revealed the overrepresented site pairs for every run

(every “starting” gene).

Noticeably, some of the observed

overrepresented site pairs were documented before.

For instance, the interaction of Bcd proteins was

shown to be important for transcriptional regulation

of genes hb and kni (Lebrecht, 2005). This is

consistent with our observations that Bcd-Bcd site

pair is overrepresented in the regulatory regions

found by the hb- and kni-trained models. Also, the

Hb-Hb and Cad-Cad correlations have been recently

shown in (Papatsenko, 2009), which also fits well to

our predictions. Moreover, according to our

predictions, the site-to-site distances in the Hb-Hb

site pair have a periodic helical distribution (Figure

3A), which also has been observed in (Papatsenko,

2009).

Interestingly, although for different “starting”

genes we observe different sets of overrepresented

site pairs, some of the pairs are typical for several

genes simultaneously. This phenomenon may be

interpreted as a characteristic of the whole

regulatory system. For example, the site pair

Hb<Hb< (two Hb binding sites, the direction of an

“arrow” ('<' or '>') shows the direction of the site

relative to the gene direction) is significantly

overrepresented for 10 starting genes and in all cases

the distance between the sites is distributed

according to the damped sinusoid (Figure 3A).

An example of a distance distribution, which is

not included in the model, but still is observed in the

predicted regulatory regions, is provided by the

distribution for the pair Bcd>Bcd> (two Bcd binding

sites, both situated on the positive DNA strand

relative to the gene direction). This site pair is

overrepresented for six “starting” genes and in all

cases the site-to-site distance distribution has an

unusual high peak at distance 190-191 bp, as well as

at distances 200-202 bp and 171-172 bp (Figure 3B).

BIOINFORMATICS 2012 - International Conference on Bioinformatics Models, Methods and Algorithms

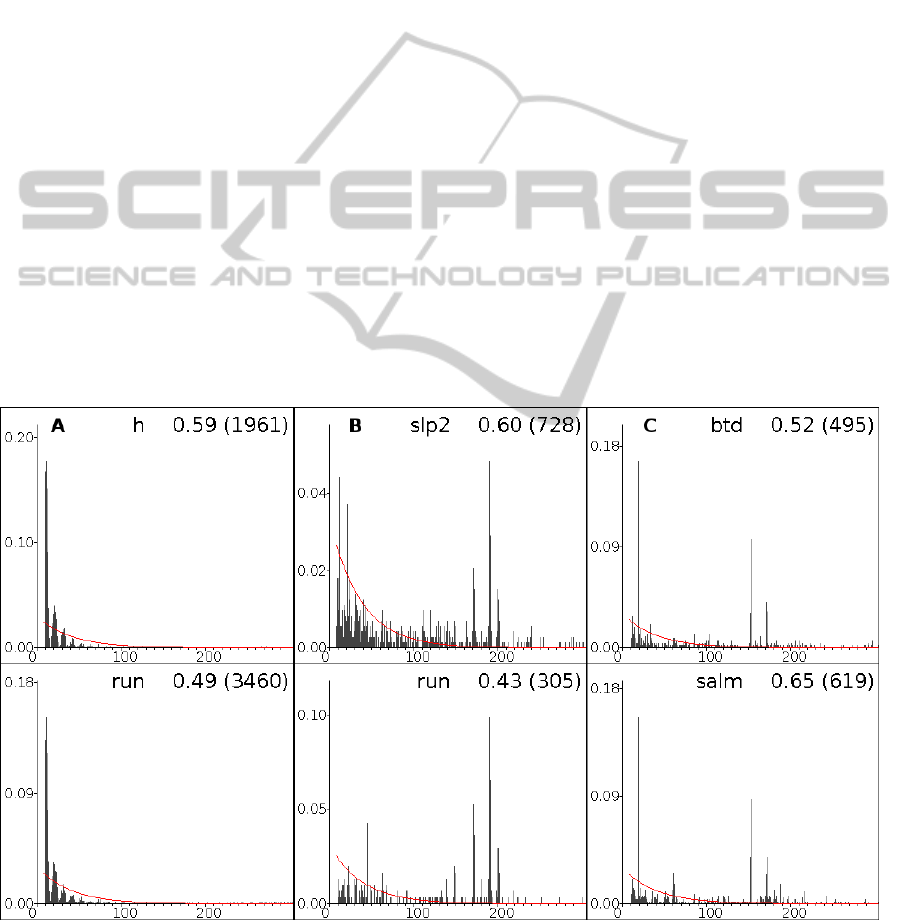
Such long distances between sites are rather

uncommon and perhaps could indicate that the

corresponding TFs interact with DNA wound around

a histone protein core.

Similarly interesting are the site-to-site distance

distributions for the pair Tll<Tll<. This pair is

overrepresented only for three starting genes but for

all of them most Tll<Tll< site pairs have

characteristic distances: 19 bp, 152-153 bp, and 171-

172 bp (Figure 3C).

One more observation on the site relative

arrangements is that the relative orientation of the

sites in a pair seems to be important. For most TF

pairs we found an overrepresentation for only some

orientation arrangements. For instance, for the

predictions made by the h-trained model, only two

types of the Kni site pairs were overrepresented:

Kni>Kni> and Kni<Kni<, which are pairs of sites on

the same DNA strand. The orientation relative to the

regulated gene also could be of importance: only site

pair Hb<Hb< is significantly overrepresented for the

starting gene h and several other genes.

These observations demonstrate that TFs

function cooperatively: if two TFs interact with each

other when binding the DNA, the orientation of their

binding sites should be crucial for successful

regulation.

4.2 Structural Analysis of CRMs In

Vertebrate Genomes

For the regulatory regions predicted by the model

trained on the muscle genes we also observe

overrepresented site pairs, most of which are

supported by the experimental data. For example,

binding sites of TFs Myf and Mef2, as well as Sp1

and Myf, occur next to each other unexpectedly

often in the predicted modules; the validity of this is

confirmed by the data from the database of

composite elements TransCompel (Matys, 2006).

Predicted interaction of the TFs Tef and Mef2 is

confirmed by (Maeda, 2002).

For this regulatory system, we also observe the

importance of specific sites relative orientation.

Thus, for Sp1 TF only S1>Sp1> and Sp1<Sp1<

site pairs are overrepresented, while the pair

Sp1>Sp1< is underrepresented.

The results presented in this section argue that in

many cases the regulatory structure is important and

could be used as an additional information for the

prediction of functional CRMs and understanding of

the transcriptional regulation mechanisms in

eukaryotes.

Figure 3: Examples of distributions of distances between adjacent sites for pairs Hb<Hb< (A), Bcd>Bcd> (B) и Tll>Tll>

(C) in the regulatory modules, predicted for models trained on different starting genes. The starting (training) gene, the

correlation coefficient and the number of observed pairs (in brackets) are given at each plot. The random distance

distribution is shown by the red line.

A GENERALIZED HIDDEN MARKOV MODEL FOR PREDICTION OF CIS-REGULATORY MODULES IN

EUKARYOTE GENOMES AND DESCRIPTION OF THEIR INTERNAL STRUCTURE

5 CONCLUSIONS

We have developed a new algorithm

CORECLUST based on generalized hidden

Markov models, which is able to successfully

predict regulatory modules in eukaryotic genomes

for a set of PWMs starting from a set of co-

regulated and/or orthologous genes. CORECLUST

utilizes the cross-species conservation without

relying on multiple alignment, which can be useful

for analysis of poorly alignable intergenic regions.

The main disadvantage of the algorithm is the

limitation of number of used PWMs, as it causes

the increase of the HMM parameters, which can

result in model overfitting. The future work aims

to overcome this limitation by reducing the number

of training parameters to only significant ones.

Nevertheless, CORECLUST demonstrates better

performance than other methods. The main

biological advantage of the method is that it

reveals regulatory regions structure, which could

help in better understanding of the transcriptional

regulation process.

ACKNOWLEDGEMENTS

We are grateful to Mikhail Gelfand and Dmitri

Pervouchine for useful discussions and

encouragement, and to Dmitry Vinogradov for

technical assistance.

REFERENCES

Moore, R., Lopes, J., 1999. Paper templates. In

TEMPLATE’06, 1st International Conference on

Template Production. SciTePress.

Smith, J., 1998. The book, The publishing company.

London, 2

edition.

Aerts, S., Van Loo, P., Thijs, G., Moreau, Y., De Moor,

B., 2003. Computational detection of cis -regulatory

modules. In Bioinformatics, 19 Suppl 2.

Bailey, T. L., Noble, W. S., 2003. Searching for

statistically significant regulatory modules. In

Bioinformatics, 19 Suppl 2.

Baum L., 1972. An equality and associated

maximization technique in statistical estimation for

probabilistic functions of Markov processes. In

Inequalities, 3.

Fariselli, P., Martelli, P. L., Casadio, R., 2005. A new

decoding algorithm for hidden Markov models

improves the prediction of the topology of all-beta

membrane proteins. In BMC Bioinformatics.

Frith, M. C., Hansen, U., Weng, Z., 2001. Detection of

cis-element clusters in higher eukaryotic DNA. In

Bioinformatics, 6 Suppl 4.

Frith, M. C., Hansen, U., Weng, Z., 2001. Detection of

cis-element clusters in higher eukaryotic DNA. In

Bioinformatics,17, no. 10.

Frith, M. C., Li, M. C., Weng, Z., 2003. Cluster-Buster:

finding dense clusters of motifs in DNA sequences.

In Nucleic Acids Research, 31, no. 13.

Halfon, M. S., Gallo, S. M., Bergman, C. M., 2008.

REDfly 2.0: an integrated database of cis-regulatory

modules and transcription factor binding sites in

Drosophila. In Nucleic Acids Research, 36.

Hallikas, O., Palin, K., Sinjushina, N., Rautiainen, R.,

Partanen, J., Ukkonen, E., Taipale, J., 2006.

Genome-wide Prediction of Mammalian Enhancers

Based on Analysis of Transcription-Factor Binding

Affinity. In Cell, 124(1).

Hu, J., Hu, H., Li, X., 2008. MOPAT: a graph-based

method to predict recurrent cis-regulatory modules

from known motifs. In Nucleic Acids Research,

36(13).

Johansson, O., Alkema, W., Wasserman, W. W.,

Lagergren, J., 2003. Identification of functional

clusters of transcription factor binding motifs in

genome sequences: the MSCAN algorithm. In

Bioinformatics, 19 Suppl 1.

Kel, A., Konovalova, T., Waleev, T., Cheremushkin, E.,

Kel-Margoulis, O., Wingender, E., 2006. Composite

Module Analyst: a fitness-based tool for

identification of transcription factor binding site

combinations. In Bioinformatics, 22(10).

Klepper, K., Sandve, G. K., Abul, O., Johansen, J.,

Drablos, F., 2008. Assessment of composite motif

discovery methods. In BMC Bioinformatics, 9.

Lebrecht, D., Foehr, M., Smith, E., Lopes, F. J. P.,

Vanario-Alonso, C. E., Reinitz, J., Burz, D. S., et al.,

2005. Bicoid cooperative DNA binding is critical for

embryonic patterning in Drosophila. In

Proceedings

of the National Academy of Sciences of the United

States of America, 102(37).

Maeda, T., Gupta, M. P., Stewart, A. F. R., 2002. TEF-1

and MEF2 transcription factors interact to regulate

muscle-specific promoters. In Biochemical and

Biophysical Research Communications, 294(4).

Makeev, V. J., Lifanov, A. P., Nazina, A. G.,

Papatsenko, D. A., 2003. Distance preferences in the

arrangement of binding motifs and hierarchical

levels in organization of transcription regulatory

information. In Nucleic Acids Research, 31(20).

Matys, V., Kel-Margoulis, O. V., Fricke, E., Liebich, I.,

Land, S., Barre-Dirrie, A., Reuter, I., et al., 2006.

TRANSFAC and its module TRANSCompel:

transcriptional gene regulation in eukaryotes. In

Nucleic Acids Research, 34.

Papatsenko, D., Goltsev, Y., Levine, M., 2009.

Organization of developmental enhancers in the

Drosophila embryo. In Nucleic Acids Research, 37,

no. 17.

Rabiner, L. R., 1989. A tutorial on hidden markov

models and selected applications in speech

BIOINFORMATICS 2012 - International Conference on Bioinformatics Models, Methods and Algorithms

recognition. In PROCEEDINGS OF THE IEEE, 77.

Sinha, S., van Nimwegen, E., Siggia, E. D., 2003. A

probabilistic method to detect regulatory modules. In

Bioinformatics, 19 Suppl 1.

Wasserman, W. W., Fickett, J. W., 1998. Identification

of regulatory regions which confer muscle-specific

gene expression. In Journal of Molecular Biology,

278(1).

Zhou, Q., Wong, W. H., 2004. CisModule: De novo

discovery of cis-regulatory modules by hierarchical

mixture modeling. In Proceedings of the National

Academy of Sciences of the United States of

America, 101(33).

A GENERALIZED HIDDEN MARKOV MODEL FOR PREDICTION OF CIS-REGULATORY MODULES IN

EUKARYOTE GENOMES AND DESCRIPTION OF THEIR INTERNAL STRUCTURE