THE DESIGN OF AN AUTONOMIC CONTROLLER FOR

SELF-MANAGED EMERGENCY DEPARTMENTS

Serene Almomen

and Daniel A. Menasc´e

Volgenau School of Engineering, George Mason University, 4400 University Drive, Fairfax,VA 22030, U.S.A.

Department of Computer Science, George Mason University, 4400 University Drive, Fairfax,VA 22030, U.S.A.

Keywords:

Autonomic computing, Healthcare, Emergency department, Quality of service, Length of stay, Self-managed

system, Simulation, Combinatorial search.

Abstract:

Improving the operational efﬁciency of an Emergency Department (ED) is a complex task due the very large

number of ED conﬁgurations that involve human and physical resources and due to the unpredictable nature

of the ED’s workload. Thus, managing the performance of EDs becomes difﬁcult and expensive when carried

out by human beings alone. A new approach, called self-managed EDs, consists of building into the ED the

mechanisms required to self-adjust the ED’s conﬁguration parameters so that its Quality of Service (QoS) is

constantly met. This paper presents the design of an autonomic controller for a self-managed Emergency De-

partment and evaluates its effectiveness in maximizing a utility function of the ED subject to cost-constraints.

The controller uses a combination of combinatorial search techniques with simulation models. Experimental

results illustrate the operation of the controller and how it reacts to variations of patient interarrival times.

1 INTRODUCTION

In hospitals all over the country, healthcare Emer-

gency Departments are known to be dynamic in na-

ture making them complex environments to manage.

The complexity stems from the sudden changes to the

workload of an ED due to emergencies such as ﬁre,

natural disasters, and terrorist attacks that are hard to

predict. An ED consists of both human (e.g., doctors,

nurses, and technicians) and physical (e.g., X-ray ma-

chines and CT-scan) resources and is one of the most

critical units in any healthcare organization. Therfore,

it is vital to improve its efﬁciency to increase patient

satisfaction and reduce operational cost.

Quality improvement principles and benchmark-

ing for EDs are increasingly becoming important for

the success of hospitals. Emergency physicians and

nurses are now being asked to provide safe, timely,

efﬁcient, and cost-effective care. Many QoS metrics

are currently being collected at EDs to proactively as-

sess performance and identify opportunities for qual-

ity improvement. These QoS metrics, also known as

Core Measures, can be time measures or proportion

measures (Welch et al., 2006). Time measures in-

clude arrival time to ﬁrst seen by a doctor, disposi-

tion to discharge, and overall patient length of stay

(LOS). Proportion measures include things like num-

ber of patients who left before they were supposed to,

hospital diversion, and ED patient ﬂow (ACEP,2010).

It is widely known that EDs suffer from crowding

problems that impact the performance and QoS pro-

vided to patients. Many studies have been conducted

to ﬁnd the cause of crowding in EDs and some solu-

tions have been suggested. For example, calculus and

chaos theory have been used to model ED crowding

and to identify variables and formulas that can pre-

dict when orderly patient ﬂow succumbs to crowd-

ing (Fields, 2003). In a related attempt, Asplin et.

al. (Asplin et al., 2003) present a conceptual model

that partitions ED crowding into three interdependent

components(input, throughput, and output) which ex-

ist within an acute care system that delivers unsched-

uled care. The goal of this model is to provide a prac-

tical framework to faciliate ED crowding solutions.

Another study used both log-rank tests and time-to-

wait (survival) proportional-hazard regression mod-

els to determine variables affecting ED QoS metrics

such as door-to-doctor and dwell times (Arkun et al.,

2009). Results showed that factors such as triage cat-

egory, ED occupancy, and day of the week contribute

to decreased patient ﬂow through the ED. Roberts

et. al. suggest the use of simulation modeling com-

bined with Six Sigma techniques to address issues of

length of stay (LOS) and patient satisfaction in the

174

Almomen S. and A. Menascé D..

THE DESIGN OF AN AUTONOMIC CONTROLLER FOR SELF-MANAGED EMERGENCY DEPARTMENTS.

DOI: 10.5220/0003737201740182

In Proceedings of the International Conference on Health Informatics (HEALTHINF-2012), pages 174-182

ISBN: 978-989-8425-88-1

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

ED (Roberts et al., 2006).

Managing the performance of complex environ-

ments, such as an ED, is difﬁcult and expensive when

carried out by human beings alone. A new approach,

called self-managed ED, is discussed here. The pa-

per discusses the mechanisms required to self-adjust

the conﬁguration parameters of an ED so that its QoS

goals are constantly met. In (Almomen and Menasc´e,

2011) we discussed the potential beneﬁts of apply-

ing autonomic computing (Huescher and McCann,

2008) techniques to design self-managed EDs. In

this paper we provide a detailed design of an au-

tonomic controller for a self-managed ED. Our ap-

proach combines an ED simulator with combinatorial

search techniques (Rayward-Smith et al., 1996) to de-

sign controllers that run periodically (e.g., every few

hours) to determine the best possible conﬁguration

for an ED given its current and predicted workload.

The paper also demonstrates the operation of the au-

tonomic controller as it maximizes a utility function

of the ED subject to cost-constraints.

The rest of the paper is organized as follows. Sec-

tion 2 presents the architecture and the algorithm used

by the ED controller of the self-managed ED. Section

3 presents the experimental setting and the next sec-

tion describes the results under various circumstances

to illustrate the operation of the method. Finally, Sec-

tion 5 presents some concluding remarks.

2 CONTROLLER APPROACH

Our framework, discussed initially in (Almomen and

Menasc´e, 2011), consists in developing an autonomic

controller for a self-managed ED system that can reg-

ulate and maintain itself with minimal human inter-

vention. This is ideal in an ED environment since the

goal is to create a system that is able to adapt to a con-

stantly changing environment (such as patient ﬂow,

workload, and resource availability) in a way that pre-

serves given operational goals (such as performance

goals or QoS goals).

2.1 The Control Loop

This framework, implements the MAPE-K (Monitor/

Analyze/ Plan/ Execute - Knowledge)model (Kephart

and Chess, 2003) in an ED environment as shown

in Fig. 1. Within the ED context, autonomic man-

agers deﬁne a control loop (the MAPE-K loop) that

continuously monitor the environment and handles

events that need action to be taken. Changes are

made through action operations. Sensors determine

the state of the managed ED resources and action

operations may change the current state. The entire

ED environment is a set of managed resources (e.g.,

doctors, nurses, lab technicians, X-ray machines, CT-

scan machines, beds). Autonomic managers contin-

uously monitor the system and record the values of

various performance metrics (e.g., Length of Stay,

throughput, and utilization of various resources). A

group of stakeholders (e.g., managers and executives)

deﬁne a utility function to be maximized. This func-

tion measures how well the ED is meeting its goals

and is a function of its various performance metrics.

For example, the utility of the ED decreases as the

Length of Stay (LOS) increases and increases as its

throughput increases. Based on the deﬁned utility

function, the autonomic manager then plans and ex-

ecutes any speciﬁc actions needed to maximize the

utility function and optimize pertinent QoS metrics.

The steps of monitoring, analyzing, planning, and ex-

ecuting may be executed concurrently.

It is worth noting that our model takes into account

the Human-in-the-loop(HITL) element (Parasuraman

et al., 2000) (see Fig. 1). This means that in order for

the ED autonomic manager to work sucessufully, hu-

man interaction is required. The resource in charge of

managing the ED, such as a charge nurse, will be part

of the decision making process of the autonomic man-

ager and will be able to change the outcome, or re-

conﬁguration commands, of the autonomic manager.

HITL is important in our model because we realize

that in the ED, an expert nurse can inﬂuence the out-

come of the system in a way that is difﬁcult if not im-

possible to autonomically reproduce exactly. HITL in

the ED environment also readily allows for the iden-

tiﬁcation of problems and requirements that may not

easily be identiﬁed by other means of the system. Uti-

lizing HITL provides a more realistic implementation

approach to a self-managed ED.

2.2 Architecture of the Controller

Figure 2 shows details of the autonomic manager in

an ED. The ED autonomic manager is based on the

notion that the ED is enhanced with an ED controller

that monitors the ED performance, monitors the re-

source utilization of the various resources of the ED,

and executes, at regular intervals called controller in-

tervals (CI), a controller algorithm to determine the

best conﬁguration for the ED. As a result of running

the controller algorithm, reconﬁguration options are

generated that will help charge nurses change the ED

conﬁguration to maintain optimal QoS. As shown in

Fig. 2, the ED controller has four main components:

Utility Function Computation, ED Simulator, Work-

load Analyzer, and Controller Driver.

THE DESIGN OF AN AUTONOMIC CONTROLLER FOR SELF-MANAGED EMERGENCY DEPARTMENTS

175

Figure 1: ED Autonomic Control Loop.

Figure 2: Architecture of the Autonomic Controller for the

ED.

The Utility Function Computation component col-

lects QoS metrics from the ED, such as resource uti-

lization and patient length of stay (LOS), to compute

the ED utility functions. The utility function is the

goal to be optimized by the controller. The Workload

Analyzer component analyzes the stream of arriving

patients and forecasts the workload intensity values

(e.g., average arrival rates) for the forthcoming peri-

ods. The predicted workload intensity values(1) com-

puted by this component are used as input parameters

to the ED Simulator. The ED Simulator receives re-

quests (2) from the Controller Driver to run the ED

Simulator corresponding for a speciﬁc conﬁguration

of the ED. The ED Simulator takes as input parame-

ters conﬁguration parameter values (2), and worload

intensity values (1). The output of the ED Simulator is

a resulting set of QoS values (3) for the conﬁguration

used as input by the Controller Driver. The Controller

Driver then sends a request (4) to the Utility Function

Computation component to compute the value of the

utility function for the QoS values obtained from the

ED Simulator. The corresponding value of the util-

ity function (5) is returned to the Controller Driver.

This last two steps are repeated for every point in each

neighborhood visited by the Controller Driver, which

executes a combinatorial search algorithm to deter-

mine the optimal conﬁguration for the ED.

At the begining of each controller interval, the

Controller Driver runs the combinatorial search en-

gine, which takes into account the desired utility func-

tion and performs a combinatorial search (e.g., beam

search or hill-climbing) (Rayward-Smith et al., 1996)

of the state space of possible conﬁguration points in

order to ﬁnd a near-optimal conﬁguration. The QoS

values have to be computed by the ED simulator for

each point in the space of conﬁguration points exam-

ined by the Controller Driver. Once the Controller

Driver determines the best conﬁguration for the work-

load intensity levels provided by the Workload Ana-

lyzer, it sends reconﬁguration commands to the ED.

The Control Parameters shown in Fig. 2 provide

for Controller Driver’s settings such as the maximum

number of conﬁguration points to be searched before

the search engine stops and the length of the controller

interval (CI).

2.3 Combinatorial Search Engine

This section describes the combinatorial search al-

gorithm used by the ED Controller. This algo-

rithm, which is based on hill-climbing (Rayward-

Smith et al., 1996), is used to obtain a near-optimal

conﬁguration

C = (c

,...,c

) for the ED without per-

forming an exhaustive search of the space of all pos-

sible conﬁgurations.

We consider that the patients that arrive at the ED

are categorized into tracks according to the resources

they need and their workﬂow through the ED.

Let

W be the vector of workload intensity (e.g.,

patient average arrival rate) values for each track. Let

curr

be the vector of current conﬁguration parameters

for the ED and let

ﬁn

be the vector of ﬁnal conﬁgu-

HEALTHINF 2012 - International Conference on Health Informatics

176

ration parameters for the ED determined by the com-

binatorial search algorithm. In the example described

here, a conﬁguration vector

C is a tuple (n,d,t) where

n is the number of nurses, d the number of doctors,

and t the number of lab technicians.

Let U(

Q) = f(

W ,

C) be the value of the utility of

the ED as a function of a vector

Q of QoS values for

the ED. The values in

Q for a given conﬁguration

and workload intensity vector

W are computed by a

function f, which implements a simulation of the ED.

In the example presented in this paper, we use LOS as

the single QoS metric. Thus,

Q = (LOS).

The utility function, U(LOS), used in this paper

follows a sigmoid curve of the type

U(LOS) = K

α (β−LOS)

1+ e

α (β−LOS)

(1)

where K is a normalizing factor equal to

K = (1+ e

αβ

)/e

αβ

(2)

and β is the QoS goal for the LOS, which is equal to

90 minutes in our experiments, and α is a sensitivity

parameter that deﬁnes the sharpness of the curve. Sig-

moids are commonly used as utility functions when

the QoS metric is LOS or response time. We used

α = 0.05 in our experiments. Note that the utility is a

dimensionless quantity in the interval [0, 1].

Figure 3 depicts U(LOS) according to Eq. (1) and

the parameters deﬁned above. As it can be seen, the

utility is 1 when the LOS is zero. As the LOS in-

creases, the utility decreases asymptotically to zero.

When the LOS is equal to its QoS goal, the utility is

equal to 0.5. Note that any other utility function de-

ﬁned by the stakeholders could be used.

0.0

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

1.0

120

160

200

Utility

Length of Stay (in minutes)

Figure 3: Utility as a function of Length of Stay (in min-

utes).

Each conﬁguration

C has a cost C (

C) associated

to it. The optimization problem implemented by the

combinatorial search engine can be formally deﬁned

Maximize U(LOS) = f(

W ,

s.t.

C (

C) ≤ COST

max

min

≤ c

max

···

min

≤ c

max

Hill-climbing works by analyzing the neighboring

conﬁgurations of a conﬁguration being visited, deter-

mining the one with the highest utility, and moving

to that point as the next point to visit. Let N (

C) be

the set of neighbors of conﬁguration

C in the space of

possible conﬁgurations for the ED.

Typically, a neighbor of a given conﬁguration is

deﬁned by a small perturbation in one of the elements

of that conﬁguration (e.g., increasing or decreasing

by one the number of nurses of a given type). In

our example, the neighbors of a conﬁguration (n,d,t)

are (n ⊕ 1, d,t), (n⊖ 1,d,t), (n,d ⊕ 1,t), (n, d ⊖ 1,t),

(n,d,t ⊕ 1), and (n, d,t ⊖ 1). The operator ⊕ is de-

ﬁned as x ⊕ 1 ← x + 1 if x < x

max

else x ← x

min

. In

other words, the addition wraps around to x

min

. Sim-

ilarly, ⊖ is deﬁned as x ⊖ 1 ← x − 1 if x > x

min

else

x ← x

max

The search engine algorithm is given below.

• Step 1: (Initialization): NumIterations ← 0;

C ←

curr

; U ← f(

W ,

C).

• Step 2: Find the conﬁguration

max

that has the

largest utility among the conﬁgurations in {

C ∈

N (

C) | C (

C) ≤ COST

max

• Step 3: U

max

← f(

W ,

max

)

• Step 4: If U

max

> U then

{

C ←

max

;

U ← U

max

}

Else {

ﬁn

←

C; Stop};

• Step 5: NumIterations ← NumIterations + 1;

• Step 6: If NumIterations < MaxIterations then go

to Step 2 else

ﬁn

←

The function f, i.e., the ED simulation, has to be

run as many times as the number of points visited in

the search space. This number is roughly equal to

MaxIterations ×

N, where

N is the average size of a

neighborhood of a point in the conﬁguration space.

Assuming that each of the p parameters of a point

in the conﬁguration space can vary in two possible

ways,

N can be estimated as 2× p. One can reduce

the number of times the simulation has to be run by

THE DESIGN OF AN AUTONOMIC CONTROLLER FOR SELF-MANAGED EMERGENCY DEPARTMENTS

177

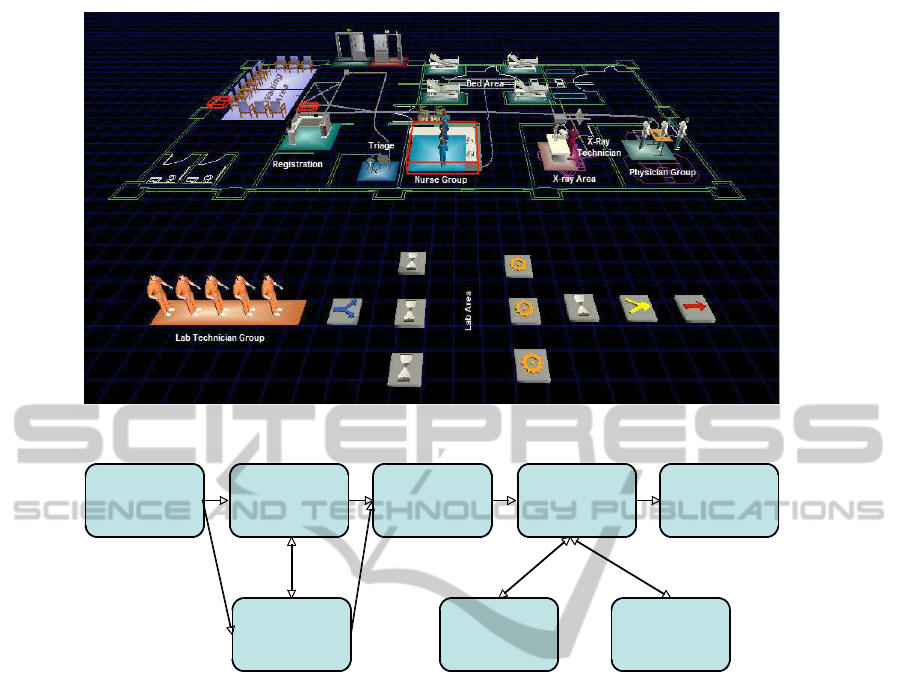
Figure 4: Simulated Emergency Department.

Patient Arrival

Area

Registration

Area

Triage

Area

Bed

Area

Patient

Exit Area

Waiting

Room Area

X-Ray

Area

Lab

Area

Figure 5: ED Model - Patient Workﬂow.

storing the results of simulation runs in a hash table

indexed by the conﬁguration. This avoids re-running

the simulation when a point is visited more than once,

which occurs when neighborhoods overlap.

3 THE EXPERIMENTAL

SETTING

In order to illustrate the operation of the controller de-

scribed above, we developed an ED simulation model

combined with a combinatorial search technique. Our

experiment uses Flexsim HC Simulation Software

(see www.ﬂexsim. com/products/healthcare/) to sim-

ulate an Emergency Department (ED) that consists of

a ﬁnite number of resources including beds, nurses,

doctors, lab technicians, imaging machines, and labs

(see Fig. 4). No patient is rejected from being seen

in the ED. Arriving patients are required to register at

check in.

A triage nurse performs a preliminary assessment

of each ED patient. If no nurse is available, the patient

waits in the waiting area. After triaging, an available

staff nurse escorts the patient to the treatment area of

the ED. If the treatment area is full, the patient waits

in the triage area until the next room is available. In

the treatment area, the patient is seen by a physician

and a staff nurse for diagnosis. The ED patient ﬂow

is depicted in Fig. 5. Our experiment considers three

patient tracks. A track is an easy way to break patients

into different types that deﬁne possible pathways in

the course of an ED visit. The different tracks are

identiﬁed by the type of tests and/or screening, if any,

the patient will need to take.

More speciﬁcally, the tracks considered here are:

• Basic: Patients in this track are discharged after

being treated without the need for X-Ray screen-

ing or lab tests.

• X-Ray: Patients in this track need X-Ray screen-

ing before being discharged.

• X-Ray and Lab Test: Patients in this track need

both X-Ray screening and three lab tests before

being discharged.

The length of stay (LOS) for each patient can

HEALTHINF 2012 - International Conference on Health Informatics

178

Table 1: Initial Resource Settings.

Resource Value

Nurse group 4

Physician group 3

Lab Technician group 5

X-ray Technician group 1

Bed 4

X-ray machine 1

Labs 3

Table 2: Workload characteristics for the three tracks for

experiments 1 and 2.

Track Routing Interarrival

Probability Time (min)

Experiment 1

Basic 60% 40

X-ray 20% 45

X-Ray & Lab Test 20% 50

Experiment 2

Basic 60% 30

X-ray 20% 35

X-Ray & Lab Test 20% 40

therefore be broken down into the waiting time at the

waiting area, triage station, treatment area, and X-Ray

or Lab (if required). Again, the LOS is the QoS met-

ric measured in our experiment and used to calculate

the utility function U(LOS) to determine the optimal

conﬁguration of the ED. Additionally, we run the sim-

ulation with two different interarrival times (low and

high intensity) and compare the results of the opti-

mal ED conﬁguration to illustrate our approach under

varying interarrival times. The intearrival times and

patient routing probabilities for the different tracks in

each experiment are shown in Table 2.

In our experiment, we also assume that the num-

ber of X-ray technicians, beds, X-ray machines and

labs is constant. Thus, the three conﬁgurable param-

eters to be changed by the contorller are the values of

n, d, and t. The conﬁgurable parameters (n,d,t) of

the ED simulator are consequently adjusted dynam-

ically at the end of every controller interval so that

the utility is maximized. In addition, COST

max

is set

as $6,000.00/hr based on the following industry av-

erage fully loaded hourly rates: $75.00/hr for nurses,

$250.00/hr for ED doctors, $30.00/hr for lab techni-

cian. In Flexsim Simulation, the Stafﬁng Cost is cal-

culated as:

∑

∀ staff

StaffPayRate ×(StaffTravelTime+

StaffServiceTime). (3)

According to Eq. (3), the hourly cost of the ED is

a function of the time spent by its staff serving pa-

tients and therefore a function of the patient vol-

ume (Bamezai et al., 2005).

The initial values of the resources are shown in

Table 1. The conﬁgurable parameters of the tuple

(n,d,t) are also limited by the following [min, max]

values:

• Nurse: n ∈ [2,4]

• Physician d ∈ [1,3]

• Technician t ∈ [3,5]

Consequently the state space of possible conﬁgu-

rations consists of N × D× T points where N,D, and

T are, respectively, the possible number of nurses,

physicians, and technicians. In our small example,

the size of the state space is 3 × 3× 3 = 27. In gen-

eral, the state space can be much larger as the number

of controllable resources and the number of possible

instances of these resources grows.

4 RESULTS

This section shows the results of the execution of the

ﬁrst two iterations of the ED controller algorithm dis-

cussed in section 2.3 for two experiments that have

different interarrival times for the three tracks (see Ta-

ble 2). The percentage of patients in each track is the

same in both experiments but the interarrival times are

lower for experiment 2, which indicates a higher traf-

ﬁc intensity. The warmup time for the experiments

was set to 60 minutes and the ED simulator simulates

24 hours, or a full day, in the modeled ED. Each con-

ﬁguration point was replicated 40 times in the simu-

lator to achieve maximum accuracy and repeatability.

Simulation results are reported with 95% conﬁdence

intervals. We assume that COST

max

= $6,000.00/hr.

Table 3 shows the results of the controller’s ﬁrst it-

eration for Experiment 1 (total arrivalrate of about 1.4

patients/hr) using the controller algorithm discussed

above. Based on the algorithm, the optimal U(LOS)

value for this iteration is for conﬁguration (4, 2,5).

However, due to the COST

max

constraint of $6,000/hr,

this conﬁguration is not feasible according to Eq. (3).

Consequently, based on both the U(LOS) value and

theCOST

max

constraint, the optimal ED conﬁguration

is actually (3, 3,5), which means three nurses, three

doctors, and ﬁve lab technicians. Using this new con-

ﬁguration as the starting point for the second iteration

(Iteration 1) of Experiment 1, we obtain the values

in Table 4. The table shows that the optimal conﬁg-

uration for the ED remains at (3, 3,5) with a cost of

$5,785.00/hr. The average LOS for this conﬁguration

is 54 minutes and the 95% conﬁdence interval for the

LOS is [51 minutes, 57 minutes].

THE DESIGN OF AN AUTONOMIC CONTROLLER FOR SELF-MANAGED EMERGENCY DEPARTMENTS

179

Table 3:

, LOS, utility values, and cost for experiment 1.

n d t LOS (min) U(LOS) Cost ($/hr) Feasible

4 3 5 56± 3.5 0.963 $6,044.00 ×

3 3 5 54± 3.0 0.967 $5,785.00 X

2 3 5 66± 5.5 0.939 $6,155.00 ×

4 2 5 53± 2.5 0.968 $6,027.00 ×

4 1 5 58± 3.5 0.959 $4,951.00 X

4 3 4 59± 4.5 0.957 $5,993.00 X

4 3 3 57± 3.5 0.961 $5,971.00 X

Table 4:

, LOS, utility values, and cost for experiment 1.

n d t LOS (min) U(LOS) Cost ($/hr) Feasible

3 3 5 54± 3.0 0.868 $5,785.00 X

2 3 5 66± 5.5 0.777 $6,155.00 ×

4 3 5 56± 3.5 0.855 $6,044.00 ×

3 2 5 58± 3.5 0.841 $5,357.00 X

3 1 5 58± 3.5 0.841 $6,003.00 ×

3 3 4 57± 3.5 0.848 $6,053.00 ×

3 3 3 55± 3.5 0.861 $6,061.00 ×

Experiment 2 has an increased total workload in-

tensity of about 1.8 patients/hr. Iteration 0 of the ED

Controller for this experiment suggests an optimal

conﬁguration of (4, 1,5) with a cost of $5,975.00/hr

(see Table 5). Iteration 1 provides an improved con-

ﬁguration of (3,1, 5) with a cost of $5,521.00/hr (see

Table 6). The average LOS for this conﬁguration is 79

minutes and the 95% conﬁdence interval for the LOS

is [69 minutes, 89 minutes]. Note that the 95% con-

ﬁdence interval for the (4, 1,5) conﬁguration is [76

minutes, 96 minutes]. These two conﬁgurations are

not statistically different in terms of LOS at the 95%

level because the average LOS of one conﬁguration

falls in the conﬁdence interval of the other and vice

versa (Jain, 1991). However, conﬁguration (3,1,5) is

preferable because it uses one less nurse and is less

expensive.

Figure 6 shows other details for the optimal con-

ﬁguration for Experiment 2: patient throughput per

track (i.e., number of patients in each track processed

by the ED during the day), the evolutionof throughput

over time, the evolution of the number of patients in

each track at each hour of the day, and the utilization

of various resources (nurse group, physician group,

X-ray technicians, and lab technicians).

As shown in Table 7, the ED Controller was able

to ﬁnd an optimal conﬁguration in Experiment 1 that

consists of only one nurse less than the maximum

number of nurses available and has an average LOS

that is lower than the desired LOS of 90 minutes. The

cost of this conﬁguration is 4% lower than the initial

conﬁguration that uses the maximum ED resources.

The ED Controller was able to ﬁnd in the second

iteration of Experiment 2 an optimal conﬁguration for

the higher intensity workload that is still below the

desired LOS goal and at the same time allows a 27%

cost saving with respect to the cost $7,588.00 of the

initial conﬁguration (4,3,5) for that experiment (see

Table 5).

We only showed two iterations of the controller

in this paper to illustrate its operation. In practice,

the controller will run until the maximum number of

iterations is achieved or until it cannot ﬁnd a better

solution.

5 CONCLUDING REMARKS

Deciding on the best ED conﬁguration given the

ED resource limitations, cost constraints, and unpre-

dictable workload is a complex task. It is extremely

difﬁcult for human beings to solve problems of such

complexity. Consequently, using the proposed self-

managed ED to assist charge nurses with the decision

making process and managing EDs efﬁciently may

prove to be advantageous.

This paper provides a novel use for a controller-

based autonomic system to implement a self-managed

ED that can help improve the ED’s performance. This

autonomic system is effective in providing best con-

ﬁguration parameters for EDs subject to cost con-

straints and varying workloads. The experiments re-

ported in this paper clearly show the effectiveness of

combining combinatorial search techniques with sim-

HEALTHINF 2012 - International Conference on Health Informatics

180

Table 5:

, LOS, utility values, and cost for experiment 2.

n d t LOS (min) U(LOS) Cost ($/hr) Feasible

4 3 5 81± 8.5 0.617 $7,558.00 ×

3 3 5 80± 7.7 0.629 $7,468.00 ×

2 3 5 114± 13 0.234 $7,642.00 ×

4 2 5 92± 14 0.480 $7,511.00 ×

4 1 5 86± 10 0.556 $5,975.00 X

4 3 4 87± 8.5 0.543 $7,683.00 ×

4 3 3 87± 11 0.543 $7,469.00 ×

Table 6:

, LOS, utility values, and cost for experiment 2.

n d t LOS (min) U(LOS) Cost ($/hr) Feasible

4 1 5 86± 10 0.556 $5,975.00 X

3 1 5 79± 10 0.641 $5,521.00 X

2 1 5 100± 12 0.382 $5,205.00 X

4 3 5 81± 8.5 0.617 $7,558.00 ×

4 2 5 92± 14 0.480 $7,511.00 ×

4 1 4 83± 9.5 0.593 $5,315.00 X

4 1 3 90± 13.5 0.506 $5,434.00 X

Table 7: Comparison of experiments 1 and 2.

Experiment Optimal Con-

ﬁguration

(n,d,t)

LOS (in min) U(LOS) Cost ($/hr)

1 (3,3,5) 54 ± 3 0.868 $5,785.00

2 (3,1,5) 79 ± 9 0.641 $5,521.00

Figure 6: Experiment 2 - ED Optimal Conﬁguration QoS.

THE DESIGN OF AN AUTONOMIC CONTROLLER FOR SELF-MANAGED EMERGENCY DEPARTMENTS

181

ulation models when used for QoS control. Not only

is the controller able to ﬁnd the optimal conﬁguration,

but it does fast enough to afford its utilization in real-

world settings to maintain optimal ED QoS metrics.

In fact, simulating 40 replicas of one conﬁguration

takes approximately 70 seconds on a 1.73-GHz Intel

Core i7 processor.

We are currently working on implementing the re-

sults of this paper in a real-world ED and analyzing

the controller’s effectiveness under cost constraints

and actual varying patient arrival rates.

ACKNOWLEDGEMENTS

The authors would like to thank FlexSim Software

Products, Inc. for providing the FlexSim Healthcare

Simulation software to complete this research. In par-

ticular, the support of Mr. Roger Hullinger and his

team at FlexSim Software Products is highly appreci-

ated.

REFERENCES

ACEP (2010). Meeting the challenge of emergency de-

partment overcrowding/boarding. American College

of Emergency Physicians.

Almomen, S. and Menasc´e, D. (2011). An autonomic com-

puting framework for self-managed emergency de-

partments. In International Health Informatics Con-

ference, Rome.

Arkun, A., Briggs, W. M., Patel, S., Datillo, P. A., Bove, J.,

and Birkhahn, R. H. (2009). Emergency department

crowding: Factors inﬂuencing ﬂow. Western Journal

of Emergency Medicine, pages 10–15.

Asplin, B. R., Magid, D. J., Rhodes, K. V., Solberg, L. I.,

Lurie, N., and Camargo, C. A. (2003). A conceptual

model of emergency department crowding. Annuals

of Emergency Medicine, pages 173–180.

Bamezai, A., Melnick, G., and Nawathe, A. (2005). The

cost of an emergency department visit and its rela-

tionship to emergency department volume. American

College of Emergency Physicians, pages 483–490.

Fields, W. W. (2003). Calculus, chaos, and other models of

emergency department crowding. Annuals of Emer-

gency Medicine, pages 181–184.

Huescher, M. C. and McCann, J. A. (2008). A survey of

autonomic computing: Degrees, models,and applica-

tions. ACM Computing Surveys, pages 1–28.

Jain, R. (1991). The Art of Computer System Performance

Evaluation. John Wiley & Sons, New York.

Kephart, J. and Chess, D. (2003). The vision of autonomic

computing. IEEE Internet Computing, pages 41–50.

Parasuraman, R., Sheridan, T. B., and Wickens, C. D.

(2000). A model for types and levels of human in-

teraction with automation. IEEE Systems, Man, and

Cybernetics Society, 30:286–297.

Rayward-Smith, V., Osman, I., and Reeves, C. (1996).

Modern Heuristic Search Methods. John Wiley &

Sons.

Roberts, L., Johnson, D. C., Shanmugam, D. R., Malho-

tra, S., Zinkgraf, D. S., Young, M., Putnam, J., and

Cameron, L. (2006). Computer simulation and six-

sigma tools applied to process improvement in an

emergency department. Institue of Industrial Engi-

neers Society for Health Systems.

Welch, S., Augustine, J., Camargo, C. A., and Reese, C.

(2006). Emergency department performance mea-

sures and benchmarking summit. Academic Emer-

gency Medicine, pages 1074–1080.

HEALTHINF 2012 - International Conference on Health Informatics

182