
A SEARCH-BASED APPROACH TO ANNEXATION AND MERGING
IN WEIGHTED VOTING GAMES
Ramoni O. Lasisi and Vicki H. Allan
Department of Computer Science, Utah State University, Logan, U.S.A.
Keywords:
Agents, Weighted voting games, Power indices, False-name manipulation, Annexation, Merging.
Abstract:
Weighted voting games are classic cooperative games which provide a compact representation for coalition
formation models in multiagent systems. We consider manipulation in weighted voting games via annexation
and merging, which involves an agent or some agents misrepresenting their identities in anticipation of gaining
more power at the expense of other agents in a game. We show that annexation and merging in weighted voting
games can be more serious than as presented in the previous work. Specifically, using similar assumptions as
employed in a previous work, we show that manipulators need to do only a polynomial amount of work
to find a much improved power gain, and then present two search-based pseudo-polynomial algorithms that
manipulators can use. We empirically evaluate our search-based method for annexation and merging. Our
method is shown to achieve significant improvement in benefits for manipulating agents in several numerical
experiments. While our search-based method achieves improvement in benefits of over 300% more than those
of the previous work in annexation, the improvement in benefits is 28% to 45% more than those of the previous
work in merging for all the weighted voting games we considered.
1 INTRODUCTION
False-name manipulation in weighted voting games
(WVGs), which involves an agent or some agents
misrepresenting their identities in anticipation of
power increase, has been identified as a problem. This
is because the anticipated power gain by manipulat-
ing agents is at the expense of other agents in the
game. The menace can take different forms. With an-
nexation, an agent, termed, an annexer, takes over the
voting weights of some agents in a game. Power is not
shared with the annexed agents. Forming an alliance
or merging involves voluntary merging of weights by
two or more agents to form a single bloc (Machover
and Felsenthal, 2002; Aziz et al., 2011; Lasisi and Al-
lan, 2011). Merged agents expect to be compensated
with their share of the power gained by the bloc. The
agents whose voting weights are taken over or merged
into a bloc are referred to as assimilated agents. When
agents engage in these manipulations, it becomes dif-
ficult to establish or maintain trust, and more impor-
tantly it becomes difficult to assure fairness in such
games.
WVGs are classic cooperative games which pro-
vide a compact representation for coalition formation
models in multiagent systems. Each agent in a WVG
has an associated weight. A subset of agents whose
total weight meets or exceeds a specified quota is
called a winning coalition. The weights of agents in a
game correspond to resources or skills available to the
agents, while the quota is the amount of resources or
skills required for a task to be accomplished. For ex-
ample, in search and rescue, robotic agents put their
resources (i.e., weights) together in large natural dis-
aster environments to reach the necessary levels (i.e.,
quota) to save life and property.
We are concerned with the ways in which agents
that complete a task are compensated from their
jointly derived payoff, taking into account each
agent’s resource (weight) contribution. The relative
power of each agent reflects its significance in the
elicitation of a winning coalition. Although a larger
weight by an agent makes it more likely that an agent
can affect the outcome of a WVG, the weight of an
agent in a game is not always proportional to its power
(Aziz et al., 2011). A widely accepted method for
measuring such relative power in WVGs uses power
indices. The two best-known and most used indices
for measuring power in WVGs are Shapley-Shubik
(Shapley and Shubik, 1954) and Banzhaf (Banzhaf,
1965) power indices.
WVGs can be viewed as a form of competi-
tion among agents to share the available fixed power
whose total value is always assumed to be 1. Agents
44
O. Lasisi R. and H. Allan V..
A SEARCH-BASED APPROACH TO ANNEXATION AND MERGING IN WEIGHTED VOTING GAMES.
DOI: 10.5220/0003741300440053
In Proceedings of the 4th International Conference on Agents and Artificial Intelligence (ICAART-2012), pages 44-53
ISBN: 978-989-8425-96-6
Copyright
c
2012 SCITEPRESS (Science and Technology Publications, Lda.)

may thus resort to a form of false-name manipula-
tion (annexation or merging) to improve their influ-
ence in anticipation of gaining more power. This pa-
per continues the work studied originally by (Ma-
chover and Felsenthal, 2002), (Aziz et al., 2011), and
(Lasisi and Allan, 2011) on annexation and merging
in WVGs. We extend the framework of (Lasisi and
Allan, 2011) on susceptibility of power indices to an-
nexation and merging in WVGs to consider a much
improved power gain or benefit for manipulators.
Consider a WVG of n agents. The simulation of
(Lasisi and Allan, 2011) for annexation and merging
is based on a random approach where some agents,
say k < n, in the game are randomly selected to
be assimilated in annexation, and to form a volun-
tary bloc of manipulators in merging. This simple
random approach shows that on average, annexa-
tions can be effective for manipulators using both the
Shapley-Shubik and Banzhaf power indices to com-
pute agents’ power. Their results also show that merg-
ing only has a minor effect on the power gained for
manipulators using the Shapley-Shubik index, while
it is typically non-beneficial (i.e., no power is gained)
for manipulators using the Banzhaf index. We note
that randomly selecting the k agents to be assimilated
for both annexation and merging this way fails to con-
sider the benefits of a more strategic approach.
We show that manipulation via annexation and
merging can be more serious than as presented in
the previous work. Specifically, we show, using sim-
ilar assumptions for annexation and meging as em-
ployed in the simple random simulation of (Lasisi
and Allan, 2011), that manipulators need to do only a
polynomial amount of work to find a much improved
power gain during manipulation. Given that the prob-
lem of computing the Shapley-Shubik and Banzhaf
power indices of agents is already NP-hard, and only
pseudo-polynomial or approximation algorithms are
available to compute agents’ power, we then present
two search-based pseudo-polynomialtime algorithms
that manipulators can use to find a much improved
power gain. Furthermore, for reasons of efficiency, we
do not implement the two algorithms exactly. Rather,
we employ informed heuristic search strategies to
complement the performance of the algorithms, while
taking into consideration the two power indices in the
design of the heuristics.
We empirically evaluate our search-based method
for annexation and merging. Our method is shown
to achieve significant improvement in benefits over
previous work for manipulating agents in several nu-
merical experiments. Thus, unlike the simple random
simulation of (Lasisi and Allan, 2011) where merging
has little or no benefits for manipulators using both
the Shapley-Shubik and Banzhaf indices, results from
our experiments suggest that manipulation via merg-
ing can be highly effective for manipulators. The sim-
ple random approach to manipulation via annexation
and merging seems unintelligent, thus, it is imprac-
tical that strategic agents would be keen in employ-
ing such method. In view of this, we modify the sim-
ple random approach to select the best power gain or
benefit from three random choices (which we refer to
as best-of-three) and compare with our search-based
method. We note that this simple modification pro-
vides higher average benefits to the manipulators than
those of the simple random approach.
The remainder of the paper is organized as fol-
lows. Section 2 provides some preliminaries. Section
3 demonstrates examples of annexation and merg-
ing in WVGs. We present our search-based approach
to annexation and merging in Section 4. In Section
5, we consider informed heuristic search strategies
to complement the performance of the search-based
method. In Section 6, we present results of empirical
evaluation of our search-based method. Section 7 dis-
cusses related work. We conclude in Section 8.
2 PRELIMINARIES
2.1 Weighted Voting Games
Let I = {1, ··· , n} be a set of n agents and the cor-
responding positive weights of the agents be w =
{w
1
, · ·· , w
n
}. Let a coalition S ⊆ I be a non-empty
subset of agents. A WVG G with quota q involving
agents I is represented as G = [w
1
, · ·· , w
n
;q]. Denote
by w(S), the weight of a coalition, S, derived as the
summation of the weights of agents in S, i.e., w(S) =
∑
j∈S
w
j
. A coalition, S, wins in game G if w(S) ≥ q,
otherwise it loses. WVGs belong to the class of simple
voting games. In simple voting games, each coalition,
S, has an associated function v : S → {0, 1}. The value
1 implies a win for S and 0 implies a loss. So, v(S) = 1
if w(S) ≥ q and 0 otherwise.
2.2 Power Indices
We provide brief descriptions of the two power
indices we use in computing agents’ power in
WVGs. For further discussion, we refer the reader to
(Felsenthal and Machover, 1998; Laruelle, 1999).
Shapley-Shubik Power Index
The Shapley-Shubik index quantifies the marginal
contribution of an agent to the grand coalition (i.e.,
A SEARCH-BASED APPROACH TO ANNEXATION AND MERGING IN WEIGHTED VOTING GAMES
45

a coalition of all the agents). Each permutation (or or-
dering) of the agents is considered. We term an agent
to be pivotal in a permutation if the agents preceding
it do not form a winning coalition, but by including
this agent, a winning coalition is formed. Shapley-
Shubik index assigns power to each agent based on
the proportion of times it is pivotal in all permuta-
tions. We specify the computation of the power in-
dex using notation of (Bachrach et al., 2010). Denote
by π a permutation of the agents, so π : {1, . . . , n} →
{1, . . . , n}, and by Π the set of all possible permuta-
tions. Denote by S
π
(i) the predecessors of agent i in
π, i.e., S
π
(i) = { j : π( j) < π(i)}. The Shapley-Shubik
index, ϕ
i
(G), for each agent i in a WVG G is
ϕ
i
(G) =
1
n!
∑
π∈Π
[v(S
π
(i) ∪ {i}) − v(S
π
(i))]. (1)
Banzhaf Power Index
The Banzhaf power index bases power on an agent
being able to turn a losing coalition into a winning
coalition by its vote. An agent i ∈ S is referred to as
being critical in a winning coalition, S, if w(S) ≥ q
and w(S\{i}) < q. The Banzhaf power index compu-
tation for an agent i is the proportion of times i is crit-
ical compared to the total number of times any agent
in the game is critical. The Banzhaf index, β
i
(G), for
each agent i in a WVG G is given by
β
i
(G) =
η
i
(G)
∑
j∈I
η
j
(G)
(2)
where η
i
(G) is the number of coalitions for which
agent i is critical in G.
2.3 Annexation and Merging
Let G be a WVG. Let Φ be any of Shapley-Shubik or
Banzhaf power indices. We denote the power index of
an agent i in G by Φ
i
(G). Also, consider a coalition
S ⊆ I, we denote by &S a bloc of assimilated voters
formed by agents in S. We say that a power index
Φ is susceptible to manipulation whenever a WVG
G is altered by an agent i (in the case of annexation
or some agents in the case of merging) and such that
there exists a new game G
′
where Φ
i
(G
′
) > Φ
i
(G). In
other words, Φ is susceptible to manipulation when
the power index of the agent in the altered game is
more than its power index in the original game.
Definition 1. (Manipulation by Annexation).
Let agent i alter game G by annexing a coalition S
(i assimilates the agents in S to form a bloc &(S ∪
{i})). We say that Φ is susceptible to manipula-
tion via annexation if there exists a new game G
′
such that Φ
&(S∪{i})
(G
′
) > Φ
i
(G); the annexation is
termed advantageous. The factor of increment by
which the annexer gains is given by
Φ
&(S∪{i})
(G
′
)
Φ
i
(G)
. If
Φ
&(S∪{i})
(G
′
) < Φ
i
(G), then the annexation is disad-
vantageous.
Definition 2. (Manipulation by Merging).
Let a manipulators’ coalition, S, alter G by merging
into a bloc &S. We say that Φ is susceptible to ma-
nipulation via merging if there exists a new game
G
′
such that Φ
&S
(G
′
) >
∑
j∈S
Φ
j
(G); the merging
is termed advantageous. The factor of increment by
which the manipulators gain is given by
Φ
&S
(G
′
)
∑
j∈S
Φ
j
(G)
. If
Φ
&S
(G
′
) <
∑
j∈S
Φ
j
(G), then the merging is disad-
vantageous. The agents in a bloc formed by merging
are assumed to be working cooperatively and have
transferable utility. For the sake of simplicity in our
analysis, we also refer to the factor of increment as
power gain or benefit.
3 EXAMPLES OF ANNEXATION
& MERGING IN WVGs
We provide examples to illustrate annexation and
merging in WVGs. We have used Banzhaf power in-
dex as a reference for these examples. The annexer
and assimilated agents are all shown in bold.
Example 1. (Manipulation by Annexation).
Let G = [12, 16, 18, 19, 23, 26, 43, 46, 50;195] be a
WVG. The power index of agent 1 with weight 12
is β
1
(G) = 0.026. Suppose the agent annexes agents
3 and 4 with weights 18 and 19. An assimilated
bloc of weight 49 is formed in the new game G
′
=
[49, 16, 23, 26, 43, 46, 50;195]. The new power index
of the annexer β
1
(G
′
) = 0.177 > β
1
(G). The agent
gains from the annexation and increases its power in-
dex by a factor of
0.177
0.026
= 6.81.
Example 2. (Manipulation by Merging).
Let G = [12, 16, 18, 19, 23, 26, 33, 40, 45;155] be a
WVG. The last four agents in the game are des-
ignated as would-be manipulators. The Banzhaf
power indices of these agents are: β
6
(G) = 0.116,
β
7
(G) = 0.142, β
8
(G) = 0.174, and β
9
(G) =
0.200. So,
∑
9
j=6
β
j
(G) = 0.632. Suppose the agents
decide to merge their weights. A merged bloc of
weight 144 is formed in the new game G
′
=
[12, 16, 18, 19, 23, 144;155]. The power index of the
bloc β
6
(G
′
) = 0.861 > 0.632. The manipulators gain
ICAART 2012 - International Conference on Agents and Artificial Intelligence
46

from the merging and increase their power indices by
a factor of
0.861
0.632
= 1.36.
There exist examples where the two forms of ma-
nipulation may not be beneficial using the two power
indices. However, (Machover and Felsenthal, 2002)
haveshownthat, in the case of annexation, it is always
beneficial for an annexerto assimilate other agents us-
ing Shapley-Shubik power index.
4 SEARCH-BASED APPROACH
TO ANNEXATION & MERGING
4.1 Overview
As noted in the introduction, randomly selecting
agents to be assimilated in annexation, or to form a
voluntary bloc in merging fails to consider the ben-
efits of a more strategic approach to false-name ma-
nipulation. In this section, we extend the simple ran-
dom simulation of (Lasisi and Allan, 2011) for annex-
ation and merging in WVGs. We propose a search-
based approach for the two forms of manipulation
(annexation and merging) using the Shapley-Shubik
and Banzhaf indices to compute agents’ power.
In considering our search-based approach to an-
nexation and merging, we have implemented two
pseudo-polynomial manipulation algorithms, one for
each form of manipulation. To begin with, we recall
that the problem of calculating the Shapley-Shubik in-
dices and Banzhaf indices for WVGs is NP-hard, and
both admit pseudo-polynomial algorithms using dy-
namic programming (Matsui and Matsui, 2000; Mat-
sui and Matsui, 2001) or generating functions (Brams
and Affuso, 1976; Bilbao et al., 2000) assuming the
weights of agents in the games are polynomial in the
number of agents.
Given that computing the two power indices is
already NP-hard, and only pseudo-polynomial or
approximation algorithms are available to compute
agents’ power, it is reasonable that the manipulation
algorithms we propose are also pseudo-polynomial
since we necessarily need to use these power in-
dices in computing agents’ benefits during manipu-
lation. (Aziz et al., 2011) have also shown that deter-
mining if there exists a beneficial merge is NP-hard
using either the Shapley-Shubik or Banzhaf power in-
dices. The same is true for determining the existence
of beneficial annexation using the Banzhaf index.
4.2 Manipulation Algorithm for
Merging
The brute force approach to determine a coalition
that yields the most improved benefit in merging in
a WVG is to simply enumerate all the possible coali-
tions of agents in the game and compute for each of
these coalitions its benefit. We can then output the
coalition with the highest value. Unfortunately, enu-
merating all the possible coalitions is exponential in
the number of agents. Also, computing the power in-
dices (to determine the factor of increment of each
coalition) naivelyfrom their definitions means that we
have two exponential time problems to solve. We pro-
vide an alternative approach.
Let procedure PowerIndex(G, i) be a pseudo-
polynomial algorithm for computing the power in-
dex of an agent i in a WVG G of n agents for any
of Shapley-Shubik and Banzhaf power indices ac-
cording to (Matsui and Matsui, 2000). We first use
PowerIndex(G, i) as a subroutine in the construc-
tion of a procedure, GetMergeBenefit(G,S). Proce-
dure GetMergeBenefit(G, S) accepts a WVG G and
a would-be manipulators’ coalition, S. It first com-
putes the sum of the individual power index of the
assimilated agents in S using PowerIndex(G,i). Then,
it alters G by replacing the sum of the weights of
the assimilated agents in G with a single weight in
a new game G
′
before computing the power of the
bloc &S in G
′
. Finally, GetMergeBenefit(G, S) returns
the factor of increment of the merged bloc &S. Let
A(G) be the pseudo-polynomialrunning time of Pow-
erIndex(G, i). Now, since |S| ≤ |I| = n, procedure
GetMergeBenefit(G,S) takes at most O(n·A(G)) time
which is pseudo-polynomial.
We now use GetMergeBenefit(G, S) to construct
an algorithm that manipulators can use to determine
a coalition that yields a good benefit in merging. We
first argue that manipulators tend to prefer coalitions
which are small in size because they are easier to form
and manage. Also, intra-coalition coordination, com-
munication, and other overheads increase with coali-
tion size. Thus, we suggest a limit on the size of the
manipulators’ coalitions since it is unrealistic and im-
practical that all agents in a WVG will belong to the
manipulators’ coalition. This is also consistent with
the assumptions of the previous work on annexation
and merging (Aziz et al., 2011; Lasisi and Allan,
2011). We note, however, that limiting the manipu-
lators’ coalitions size this way does not change the
complexity class of the problem as finding the coali-
tion that yields the most improved benefit remains
NP-hard even with such limitation.
Consider a WVG of n agents. Suppose the manip-
A SEARCH-BASED APPROACH TO ANNEXATION AND MERGING IN WEIGHTED VOTING GAMES
47

ulators’ coalitions have a limit, k < n, on the size of
the members of the coalitions, i.e., the manipulators’
coalitions, S, are bounded as 2 ≤ |S| ≤ k. In this case,
the number of coalitions that the manipulators need
to examine is at most O(n
k
) which is polynomial in
n. Specifically, the total number of these coalitions is:
n
2
+
n
3
+ · ·· +
n
k
=
k
∑
j=2
n
j
. (3)
So, we have
k
∑
j=2
n
j
=
k
∑
j=2
n(n− 1)···(n− j + 1)
j!
≤
k
∑
j=2
n
j
j!
≤
k
∑
j=2
n
j
2
j−1
=
n
2
2
1
+
n
3
2
2
+ · ·· +
n
k
2
k−1
= O(n
k
).
Running GetMergeBenefit(G,S) while updating
the most
1
improved benefit found so far from each
of these coalitions requires a total running time of
O(n
k
· A(G)) which is pseudo-polynomial time, and
thus becomes reasonable to compute.
4.3 Manipulation Algorithm for
Annexation
Our pseudo-polynomial manipulation algorithm for
annexation provides a basic modification of the merge
algorithm above. Specifically, we first replace the
procedure GetMergeBenefit(G, S) with another pro-
cedure, GetAnnexationBenefit(G, i, S). The procedure
GetAnnexationBenefit(G, i, S) accepts a WVG G, an
annexer, i, and a coalition S to be assimilated by i. The
procedure then returns the factor of increment or ben-
efit of the assimilated bloc &(S∪ {i}).
Again, we use GetAnnexationBenefit(G, i, S) to
construct an algorithm that the annexer can use to de-
termine the coalition that yields the most improved
benefit in annexation. The method of construction of
the algorithm is the same as that of the previous ma-
nipulation algorithm for merging with the exception
that we add the weight of an annexer i to the weight
of each coalition S and compare the power index
Φ
&(S∪{i})
(G
′
) of the assimilated bloc in a new game
G
′
to the power index Φ
i
(G) of the annexer in the
1
We refer to the most improved benefit among the O(n
k
)
polynomial coalitions and not from the original 2
n
coali-
tions since we have restricted each manipulators’ coalition
size to a constant k < n.
original game G. The annexer examines a polynomial
number of coalitions of the agents assuming a limit
k < n on the size of each coalition. Since any of the n
agents can be an annexer and the annexer will belong
to any of the coalitions it annexes, the total number of
coalitions examined by all the annexers is:
n
1
n− 1
1
+
n− 1
2
+ ·· · +
n− 1
k− 1
=
n
1
k−1
∑
j=1
n− 1
j
. (4)
Bounding this equation using similar approach as
in Equation 3 shows that Equation 4 is O(n
k
). Thus,
as before, the manipulation algorithm for annexation
also runs in pseudo-polynomialtime, with a total run-
ning time of O(n
k
· A(G)).
5 INFORMED HEURISTIC
SEARCH STRATEGIES
To further improve the performance of the manipu-
lation algorithms, we use heuristics. In this section,
we provide descriptions of search infrastrutures and
enhancements to complement the performance of the
manipulation algorithms.
5.1 Merging Heuristics
The search space for the manipulation algorithm for
merging is the polynomial number of coalitions of
size at most k (see Equation 3) as described ear-
lier. It is important to point out that the computation of
the power indices of the manipulators in the original
game and the power index of the bloc formed by these
agents in a new game account for most of the compu-
tational time required by this algorithm. We also note
that it is unclear to the manipulators on how to deter-
mine a coalition that is beneficial without having to
compute and compare the power indices of the ma-
nipulators in both games.
Since we seek to find the coalition with the most
improved benefit among these coalitions, it is not dif-
ficult to see that the algorithm is prone to engaging in
irrelevant computation of power indices of agents in
the two games for coalitions whose merging are dis-
advantageous. We define evaluation criteria that we
use to prune away such coalitions without having to
compute the power indices of the blocs in the new
games, thus gaining ample computational time. The
basic idea of the evaluation criteria is to prune away
all coalitions havingtheir factor of increment less than
ICAART 2012 - International Conference on Agents and Artificial Intelligence
48

or equal to the estimated minimum possible factor of
increment in the altered WVGs. The criteria are de-
fined for both Shapley-Shubik and Banzhaf indices.
First, consider merging using the Shapley-Shubik
index. Let G be a WVG of n agents. Let the Shapley-
Shubik power index of an agent i in a game G be
ϕ
i
(G). Consider a manipulators’ coalition S ⊆ I with
k agents. Let agents i
1
, i
2
, . . . , i
k
be the distinguished k
manipulators in S that want to merge into a single bloc
&S. Let Π
n−k
be the set of all permutations of the re-
maining n−k agents in G (i.e., not including the k ma-
nipulators). Consider a certain permutation π ∈ Π
n−k
in which we insert all the k manipulators starting from
the r-th position in π (where r is any arbitrary position
in π), and such that one of the manipulators is pivotal
for π. There are k! permutations in G for π in which
the members of S occur together beginning at posi-
tion r. For example, consider a permutation π = 1, 2, 3
of other agents in G which excludes the three ma-
nipulators i
1
, i
2
, and i
3
. The 3! permutations in G
for π when all the manipulators appear together and
starting at the 3-rd position are: π
1
= 1, 2, i
1
, i
2
, i
3
, 3,
π
2
= 1, 2, i
1
, i
3
, i
2
, 3, π
3
=, ···,π
6
= 1, 2, i
3
, i
2
, i
1
, 3.
Now, consider a permutation f(π) of agents in
the altered game G
′
obtained from π by inserting the
bloc &S (formed by agents i
j
∈ S) at the r-th posi-
tion in f(π). It is easy to see that the k! permutations
π
1
, · ·· , π
k!
for π in G when the manipulators appear
together from the r-th position correspond to exactly
one permutation f(π) in G
′
. Also, since one of the
manipulators is pivotal for each of the permutations
π
1
, · ·· , π
k!
for π in G, &S is also pivotal for the corre-
sponding f(π) in G
′
. Observe that counting the num-
ber of distinct permutations π ∈ Π
n−k
in G in which
we insert all the manipulators at certain positions and
such that one of them is pivotal for each π provides a
lower bound on the number of times the blocs formed
by these agents in G
′
will be pivotal. That it is a lower
bound is clear as the manipulators may also be pivotal
in other cases when they do not all appear together.
In our implementation, we first count the num-
ber of times each of the manipulators is pivotal when
they all follow one another in G. We then pick the
smallest among these numbers denoted by |Π
∗
n
|. Now,
if S merges to form a bloc &S, then, the number of
agents in the new game G
′
is n − k + 1. We estimate
the Shapley-Shubik power index of the bloc in G
′
as
|Π
∗
n
|
(n−k+1)!
. We compare the estimated power index of
the bloc in G
′
to the sum of the Shapley-Shubik power
indices,
∑
i∈S
ϕ
i
(G), of the manipulators in G. Specif-
ically, if
|Π
∗
n
|
(n−k+1)!
≤
∑
i∈S
ϕ
i
(G), we eliminate the ma-
nipulators’ coalition S as the coalition cannot possibly
be a candidate coalition that provides the most im-
proved benefit to the manipulators.
Second, consider merging using Banzhaf in-
dex. Let η
i
(G) be the number of coalitions for which
an agent i is critical in G. Also, denote by β
i
(G)
the Banzhaf power index of agent i in G. As before,
we consider a manipulators’ coalition S ⊆ I with k
agents. Let agents i
1
, i
2
, . . . , i
k
be the distinguished k
manipulators in S that want to merge into a single bloc
&S. Let Γ
n−k
be the set of all losing coalitions of the
remaining n − k agents in G (i.e., not including the k
manipulators). Consider a certain coalition C ∈ Γ
n−k
in which the inclusion of at least one of agents i
j
∈ S
makes C ∪ {i
j
} a winning coalition and such that at
least one of agents i
j
is critical for C∪ {i
j
}. There are
multiple such winning coalitions that can be formed
from the union of C and the subsets of S depending
on the quota of the game.
For example, let G = [23, 20, 10, 11, 15;50] be a
WVG of five agents I = {1, 2, 3, 4, 5} in order. Let
S = {3, 4, 5} be a set of manipulators. Consider a los-
ing coalition C = {1, 2} which excludes the three ma-
nipulators. There are three winning coalitions: C
w
1
=
C∪ {3}, C
w
2
= C ∪ {4}, and C
w
3
= C ∪ {5} that can be
formed from the union of C and the subsets of S such
that at least one agent in S is critical in the resultant
set. Note that adding two members of S to C would
yield coalitions in which no agent is critical.
Now, consider a winning coalition f(C) of agents
in the altered game G
′
obtained from the union of the
losing coalition C in game G and the bloc &S (formed
by agents i
j
∈ S). It is easy to see that all the winning
coalitions C
w
1
, · ·· ,C
w
m
(where m ∈ N) obtained from C
in G correspond to exactly one winning coalition f (C)
in G
′
. Also, since at least one of the manipulators is
critical for each of the winning coalitions C
w
1
, · ·· ,C
w
m
,
the bloc &S is also critical for the corresponding win-
ning coalition f(C) in G
′
. Observe that counting the
number of distinct losing coalitionsC ∈ Γ
n−k
in which
the inclusion of agents i
j
∈ S makes C ∪ {i
j
} a win-
ning coalition and such that at least one of agents i
j
is critical for C ∪ {i
j
} gives the number of times the
bloc formed by the manipulators in G
′
is critical.
In our implementation, we compute the sum
∑
i∈S
η
i
(G) of the number of times all the manipula-
tors are critical in G, and then compute the number
η
&S
(G
′
) of times the bloc formed by the manipula-
tors will be critical in G
′
as described above. In or-
der to estimate the power of the bloc &S in G
′
we
need to know the number of times for which each of
the other agents in G
′
other than the bloc is also crit-
ical. These numbers are not available. Since we al-
ready know the number of times all agents in G are
critical, we estimate the number of times for which
each agent i (other than &S) in game G
′
would be crit-
ical as η
i
(G
′
) =
η
i
(G)
τ
, where τ is defined as a measure
A SEARCH-BASED APPROACH TO ANNEXATION AND MERGING IN WEIGHTED VOTING GAMES
49

to scale down the number of times an agent is criti-
cal in G to G
′
. This is required since there are more
agents in the original game G than G
′
. The number of
coalitions for which the non manipulating agents in
G is critical is always more than the number of coali-
tions for which they are critical in G
′
. More precisely,
we estimate the scaling factor between the two games
using the following ratio τ =
∑
i∈S
η
i
(G)
η
&S
(G
′
)
. We now com-
pute the estimated Banzhaf power index of the bloc in
G
′
as β
&S
(G
′
) =
η
&S
(G
′
)
η
&S
(G
′
)+
∑
i∈I\S
η
i
(G
′
)
. We compare the
estimated power index of the bloc in G
′
to the sum
of the Banzhaf power indices,
∑
i∈S
β
i
(G), of the ma-
nipulators in G. Specifically, if β
&S
(G
′
) ≤
∑
i∈S
β
i
(G),
we prune the manipulators’ coalition S as the coalition
cannot possibly be a candidate coalition that provides
the most improved benefit to the manipulators.
5.2 Annexation Heuristic
We recall the definition of annexation in Section 2
and from (Machover and Felsenthal, 2002; Aziz et al.,
2011), the power of the assimilated bloc in an altered
WVG is compared to the power of the annexer in the
original game. By this definition, intuition suggests
that annexation should always be advantageous. This
intuition is indeed true using the Shapley-Shubik in-
dex to compute agents’ power. However, there exists
situations where annexation is disadvantageous for
the annexer using the Banzhaf index. See (Machover
and Felsenthal, 2002; Aziz and Paterson, 2009; Aziz
et al., 2011) for different examples of WVGs where
annexation is disadvantageous for the annexer using
the Banzhaf index. This case where annexation results
in power decrease for the annexer is refer to as the
bloc paradox (Machover and Felsenthal, 2002). Fur-
thermore, (Aziz et al., 2011) have also shown that de-
termining whether a player can benefit from annexing
a given coalition is NP-hard for the Banzhaf index.
Recall again from Equation 4 that the annexer
needs to examine only a polynomial number of as-
similated coalitions of size at most k − 1 to find the
most improved power gain. It is also known that in
computing agents’ power index in a WVG using both
the Shapley-Shubik and Banzhaf indices, the power
index of an agent with a higher weight cannot be
less than the power index of an agent with a smaller
weight (Bachrach et al., 2010). In our case, since we
are restricting the manipulators’ coalition size to k,
the assimilated coalitions with maximal weights are
those of size k − 1. Based on this observation and
the fact due to the bloc paradox as discussed above,
it is enough to check only the assimilated coalitions
of size exactly k − 1 in order for an annexer to find
the coalition with the most improved benefit using the
two power indices. There are only
n
1
n− 1
k− 1
such assimilated coalitions to be considered when the
n agents act as an annexer in turn.
6 EXPERIMENTAL RESULTS
We have studied the performance of the two ma-
nipulation algorithms. As noted in the introduction,
the simple random approach to manipulation via an-
nexation and merging seems unintelligent. Thus, it
is impractical that strategic agents would employ
such method. We make a simple modification to this
method which provides manipulators with higher av-
erage factor of increment. The modification involves
the selection of the best factor of increment from three
random choices (which we refer to as the best-of-three
method). We compare the results of our search-based
method with those of the simple random and best-of-
three methods. However, for clarity of presentation,
we show our results compared with only those of the
best-of-three method.
We randomly generate WVGs. The weights of
agents in each game are randomly chosen so that
all weights are integers and drawn from a uni-
form distribution over the range [1,W], where W ∈
{10, 20, 30, 40, 50}. We have chosen different weight
distributions in order to provide some generalization
of the performanceof the two methods under different
conditions. We run two different set of tests in which
the number of agents, n, in each of the original WVGs
is either 10 or 20 while the number of assimilated
agents, k, is chosen to be either 5 or 10. When creat-
ing a new game, the quota, q, of the game is randomly
generated such that
1
2
w(I) < q ≤ w(I), where w(I) is
the sum of the weights of all agents in the game.
Using the manipulation algorithms, the simple
random and the best-of-three methods, the power in-
dex of an assimilated bloc formed by annexation in
an altered game is compared to the power index of
the annexer in the original game. Similarly, the power
index of the assimilated bloc formed by merging is
compared to the sum of the original power indices of
the agents in the merged bloc. The factor of increment
(decrement) by which the annexer (or the merged
bloc) gains (loses) in the annexation (or merging) is
computed. We repeat each experiment 100 times and
compute the average factor of increment.
6.1 Results for Merging
Figure 1 shows the benefits from merging for both the
ICAART 2012 - International Conference on Agents and Artificial Intelligence
50
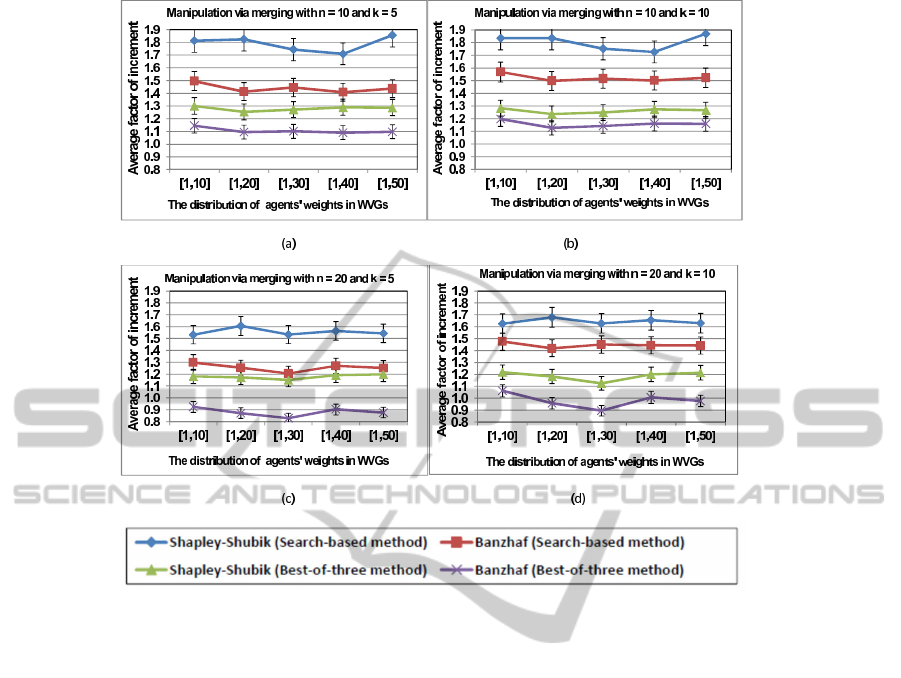
Figure 1: The average factor of increment for merging for the search-based and best-of-three methods using different agents’
weights distributions. (a) n = 10 and k = 5 (b) n = 10 and k = 10 (c) n = 20 and k = 5 (d) n = 20 and k = 10.
best-of-three method and our search-based approach
for various values of n, k, and W using the two power
indices. The x-axis indicates the weight distributions
of agents while the y-axis is the average factor of in-
crement achieved by manipulating agents. The error
bars in this and the subsequent figure indicate 5% er-
ror amounts in the average factor of increment.
We found from the data of Figures 1(a)-(d) that
our search-based method achieves improvement in
benefits of 28% to 45% more than those of the best-
of-three method in merging for various values of n, k,
and W, and for the two power indices. Since this per-
centage increment of the search-based approach over
the best-of-three method can be achieved with only a
polynomial amount of work, then, manipulators are
more likely to seek a much improved power gain in
merging using the search-based approach.
6.2 Results for Annexation
Figure 2 shows the average factor of increment from
annexation for both the best-of-three method and the
search-based approach for various values of n, k, and
W using the two power indices.
It is clear from the figure that the average factor
of increment found by the search-based approach for
the two power indices are higher than those of the
corresponding power indices using the best-of-three
method. Specifically, we found from the data of Fig-
ures 2(a)-(d) that the search-based method achieves
improvement in benefits of over 300% more than
those of the best-of-three method in annexation for
various values of n, k, and W, and for the two power
indices. Again, this percentage increment of the
search-based approach over the best-of-three method
can be achieved with only a polynomial amount of
work. Thus, we conclude that manipulation via merg-
ing and annexation is more serious than was presented
in the simple random simulation of the previous work.
7 RELATED WORK
Weighted voting games and power indices are widely
studied (Brams, 1975; Felsenthal and Machover,
1998; Laruelle, 1999). Prominent real-life situations
where WVGs have found applications include the
United Nations Security Council, the International
Monetary Fund (Leech, 2002; Alonso-Meijide and
Bowles, 2005), the Council of Ministers, and the Eu-
A SEARCH-BASED APPROACH TO ANNEXATION AND MERGING IN WEIGHTED VOTING GAMES
51
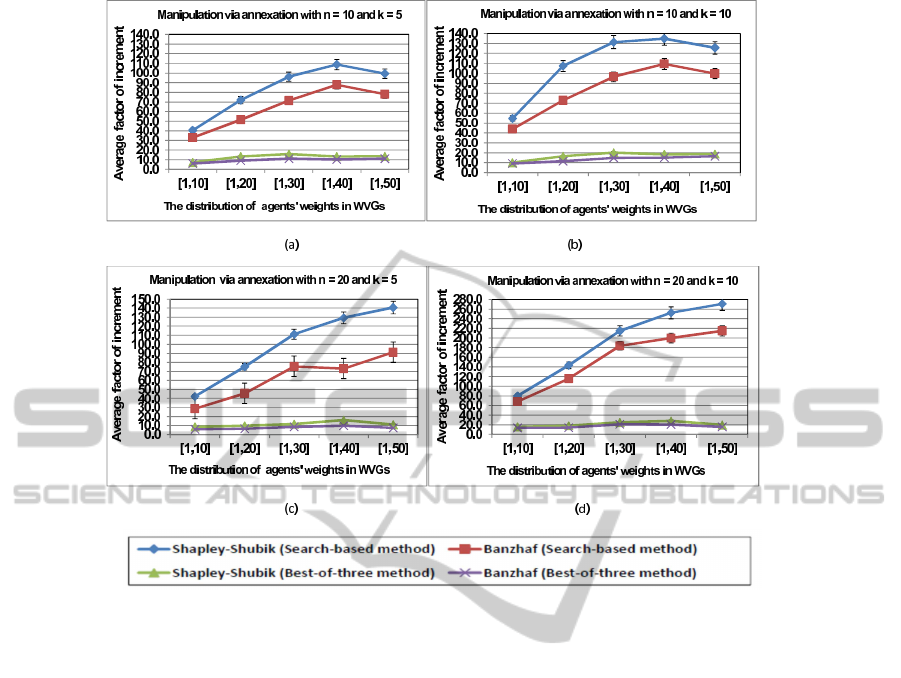
Figure 2: The average factor of increment for annexation for the search-based and best-of-three methods using different
agents’ weights distributions. (a) n = 10 and k = 5 (b) n = 10 and k = 10 (c) n = 20 and k = 5 (d) n = 20 and k = 10.
ropean Community (Felsenthal and Machover, 1998).
The need to compensate agents from jointly de-
rived payoff in WVGs has also necessitated the as-
signment of power to players. A widely accepted
method for measuring power of agents in WVGs
uses power indices. Fairness in the assignment of
power to players in a game is also a concern of most
of the power indices. The two most prominent and
widely used power indices are Shapley-Shubik(Shap-
ley and Shubik, 1954) and Banzhaf (Banzhaf, 1965)
power indices. Other power indices found in the lit-
erature include Deegan-Packel (Deegan and Packel,
1978), Johnsoton (Johnston, 1978), and Holler-Packel
(Holler and Packel, 1983) power indices.
Computing the Shapley-Shubik and Banzhaf
power indices of players in WVGs is NP-hard (Mat-
sui and Matsui, 2001). The power indices of voters
using any of Shapley-Shubik and Banzhaf power in-
dices can be computed in pseudo-polynomial time
using dynamic programming (Matsui and Matsui,
2000). Efficient exact algorithms using generating
functions (Brams and Affuso, 1976; Bilbao et al.,
2000) also exist for both the Shapley-Shubik and
Banzhaf power indices for WVGs where the weights
of all agents are restricted to integers. There are
also approximation algorithms (Fatima et al., 2007;
Bachrach et al., 2010) for computing the Shapley-
Shubik and Banzhaf power indices in WVGs.
We now consider false-name manipulation via
annexation and merging in WVGs. (Machover and
Felsenthal, 2002) originally studied annexation and
alliance (or merging) in WVGs. They consider when
the blocs formed by annexation or merging are ad-
vantageous or disadvantageous. They show that using
the Shapley-Shubikpower index, it is always advanta-
geous for a player to annex some other players in the
game. However, this is not true for Banzhaf power
index. Furthermore, they show that merging can be
advantageous or disadvantageous for the two power
indices. In contrast to our work, they do not consider
the extent to which the agents involved in annexation
or merging may gain, which we study in this paper.
(Aziz et al., 2011) have also considered the com-
putational aspects of the problem of annexation and
merging in WVGs. They show that determining if
there exists a beneficial merge in a WVG is NP-hard
using both Shapley-Shubik and Banzhaf indices. The
same is also true for determining the existence of ben-
eficial annexation using the Banzhaf index. Our work
differ from that of these authors as we provide a com-
ICAART 2012 - International Conference on Agents and Artificial Intelligence
52

parison of the extent of power gain or benefits that are
possible for manipulating agents in a restricted ver-
sion of this problem using the two indices.
8 CONCLUSIONS
We extend the simple random simulation of (Lasisi
and Allan, 2011) on susceptibility of power indices
to annexation and merging in WVGs to consider a
much improved benefit achievable by manipulating
agents. Using similar assumptions for annexation and
meging as employed in the simulation of (Lasisi and
Allan, 2011), we show that manipulators need to do
only a polynomial amount of work to find a much
improved benefit and then present two search-based
pseudo-polynomial manipulation algorithms that ma-
nipulators can use.
We provide a modified version of the simple ran-
dom approach that considers the best benefit from
three random choices (which we refer to as the
best-of-three method) that we compare results of
our search-based approach with. Experimental results
show that our search-based method achievesimprove-
ment in benefits of over 300% more than those of the
best-of-three approach in annexation, while the im-
provement in benefits is 28% to 45% more than the
best-of-three method in merging for all the WVGs
we considered. We conclude that since this percent-
age increment of the search-based approach over the
best-of-three method for both annexation and merg-
ing can be achievedwith only a polynomial amount of
work, and using pseudo-polynomial algorithms, then,
manipulators are more likely to seek for a much im-
proved power gain when faced with annexation and
merging in WVGs. Thus, we advance the state of the
art by showing that annexation and merging can be
more serious than as presented in the previous work.
ACKNOWLEDGEMENTS
This work is supported by NSF research grant
#0812039 entitled “Coalition Formation with Agent
Leadership”.
REFERENCES
Alonso-Meijide, J. M. and Bowles, C. (2005). Generating
functions for coalitional power indices:an application
to the IMF. Annals of Oper. Res., 137:21–44.
Aziz, H., Bachrach, Y., Elkind, E., and Paterson, M. (2011).
False-name manipulations in weighted voting games.
Journal of Artificial Intelligence Research, 40:57–93.
Aziz, H. and Paterson, M. (2009). False-name manipula-
tions in weighted voting games: splitting, merging and
annexation. In 8th Intl. Conf. of AAMAS, pages 409–
416, Budapest, Hungary.
Bachrach, Y., Markakis, E., Procaccia, A. D., Rosenschein,
J. S., and Saberi, A. (2010). Approximating power in-
dices - theoretical and empirical analysis. Autonomous
Agents and Multiagent Systems, 20(2):105–122.
Banzhaf, J. (1965). Weighted voting doesn’t work: a math-
ematical analysis. Rutgers Law Review, 19:317–343.
Bilbao, J. M., Fernndez, J. R., Losada, A. J., and Lpez, J. J.
(2000). Generating functions for computing power in-
dices eciently. TOP: An official Journal of the Spanish
Society of Statistics and Oper. Res., 8(2):191–213.
Brams, S. J. (1975). Game Theory and Politics. Free Press,
New York.
Brams, S. J. and Affuso, P. J. (1976). Power and size: a new
paradox. Theory and Decision, 7:29–56.
Deegan, J. and Packel, E. W. (1978). A new index of power
for simple n-person games. International Journal of
Game Theory, 7:113–123.
Fatima, S. S., Wooldridge, M., and Jennings, N. R. (2007).
A randomized method for the Shapley value for the
voting game. In 6th Intl. Conf. of AAMAS, pages 959–
966, Honolulu, Hawaii.
Felsenthal, D. S. and Machover, M. (1998). The Measure-
ment of Voting Power: Theory and Practice, Problems
and Paradoxes. Edward Elgar, Cheltenham.
Holler, M. J. and Packel, E. W. (1983). Power, luck and the
right index. Journal of Economics, 43:21–29.
Johnston, R. J. (1978). On the measurement of power: some
reactions to Laver. Environment and Planning,
10:907–914.
Laruelle, A. (1999). On the choice of a power index.
Instituto Valenciano de Investigaciones Economicas,
2103:99–10.
Lasisi, R. O. and Allan, V. H. (2011). Annexations and
merging in weighted voting games - the extent of
susceptibility of power indices. In 3rd Int. Conf. of
ICAART, pages 124–133, Rome, Italy.
Leech, D. (2002). Voting power in the governance of the
International Monetary Fund. Annals of Operations
Research, 109(1):375–397.
Machover, M. and Felsenthal, D. S. (2002). Annexation
and alliances: When are blocs advantageous a priori.
Social Choice and Welfare, 19(2):295–312.
Matsui, T. and Matsui, Y. (2000). A survey of algorithms
for calculating power indices of weighted majority
games. Journal of the Oper. Res. Soc. of Japan, 43(1).
Matsui, T. and Matsui, Y. (2001). NP-completeness for cal-
culating power indices of weighted majority games.
Theoretical Computer Science, 263((1-2)):305–310.
Shapley, L. S. and Shubik, M. (1954). A method for evalu-
ating the distribution of power in a committee system.
American Political Science Review, 48:787–792.
A SEARCH-BASED APPROACH TO ANNEXATION AND MERGING IN WEIGHTED VOTING GAMES
53
