
A GRAPH-SEARCH APPROACH ON RESOURCE-CONSTRAINED
SCHEDULING PROBLEMS AND ITS APPLICATION TO
ADVANCED DRIVER ASSISTANCE SYSTEMS
Christoph Endres and Christian M
¨
uller
German Research Center for Artificial Intelligence, DFKI GmbH, Saarbruecken, Germany
Keywords:
Automotive, Presentation scheduling, Conflict resolution.
Abstract:
In this paper we present a problem which is a variation of the resource-constrained project scheduling problem
and a graph-based approach to solve it. The problem is defined as resource-constrained scheduling problem
(RCSP). Particularly, we apply the approach to the problem of scheduling a large number of driver warnings
based on car-to-car communication (also known as cooperative vehicles). Data is presented from the project
SIM
TD
, a large-scale field test in the area of the Hessian city of Frankfurt, where 120 cars participate in a
number of controlled tests in three main scenarios: the rural road scenario (basic complexity), the motorway
scenario (intermediate complexity), and the urban road scenario (high complexity). We argue that, due to its
run-time behaviour, our graph-based approach is suitable for the particular application domain at hand. Results
are presented in terms of quality of the solution (conflict resolution), runtime behavior and pruning effects to
the size of the search tree. In addition to the scenarios derived from the actual field test, a hyper-real stress test
is presented to demonstrate the performance of our solution.
1 INTRODUCTION
The resource-constrained project scheduling problem
(RCPSP) is a combinatorial optimization problem
(Blazewicz et al., 1983). Due to its high practical
importance, it has been analyzed for several decades
now. RCPSP is an extension of the job shop schedul-
ing problem (JSP). (Garey and Johnson, 1979) pro-
vides the following definition, which is used as a basis
here.
Definition 1 (JSP). The job shop scheduling problem
(JSP) consists of a set A of activities each with a pos-
itive integer-valued duration, d
i
. A is partitioned into
projects (jobs), and with each project is associated a
total ordering on that set of activities. Each activity
specifies a resource on which it must execute without
interruption. No activities that require the same re-
source can overlap in their execution.
Finding a solution to this problem with minimal
makespan (difference between minimum start time
and maximum end time) is NP-hard. RCPSP is more
complicated than JSP, since each task requires not
only a processor but also additional scarce resources.
Since it can be reduced to the simpler JSP, it is NP-
hard as well (Garey and Johnson, 1979; Blazewicz
et al., 1983).
In this paper, we introduce the resource-constrained
scheduling problem (RCSP), which is similar but adds
additional constraints to start- and endtime of activ-
ities. Unlike the original RCPSP, it has a dynamic
component from disruption management. (Clausen
et al., 2001) defines a disruption as ”a state during
the execution of the current operation, where the de-
viation from plan is sufficiently large that the plan
has to be changed substantially.” In a similar manner,
(Kuster et al., 2007) defines disruption management
(DM) as ”the process of responding to an unforseen
disturbance occuring during the execution of planned
and scheduled operations.”. According to the author,
DM aims at the selection of appropriate repair actions
to minimize the negative impact typically associated
with disruption.
In the automotive domain, particularly in the field
of Advanced Driver Assistance Systems (ADAS), we
face the challenge of scheduling a growing number of
assistance systems trying to communicate simultane-
ously with the driver over a limited amount of com-
munication channels. This differs from RCPSP in a
way that scheduling priority lies not on the order of
activities but on preserving the requested presentation
times as good as possible. Moreover, following (Baier
334
Endres C. and Müller C..
A GRAPH-SEARCH APPROACH ON RESOURCE-CONSTRAINED SCHEDULING PROBLEMS AND ITS APPLICATION TO ADVANCED DRIVER
ASSISTANCE SYSTEMS.
DOI: 10.5220/0003743303340339
In Proceedings of the 4th International Conference on Agents and Artificial Intelligence (ICAART-2012), pages 334-339
ISBN: 978-989-8425-95-9
Copyright
c
2012 SCITEPRESS (Science and Technology Publications, Lda.)

rural road scenario
motorway scenario
urban road scenario
!"#$%
!"#$%
!"#
!"#
Wöllstadt
Bad Vilbel
Friedberg
Jctn Bad Nauheim
!"#$%
Jctn Friedberg
IS Bad Homburg
IS Preungesheim
!""#$
!""#$
!"#$
IS Offenbach
IS F South
IS Frankfurt
IS F West
IS F North West
30 mls
14 mls
I
II
III
IV
!""#$
400
Figure 1: The SIM
TD
test field around Frankfurt/Main, Ger-
many, is comprised of three test scenarios that imply differ-
ent degrees of resource utilization from low (rural road sce-
nario) to high (urban road scenario). 120 cars are involved
in the field test.
et al., 2007), we do not only need to be able to distin-
guish between plans that satisfy goals and those that
do not without providing further means of discrimina-
tion between successful plans. For the application at
hand, we need to have information about how ”good”
a plan is, thus ”enabling the planner to distinguish be-
tween successful plans of differing quality” (ibid.).
Furthermore, the nature of the application demands
for an anytime behaviour. The desired algorithm to
solve the problem should be able to output a solution
at any time, which should be as close as possible to
the optimal solution.
2 BACKGROUND
RCSP consists of a set of tasks (activities) with fixed
start times and durations, which should be executed
without interruption on a given (limited) resource.
Thus, conflicts occur when two or more tasks attempt
to use the same resource simultaneously. The objec-
tive is to resolve all conflicts while modifying the set
of tasks as little as possible.
For RCPSP, several algorithms have been pro-
posed, reaching back to the 1960’s with a Branch-and-
Bound approach by (Johnson, 1967), adopted later
by (Stinson et al., 1978; Christofides et al., 1987;
Brucker et al., 1998). (Pritsker et al., 1969; Patterson
and Roth, 1976) proposed Zero-One programming
solutions, while more recent approaches use Linear
(Brucker and Knust, 2000), Constraint (Demassey
et al., 2005) and Genetic Programming (Kuster et al.,
2007).
The Branch-and-Bound approach is closest to our
solution presented here. It is based on graph search
and effective bounding (e.g. pruning). Linear, Integer
and Zero-One-Programming are variations of a stan-
dard optimization problem. Genetic programming is
a search heuristic which mimics natural selection be-
haviour.
It is important to keep in mind that our problem
presented here differs significantly from the original
RCPSP and thus, the approaches mentioned here can-
not simply be adopted.
For solving RCSP in the given highly dynamic do-
main, we need an anytime algorithm which finds a
good (not necessary perfect) solution very fast. Both
tree search and genetic algorithms fulfill these re-
quirements. In this paper, we present a tree search
approach with effective pruning.
3 APPLICATION DOMAIN
We apply the approach to the problem of scheduling
a large number of driver warnings based on car-to-car
communication (also known as cooperative vehicles).
Particularly, the system is developed for the project
SIM
TD
.
The SIM
TD
test field is located in the Frankfurt-
Rhine-Main area of Hessen, Germany. With up to 120
vehicles and more than 100 roadside stations installed
by the Hessian traffic centre (VZH) and the Integrated
Traffic Management Center Frankfurt (IGLZ), car-
to-x communication is tested under real conditions.
The Frankfurt-Rhine-Main area is an important Ger-
man traffic hub with major traffic generators such as
Frankfurt Airport, Frankfurt Trade Fair and the sta-
dium. Large parts of the area are characterised by
high traffic density and therefore allow experiments
on all road safety and traffic efficiency functions un-
der normal as well as high load conditions. Figure 1
shows a map of the test field. It is comprised of three
scenarios: I Rural road, II / III Motorway, and IV Ur-
ban road. The order of the scenarios represents their
increasing use of the limited HMI resources. These
assumptions are based on the number of applications
active in the respective area, the traffic density as well
A GRAPH-SEARCH APPROACH ON RESOURCE-CONSTRAINED SCHEDULING PROBLEMS AND ITS
APPLICATION TO ADVANCED DRIVER ASSISTANCE SYSTEMS
335

as the density of road site stations (stationary wireless
communication units) used in the field test.
Figure 2 gives an overview on the complexity
of the scenarios and specifies the role of RCSP in
the given application context. A large number of
presentations try to access (potentially) simultane-
ously a limited resource (the Human-Machine Inte-
face, HMI). Not all requests are equally important.
Output channels are distributed over different modal-
ities: multiple visual channels (symbols and main
screen), auditory outputs, and text-to-speech (TTS).
Hence, unlike traditional presentation planning, we
look at a highly dynamic scenario in which presen-
tation requests come in at any time during runtime.
As indicated by the dashed triangle, a second re-
source limitation has to be taken into account: the
limited cognitive resource of the driver. Here ques-
tions should be addressed like for example, how long
the minimal display time for an information should
be, or wether or not overlapping presentations on dif-
ferent channels (TTS for one message and simultane-
ous display of another message) is beneficial. How-
ever, this is beyond the scope of this paper. We refer
the interested reader to (Cao et al., 2009; Cao et al.,
2010; Mahr et al., 2010).
So called presentation requests are issued by the
”functions” listed on the right side of Figure 2. Func-
tions act as individual subsystems that have no knowl-
edge on the available resources and activities of other
functions. Presentation requests are issued (”an-
nounced”) as soon as the need for a warning becomes
apparent. Hence, the scheduler can allocate the HMI
resources beforehand (planning time does not delay
crucial warning messages). Nevertheless, the scenario
involves a multiplicity of presentations and is highly
dynamic.
4 PROPOSED GRAPH-BASED
SOLUTION
In short, our problem is a dynamic set of tasks (pre-
sentation requests) simultaneously trying to access a
limted resource. Tasks have a start time, duration, a
hard minimal duration, a priority, and a desired re-
source (presentation strategy). We look for a solution
which resolves resource conflicts while modifying the
tasks as little as possible. A more formal defnition is
given below.
We propose a two-step graph-based solution to the
problem. Step one is transforming dynamic planning
to static planning at runtime. Dynamic planning thus
is by construction equivalent to having a series of
static planning problems. The main problem here is
to identify subsets of the set of presentation tasks and
the appropriate order of resolving multiple different
conflict sets. Identifying overlapping presentations is
a straightforward task at first sight. However, since
the solution to that conflict could again cause other
conflicts, the appropriate set of tasks to be included in
the conflict set is not always obvious. Here we have to
solve the trade-off between scope of the solution and
runtime, which is heavily depending on the amount of
tasks in the conflict set.
Step two of our approach is transforming our
problem into a tree search problem for which well
known algorithms can be applied.
Let T be a set of presentation tasks T =
{t
1
,t
2
,...,t
M
}. Let each presentation task t
i
consist
of a start time, an end time, a priority and additional
information about the presentation such as rendering
information, distance to event, etc. which are not of
immediate relevance for the scheduling.
Definition 2 (Scheduling Problem RCSP). The RCSP
P is defined as:
P = < T
C
,M > where
• T
C
is a set of conflicting presentation tasks, T
C
= {t
C
1
, t
C
2
,..., t
C
M
}.
• M is a set of modifying actions (short: modi-
fications) as conflict resolving strategies, M =
{m
1
,...,m
N
}
In our implementation, modifications are postpon-
ing, preponing, shortening (beginning or end of task),
switching resource (not considered in this paper) and
canceling a task.
Definition 3 (Search Tree). We define a search tree
S(P ) as follows:
• The root R of the tree contains the set of conflict-
ing tasks T
C
• Each edge e is a pair of a presentation task and a
modification applied to it, e = < t
C
i
,m
j
>
• A cost function p(E), which defines a positive in-
teger penalty for each edge, based on the severity
of the modification (see Definition 5).
• Each node is the result of the modification of the
previous edge to the parent node
• The penalty p(n) of a node n is the sum of the
penalties of all edges on the branch leading to it
• A node n containing a presentation task set T
without conflicts is a leaf.
By design, the leaf with the lowest cost is the best so-
lution to our problem. Using the tree S (P ) described
in Definition 3, we can now search the solution with
the Breadth First Search (BFS) Algorithm 1.
ICAART 2012 - International Conference on Agents and Artificial Intelligence
336

IV Urban road scenario
II"/"III"Motorway"Scenario"
I Rural road scenario
Traffic flow information and navigation
1 Foresighted road/traffic information
2 Road works information system
3 Advanced route guidance and navigation
Local danger alert
5 Obstacle warning
6 Congestion warning
7 Road weather warning
8 Emergency vehicle warning
Driving assistance
9 In-vehicle signage/traffic rule violation warning
10 Traffic light phase assistant/ violation warning
11 Extended electronic brake light
12 Intersection and cross traffic assistance
Additional services
13 Internet-based usage of services
14 Location-dependent services
limited resource
attention, decision
making**
1
3
4
5
6
7
8
9
10
14
13
11
Traffic management
4 Alternative route management
limited resource
Human-Machine
Interface
(HMI)
2
1
6
3
4
3
2
9
9
12
1
11
5
Resource-
constraint
scheduling
problem*
*addressed here **not addressed here but part of our research
Figure 2: Complexity of the scenarios I – IV and the role of RCSP in the given application context.
Algorithm 1: Scheduling using BFS tree search.
1: solution ← nil
2: minPenalty ← ∞
3: i ← 0
4: N
0
← {R}
5: while |N i| > 0 do
6: for all n ∈ N
i
do
7: for all m ∈ M do
8: if applicable(m,n) then
9: n’ ← apply(m,n)
10: N
i+1
← N
i+1
∪ {n’}
11: if isSolution(n’) and p(n’)<minPenalty
then
12: minPenalty ← p(n’)
13: solution ← n’
14: end if
15: end if
16: end for
17: end for
18: i ← i+1
19: end while
Pruning. In order to reduce complexity and run-
time, several pruning mechanisms are applied in the
algorithm: A branch with a total penalty bigger than
the best solution found so far minus the minimum ac-
tion penalty will be pruned; a branch that encodes a
solution already encoded in another branch (maybe
with permutated actions) will be pruned. Additional
implicit pruning is achieved using the function appli-
cable(a,n) (see line 8 of Algorithm 1):
Definition 4 (applicable(m,n)). A modification m is
applicable to a node n if and only if:
• n is not a leaf
• applying m to n will not create another conflict
• m will not shorten any task below a given minimal
display time
• p(n’) < minPenalty
• n’ /∈ N
j
, 0 ≤ j ≤ i + 1
• m will not move any task completely out of its
original scope
Anytime Behavior. Our algorithm shows an ”any-
time” behavior, i.e. it incrementally finds better plans
(Baier et al., 2007). Once a solution is found, its met-
ric value can be used as a bound for future solutions.
The metric we use here is a penalty of the actions
needed in order to modify the conflict set to a conflict-
free set. It is defined in more detail below.
5 EMPIRICAL EVALUATION
In preparation of the SIM
TD
field test which will be-
gin in 2012, applications are tested on the basis of
pre-recorded traces containing GPS positions, car-to-
car communication messages, and vehicle data (ve-
locity, heading, gas pedal status, break pedal status,
index lights, etc.). The scenarios lined-up at the X-
axis in Figure 3 correspond to what we have seen ear-
lier in Figures 1 and 2. Additionally, a scenario with
hyper-realistic complexity was added (here denoted
Scenario V). Each scenario was further specified with
three concrete evaluation cases (I.1, I.2, I.3, .... V.3).
The dashed black line corresponds to the actual com-
plexity of the evaluation cases:
Definition 5 (Complexity). The complexity of a con-
flict set T
C
is
cx(T
C
) =
∑
ol(t
C
i
,t
C
j
)
ms
· |T
C
| · |ol(t
C
i
,t
C
j
)| · alloc(ms),
A GRAPH-SEARCH APPROACH ON RESOURCE-CONSTRAINED SCHEDULING PROBLEMS AND ITS
APPLICATION TO ADVANCED DRIVER ASSISTANCE SYSTEMS
337
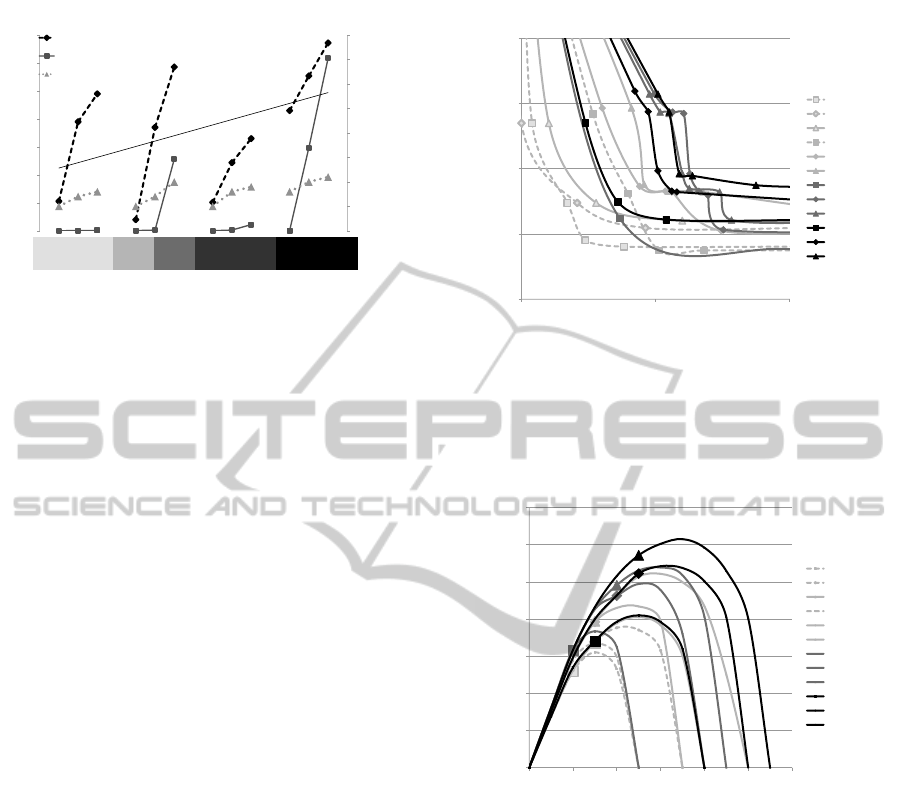
!"
#"
$!"
$#"
%!"
%#"
&!"
&#"
'!"
!"
#!"
$!!"
$#!"
%!!"
%#!"
&!!"
&#!"
()*+,-./01"
2345*-"678"
9:--;-+0<"
I Rural road
scenario
IV Urban road
scenario
V Hyper-realistic
scenario (I, II/III, IV)
II / III Motorway(
Scenario(
complexity
(see definition in the text)
runtime (s)
treedepth
4
I.1 I.2 I.3 II.2 II.1 III.1 IV.1 IV.2 V.1 V.3 IV.3
V.2
Figure 3: For each type of scenario, several examples of
varying complexity based on field data are used to test the
algorithm presented in this paper. Hyperrealistic in the
sense of unrealistic high) scenarios are used for stress test-
ing. Runtime and tree depth match the tendency of growing
complexity from left to right in each scenario type.
where ol is the temporal overlap of two conflicting
tasks in milliseconds and alloc(ms) is the percentage
of the makespan allocated by the unmodified tasks.
Figure 3 shows that the complexity of the test
cases has a positive trend from left to right(see solid
black trend line), which appeals to our intuition. Nev-
ertheless, there is a significant case-specific complex-
ity within each of the scenarios. We see, for exam-
ple, that the variance of complexity in Motorway sce-
nario is higher than both Rural road scenario and Ur-
ban road scenario. Note that the complexity of V.1 is
lower than the ones of I.3 and III.1. This is because
V.1 is a hyper-real Rural road test case, V.2 is hyper-
real Motorway test case, and V.3 is a hyper-real Urban
road test case.
Both run-time as well as tree-depth differed sig-
nificantly, which can be seen by regarding the grey
(square) solid lines respectively the dashed (triangle)
lines. Runtime relates to the time needed to find the
optimal solution. It was measured on a regular state-
of-the-art desktop PC.
For each of the evaluation cases, a solution was
found by the scheduling algorithm. In order to be able
to distinguish between successful solutions of differ-
ent quality, we define quality via a penalty for the
modifying actions it involves: the fewer the modifi-
cations, the better the solution.
Definition 6 (Penalty of a RCSP Solution). Be M a
set of modifications, M = {m
1
,...,m
N
} and t a task
with given positive priority prio(t). The penalty p for
m applied to t is p(m,t) = d(m) · prio(t) · ∆, where
d(m) defines the general desirablility of an action as
positive interger value and ∆ specifying the temporal
aspect of the modification (e.g. postponing or short-
ening).
The penalty of a solution is then defined as
penalty (log)
(see definition in the text)
time in ms (log)
50#
500#
5.000#
50.000#
500.000#
5# 50# 500#
I.1
I.2
I.3
II.1
II.2
III.1
IV.1
IV.2
IV.3
V.1 (I)
V.2 (III)
V.3 (IV)
Figure 4: Quality of a solution annotated as penalty (see
Definition 6) as a function of runtime (ms). Solutions with
qualities close to the respective optimal solutions are found
after a very short time. Note that presentation tasks are is-
sued at least a few seconds before start time. Hence, the
planning time does not delay the warning.
!"
!#"
!##"
!###"
!####"
!#####"
!######"
!#######"
#" $" %" &" '" !#" !$"
I.1
I.2
I.3
II.1
II.2
III.1
IV.1
IV.2
IV.3
V.1 (I)
V.2 (III)
V.3 (IV)
number of nodes
tree depth
Figure 5: Number of nodes as a function of tree depth show-
ing the effect of pruning. The symbols correspond to the
point when the optimal solution was found.
∑
p(m,t) of all (m,t) contained in it.
The order of steps taken towards a certain solu-
tion is in our case not important. This is respected by
pruning duplicate and redundant solutions. As a side
effect, the penalty for a solution is well defined and
independent of the way it was constructed.
Figure 4 shows the correlation between runtime
and solution quality in terms of the penalty we de-
fined. Our algorithm provides a first solution typi-
cally in the first few milliseconds and then finds in-
creasingly better solutions fast. After 50-100 ms, we
are very close to, or in some cases already at, the op-
timal solution. Note that the optimal solution is not
at penalty zero, so the asymptotic behaviour of the
graph is not aimed towards the X-axis. Interrupting
ICAART 2012 - International Conference on Agents and Artificial Intelligence
338

the scheduling process at this point leads to a satis-
factory result.
In Figure 5, the effects of pruning are depicted.
The tree depth is correlated to the number of nodes
calculated on that level using our BFS tree search. If
no pruning was applied, the graph would be a straight
line on the logarithmic scale. Using the penalty of the
best solution found so far (which drops rather rapidly
as we saw in Figure 4) as an upper bound enables us
to severly prune the tree fast. The symbols correspond
to the point when the optimal solution was found.
6 CONCLUSIONS AND
OUTLOOK
In this paper, we presented the Resource-constrained
Scheduling Problem (RCSP), which is like the well
known Resource-constrained Project Scheduling
Problem (RCPSP) a combinatorial optimization
problem. The automotive domain, in which we
encountered this problem, is highly dynamic and
requires fast responses, e.g. an anytime behaviour of
the algorithm tackling this problem. We presented
a tree-search based solution for the RCSP, analyzed
its runtime behaviour, solution quality increase and
space consumption. Although the algorithm is space-
consuming when running until termination, very
good results are produced fast and the calculation can
be stopped then. We argue that the solution presented
is suitable for the scenario at hand. As a next step,
we will alternatively implement a genetic algorithm
for the problem, analyze it and compare it to the
performance of the algorithm presented here. This
will, based on a categorization of problems according
to its complexity, lead to a hybrid approach using the
most suitable mechanism for each problem.
This work was funded within the project SIM
TD
by the German Federal Ministries of Economics
and Technology as well as Education and Research,
and supported by the Federal Ministry of Transport,
Building and Urban Development.
REFERENCES
Baier, J. A., Bacchus, F., and McIlraith, S. A. (2007). A
heuristic search approach to planning with temporally
extended preferences. In Proce. 20th International
Joint Conference on AI (IJCAI-07), pages 1808–1815.
Blazewicz, J., Lenstra, J., and Kan, A. R. (1983). Schedul-
ing subject to resource constraints: Classification and
complexity. Discrete Applied Mathematics, 5:11–24.
Brucker, P. and Knust, S. (2000). A linear programming
and constraint propagation-based lower bound for the
rcpsp. European Journal of Operational Research,
127(2):355–362.
Brucker, P., Knust, S., Schoo, A., and Thiele, O. (1998).
A branch and bound algorithm for the resource-
constrained project scheduling problem. European
Journal of Operational Research, 107(2):272–288.
Cao, Y., Mahr, A., Castronovo, S., and M
¨
uller, C. (2009).
On timing and modality choice with local danger
warnings for drivers. In Proc. of the 1st Intern. Conf.
on Automotive User Interfaces and Interactive Vehic-
ular Applications (AutomotiveUI 2009), pages 75–78,
Essen. ACM Press.
Cao, Y., Mahr, A., Castronovo, S., Theune, M., Stahl, C.,
and M
¨
uller, C. (2010). Local danger warnings for
drivers: The effect of modality and level of assis-
tance on driver reaction. In Proc. Intern. Conf. on In-
telligent User Interfaces (IUI 2010), pages 239–248,
Hong Kong. ACM.
Christofides, N., Alvarez-Valdes, R., and Tamarit, J. M.
(1987). Project scheduling with resource constraints:
A branch and bound approach. European Journal of
Operational Research, 29(3):262–273.
Clausen, J., Larsen, J., Larsen, A., and Hansen, J. (2001).
Disruption management - operations research be-
tween planning and execution. Technical report, Infor-
matics and Mathematical Modelling, Technical Uni-
versity of Denmark, DTU, Richard Petersens Plads,
Building 321, DK-2800 Kgs. Lyngby.
Demassey, S., Artigues, C., and Michelon, P. (2005).
Constraint-propagation-based cutting planes: An ap-
plication to the resource-constrained project schedul-
ing problem. INFORMS JOURNAL ON COMPUT-
ING, 17:52–65.
Garey, M. R. and Johnson, D. S. (1979). Computers
and Intractability: A Guide to the Theory of NP-
Completeness (Series of Books in the Mathematical
Sciences). W. H. Freeman, first edition edition.
Johnson, T. (1967). An algorithm for the resource-
constrained project scheduling problem. PhD thesis,
M.I.T., Boston.
Kuster, J., Jannach, D., and Friedrich, G. (2007). Handling
alternative activities in resource-constrained project
scheduling problems. In Proc of 20th Intern. Joint
Conference on AI (IJCAI-07), pages 1960–1965.
Mahr, A., Cao, Y., Theune, M., Schwartz, T., and M
¨
uller,
C. (2010). What if it Suddenly Fails? Behavioural
Aspects of Advanced Driver Assistant Systems on the
Example of Local Danger Alerts. In Proc. 19th Europ.
Conf. on AI (ECAI 2010), pages 1051–1052, Lisbon.
IOS Press, Amsterdam.
Patterson, J. and Roth, G. (1976). Scheduling a project
under multiple resource constraints: a zero-one pro-
gramming approach. AIIE Transactions, 8:449–455.
Pritsker, A. A. B., Watters, L. J., and Wolfe, P. M. (1969).
Multiproject scheduling with limited resources: A
zero-one programming approach. Management Sci-
ence, 16:93–108.
Stinson, J. P., Davis, E. W., and Khumawala, B. M.
(1978). Multiple resource-constrained scheduling us-
ing branch and bound. IIE Transactions, 10:252–259.
A GRAPH-SEARCH APPROACH ON RESOURCE-CONSTRAINED SCHEDULING PROBLEMS AND ITS
APPLICATION TO ADVANCED DRIVER ASSISTANCE SYSTEMS
339
