
A COMBINED UNIFORM AND HEURISTIC SEARCH ALGORITHM
FOR MAINTAINING SHORTEST PATHS ON FULLY DYNAMIC
GRAPHS
Sandro Castronovo
1
, Bj
¨
orn Kunz
1
and Christian M
¨
uller
1,2
1
German Research Center for Artificial Intelligence (DFKI), Campus D3.2, Saarbr
¨
ucken, Germany
2
Action Line Intelligent Transportation Systems, EIT ICT labs, Saarbr
¨
ucken, Germany
Keywords:
Graph theory, Dynamic graphs, Heuristic search, Shortest paths.
Abstract:
Shortest-path problems on graphs have been studied in depth in Artificial Intelligence and Computer Science.
Search on dynamic graphs, i.e. graphs that can change their layout while searching, receives plenty of attention
today – mostly in the planning domain. Approaches often assume global knowledge on the dynamic graph, i.e.
that topology and dynamic operations are known to the algorithm. There exist use-cases however, where this
assumption cannot be made. In vehicular ad-hoc networks, for example, a vehicle is only able to recognize
the topology of the graph within wireless network transmission range. In this paper, we propose a combined
uniform and heuristic search algorithm, which maintains shortest paths in highly dynamic graphs under the
premise that graph operations are not globally known.
1 INTRODUCTION
Shortest path problems on graphs have been thor-
oughly studied in Artificial Intelligence and Com-
puter Science literature. Single-source shortest path
or all-pair shortest path problems with positive edge
weights can be solved using widely known algo-
rithms, such as Dijkstra (Dijkstra, 1959) and A*.
There are a large number of applications: modern
navigation systems, for example, use implementa-
tions of these algorithms for route planning, network
protocols use them in order to route data packets from
one physical location to another and many planning
systems in Artificial Intelligence use variants of these
algorithms.
The problem becomes significantly more chal-
lenging when we allow certain dynamic operations on
the graph while searching, such as insertions or dele-
tions of vertices as well as changes of edge weights.
This problem drew attention of research in Artificial
Intelligence and related Computer Science fields. Ap-
proaches by (Nannicini and Liberti, 2008; Koenig
et al., 2004; Misra and Oommen, 2004; Cicerone
et al., 2003; Demetrescu and Italiano, 2003; Frigioni
et al., 2000) among others assume global knowledge
on the performed graph operations. This means they
are only applicable on graphs, for which the topol-
ogy and all executed operations are known at every
point in time. (Koenig et al., 2004), for example, as-
sume that every vertex stores its distance to a start
vertex of a shortest path. They modify this informa-
tion on every graph operation and use the result for
re-calculating. Work by (Misra and Oommen, 2004)
transfers the problem into the domain of Learning Au-
tomata but also allows access to the entire topology of
the dynamic graph.
There exist applications, however, in which this
knowledge can neither be assumed nor derived. Con-
sider a vehicular ad-hoc network, for example, where
vertices are vehicles, edges are wireless connections
between two vehicles, the task is to send data from
car A to car B, and B is not in A’s transmission range.
While searching a path to B, all of the operations
above can occur in arbitrary order and number, be-
cause the topology of the underlying graph is subject
to fast deletion and insertions of vertices and the algo-
rithm has no information about these changes. Hence,
we look at a ”fully dynamic problem” (Dynamic Sin-
gle Source Shortest Path Problem, or DSSSP). In our
example, the dynamic operations may even break the
connection between vertices. Furthermore, it is not
efficient and sometimes even not feasible to visit ev-
ery vertex after a graph operation. Network band-
width is considered a limited resource in vehicular
ad-hoc networks, which is also a reason why the cited
algorithms are not applicable here.
119
Castronovo S., Kunz B. and Müller C..
A COMBINED UNIFORM AND HEURISTIC SEARCH ALGORITHM FOR MAINTAINING SHORTEST PATHS ON FULLY DYNAMIC GRAPHS.
DOI: 10.5220/0003743401190126
In Proceedings of the 4th International Conference on Agents and Artificial Intelligence (ICAART-2012), pages 119-126
ISBN: 978-989-8425-95-9
Copyright
c
2012 SCITEPRESS (Science and Technology Publications, Lda.)

In this paper, we propose a combined uniform and
heuristic search algorithm, which is able to solve the
single-source shortest path problem under unknown
topology changes in fully dynamic graphs. In order
to do so we instantiate two graphs: The first, G =
(V, E), is static. We solve the single-source shortest
path problem on G using Dijkstra’s algorithm. The
second,
˜
G = (
˜
V ,
˜
E), is subject to the described graph
operations. We then exploit domain specific relations
between the two graphs and approximate the shortest
path identified on G in
˜
G. Our algorithm only depends
on local information about graph operations in order
to heuristically maintain or alter the initial path found
in G.
2 RELATED WORK
(Koenig et al., 2004) propose an incremental ver-
sion of the popular A* algorithm based on a dynamic
gridworld. This world consists of cells which de-
note vertices. Edges are drawn between neighbour-
ing cells. The algorithm continously finds shortest
paths between a start cell s
start
and a goal cell s
goal
.
Their approach is incremental since they reuse results
from previous searches. However, they assume global
knowledge about the gridworld: The algorithm holds
data structures for the start distance of every cell as
well as a list of traversable and blocked cells. In our
application domain this assumption cannot be made.
The approach of (Misra and Oommen, 2004)
transfers the DSSSP problem into the domain of
Learning Automata. They establish three compo-
nents: The learning automaton (LA), which is in-
stantiated in every vertex, the random environment
(RE) and a penalty/reward system. RE changes edge
weights using stochastic information and LA con-
stantly interacts with this environment by guessing
whether or not a node belongs to the shortest path.
The LA constantly receives rewards or penalties de-
pending on whether its guess was right or not. Al-
though the distribution of the weight changes by the
RE are unknown to LA, it is allowed to retrieve a
snapshot of the whole graph and its current edge
weights. Basically, this snapshot, Dijkstra’s algorithm
and the received penalities/rewards are used for short-
est path computation. It is obvious that in our domain
such a snapshot of the whole graph is not available.
(Frigioni et al., 2000) propose fully dynamic al-
gorithms for solving DSSSP by counting the vertices
affected by changes of the graph. When increasing
the weight of an edge, the affected vertices are those
which change the distance from the start vertex. The
algorithm marks vertices according to their status af-
ter a graph operation; White marked vertices were
not affected by an operation. Neither the distance
from the source nor the parent in the shortest path
tree changed. Red marked vertices increased their
distance from the source while the distance of the
ones marked pink remained constant but it replaces
the old parent in the shortest path tree. Obviously,
this approach also relies on global knowledge about
the graph topology and the operations on it.
(Seet et al., 2004) (SEET) and (Granelli et al.,
2007) (GRANELLI) are both routing protocols for ve-
hicular ad-hoc networks. Both implementations have
to solve the single-source shortest path problem in dy-
namic graphs having no knowledge about its topol-
ogy by the very nature of their application domain.
The approach by (Seet et al., 2004) is to employ two
graphs: One fixed, one dynamic. There exists a con-
nection between the two in a way such that the topol-
ogy of the fixed graph correlates with the dynamic
one. By solving the SSSP on the fixed graph they
try to approximate this path in the dynamic one. We
adopt this idea but also take local information about
graph operations into account allowing us to dynami-
cally assign lower weights to edges in the fixed graph
for solving the SSSP. This allows our algorithm to
adapt the path on the static graph according to the lo-
cally known changes in the dynamic one.
The key idea behind (Granelli et al., 2007) is to
estimate the topology of the dynamic graph by using
information about the neighbouring vertices. More
precisely they try to estimate the position of neigh-
bouring vehicles by using their respective velocity
and direction vector. Our approach also assumes cer-
tain knowledge, e.g. the route on the map a vehicle
is driving along, about the surrounding topology of a
given vertex (see Section 3) thus allowing us more ac-
curate position information since we can also take the
curvature of a street into account by computing the
position along it.
3 SHORTEST PATH
COMPUTATION UNDER
UNKNOWN GLOBAL GRAPH
OPERATIONS
Let G = (V, E) be a weighted, directed graph, which
is fixed, i.e., no insertions and deletions are allowed.
The topology of G is known to the algorithm. Fur-
thermore,
˜
G = (
˜
V ,
˜
E) denotes a fully dynamic graph.
˜
N is a list containing all vertices, which are reachable
from a vertex ˜v ∈
˜
G with distance 1 (direct connec-
tion by one edge). Only the vertices in
˜
N are known
ICAART 2012 - International Conference on Agents and Artificial Intelligence
120

to the algorithm. The remaining topology of
˜
G is hid-
den: Neither the number of vertices is known nor the
edges between them. In order to give the reader a
clear understanding of these notions, Figure 1 exem-
plifies these terms when applied to the domain of ve-
hicular ad-hoc networks: Our algorithm is running on
green Vehicle 1. Black points mark vertices v ∈ G,
here: junctions. Connecting lines in between mark
edges e ∈ G (streets). All vehicles in light blue are lo-
cated within transmission range and thus are elements
of list
˜
N. Vehicles form vertices of dynamic graph
˜
G. Dotted lines between them mark edges ˜e ∈
˜
G, e.g.
wireless connections. Note, that there is no (direct)
edge between vehicle 1 and black vehicles 6,7 and 8
since they are out of transmission range.
Figure 1: Notations used throughout the paper on the exam-
ple of vehicular ad-hoc networks.
We define a set of functions that can be queried by
every vertex in
˜
G:
1. A function
˜
f :
˜
V × T → E × R
+
maps a vertex
˜v ∈
˜
G to exactly one edge e ∈ E. Moreover, it
generates a virtual edge between the vertex ˜v and
the start vertex of the assigned edge e and sets a
weight depending on the specific application do-
main. For example, we can interpret this as the
distance vehicle ˜v travelled along a road e.
˜
f up-
dates this mapping and weight in specific time in-
tervals thus enabling the algorithm to see a snap-
shot of the neighbouring topology of
˜
G at a point
in time t ∈ T . Hence, a request to
˜
f requires a
time t ∈ T. Note, that a vertex ˜v ∈
˜
G is only al-
lowed to query vertices in
˜
N, which contains di-
rect neighbours within transmission range. Fur-
thermore, queries to future edge weights return
null. Also note, that the dynamic graph changes
very quickly and
˜
f only provides a snapshot of
the neighbouring topology of
˜
G.
2. A function w : V ×
˜
V × T → R
+
returns a weight
of a virtually drawn edge between a vertex in
˜
G
and a vertex in G. Only queries to elements in
˜
N
are allowed since the knowledge in a vertex ˜v ∈
˜
V
is restricted to its direct neighbours. In contrast
to the virtual edge in
˜
f for vehicular ad-hoc net-
works this gives us the euclidian distance of a ve-
hicle ˜v ∈
˜
V to a crossing v ∈ V .
3. A function ˜g :
˜
V → List < E > maps every ˜v ∈
˜
V
to a sequence of edges e
1
, ..., e
n
∈ E effectively
describing the path of ˜v on G. In vehicular ad-hoc
networks this maps to the most probable path of a
vehicle.
After solving the SSSP on fixed graph G yielding
shortest path P, the algorithm’s task is now to approx-
imate P in
˜
G by making use of the information avail-
able from the defined functions
˜
f ,w and ˜g. In the fol-
lowing, we denote the aproximated shortest path as
˜
P.
Note, that P is an array of vertices in G (in ascending
order).
Our algorithm is divided into seven steps, which
are summarized in Table 1. First, we check if the des-
tination vertex
˜
d ∈
˜
V is a direct neighbour, e.g. an
element in
˜
N. In this case, no shortest path compu-
tation is necessary and the algorithm terminates after
adding ˜v to
˜
P.
If the destination vertex is not contained in
˜
N, we
proceed with solving SSSP on G using a modified Di-
jkstra: Our Dijkstra implementation takes the number
of mappings of all ˜v ∈
˜
N by ˜g to edges in G into ac-
count (as far this can be determined by the vertices
contained in
˜
N and queries to ˜g). It assigns lower
weights on edges in G where density of mappings
is higher. This is done before every vertex decision
for
˜
P to accomodate fast topology changes within the
graph.
We then estimate future edge weights of all ver-
tices in
˜
N to the start vertices of their mapped edge
in G. This is especially necessary at low update rates
by
˜
f to the vertices in
˜
N. Since our application do-
main are vehicular ad-hoc networks we have to con-
sider this fact. A car traveling by 36 m/s on a motor-
way covers a substantial amount of a car’s transmis-
sion range between two position updates. Hence an
update by
˜
f could delete an edge in
˜
G.
The following three steps are crucial for the algo-
rithm since the decision on next vertex for
˜
P depends
on them. Every vertex in
˜
N gets assigned three heuris-
tics within the interval of [0, 1] where higher values
denote higher priority in selecting the next vertex for
˜
P. The three heuristics are given in Table 1, rows 4 –
6.
A COMBINED UNIFORM AND HEURISTIC SEARCH ALGORITHM FOR MAINTAINING SHORTEST PATHS ON
FULLY DYNAMIC GRAPHS
121

Table 1: High level steps and actions of the search algo-
rithm.
# Step Action(s)
1 Check necessitiy
of Single Source
Shortest Path
computation
Check if a ˜v ∈
˜
N is a destina-
tion. Add ˜v to
˜
P and termi-
nate if true or continue other-
wise
2 Solve single-source
shortest path prob-
lem on G
Change weights of edges in
G according to number of
mappings of vertices ∈
˜
N
to edges ∈ G. Use Dijk-
stra’s Algorithm to compute
the shortest path from source
to destination
3 Update neighbour
weights
Calculate estimated weights
∀ ˜v ∈
˜
N to the start vertex of
their mapped edges in G
4 Calculate edge
weights between
v ∈ P and ˜v ∈
˜
N
Prefer vertices with minimal
edge weight between virtu-
ally drawn edges between
vertices v ∈ P and vertices
˜v ∈
˜
N. Weight the result with
predefined α
5 Calculate mappings
of ˜v ∈
˜
N with with
edges in P
Prefer vertices whose map-
ping by
˜
f is close to edges in
P over others. Weight the re-
sult with predefined β
6 Calculate edge
weights along P
Prefer vertices in with larger
sum of edge weights on P be-
fore others. Weight the result
with predefined γ
7 Update
˜
P Select a vertex ˜v ∈
˜
N accord-
ing to computed heuristics in
steps 4 – 6 and add it to
˜
P or
wait until next update from f
to
˜
N if no vertex can be se-
lected. Repeat steps 1 – 7 un-
til destination reached
Each heuristic is multiplied by a weight of α, β
and γ respectively. The computations of the three
heuristics are described in detail below. The final step
is to select a vertex in
˜
N for
˜
P based on the heuris-
tics computed in the steps before or restart the algo-
rithm on the vertex until we have have reached a ver-
tex close to destination vertex d.
Estimating Future Weights. The procedure for es-
timating future weights is given in Algorithm 1. Since
˜
f updates
˜
N only in specific intervals and the topol-
ogy of
˜
G changes very quickly we try to estimate the
topology of the neighbouring vertices in
˜
G. The idea
is to query
˜
f on the edge weights of all vertices con-
tained in
˜
N at time t and t − 1. We then use the delta
of the two weights and add it to the current weight of
a vertex in
˜
N. We have to distinguish two cases here:
(1) At time t and time t
t−1
vertex ˜v maps to the same
edge in G, (2) At time t and time t
t−1
vertex ˜v maps to
different edge in G (line 4). This influences how ∆w
is calculated (lines 5 – 10).
If the estimated edge weight is larger than the
weight of the currently assigend edge of ˜v we do not
only estimate the weight, we also set the future as-
signed edge of ˜v using ˜g.
We store the updated values directly in ˜v.
Algorithm 1: Estimate future edge weights.
1: for all (˜v ∈
˜
N) do
2: w
t
←
˜
f ( ˜v,t).w
3: w
t−1
←
˜
f ( ˜v,t
t−1
).w
4: if (
˜
f ( ˜v,t).e ==
˜
f ( ˜v,t
t−1
).e) then
5: ∆w ← w
t
− w
t−1
6: w
est
← w
t
+ ∆w
7: else
8: w
t−1
←
˜
f ( ˜v,t
t−1
).e.w −
˜
f ( ˜v,t
t−1
).w
9: ∆w ← w
t
+ w
t−1
10: w
est
← w
t
+ ∆w
11: end if
12: if (w
est
>
˜
f ( ˜v,t).e.w) then
13: E ← ˜g( ˜v)
14: for (i ← 0; i < E.length − 1; i + +) do
15: if (E[i] ==
˜
f ( ˜v,t).e) then
16: ˜v.e ← E[i + 1]
17: ˜v.w ← w
est
− E[i].w
18: end if
19: end for
20: else
21: ˜v.w ← w
est
22: end if
23: end for
Heuristic 1: Edge Weights between v ∈ P and ˜v ∈
˜
N. Alogrithm 2 shows how the first heuristic is com-
puted for selecting the next vertex for
˜
P. The idea here
is to use w in order to identify the vertex ˜v ∈
˜
N with
minimum weight to a vertex v ∈ P. It is obvious to
prefer these edges for
˜
P since they come close to the
initial found path P.
The code is executed for ∀ ˜v ∈
˜
N from the previ-
ous step and computes ∀v ∈ P the weight of an edge
between a vertex ˜v ∈
˜
G to a vertex v ∈ G (line 4-
7). We only consider vertices up to a certain weight
w
max
. (lines 8-10). Heuristic 1 is then defined as
m
1
= α ∗ (1 −
w
w
max
) (line 11). Remember, that higher
values denote higher priority in selecting the next ver-
tex for
˜
P. Heuristic 1 is optimizing the stability of the
path
˜
P since it prefers vertices ˜v ∈
˜
V that are close to
the path vertices in P. In vehicular ad-hoc networks
we can interpret this as prefering vehicles that are on
street junctions which form natural turning points in
the street graph.
ICAART 2012 - International Conference on Agents and Artificial Intelligence
122

Algorithm 2: Heuristic 1: Edge weights between v ∈ P and
˜v ∈
˜
N.
1: for all ( ˜v ∈
˜
N) do
2: w ← ∞
3: for all (v ∈ P) do
4: if (w(v, ˜v, t) < w) then
5: w ← w(v, ˜v, t)
6: end if
7: if (w > w
max
) then
8: w ← w
max
9: end if
10: end for
11: ˜v.h
1
← α ∗ (1 −
w
w
max
)
12: end for
Heuristic 2: Mappings of ˜v ∈
˜
N with Edges in P.
Heuristic 2 is computed as stated in algorithm 3. As
for heuristic 1, the code is executed ∀ ˜v ∈
˜
N. It scores
vertices in
˜
N higher whose mappings to edges in G
matches more edges in P over others. Furthermore,
we take the direction of the edge into account: An
exact match gets assigned a score of ω. If the mapped
edge of ˜v is the opposite of an edge in P we assign
τ. If no match is detected, we assign a score of 0.
Note, that we require ω > τ. The actual values used
for evaluation are given in table 2.
Score
max
is defined as
∑
|P|−1
i=0
ω. Heuristic 2 is de-
fined as β ∗
score
score
max
, yielding to a value in the range
[0, 1] where larger values denote higher priority in se-
lecting the next vertex for
˜
P. Finally, we assign the
weight β and store heuristic h
2
in ˜v (line 14). Heuris-
tic 2 is trying to optimize path stability by prefering
˜v ∈
˜
V whose own path along G covers more of path
P, the idea being that if ˜v cannot find next vertex for
˜
P it at least gets closer to the destination. In vehicular
ad-hoc network terms we can interpret this as prefer-
ing a vehicle that can carry the message closer to the
destination in the case when a more suitable vehicle
cannot be found.
Heuristic 3: Edge Weights along P. The pseu-
docode for the third heuristic is given in Algorithm
4. It favours vertices in
˜
N with larger sum of edge
weights on P before others. We first look at the cur-
rent mapping of vertex ˜v ∈
˜
N to an edge in G and
distinguish two cases:
• P contains the Current Mapping. We add up
the weight of edges e ∈ P starting from P[0] to the
current mapping of ˜v (lines 5-13)
• P doesn’t Contain the Current Mapping. We
add up the weight of every edge e ∈ P until the
vertex with the least weight from ˜v to a vertex v ∈
P (lines 15-30)
Algorithm 3: Heuristic 2: Mappings of ˜v ∈
˜
N with with
edges in P.
1: for all ( ˜v ∈
˜
N) do
2: currentScore ← 0
3: for (i ← 0; i < P.size − 2; i + +) do
4: p
1
← P[i]
5: p
2
← P[i + 1]
6: if (edge(p
1
, p
2
) ∈ ˜g( ˜v)) then
7: currentScore ← currentScore + ω
8: else
9: if (edge(p
2
, p
1
) ∈ ˜g( ˜v)) then
10: currentScore ← currentScore + τ
11: end if
12: end if
13: end for
14: ˜v.h
2
← β ∗ (
currentScore
score
max
)
15: end for
Like before, we calculate a heuristic in the interval
(0,1) We multiply by a weight of γ (line 31). Also
here, larger values denote higher priority in selecting
the next vertex for
˜
P. In constrast to heuristic 1 and
2 this heuristics tries to optimize progress towards the
destination by choosing the next vertex ˜v ∈
˜
V that is
furthest along P. In vehicular ad-hoc networks this
means choosing the vehicle furthest along the guiding
path on the street map.
Selecting the Next Vertex for
˜
P. After calculating
the heuristics described in the previous sections we
can now select a vertex in
˜
N for
˜
P. Let H be the
set containing the sums of h
1
, h
2
, h
3
∀n ∈
˜
N. Then,
the next vertex for
˜
P is defined as the vertex with the
largest sum in H.
If the next vertex is
˜
P[
˜
P.length − 1] we re-calculate
after the next update of
˜
f .
4 EVALUATION
We integrated our algorithm into the transportation
layer of a network stack and performed a simple
point-to-point sending task in a simulator for evalu-
ation of vehicular ad-hoc network applications (V2X
Simulation Runtime Infrastructure or short VSimRTI
(N. Naumann, 2009)). VSimRTI integrates and co-
ordinates different simulators and constitutes a mid-
dleware between the individual simulators. For re-
alistic simulation we used the wireless network sim-
ulator Jist/Swans (Barr et al., 2005) and the traffic
simulation SUMO (Krajzewicz et al., 2002). We fur-
thermore integrated the effect of buildings on wireless
transmission into the simulator. Two vehicles are only
A COMBINED UNIFORM AND HEURISTIC SEARCH ALGORITHM FOR MAINTAINING SHORTEST PATHS ON
FULLY DYNAMIC GRAPHS
123

Algorithm 4: Heuristic 3: Edge weights along P.
1: w
P
← P.totalWeight
2: for all ( ˜v ∈
˜
N) do
3: e
˜v
←
˜
f ( ˜v,t).e
4: w ← 0
5: if (e
˜v
∈ P) then
6: for (i ← 0; i < P.size − 2; i + +) do
7: if (e
˜v
== edge(P[i], P[i + 1])) then
8: w ← w +
˜
f ( ˜v,t).w
9: break
10: else
11: w ← w + edge(P[i],P[i + 1]).w
12: end if
13: end for
14: else
15: leastWeight ← ∞
16: v ← nil
17: for (i ← 0; i < P.size − 1; i + +) do
18: if (w(P[i], ˜v, t) < leastWeight) then
19: leastWeight ← w(P[i], ˜v, t)
20: v ← P[i]
21: end if
22: end for
23: for (i ← 0; i < P.size − 2; i + +) do
24: if (P[i] == v) then
25: break
26: else
27: w ← w + edge(P[i],P[i + 1]).w
28: end if
29: end for
30: end if
31: ˜v.h
3
← γ ∗ (
w
w
P
)
32: end for
able to communicate if and only if there is a line of
sight between them. This serves as a lower bound on
the connection between the vehicles in the network
simulator.
We compare the performance of our algorithm
with SEET (Seet et al., 2004) and GRANELLI
(Granelli et al., 2007) in terms of path discovery ra-
tio (PDR) and path discovery time (PDT). The first
metric measures the ratio
PDR =
Success f ulShortestPathDiscoveries
TotalShortestPathSearches
and the second indicates time from beginning to end
of shortest path search PDT = t
end
−t
start
.
4.1 Implementation of
˜
f , w and ˜g
Remember that graph G = (V, E) is represented by
the underlying city map. Junctions are vertices v ∈ V ,
road segments denote edges e ∈ E.
˜
G = (
˜
V ,
˜
E) is
spanned by the vehicular ad-hoc network. Vehicles
are represented by ˜v ∈
˜
V , edges ˜e ∈
˜
E are considered
as wireless connection between two vehicles. The ab-
stract defined functions
˜
f , w and ˜g of Section 3 are
then implemented as follows: Given a time t,
˜
f as-
signs vehicles to specific road segments. Weight is
calculated out of the distance to the beginning of the
assigned road segment. In our application domain,
˜
f is responsible for controlling and updating posi-
tions of vehicles therefore realizing vehicle move-
ments over time. Function w returns the distance be-
tween a vehicle in transmission range and a junction
of the city map. The vehicles further include the road
segments which they have passed as well as their most
probable path in their position updates. This realizes
function ˜g.
4.2 Scenario
Evaluation was done in a scenario where every vehi-
cle starts one shortest path computation to a given car,
e.g. the center of the underlying city map. The des-
tination car remained stationary while all others were
driving a route on the map.
We optimzed weights for heuristics 1 – 3 introduced
in Section 3 on a randomly generated map shown in
Figure 2 (left). Weights and values for ω and τ, which
were found to be optimal for our algorithm, are given
in Table 2. We optimized for high PDR.
Figure 2: Fixed graphs used for parameter optimization and
evaluation. Left: Random generated, used for parameter
optimization (1200m x 1200m). Right: Graph generated
based on an existing road network of the city of Heidelberg,
Germany used for evaluation (1200m x 1200m).
After optimization, evaluation was done on a map
generated out of an existing city environment (Heidel-
berg, Germany, Figure 2, right). Evaluation runtime
was 120 seconds where we started shortest path com-
putation after 20 seconds simulation time. This en-
sured a fair distribution of vehicles on the map. n ve-
hicles per second were placed on the map by the sim-
ulator and removed after they completed their route
where n ∈ {1, 2, 3, 4}. For n = 1 this resulted in 120
path computations. We repeated every run three times
for every n and algorithm. This means 120 ∗ 3 = 360
path computations for n = 1 in total per algorithm and
720, 1080, 1440 for n = 2, 3, 4 respectively resulting
in a total of 3600 path searches per algorithm.
ICAART 2012 - International Conference on Agents and Artificial Intelligence
124

Figure 3: Voronoi diagrams visualizing PDR and PDT. Dots mark nodes in which path computation started, color denotes
average time until shortest path completed in the enclosed region. Left: GRANELLI (n = 4), fast but unreliable; middle: SEET
(n = 4), slower but more reliable than GRANELLI due to taking correlation of
˜
G and G into account; right: Our approach,
n = 4, taking correlation between
˜
G and G as well as local information on dynamic graph operations into account outperforms
GRANELLI and SEET.
Table 2: Values of the various weights used during the eval-
uation. The three on the left side denote the weights for the
different heuristics while the two on the right were used for
score computation of Heuristic 2 (see Algorithm 3).
Heuristic Weight Heuristic 2 score
weight value score value
α 0.5 ω 2
β 0.3 τ 1
γ 0.2
4.3 Results and Analysis
Results in Figure 4 and Figure 5 show that our ap-
proach outperforms SEET and GRANELLI in means
of PDR. As expected, PDR increases with increas-
ing traffic density. SEET obviously benefits from the
available information about the underlying city map
(the static graph G). GRANELLI lacks this kind of
information which results in a lower PDR. As our
approach also takes local information about graph
operations in
˜
G (the vehicular ad-hoc network) into
account, it scores higher PDR than both SEET and
GRANELLI. The results are statistically significant
(p < .001 according to a χ
2
test).
However, by means of PDT, GRANELLI is su-
perior to SEET and our approach. Both, SEET and
our approach re-schedule path searching in a vertex
when no suitable successor vertex could be identified
for the shortest path (see Section 3). GRANELLI’s
behaviour in such a situation is to greedily select
a next vertex out of the neighbouring vertices and
do no re-scheduling at all. This also justifies low
PDR for GRANELLI. Interestingly, PDT increases for
GRANELLI but decreases for both SEET and our ap-
proach when there are more vehicles on the graph.
In this case both, SEET and our approach have an
0
0,23
0,45
0,68
0,90
120 240 360 480
GRANELLI
SEET
Our approach
Figure 4: Path Discovery Ratio (PDR) results for all three
algorithms. X-Axis gives the number of path searches, y-
axis gives the percentage of successful path searches. As
expected, PDR increases with a larger number of cars on
the evaluation scenario.
increased number of vertices available for choosing
the next vertex for the shortest path and the propa-
bility of finding a suitable one also increases since
re-computing time for heuristics is lower than the re-
scheduling interval PDT decreases in this case. Be-
cause our approach considers local information about
graph operations it superseeds SEET by means of
PDT over time which results in a lower number of
re-schedules.
Figure 3 depicts voronoi visualizations for all
three algorithms after a run with n = 4. Black dots
mark starting positions for shortest path computation.
Enclosing colored areas denote PDT to the centre of
the map for an individual path in ms (more red ar-
eas mark higher PDT). After a threshold of 15000 ms
path computation was stopped and marked as failed.
A COMBINED UNIFORM AND HEURISTIC SEARCH ALGORITHM FOR MAINTAINING SHORTEST PATHS ON
FULLY DYNAMIC GRAPHS
125
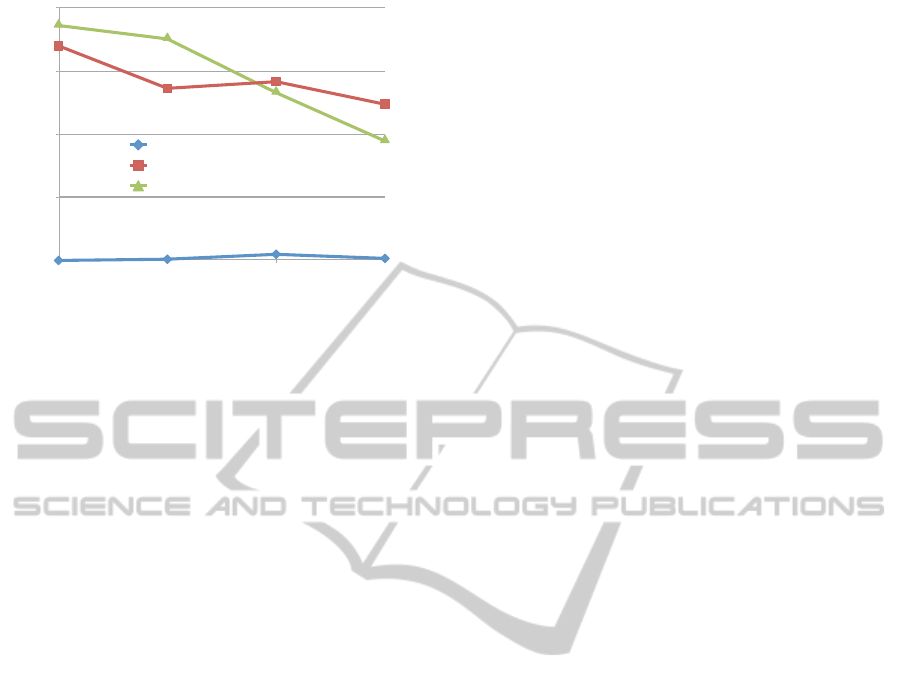
0
1500
3000
4500
6000
120 240 360 480
GRANELLI
SEET
Our approach
Figure 5: Path Discovery Time (PDT) for all three algo-
rithms. X-Axis gives the number of path searches, y-axis
gives the time in ms. GRANELLI does not reschedule when
no suitable successor vertex for the shortest path can be
found. By increasing the number of vertices in the graph,
PDT gets lower for SEET and our approach.
One clearly recognizes short PDT of GRANELLI but
low PDR: Paths are found quickly or not at all. Re-
scheduling in cases when no successor vertex for
the shortest path can be identified results in stepwise
PDTs. Results of our approach reflect high PDR even
for large path lenghts due to exploiting local informa-
tion on dynamic graph operations.
5 CONCLUSIONS
In this paper, we developed a combined uniform
and heuristic search algorithm for maintaining short-
est paths in fully dynamic graphs. While other
approaches assume global knowledge on performed
graph operations, we argued that there exist use cases
where this information is not available. Our approach
shows that in those cases the algorithms’ performance
can greatly benefit from considering domain specific
knowledge. In our example, we instantiated two
graphs: A static and dynamic one. We exploited do-
main specific relations between these graphs in or-
der to heuristically maintain a shortest path in a dy-
namic graph. The used heuristics are also tailored
to the domain. We applied our approach to vehicu-
lar ad-hoc networks and integrated it into the trans-
portation layer of a network stack to use it for routing
data packets between two vehicles. Evaluation was
performed against two other routing algorithm of this
domain. Due to re-scheduling when no neighbouring
vertex could be identified during shortest path search,
the approach of GRANELLI is superior to our imple-
mentation in means of PDT. However, our approach
outperformed SEET and GRANELLI in means of PDR.
REFERENCES
Barr, R., Haas, Z. J., and van Renesse, R. (2005). Jist:
An efficient approach to simulation using virtual ma-
chines. Software Practice & Experience, 35(6):539–
576.
Cicerone, S., Stefano, G. D., Frigioni, D., and Nanni, U.
(2003). A fully dynamic algorithm for distributed
shortest paths. Theoretical Computer Science, 297:1–
3.
Demetrescu, C. and Italiano, G. F. (2003). A new approach
to dynamic all pairs shortest paths. In Proceedings
of the thirty-fifth annual ACM symposium on Theory
of computing, STOC ’03, pages 159–166, New York,
NY, USA. ACM.
Dijkstra, E. W. (1959). A note on two problems in con-
nection with graphs. Numerische Mathematik, 1:269–
271.
Frigioni, D., Spaccamela, A. M., and Nanni, U. (2000).
Fully dynamic algorithms for maintaining shortest
path trees. Algorithms, 34(2):251–281.
Granelli, F., Boato, G., Kliazovich, D., and Vernazza, G.
(2007). Enhanced gpsr routing in multi-hop vehicular
communications through movement awareness. IEEE
COMMUNICATIONS LETTERS, 11(10):781–783.
Koenig, S., Likhachev, M., and Furcy, D. (2004). Lifelong
planning A*. Artif. Intell., 155:93–146.
Krajzewicz, D., Hertkorn, G., R
¨
ossel, C., and Wagner, P.
(2002). Sumo (simulation of urban mobility); an
open-source traffic simulation. In Proceedings of the
4th Middle East Symposium on Simulation and Mod-
elling.
Misra, S. and Oommen, B. J. (2004). Stochastic learn-
ing automata-based dynamic algorithms for the sin-
gle source shortest path problem. In Proceedings of
the 17th international conference on Innovations in
applied artificial intelligence, IEA/AIE’2004, pages
239–248. Springer Springer Verlag Inc.
N. Naumann, B. Schuenemann, I. R. (2009). Vsimrti - sim-
ulation runtime infrastructure for v2x communication
scenarios. In Proceedings of the 16th World Congress
and Exhibition on Intelligent Transport Systems and
Services.
Nannicini, G. and Liberti, L. (2008). Shortest paths on dy-
namic graphs.
Seet, B., Liu, G., Lee, B., Foh, C., and Wong, K.-J. (2004).
A-star: A mobile ad hoc routing strategy for metropo-
lis vehicular communications. In Lecture Notes in
Computer Science Vol. 3042: IFIP-TC6 Networking
Conference.
ICAART 2012 - International Conference on Agents and Artificial Intelligence
126
