A COOPERATIVE MODEL FOR MULTI-CLASS PEER-TO-PEER

STREAMING NETWORKS

Pablo Romero, Mar

ıa Elisa Bertinat, Dar

ıo Padula, Pablo Rodr

ıguez-Bocca

and Franco Robledo Amoza

Laboratorio de Probabilidad y Estad

ıstica, Facultad de Ingenier

ıa, Universidad de la Rep

ublica, Montevideo, Uruguay

Keywords:

Peer-to-peer, Piece selection strategies, Bandwidth, Free-riding.

Abstract:

Peer-to-peer networks are strongly based on cooperation. The users, called peers, communicate basically in

a three-level based policy. In the ﬁrst one, peers discover others interested in the same content, and is called

swarm selection strategy (or swarming). Then, peers must select the best ones to cooperate, what is called

peer selection strategy. Finally, peers cooperate sending pieces to each other, and the planning must attend the

piece selection strategy.

In this paper we propose an extension of a simple model based on cooperation for peer-to-peer video streaming

networks. We assume that the swarming classiﬁes peers according to their bandwidth. In this model we meet

both the peer and the piece selection strategies, for simpliﬁed scenarios. The aim is to design network policies

in order to achieve the highest continuity of video reproduction when peers reach a stationary state. We show

that under full knowledge, the network can scale even under free-riding effects. At the same time, we provide

theoretical results that reveal Rarest First has a poor performance in comparison with other techniques. Finally,

we analyze the scalability in a worst-case scenario when a variable amount of special peers are included in the

network.

1 INTRODUCTION

An important amount of today’s Internet trafﬁc is

due to live video streaming (Bertinat et al., 2009c).

For this reason, several peer-to-peer streaming net-

works were developed in the last years. The most

successful ones are PPlive(Liu et al., 2009; Huang

et al., 2008), TVUnetwork(TVUnetworks home page,

2007), SopCast(SopCast - Free P2P internet TV,

2007), with proprietary and unpublished mesh-based

protocols (Rodr

ıguez-Bocca, 2008). Mesh-based P2P

networks are virtual unstructured networks devel-

oped at the application layer, over the Internet in-

frastructure. Bittorrent is the best known mesh-based

P2P protocol, originally created for ﬁle sharing pur-

poses (Cohen, 2003). The users, called peers, offer

their resources (bandwidth in a streaming application)

to others, basically because they share common inter-

ests. They can connect and disconnect freely. This

makes P2P networks an attractive tool for them, but

increases P2P’s design challenges, because the re-

source availability depends on them.

In P2P, the cooperation is the key element in or-

der to assure a certain quality of experience to end-

users (Rodr

ıguez-Bocca, 2008). There are three main

steps in all mesh-based P2P protocols for cooperation.

First, when a peer enters the net it should discover

other peers sharing the same content, which is called

swarm selection strategy. Once a new peer knows

other peers in his swarm, he must select the best ones

to cooperate, what is called peer selection strategy.

Once a new peer handshakes other peers, it should de-

cide which pieces of the streaming content should be

asked ﬁrst, called the piece selection strategy (Berti-

nat et al., 2009b).

The research literature related on Peer-to-Peer net-

works focused, from the beginnings, in system de-

sign and trafﬁc measurements for ﬁle sharing (Ri-

peanu, 2001; Cohen, 2003). The new challenges

adopted for streaming purposes inspired the scien-

tiﬁc community to elaborate diverse mathematical

models to understand the behavior and scalability of

streaming systems, including Markov Chains, Fluid

Models, Branching Processes and Marginal Probabil-

ities (Zhou et al., 2007; Zhao et al., 2009) . In this

work we propose an extension of the simple model

for cooperation deﬁned in (Zhou et al., 2007). There,

a pull process is considered, in which peers cooperate

with each other in order to recover a video stream-

ing content which is delivered by a server. The aim

274

Romero P., Elisa Bertinat M., Padula D., Rodríguez-Bocca P. and Robledo Amoza F..

A COOPERATIVE MODEL FOR MULTI-CLASS PEER-TO-PEER STREAMING NETWORKS.

DOI: 10.5220/0003744502740282

In Proceedings of the 1st International Conference on Operations Research and Enterprise Systems (ICORES-2012), pages 274-282

ISBN: 978-989-8425-97-3

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

is to ﬁnd an optimal permutation, that dictates the

order in which pieces must be downloaded in or-

der to achieve high continuity of video reproduction.

This model has been extensively analyzed in (Berti-

nat et al., 2009a; Bertinat et al., 2009b; Romero et al.,

2010; Rodr

ıguez, 2009; Zhao et al., 2009). Speciﬁ-

cally, in (Zhao et al., 2009) the authors state properties

of the optimal permutation for highly populated sce-

narios of identical peers, and a server with bounded

uploading capacity.

This paper is structured as follows. Section 2 de-

tails the simple model for cooperation in peer-to-peer

streaming networks originally deﬁned in (Zhou et al.,

2007). In Section 3 we summarize the main results of

combinatorial problems concerning the simple model

for cooperation. The contributions of this paper are

the introduction of an extension of this mathemat-

ical model considering different peer classes (free-

riders, normal peers, double-bandwidth peers and

super-peers), an analysis of this new model under dif-

ferent scenarios and discussion of this results. At the

same time we provide theoretical results that conﬁrm

super-peers can highly outperform the Rarest First

strategy, which is widely used nowadays for ﬁle shar-

ing purposes. We will work between the performance

of the Rarest First and super-peer strategy, given that

the performance of super-peers is not achievable in

practice. This latter fact will be also proved.

Section 4 contains a generalization of the simple

model, and an analysis of different scenarios. More

speciﬁcally, Subsection 4.1 presents the Extended

Model (EM for short). In Subsection 4.2 we show

that super-peers achieve an upper bound in the per-

formance of every possible piece selection strategy

in the simple model. Super-peers play a prestigious

role in the new model here proposed. Subsection 4.3

shows that the EM is in fact an extension of the sim-

ple model, and consequently the computational com-

plexity of its resolution is higher than the complexity

of the simple model. Subsection 4.4 shows how to

deal with free-riders under the extended model. We

deﬁne a natural hypothesis of full knowledge in the

network, in which the network scales even under pres-

ence of free-riders. However, we show that the perfor-

mance dramatically decreases if peers (or the server)

cannot recognize the different classes of peers in the

network, unless super-peers are included in the net-

work. In fact, under full knowledge (when the server

and peers can recognize the different classes of peers),

the network always scales, meaning that the continu-

ity of the video reproduction will remain high inde-

pendently of the number of peers in the network. This

fact is proved in Subsection 4.5.

The most complex interaction is between normal

and double-bandwidth peers. We analyze this sce-

nario in Section 5. Speciﬁcally, the study is focused

on the scalability of the network when a variable

amount of superpeers is present. Finally, Section 6

contains the main conclusions of this work.

2 A SIMPLE MODEL FOR

COOPERATION

Consider a static network with M identical peers with

buffer size N, and one server that contains the original

video content. The server cuts the video into pieces

and shares them in order. In each time slot, it chooses

only one peer randomly to send one piece. That peer

places the piece in the ﬁrst buffer position, and that

piece will advance one buffer position in each time

slot, until it reaches position N. Pieces from position

N are displayed at the screen of that user. It is as-

sumed that all peers are synchronized with time (i.e.

every peer plays the piece at position N, see Figure 1

for a graphical description).

Figure 1: Buffer model for each peer. Position 1 represents

the newest video piece in the network, and N the next piece

to be displayed.

All peers can also communicate with each other

in order to ask for pieces. In each time slot, every

peer chooses one of the M − 1 other peers at ran-

dom, and can get no more than one piece during that

time slot. The piece selection strategy works as fol-

lows: each peer chooses a permutation π of the set

B = {1,..., N − 1}. Each element of B represent one

position of the buffer size, without regarding the last

(position N), which is expected to be played on that

time slot. Suppose peer P

chooses peer P

. Then P

looks for position π

of its own buffer. If it has that

piece, it looks for π

and so on. Otherwise, it checks

if peer P

has that piece, and takes it. This process

is repeated until either P

gets one piece during that

time slot or it checks with no success every place of

its buffer. In the former (latter) case we say peer P

had a good (resp. bad) time slot.

In (Zhou et al., 2007), a symmetric strategy is con-

sidered, which means that every peer follows the same

piece selection strategy π. Let us call p

the proba-

bility that a peer has piece i ∈ {1, ...,N} under sta-

tionary state (this probability is the same for differ-

A COOPERATIVE MODEL FOR MULTI-CLASS PEER-TO-PEER STREAMING NETWORKS

275

ent peers because of the symmetry). It can be proved

that (Zhou et al., 2007):

(

i+1

= p

+ (1 − p

,∀i ∈ B.

(1)

Clearly, the probability of a given peer to be chosen

by the server is one out of M, so p

. We know

that under steady state we have that p

(t) = p

, so the

probability vector does not depend on time. As a con-

sequence, the piece at position i + 1 can be obtained

in two different ways. The ﬁrst one is by promotion

with time of piece at position i (with probability p

The second is because the peer did not have the piece

i (event with probability 1 − p

) but the requested peer

did (probability p

) and piece at position i was chosen

to be downloaded in the previous time slot (event with

probability s

). The strategic sequence s

represents

the probability of taking the piece at position i, given

that the requesting peer does not have that piece and

the requested does. Note that s

will depend on the

permutation, and under this model we identify piece

selection strategies with one permutation of the ele-

ments in the set B.

3 ANALYSIS OF THE SIMPLE

MODEL

The previous model was originally proposed in (Zhou

et al., 2007), and was extensively analyzed in (Berti-

nat et al., 2009a; Bertinat et al., 2009b; Romero et al.,

2010; Rodr

ıguez, 2009). Here, we summarize the

main results, and provide a new pessimistic one, that

assures the Rarest First strategy (a widely developed

technique used in BitTorrent (Cohen, 2003)) has a low

(linear) convergence rate to the perfect video quality,

when the buffer size tends to inﬁnity. At the same

time, we will show that is impossible to achieve more

than a quadratic convergence rate. Consequently, we

will work between linear and quadratic convergence

to the perfect video quality (outperforming Rarest

First), whenever the buffer tends to be unlimited. We

will formalize these ideas next. We suppose a sym-

metric network in steady state:

Deﬁnition 3.1. The continuity of the video reproduc-

tion is measured by c = p

Deﬁnition 3.2. The buffering time is L =

∑

i=1

Deﬁnition 3.1 is clear: count the number of pieces

showed at the screen and divide it by the total number

of time slots. When the number of time slots tends to

inﬁnity, we have the continuity of the video reproduc-

tion.

Deﬁnition 3.2 deserves an explanation. Suppose a

new peer P enters to that static network with an empty

buffer. In the next time slots, it will get many pieces

with high probability via requests. More precisely,

the expected number of time slots needed to reach the

steady state is the expected number of pieces of a peer,

or p

+ . .. + p

In (Zhou et al., 2007), the performance of classical

strategies are studied, named Rarest First, the Greedy

strategy, and a Mixture of them. The name Rarest

First is inspired by BitTorrent (Cohen, 2003). This

piece selection policy tries to achieve uniform distri-

bution, copying the rarest pieces in the network. In

this way, it assures that rarest pieces are easier to ﬁnd

via requests. Under this model, observe that the vec-

tor (p

)

1≤i≤N

is monotonous increasing. Then, Rarest

First takes the identity permutation π

= i, ∀i ∈ B

(ask for the ﬁrst piece in the buffer, then the second

and so on until either downloading a piece or com-

pleting a bad time slot). The strategic sequence in

Rarest First is:

= (1 −1/M)

i−1

∏

j=1

+ (1 − p

)

] (2)

Expression 2 has a simple interpretation. In order to

download the piece at position i ∈ B, the peer must fail

in all previous positions j = 1,... , i − 1 and must not

be chosen by the server (with probability 1−1/M). A

fail at position j occurs when the peer already has a

piece at position j (with probability p

) or it does not

have that piece but neither the requested peer (event

with probability (1 − p

)

). A direct induction for

i ∈ {1,... ,N} shows that s

= 1 − p

holds for Rarest

First (Zhou et al., 2007).

On the other hand, the greedy notion of the problem is

to ask ﬁrst for the nearest piece to be played (i.e. the

piece at position N − 1, because that one at position

N is being played). Then, the Greedy strategy con-

siders the permutation π

= N − i,∀i ∈ B. Its strategic

sequence is:

= (1 −1/M)

N−1

∏

j=i+1

+ (1 − p

)

] (3)

The interpretation is analogous to that of Rarest First,

but reading the buffer in the opposite way. A mixture

of both strategies can be obtained reading the buffer in

the increasing way (using Rarest First) until a certain

buffer position m : 1 < m < N, and then completing

the buffer using Greedy from position N − 1 down-to

m + 1. The “Mixture” strategies are deﬁned depend-

ing on m.

There are piece selection strategies that outperform

classical strategies, as well as the Mixture strategy.

ICORES 2012 - 1st International Conference on Operations Research and Enterprise Systems

276

In fact, in (Bertinat et al., 2009a) a subfamily of per-

mutation strategies was deﬁned with polynomial size.

That subfamily contains the classical strategies, as

well as their mixtures, and has a polynomial cardinal-

ity in terms of the buffer size. An exhaustive search

in this family permits to achieve higher continuities,

keeping at the same time reduced buffering times. A

more sophisticated design of piece selection strategies

can be found in (Romero et al., 2010). There, a sin-

gle objective function was deﬁned, which captures the

continuity and latency:

Theorem 3.3. If π is an arbitrary permutation of B

and X

is the random variable that counts the number

of steps in a good time slot, then its expected value is:

E(X

) =

M − 1

N−1

∑

i=1

i+1

− p

) (4)

Note that in Rarest First we get E(X

) ∝ N p

−

L. The convex combination of continuity and la-

tency takes a natural form in this combinatorial prob-

lem (maximize E(X

) choosing the best permutation

π). We translated this problem in a second oppor-

tunity into a suitable Asymmetric Traveling Sales-

man Problem (ATSP). Finally, an Ant Colony-based

search (Dorigo and Stutzle, 2004) permits to ﬁnd

cheap tours (or equivalently permutations) and this

permutations had a direct interpretation in the simple

model, outperforming again classical selection strate-

gies. We refer the reader to (Romero et al., 2010) for

an overview.

In the next section, we will enrich the simple

model by considering different classes of peers, ac-

cording to a swarm selection policy based on band-

width. The analysis is primarily focused on extreme

scenarios, attending the interaction of four classes of

peers: free-riders (Class 0 with zero upload band-

width), normal peers with unit bandwidth (Class 1),

double-peers with double bandwidth (Class 2) and

super-peers with unlimited bandwidth (Class 3). All

peers have unlimited downloading capacities (so, the

limitation is in the uploading bandwidth). The main

issue is to plan the network in order to maximize the

continuity of reproduction, in a more realistic model.

4 A GENERALIZATION OF THE

SIMPLE MODEL

4.1 Deﬁnition of the Extended Model

Suppose a static network that has M peers of Class X,

peers of Class Y and a server that has the original

video content (where X,Y ∈ {0,1,2,3}). The server

cuts the video into small pieces, and shares them in

turns. In each time slot, the server chooses one peer at

random from Class X with probability α, or one peer

at random from Class Y with probability 1 − α, and

sends one piece to that peer. As in the simple model,

peers can cooperate. More precisely, one peer from

Class X either chooses with probability β another peer

at random from its own class or a peer from Class Y at

random with probability 1 − β. Symmetrically, peers

from Class Y can request other peers from their own

class (chosen at random) with probability β

, or from

Class X (with probability 1 − β

). Every peer tries to

download the highest number of pieces during each

time slot, and that number will depend on the upload-

ing bandwidth of the contacted class. For example,

if a peer requests a double-peer (with double band-

width), it will be able to download two pieces during

the same time slot. The process of the request is iden-

tical to that of the simple model, but it may continue

after one piece is obtained.

Deﬁnition 4.1. A free-rider is a peer that has inﬁ-

nite downloading bandwidth, but no uploading band-

width. When a peer requests a free rider, it will get no

piece on that time slot.

In other words, it is a selﬁsh peer, that asks for

pieces but does not share them.

Deﬁnition 4.2. A normal peer has inﬁnite download-

ing bandwidth and unit uploading bandwidth. When

a peer requests a normal peer, the time slot works as

in the simple model.

Deﬁnition 4.3. A double-bandwidth peer has inﬁnite

downloading bandwidth and double uploading band-

width. When a peer requests a double-bandwidth

peer, it can get zero, one or two pieces.

For example, if one peer follows the Rarest First

strategy and requests a double-bandwidth peer, then

the request works as in the simple model. However,

if a download occurs, the peer goes on asking for the

next pieces, until downloading another one or reach-

ing position N − 1 of its buffer. An analogous request

occurs when the piece selection strategy is identiﬁed

with an arbitrary permutation.

Deﬁnition 4.4. A super-peer has both inﬁnite down-

loading and uploading bandwidth. When a peer re-

quests a super-peer, it will take all pieces in only one

time slot.

The optimization problem is speciﬁed next. The

two classes X and Y , the number of peers M and M

and the buffer size N are given. We want to plan the

network by choosing the parameters α, β and β

well as the permutation strategy π, in order to maxi-

mize the average continuity of reproduction in the net-

work. More speciﬁcally, the Extended Model (from

A COOPERATIVE MODEL FOR MULTI-CLASS PEER-TO-PEER STREAMING NETWORKS

277

now on the EM) is captured with the next optimiza-

tion problem:

max f (π,M,N,α,β) =

M p

+ M

M + M

(5)

s.t.











1−α

i+1

= p

+ (1 − p

)[βp

(X,X,π)

+ (1 − β)p

(X,Y,π)

]

i+1

= p

+ (1 − p

)[β

(Y,Y,π)

+ (1 − β

(Y,X ,π)

]

α,β,β

∈ [0,1]

where s

(X,Y,π)

is the probability that a peer from class

X is using the permutation strategy π (which is a per-

mutation of the set {1,.. .,N − 1}) and requesting a

peer from class Y takes piece at position i. These ex-

pression will be analyzed for each possible scenario.

The objective is to maximize the average quality of

experience of all peers in the network (identifying

quality with continuity of reproduction). If we re-

call that the server sends with probability α one peer

from Class X at random, then obviously p

= α/M

and p

= (1 − α)/M

hold. The next equations are

correct under steady state, and take into account the

fact that the requested peer can be from their own

class or the foreign class. We shall ﬁx the parame-

ters β and β

according to random peer selection (i.e.

β = M/(M + M

) and β

= M

/(M + M

)). In fact,

we will show that under a full knowledge assump-

tion, the network can work in optimal conditions and

the combinatorial problem is reduced to the simple

model, which has been extensively analyzed in pre-

vious works (Bertinat et al., 2009a; Bertinat et al.,

2009b; Romero et al., 2010; Rodr

ıguez, 2009). The

intuition here is that if the server as well as the peers

can discover which peers have the highest bandwidth,

then the server will send pieces to them, and all peers

will direct requests to this powerful peers (which play

the role of intermediate nodes of a tree-like structure).

There are exactly 4

−C

= 10 different interac-

tion of pairs of the four classes (we are considering

only once the cases of interaction between classes X

and Y , when X 6= Y ). Moreover, the cases of self-

interaction can be reduced to the simple model. More

precisely, the self-interaction between free-riders is

strictly inadmissible, and does not deserve our atten-

tion. The interaction between normal peers behaves

exactly as in the simple model, and between double-

bandwidth peers translates proportionally to the case

of the simple model (in fact, cut the time slot into two

half). There is something to say for the case of self-

interaction between super-peers. As a consequence,

we will focus on 7 scenarios: the six different pairs of

classes, and the simple model with inﬁnite bandwidth.

4.2 The Best Strategy for the Simple

Model

Certainly, the best piece selection strategy for the sim-

ple model occurs when all peers in the network have

inﬁnite bandwidth, and they can download all pieces

in only one time slot. In fact, in steady state the strate-

gic sequence for this case is s

= 1. This means that if

one peer does not have a piece and the requested does,

the peer always downloads that piece. Naturally, the

sequence p

is the highest possible, because:

i+1

= p

+ (1 − p

≥ p

+ (1 − p

, (6)

whenever s

≤ 1, which is obvious (s

is a probability

for every i ∈ B). Hence, the probability p

is never ex-

actly 1 (as a trivial induction can show), but the high-

est possible. By technological reasons, it is natural

to ask what happens in the case of unlimited storage

(when the buffer size N tends to inﬁnity).

Theorem 4.5. Under the simple model, the super-

peers tend to experiment perfect continuity when the

buffer tends to inﬁnity:

lim

N→∞

= 1. (7)

Moreover, the convergence order is quadratic.

Proof. Super-peers are characterized by s

= 1. Sub-

stituting in (1) we have that:

i+1

= p

(2 − p

),i ∈ B

Taking i = N − 1 we have that p

= p

N−1

(2 − p

N−1

The sequence (p

)

1≤i≤N

is monotonous increasing

and bounded by 1; hence it has a limit a. Taking N

tending to inﬁnity:

a = a(2 − a) (8)

So a = 0 or a = 1. But p

= 1/M > 0 and (p

)

1≤i≤N

is monotonous increasing. Consequently a = 1, and

lim

N→∞

= 1. (9)

Finally, its convergence order can be found easily:

lim

N→∞

1 − p

(1 − p

N−1

)

lim

N→∞

1 − p

N−1

(2 − p

N−1

)

(1 − p

N−1

)

= 1.

Hence, its convergence order is 2, and the result holds.

Observe also that super-peers achieve the smallest

buffering times, because if one super-peer enters the

network in steady state, then in one time slot reaches

the state of another super-peer.

It is interesting to compare this performance with re-

spect to the one obtained following Rarest First:

ICORES 2012 - 1st International Conference on Operations Research and Enterprise Systems

278

Theorem 4.6. The Rarest First strategy tends to have

perfect continuity when the buffer size tends to inﬁn-

ity, but its convergence order is linear.

Proof. In Rarest First s

= 1 − p

holds for all i ∈ B.

As a consequence:

(

i+1

= p

+ (1 − p

)

Again, the limit of the sequence (p

)

1≤i≤N

exists

when N tends to inﬁnity (it is a bounded increas-

ing real sequence). The limit a must comply that

a = a + (1 − a)

a. Then a = 0 or a = 1. The null

limit is discarded because the sequence (p

)

1≤i≤N

monotonous increasing and p

> 0. Hence, a = 1.

Finally, the convergence order is linear, given that:

lim

N→∞

1 − p

N−1

lim

N→∞

1 − p

N−1

− p

N−1

(1 − p

N−1

)

1 − p

N−1

= 1.

As a consequence, the piece selection strategies

will always work with convergence order p such that

1 < p < 2 when the buffer increases. In fact, we know

there are better strategies than Rarest First, and that

there is no strategy better than the one of super-peers

(download the whole buffer of the requested peer).

4.3 The EM under Full-Knowledge

From now on, we study the EM (Extended Model)

when different classes interact (i.e. X 6= Y ).

Deﬁnition 4.7. We say that the network in the EM

has full knowledge, when the server can recognize

the different classes of peers in the network, and peers

can deduce the best class-request (if it is better to ask

one peer from its own class or the foreign class).

Deﬁnition 4.8. A peer-class has higher level than

other when it has higher uploading bandwidth.

Deﬁnition 4.9. We say that the server is fair when

each peer in the network has the same probability of

getting a piece from it.

Deﬁnition 4.10. We say that the network is balanced

when the peer selection strategy is at random.

Theorem 4.11. The EM is computationally more

complex than the Simple Model.

Proof. We will prove that the EM is trivially re-

duced to the simple model under full knowledge and

fairness. Without loss of generality, suppose X has

higher class than Y . Then clearly a peer has more

chances to download piece at position i requesting

peers from class X rather than from class Y , and

(X,X,π)

≥ s

(X,Y,π)

. Given that peer can recognize the

highest class, then they will always choose peers from

class X to ask for pieces, so β = 1 and β

= 0. By

symmetry, observe that s

(Y,X ,π)

= s

(X,X,π)

. Denote this

number with s

for brevity. Substituting in the EM we

have that:

1 − α

i+1

= p

+ (1 − p

)[p

]

i+1

= p

+ (1 − p

)[p

]

α ∈ [0,1]

Assuming fairness, the server will send pieces

with probability α = M/(M +M

). As a consequence,

= p

= 1/(M + M

). Hence, both recursive ex-

pressions are the same, and the sequences p

and p

coincide. Moreover, the problem was reduced to:

(

i+1

= p

+ (1 − p

(10)

being π a permutation, which is exactly the simple

model with M + M

peers.

So far, we know that the peers with higher class

perform better under the simple model, and super-

peers achieve the best performance, with unit strategic

sequence (s

= 1).

4.4 Dealing with Free-riders

As we said before, the self-interaction of free-riders is

not admissible (it is evident that without cooperation

the network does not work). The reader can check

that if all peers are free-riders then p

= p

= β/M <

1/M,∀i, and this performance is not acceptable since

the network normally works with hundreds or thou-

sands of peers. Similar results are obtained for the

second class: p

= (1 −β)/M

is constant.

The interaction between free-riders and other

classes has a special treatment. Particularly, suppose

that X = 0 (free-rider class) and Y 6= 0. Under full

knowledge, the server will always choose to send

pieces to peers from class Y , so α = 0. Moreover,

free-riders will choose to complete requests consider-

ing peers from Class Y , which will prefer to do self-

requests, so β = 0 and β

= 1. Substituting in the EM:

A COOPERATIVE MODEL FOR MULTI-CLASS PEER-TO-PEER STREAMING NETWORKS

279











= 0

i+1

= p

+ (1 − p

(X,Y,π)

i+1

= p

+ (1 − p

(Y,Y,π)

As a consequence, the quality of all non-free-riders

in the network is equivalent to that of the simple

model. Note that p

= 0 but p

> 0. For example, if

the Rarest First strategy is applied, then the sequence

}

1≤i≤N

converges to 1 as N tends to inﬁnity, and

behaves exactly the same as {p

}

1≤i≤N

but with a

shift. In this way, the free-riders follow the perfor-

mance of the other class, and the network scales.

The previous discussion shows that with full

knowledge, the planning of the network reduces to

choose a piece selection strategy, or a permutation

π, as in the case of the simple model (which has

been extensively analyzed already). However, if the

server cannot identify classes, it will tune α 6= 0,

and the performance of the network dramatically

decreases, because pieces given to free-riders will be

missing for all but only one peer. Hence, the network

scales if and only if α = 0. This results outstand

the importance of the recognition of free-riders,

under this new extension of the simple model. The

full-knowledge hypothesis is strictly necessary in this

case. This is an evidence of the empirical complexity

of designing a scalable streaming network: normally

the broadcaster does not have full knowledge, and

neither peers do.

4.5 The Network with Super-peers

Naturally, when one of the classes working in the net-

work are super-peers, the cooperation is easier. With

full knowledge of the network (i.e. the server as well

as peers can recognize classes of different peers), the

server will always send pieces to super-peers, and the

other class will be pleased to complete full requests

to them, making the network scalable. The quality of

experience of every peer in the network follows, un-

der these circumstances, the one of super-peers (as if

there were no other class) in the simple model. As a

consequence, all peers will have (discarding the small

initial shift) the next probabilities:

(

= 1/M

i+1

= p

(2 − p

),∀i ∈ B,

(11)

being M the number of super-peers in the network and

the continuity of video reproduction of each peer.

When free-riders or super-peers are present inside the

network, the analysis of the EM is trivial (because the

strategic sequence is reduced to 0 or 1 respectively).

In the next section we analyze the most complex in-

teraction.

5 INTERACTION BETWEEN

NORMAL AND

DOUBLE-BANDWIDTH PEERS

5.1 Presentation of the Problem

This case is clearly the most complex to analyze. In-

tuitively, the server should send pieces to the double-

bandwidth peers, and the request always directed to

them. Under full knowledge this will happen, and

normal-peers will tend to follow the quality of double-

bandwidth peers.

Let us focus on a more realistic scenario. Choose X

as normal peers and Y double-bandwidth peers. Now,

we will ﬁnd an expression for the sequences s

(X,Y,π)

and s

(Y,Y,π)

(the other two cases are self-requests, and

expressed as in the simple model). For brevity, s

de-

notes the probability that normal-peers have to take

the ﬁrst piece from a double-bandwidth peer. If k is

such that π

k+1

= i then:

= (1 −α/M)

∏

j=1

[1 − (1 − p

] (12)

Expression (15) deserves an explanation. One peer

from class X will download the ﬁrst piece at posi-

tion i from class Y following the permutation strat-

egy π whenever it fails in all previous positions (and

success at position i) and is not chosen by the server

(with probability p

= 1 − α/M). Hence, a fail at all

positions π

, j = 1,..., k −1 such that π

= i must oc-

cur. Moreover, a fail at position π

occurs when it

is not the case that the requesting peer does not have

that piece (with probability 1− p

) and the requested

peer does (event with probability p

). Then, a fail at

position π

has probability 1 − (1 − p

Now, we are ready to express the sequence s

(X,Y,π)

= s

+ s

k−1

∑

j=1

(1 − p

1 − (1 − p

(13)

When asking a double-bandwidth peer, we can down-

load piece at position i in the ﬁrst chance (the ﬁrst

term) or we downloaded a previous position π

, j =

1,... ,k − 1 with success. The factor

(1 − p

/[1 − (1 − p

ICORES 2012 - 1st International Conference on Operations Research and Enterprise Systems

280

represents a replace of a success instead of a fail at

position π

in the expression s

In a similar way, the strategic sequence s

(Y,Y,π)

is:

(Y,Y,π)

= s

∗

+ s

∗

k−1

∑

j=1

(1 − p

1 − (1 − p

, (14)

where

∗

= (1 −(1 − α)/M)

k−1:π

∏

j=1

[1 − (1 − p

(15)

The EM can be obtained for this interaction by sub-

stitution.

5.2 Empirical Results

We will concentrate on a worst case scenario, by tak-

ing the Rarest First strategy (i.e. π

= i), and ana-

lyzing the scalability of the network under different

mass of double-bandwidth peers, with no knowledge

of the network, which imples that the peer selection is

balanced: β = M/(M + M

) and β

= M

/(M + M

Consider the common-network values M +M

= 1000

and N = 40. Table 1 presents the objective function

f (α,M) = (M p

+ M

)/(M + M

) when the mass

of double-bandwidth peers is variable accordingly

with M

∈ {350,250,150,100,0} double-bandwidth

peers and correspondingly M = 1000 − M

normal

peers. Table 2 contains the function p

− p

taking

the same set for M and probability α.

Table 1: Expected continuity f (α,M) for a balanced net-

work with different number of double-bandwidth peers.

α 350 250 150 100 0

0.0 1.0000 0.9998 0.9979 0.9941 0.9666

0.1 1.0000 0.9998 0.9979 0.9940 0.9665

0.2 1.0000 0.9998 0.9978 0.9939 0.9663

0.3 1.0000 0.9998 0.9978 0.9938 0.9661

0.4 1.0000 0.9998 0.9977 0.9937 0.9658

0.5 1.0000 0.9998 0.9977 0.9936 0.9655

0.6 1.0000 0.9998 0.9976 0.9934 0.9651

0.7 1.0000 0.9997 0.9975 0.9932 0.9646

0.8 1.0000 0.9997 0.9974 0.9929 0.9638

0.9 1.0000 0.9997 0.9972 0.9925 0.9625

1.0 1.0000 0.9997 0.9970 0.9918 impossible

It can be appreciated from Table 1 that the net-

work always scales, although the server cannot recog-

nize peers and tunes incorrectly the parameter α. Cer-

tainly, the performance is the best when α = 0 (that

is, to choose always double-bandwidth peers to send

pieces). It can be noticed that the average continuity is

higher than 96% in all instances, so the video quality

is high. It is interesting to analyze if the video qual-

ity of normal peers is similar to double-peers or not.

Table 2 contains the difference of continuity p

− p

Table 2: Difference in continuity p

− p

between double-

bandwidth peers and normal peers, with different number

of normal peers.

α 350 250 150 100 0

0.0 0.0002 0.0013 0.0067 0.0117 0.0006

0.1 0.0001 0.0010 0.0055 0.0094 0.0005

0.2 0.0001 0.0008 0.0041 0.0071 0.0004

0.3 0.0001 0.0005 0.0028 0.0048 0.0002

0.4 0.0000 0.0003 0.0014 0.0024 0.0001

0.5 0 0 0 0 0

0.6 -0.0000 -0.0003 -0.0015 -0.0025 -0.0001

0.7 -0.0001 -0.0006 -0.0030 -0.0051 -0.0003

0.8 -0.0001 -0.0009 -0.0047 -0.0077 -0.0004

0.9 -0.0002 -0.0013 -0.0065 -0.0106 -0.0006

1.0 -0.0002 -0.0017 -0.0086 -0.0140 impossible

It is obvious that when the parameter α increases, the

quality of normal peers is increased as well. More-

over, in the case α = 0.5 both classes of peers exper-

iment the same video quality, and there is a symme-

try in the instances α = i/10 and α = (10 − i)/10.

It is evident that peers can follow double-bandwidth

peers, and peers have better continuity than super-

peer when α > 0.5. This empirical analysis shows

that the network scales when peers and double-peers

interact, even under pessimistic scenarios. A further

experiment with the balanced case of α = 0.5 shows

the scalability property of this network when the stor-

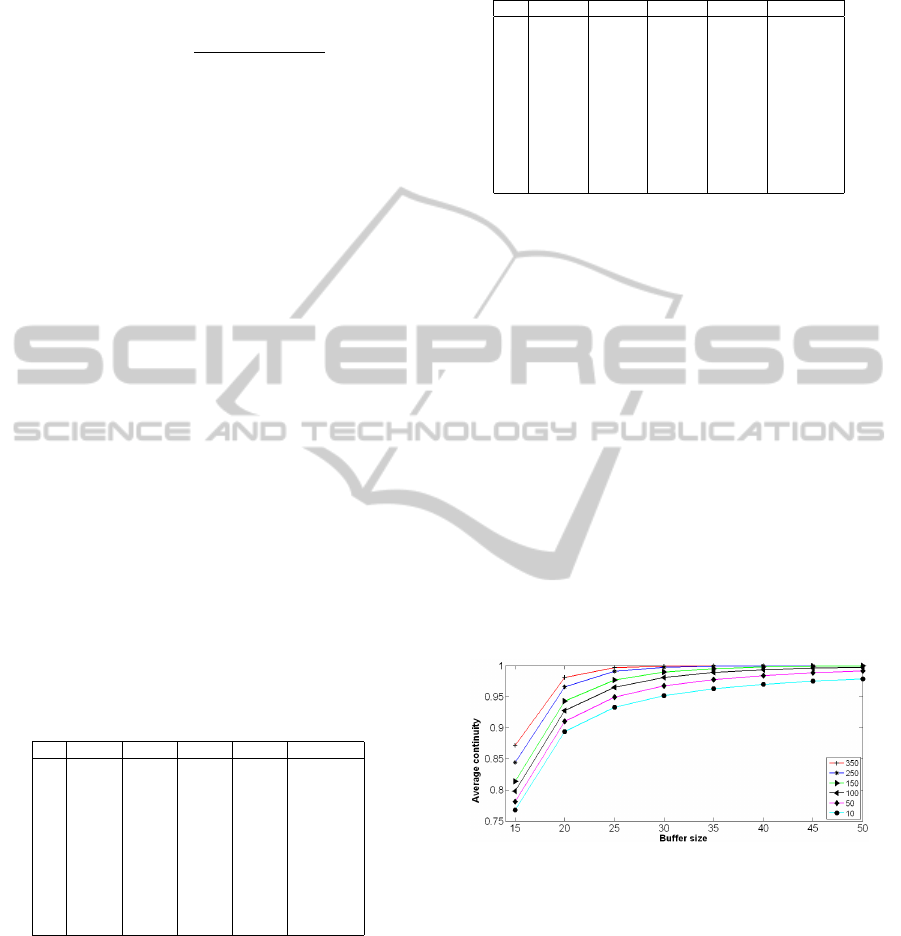
age size increases. Figure 2 reveals the average con-

tinuity of normal (and double-bandwidth) peers as a

function of the buffer size N, considering again dif-

ferent amounts of double-bandwidth peers. It can be

appreciated that the average continuity is higher than

90% when the storage capacity is higher than 25, even

when the number of double-bandwidth peers is small.

Figure 2: Evolution of the average continuity of peers as a

function of the buffer storage capacity N.

6 CONCLUSIONS AND FUTURE

WORK

This paper proposes an extension of a simple model

for cooperation in peer-to-peer streaming networks.

This model assumes a swarming policy based on up-

loading bandwidth, classifying peers as free-riders,

normal, double-bandwidth and super-peers with inﬁ-

nite bandwidth. A primitive analysis demonstrates the

strength of the full knowledge hypothesis in the net-

A COOPERATIVE MODEL FOR MULTI-CLASS PEER-TO-PEER STREAMING NETWORKS

281

work. In fact, the scalability of the network is guaran-

teed whenever the server as well as peers can recog-

nize different classes. When free-riders interact with

other classes, peers will always experiment cuts in the

video content, unless the server sends pieces to non-

free-riders. On the other hand, when super-peers take

part of it, the network scales.

The performance of the Rarest First strategy was con-

trasted with the one of super-peers. Particularly, the

convergence to the perfect probability is faster for

super-peers. Moreover, there is no real strategy that

can achieve quadratic convergence to the perfect con-

tinuity, even with high buffer size. Finally, the most

complex scenario considered the interaction between

normal and double-bandwidth peers, and was ana-

lyzed via simulations. Although there exist many

piece selection strategies with higher performance

than Rarest First, the results show that the network

scales using the latter strategy. This is an encourag-

ing result, which motivates to apply different piece

selection strategies. We have extensively analyzed

the simple model, and we are currently approaching

the general EM via metaheuristics. As a future work,

we point to apply the results in a real peer-to-peer

platform named GoalBit, an open source real plat-

form that widely offers live video-streaming to end

users(Bertinat et al., 2009c). It is worth to mention

that we do not know a global model for peer-to-peer

streaming networks that integrates swarming, peer se-

lection and piece selection strategies. It sounds ambi-

tious, and the model here proposed takes into account

peers as well as piece selection strategies, in a coop-

erative simpliﬁed environment.

ACKNOWLEDGEMENTS

The authors are pleased to thank the reviewers for

their constructive comments, and Lic. Fernanda

Fern

andez for her corrections. This work was par-

tially supported by project “Sistema eﬁciente de dis-

tribuci

on de video y TV en tiempo real”, for the na-

tional telephony operator ANTEL.

REFERENCES

Bertinat, M. E., Vera, D. D., Padula, D., Robledo, F.,

Rodr

ıguez-Bocca, P., and Romero, P. (2009a). Sys-

tematic procedure for improving continuity and la-

tency on a p2p streaming protocol. In Proceedings

of the 1th IEEE Latin-American Conference on Com-

munications (LatinCom’09), Washington, DC, USA.

IEEE Computer Society.

Bertinat, M. E., Vera, D. D., Padula, D., Robledo, F.,

Rodr

ıguez-Bocca, P., Romero, P., and Rubino, G.

(2009b). A cop for cooperation in a p2p stream-

ing protocol. In Proceedings of the IEEE Inter-

national Conference on Ultra Modern Telecommuni-

cations (ICUMT’09), Washington, DC, USA. IEEE

Computer Society.

Bertinat, M. E., Vera, D. D., Padula, D., Robledo, F.,

Rodr

ıguez-Bocca, P., Romero, P., and Rubino, G.

(2009c). Goalbit: The ﬁrst free and open source peer-

to-peer streaming network. In Proceedings of the 5th

international IFIP/ACM Latin American conference

on Networking (LANC’09), pages 83–93, New York,

USA. ACM.

Cohen, B. (2003). Incentives build robustness in bittorrent.

www.bramcohen.com, 1:1–5.

Dorigo, M. and Stutzle, T. (2004). Ant Colony Optimiza-

tion. MIT Press.

Huang, Y., Fu, T. Z., Chiu, D.-M., Lui, J. C., and Huang,

C. (2008). Challenges, design and analysis of a large-

scale P2P-VoD system. In ACM SIGCOMM 2008 con-

ference on Data communication, Linkoping, Swede.

Liu, Y., Guo, L., Li, F., and Chen, S. (2009). A Case Study

of Trafﬁc Locality in Internet P2P Live Streaming

Systems. In International Conference on Distributed

Computing Systems, ICDCS 2009, pages 423–432.

Ripeanu, M. (2001). Peer-to-peer architecture case study:

Gnutella network. In First International Conference

on Peer-to-Peer Computing, pages 99–100, Linkop-

ing, Sweden.

Rodr

ıguez, P. R. (2009). Optimizaci

on de la Estrategia de

Selecci

on de Piezas de Video en Redes P2P. Univer-

sidad de la Rep

ublica, Facultad de Ingenier

ıa, Insti-

tuto de Investigaci

on : LPE - IMERL. Montevideo,

Uruguay.

Rodr

ıguez-Bocca, P. (2008). Quality-centric design of Peer-

to-Peer systems for live-video broadcasting. PhD the-

sis, INRIA/IRISA, Universit

e de Rennes I, Rennes,

France.

Romero, P., Robledo, F., Rodr

ıguez-Bocca, P., Padula, D.,

and Bertinat, M. E. (2010). A cooperative network

game efﬁciently solved via an ant colony optimization

approach. In Proceedings of the Seventh International

Conference of Swarm Intelligence (ANTS’10), Lon-

don, UK. Springer, Lecture Notes in Computer Sci-

ence.

SopCast - Free P2P internet TV (2007). http://

www.sopcast.org.

TVUnetworks home page (2007). http://tvunetworks.com/.

Zhao, B., Lui, J., and Chiu, D.-M. (2009). Exploring the

optimal chunk selection policy for data-driven P2P

streaming systems. In IEEE Ninth International Con-

ference on Peer-to-Peer Computing, pages 271–280,

Hong Kong, China.

Zhou, Y., Chiu, D. M., and Lui, J. (2007). A Simple Model

for Analyzing P2P Streaming Protocols. In Proceed-

ing of the IEEE International Conference on Network

Protocols (ICNP’07), pages 226–235, Beijing, China.

ICORES 2012 - 1st International Conference on Operations Research and Enterprise Systems

282