COMPUTING THE REEB GRAPH FOR TRIANGLE MESHES WITH

ACTIVE CONTOURS

Laura Brandolini and Marco Piastra

Computer Vision and Multimedia Lab, Universit`a degli Studi di Pavia, via Ferrata 1, 27100 Pavia, Italy

Keywords:

Reeb graph, Active contours, Triangle mesh, Segmentation.

Abstract:

This paper illustrates a novel method to compute the Reeb graph for triangle meshes. The algorithm is based

on the deﬁnition of discrete, active contours as counterparts of continuous level lines. Active contours are

made up of edges and vertices with multiple presence and implicitly maintain a faithful representation of the

level lines, even in case of coarse meshes with higher genus. This approach gives a great advantage in the

identiﬁcation of the nodes in the Reeb graph and also improves the overall efﬁciency of the algorithm in that at

each step only the information local to the contours and their immediate neighborhood needs to be processed.

The validation of functional integrity for the algorithm has been carried out experimentally, with real-world

data, without mesh pre-processing.

1 INTRODUCTION

Reeb graphs are compact shape descriptors that play

a fundamental role in different ﬁelds of computer

graphics: shape matching and encoding (Sebastian

et al., 2002; Sundar et al., 2003), mesh deformation

(Tierny et al., 2006; Schaefer and Yuksel, 2007), 3D

search (Hilaga et al., 2001), mesh compression (Bia-

sotti et al., 2000), medical imaging and several other

ﬁelds. Reeb graphs enclose important shape prop-

erties like connectivity, length, width, direction and

genus in a faithful fashion.

This paper illustrates a new robust method for con-

structing Reeb graphs for 2-manifold, triangle meshes

using a predeﬁned Morse function. In the literature

there are other methods for Reeb graphs extraction,

as it will be described in Section 3. In Section 4

we propose an approach in which the Reeb graph is

constructed incrementally by evolving discrete, active

contours overthe mesh, starting from relevantminima

of the Morse function. A key aspect in the active con-

tours proposed is that both vertices and edges could

have a multiple presence and this allows a faithful

representation of the level lines of the Morse function

even when these lines are too close to each other with

respect to mesh sampling.

Experimental evidence, illustrated in Section 5,

shows that this algorithm is effective with real-world

data, without the need of pre-processing, and there-

fore suitable for practical applications.

2 THEORETICAL PRELUDE

Morse theory (Milnor, 1963) is a classical mathemat-

ical approach that has found many applications in the

ﬁeld of computationaltopology. The Morse function f

is a real-valued function deﬁned on a compact smooth

manifold M (Biasotti et al., 2008). A point x of M

where all the partial derivatives of f are zero is a crit-

ical point. A critical point x is non-degenerate if the

matrix of second order partial derivatives (Hessian)

of f at x is non-singular. A non-degenerate critical

point can only be a maximum, a minimum or a sad-

dle, while other points are called regular. We can

then deﬁne a Morse function as a smooth function f

deﬁned on M that has no degenerate critical points.

The function f is frequently required to be simple,

i.e. f(x) 6= f(y) for any pair x and y of distinct crit-

ical points.

Reeb graphs have been deﬁned by George Reeb in

1946 (Reeb, 1946). Given a compact, smooth mani-

fold M and a Morse function f deﬁned on it, the Reeb

graph “is the quotient space deﬁned by the equiva-

lence relation that identiﬁes the points belonging to

the same connected component of the level-set of f”.

Each point in a Reeb graph corresponds to a con-

nected component of a level set of the Morse function

f. In particular, each point of the arcs in the graph cor-

responds to a regular value of f, whereas each node

corresponds to a critical value of f. Reeb graphs are

compact shape descriptors which convey topological

Brandolini L. and Piastra M. (2012).

COMPUTING THE REEB GRAPH FOR TRIANGLE MESHES WITH ACTIVE CONTOURS.

In Proceedings of the 1st International Conference on Pattern Recognition Applications and Methods, pages 80-89

DOI: 10.5220/0003745500800089

 SciTePress

informationabout the shape of the manifold M. In par-

ticular for orientable, closed 2-manifolds the number

of loops in the Reeb graph corresponds to the genus of

the manifold (Cole-McLaughlin et al., 2003) and this

property does not depend on the choice of the Morse

function f.

(a) (b)

Figure 1: A discrete Morse function with two minima (see

text) (a); the corresponding discrete Reeb graph (in red),

where the nodes are emphasized in orange (b).

3 RELATED WORK

Reeb graphs have been extensively applied in recent

years in different ﬁelds of computer science, thus a

complete exploration of all the contributions about

this matter is beyond the scope of this paper. De-

tailed works on the subject of Reeb graphs for shape

analysis can be found in (Biasotti et al., 2008). The

introduction of Reeb graphs in computer graphics is

due to (Shinagawa et al., 1991) and the ﬁrst algo-

rithm to automatically compute Reeb graphs is de-

scribed in (Shinagawa and Kunii, 1991). This algo-

rithm automatically constructs the Reeb graph of a

2D manifold surface embedded in 3D using surface

contours, a weight function and an a priori knowl-

edge of the number of holes of the object. In their

work (Lazarus and Verroust, 1999) describe an algo-

rithm that constructs level-set diagrams for 0-genus

polyhedrons using geodesic distance from a source

point. (Tierny et al., 2006) propose a smart approach

based on a good choice of the Morse function f, tak-

ing feature points as the origin of function f, but the

strategy adopted for evolving contours leads to critical

contour conﬁgurations, especially in case of coarse,

real-world meshes. (Pascucci et al., 2007) propose an

on-line algorithm for Reeb graphs construction and

test its performance with different Morse functions.

Their algorithm has an iterative approach that requires

taking into account all the simplicial elements of the

mesh (vertices, edges and triangles) during the com-

putation: at each step, a new simplicial element is

considered and the Reeb graph is incrementally up-

dated, until all simplicial elements have been con-

sidered. (Shapira et al., 2008) propose an algorithm

for mesh decomposition and skeletonization using a

shape diameter function (SDF), i.e. a scalar func-

tion deﬁned on mesh faces. This technique is pose-

invariant in general, but there are positions for which

smoothing and ﬁltering are necessary. In (Edelsbrun-

ner et al., 2008) an algorithm is presented to calculate

the Reeb graph of a time-varying continuous function

deﬁned in the tridimensional space. They give also

a classiﬁcation of the combinatorial changes in the

evolution of the Reeb graph of a time-varying Morse

function. (Doraiswamy and Natarajan, 2009) propose

an approach for computing Reeb graphs with the use

of dynamic graphs, but also in this case a global sort-

ing step is needed to start the computation. A work by

(Berretti et al., 2009) proposes a 3D mesh segmenta-

tion using Reeb graphs. As in (Hilaga et al., 2001) this

work uses AGD (average geodesic distance) calcu-

lated from a small set of evenly-spaced vertices (base

vertices) and this choice leads to inaccurate results

with certain type of meshes. (Patane et al., 2009)

propose an approach for building the Reeb graph of

a mesh using critical points and their isocontours,

which is particularly suited for large meshes with

small genus and really smooth functions (with a small

number of critical points), but is not suited for coarse

meshes with higher genus.

4 THE ALGORITHM

A key aspect in the algorithm proposed are active con-

tours, namely ensembles of vertices and edges with

possible multiple presence, that represent the level

lines of the Morse function.

On a 2-manifold and away from critical points,

each level line is a 1-manifold, possibly with more

than one connected component, which become ei-

ther a point or a self-intersecting line when critical

points are met. The representation of each connected

component by an active contour relies on the multi-

ple presence of vertices and edges in order to pre-

serve such 1-manifoldness for all regular values. In

fact, when the mesh is coarse, the immediate dis-

crete representation would not be a 1-manifold (see

for instance Figures 3(a) and 4(a)). In addition, as

we will see, the multiple presence of vertices in ac-

tive contours simpliﬁes the detection of saddles, i.e.

where active contours either split or merge. Indeed,

as it will be seen later on, in our algorithm split and

merge events can only occur with vertices with pres-

ence greater than 1 in either the same contour (split)

or in two different contours (merge). The mesh seg-

mentation is generated as a by-product, by associating

COMPUTING THE REEB GRAPH FOR TRIANGLE MESHES WITH ACTIVE CONTOURS

to each active contour a segment, which is closed and

created anew whenever a critical point is met.

The overall algorithm can be summarised as fol-

lows:

• compute the values of the Morse function for each

vertex;

• identify the prominent points of the mesh - i.e.

feature points - each corresponding to relevant

minima in the Morse function;

• initialize an active contour at each feature point;

• evolve incrementally all the active contours in the

direction of increasing values of the Morse func-

tion;

• perform either split or merge operations each time

a critical point is detected (see Figure 1(b));

• terminate the execution when all active contours

have reached a maximum.

4.1 Which Morse Function

We opted for the same Morse function adopted in

(Tierny et al., 2006). This particular function is bound

to intrinsic shape properties, as described in the above

paper, and therefore is both robust in front of variation

in mesh sampling and invariant to mesh rotation and

deformation.

The Morse function in point is based on the con-

cept of geodesic distance on a mesh (Novotni et al.,

2002), meant as the length of the shortest path con-

necting each two vertices. A derived concept is that of

diameter vertices: i.e. a pair of vertices that are at the

maximum geodesic distance on the mesh. A pair of

diameter vertices can be found with a recursive algo-

rithm, as illustrated in (Lazarus and Verroust, 1999).

The Morse function is computed through the fol-

lowing steps:

• ﬁnd the two diameter vertices (see above) and

calculate the two distance functions from these

points with the Dijkstra algorithm (Dijkstra,

1959);

• ﬁnd the local maxima and minima of the two dis-

tance functions, i.e. the local extrema;

• identify the feature points (FP) by merging local

extrema with some tolerance (see below);

• calculate the Morse function, deﬁned as the

geodesic distance between each vertex and the

closest FP, with the Dijkstra algorithm.

4.1.1 Find Diameter Vertices and Mesh

Maximum Distance

The algorithm randomly chooses a starting vertex in

the mesh and sets it as the currentVertex. Then it cal-

culates the distance map, with the Dijkstra algorithm,

and ﬁnds the most distant vertex. The latter is selected

as the next currentVertex and the algorithm repeats it-

self until currentVertex and its most distant vertex in

2 consecutive loops coincide. We call these two ver-

tices diameter vertices V1 and V2 respectively. It is

worth highlighting that this method is fairly robust in

practise, in that the resulting diameter vertices depend

only weakly on the choice of the starting vertex.

The two diameter vertices deﬁne two distance

functions:

• δ

: the distance from diameter vertex V1

• δ

: the distance from diameter vertex V2

The distance between the couple of points V1 and

V2 is deﬁned as the maxDistance and will be used

to normalize all distances in the mesh. In this way

the value of the parameters in the algorithm will be

independent from the actual size of the mesh.

4.1.2 Identiﬁcation of Feature Points

Feature points (FP) are usually deﬁned in the liter-

ature (Mortara and Patane, 2002) (Katz et al., 2005)

(Tierny et al., 2006) as the vertices in the mesh that are

furthest away from every other mesh vertex. Typically

they are located on mesh prominent components.

(a) (b)

Figure 2: Feature points (in red) (a) and the resulting dis-

tance function δ (b).

Following (Tierny et al., 2006) we identify fea-

ture points by merging the local extrema of the two

distance functions δ

and δ

. Local minima and lo-

cal maxima from either functions that are not farther

away than a certain predeﬁned tolerance value rein-

force each other and are merged in a common feature

ICPRAM 2012 - International Conference on Pattern Recognition Applications and Methods

point, whereas isolated extrema are simply discarded

(see Figure 2(a)).

4.1.3 The Morse Function

The Morse function of our choice is deﬁned as the

normalized geodesic distance between each vertex

and the closest feature point (see Figure 2(b)). In

agreement with (Tierny et al., 2006) we also perform

a post-processing step in order to ensure that no two

vertices have the same value of the Morse function.

4.2 Computing the Reeb Graph

4.2.1 Discrete Contours as Multisets

In a theoreticalframework, a Morse function f deﬁned

on a continuous and smooth surface implicitly deﬁnes

level lines that join all the points at the same value of

f. In our context, the Morse function f is deﬁned only

at mesh vertices and, per choice, the discrete repre-

sentation of level lines is made only of mesh edges

and vertices. Besides the loss of precision, which is

easily addressable, a critical problem is that the dis-

crete representation of a level line might no longer

be 1-manifold. As a matter of fact, this problems

occurs frequently on coarse meshes (see Figure 3(a)-

4(a)). In order to solve this we borrow an idea from

(Edelsbrunner et al., 2003) in that we introduce multi-

ple presence of both edges and vertices in the discrete

representation of level lines.

(a) (b)

Figure 3: The continuous level line - in red - is a 1-manifold,

while its discrete representation is not (a). In the represen-

tation with multiple presence (double vertices and edges -

in green) the 1-manifoldness of the level line is implicitly

maintained (b).

(a) (b)

Figure 4: In this case the discrete representation with mul-

tiple presence maintains the 1-manifoldness of each corre-

sponding level lines.

In other words, what we will call in the following

an active contour γ, is made of two multisets (Knuth,

1998) of vertices and edges respectively.

As shown in Figures 3(b) and 4(b), active contours

maintain the representation of discrete contours faith-

ful with respect to the continuous level lines.

Due to obvious topological reasons, in a triangle

mesh, the vertices with multiple presence can only

exist in an active contour in a ﬁxed number of pat-

terns, as represented in Figures 5,6,7. These ﬁgures

describe all the possible, base conﬁgurations of a seg-

ment of the discrete contour, with multiple presence

of vertices up to 3 and multiple presence of edges up

to 2.

p=2

p=1

(a)

p=1

(b)

Figure 5: The catalog of all possible conﬁgurations of one

vertex with presence 1 in a contour.

p=2

(a)

p=2

p=1

p=2

p=1

(b) (c)

Figure 6: The catalog of all possible conﬁgurations of one

vertex with presence 2 in a contour.

p=3

p=2

(a)

p=3

p=2

(b)

p=3

p=2

(c)

p=3

p=1

(d)

Figure 7: The catalog of all possible conﬁgurations of one

vertex with presence 3 in a contour.

In our experience, with meshes up to genus 22,

we found no evidence of presences higher than the

ones above. We suspect the existence of a theoretical

limit about those values, given suitable quality con-

ditions for the mesh. In any case multiple presences

with greater values could be accommodated by mod-

ifying the algorithm accordingly.

The multiple presence of vertices and edges re-

sults in a great advantage in detecting split or merge

COMPUTING THE REEB GRAPH FOR TRIANGLE MESHES WITH ACTIVE CONTOURS

events. Indeed, as it will be shown in 4.2.3, split and

merge events can only occur at vertices with presence

greater than 1.

4.2.2 The Main Algorithm

Initially all feature points become an active contour

and active contours evolve in a way that is shown in

detail in Algorithm 4.1.

There are two crucial events in contour evolution:

Split: when a single contour separates in two differ-

ent, disconnected contours.

Merge: when two contours melt in one unique, con-

nected contour.

Active contours γ sweep the mesh, following the

direction of ascending values of the Morse function.

γ is made of two multisets:

• V: active contours vertices

• E: active contours edges

The ensemble of segments σ is extracted during

the evolution of active contours. Each segment σ is

made of:

• γ: the active contour of the segment (used in read-

write for segmentation)

• V: the visited vertices of the segment (used as

write-only repository during segmentation)

The set that collects all active segments is called

Σ. Once an event occurs (either merge or split) the

active segments involved are closed and stored in Σ

the set of segments that have already been closed.

4.2.3 Evolution of Active Contours

In the main loop, at each step, a candidate vertex v

selected as the one with the lowest value of the Morse

function in all active contours.

σ = nearest(Σ), v

= nearest(σ.γ) (1)

The algorithm ﬁrst checks the presence of the can-

didate vertex v

in the active contour, as a presence

greater than one would reveal a split event, then it

checks for the presence of v

in other contours, in

order to detect a merge event. Then the contour is

updated locally.

This operation is described in detail in Algorithm

4.2 and illustrated in Figure 8. In the description that

follows we use the concepts of star and link of a ver-

tex in a simplicial complex - see for instance (Edels-

brunner, 2001) for details. In the basic step of con-

tour evolution, the star of v

on the contour (see Fig-

ure 8(a)) is replaced by a subset of the link of v

on the

mesh (see Figure 8(b)), in the direction of advance-

ment. More precisely, the replacing subset of the link

of v

on the mesh, which we call the link

, has a fairly

subtle deﬁnition. The link of v

is divided by the ver-

tices that also belong to the active contour into con-

nected subsets. By deﬁnition, the link

is obtained

by subtracting from the link of v

all the connected

components that contain at least one vertex having a

value of the Morse function which is lower than the

one on v

link

(a)

(b)

Figure 8: Local update of the contour: the star of v

on the

contour (a) is replaced by the link

, i.e. a subset of the link

of v

on the mesh (b).

4.2.4 Finding Connected Components

If each active contour was composed only of vertices

and edges with a single presence, the separation of

connected subsets would be straightforward.

The multiple presence of both edges and vertices

makes the problem more complex, as shown in Fig-

ure 9. In particular, when visiting the double branch

(i.e. the green segment containing double presence

edges and vertices) from one side, it is crucial to exit

from “the right side” of the contour, i.e. without

crossing over. In our method it is possible to discrim-

(a)

(b)

Figure 9: Finding connected components in an active con-

tour: how to walk a double branch.

inate the direction to be kept by inspecting the val-

ues of the Morse function in the local neighborhoods.

In Figure 9(a) we identify the subset of the link (in

blue) of an entrance vertex a, as the one being delim-

ited by two contour vertices and containing the vertex

that is the intersection between the link of the vertex a

and the subsequent vertex b, with a lower value of the

Morse function and not belonging to the active con-

tour. This lets us determine by intersection the right

subset (in violet) of the link of the subsequent vertex

b. The procedure can be repeated until the entire dou-

ble branch has been visited. Figure 9(b) shows that

the visiting procedure exits from the right side in that

it properly selects vertex e over vertex f as the exit

vertex.

ICPRAM 2012 - International Conference on Pattern Recognition Applications and Methods

Algorithm 4.1: SEGMENTATION(FPs)

main

INITIALIZE(FPs)

while not(Σ =

σ = nearest(Σ), v

= nearest(σ.γ)

if presence(v

, σ.γ) > 1

then SPLIT(v

, σ)

else







if ∃σ

: v

∈ σ

.γ

then MERGE(σ, σ

)

else ADVANCECONTOUR(v

, σ)

procedure INITIALIZE(FPs)

Σ, Σ

= {

for each fp ∈ FPs











σ = new(σ)

σ.γ.V = σ.γ.V ∪ {fp}

σ.V = σ.V ∪ {fp}

Σ = Σ∪ σ

procedure ADVANCECONTOUR(v

, σ)

linkPlus = FINDLINKPLUS(v

, σ.γ)

updated

= updateContour(σ, v

, linkPlus)

removeFolds(σ

updated

.γ)

Σ = Σ∪ σ

updated

− σ

procedure MERGE(σ

, σ

)

merged

.γ.V = σ

.γ.V ∪ σ

.γ.V

merged

.γ.E = σ

.γ.E ∪ σ

.γ.E

linkPlus = FINDLINKPLUS(v

, σ

merged

.γ)

updated

= updateContour(σ

merged

, v

, linkPlus)

removeFolds(σ

updated

.γ)

setAdjacence(σ

, σ

updated

)

setAdjacence(σ

, σ

updated

)

= Σ

∪ {σ

, σ

}

Σ = Σ∪ σ

updated

− {σ

, σ

}

Γ = connectedComponents(σ

updated

.γ)

if Γ.size > 1

then











= splitSegment(σ

updated

, Γ[0])

= splitSegment(σ

updated

, Γ[1])

setAdjacence(σ

, σ

updated

)

setAdjacence(σ

, σ

updated

)

Σ = Σ∪ {σ

, σ

} − σ

updated

= Σ

∪ σ

updated

procedure SPLIT(v

, σ)

linkPlus = FINDLINKPLUS(v

, σ.γ)

updated

= updateContour(σ, v

, linkPlus)

removeFolds(σ

updated

.γ)

Γ = connectedComponents(σ

updated

.γ)

if Γ.size > 1

then











= splitSegment(σ, Γ[0])

= splitSegment(σ, Γ[1])

setAdjacence(σ

, σ)

setAdjacence(σ

, σ)

= Σ

∪ {σ}

Σ = Σ∪ {σ

, σ

} − σ

else Σ = Σ∪ σ

updated

− σ

Algorithm 4.2: FINDLINKPLUS(v

, γ)

main

link = ﬁndLink(v

)

adjacents = ﬁndAdjacent(v

, γ)

link.V = link.V − adjacents

stack =

for each presence(v

, γ)











= FINDPREDECESSOR(link.V)



if δ(v

) > δ(v

)

then break

stack = stack+ v

while not (stack =











intersections = getLinkIntersections(v

, v

)

for each v

∈ intersections



if (v

∈ link.V) and not (v

∈ stack))

then stack = stack+ v

link.V = link.V − v

stack = stack− v

= next(stack)

for each v

∈ adjacents







edge = ﬁndEdgeConnecting(v

, v

)

if presence(edge, γ) > 1

then adjacents = adjacents− (v

)

for each edge ∈ link.E







if not ((edge.start or edge.end) ∈ link.V) or

not ((edge.start or edge.end) ∈ adjacents)

then link.E = link.E − edge

return (new(γ(link))

procedure FINDPREDECESSOR(link)

predecessor =

0, d = ∞

for each v ∈ link







if δ(v) < d

then



d = δ(v)

predecessor = v

return (predecessor)

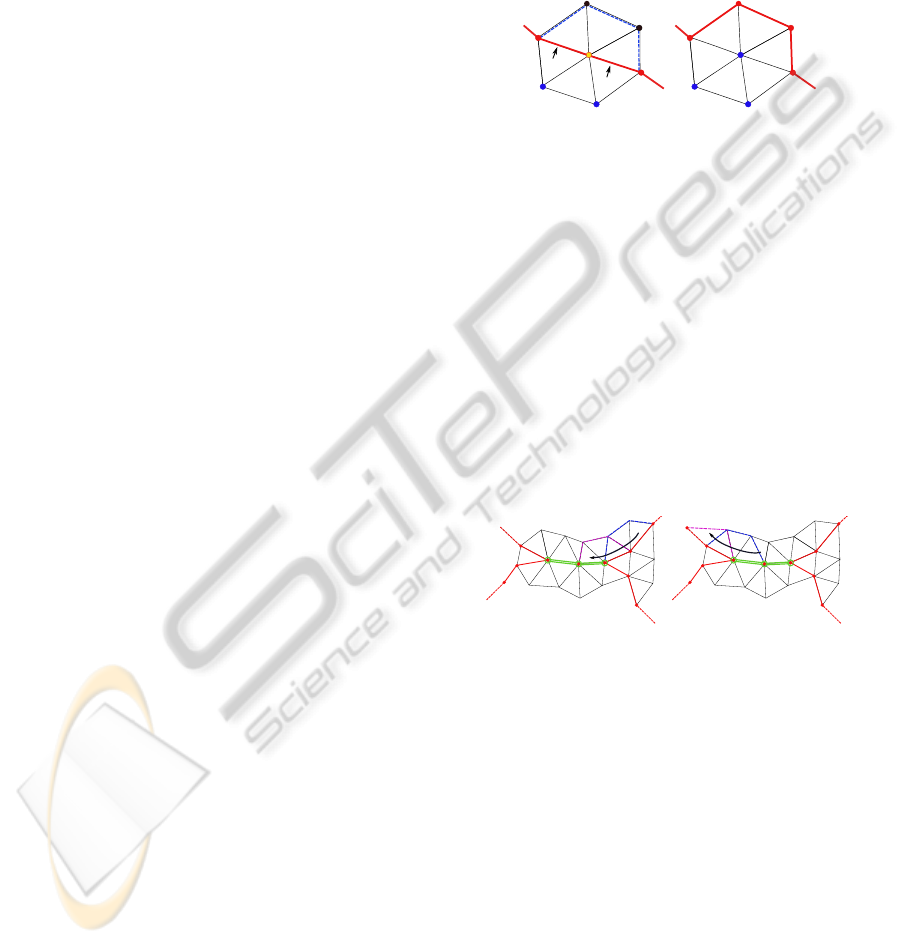
4.2.5 Contour Split

The ﬁrst condition to be checked for in order to detect

split events is the multiple presence of v

in the active

contour (see Figure 10). Only when this condition

occurs the entire active contour is explored, in order

to isolate the connected sub-components.

When dealing in particular with coarse meshes

with high genus, split and merge events can occur

with high frequency and, omitting details, the result-

ing segments could be either fragmented or not sim-

ply connected. For this reason, after having detected

a split event, it is important to determine which seg-

ment each contour vertex will belong after the split.

In our method, after a split event, each of the two new

segments will contain a connected subset of the split-

ting contour; this same connected subset is deemed

COMPUTING THE REEB GRAPH FOR TRIANGLE MESHES WITH ACTIVE CONTOURS

(a) (b)

Figure 10: Split event: the candidate vertex v

(in orange)

has a double presence in the active contour (a); the contour

is split into two distinct ones (b).

the originating vertices of the segment. As a mat-

ter of fact, it can happen that the active contour γ

that is splitting could contain one or more vertices

belongings to the originating vertices of its own seg-

ment σ. If those vertices were simply passed to the

two new segments, interruptions could be generated

and the connectedness of the previous segment could

be compromised. For this reason we introduce the

idea of multiple vertex membership: vertices belong-

ing to the originating vertices of a segment, if passed

to other segments, will be marked as belongings to

all involved segments. Figure 11 shows an example

of multiple vertex membership: vertices with multiple

membership are highlighted with a different border

color. Inside vertex color represents parent segment

belonging, border color represents child segment be-

longing. Higher level of sharing (e.g. vertices shared

between three or more segments) can occur in practise

for coarse meshes with higher genus.

Figure 11: Vertices with multiple membership are in the

highlighted areas in red.

4.2.6 Merge Between Contours

In analogy of the case of the split, the fundamental

condition to be checked for in order to detect the oc-

currence of the merge event is the simultaneous pres-

ence of v

in two contours (see Figure 12). When

this is true, the two merging segments σ

and σ

are

closed and stored in Σ

and a new segment σ

merged

created. The merged active contour will also repre-

sent the originating vertices for the segment σ

merged

4.2.7 Removing Folds

One of the real plagues of Morse functions, dis-

cretized in the way here described, is the presence

(a) (b)

Figure 12: Merge event: the candidate vertex v

(in orange)

belongs to two distinct contours (a); the two distinct con-

tours are merged into one (b).

of multiple, spurious, local saddles, as analyzed in

(Tierny et al., 2006). The algorithm could originate

false splits when encountering those spurious saddles

(see Figure 13). Indeed, in those cases, if we actu-

ally made a split, we would produce “anomalous con-

tours”, composed only by individual isolated vertices

or contours where every edge would have a presence

greater than one. We named situations like the one

described in Figure 13 as contour folds and in our al-

gorithm they are removed as soon as they occurs. Al-

though we do not have a theoretical proof of the com-

pleteness of this solution, we tested it extensively and

in our experimental evidence it solved the problem of

spurious saddles completely. As shown in Figure 14

the check for fold presence can be performed once

again in the basic step of active contour evolution: a

fold is certainly present whenever a vertex with a sin-

gle presence is connected with an edge with double

presence. The fold-removing procedure is recursive

in that it follows the fold “branch” until the latter is

removed completely from the active contour. Obvi-

ously, the topology of the contour is unaffected by the

fold-removing procedure.

Figure 13: The candidate vertex v

(in orange) is a spurious

saddle.

(a) (b) (c)

Figure 14: Removing folds: candidate v

(in orange) is se-

lected (a); a fold has been generated (in green) (b); the fold

has been removed: the topology of the contour is unaffected

(c).

ICPRAM 2012 - International Conference on Pattern Recognition Applications and Methods

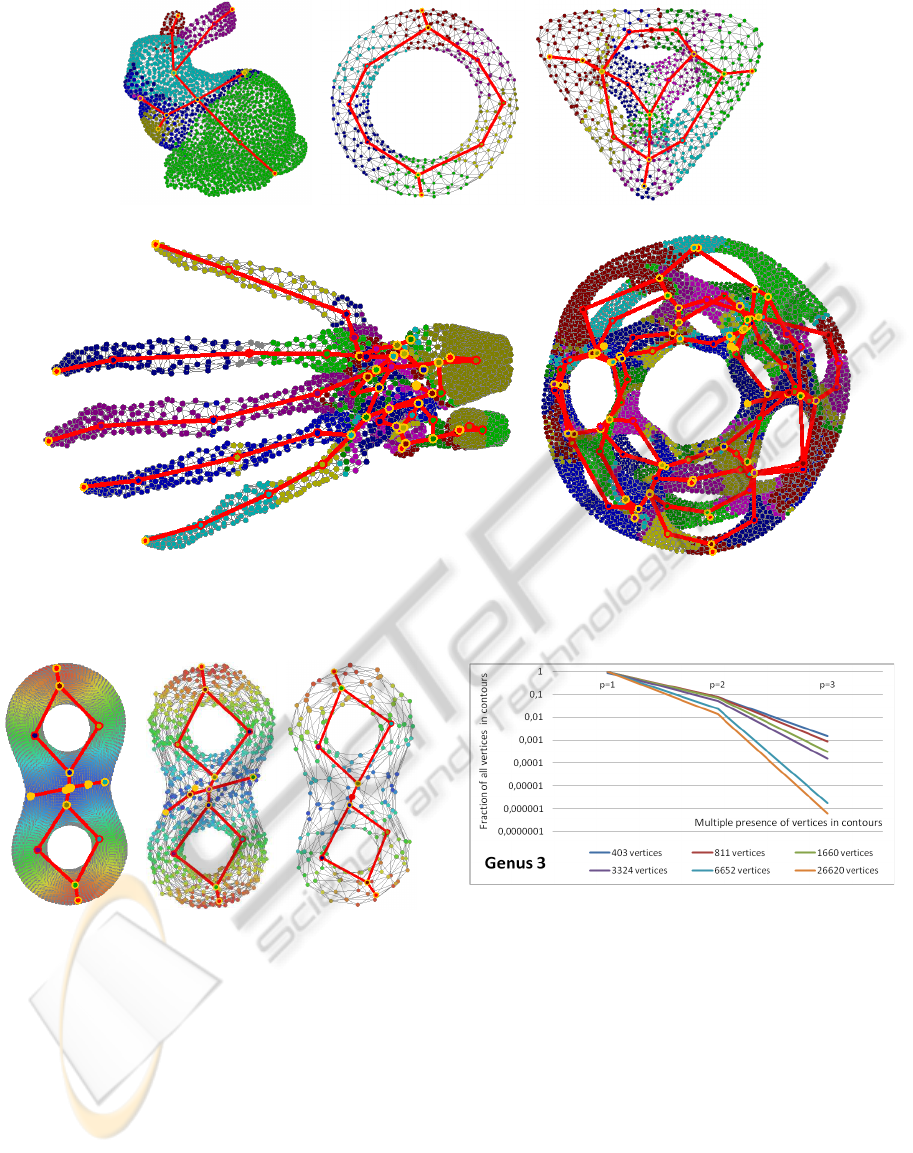
(a) Genus 0 (b) Genus 1 (c) Genus 3

(d) Genus 5 (e) Genus 22

Figure 16: A few meshes in the test set: Reeb graphs are painted in red, segmentations are highlighted with different vertices

colors. Multiple vertex memberships are not represented in these images.

(a) (b) (c)

Figure 15: The original, high-resolution mesh with 12286

vertices (a), two increasingly decimated versions with ran-

dom noise added, with 766 vertices (b) and 190 vertices (c).

4.2.8 Constructing the Reeb Graph

In the output of our algorithm, each segment σ is a

node in the Reeb graph and each arc corresponds to

an adjacency relation between two segments, as de-

scribed in Algorithm 4.1. The Reeb graph is built dur-

ing active contour evolution. Every time an event oc-

curs (either merge or split) and segments are stored in

, adjacency relations are also updated accordingly:

after a merge the two merging segments are declared

Figure 17: Progressive coarsening of the same mesh (Genus

3): a smaller number of vertices causes an increase of mul-

tiple presences in contours.

adjacent to the newly generated one; after a split the

parent segment is declared adjacent to the two new

ones.

5 EXPERIMENTAL EVIDENCE

In order to verify the correctness and effectiveness of

the proposed algorithm we carried out extensive tests

with a great number of meshes having different genus

and density. We present here some of the most rel-

evant results in our tests. Most of the meshes have

COMPUTING THE REEB GRAPH FOR TRIANGLE MESHES WITH ACTIVE CONTOURS

been taken from the AIM@Shape database (Falci-

dieno, 2004) and range from genus 0, both with great

and small number of vertices, to genus 22 with over

ten thousand vertices.

We used a non-optimized Java implementation be-

cause, at present, our main interest is the validation of

the algorithm.

Since the algorithm contains a random choice of

the starting point (see 4.1.1), our tests were carried

out in an exhaustive way even with respect to the cal-

culation of the diameter vertices. As a matter of fact,

in order to test all the variants of the Morse function,

we carried out, for each mesh, n test runs (with n be-

ing the number of mesh vertices), selecting at every

run a different starting point, until every mesh vertex

has been selected.

In order to validate the properties of the Reeb

graphs obtained, we used the procedure described in

(Safar et al., 2009) to compute the minimum cycle ba-

sis and hence the number of loops in each of those

graphs. The number of loops must be equal to the

genus of the corresponding mesh, which can be com-

puted with the well-known Euler equation:

v− e +t = 2− 2g (2)

where v is the number of vertices in the mesh, e is the

number of edges and t is the number of triangles.

With all the variants of the Morse function and for

each of the meshes shown in Table 1, the proposed

algorithm computes the Reeb graph corresponding to

the correct genus. The meshes in the test set are also

illustrated in Figure 16, together with the Reeb graphs

and the segmentations obtained.

Finally, Figure 17(a) shows how coarser meshes

lead to more complex active contours. The same

mesh shown in Figure 16(c) has been considered at

ﬁrst with high resolution and then progressively dec-

imated: in the statistics of these experiments multi-

ple presences increase by orders of magnitude as the

number of vertices decreases.

Table 1: Some of the meshes used to check the validity of

the algorithm, with their genus and number of vertices.

Mesh Name Genus Vertices

Bunny 0 3052

Torus 1 359

Double torus-12286 2 12286

Double torus-766 2 766

Double torus-190 2 190

Genus3 3 782

HandG5 5 4037

HandG8 8 3639

Eptoroid 22 10851

6 CONCLUSIONS

As we have seen, the key aspect in the algorithm

presented is the way in which active contours are

evolved. Using the properties of the Morse func-

tion and the discrete topology of the triangle mesh,

the evolution process can be performed by relying al-

most entirely on information being local to the ver-

tices in the contours and their immediate neighbor-

hood. In particular, it is not even necessary to verify

at each step the connectedness of each active contour,

because both split and merge events can only occur

when the candidate vertex has multiple presence on

one or more contours. A more complex test on the

entire contour is only required when dealing with a

split event, since the multiple presence of vertices and

edges can make it more difﬁcult to detect the con-

nected components after the split.

Even if the theoretical validation of the correct-

ness of the algorithm remains to be assessed, the ex-

perimental evidence presented supports the idea that

the algorithm proposed could be effective for a wide

class of real-world meshes.

ACKNOWLEDGEMENTS

The authors want to thank an anonymous reviewer for

the precious comments and suggestions received.

REFERENCES

Berretti, S., Del Bimbo, A., and Pala, P. (2009). 3d mesh

decomposition using reeb graphs. Image and Vision

Computing, 27(10):1540 – 1554. Special Section:

Computer Vision Methods for Ambient Intelligence.

Biasotti, S., Giorgi, D., Spagnuolo, M., and Falcidieno, B.

(2008). Reeb graphs for shape analysis and applica-

tions. Theoretical computer science, 392:5–22.

Biasotti, S., Mortara, M., and Spagnuolo, M. (2000).

Surface compression and reconstruction using reeb

graphs and shape analysis. In Proceedings of 16th

Spring Conference on Computer Graphics, pages

175–184. ACM press.

Cole-McLaughlin, K., Edelsbrunner, H., Harer, J., Natara-

jan, V., and Pascucci, V. (2003). Loops in reeb graphs

of 2-manifolds. In Proceedings of the nineteenth an-

nual symposium on Computational geometry, SCG

’03, pages 344–350, New York, NY, USA. ACM.

Dijkstra, E. W. (1959). A note on two problems in connex-

ion with graphs. Numerische Mathematik, 1:269271.

Doraiswamy, H. and Natarajan, V. (2009). Efﬁcient algo-

rithms for computing reeb graphs. Computational Ge-

ometry, 42(6-7):606 – 616.

ICPRAM 2012 - International Conference on Pattern Recognition Applications and Methods

Edelsbrunner, H. (2001). Geometry and Topology for Mesh

Generation. Cambridge University Press, New York,

NY, USA.

Edelsbrunner, H., Harer, J., Mascarenhas, A., Pascucci, V.,

and Snoeyink, J. (2008). Time-varying reeb graphs

for continuous space-time data. Computational Ge-

ometry, 41(3):149 – 166.

Edelsbrunner, H., Harer, J., and Zomorodian, A.(2003). Hi-

erarchical morse-smale complexes for piecewise lin-

ear 2-manifolds. Discrete and Computational Geom-

etry, 30(1):87–107.

Falcidieno, B. (2004). Aim@shape project presentation.

In Shape Modeling Applications, 2004. Proceedings,

page 329.

Hilaga, M., Shinagawa, Y., Kohmura, T., and Kunii, T. L.

(2001). Topology matching for fully automatic simi-

larity estimation of 3d shapes. In Proceedings of the

28th annual conference on Computer graphics and

interactive techniques, SIGGRAPH ’01, pages 203–

212, New York, NY, USA. ACM.

Katz, S., Leifman, G., and Tal, A. (2005). Mesh segmen-

tation using feature point and core extraction. The

Visual Computer, 21:649–658. 10.1007/s00371-005-

0344-9.

Knuth, D. E. (1998). The Art of Computer Programming

Vol. 2: Seminumerical Algorithms. Addison Wesley,

3rd edition.

Lazarus, F. and Verroust, A. (1999). Level set diagrams

of polyhedral objects. In Fifth Symposium on Solid

Modeling, pages 130–140. ACM.

Milnor, J. (1963). Morse Theory. Princeton University

Press.

Mortara, M. and Patane, G. (2002). Afﬁne-invariant skele-

ton of 3d shapes. Shape Modeling and Applications,

International Conference on, 0:245–252.

Novotni, M., Klein, R., and Ii, I. F. I. (2002). Computing

geodesic distances on triangular meshes. In In Proc.

of WSCG2002, pages 341–347.

Pascucci, V., Scorzelli, G., Bremer, P.-T., and Mascarenhas,

A. (2007). Robust on-line computation of reeb graphs:

simplicity and speed. ACM Trans. Graph., 26.

Patane, G., Spagnuolo, M., and Falcidieno, B. (2009). A

minimal contouring approach to the computation of

the reeb graph. IEEE Transactions on Visualization

and Computer Graphics, 15:583–595.

Reeb, G. (1946). Sur les points singuliers d une forme de

pfaff completement integrable ou d une fonction nu-

merique. In Comptes rendus de l’Academie des Sci-

ences 222, pages 847–849.

Safar, M., Alenzi, K., and Albehairy, S. (2009). Counting

cycles in an undirected graph using dfs-xor algorithm.

In Networked Digital Technologies, 2009. NDT ’09.

First International Conference on, pages 132 –139.

Schaefer, S. and Yuksel, C. (2007). Example-based skeleton

extraction. In Proceedings of the ﬁfth Eurographics

symposium on Geometry processing, pages 153–162,

Aire-la-Ville, Switzerland. Eurographics Association.

Sebastian, T., Klein, P., and Kimia, B. (2002). Shock-based

indexing into large shape databases. In Computer

Vision ECCV 2002, volume 2352 of Lecture Notes

in Computer Science, pages 83–98. Springer Berlin /

Heidelberg.

Shapira, L., Shamir, A., and Cohen-Or, D. (2008). Consis-

tent mesh partitioning and skeletonization using the

shape diameter function. Visual Comput, 24:249–259.

Shinagawa, Y. and Kunii, T. (1991). Constructing a reeb

graph automatically from cross sections. Computer

Graphics and Applications, IEEE, 11(6):44 –51.

Shinagawa, Y., Kunii, T., and Kergosien, Y. (1991). Surface

coding based on morse theory. Computer Graphics

and Applications, IEEE, 11(5):66 –78.

Sundar, H., Silver, D., Gagvani, N., and Dickinson, S.

(2003). Skeleton based shape matching and retrieval.

In Shape Modeling International, 2003, pages 130 –

139.

Tierny, J., Vandeborre, J., and Daoudi, M. (2006). 3d mesh

skeleton extraction using topological and geometrical

analyses. In 14th Paciﬁc Conference on Computer

Graphics and Applications. Paciﬁc Graphics.

COMPUTING THE REEB GRAPH FOR TRIANGLE MESHES WITH ACTIVE CONTOURS