EXTRACTING TOPOLOGICAL INFORMATION FROM

GRID MAPS FOR ROBOT NAVIGATION

David Portugal and Rui P. Rocha

Institute of Systems and Robotics, University of Coimbra, 3030-290 Coimbra, Portugal

Keywords:

Robot navigation, Graphs, Topological maps, Voronoi diagrams.

Abstract:

In many robotic navigation-related tasks, abstracting the environment where mobile robots carry out some

mission can be of a great beneﬁt. In particular, extracting a simple topological graph-like representation from

a more complex and detailed metric map is often required for path-planning and navigation. In this work, an

approach to perform such extraction in grid maps is presented. The focus is not only on obtaining a diagram or

visual representation of possible paths, but also to propose a new way to obtain graph data information related

to the connectivity of the environment that can be passed to robots or to a centralized planner, in order to assist

the navigation task. The approach proposed is based on image processing techniques. Simulation results prove

its simplicity, accuracy and efﬁciency.

1 INTRODUCTION

In the context of robotics, it is very important for au-

tonomous mobile robots to learn and preserve models

of the environment. Without an internal description

of the environment, and information of their position

and orientation with respect to this map, most mobile

robotic tasks, like driving while avoiding collisions

and navigating, would become impractical.

In navigation tasks, it is normally assumed that

the environment is known a priori. On the other

hand, exploration is generally related to completely

or partially unknown environments. For both cases,

maintaining or building internal representations of the

infra-structure is one of the key issues to the success-

ful completion of the task.

The two major distinct paradigms for mapping in-

door environments are grid-based maps and topologi-

cal maps (Thrun, 1998). In the present work, we focus

on the latter one.

Grid-based methods produce accurate metric

maps, are easy to build, represent and maintain, but

often suffer from memory space and time complex-

ity, because of its ﬁne resolution restrictions which

results in memory problems and also harder efﬁcient

planning and navigating in large-scale infrastructures.

Topological maps, on the other hand, produce graph-

like maps that can be used much more efﬁciently.

They are simpler, permit efﬁcient planning and do

not require accurate determination of the robot’s posi-

tion. In these maps, vertices correspond to important

places or landmarks, which are connected by edges

that represent paths between them. However, its in-

accuracy makes it harder to maintain consistency in

large scale environments, which results in difﬁculties

in recognizing similar places that look alike. There

are some other constraints related to navigation us-

ing topological maps. Some limitations previously

identiﬁed (Zimmer et al., 1994) were: handling in-

accurate position and orientation information and de-

tecting neighbor vertices in the topological map by

traversing them, as opposed to sensing or recogniz-

ing them. Despite these constraints, the path planning

method that was used produced adequate results.

In addition, map validation and self-localization in

topological maps is also an important issue for correct

robot navigation, which has been extensively stud-

ied (Dudek et al., 1997). As seen before, topologi-

cal maps can be a very important tool for most tasks

using mobile robots. Many works exploit this simple

representation to employ correct robot navigation. In

Ferreira et al. (Ferreira et al., 2007), a robot drives

around the environment and self-localizes, while us-

ing a place recognition technique to build 3D point

cloud sets for monitoring changes that might take

place in the environment.

In this work, the focus is mainly on obtaining a

global topological abstraction from a preexisting met-

ric representation of an environment. For example,

for surveillance, monitoring and patrolling tasks with

137

Portugal D. and P. Rocha R..

EXTRACTING TOPOLOGICAL INFORMATION FROM GRID MAPS FOR ROBOT NAVIGATION.

DOI: 10.5220/0003746401370143

In Proceedings of the 4th International Conference on Agents and Artiﬁcial Intelligence (ICAART-2012), pages 137-143

ISBN: 978-989-8425-95-9

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

multiple robots, it is common to rely on topological

maps for navigation issues. In a previous work (Por-

tugal and Rocha, 2010), we presented a novel multi-

robot patrolling algorithm based on topological maps.

In this article, we describe in detail how complete

topological information is extracted from an existing

2D grid map representation of the area to be patrolled,

which in turn can be obtained with a state-of-the-art

robotic mapping technique, e.g. (Thrun et al., 2000).

The next section presents a survey of previous

techniques for extracting topological representations

like diagrams and graphs from metric representations

given a priori. Typically, these metric representations

are occupancy grids, which are probabilistic maps

wherein each cell of the grid contains a probability

value that indicates whether the related location is free

space or part of an obstacle (Elfes, 1989). These grids

are usually obtained in a preceding exploration phase.

In Section III, we state the problem to be addressed

and Section IV presents the algorithm proposed to

solve it. Later on, results are presented and the article

ends with conclusions and future work.

2 RELATED WORK

In the literature, there are a few existing techniques to

extract topological representations using metric maps.

In particular, Voronoi Diagrams (Voronoi, 1908) have

been extensively used to plan a path that stays away

from obstacles as far as possible. In addition, the Gen-

eralized Voronoi Diagram (GVD) (Wallgr

un, 2004)

was described as a “retraction of the free space of

the working space onto a network of one-dimensional

curves reﬂecting the connectivity of free space” and

a hierarchically organized Voronoi-based route graph

representation for robot navigation in indoor scenar-

ios was proposed.

Furthermore, the Extended Voronoi Graph (EVG)

(Beeson et al., 2005) has been presented more re-

cently. In this new approach, the diagram (or skele-

ton) computation overcomes limitations in the sen-

sory horizon of robots by clearly deﬁning a tran-

sition from corridor-following to wall-following in

large rooms. Although deﬁned as a graph, beyond the

actual diagram no information about vertices or edges

is available after the ﬁnal computation.

Additionally, Kolling and Carpin (Kolling and

Carpin, 2008) proposed a method to extract graph

representations from occupancy grids for surveillance

tasks, based on the GVD. Graph modiﬁcations, called

contractors, are promoted to simplify the surveillance

problem towards solving it using fewer robots.

Another commonly used technique when extract-

ing graphs is the Delaunay triangulation (DT) (Delau-

nay, 1934). In fact, the DT of a discrete point set gen-

erally corresponds to the dual graph of the Voronoi

diagram for the same point set.

Katsilieris et al. (Katsilieris et al., 2010) extract

the traversability graph from the original metric map

in the context of searching intruders with a team of

robots. Firstly, the obstacle-free area is triangulated

and then triangles are merged to form large convex

regions where the vertices are extracted. The set of

edges consists of all pairs of regions that share a side.

In addition, a technique called Reduced Con-

strained Delaunay Triangulation to build graphs is

also becoming popular. This technique is based on

a DT computation together with a mechanism to re-

duce the graph by minimizing the distance each robot

has to traverse. It was applied by Fazli et al. (Fazli

et al., 2010) in the context of a multi-robot area cov-

erage task in a known and static 2D environment.

Another method presented in the literature to ex-

tract the graph of an environment is the visibility

graph (Lozano-P

erez and Wesley, 1979), which is

composed of straight lines joining a sequence of ver-

tices that are normally placed near the limits of obsta-

cles in the environment (considering the dimension

and pose of the robot). The graph is created connect-

ing all vertices that can “see” each other, hence the

name visibility graph.

Among the most used techniques are also thinning

(Ko et al., 2004) and skeletonization (Szab

o, 2004)

methods. These are operations used to remove the

foreground pixels from binary images, analogously

to peeling an onion. They provide a skeleton of the

image, reducing all lines to a single pixel thickness.

The output of such techniques is similar to the GVD.

Szab

o (Szab

o, 2004) also refers in his work some

other methods for extracting topological maps from

occupancy grids, namely sparse pixel approaches and

matching opposite contours. Moreover, another tech-

nique called C-cells can be found in the literature

(Machado, 2002). It has the principle to divide the

space not occupied by obstacles into convex polygons

and the vertices of the graph are positioned in the cen-

ter of those polygons, having each vertex connected in

a straight line to the closest visible vertex.

Most previous works mentioned above present

methods to visually extract the topological represen-

tation. However, many of these do not correctly char-

acterize vertices and edges on the graph (like Voronoi

Diagrams, EVG, thinning or skeletonization). As for

those that do, the methods which are based on De-

launay Triangulation need a manual deﬁnition of the

vertices in the environment to compute the topology

and usually generate non-elegant and unbalanced rep-

ICAART 2012 - International Conference on Agents and Artificial Intelligence

138

resentations. In the case of visibility graphs, highly

inadequate topologies are produced since the vertices

are positioned very close to obstacles, which is unnat-

ural for robot navigation. The Generalized Voronoi

Graph (GVG), which consists of a vertex for every

meet and end point of the GVD and edges reﬂect-

ing the connectivity of the GVD, results in very com-

plex graphs with a large number of vertices and edges

that are mostly redundant, especially when consid-

ering navigation tasks for robots. In addition, all of

these methods assume that the edges connecting pairs

of neighboring vertices must be a straight line, which

is not necessarily true for robots with the ability to

locally plan paths between two vertices.

In this work, we intend to go further ahead, by

ﬁrstly extracting an elegant topological representation

and then focusing on identifying vertices, edges and

their length (i.e., their weight) and obtaining relevant

data concerning the vertices and the connectivity be-

tween areas of the map so as to assist robots navi-

gation in tasks like patrolling, coverage, monitoring,

surveillance, pursuit-evasion and others.

3 PROBLEM STATEMENT

In this work, the environment is assumed to be known

a priori and a metric representation, typically with the

form of an occupancy grid, is available. The goal is

to abstract the environment through a topological rep-

resentation, i.e., a graph, and obtain all information

about the graph’s connectivity.

The techniques described in the previous section

will lead to different graph representations, like plac-

ing vertices close to obstacles, inserting them halfway

between obstacles or positioning them in a uniform

way along the terrain. Having this in mind, a careful

choice should be made, considering the applications

in which the extraction is applied.

We start with a skeleton representation and then

focus on extracting topological information to char-

acterize the connectivity of the environment. There

are several techniques to compute the initial skele-

ton as seen previously in section II. In this work, it

is obtained via the EVG computation, mainly because

of its results in terms of producing visually attrac-

tive path representations that stay away from obsta-

cles and that consider the sensing range of the robots

as an input of the method. Additionally, it is a rela-

tively recent technique, which is open source and is

easily adaptable to the code that was developed. Hav-

ing the representation of the skeleton, the graph is ob-

tained through image processing techniques by cor-

rect identiﬁcation of vertices and edges. The topolog-

ical map is modeled as an undirected graph. Vertices

represent places and edges represent the connectivity

(in both directions) between those places.

In the next section, we present the algorithm to

extract the complete topological information and its

simplicity and efﬁciency becomes clear.

4 THE ALGORITHM

In a previous work (Portugal and Rocha, 2010) a pa-

trolling simulator was used to validate a multi-robot

patrolling approach based on balanced graph parti-

tioning. Here, we show how the pre-assumed graph

is provided to the patrolling simulator. The algorithm

is comprised of 4 steps which are detailed below.

4.1 Acquiring the Skeleton

A tool named EVG-THIN developed by Patrick Bee-

son (Beeson et al., 2005) was used to acquire skele-

tons from occupancy grids in this project. “EVG”

stands for the Extended Voronoi Graph, which al-

though being called a graph, does not present out-

put related to information about vertices and edges

on the graph, giving instead an enhanced skeleton

on top of a grid map, when compared to the GVD.

“THIN” accounts for the pixel-based thinning algo-

rithm that ﬁnds skeletons of bitmaps, which is a fast

approximation of the Voronoi diagram. Its code was

written to be applied in real-time to occupancy grids,

where cells are either occupied, free, or unknown,

but it also works on any grayscale bitmap image in

other domains. This command-line application runs

in any Linux console upon the deﬁnition of some pa-

rameters, such as the pixels’ threshold for considering

them free, unknown or occupied; or the robot’s mini-

mum distance to an obstacle to account for the robot’s

geometric dimension and sensing range when navi-

gating in the map. Setting these parameters correctly

is important, because the computed skeleton and ﬁnal

topology depends substantially on those parameters.

The Patrolling Simulator interface displays a win-

dow to set all the input parameters reusing and evolv-

ing the EVG-THIN’s code, which is run in back-

ground

, obtaining the 1 pixel-thin skeleton of the en-

vironment, as seen on Figure 1 (right).

Note that this program is released under the GNU Gen-

eral Public License (GPL), which is intended to guarantee

the freedom to share and change free software.

EXTRACTING TOPOLOGICAL INFORMATION FROM GRID MAPS FOR ROBOT NAVIGATION

139

Figure 1: EVG-THIN incorporated in the simulator.

4.2 Cluster Image Removal

Due to aliasing, sometimes the skeleton representa-

tion generated in the previous section presents clus-

ters, i.e., sets of 4 pixel squares, as shown on Figure 2.

These clusters are problematic, in the sense that they

interfere with the subsequent detection of vertices in

the graph, due to the 1 pixel-thin skeleton assumption.

Therefore, an intermediate phase to avoid future data

corruption when detecting the vertices and edges is

necessary: Cluster Removal.

Figure 2: Cluster detection and correction. The blue dots

correspond to vertices subsequently identiﬁed.

A protective ﬁlter was developed to detect and re-

move such clusters. Basically, it sweeps the image

and when a cluster is detected, two actions are possi-

ble:

• Pixel Removal: Eliminate unnecessary pixels

from the cluster;

• Pixel Shifting: Move pixels to the cluster’s

neighborhood.

These actions are conducted without affecting the

connectivity of the graph. In Figure 3, on the left side,

two examples of their application are shown. On top,

the 2 pixels marked by a cross are removed, because

they are unnecessary to guarantee the connection be-

tween all branches.

When a cluster is identiﬁed, the ﬁlter checks the

implications of removing pixels; more speciﬁcally it

guarantees that no disconnections resulting from eras-

ing pixels will exist, by inspecting all the neighbor

pixels around the cluster.

Erasing pixels is not always possible, as it can be

observed in the bottom left of Figure 3, where remov-

ing red pixels would create gaps in the skeleton un-

derneath. Hence, a pixel shifting strategy was created

to remedy such situations.

4.3 Detecting Vertices

Having the cluster-free skeleton, the next step is ex-

tracting all vertices of the graph by image process-

ing, which is done on top of the previously generated

skeleton. The process is fairly simple, due to the 1-

pixel thin assumption. Vertices correspond to single

pixels that are placed in two speciﬁc locations:

• Dead-ends: Pixels that typically only have one

neighbor pixel that also belongs to the skeleton. They

originate vertices with degree

one.

• Branch intersections: Crucial pixels that corre-

spond to crossings of the branches of the skeleton.

They usually have three or more neighbor pixels that

also belong to the skeleton, within the eight pixels

around them. They originate higher degree vertices.

Figure 3: On the left side: Cluster Analysis - Pixel removal

on top and pixel shifting below. On the right side: Possible

neighbor directions.

The process shown in pseudo-code by Algorithm

1 is conducted to identify all vertices in the graph.

Basically, the intent is to inspect the 9-pixel window

centered on the analyzed pixel of the skeleton and ver-

ify if it is a dead-end or a branch intersection. When

the vertex is identiﬁed, a single blue pixel is drawn in

“The degree (or valency) d

(v) = d(v) of a vertex v

is the number |E(v)| of edges at v (...), this is equal to the

number of neighbours of v” (Reinhard, 2010).

ICAART 2012 - International Conference on Agents and Artificial Intelligence

140

1 foreach pixel p of the image do

2 if p is red then

3 count ← number of red pixels inside

9-pixel window centered on p;

4 else

5 count = 0;

6 end

7 if count > 3 then // Exclude pixels with 3 or

more neighbors that do not correspond to

branch intersections.

8 foreach two adjacent red pixels around

p do

9 count = count −1;

10 end

11 foreach three adjacent red pixels

around p do

12 count = count −2;

13 end

14 else if count = 3 then // Dead-end (with more

than one neighbor pixel)

15 if two adjacent red pixels around p then

16 count = count +1;

17 end

18 end

19 if count > 3 ∨ count = 2 then

20 p is a vertex ⇒ blue pixel in p;

21 end

22 end

Algorithm 1: Pseudo-Code of the vertex detection process.

the correct spot. Note that this algorithm relies on the

fact that no clusters exist in the graph.

After running the algorithm, the visual represen-

tation of the graph on top of the grid is complete, as

it will be shown on the results section, where the ver-

tices were highlighted for better identiﬁcation.

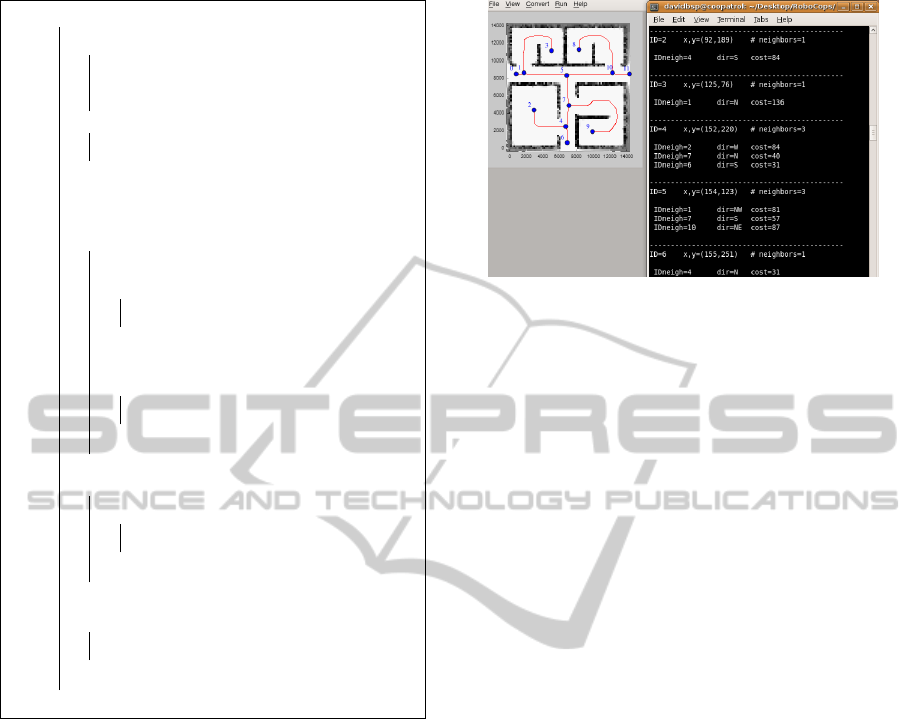
4.4 Extracting Relevant Topological

Information

The last step of the algorithm is to compute the rest

of the topological information to completely charac-

terize the graph (edges, connectivity, etc.). In this

work, each vertex data structure will have the follow-

ing ﬁelds associated to it:

• ID

• Coordinates (x, y)

• Degree

• Neighbors (Vertex Degree)={ID, direction, edge

weight}

Figure 4: Extracting the graph and relevant topological in-

formation. Example of a simple tree-like graph with 12 ver-

tices.

In this step, the main concern is to convert visual

information into graph data that can be used by robots

to abstract the environment.

The ID and coordinates (x, y) of each vertex are

easily extracted by looking for the blue pixels in the

picture and assigning them ID’s and saving their (x,

y) pixel coordinates.

The other ﬁelds are obtained subsequently, also by

image processing, by following all branches leaving

the vertices via the red pixels’ routes. When a blue

pixel is found at the end of a route, a neighbor ver-

tex is recognized, therefore the degree of the initial

pixel is incremented, and a new entry to the neigh-

bors table of the initial vertex is ﬁlled: the ID of the

newly-detected neighbor vertex, its direction related

to the initial vertex and the edge weight between the

2 vertices.

The ID is obtained by relating the coordinates of

the newly-detected vertex to the ID list previously

computed. The direction is deﬁned in a similar way

to the compass rose designation, as show on the right

side of Figure 3, e.g., if the direction of the route lead-

ing to the neighbor vertex starts in the pixel above

the examined vertex, than the direction is deﬁned as

North (N). Also, the edge weight between vertices is

deﬁned as the cost of travelling from one vertex to an-

other in pixel units, more speciﬁcally, the number of

red pixels in the edge between both vertices.

Every vertex is identiﬁed by a single blue pixel, as

shown previously in Figure 2. After obtaining all the

data ﬁelds, each vertex will have a table of neighbors

with the size of its degree and all the edges and the

connectivity between neighbor vertices will be well

characterized. This is clear in Figure 4. Having all

this information, the framework for agents’ naviga-

tion in the Patrolling Simulator is ﬁnally created.

EXTRACTING TOPOLOGICAL INFORMATION FROM GRID MAPS FOR ROBOT NAVIGATION

141

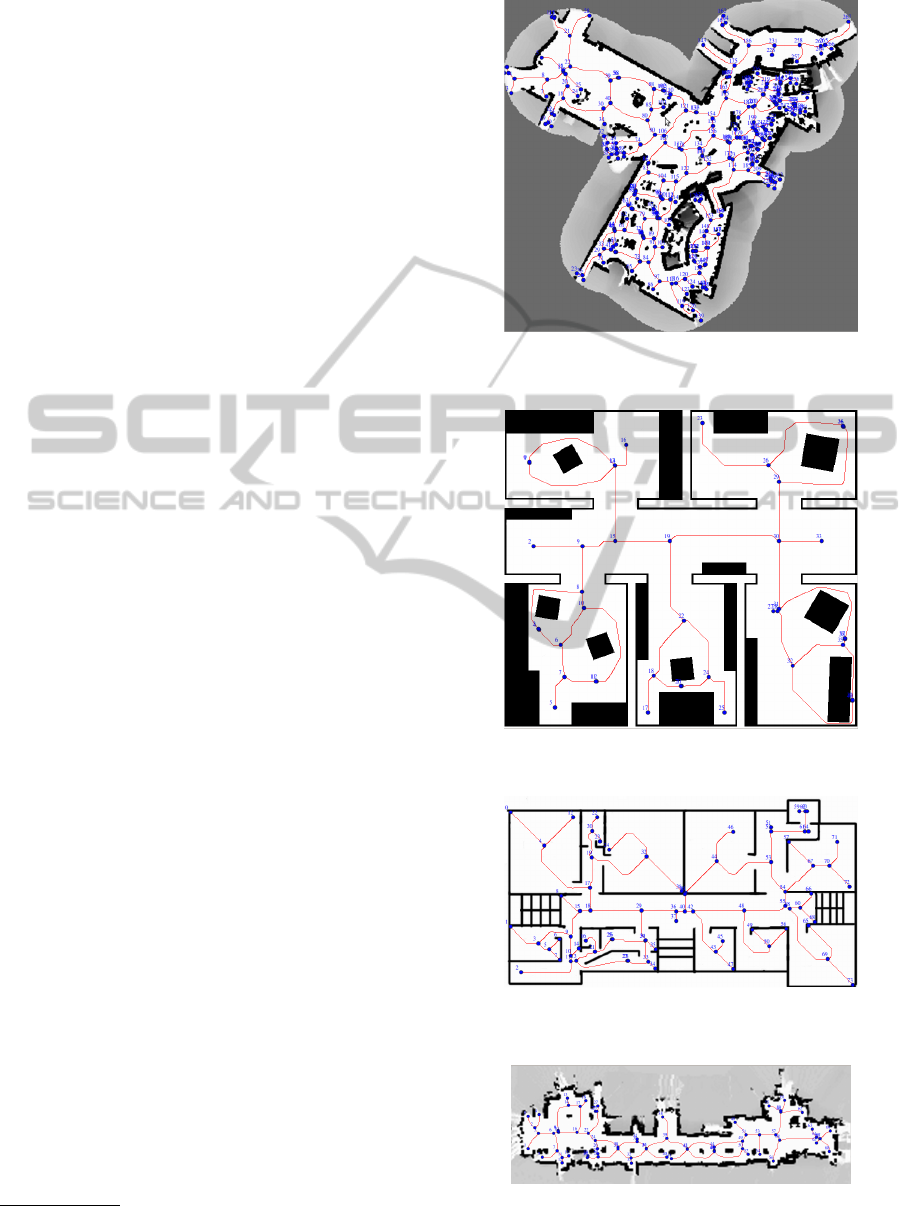
5 RESULTS AND DISCUSSION

The algorithm presented in this article was tested us-

ing a large diversity of maps that generated elegant

and balanced representations that range from simple

topologies to complex ones. An important aspect is

that the complexity of the topological maps extracted

has no relation to the dimension of the environment

(in terms of Cartesian distances). The algorithm at-

tained clear and visually attractive graph representa-

tions from metric maps of all sizes and shape, pre-

senting no vertices with self-loops, staying away from

obstacles and considering the sensing range of the

robots; showing that it scales well in terms of envi-

ronment, as shown in Figures 5-8. Beyond the ac-

curate results obtained, the algorithm has shown to

be computationally efﬁcient. The C++ programming

language was used and the Graphical User Interface

(GUI) for the Patrolling Simulator was implemented

using QT Open Source Edition 4.4.3, which is also

based on C++ Language

. The system ran on Ubuntu

8.10 Intrepid on an AMD Athlon 64 Processor 3500+,

2.21GHz, with 1GB RAM.

Table 1 illustrates the time taken by the algorithm

to extract all information from diverse metric maps,

which is dependent not only on the amount of pix-

els in the free area of each metric map, as well as the

complexity of the generated graph. Around 95% of

the time values shown is spent computing the skele-

ton of the environment (ﬁrst step of the Algorithm),

which is the responsibility of EVG-THIN. The three

other steps of the approach are computed in a few

hundredths of second, which is extremely fast con-

sidering the application for which it was designed for.

The image pixels presented in the table do not re-

late in the same way, for every case, to the free pixels

detected in each image. It is also clear that the com-

putation time does not depend exclusively on this. It

also depends on the graph’s dimension as, for exam-

ple, the fourth and ﬁfth line of the table highlights.

These results attest to the applicability of the

method proposed herein. It is a valuable method for

obtaining a topological map of the environment from

either an a priori known metric map or a metric map

being built on the ﬂy.

6 CONCLUSIONS AND FUTURE

WORK

In this article, a novel way to extract topological maps

The Patrolling simulator code is available at:

http://paloma.isr.uc.pt/%7Edavidbsp/packages

Figure 5: Results for a complex graph (268 vertices) with

high connectivity.

Figure 6: Results for a medium graph (41 vertices) with

deﬁned connectivity.

Figure 7: Results for a medium graph (74 vertices) with

deﬁned connectivity.

Figure 8: Results for a graph with 70 vertices and a few

connectivity constraints.

ICAART 2012 - International Conference on Agents and Artificial Intelligence

142

Table 1: Computation time for different metric maps.

Image Pixels # Vertices Time (s)

90K 12 0.40

341K 74 1.38

379K 20 1.42

343K 66 1.57

509K 206 1.61

544K 268 1.63

815K 135 3.62

and connectivity information from standard grid-like

grayscale representations is described. The approach

presented gains advantage from its simplicity, accu-

racy and performance. One possible disadvantage of

using the EVG-THIN method to compute the skeleton

of the grid map is the dependency on the correct pa-

rameterization, which is not straightforward for most

cases. However, the approach presented in this pa-

per is not limited to the use of EVG-THIN to extract

the skeleton, other techniques like those mentioned in

Section II, can also be used.

Unlike most previous works in this area, here the

intent is not to present solely a representation of the

graph on top of the grid, but also to give one step

ahead by proposing a way to convert visual informa-

tion into data structures, by means of image process-

ing techniques as described.

The proposed approach offers, as output, a com-

plete characterization of the topological aspects of the

environment, which has the ability to assist robot’s

navigation in a broad spectrum of activities, espe-

cially those that include path planning.

As for future work, it would be interesting to test

this approach using different methods in the literature

to obtain the underlying diagram to check whether it

is possible to speed up the ﬁrst step of the algorithm

without losing quality on the topological representa-

tion. Additionally, some questions are still left open

like addressing fast update of the Voronoi Diagram

given dynamic changes in the environment as well as

considering 3D models and deal with topological nav-

igation using mobile robots in real world scenarios.

REFERENCES

Beeson, P., Jong, N., and Kuiper, B. (2005). Towards au-

tonomous topological place detection using the ex-

tended voronoi graph. In Int. Conf. on Robotics and

Automation (ICRA’05), pages 4373–4379, Barcelona.

Delaunay, B. (1934). Sur la sph

ere vide. Izvestia Akademii

Nauk SSSR, Otdelenie Matematicheskikh i Estestven-

nykh Nauk, 7(6):793–800.

Dudek, G., Jenkin, M., Milios, E., and Wilkes, D. (1997).

Map validation and robot self-location in a graph-like

world. Robotics and Autonomous Systems, 22(2):159–

178. Elsevier, Ltd.

Elfes, A. (1989). Using occupancy grids for mobile robot

perception and navigation. Computer, 22(6):46–57.

Fazli, P., Davoodi, A., Pasquier, P., and Mackworth, A.

(2010). Fault-tolerant multi-robot area coverage with

limited visibility. In 2010 IEEE Int. Conf. on Robotics

and Automation (ICRA’10), Anchorage, Alaska, USA.

Ferreira, F., Davim, L., Rocha, R., Dias, J., and Santos, V.

(2007). Presenting a technique for registering images

and range data using a topological representation of a

path within an environment. J. of Automation, Mobile

Robotics & Intelligent Systems, 1(3):47–55.

Katsilieris, F., Lindh

e, M., Dimarogonas, D.,

Ogren, P., and

Johansson, K. (2010). Demonstration of multi-robot

search and secure. In Int. Conf. on Robotics and Au-

tomation (ICRA’10), Anchorage, Alaska, USA.

Ko, B., Song, J., and Lee, S. (2004). Realtime building

of thinning-based topological map. In lnt. Conf. on

Intelligent Robots and Systems, Sandal, Japan.

Kolling, A. and Carpin, S. (2008). Extracting surveil-

lance graphs from robot maps. In IEEE/RSJ Interna-

tional Conference on Intelligent Robots and Systems

(IROS’08), pages 2323–2328, Nice, France.

Lozano-P

erez, T. and Wesley, M. (1979). An algorithm for

planning collision-free paths among polyhedral obsta-

cles. Communications of the ACM, 22(10):560–570.

Machado, A. (2002). Patrulha multiagente: Uma an

alise

emp

ırica e sistem

atica. Master’s thesis, Centro de

Inform

atica, Universidade Federal de Pernambuco

(UFPE), Recife, Brasil.

Portugal, D. and Rocha, R. (2010). Msp algorithm: Multi-

robot patrolling based on territory allocation using

balanced graph partitioning. In 25th ACM Sympo-

sium on Applied Computing (SAC’2010), pages 1271–

1276, Sierre, Switzerland.

Reinhard, D. (2010). Graph Theory. Springer-Verlag Hei-

delberg, New York, electronic edition.

Szab

o, R. (2004). Topological navigation of simulated

robots using occupancy grid. Int. J. of Advanced

Robotic Systems, 1(3):201–206.

Thrun, S. (1998). Learning maps for indoor mobile robot

navigation. Artiﬁcial Intelligence, 99:21–71. Elsevier

Science Ltd.

Thrun, S., Bugard, W., and Fox, D. (2000). A real-time al-

gorithm for mobile robot mapping with applications to

multi-robot and 3d mapping. In Int. Conf. on Robotics

and Automation, pages 321–328, San Francisco.

Voronoi, G. (1908). Nouvelles applications des param

etres

continus

a la th

eorie des formes quadratiques. Journal

ur die Reine und Angewandte Mathematik, 134:198–

287.

Wallgr

un, J. (2004). Hierarchical voronoi-based route graph

representations for planning, spatial reasoning, and

communication. In 4th Int. Cognitive Robotics Work-

shop (CogRob-2004), pages 64–69.

Zimmer, U., Fischer, C., and Puttkamer, E. V. (1994). Nav-

igation on topologic feature-maps. In 3rd Interna-

tional Conference on Fuzzy Logic, Neural Nets and

Soft Computing, pages 131–132, Fukuoka, Japan.

EXTRACTING TOPOLOGICAL INFORMATION FROM GRID MAPS FOR ROBOT NAVIGATION

143