ON COMPLEXITY OF VERIFYING NESTED WORKFLOWS

WITH EXTRA CONSTRAINTS

Roman Barták

Faculty of Mathematics and Physics, Charles University in Prague, Praha, Czech Republic

Keywords: Workflow, Verification, Complexity, Scheduling.

Abstract: Workflow is a formal description of a process or processes. There exist tools for interactive and visual

editing of workflows such as the FlowOpt Workflow Editor. During manual editing of workflows, it is

common to introduce flaws such as cycles of activities. Hence one of the required features of workflow

management tools is verification of workflows, which is a problem of deciding whether the workflow

describes processes that can be realized in practice. In this paper we deal with the theoretical complexity of

verifying workflows with a nested structure and with extra constraints. The nested structure forces users to

create valid workflows but as we shall show, introduction of extra causal, precedence, and temporal

synchronization constraints makes the problem of deciding whether the workflow represents a realizable

process hard. In particular, we will show that this problem is NP-complete.

1 INTRODUCTION

Workflow optimization is an important aspect of

many problems including project management and

manufacturing scheduling. There exist many formal

models to describe the workflows (van der Aalst and

Hofstede, 2005) typically using temporal networks

where the nodes correspond to activities and arcs are

annotated by the temporal relations between the

activities. In this paper we focus on the models

describing optional ways how to realize the

workflow. We mean that the workflow describes

alternative processes and a particular process is

selected based on specified criteria such as

availability of resources or required completion

times. Optional (alternative) activities were

introduced to the scheduling workflows in (Beck and

Fox, 2000) and in this paper we use the formal

model of such workflows called Temporal Networks

with Alternatives (TNA) (Barták and Čepek, 2007).

This model is based on parallel and alternative

splitting and joining of processes that is also known

as AND-split and OR-split (and AND-join, OR-join)

in traditional workflow management systems (van

der Aalst and Hofstede, 2005) (Bae et al., 2004). It

has been shown in (Barták and Čepek, 2007) that the

problem whether it is possible to select a process

from a TNA such that the process contains a specific

node and satisfies the branching constraints (defined

by splitting and joining of processes) is NP-complete

even if no temporal constraints are imposed (the arcs

describe the precedence constraints only). This

implies that verifying general TNA workflows,

which is the task of deciding whether for any node

(activity) there exists a valid process, is NP-

complete. When a TNA is restricted to a nested

structure – we are talking about a Nested TNA – then

the above decision problem is solvable in

polynomial time provided that only the precedence

constraints are used between the nodes (Barták and

Čepek, 2008). Unfortunately, when the simple

temporal constraints are allowed in a Nested TNA

then the problem of deciding about the existence of a

valid process becomes NP-complete again (Barták,

Čepek, Hejna, 2008).

This paper addresses the problem of verifying a

Nested TNA with precedence constraints and some

extra constraints. We will first give necessary

background on Nested TNAs and explain the

semantics of custom constraints added to these

workflows to simplify modeling of real-life

processes. Then, we will look separately on the

problems of verifying workflows with causal,

precedence, and synchronization constraints. We

will show that the problem whether there exists a

valid process where these extra constraints are

enforced is NP-complete in general.

346

Barták R..

ON COMPLEXITY OF VERIFYING NESTED WORKFLOWS WITH EXTRA CONSTRAINTS.

DOI: 10.5220/0003748003460354

In Proceedings of the 4th International Conference on Agents and Artiﬁcial Intelligence (ICAART-2012), pages 346-354

ISBN: 978-989-8425-95-9

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

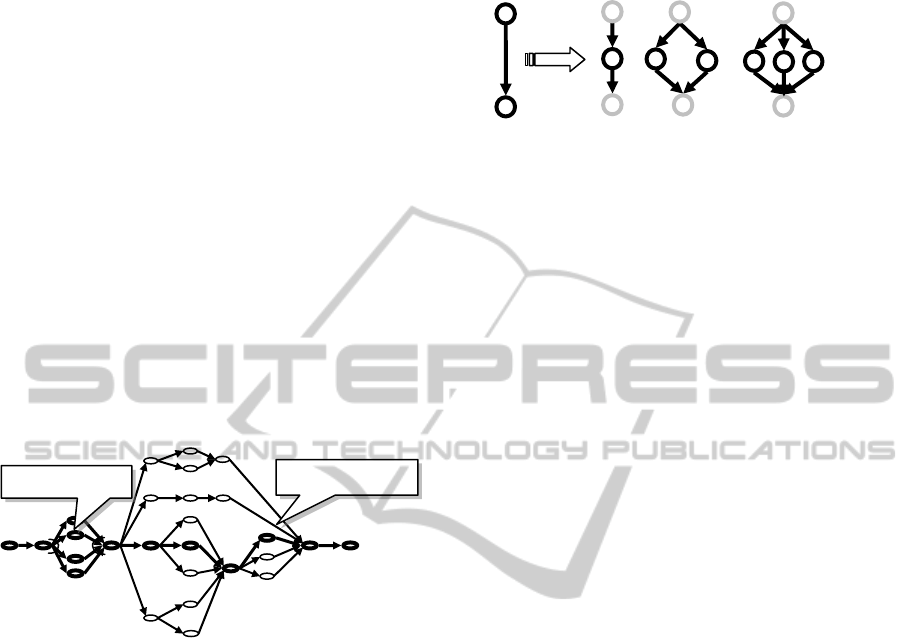
2 BACKGROUND

A Temporal Network with Alternatives (Barták and

Čepek, 2007) is a directed acyclic graph where the

nodes describe the activities and the arcs specify the

precedence constraints between the activities (in

general, simple temporal constraints are allowed, but

we restrict to the precedence constraints which

seems enough for the description of most processes).

When there are more arcs going from (to) a node,

then the type of branching must be specified.

Parallel output (input) branching means that the

node is present in the process if and only if all

directly following (preceding) nodes are present.

Alternative output (input) branching means that the

node is present in the process if and only if exactly

one of the directly following (preceding) nodes is

present. If the node is not present in the process then

none of the directly following (preceding) nodes is

present. Figure 1 gives an example of TNA with one

selected valid process.

Figure 1: A Temporal Network with Alternatives with a

single selected valid process.

Obviously, the branching constraints restrict

which nodes can be present together in a valid

process. An empty process is always valid, but if a

particular node must be included in the process then

the problem of deciding whether such a process

exists or not is NP-complete (Barták and Čepek,

2007). Therefore a restricted form of a TNA, called

a Nested TNA, was proposed in (Barták and Čepek,

2008) to make this decision problem tractable. The

idea is that a Nested TNA is obtained by a sequence

of arc decomposition operations starting with a

trivial TNA consisting of a single arc. Briefly

speaking, an arc is decomposed by adding several

new nodes and connecting them to the original end

nodes of the arc as Figure 2 shows. Each such

decomposition is marked either as a parallel or an

alternative decomposition which corresponds to the

branching constraints from the TNA. The obtained

structure called a nest enforces each output

branching to be “closed” by an input branching of

the same type downstream the graph. The TNA in

Figure 1 is actually a Nested TNA.

Figure 2: Arc decompositions to obtain a Nested TNA.

The nested structure is quite typical for real-life

processes (Bae et al., 2004). It naturally forces the

workflow to be always valid meaning that for each

node (activity) there exists a valid process

containing it. That is the reason why this model was

adapted in the FlowOpt system developed for

modeling and optimizing manufacturing processes

(Barták et al., 2011). To increase flexibility, the

FlowOpt workflow model allows adding extra

constraints to the core nested structure.

2.1 Nested Workflows with Extra

Constraints

The FlowOpt system adapted the idea of a Nested

TNA where instead of decomposing the arcs the

tasks are being decomposed (decomposing tasks

seems more natural for the end users). Basically the

nested workflow is obtained from a single (root) task

by repeated application of the decomposition

operations. Three decomposition operations can be

applied, namely serial, parallel, and alternative

decompositions (Figure 3). There is obvious

similarity to the arc-decomposition operations in a

Nested TNA (compare Figures 2 and 3). These

decomposition operations are applied repeatedly

until non-decomposable base activities are obtained.

By building the workflows using the above

decomposition operations only, a specific nested

structure of the workflow is forced. Such workflows

are always valid because any activity can be a part

of some process defined by the workflow. Moreover,

as we discussed above, it is easy (in polynomial

time) to verify whether a process containing specific

activities exists or not (Barták and Čepek, 2008).

This is not surprising as the nested structure has

inherently a hierarchical (tree) structure describing

how the top task decomposes into sub-tasks and

activities. This simplifies reasoning significantly

because the activities in different nests are related

only through a common ancestor task in the

hierarchical structure.

The base nested structure is not always enough to

describe the peculiarities of real-life processes and

parallel branching

alternative branching

...

ON COMPLEXITY OF VERIFYING NESTED WORKFLOWS WITH EXTRA CONSTRAINTS

347

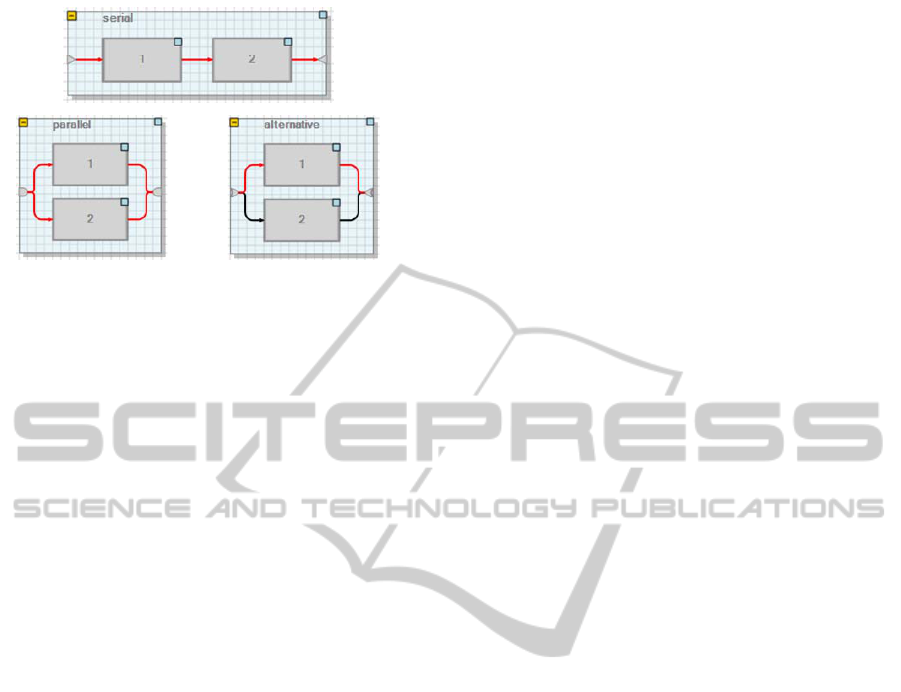
Figure 3: Serial, parallel, and alternative decompositions

of nested workflows as they appear in the FlowOpt

Workflow Editor.

hence the FlowOpt system supports additional

constraints beyond the nested structure. These

constraints express binary relations between the

tasks and activities in the workflow. For example,

the users can connect alternatives in different tasks

and describe that selecting a particular alternative

branch forces (or forbids) selecting a specific

alternative branch in a different task. This is a form

of causal relation between the tasks. Three types of

additional constraints are supported in the FlowOpt

system:

 precedence constraints between any pair of

tasks meaning that if both tasks are selected in

the process then the specified ordering must

hold,

 temporal synchronization constraints

describing that two tasks start or end at the

same time or that one task must start exactly

when another task finishes,

 logical constraints describing causal relations

between the tasks beyond the nested structure

(mutual exclusion, equivalence, and

implication are supported).

We will now study the problem of verifying such

workflows.

2.2 Workflow Verification

When the user specifies the workflow structure, it is

important to ensure that this structure is “correct”.

This process is called workflow verification and it

should be an integral part of workflow management

systems (Giro, 2007). Workflow verification means

checking that for any activity in the workflow there

is a valid process containing this activity. By the

valid process we mean a process selected from the

workflow and satisfying all the workflow and extra

constraints. If some activity cannot be included in

any valid process then it indicates a flaw in the

workflow – such activity should not be a part of the

workflow specification at all. Note that during the

workflow verification, we treat each workflow

separately and we do not assume resource

constraints. We only deal with the temporal and

causal relations between the tasks and activities and

we assume that the activities have non-negative

duration. In particular, we study a sub-problem of

the workflow verification where we verify whether

or not it is possible to select a process from the

workflow satisfying all the workflow constraints and

the extra constraints. This is a verification problem

where only the presence of the root task in the

workflow is checked.

Workflow verification has been studied for some

time. Various methods of verification have been

proposed, for example using Petri Nets (van der

Aalst and Hofstede, 2000), graph reductions (Sadiq

and Orlowska, 2000), or logic-based verification (Bi

and Zhao, 2004). These methods deal with complex

workflow structures that are used for example to

model business processes. A Nested TNA can be

seen as a subset of the workflow models such as

YAWL though using the extra constraints increases

the modeling power of a Nested TNA in some sense

beyond the traditional workflow models. Our

approach to verification is close to logic-based

verification as for example presented in (Bi and

Zhao, 2004). However, in this paper we study

merely the theoretical complexity of the verification

problem rather than proposing a novel verification

technique. Nevertheless, we will also describe some

easily verifiable cases at the end of the paper.

3 NESTED WORKFLOWS WITH

CAUSAL CONSTRAINTS

Let us first formally introduce the causal relations

supported by the FlowOpt system. Causal relations

are binary logical relations between the tasks and

activities in the workflow that describe how the

tasks or activities may appear in the solution.

Because the activities are just a special case of the

tasks (a task that is not decomposed is filled by an

activity), we will be using the word task further. In

the paper we will describe two types of causal

relations, namely implication and mutual exclusion.

If tasks A and B are connected by the implication

relation A ⇒ B then if task A appears in the process

then also task B must appear in the same process.

The mutual exclusion relation, shortly mutex,

between tasks A and B means that these two tasks

ICAART 2012 - International Conference on Agents and Artificial Intelligence

348

cannot appear together in a single process. It means

that either task A appears in the process, but not task

B, or task B appears in the process, but not task A,

or none of these tasks appear in the process. Notice

that the mutex relation looks similar to classical

XOR relation, but it is slightly different as XOR

requires that exactly one of the tasks appears in the

process.

In the rest of this section we will show that if the

implication or mutex relations appear in a nested

workflow then the problem of checking validity of

the workflow is NP-complete. We will show that the

problem of deciding satisfiability of a Boolean

formula in a conjunctive normal form where each

clause contains three literals – this is a well known

3SAT problem that has been shown to be NP-

complete (Garey and Johnson, 1979) – can be

converted in polynomial time to a problem of

deciding whether the nested workflow with some

additional constraints has a solution. Briefly

speaking, we will present how to convert any 3SAT

formula to a nested workflow that uses either the

implication constraints or the mutex constraints.

Then we will prove that the solutions to this nested

workflow correspond to the solutions of the original

Boolean formula.

Proposition 1: The problem of deciding validity of a

nested workflow with additional implication

constraints is NP-complete.

Proof: If we have a selection of activities belonging

to the solution then it is easy to check in polynomial

time whether the workflow and implication

constraints are satisfied. Hence the problem belongs

among the NP problems.

Let us assume that we have a 3SAT formula,

which is a conjunction of clauses, where each clause

is a disjunction of three literals and a literal is a

variable or a negation of the variable. We will

represent this formula as a nested workflow

consisting of a sequence of tasks where first there

are tasks for the variables followed by a single task

for the formula. For each variable there is exactly

one task (the order of the tasks does not matter)

which decomposes to two activities, one

representing value true and the other one

representing value false – let us call them value

activities. The task representing the formula

decomposes into parallel tasks where each task

represents one clause in the formula – we will call

them clause tasks. Figure 4 shows this

representation. Notice that using serial or parallel

decomposition does not matter here and it is possible

to use any of these types of task decomposition. We

Figure 4: The core concept of representing a 3SAT

formula as a nested workflow.

will now show on a single example how to represent

the clause, in particular how clause X ∨ Y ∨ ¬ Z is

represented using an alternative decomposition of

the clause task. There are seven possible

assignments of variables X, Y, and Z satisfying this

clause; X = true, Y = true, Z = true is one of them.

To satisfy the clause exactly one of these satisfying

assignments must be used. To model this feature we

decompose the clause task into seven alternative

activities, each one representing one satisfying

assignment – let us call them assignment activities.

Now we need to ensure that these assignment

activities are selected only when the corresponding

value activities are selected. This is achieved by

using the implication constraints going from the

assignment activities to the value activities. Let the

assignment activity correspond to assignment

X = true, Y = true, Z = true. Then we include the

implication constraints from the assignment activity

to the corresponding value activities of tasks

representing variables X, Y, and Z as Figure 5

shows. By this construction we obtain a nested

workflow whose size is polynomial in the size of the

3SAT formula. In particular if we have a formula

with n variables and m clauses then we obtain a

nested workflow with 2n + 7m activities (the number

of tasks is 3n + 8m + 2) and 21m additional

implication constraints.

The last step of the proof is to show that the

nested workflow has a solution if and if only the

formula is satisfiable. We will show that each

satisfying assignment of the variables corresponds to

one solution of the workflow. If we have a satisfying

assignment then we select in the workflow the value

activities corresponding to the values in the

assignment and the assignment activities compatible

with the assignment. Obviously the implication

constraints are satisfied by this selection. Moreover

from each task corresponding to a variable we

ON COMPLEXITY OF VERIFYING NESTED WORKFLOWS WITH EXTRA CONSTRAINTS

349

Figure 5: Selected custom implication constraints

connecting the assignment and value activities in the

model of a 3SAT formula.

selected exactly one activity (the variable is

instantiated to some value) and from each task

corresponding to a clause, exactly one activity is

selected because the clause is satisfied by the

assignment. Together the selected activities form the

process satisfying the workflow constraints as well

the additional causal constraints. Vice versa, let us

have a process selected from the workflow. Then

exactly one value activity is selected for each task

representing a variable – this activity determines the

value of that variable. For each task corresponding

to a clause, one assignment activity is selected. As

implication constraints from this assignment activity

must be satisfied, the value activities corresponding

to the assignment must also be selected which means

that the values assigned to the variables satisfy the

clause. Together, the selected process defines an

assignment of variables that satisfies all clauses in

the formula and hence the formula is satisfiable.

We have shown that the solutions of the nested

workflow with additional implication constraints

correspond to the solutions of the 3SAT formula.

Hence the problem to decide whether the nested

workflow with implication constraints has a solution

is NP-complete.

We will now use similar arguments to show that

the problem of verifying nested workflows with

additional mutex constraints is also NP-complete.

Proposition 2: The problem of deciding validity of a

nested workflow with additional mutex constraints is

NP-complete.

Proof: We will again use the transformation of a

3SAT formula to a nested workflow. In fact, we

will use exactly the same core structure of the nested

workflow as in the proof of proposition 1 (also

shown in Figure 4), we shall only introduce mutex

constraints instead of the implication constraints.

Let us assume that for a given 3SAT formula we

generated a nested workflow with the structure

shown in Figure 4, that is, with the pairs of value

activities for the propositional variables and with the

clause tasks each containing seven assignment

activities. We shall introduce the mutex constraints

as follows. Assume that an assignment activity

corresponds to a satisfying assignment X = true,

Y = true, Z = true. Then we introduce the mutex

constraints between this activity and the value

activities for X = false, Y = false, and Z = false.

These mutex constraints ensure that the assignment

activity cannot be selected together with the

incompatible value activities. In other words

selection of an assignment activity forces selection

of compatible value activities (recall that for each

propositional variable exactly one value activity is

selected). Figure 6 shows these additional mutex

constraints. Like before, for a formula with n

variables and m clauses we obtain a nested workflow

with 2n + 7m activities (the number of tasks is

3n + 8m + 2) and 21m additional mutex constraints

so the size of the nested workflow is polynomial in

the size of the 3SAT formula.

Now, it is straightforward to show that the

satisfying assignments to a given 3SAT formula

correspond one-to-one to the solutions of the

constructed nested workflow. If we have a satisfying

assignment of the propositional variables then we

select the value and assignment activities

corresponding to this assignment. Consequently, for

each task describing a variable exactly one value

activity is selected and for each clause task exactly

one assignment activity is selected. As described in

the previous paragraph this selection satisfies the

mutex constraints. Vice versa, the selection of

activities satisfying the workflow and the mutex

constraints defines a satisfying assignment of the

3SAT formula.

Figure 6: Selected custom mutex constraints connecting

assignment and value activities in the model of a 3SAT

formula.



ICAART 2012 - International Conference on Agents and Artificial Intelligence

350

We have shown that the solutions of the nested

workflow with additional mutex constraints

correspond to the solutions of the 3SAT formula.

Hence the problem to decide whether the nested

workflow with mutex constraints has a solution is

NP-complete.

The problem of deciding whether a given

workflow has a solution, that is, finding whether it is

possible to select a subset of activities satisfying the

workflow constraints, is NP-complete if additional

causal constraints are added. Consequently the

problem of verifying the nested workflows with

causal constraints is also NP-complete.

4 NESTED WORKFLOWS WITH

PRECEDENCE CONSTRAINTS

Let us now look at the nested workflows where

additional precedence constraints are added. Recall

that the nested workflows already include implicit

precedence constraints. Namely each arc in the

graphical representation of the workflow represents

a precedence relation between the tasks and

activities. These precedence relations are introduced

during the task decomposition. To check consistency

of the precedence relations, it is enough to ensure

that the graph is acyclic (we assume that the

activities have positive duration). This is always the

case for implicit precedence relations introduced

during task decomposition as the decomposition will

never introduce a cycle. If we allow adding extra

precedence constraints then directed cycles may be

introduced to the workflow. This does not

necessarily mean inconsistency of the workflow

because not all tasks/activities are present together in

valid processes selected from the workflow. We just

need to ensure that every directed cycle of the

precedence constraints can be broken by omitting at

least one of the activities from the cycle in the

solution. We will show now that the problem of

detecting whether breaking the cycles is possible is

an NP-hard problem. We will again use the

conversion of a 3SAT formula to a nested workflow

as shown in Figure 4. In fact we will use a similar

idea to exploiting the mutex constraints. Notice that

a cycle of two activities is semantically identical to a

mutex relation between the same activities – these

two activities cannot be present in the solution

together.

Proposition 3: The problem of deciding validity of a

nested workflow with additional precedence

constraints is NP-complete.

Proof: The proof is identical to the proof of

Proposition 2 where mutex constraints are used. The

only difference is that the precedence constraints are

used instead of the mutex constraints as Figure 7

shows. Let us also set the duration of all activities to

one to highlight that the loops are forbidden because

the activities in the loop cannot be allocated

consistently to time in such a way that the

precedence constraints are satisfied (a TNA expects

a unique appearance of each activity in the process

which differentiates it from workflow formalisms

such as YAWL (van der Aalst and Hofstede, 2005)).

Figure 7: Selected custom precedence constraints

connecting assignment and value activities in the model of

a 3SAT formula.

Assume that an assignment activity corresponds

to a satisfying assignment X = true, Y = true,

Z = true. Then we introduce the precedence

constraints leading from this activity to the value

activities for X = false, Y = false, and Z = false.

Because the value activities are before all the

assignment activities in the workflow, the added

precedence constraints introduce directed cycles to

the workflow. These directed cycles consist of tasks

encapsulating the value activities (these tasks must

always be in the solution process) and two activities

connected by the extra precedence constraints.

Hence one of these two activities must be omitted

from the process to break the cycle so the semantic

of such precedence constraints is identical to the

mutex constraints between the same pair of

activities. Therefore the arguments from the proof of

Proposition 2 can be re-used there. We should only

show that the problem belongs to the NP class which

is easy to realize as checking validity of the solution

means checking the workflow constraints as before

and checking that there is no directed cycle between

the selected activities which can be done in

polynomial time for example by topological sorting.

ON COMPLEXITY OF VERIFYING NESTED WORKFLOWS WITH EXTRA CONSTRAINTS

351

5 NESTED WORKFLOWS WITH

SYNCHRO CONSTRAINTS

Finally, we will study the workflows with additional

temporal synchronization constraints. Temporal

synchronization constraints are useful to express

relations such as that two activities should start or

finish at the same time or that an activity should start

exactly at the time when the preceding activity

finished. Some of these relations are hidden in the

core structure of the nested workflow. In particular,

we assume that the task starts exactly at the time

when the earliest of its sub-tasks starts and the task

finishes exactly when the latest of its sub-tasks

finishes (note that we assume only those sub-tasks

that are selected in the solution). Naturally, when

working with the temporal relations, we assume that

all activities have non-negative duration (zero

duration is allowed to model milestone activities).

It is practically useful to express some temporal

synchronization constraints explicitly even between

the tasks that do not belong to the same nest in the

workflow. In particular, the FlowOpt system

supports temporal synchronization constraints that

are known as start-start, end-end, end-start, and

start-end. Unfortunately, as we shall show adding

these extra constraints to nested workflows makes

the problem of deciding whether or not the

workflow has a solution intractable. Differently from

the previous sections, we will now use a subset-sum

problem to prove the above claim. This is motivated

by a similar approach used in (Barták, Čepek, Hejna,

2008). A subset-sum problem is a known NP-

complete problem (Garey and Johnson, 1979) that is

formulated as follows. Given a set of positive

integers Z

and integer K, does the sum of some

subset of {Z

| i= 1,…,n} equals K? We shall show

that this problem can be represented as a nested

workflow with extra synchronization constraints.

Proposition 4: The problem of deciding validity of a

nested workflow with additional synchronization

constraints is NP-complete.

Proof: The structure of the proof is similar to the

proofs of previous propositions in the paper. First, it

is easy to verify in a polynomial time that a given

selection of activities allocated to time satisfies the

workflow constraints as well as the additional

temporal synchronization constraints. Hence the

problem belongs to the NP class.

We shall show now that a subset-sum problem

can be modeled as a nested workflow with

synchronization constraints. Assume the numbers K,

,…, Z

from the subset-sum problem. We use a

workflow with two parallel tasks. One task contains

a single activity with duration K – let us call it a

bound activity – and the other task is a serial

decomposition with n value tasks. Each of the value

tasks decomposes further into two alternative

activities – we call them value activities. One of

these activities has zero duration and the other

activity has duration Z

in the i-th value task. The

idea is that we need to select the value activities

such that the sum of their durations equals the

duration of the bound activity. To ensure this feature

we introduce the following synchronization

constraints. The bound activity must start exactly at

the same time as the first value task (start-start

synchronization) and it must finish exactly when the

last value task finishes (end-end synchronization).

Moreover, the i-th value task must finish exactly

when the (i+1)-th value task starts (end-start

synchronization). Figure 8 gives an example of such

a nested workflow with above described

synchronization constraints.

Figure 8: Representation of the subset-sum problem as a

nested workflow with synchronization constraints.

Obviously, each solution to the subset-sum

problem corresponds to a selection of certain value

activities and this selection satisfies the

synchronization constraints. Vice versa, a set of

activities satisfying the workflow and

synchronization constraints defines a solution of the

subset-sum problem. The bound activity is always

selected and from each value task exactly one value

activity is selected. The sum of durations of selected

value activities equals the duration of the bound

activity which complies with the specification of the

subset-sum problem. Hence the subset-sum problem

can be formulated as the problem of selecting

activities from the nested workflow which proves

that verification of nested workflows with

synchronization constraints belong among the NP-

hard problems.

6 CONCLUSIONS

In this paper we showed that the problem of

ICAART 2012 - International Conference on Agents and Artificial Intelligence

352

verifying whether or not there exists a feasible

process selected from a nested workflow with

additional constraints is NP-complete. We used

workflows modeling 3SAT and subset-sum

problems in the proofs and these workflows have a

structure that is not typical for real-life workflows.

Hence, there is a hope that real-life workflows can

still be verified in a reasonable time in practice. The

next step is to find such a procedure that can do

verification of nested workflows with additional

constraints efficiently in practice. Note that this

verification procedure should work with constraints

of all types mentioned in the paper together.

Figure 9: A tree representation of nested workflows.

Some of the extra constraints can be verified

easily. Notice that a Nested TNA can be represented

as a tree showing how the root task is decomposed

into sub-tasks and so on until activities are obtained

in the leafs (Figure 9). There are basically two

different locations where the binary custom

constraint can be placed in this tree. Either the

constraint connects two tasks on the same

path/branch to the root task (for example the

constraint between tasks A and B in Figure 9) or the

constraint connects the tasks from different sub-trees

with a common ancestor task (for example the

constraint between tasks C and D in Figure 9). The

constraints along the path to the root are those

constraints that are easy to verify as they are

frequently redundant (entailed by the workflow

constraints) or inconsistent. The constraints between

tasks from different sub-trees are easy to verify if

their common ancestor (task E in Figure 9)

decomposes alternatively. The only situation which

makes verification non-trivial is when task E is a

serial or parallel decomposition as in Figure 9. This

is exactly the case of the nested workflows used in

the proofs of NP-completeness in this paper. For

these cases a straightforward approach is using a

search procedure that finds for each activity a valid

process containing this activity. If no valid process is

found, the activity is reported to the user as a

problematic activity. In such a case, it is not always

clear which custom constraints cause the problem.

Providing the most accurate explanation is an

interesting open problem.

ACKNOWLEDGEMENTS

The research is supported by the Czech Science

Foundation under the contract P202/10/1188. The

author would like to thank Vladimír Rovenský for

implementing the FlowOpt Workflow Editor;

screenshots from this software are used in the paper.

REFERENCES

Bae, J., Bae, H., Kang, S.-H., Kim, Z., 2004. Automatic

Control of Workflow Processes Using ECA Rules.

IEEE Transactions on Knowledge and Data Enginee-

ring, vol. 16, no. 8, pp. 1010-1023.

Barták, R., Čepek, O., 2007. Temporal Networks with

Alternatives: Complexity and Model. In Proceedings

of the Twentieth International Florida AI Research So-

ciety Conference (FLAIRS), AAAI Press, pp. 641–646.

Barták, R., Čepek, O., 2008. Nested Temporal Networks

with Alternatives: Recognition, Tractability, and

Models. In Artificial Intelligence: Methodology, Sys-

tems, and Applications (AIMSA 2008), LNAI 5253,

Springer Verlag, pp. 235-246.

Barták, R., Čepek, O., Hejna, M., 2008. Temporal

Reasoning in Nested Temporal Networks with Alter-

natives. In Recent Advances in Constraints, LNAI

5129, Springer Verlag, pp. 17-31.

Barták, R., Cully, M., Jaška, M., Novák, L., Rovenský, V.,

Sheahan, C., Skalický, T., Thanh-Tung, D., 2011.

FlowOpt: A Set of Tools for Modeling, Optimizing,

Analyzing, and Visualizing Production Workflows. In

Proceedings of the ICAPS 2011 System Demonstra-

tions, pp. 6-9.

Beck, J. Ch., Fox, M. S., 2000. Constraint-directed

techniques for scheduling alternative activities. Arti-

ficial Intelligence, vol. 121, pp. 211-250.

Bi, H. H., Zhao, J. L., 2004. Applying Propositional Logic

to Workflow Verification. Information Technology

and Management, vol. 5, no 3-4, pp. 293-318.

Garey, M. R., Johnson, D. S., 1979. Computers and Intra-

ctability: A Guide to the Theory of NP-Completeness,

W. H. Freeman and Company.

Giro, S., 2007. Workflow Verification: A New Tower of

Babel. In AIS-CMS International Modeling and Simu-

lation Multiconference, Buenos Aires, Argentina.

Sadiq, W., Orlowska, M. E., 2000. Analyzing Process

Models using Graph Reduction Techniques.

Information Systems, vol. 25, no. 2, pp. 117–134.



A

B

C

D

E

ON COMPLEXITY OF VERIFYING NESTED WORKFLOWS WITH EXTRA CONSTRAINTS

353

van der Aalst, W., Hofstede, A. H. M. t., 2000.

Verification of Workflow Task Structures: A Petri-

Net-Based Approach. Information Systems, vol. 25,

no. 1, pp. 43–69.

van der Aalst, W., Hofstede, A. H. M. t., 2005. Yawl: Yet

another workflow langure. Information Systems, vol.

30, no. 4, pp. 245–275.

ICAART 2012 - International Conference on Agents and Artificial Intelligence

354