INTERBANK PAYMENT SYSTEM (RTGS) SIMULATION USING

A MULTI-AGENT APPROACH

Hedjazi Badiâa

, Ahmed-Nacer Mohamed

, Aknine Samir

and Benatchba Karima

Information Systems Division, CERIST Research Center on Scientific and Technical Information, Algiers, Algeria

Information Systems Laboratory, USTHB University, Algiers, Algeria

GAMA Laboratory, Lyon 1 University, Lyon, France

ESI, National High School of Computer Science, Algiers, Algeria

Keywords: Real Time Gross Settlement, Multi-agent system, Classifier system, Evolutionary game theory.

Abstract: This work consists in simulating a real time interbank gross payment system (RTGS) through a multi-agent

model, to analyze the evolution of the liquidity brought by the banks to the system. In this model, each bank

chooses the amount of a daily liquidity on the basis of costs minimization (costs of liquidity and delaying)

by taking into account the liquidity brought by other banks. Banks agents’ strategies are based on a liquidity

game during several payment days where each bank plays against the others. For their adaptability, we

integrate into bank agents learning classifier systems. We carry out several simulations to follow the system

total liquidity evolution as that of each bank agent with varying costs coefficients. The question to answer

is: what are the cash amounts that banks must provide and under what costs of liquidity and delaying, the

system avoids the lack of liquidity? We find that liquidity depends on costs coefficients.

1 INTRODUCTION

Real Time Gross Settlement systems (RTGS) are

real-time funds transfer systems that enable banks to

make large-value payments to one another (Devriese

and Mitchell, 2006) (Leinonen, 2005) (BIS, 1997).

Exchanged Liquidity (funds) carries "cost of

liquidity" proportional to liquidity amount. Delayed

payments imply a “cost of delaying". Therefore

several questions arise. How much liquidity must a

bank engage? What are the best values of costs’

coefficients? Cost of liquidity coefficient is the

interest rate paid to central bank and delaying cost

coefficient is a penalty. We simulate RTGS using a

multi-agent system (MAS) to show the relationship

between liquidity and costs while evolutionary game

theory (EGT) (Thisse, 2004) formalizes interbank

strategies. Section 2 presents RTGS, section 3

existing works, section 4 our model and section 5

simulation results. We conclude in section 6.

2 RTGS FUNCTIONING

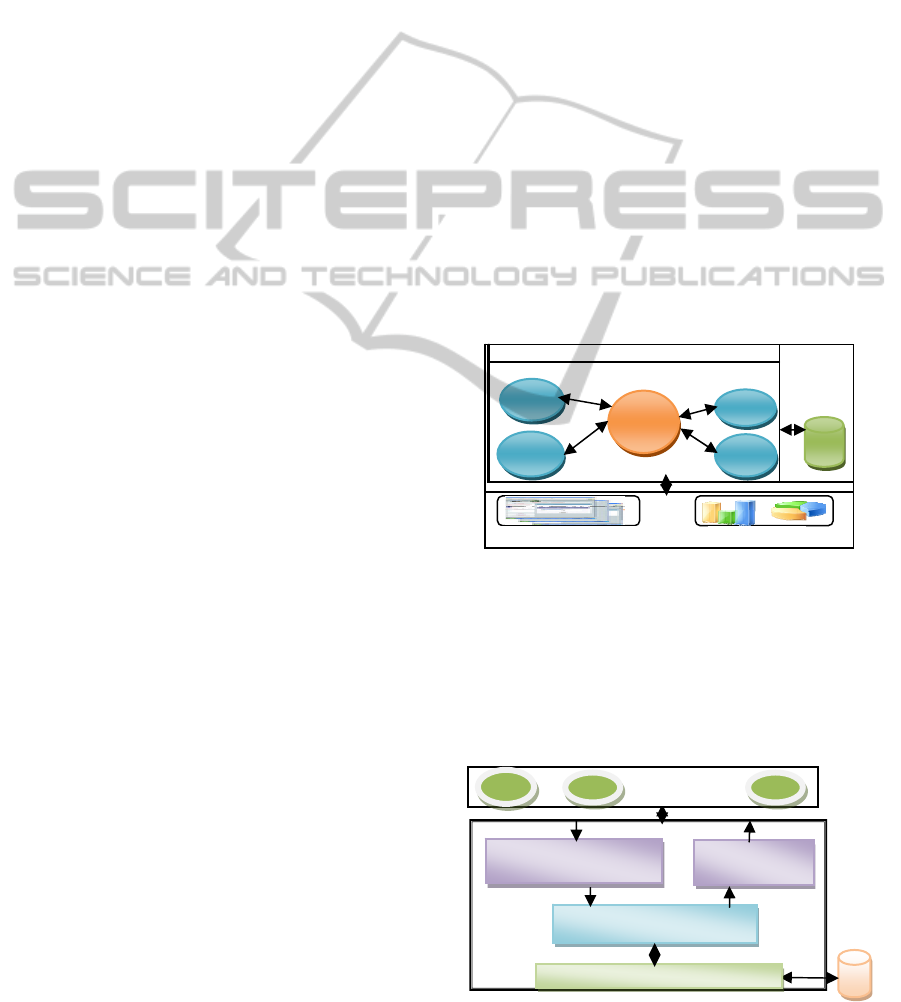
Figure 1 shows the functional architecture of a

RTGS system: (1) A bank B

submits a payment

order to RTGS. (2) Order is either executed or

queued. (3) Payment is transmitted to receiver bank

account. (4) RTGS informs receiver bank on the

transfer (Bank of International Settlements, 1997).

Figure 1: RTGS system architecture (Beyeler et al., 2007)

3 RELATED WORK

Several researchers developed mathematical

simulation models of payment systems (Koponen

and Soramäki, 1998) (Leinonen, 2005) (Devriese

and Mitchell, 2006). In the mathematical approach,

Central RTGS platform

Account

3. Final transfer

Bank

1. Irrevocable

ayment order

submission

Information

on payment

2. Payment after

checking

(Executed/putte

d in waitin

)

Payment

information

362

Badiâa H., Mohamed A., Samir A. and Karima B..

INTERBANK PAYMENT SYSTEM (RTGS) SIMULATION USING MULTI-AGENT APPROACH.

DOI: 10.5220/0003750503620365

In Proceedings of the 4th International Conference on Agents and Artiﬁcial Intelligence (ICAART-2012), pages 362-365

ISBN: 978-989-8425-96-6

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

payment systems are represented through differential

equations and banks behaviour is not endogenously

determined but assumed unchanged. Contrary to

this, multi-agent simulation describes entities

behaviours explicitly (Arciero et al., 2009) and

considers system total dynamics resulting from

entities interactions (Parunak et al., 1998).

In (Galbiati and Soramäki, 2007) model, orders

are of 1 unit only, and agents are assumed knowing

all banks’ past choices, which is unrealistic.

Game theory studies situations in which each

participant (assumed rational) fate depends on its

decisions and the others participants’ ones (Angelini,

1998). RTGS mechanisms are seen like games

where players are the banks. Evolutionary game

theory assumes that players are with bounded

rationality and remained strategies are those

obtaining the largest gains over time. In the models

of (Arciero et al., 2009) (Bech and Garratt, 2003)

(Bech and Garratt, 2006) (Galbiati and Soramäki,

2007), players’ utility is static and known in

advance. In addition, these models cannot provide

information on each entity and cannot run historical

or random data or represent components as by MAS.

4 PROPOSED RTGS MODEL

In our agent-based model, a collection of banks have

different payments during several days. Choices of a

bank agent are formalized by an evolutionary game

where a bank chooses a liquidity based on costs of

liquidity and delaying and the other banks choices.

4.1 Liquidity Game of the System

Our liquidity game is inspired from aggregate game

(Mezzetti and Dindos, 2006) where a player

considers the others as a single opponent. Our game

consists of a set of N banks. Each new day, a bank

chooses its liquidity l

(0) for its payments. Each

bank estimates the other banks average liquidity l

-i

through its neighbours. For bank i, the number of

payment orders received up to time t is z

(t). Number

of orders executed until time t is x

(t). Payment

orders number in queue at t, q

(t), is defined by (1):

(t)= z

(t) - x

(t) (1)

Payment orders are executed using the available

liquidity which is defined by (2):

(t) = l

(0) − x

(t) + y

(t) (2)

yi(t) is the payments amount that bank i received

until time t. Payments are executed in FIFO. Initial

liquidity li(0) imposes to bank i a liquidity cost (3):

(0)) = α× l

(0) (3)

α ∈ [0, 1], is cost coefficient of liquidity.

Payment received at time t

, executed at t

, queued

for ∆t=t

–t

, imposes to bank i a cost of delaying (4):

, t

) = β×Δt×Payment_amount (4)

β ∈ [0, 1] is the cost coefficient of delaying. The

global bank daily cost is the sum of the costs (5):

C = C

+ C

(5)

As the costs’ bank increase its profitability

decreases. Player i utility depends on its action l

, the

others average actions l

-i

and costs coefficients.

4.2 Multi-agent System Model

At the central level of our RTGS model, payments

are settled with liquidity brought by banks on their

RTGS accounts. Payment order with insufficient

account balance is rejected. Each bank manages its

own waiting queue. Our MAS model contains an

"RTGS agent" and "Banks agents" BAi (Figure 2).

Figure 2: General representation of the system.

4.2.1 RTGS Agent (RA)

RA is a reactive agent and represents the central

payment system (Figure 3). For each day, RA

receives and liquidity amounts of banks agents. RA

Processes banks agents’ payment orders (debits and

credits banks accounts).

Figure 3: RA internal architecture.

Messages reception (liquidity,

payment orders)

Payment orders and other messages

treatments

Messages sending

(informations)

Banks RTGS accounts management

BA1

BA2 BAn

Other agents

RTGS

Agent

Parameterization

Results

SMA

ADE

INTERBANK PAYMENT SYSTEM (RTGS) SIMULATION USING MULTI-AGENT APPROACH

363

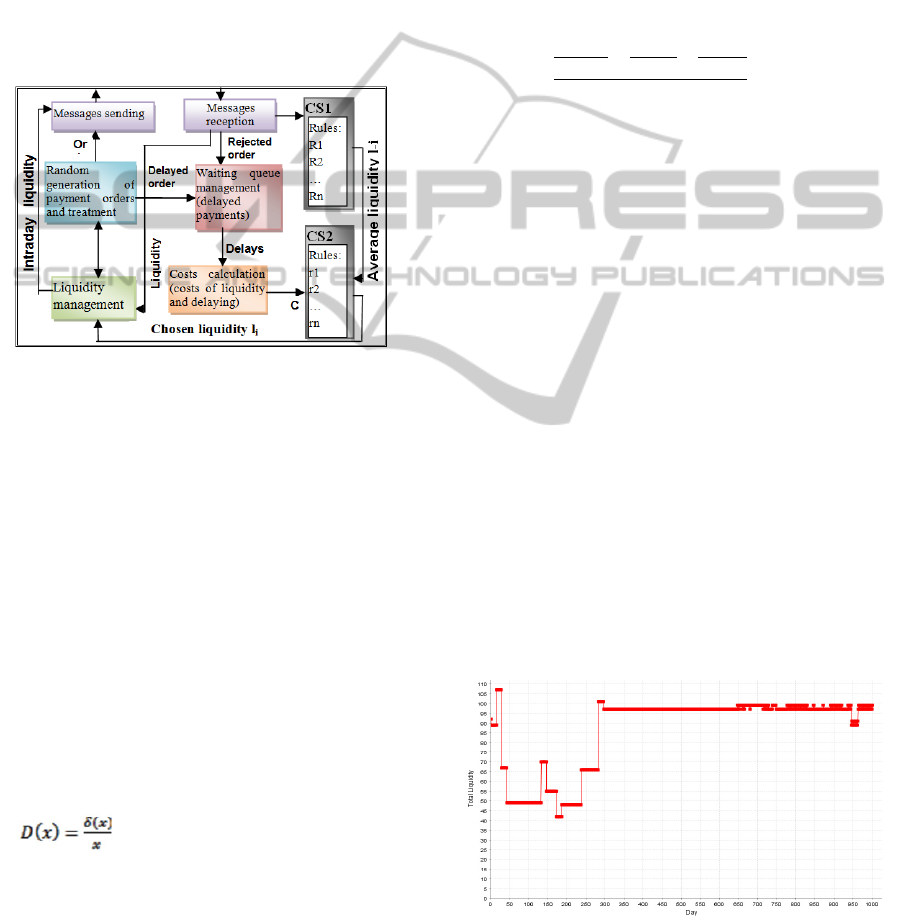
4.2.2 Banks Agents (BA)

BA exchanges payments through RA with liquidities

chosen at the beginning of each day. BA sends

random payment orders to RA and manages its

waiting queue. At the end of the day, it calculates

costs and starts a learning process. BA is cognitive.

It learns playing game to minimize costs and

improve utility with classifier systems (CS) of LCS

type (Holland, 1987). LCS is appropriate because

banks evaluate actions periodically to learn quickly.

BA is built on: (1) CS1 gives the others average

liquidity. (2) CS2 defines liquidity (Figure 4).

Figure 4: BA Internal architecture.

classifier system (CS1): CS1 estimates the others

average liquidity. Each day, each agent observes the

liquidity chosen by a reduced number (eg. 3) of

neighbours chosen randomly. CS1 generated value is

used as entry for CS2 to choose liquidity. CS1 rule is

composed of three parts:

Condition Part: has 3 attributes (Lbx, Lby, Lbz)

representing the 3 liquidity values of selected agents.

These values are in the interval [0, 15]. So this part

requires 12 bits (4 bits for each attribute).

Action Part: is coded on 4 bits, corresponding to

average liquidity l

-i

of the other agents in [0, 15].

Rules Reward: Rules are remunerated when

neighbours liquidity values are close to the average.

Dispersion coefficient is calculated then between

the three values of the condition and the action

value.

Where δ(x) is the standard

deviation.

If D(x) < 0.15 Then reward=1 Else reward=0;

classifier system (CS2): CS2 allows intraday

liquidity choice. The system evaluates costs (of

liquidity and delaying) at the end of the day and

chooses liquidity. CS2 rule consists of three parts:

Condition Part: has 2 attributes (real numbers), cost

of liquidity C

and cost of delaying C

. C

(Integer

part in [0, 15], decimal part in [0, 99]). C

is on 11

bits (4 for integer part, 7 for decimal one). C

(Integer part in [0, 1000], decimal part in [0, 99]). C

is on 17 bits (10 for integer part, 7 for decimal part).

Action Part: on 4 bits, represents the intraday

liquidity l

to be chosen in the interval [0, 15].

Rules Reward: CS2 reward depends on the action l

the average l

-i

of the neighbours obtained by CS1

and the costs of liquidity and delaying (6).







−′









(6)

With l’= l

-i

. The reward is divided by 3 to limit it

to 1. CS2 rewards actions generating less costs and

which liquidity approaches l

-i

Liquidity game strategies correspond to CS2

rules actions and utility corresponds to CS2 reward.

Heterogeneity between BA agents’ is assured by:

(1) Rules of CS1 and CS2 are initialized randomly

for each BA. (2) Random neighbours of a BA.

5 SIMULATIONS

MAS’ implementation has been done using JADE

platform and CS with ART (Artificial Reasoning

Toolkit).Our simulations duration is 1000 days with

10 BA then 20 BA and different α and β values.

Figure 5 shows the global liquidity evolution of

10 BA. For all our simulations, we notice that

liquidity and total cost of delaying (Figure 7)

stabilize at certain values. This shows that agents

performed successfully their coordination leading to

satisfaction. As costs coefficients increase, total

liquidity becomes unstable. We notice that

coefficient β destabilizes liquidity more than α.

Figure 5: Global liquidity (for 10 BA) α =1%; β=10%.

ICAART 2012 - International Conference on Agents and Artificial Intelligence

364

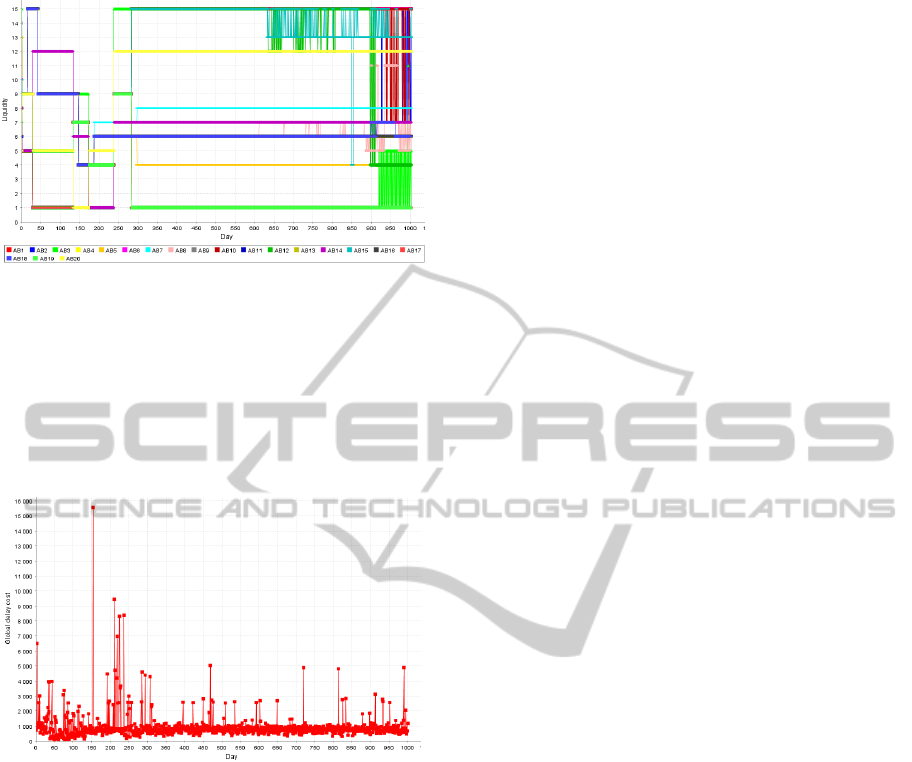
Figure 6: Liquidity of the 20 BA α =1%; β=10%.

Figure 6 shows that liquidity value for each BA

is more stable when α and β are small and that β

coefficient influences the system evolution more

than α. Figure 7 shows total cost of delaying. We

notice that as the number of BA increases, the cost

of delaying decreases. This indicates that more there

is sources of liquidity, less there is delaying.

Figure 7: Cost of delaying of 10 BA α=10%; β=10%.

These results show that the best configuration of the

coefficients is α=10%; β=1%. For these values,

global liquidity is more stable. BA agents propose

closer liquidity values and minimized costs of

delaying. All these experiments show that efficient

RTGS management is possible with smart choices of

costs coefficients. They also help to determine daily

liquidity values that stabilize the system and allow

RTGS decision makers implementing policies

specifying liquidity values that banks must choose.

6 CONCLUSIONS

In this paper, we have presented a multi-agent model

for simulating RTGS systems. This model has been

implemented and tested with different parameters.

Our tool can be used as a decision support system by

adapting it with real RTGS data in the codification

of real liquidity and cost values in CS rules.

Decision support is possible by searching liquidity

values, costs coefficients that cause stabilities or

instabilities. Our simulation model is intended for

central banks, private banks, specialists or any

person interested by RTGS systems. Some

improvements could be added to this work such as:

(1) considering payments of different priorities; (2)

taking other parameters such as bank reputation.

REFERENCES

Angelini, P., 1998. An analysis of competitive

externalities in gross settlement systems, JBF, vol.22.

Arciero, L., Biancott, C., D’Aurizio, L. L., Impenna, C.,

2009. Exploring agent-based methods for the analysis

of payment systems: a crisis model for StarLogo TNG,

Working paper, Banca d’Italia.

BIS: Bank of International Settlements, 1997. Real-Time

Gross Settlement systems, Report of the Committee on

Payment and Settlement Systems of central banks of

Group of 10 countries, www.bis.org.

Bech, M., Garratt, R., 2003. The intraday liquidity

management game, JET, vol. 109(2), pp. 198-219.

Bech, M., Garratt, R., 2006. Illiquidity in the Interbank

Payment System Following, Wide-Scale Disruptions,

Federal Reserve, New-York, Report No. 239.

Beyeler, W. E., Glass, R. J., Bech, M., Soramäki, K.,

2007. Congestion and cascades in payment systems,

Physica A, doi:10.1016/j.physa.2007.05.061.

Devriese, J., Mitchell, J., 2006. Liquidity Risk in

Securities Settlement, Journal of Banking and

Finance, vol. 30, iss. 6, pp. 1807-1834.

Galbiati, M., Soramäki, K., 2007. A competitive multi-

agent model of interbank payment systems, arXiv.org.

Holland, J. H., 1987. Genetic algorithms and classifier

systems: Foundations and future directions. In J.J.

Grefenstette, the 2

ICGAA, pp. 82-89.

Koponen, R., Soramäki, K., 1998. Intraday liquidity needs

in a modern inter-bank payment system – A

simulation approach, Studies in Economics and

Finance E: 14, Bank of Finland, Helsinki.

Leinonen, H., 2005. Liquidity, risks and speed in

payments and settlement systems - A simulation

approach, Bank of Finland Studies.

Mezzetti, C., Dindoš M., 2006. Better-reply dynamics and

global convergence to Nash equilibrium in aggregative

games, Games and Economic Behaviour, vol. 54, pp.

261-292.

Parunak, H. V. D., Savit, R., Riolo, R., 1998. Agent-based

modeling vs. equation-based modeling. In Multi-agent

systems and Agent-Based Systems, MABS'98, LNAI

1534, pp. 10-25. Springer.

Thisse, J.-F., 2004. Théorie des jeux : une introduction,

Notes de cours, Université catholique de Louvain,

Département des sciences économiques.

INTERBANK PAYMENT SYSTEM (RTGS) SIMULATION USING MULTI-AGENT APPROACH

365