WHEN YOU SAY (DCOP) PRIVACY, WHAT DO YOU MEAN?

Categorization of DCOP Privacy and Insights on Internal Constraint Privacy

Tal Grinshpoun

Department of Software Engineering, SCE – Sami Shamoon College of Engineering, Beer-Sheva, Israel

Keywords:

Distributed Constraint Optimization, Constraint Privacy.

Abstract:

Privacy preservation is a main motivation for using the DCOP model and as such, it has been the subject of

comprehensive research. The present paper provides for the ﬁrst time a categorization of all possible DCOP

privacy types. The paper focuses on a speciﬁc type, internal constraint privacy, which is highly relevant for

models that enable asymmetric payoffs (PEAV-DCOP and ADCOP). An analysis of the run of two algorithms,

one for ADCOP and one for PEAV, reveals that both models lose some internal constraint privacy.

1 INTRODUCTION

Constraint optimization (Meseguer and Larrosa,

1995) is a powerful framework for describing opti-

mization problems in terms of constraints. In many

real-world problems, such as Meeting Scheduling

problems and Mobile Sensor nets, the constraints are

enforced by distinct participants (agents). Such prob-

lems were termed Distributed Constraint Optimiza-

tion Problems (DCOPs) (Hirayama and Yokoo, 1997)

and in the past decade various algorithms for solving

DCOPs were proposed (Modi et al., 2005; Mailler

and Lesser, 2004; Petcu and Faltings, 2005; Gersh-

man et al., 2009). While these algorithms compete in

terms of reducing the run-time and/or communication

overhead, they maintain the inherent distributed struc-

ture of the original problem. Nonetheless, up until

recently there was no evidence that DCOP algorithms

outperform (in terms of run-time) state-of-the-art cen-

tralized COP methods. This observation was re-

cently challenged by methods that rely on GDL (Ste-

fanovitch et al., 2011; Vinyals et al., 2011). How-

ever, in these new set of algorithms the original dis-

tribution of variables among agents is not necessar-

ily preserved. In fact, the “distribution” of variables

among agents in these algorithms is actually only for

the means of parallelization of the problem solving

process. Hence, this new group of algorithms can be

referred to as Parallel COP algorithms as opposed to

Distributed COP algorithms.

Following the subsequent observation, the neces-

sity of “classical” DCOP search remains questionable

– if not for performance considerations, then what do

we need DCOP for? The answer to that is obviously

the will to preserve the original distributed structure

of the problem. And why should one try to preserve

this structure? The answer to the second question is

privacy. Indeed, much of DCOP research throughout

the years has focused on privacy issues (Maheswaran

et al., 2006; Greenstadt et al., 2007; Silaghi and Mitra,

2004). It turns out that the term privacy is too general

and almost every work on DCOP privacy considered

a slightly different angle of this term.

The ﬁrst contribution of the present paper is a cat-

egorization of the various aspects of DCOP privacy.

The given categorization indicates that probably the

most interesting privacy aspect in real-world DCOPs

is constraint privacy, and indeed most previous work

on DCOP privacy actually refers to constraint privacy.

This aspect is further sub-categorized into internal

and external constraint privacy.

The paper’s second contribution regards internal

constraint privacy that has not been widely stud-

ied. Two models that do consider internal constraint

privacy are examined – PEAV-DCOP (Maheswaran

et al., 2004) and ADCOP (Grubshtein et al., 2010).

Some important insights regarding internal constraint

privacy preservation in these models are given.

The rest of the paper is organized as follows. Sec-

tion 2 formally describes the DCOP model. A cate-

gorization of privacy types is given in section 3, and

is followed by a review of previous work accord-

ing to the proposed categories (section 4). Section 5

overviews the existing models that enable asymmetric

payoffs, while section 6 exhibits internal constraint

privacy loss in these models. The conclusions and

ideas for future work are given in section 7.

380

Grinshpoun T..

WHEN YOU SAY (DCOP) PRIVACY, WHAT DO YOU MEAN? - Categorization of DCOP Privacy and Insights on Internal Constraint Privacy.

DOI: 10.5220/0003752203800386

In Proceedings of the 4th International Conference on Agents and Artiﬁcial Intelligence (ICAART-2012), pages 380-386

ISBN: 978-989-8425-95-9

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

2 DCOP DEFINITION

A DCOP is a tuple < A, X , D, R >. A is a ﬁnite set

of agents A

, A

, ..., A

. X is a ﬁnite set of variables

, X

, ..., X

. Each variable is held by a single agent

(an agent may hold more than one variable). D is a

set of domains D

, D

, ..., D

. Each domain D

con-

tains a ﬁnite set of values which can be assigned to

variable X

. R is a set of relations (constraints). Each

constraint C ∈ R deﬁnes a non-negative cost for every

possible value combination of a set of variables, and

is of the form:

C : D

× D

× . . . × D

→ R

(1)

A binary constraint refers to exactly two variables and

is of the form C

i j

: D

× D

→ R

. A binary DCOP

is a DCOP in which all constraints are binary. An as-

signment is a pair including a variable, and a value

from that variable’s domain. A partial assignment

(PA) is a set of assignments, in which each variable

appears at most once. A solution is a full assignment

of aggregated minimal cost.

3 PRIVACY CATEGORIZATION

In order to categorize the different pieces of data that

one may wish to keep private during DCOP solving,

we begin with a distinction between two types of pri-

vate data. The ﬁrst type is data regarding the original

problem to be solved. This type refers to the deﬁni-

tion of a DCOP as given in section 2. The second type

is data about the search process itself.

When considering the ﬁrst type of data we refer to

the tuple < A, X , D, R >. We look at privacy from

the point of view of a variable. In most cases this

also coincides with the perspective of an agent, as it

is a common assumption in DCOP research that every

agent holds a single variable. We will refer to cases

in which this assumption does not hold in following

sections. Thus, we remain with two elements of the

tuple that a variable/agent may wish to preserve their

privacy – D and R :

• Domain Privacy – agents may desire to keep their

domains private. The standard DCOP model usu-

ally assumes that the domains of all the agents

are fully known, leading in most cases to an a-

priory loss of any domain privacy. Nevertheless,

agents may decide to abandon this assumption and

still use the standard DCOP model. Contrary to

that, in Open Constraint Optimization Problems

(OCOP) (Faltings and Macho-Gonzalez, 2005)

the domains are inherently gradually revealed in

an attempt to preserve some domain privacy.

• Constraint Privacy – agents may desire to keep

the information contained in the constraints pri-

vate. We distinguish between preserving the con-

straint information from agents participating in

the constraint (internal constraint privacy) and

preserving the constraint information from other

agents (external constraint privacy). Various

DCOP algorithms differ in their level of external

constraint privacy. For instance, in the OptAPO

algorithm (Mailler and Lesser, 2004; Grinshpoun

and Meisels, 2008) agents disclose all their con-

straint information to mediator agents, which ob-

viously leads to poor external constraint privacy

preservation. The story with internal constraint

privacy is more complicated, since the standard

DCOP model assumes that a constraint is totally

known by the agents participating in it. This ob-

viously leads to absolutely no internal constraint

privacy preservation. Two variations of the DCOP

model – PEAV-DCOP (Maheswaran et al., 2004)

and ADCOP (Grubshtein et al., 2010) – allow for

preservation of internal constraint privacy. An

overview of these models is given in section 5.

The second type of data includes information regard-

ing the current state (assignment) of a variable or the

behavior of the agent:

• Assignment Privacy – agents may desire to keep

the assigned values to their variables private. To

achieve this, agents must avoid sending their as-

signed values to other agents. This category

refers to the dynamic changes of assigned values

throughout the search process, as well as to the

assigned values in the ﬁnal solution.

• Algorithmic Privacy – It is a common as-

sumption in DCOP research that all participat-

ing agents/variables run the same algorithm –

otherwise, there seems to be no sense for the

search process. However, an agent may attempt to

“tweak” an algorithm for some personal beneﬁts.

For example, consider a scenario in which each

change of assignment applies some minor cost to

the agent holding the variable. The agents may

decide together to run the DSA algorithm (Zhang

et al., 2005) with a certain value of the p param-

eter that controls the likelihood of updating its

value if the agent attempts to do so. In this ex-

ample, an agent may decide to use a lower value

of p than initially decided, thus reducing its per-

sonal cost during the search process. Naturally,

this agent would like to keep the knowledge of its

selﬁsh behavior private.

WHEN YOU SAY (DCOP) PRIVACY, WHAT DO YOU MEAN? - Categorization of DCOP Privacy and Insights on

Internal Constraint Privacy

381

4 RELATED WORK

In light of the above categorization, we go over pre-

vious DCOP privacy studies in order to put them in

context of the proposed categorization.

A previous study has characterized different types

of DCOP privacy loss (Greenstadt et al., 2007). The

types are – initial vulnerability, intersection vulner-

ability, domain vulnerability and solution vulnerabil-

ity. While some of these types may seem similar to

our proposed categories, they actually all belong to

the same category – constraint privacy. In fact, these

all represent different vulnerabilities of DCOP search

that may lead to external constraint privacy loss. For

example, solution vulnerability refers to the external

constraint information that is revealed by the solution

itself – in some cases there may be several solutions,

and the speciﬁc solution that was chosen may reveal

some constraint information.

The above study is a very good representative of

previous work – most of the studies on DCOP privacy

actually focus on external constraint privacy. The

same study introduces an algorithm that reduces the

privacy loss of all the types except for solution vulner-

ability (Greenstadt et al., 2007). Solution vulnerabil-

ity is addressed by another study (Silaghi and Mitra,

2004). Both studies selectively use encryption tech-

niques in strategic stages of the problem solving.

In early research of DCSP and DCOP privacy, ev-

ery work had a slightly different notion of what con-

straint privacy is, which resulted in the use of various

metrics for privacy loss (Silaghi and Faltings, 2002;

Franzin et al., 2004; Silaghi and Mitra, 2004). These

metrics were all uniﬁed with the introduction of the

Valuation of Possible States (VPS) framework (Mah-

eswaran et al., 2006). This general quantitative frame-

work enables the expression, analysis, and compar-

ison of various constraint-privacy-loss metrics. The

VPS framework was later used for a comprehen-

sive privacy-loss analysis of different DCOP algo-

rithms (Greenstadt et al., 2006). Additional re-

search on DCOP external constraint privacy includes

using cryptographic techniques for Vehicle Routing

Problems (L

eaut

e and Faltings, 2011), investigating

the privacy-loss in k-optimal algorithms (Greenstadt,

2009), and integrating privacy-loss into the utility

function (Doshi et al., 2008).

In cases where the agents sharing a constraint have

equal payoffs, they naturally want to prevent other

agents from learning about their mutual constraints.

However, when this constraints symmetry does not

exist, the agents are naturally more concerned about

their private information not reaching their peers (in-

ternal privacy) than not reaching some third-party

agents that are not involved in the constraint (external

privacy). Consequently, models that enable internal

private constraint information are in the center of this

paper, and are thoroughly discussed in the following

sections. An interesting work on DCSPs has consid-

ered internal constraint privacy (Brito et al., 2009).

In this work entropy was used as a measure of pri-

vacy loss. The same paper also proposes algorithms

that account for assignment privacy as well as internal

constraint privacy.

The centralized Open Constraint Optimization

Problems (OCOP) model (Faltings and Macho-

Gonzalez, 2005) assumes that domains may be very

large and even inﬁnite, and are thus not revealed a-

priorly. In DCOP this is not the case and domains are

usually assumed to be known in advance. However,

except for values of an agent that are constrained with

values of another agent, there is no necessity to re-

veal all the domains to all the participants before the

search process begins. Therefore, in sparse and loose

problems most domain information is expected to re-

main private when using Branch & Bound algorithms.

Moreover, the ODPOP algorithm (Petcu and Faltings,

2006) reveals values in a best-ﬁrst manner and is ex-

pected to effectively preserve domain privacy.

To the best of our knowledge there has been no

research regarding algorithmic privacy. This is prob-

ably due to the fact that most DCOP studies as-

sume that the agents are cooperative (though privacy-

preserving). However, a recently proposed model,

Quantiﬁed DCOP, assumes the existence of adver-

saries (Matsui et al., 2010). This research direction

may potentially lead to algorithmic privacy issues.

5 DCOP WITH ASYMMETRIC

PAYOFFS

The standard DCOP model assumes equal payoffs for

constrained agents. When such a strong assumption

is applied, there is no meaning at all to internal con-

straint privacy, and the agents holding a constraint

only worry about the data of this constraint leaking to

other agents (external constraint privacy). However,

in many real-life situations constrained agents value

differently the results of decisions on constraint issues

even if they consider the same constraints. In fact, this

is the natural scenario in a typical Multi-Agent System

(MAS). In the meeting scheduling problem for exam-

ple, agents which attend the same meeting may derive

different utilities from it. Moreover, their preferences

and constraints regarding its time and location are ex-

pected to be different. Several alternatives for repre-

senting asymmetric constraints by DCOPs are given

next.

ICAART 2012 - International Conference on Agents and Artificial Intelligence

382

5.1 Disclosure of Constraint Payoffs

The simplest way to solve MAS problems with asym-

metric payoffs by DCOPs is through the disclosure

of constraint payoffs. That is, aggregate values of all

agents taking a joint action. However, constraint dis-

closure a-priorly reveals all internal constraint infor-

mation, and is thus an inadequate solution.

5.2 Private Events as Variables (PEAV)

The PEAV model (Maheswaran et al., 2004) suc-

cessfully captures asymmetric payoffs within stan-

dard DCOPs. The incurred cost of the PEAV model

on an agent involves one mirror variable per each of

its neighbors in the constraints graph. Consistency

with the neighbors’ original variables is imposed by a

set of hard equality constraints. One way to represent

hard constraints is to assign a cost that is calculated

for each speciﬁc problem (Maheswaran et al., 2004).

Figure 1: Example of a PEAV-DCOP.

As an example, consider the DCOP on the left-

hand side of Figure 1. The presented example in-

cludes three agents (each holding a single variable

that coincides with the agent’s name). When repre-

senting this problem as a PEAV-DCOP, each agent

needs to produce a mirror variable for each of its

neighbors in the original constraints graph. The re-

sulting problem is illustrated in the right-hand side

of Figure 1. Here the subscript in each new variable

refers to the original variable the new one represents,

whereas the superscript refers to the agent in which

this new variable resides in. So x

is the mirror vari-

able of x

in agent A

, and x

is the mirror variable

of x

in agent A

. The solid lines represent the hard

equality constraints, while the dashed lines represent

the internal constraint information.

Since the PEAV model uses the standard DCOP

model (with multiple variables per agent), any DCOP

algorithm can be used to solve the resulting PEAV-

DCOP problem. Note that most DCOP algorithms

assume a single-variable-per-agent in their original

description. Some methods for dealing with mul-

tiple variables per agent in DCSP have been sug-

gested (Yokoo, 2001). One solution is to convert

a constraint reasoning problem involving multiple

variables into a problem with only one variable by

deﬁning a new variable whose domain is the cross

product of the domains of each of the original vari-

ables. Such complex variables imply extremely large

domains, and therefore this solution is seldom used.

A more applicable method is to create multiple vir-

tual agents within a single real agent and assign one

local variable to each virtual agent.

5.3 Asymmetric DCOPs (ADCOPs)

ADCOPs (Grubshtein et al., 2009; Grubshtein et al.,

2010) generalize DCOPs in the following manner:

instead of assuming equal payoffs for constrained

agents, the ADCOP constraint explicitly deﬁnes the

exact payoff of each participant. That is, domain val-

ues are mapped to a tuple of costs, one for each con-

strained agent.

More formally, an ADCOP is deﬁned by the tu-

ple < A, X , D, R >, where A, X and D are deﬁned

exactly as in regular DCOPs. Each constraint C ∈ R

of an asymmetric DCOP deﬁnes a set of non-negative

costs for every possible value combination of a set of

variables, and takes the following form:

C : D

× D

× ···D

→ R

(2)

This deﬁnition of an asymmetric constraint is nat-

ural to general MAS problems, and requires little ma-

nipulation when formulating these as ADCOPs.

ADCOPs require that the solving process will al-

ways take into account both sides of a constraint, ren-

dering existing DCOP algorithm inapplicable. Along

with the ADCOP model, several designated ADCOP

algorithms have been proposed (Grubshtein et al.,

2009). We brieﬂy present the simplest one.

The SyncABB algorithm is an asymmetric version

of SyncBB (Hirayama and Yokoo, 1997). After each

step of the algorithm, when an agent adds an assign-

ment to the Current Partial Assignment (CPA) and

updates one direction of the bound, the CPA is sent

back to the assigned agents to update the bound by

the costs of all backwards directed constraints (back-

checking). When the bound on the CPA is exceeded,

a new value must be assigned, and the state of the

CPA must be restored. The state of the CPA in-

cludes assignments of all higher priority agents and

the cost (both backward and forward) associated with

them. As the assignment does not change when back-

checking, only the cost must be restored. More details

can be found in (Grubshtein et al., 2009).

WHEN YOU SAY (DCOP) PRIVACY, WHAT DO YOU MEAN? - Categorization of DCOP Privacy and Insights on

Internal Constraint Privacy

383

6 LOSS OF INTERNAL

CONSTRAINT PRIVACY

The ADCOP and PEAV-DCOP models were both de-

signed to not a-priorly reveal all internal constraint

data. Nevertheless, while performing search, personal

costs of agents must be revealed, aggregated and com-

pared against the value of the objective. Thus, infor-

mation may be gathered by different agents about the

nature of their peers’ private valuations (costs). We

illustrate this fact by choosing two very simple algo-

rithms, one for each model – SyncABB (ADCOP) and

SyncBB (PEAV).

Following common practice, we evaluate privacy

loss in terms of entropy (Greenstadt et al., 2006; Brito

et al., 2009). Each constraint of an agent is repre-

sented by a matrix. Each cell in the matrix represents

the agent’s valuation of the constrained tuple. The en-

tropy represents the uncertainty of the agent regarding

the content of the matrices held by other agents. The

general scheme for computing the entropy decrement

is based on knowledge gain from a received CPA.

6.1 Privacy Loss in ADCOP

In ADCOP algorithms the data is revealed in return-

ing CPAs. We require a returning CPA because only

after the initial assignment is made by the agent can

others asses its impact on them. An agent receiving

a CPA message and a cost must ﬁrst reduce the cost

incurred by itself and the initial value the CPA had

when it was last received by the agent. The remaining

cost value k represents the aggregated cost which can

be due to conﬂicts with its assignment or other inter-

agent conﬂicts. Assuming a binary ADCOP, the agent

may calculate the number of all the possible conﬂicts

that may have triggered the cost k and were not part

of the conﬂicts relevant to the previous version of the

CPA. This number of conﬂicts will be denoted by n in

the following analysis.

In our analysis, we use Asymmetric Max-DCSPs.

Max-DCSP is a subclass of DCOP in which all con-

straint costs are equal to one (Modi et al., 2005). We

use Asymmetric Max-DCSPs to simplify the privacy

loss computation. Since Asymmetric Max-DCSPs are

more restrictive than general DCOPs, their privacy

loss can actually serve as an upper bound for general

ADCOPs.

Throughout the SyncABB search process an agent

may collect samples whenever the CPA reaches it in

order to learn about the costs of its peers. When a

CPA is moving backwards for back-checking it in-

cludes one new value assignment which was not in-

cluded when it was last moved backwards for this

purpose. Thus, an agent which receives the CPA can

identify the new assignment and the difference in cost

between the current lower bound and the lower bound

which was on the CPA when it last held it. However,

the agent cannot tell which of the agents, through

which the CPA has passed, has contributed to this

change of cost. This amount of uncertainty is depen-

dent upon the number of agents which are already as-

signed on the CPA. The longer the partial assignment

is the less an agent can learn from a CPA sent back

for back-checking.

For each relevant sample the agent must calculate

the appropriate k and n values. When agent A

re-

ceives a returning CPA it can obtain data about A

the initiator of the back-checking (one of its succeed-

ing peers). When receiving a returning CPA from its

successor (A

= A

i+1

) the agent can also obtain data

about its preceding peers (∀A

|l < i). In all samples,

k is equal to the difference between the current CPA’s

cost and the value the CPA had when it was previously

received by the agent (excluding the cost incurred by

the agent itself). The value of n is determined by j,

the priority (position in the order) of the initiator of

the back-checking:

n = 2 · ( j − 1) − 1 (3)

Since internal constraint private data can be obtained

only when back-checking, the last agent (A

) cannot

learn anything about its peers.

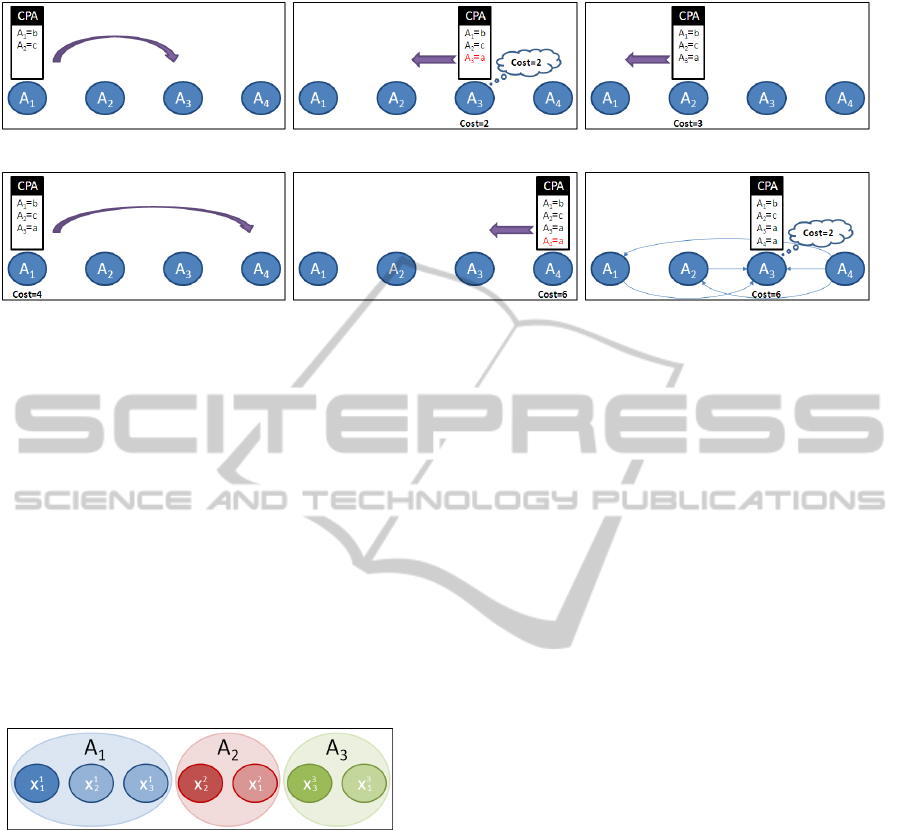
The scenario depicted in Figure 2 demonstrates

the information leak in SyncABB when running on

some asymmetric Max-DCSP example with 4 agents.

We join the example after the back-checking initiated

by A

is ﬁnished and A

sends the CPA to the next

assigning agent, which is A

(stage a). The cost in-

curred by the CPA at this point is 2. A

remembers

this cost (stage b) until the next time it receives the

CPA. During the back-checking (stages c and d) the

cost increases to 4. A

sends the CPA to the next as-

signing agent, which is A

. After A

assigns its value

the cost of the CPA increases to 6 (stage e). Following

that, the CPA returns to A

for back-checking (stage

f). A

remembers the cost from the previous time that

he held the CPA (which was 2). The difference be-

tween the new cost and the old one is k = 4. The 5

thin arrows in Figure 2(f) represent the possible con-

ﬂicts which triggered the cost k and were not part of

the conﬂicts relevant to the previous version of the

CPA. Since the initiator of this back checking is A

one can see that the value of n in the given example

coincides with Equation 3:

n = 2 · ( j − 1) − 1 = 2 · (4 − 1) − 1 = 5

ICAART 2012 - International Conference on Agents and Artificial Intelligence

384

(a) (b) (c)

(d) (e) (f)

Figure 2: Information leak in SyncABB running on an asymmetric Max-DCSP example.

6.2 Privacy Loss in PEAV

Contrary to the ADCOP case, in PEAV-DCOPs the

private information is revealed when the CPA ad-

vances forward. In fact, in most standard DCOP al-

gorithms there is no such thing as a returning CPA

(except after backtracking).

We will demonstrate the leakage of internal con-

straint information in PEAV through the simplest al-

gorithm – SyncBB (Hirayama and Yokoo, 1997). The

SyncBB algorithm requires an ordering of all partici-

pating variables. A natural example of such an order-

ing to the PEAV-DCOP that was presented in Figure 1

is given in Figure 3.

Figure 3: A variable ordering for the example in Figure 1.

In the beginning of the search process, agent A

assigns a value to variable x

. It then goes on and as-

signs values to the variables x

and x

, which are the

next variables in the ordering. At this point the CPA

holds the sum of costs of the constraints between vari-

able x

and variables x

and x

from the point-of-view

of agent A

. Let us now look at the fourth variable in

the ordering, i.e. variable x

. When the CPA reaches

it, some internal constraint information (of agent A

)

reaches agent A

. To evaluate the privacy-loss we use

the abbreviations k and n from the previous subsec-

tion. In this example we have n = 2, whereas the

value of k is exactly the current cost of the CPA. In

case k is equal to 0 or 2 (considering this is a Max-

DCSP) the internal constraint information of agent A

is completely revealed to agent A

. This example re-

sembles the initial vulnerability that was described for

external constraint privacy (Greenstadt et al., 2007).

A conclusive formula such as the one in Equation 3

cannot be given for SyncBB, since it depends on the

chosen variable ordering.

7 CONCLUSIONS

Privacy preservation is probably the main motiva-

tion for using the DCOP model. This explains the

comprehensive research on DCOP privacy through-

out the years. The present paper examines all the

data that may be accumulated during DCOP search.

This examination leads to categorization of all possi-

ble DCOP privacy types, including types that have not

been studied in the past. According to the proposed

categorization, most DCOP privacy studies in the past

have targeted constraint privacy. The paper distin-

guishes between the constraint information of agents

participating in the constraint (internal constraint pri-

vacy) and the constraint information of other agents

(external constraint privacy). While most DCOP pri-

vacy research has focused on external constraint pri-

vacy, two models, PEAV and ADCOP, inherently re-

late to internal constraint privacy.

An analysis of the run of two algorithms, one for

ADCOP and one for PEAV, reveals that both mod-

els lose some amount of internal constraint privacy.

A question remains regarding which of the two mod-

els is better when considering both privacy preserva-

tion and performance. Previous studies have shown

that PEAV is inapplicable for Local Search (Grub-

shtein et al., 2010). However, when it comes to com-

plete search both models are ﬁtting. We leave the

investigation of the privacy/performance tradeoff in

complete search for future work.

WHEN YOU SAY (DCOP) PRIVACY, WHAT DO YOU MEAN? - Categorization of DCOP Privacy and Insights on

Internal Constraint Privacy

385

REFERENCES

Brito, I., Meisels, A., Meseguer, P., and Zivan, R.

(2009). Distributed constraint satisfaction with par-

tially known constraints. Constraints, 14(2):199–234.

Doshi, P., Matsui, T., Silaghi, M., Yokoo, M., and Zanker,

M. (2008). Distributed private constraint optimiza-

tion. In IAT, pages 277–281.

Faltings, B. and Macho-Gonzalez, S. (2005). Open con-

straint programming. Artiﬁcial Intelligence, 161:1-

2:181–208.

Franzin, M. S., Rossi, F., Freuder, E. C., and Wallace, R. J.

(2004). Multi-agent constraint systems with prefer-

ences: Efﬁciency, solution quality, and privacy loss.

Computational Intelligence, 20(2):264–286.

Gershman, A., Meisels, A., and Zivan, R. (2009). Asyn-

chronous forward bounding. JAIR, 34:25–46.

Greenstadt, R. (2009). An overview of privacy improve-

ments to k-optimal dcop algorithms. In Proceedings

of The 8th International Conference on Autonomous

Agents and Multiagent Systems - Volume 2, AAMAS

’09, pages 1279–1280, Richland, SC. International

Foundation for Autonomous Agents and Multiagent

Systems.

Greenstadt, R., Grosz, B., and Smith, M. D. (2007). Ssdpop:

improving the privacy of dcop with secret sharing. In

Proceedings of the 6th international joint conference

on Autonomous agents and multiagent systems, AA-

MAS ’07, pages 171:1–171:3, New York, NY, USA.

ACM.

Greenstadt, R., Pearce, J., and Tambe, M. (2006). Analysis

of privacy loss in distributed constraint optimization.

In Proc. AAAI-06, pages 647–653, Boston, MA.

Grinshpoun, T. and Meisels, A. (2008). Completeness and

performance of the apo algorithm. J. of Artiﬁcial In-

telligence Research, 33:223–258.

Grubshtein, A., Grinshpoun, T., Meisels, A., and Zivan, R.

(2009). Asymmetric distributed constraint optimiza-

tion. In IJCAI-2009 Workshop on Distributed Con-

straints Reasoning (DCR-09), pages 60–74, Pasadena,

CA.

Grubshtein, A., Zivan, R., Grinshpoun, T., and Meisels, A.

(2010). Local search for distributed asymmetric op-

timization. In Proc. 9th Int. Conf. on Autonomous

Agents and Multiagent Systems (AAMAS 2010), pages

1015–1022, Toronto, Canada.

Hirayama, K. and Yokoo, M. (1997). Distributed partial

constraint satisfaction problem. In Proc. CP-97, pages

222–236.

eaut

e, T. and Faltings, B. (2011). Coordinating logistics

operations with privacy guarantees. In IJCAI, pages

2482–2487.

Maheswaran, R. T., Pearce, J. P., Bowring, E., Varakan-

tham, P., and Tambe, M. (2006). Privacy loss in dis-

tributed constraint reasoning: A quantitative frame-

work for analysis and its applications. Autonomous

Agents and Multi-Agent Systems, 13(1):27–60.

Maheswaran, R. T., Tambe, M., Bowring, E., Pearce, J. P.,

and Varakantham, P. (2004). Taking DCOP to the

real world: Efﬁcient complete solutions for distributed

multi-event scheduling. In Proc. AAMAS-04, pages

310–317, New York, NY.

Mailler, R. and Lesser, V. R. (2004). Solving distributed

constraint optimization problems using cooperative

mediation. In Proc. AAMAS-04, pages 438–445.

Matsui, T., Matsuo, H., Silaghi, M. C., Hirayama, K.,

Yokoo, M., and Baba, S. (2010). A quantiﬁed dis-

tributed constraint optimization problem. In Pro-

ceedings of the 9th International Conference on Au-

tonomous Agents and Multiagent Systems: volume 1 -

Volume 1, AAMAS ’10, pages 1023–1030, Richland,

SC. International Foundation for Autonomous Agents

and Multiagent Systems.

Meseguer, P. and Larrosa, J. (1995). Constraint satisfaction

as global optimization. In Proceedings of the 14th in-

ternational joint conference on Artiﬁcial intelligence

- Volume 1, pages 579–584, San Francisco, CA, USA.

Morgan Kaufmann Publishers Inc.

Modi, P. J., Shen, W., Tambe, M., and Yokoo, M. (2005).

ADOPT: asynchronous distributed constraints opti-

mizationwith quality guarantees. Artiﬁcial Intelli-

gence, 161:149–180.

Petcu, A. and Faltings, B. (2005). A scalable method for

multiagent constraint optimization. In Proc. IJCAI-

05, pages 266–271, Edinburgh, Scotland, UK.

Petcu, A. and Faltings, B. (2006). ODPOP: An algorithm

for open/distributed constraint optimization. In Proc.

AAAI-06, pages 703–708, Boston.

Silaghi, M. C. and Faltings, B. (2002). A comparison of

distributed constraint satisfaction approaches with re-

spect to privacy. In Workshop on Distributed Con-

straint Reasoning.

Silaghi, M. C. and Mitra, D. (2004). Distributed con-

straint satisfaction and optimization with privacy en-

forcement. In Proceedings of the IEEE/WIC/ACM In-

ternational Conference on Intelligent Agent Technol-

ogy, IAT ’04, pages 531–535, Washington, DC, USA.

IEEE Computer Society.

Stefanovitch, N., Farinelli, A., Rogers, A., and Jennings,

N. R. (2011). Resource-aware junction trees for efﬁ-

cient multi-agent coordination. In The Tenth Interna-

tional Conference on Autonomous Agents and Multia-

gent Systems (AAMAS 2011), pages 363–370.

Vinyals, M., Rodriguez-Aguilar, J. A., and Cerquides, J.

(2011). Constructing a unifying theory of dynamic

programming dcop algorithms via the generalized dis-

tributive law. Autonomous Agents and Multi-Agent

Systems, 22:439–464.

Yokoo, M. (2001). Distributed constraint satisfaction:

foundations of cooperation in multi-agent systems.

Springer-Verlag, London, UK.

Zhang, W., Xing, Z., Wang, G., and Wittenburg, L. (2005).

Distributed stochastic search and distributed break-

out: properties, comparishon and applications to con-

straints optimization problems in sensor networks. Ar-

tiﬁcial Intelligence, 161:1-2:55–88.

ICAART 2012 - International Conference on Agents and Artificial Intelligence

386