INVENTORY ALLOCATION FOR ONLINE GRAPHICAL DISPLAY

ADVERTISING USING MULTI-OBJECTIVE OPTIMIZATION

Jian Yang

, Erik Vee

, Sergei Vassilvitskii

, John Tomlin

1,3

Jayavel Shanmugasundaram

1,4

, Tasos Anastasakos

and Oliver Kennedy

2,5

Yahoo! Labs, 701 First Avenue, Sunnyvale, CA 94089, U.S.A.

Computer Science Department, Cornell University, Ithaca, NY 14840, U.S.A.

Currently at Marketshare LLC, Redwood Shores, CA, U.S.A.

Currently at Google, Mountain View, CA, U.S.A.

Currently at EPFL, Lausanne, Switzerland

Keywords:

Advertising, Inventory allocation, Multi-objective optimization.

Abstract:

We discuss a multi-objective/goal programming model for the allocation of inventory of graphical advertise-

ments. The model considers two types of campaigns: guaranteed delivery (GD), which are sold months in

advance, and non-guaranteed delivery (NGD), which are sold using real-time auctions. We investigate various

advertiser and publisher objectives such as (a) revenue from the sale of user visits, clicks and conversions,

(b) future revenue from the sale of NGD inventory, and (c) “fairness” of allocation. While the ﬁrst two ob-

jectives are monetary, the third is not. This combination of demand types and objectives leads to potentially

many variations of our model, which we delineate and evaluate. Our experimental results, which are based on

optimization runs using real data sets, demonstrate the effectiveness and ﬂexibility of the proposed model.

1 INTRODUCTION

Online graphical display advertising is a form of on-

line advertising where advertisers can explicitly or

implicitly target users visiting Web pages, and show

graphical (e.g., image, video) ads to those users. For

instance, a brokerage ﬁrm may wish to target Males

from California who visit a Finance web site in the

month of November 2011, and show an ad promoting

its special offers to those users. Similarly, a differ-

ent advertiser may wish to automatically target users

who visit a Finance web site, speciﬁcally those who

are likely to click on their ad highlighting a lower

mortgage rate. Online graphical display advertising

is a multi-billion dollar industry that is related to, but

distinct from, sponsored search advertising (Aggar-

wal et al., 2006), where advertisers bid for keywords

entered by users on a search page, and from content

match advertising (Broder et al., 2007), where adver-

tisers bid for clicks and text-matching techniques (as

opposed to user targeting) are used to show contextu-

ally relevant text advertisements on Web pages.

As with most forms of online advertising (Broder,

2008), one of the central questions that arises in the

context of online graphical display advertising is that

of inventory allocation, i.e., determining how to allo-

cate supply/inventory (user visits) to demand (adver-

tiser campaigns) so as to optimize for various pub-

lisher and advertiser objectives. However, even for-

mulating the inventory allocation problem for online

graphical display advertising is quite challenging, for

two reasons.

First, the same inventory can be sold in two differ-

ent forms: guaranteed delivery and non-guaranteed

delivery. In guaranteed delivery, an advertiser can

purchase a certain number of targeted user visits from

a publisher several months in advance, and the pub-

lisher guarantees these visits and incurs penalties if

the guarantees are not met. For instance, an adver-

tiser may wish to purchase 100 million user visits

by Males in California on a Sports web site during

the 2012 Olympics, and the Sports web site publisher

will guarantee these user visits even though the serv-

ing date is months away from the booking date. On

the other hand, in non-guaranteed delivery, advertis-

ers can bid in real-time in a spot market for user vis-

its, and the highest bidder obtains the right to show

an ad to the user. For instance, if a user visits a Fi-

nance web page, then there may be multiple advertis-

ers bidding for the ad slot on the page, and the highest

293

Yang J., Vee E., Vassilvitskii S., Tomlin J., Shanmugasundaram J., Anastasakos T. and Kennedy O..

INVENTORY ALLOCATION FOR ONLINE GRAPHICAL DISPLAY ADVERTISING USING MULTI-OBJECTIVE OPTIMIZATION.

DOI: 10.5220/0003752802930304

In Proceedings of the 1st International Conference on Operations Research and Enterprise Systems (ICORES-2012), pages 293-304

ISBN: 978-989-8425-97-3

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

bidder can show an ad to the user. An interesting as-

pect is that the same user visits are eligible for both

guaranteed delivery and non-guaranteed delivery. A

typical use case is that some inventory not fully al-

located to guaranteed campaigns can be sold to non-

guaranteed campaigns. However, not all visits from

this inventory will fetch the same price in the spot-

market. This leads to the ﬁrst question addressed by

this work: How does a publisher allocate inventory

to both guaranteed and non-guaranteed advertising

campaigns, while still ensuring that the guaranteed

advertiser objectives are met, and publisher revenue

is maximized?

Second, unlike sponsored search and content

match advertising, where the goals of advertisers are

to obtain clicks/ conversions on ads, the goals of ad-

vertisers in online graphical display can be quite var-

ied. At one end of the spectrum are brand advertisers

(e.g., major department stores), whose primary goal

is to reach a large and diverse audience and promote

their brand, rather than immediate clicks or purchases.

At the other end of the spectrum are performance ad-

vertisers (e.g., credit card companies), whose primary

goal is to obtain immediate online clicks and con-

versions. In the middle, there are performance-brand

advertisers (e.g., car companies), whose goal is both

to promote the brand, as well as to obtain immedi-

ate leads of users who are in the market to buy a car.

The varied goals of advertisers also lead to multiple

currencies by which graphical display advertisements

are bought: brand advertisers typically buy user visits

(expressed in CPM, or Cost Per Mille (1000 user vis-

its)), while performance advertisers typically pay per

click (CPC or Cost Per Click) or conversion (CPA, or

Cost Per Action), while brand-performance advertis-

ers may use a combination of CPM and CPC/CPA.

Thus, the second question we address is: How does

a publisher allocate inventory across diverse adver-

tisers and payment types so that advertiser and pub-

lisher objectives are met?

1.1 Contributions

Given the aforementioned unique requirements for

online graphical display advertising, one of the main

technical contributions of this paper is an inventory al-

location optimization model that can capture these re-

quirements. At a high-level, the proposed allocation

model represents forecasts of future inventory (user

visits) and guaranteed advertiser campaigns as nodes

in a bipartite graph. Each edge of the bipartite graph

connects a user visit to an eligible guaranteed adver-

tiser campaign. In addition, each user visit is anno-

tated with a forecast of the highest bid fetched on the

non-guaranteed marketplace and a forecast of the ex-

pected pay-out. Similarly, each edge of the graph is

annotated with a forecast of the click or conversion

probability for the advertiser campaign and the spe-

ciﬁc user visit.

Given the previous model, the objectives for on-

line graphical display advertising are captured as fol-

lows. There are two parts to the objective function:

one that captures guaranteed campaigns, and the other

that captures non-guaranteed campaigns. The ob-

jective for the latter is simply to maximize the rev-

enue for the publisher, since advertisers only bid for

what the user visit is worth to them. The objec-

tive for the guaranteed campaigns, on the other hand,

is more complex because advertisers could be inter-

ested in brand awareness, or performance, or both.

Furthermore, the publisher faces penalties for under-

delivering – that is displaying an advertisement to

fewer users than agreed on.

In our model, delivery guarantees are treated as

feasibility constraints. (If the instance is infeasible,

we trim the demand to ﬁnd the feasible solution with

the minimum under-delivery penalties.) The objec-

tive for guaranteed contracts has two parts. The brand

awareness objective is captured in terms of “represen-

tativeness” (Ghosh et al., 2009), which tries to max-

imize the reach of the guaranteed campaign by uni-

formly distributing the contracts among the user visits

to the extent possible. The performance objectives for

guaranteed campaigns are captured as the expected

pay-out, i.e., the probability of clicks and conversions,

times the value of each click and conversion.

Consequently, the ﬁnal allocation objective has

three parts: non-guaranteed revenue, guaranteed rep-

resentativeness, and guaranteed clicks/conversions.

While multi-objective programming has been a stan-

dard technique for some time, previous optimization

models for online advertising (see e.g. (Langheinrich

et al., 1999) and (Nakamura and Abe, 2005)) have

used a single objective function. One of our major

contributions is to use the multi-objective optimiza-

tion framework (Steuer, 1986) to model the some-

times conﬂicting objectives in a rigorous way.

While the multi-objective optimization model de-

scribed above captures the various objectives, it also

introduces a new set of challenges both in terms of

operability and in terms of computational feasibility.

Speciﬁcally, with regard to operability, the question

that arises is: how do we trade-off between the var-

ious objectives (such as representativeness and non-

guaranteed revenue), which do not even have the same

units? With regard to computational feasibility, the

question that arises is: how do we solve a multi-

objective formulation efﬁciently over large volumes

ICORES 2012 - 1st International Conference on Operations Research and Enterprise Systems

294

of data (tens of billions of user visits per day and hun-

dreds of thousands of advertiser campaigns per year)?

Another key technical contribution of this paper is a

method that enables operators of the system to trade-

off between multiple objectives based on the mone-

tary unit of a single objective. For instance, an op-

erator can trade-off representativeness in terms of the

impact it has on non-guaranteed revenue, which is ex-

pressed in monetary units. A signiﬁcant advantage of

this method is that it also allows for an efﬁcient so-

lution, which can be solved on a small sample of the

original bipartite graph, without signiﬁcantly compro-

mising accuracy.

We have implemented the proposed inventory al-

location model and the solution techniques, motivated

by the context of an operational online graphical dis-

play advertising system. Our results using real user

visits, guaranteed campaigns, non-guaranteed bids,

and click/conversion data, indicate that the proposed

approach is both versatile in capturing and trading off

between various advertiser and publisher objectives,

as well as efﬁcient to solve with high accuracy.

2 LITERATURE REVIEW

Operations Research techniques, and optimization in

particular, have been used for decades in planning ad-

vertising campaigns in other media, such as print, ra-

dio and television (Bollapragada et al., 2002). The

potential of the WWW for more targeted advertis-

ing was realized in the 1990’s and became a sub-

ject of research. A study was reported in (Langhein-

rich et al., 1999) where they attempted to target dis-

play ads to users in order to optimize expected rev-

enue, without using intrusive data gathering tech-

niques. While “unintrusiveness” seems to have be-

come less of a concern to advertisers and publishers,

their optimization approach was inﬂuential. Noting

a similarity between this problem and the trafﬁc dis-

tribution model (Wilson, 1970), (Tomlin, 2000) sug-

gests adding an entropy term to the linear cost func-

tion proposed in (Langheinrich et al., 1999) to essen-

tially smooth the allocations and prevent “bang-bang”

solutions; characteristic of LP models. A good survey

of these and later developments is given in (Nakamura

and Abe, 2005).

Since that time, the development of Computa-

tional Advertising as a discipline has led to the con-

sideration of many variants of the graphical advertis-

ing allocation problem. A crucial development in this

process was the promulgation of the concept of “fair-

ness” in allocation (Ghosh et al., 2009) to offset ex-

treme LP solutions. (Yang and Tomlin, 2008) pro-

poses a multi-objective model for advertising inven-

tory allocation to balance the short-term objective of

revenue and long-term objective of “fairness”. This

model is further extended by (Yang, 2009) for uniﬁed

marketplace, where user visits can not only be sold

to, but also be purchased from, and by (Yang, 2010)

for malleable supply. (Feldman et al., 2009) consid-

ers the online ad allocation problem in the more gen-

eral setting of the matching problem, while (Roels

and Fridgeirsdottir, 2009) considers a dynamic ver-

sion assuming the inventory follows a Markov pro-

cess. (Easterly, 2009) and (Han, 2009) discuss on-

line advertising from a Revenue Management point

of view.

Two other modules in the online advertising sup-

ply chain make use of the results of an allocation

model such as we have described. These are Ad Serv-

ing and Admission Control. The Ad Server interprets

the output of the allocation model as a set of frequen-

cies with which speciﬁc ads should be shown to users

in the supply pools when they visit a web page. Con-

siderable practical advantages ensue when the solu-

tion can be stored in compact form and rapidly re-

constructed on the ﬂy by the ad server when a page

requests ads. This process has been studied by (Deva-

nur and Hayes, 2009) and (Vee et al., 2009), using the

dual values associated with the demand constraints

and, implicitly, the graph structure to determine the

contracts for which a new arriving user visit is eligi-

ble. The optimization models we have studied pro-

vide the necessary dual values, but online ad serving

is not considered in this paper.

Admission Control is the process of determining

whether a proposed new guaranteed campaign should

be accepted, that is whether the existing obligations

can still be satisﬁed in a modiﬁed solution if the

new contract is accepted. Versions of this problem

have been studied by (Feige et al., 2008) and (Aleai

et al., 2009) and considered as an NP-hard combina-

torial optimization problem. (Radovanovic and Zeevi,

2009) have proposed a relaxed, more tractable, vari-

ant of the Admission Control process.

3 MODEL AND OBJECTIVES

We begin by ﬁrst deﬁning some notation, and then

motivating and formalizing the various objectives in

online graphical display advertising.

3.1 Supply and Demand Model

As mentioned earlier, the main goal of inventory al-

location is to match supply (user visits) and demand

INVENTORY ALLOCATION FOR ONLINE GRAPHICAL DISPLAY ADVERTISING USING MULTI-OBJECTIVE

OPTIMIZATION

295

(advertising campaigns). We thus begin by modeling

user visits, advertising campaigns, and their interac-

tion.

User visits can be represented as attribute-value

pairs, where the attributes represent the properties of

a user, the properties of the page they visit, as well

as the time stamp of the visit. An example user visit

could be represented as: Gender = Male, AgeGroup

= 30-40, Interests = {Sports, Finance}, Location =

California, ..., PageCategory = {Sports}, ..., Day = 27

Jul 2012, Time = 12:35pm GMT.

A display advertising campaign targets a subset of

user visits by specifying a targeting predicate. For

instance, an advertising campaign that targets Males

in California visiting Sports pages during the 2012

Olympics can be represented as: Gender ∈ {Male} ∧

Location ∈ {California} ∧ PageCategory ∈ {Sports}

∧ Duration ∈ [27 Jul 2012 - 12 Aug 2012]. A user

visit is said to be eligible for an advertising campaign

if the attribute-value pairs of the user visit satisfy the

targeting predicate of the advertising campaign. In the

rest of this paper, we will focus on just the eligibility

relationship between user visits and advertising cam-

paigns, and not on the speciﬁc attribute-value pairs or

the targeting predicates.

Advertising campaigns can be of two types: guar-

anteed campaigns, whereby the publisher guarantees

a ﬁxed number of user visits to an advertiser in ad-

vance, and non-guaranteed campaigns, where adver-

tisers bid in real-time for user visits. Both guaranteed

and non-guaranteed campaigns can have one or more

advertiser goals: to obtain user visits (this is the only

goal that is guaranteed in a guaranteed campaign), to

obtain clicks, and/or to obtain conversions. In non-

guaranteed campaigns, however, these objectives are

converted into a bid by a bidding agent and thus, for

the purpose of modeling, they can be represented as

a bid for each user visit. Guaranteed campaigns, on

the other hand, need to be modeled in more detail.

Speciﬁcally, a guaranteed campaign has a user visit

goal (the guarantee), a penalty function that speciﬁes

the penalty to be paid by the publisher if the guarantee

is not met, and a value for each click and/or conver-

sion. A key aspect that enables yield optimization for

clicks and/or conversions is the probability of a click

and/or conversion given a user visit.

Finally, for reasons of scale, it is usually not prac-

tical to work with all future user visits for a duration

of many months (many large publishers have billions

of user visits per day). Consequently, the inventory

allocation problem often has to be solved on a sam-

ple of user visits, and thus each sampled user visit is

annotated with a sample weight.

The following notation summarizes the above dis-

Figure 1: Example of allocation graph.

cussion:

• I : Set of user visits.

• s

: Sample weight of user visit i ∈ I .

• r

: The payout for user visit i ∈ I by non-

guaranteed campaigns.

• J : Set of guaranteed campaigns.

• d

: User visit goal for guaranteed campaign j ∈

J .

• P

: N → R: Penalty function for guaranteed

campaign j ∈ J , which maps under-delivery

(how much a guarantee is missed) to a penalty.

• W

: The value of a click for a guaranteed cam-

paign j ∈ J .

• W

: The value of a conversion (action) for a

guaranteed campaign j ∈ J .

• p

i j

: The probability that a user corresponding to

user visit i ∈ I clicks on an ad corresponding to

guaranteed campaign j ∈ J .

• p

i j

: The probability that a user corresponding to

user visit i ∈ I converts on an ad corresponding

to guaranteed campaign j ∈ J .

• B

: Subset of user visits I that are eligible for

guaranteed campaign j ∈ J .

It is often convenient to view the user visits and

guaranteed campaigns in a bipartite graph, with user

visits I on one side, guaranteed campaigns J on the

other. An edge (i, j) connects a user visit i and a guar-

anteed campaign j if i ∈ B

, that is if i satisﬁes the

targeting predicates of j. An example of such a graph

is shown in Figure 1.

It should be noted that the construction of this

graph, which may involve tens of thousands of nodes

and millions of edges, is in itself a major computa-

tional task.

3.2 Objectives

In this section, we motivate and formalize the various

objectives that are relevant to the inventory allocation

problem. In the next section, we introduce a mathe-

matical model to trade-off and optimize across these

different objectives.

ICORES 2012 - 1st International Conference on Operations Research and Enterprise Systems

296

An overriding objective of publishers is to min-

imize the penalties incurred in case guarantees are

not met. Minimizing penalties is important not only

because the publisher incurs an immediate mone-

tary loss, but also because the publisher could suffer

longer-term losses due to advertiser attrition. Deﬁne

i j

as the weight of user i ∈ I that is allocated to guar-

anteed campaign j ∈ J . Then the amount of user visits

delivered to a guaranteed campaign j is

∑

i j

, and the

objective of minimizing penalties can be formalized

as:

min

∑

−

∑

i j

) (1)

In this paper, we always ensure feasibility before tak-

ing care of other objectives (see section 4.1).

At a high-level, there are two parts to the inventory

allocation problem, corresponding to non-guaranteed

and guaranteed campaigns. The objective for non-

guaranteed campaigns is simple: to maximize the rev-

enue for the publisher, since advertisers only bid what

each user visit is worth to them. Modeling the objec-

tives for guaranteed campaigns, on the other hand, is

more complex because advertisers could be interested

in brand awareness/reach or performance (clicks, con-

versions) or both. We thus have three objectives: non-

guaranteed revenue, brand awareness/reach, and per-

formance.

Before formalizing the above objectives, we intro-

duce some notation:

• z

= s

−

∑

i j

: The weight of user visit i ∈ I that

is allocated to non-guaranteed campaigns

• S

∑

i∈B

: The total amount of user visits el-

igible for guaranteed campaign j ∈ J

• θ

i j

= s

: The ideal fully representative target

allocation fraction of user visit i ∈ I to guaran-

teed campaign j ∈ J (motivated further below)

3.2.1 Non-guaranteed Revenue

The prices paid by non-guaranteed advertisers depend

heavily on the particular user. Therefore, a natural

goal of an allocation is to maximize the publisher’s

revenue by allocating the highest valued user visits

to the non-guaranteed contracts. Since the amount of

revenue that a publisher obtains from a user visit i is

, this objective is written as:

max

∑

(2)

3.2.2 Brand Awareness/Reach

There are two primary reasons why it is important to

have a brand awareness/reach objective. The ﬁrst rea-

son is that brand advertisers typically want to reach

a large swath of their target audience. For instance,

a brand advertiser who targets user visits from the

US will likely be quite unhappy if all of their deliv-

ered user visits are from fourteen year old males in

Wyoming, and none from the rest of the population

(even though all the delivered user visits technically

satisfy the targeting predicate of the advertiser). In

other words, brand advertisers often want a represen-

tative subset of their target audience.

The second reason for having a brand awareness

and reach objective is more subtle, and it relates to the

interaction with non-guaranteed campaigns. Speciﬁ-

cally, if the primary goal of the publisher was to max-

imize short-term revenue, then he could allocate all of

the high-value user visits to the highest bidding non-

guaranteed campaigns, and allocate only the remain-

ing user visits to the guaranteed campaigns. How-

ever, this is clearly detrimental to the advertiser, and

is also a dangerous road to take for the publisher: by

selectively allocating the most expensive user visits

to the non-guaranteed contracts, the publisher risks

alienating in the long term the guaranteed advertisers,

many of whom pay a large premium for guarantees.

In fact as (Ghosh et al., 2009) argued, in these situ-

ations price serves as a signal of value, thus the user

visits with the highest r

may also be the ones most

desired by the guaranteed contracts.

Therefore, it is in the long-term interests of pub-

lishers to allocate each guaranteed campaign a repre-

sentative subset of targeted user visits. Ideally, every

eligible user visit i ∈ B

should be equally likely to

see an ad from j. A similar argument holds on a tem-

poral scale. A week long contract should have the

same probability of being displayed on all days of the

week. That is, it should be allocated uniformly dur-

ing the course of the week—after all, if an advertiser

wanted the contract to be shown only on Tuesday, she

would have added that to the targeting constraints.

To model these representativeness constraints, let

i j

be the ideal target allocation. Note that θ

i j

directly

encodes the fact that no user visit i is preferred by j

over others. To maximize long term revenue, the pub-

lisher should strive to ﬁnd an allocation close to θ

i j

In this paper we use the L

-norm distance to measure

closeness to the target allocation. We denote V

the

importance of a representative allocation to advertiser

j and write the objective as:

min

∑

i∈B

2θ

i j

− θ

i j

)

(3)

For consistency with other objectives, we will use

the maximization form:

max −

∑

i∈B

2θ

i j

− θ

i j

)

(4)

INVENTORY ALLOCATION FOR ONLINE GRAPHICAL DISPLAY ADVERTISING USING MULTI-OBJECTIVE

OPTIMIZATION

297

Note that alternative forms such as an entropy

function or K-L divergence can also be used, as they

retain the essential features of separability (by adver-

tiser) and convexity. Similarly, other target alloca-

tions besides the perfectly uniform target allocation

can also be considered but these variants are beyond

the scope of this paper.

3.2.3 Clicks/Conversions

An advertiser in a guaranteed campaign may have

multiple objectives, such as clicks and conversions,

besides obtaining the guaranteed user visits. The pub-

lisher’s objective is to maximize the yield from such

goals, while also directing such clicks and conver-

sions to the advertisers who value them the most. This

can be modeled as trying to maximize the expected

value of clicks and conversions across all user visits:

∑

i∈B



i j



For compactness we deﬁne:

i j

= W

i j

. (5)

Then we can rewrite the performance objective as:

max

∑

i∈B

i j

. (6)

Note that when we refer to “clicks” below, it is to

be understood to include the subsequent conversions.

4 SOLUTION APPROACHES

In the previous section we described the competing

objectives faced by a publisher in allocating user vis-

its to guaranteed contracts. In this section we for-

mally state the mathematical problem that incorpo-

rates these objectives subject to the feasibility con-

straints.

There are three types of constraints that the allo-

cation must satisfy to be feasible. First, the desired

number of user visits must be allocated for each guar-

anteed contract:

∀ j

∑

i∈B

i j

= d

(Demand Constraints)

Next, each user visit can be allocated to exactly one

guaranteed contract or the non-guaranteed market:

∀i

∑

j|i∈B

i j

+ z

= s

(Supply Constraints)

Finally, we must ensure that the allocation is always

non-negative:

∀i, j y

i j

≥ 0 (Non-Negativity Constraints)

∀i, z

≥ 0

Putting together the objectives from the previous

section with the set of constraints, we may state our

generic multi-objective optimization:

max







−

∑

i∈B

2θ

i j

− θ

i j

)

∑

i∈B

i j

∑







(7)

subject to

∑

i∈B

i j

= d

∀ j (8)

∑

j|i∈B

i j

+ z

= s

∀i (9)

i j

≥ 0 ∀i, j (10)

≥ 0 ∀i (11)

Note that the non-negative variables z

transform

what would be inequality supply constraints into

equalities. Since z

is actually the leftover supply in-

ventory that will be sold to the non-guaranteed mar-

ket, the term

∑

can be viewed as the total non-

guaranteed revenue that can be obtained for an alloca-

tion y, with remnant inventory z. The second objective

is the revenue obtained from clicks on the displayed

advertisements.

4.1 Ensuring Feasibility

In this model formulation, guarantees are treated as

constraints (Demand Constraints). Consequently, be-

fore we optimize for the other objectives, we need to

ensure that the model is feasible, i.e., there is suf-

ﬁcient supply for guaranteed campaigns. Note that

even if a publisher is careful to accept only guaran-

teed campaigns that are feasible at the time of book-

ing, the model could become infeasible at a later point

because forecasts of user visits could change due to

unforeseen events.

In order to make the model feasible, we add

dummy user visits that have unlimited supply but a

very high cost of being used, and connect them to all

the guaranteed campaigns. The cost associated with

using each dummy user visit for a guaranteed cam-

paign j corresponds to the penalty P

> 0 incurred

by that guaranteed campaign in case of under-delivery

(note that if P

has multiple penalty values for under-

delivery, then these can be represented as multiple

dummy user visits, each with a different cost of be-

ing used). The cost associated with using real user

visits is 0.

Given the above set up, the goal is to ﬁnd the min-

imum cost allocation to guaranteed campaigns. Since

this problem is a pure network with a linear objective

function, it can be solved very efﬁciently (Bertsekas,

1998). If the cost of the optimal allocation is 0, then it

implies that all the guaranteed campaigns can be sat-

isﬁed, and hence that the original model is feasible.

ICORES 2012 - 1st International Conference on Operations Research and Enterprise Systems

298

If the cost of the optimal allocation is greater than 0,

then it implies that some guaranteed campaigns will

under-deliver. Furthermore, the optimal allocation to

the dummy user visits will indicate how much each

guaranteed campaign needs to under-deliver so that

overall penalty cost is minimized. In this case, the

user visit goal d

for each guaranteed campaign is re-

duced by the amount of allocation to the dummy user

visits in order to make the model feasible. We then

follow one of the procedures described in the remain-

der of this section.

4.2 Multi-objective Programming

We may approach a multi-objective function model

in a number of ways (Steuer, 1986). One general ap-

proach is to obtain an efﬁcient frontier of solutions

where at each point on the curve the value of one ob-

jective can only be improved at the expense of degrad-

ing another. Figure 3 shows an example of efﬁcient

frontier in the space of two objectives. The user may

then choose any point on this curve as the “solution”.

More algebraic approaches include using a

weighted sum of the multiple objectives and/or us-

ing “goal programming”, whereby the objectives are

handled sequentially, with the additional constraint(s)

that previous objectives retain a certain fraction of

their optimal value. Since we have three objectives,

there are clearly several variations, which we explore

below.

In what follows, it will be convenient to deﬁne the

three objective components as follows:

(y) = −

∑

i∈B

2θ

i j

− θ

i j

)

(12)

(y) =

∑

i∈B

i j

(13)

(z) =

∑

(14)

Depending on the data available, we may formu-

late solution strategies which employ: 1) a single-

stage optimization model, 2) a two-stage optimization

model in various ﬂavors and 3) a three-stage optimiza-

tion model, also in several ﬂavors.

4.3 Single-stage Programming

We consider a multi-component objective function:

max

{

γF

(y) +ξF

(y) +F

(z)

}

(15)

subject to (8)-(11). The parameter γ ≥ 0 is the weight

for the “representativeness” component. The param-

eter ξ, in conjunction with the w

i j

, reﬂects the means

by which we attribute value to clicks. We observe that

a feature of this model is that the shadow value β

the supply constraint i is always no less than the pay-

out for user visit i by non-guaranteed campaigns, i.e.

≥ r

The model involves the addition of a linear term in

y to the strictly convex distance function F

(y). The

objective thus remains strictly convex quadratic in y

and linear in z. Optimization of this model is straight-

forward in principle, using a commercial solver such

as XpressMP (FICO, 2010). If a sufﬁciently power-

ful large-scale nonlinear network code were available,

this could also be used since our constraints are of the

pure network type.

4.4 Two-stage Programming

If all of the above data are not available to us, we must

resort to multi-objective or goal programming. Let us

ﬁrst assume that γ is not known, but the click-related

data (ξ, w

i j

) are available. In this case, we may ini-

tially solve:

max

{

ξF

(y) +F

(z)

}

(16)

subject to (8)-(11). Note that this is a linear pure

network minimum cost ﬂow problem which can be

solved very rapidly by special purpose software (e.g.,

see (Bertsekas, 1998)). Let the optimal value of this

linear program (LP) be M

∗

. We may now append a

constraint specifying that at least a certain fraction

ψ(0 < ψ < 1) of this monetary value be preserved

and solve the model:

max F

(y) (17)

subject to (8)-(11) and

∑

i∈B

i j

∑

≥ ψM

∗

(18)

It may be shown that the unknown parameter γ is

equal to the inverse of the dual value for the constraint

(18).

Suppose now that a value for γ is available but ξ is

not. We may initially solve

max F

(y) (19)

subject to (8)-(11). Let the optimal value of this linear

program (LP) be P

∗

. We may now append a constraint

specifying that at least a certain fraction ω(0 < ω <

1) of this “click value” (however it is quantiﬁed) be

preserved, and solve the model:

max

{

γF

(y) +F

(z)

}

(20)

subject to (8)-(11) and

∑

i∈B

i j

≥ ωP

∗

(21)

INVENTORY ALLOCATION FOR ONLINE GRAPHICAL DISPLAY ADVERTISING USING MULTI-OBJECTIVE

OPTIMIZATION

299

The third variant combines the two objectives F

and F

in the second stage model, after solving a ﬁrst

stage model:

max F

(y) (22)

subject to (8)-(11). Let the optimal value of this linear

program be R

∗

. In this approach, the second model is

of the form:

max

{

γF

(y) +ξF

(y)

}

subject to (8)-(11) and

∑

≥ ηR

∗

(23)

where η(0 < η < 1) is the fraction of non-guaranteed

revenue we wish to preserve. This model would re-

quire us to have the relative weights on F

and F

available. This model is also guaranteed to be feasible

if the original constraints (8)-(11) are feasible.

4.5 Three-stage Optimization

From an operability point of view, it is unlikely that

both the parameters γ and ξ would be known, or

even understood very well. In that case, we cannot

avoid turning to goal programming and more intuitive

“knobs” for the business to use in the decision mak-

ing process. Our goal program reduces to a sequence

of three models. In principle, these models could be

solved in any order, but we take the point of view

that the nonlinear objective F

(y) should be optimized

last, in order to avoid imposing a nonlinear constraint.

Such a non-linear constraint would be computation-

ally crippling at the scale we are contemplating. The

last model therefore must optimize representativeness

subject to constraints on non-guaranteed revenue and

click value.

Since non-guaranteed revenue is undeniably mon-

etary, the most intuitive procedure might be to ﬁrst

solve for F

max F

(y) (24)

subject to (8)-(11). Let the optimum objective func-

tion value be R

∗

. Then solve for maximum click

value:

max F

(y) (25)

subject to (8)-(11) and

∑

≥ ηR

∗

(26)

Let the optimum objective function value be P

∗∗

. We

may now optimize the representativeness function:

max F

(y) (27)

subject to (8)-(11) and

∑

≥ ηR

∗

(28)

∑

i∈B

i j

≥ ωP

∗∗

(29)

Clearly we could reverse the ﬁrst two stages. This

would likely produce different results, but both would

be feasible.

5 EXPERIMENTS

We now present some experimental results using a

snapshot of real online graphical display advertising

data sets. Our speciﬁc focus is on quantifying the rel-

ative beneﬁts of the various multi-objective optimiza-

tion approaches for a given data/forecast snapshot

as compared to the more traditional single-objective

optimization approaches, rather than the online ad

serving mechanisms (Devanur and Hayes, 2009; Vee

et al., 2009) that account for forecast errors, and could

use periodic re-optimization.

5.1 Experimental Setup

The data snapshot consists of guaranteed campaigns,

forecasts of user visits, non-guaranteed bids and

clicks, all based on a subset of historical data from

an operational display advertising system. The corre-

sponding bipartite allocation graph has 32,390 supply

nodes, 2,696 demand nodes and 1,407,753 edges. The

supply weight (s

) ranges from 10.83 to 1.18 × 10

The user visit goal (d

) ranges from 1 to 6.96 × 10

The non-guaranteed price (r

) ranges from 0.046 to

4.350. The click probability (p

i j

) ranges from 1.290×

−6

to 0.947 (the experiments only evaluate clicks,

not conversions).

Figure 2 shows the experimental ﬂow. After a

snapshot of guaranteed campaigns are fetched from

the Campaign Database, the User Visit Forecasting is

invoked to generate a forecast of user visits that are

eligible for the guaranteed campaigns, and construct

the allocation graph. Then the Non-Guaranteed Fore-

casting and Click Forecasting are invoked in parallel

to annotate the allocation graph with non-guaranteed

price (r

) and click probabilities (p

i j

), respectively.

Finally the Optimizer is run to solve the various opti-

mization models proposed in the paper.

The metrics that we measure for the various opti-

mization runs are the non-guaranteed revenue, the to-

tal value of clicks, and the representativeness of guar-

anteed campaigns. The experiments are run for var-

ious values of the model parameter settings. In the

ICORES 2012 - 1st International Conference on Operations Research and Enterprise Systems

300

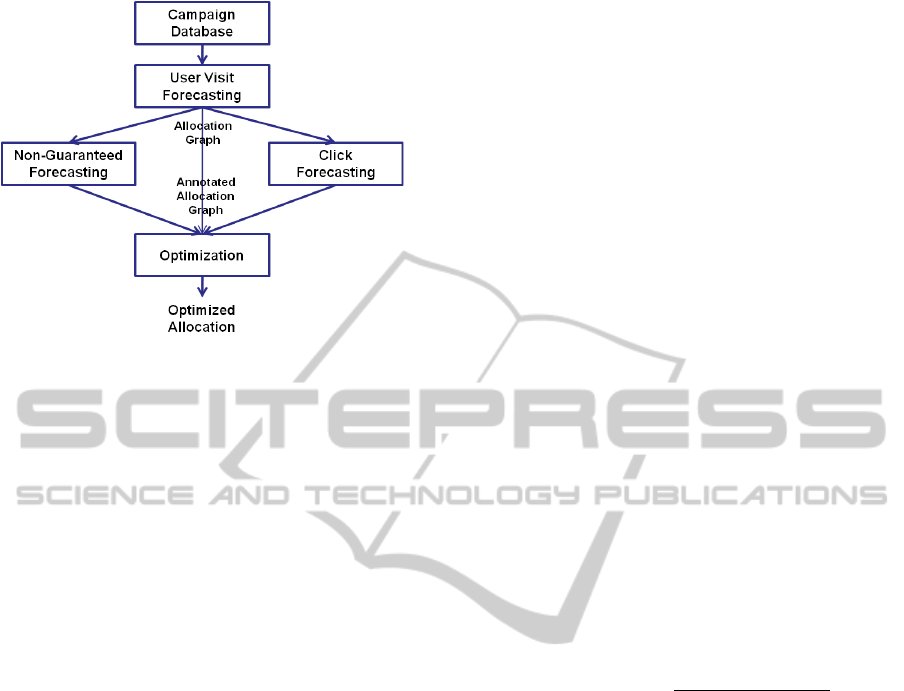
Figure 2: Experiment ﬂowchart.

experiments, all the allocation priorities V

are set to

1 and all the click values W

are set to 10.

The experiments were run on a 64bit/64GB/2GHz

Linux box using the optimization package XpressMP

from Dash Optimization of FICO (FICO, 2010).

5.2 Forecast Models

Although the forecast models used here are not the

focus of this paper, we include a brief description of

each for completeness.

5.2.1 User Visit Forecasting

User visit forecasting uses time-series trend predic-

tions to predict the trend/growth in user visits for var-

ious pockets of supply such as Sports or Finance. Our

speciﬁc implementation uses SARIMA (Shumway

and Stoffer, 2007) for time-series predictions.

In addition, to generate the allocation graph, we

need to produce a sample of user visits. For this, we

follow the sampling procedure outlined in (Vee et al.,

2009), which produces a unbiased sample for the class

of optimization models that we consider in this paper.

Speciﬁcally, for each guaranteed campaign, the sup-

ply forecast selects k eligible user visits uniformly at

random. Once all of the user visits for all campaigns

are chosen, the weights given to each user visit is nor-

malized so that the total weight of any subset of user

visits is, in expectation, equal to the predicted avail-

able supply. The allocation graph is then created by

adding edges from the campaigns to their eligible user

visits.

5.2.2 Non-guaranteed Forecasting

The goal of the Non-Guaranteed Forecasting module

is to predict the expected revenue obtained by sell-

ing a particular user visit in the non-guaranteed mar-

ketplace. We observed that the prices paid for user

visits by the non-guaranteed contracts followed a log

normal distribution, with prices ranging from under

$0.10 CPM to above $10 CPM. To predict the price

of an individual user visit, we trained a generalized

least squares regression model on the logarithm of

the prices. Each user visit was annotated with a set

of user features, for example, age, gender, etc, and

a set of page features, for example, Sports, Finance,

etc. We used the value predicted by the model as the

non-guaranteed price r

5.2.3 Click Forecasting

Click forecasting estimates the probability that a dis-

played ad will be clicked in a particular user visit

context. Estimation of click-through rates (CTR) is

extensively applied in pay-for-performance systems

that attempt to maximize expected revenue (Richard-

son et al., 2007; Shaparenko et al., 2009). The esti-

mates can be based on historical click-through perfor-

mance statistics of features that are selected as signiﬁ-

cant predictors of CTR. In this work, we use a logistic

regression model with the following functional form:

p(click|{ f

, . . . , f

}) =

1 + exp(

∑

k=1

)

(30)

where f

are predicates of features of the user visit

and the ad such as user age and gender, page con-

tent category, ad position in page, etc. Using histor-

ical data from web trafﬁc that consist of page visits

with corresponding user visit and click statistics, we

learned the logistic regression parameters.

Finally, each edge in the allocation graph, which

represents a contract and a corresponding eligible user

visit, is annotated with features f

. The click model is

used to produce an estimate of the probability of click

i j

for each graph edge.

5.3 Experimental Results

We now present our experimental results for various

models and parameter settings. Each optimization for

a particular parameter combination takes about 5 to

10 minutes, which is quite acceptable as an ofﬂine

optimization step that can inform online serving algo-

rithms (Devanur and Hayes, 2009; Vee et al., 2009).

INVENTORY ALLOCATION FOR ONLINE GRAPHICAL DISPLAY ADVERTISING USING MULTI-OBJECTIVE

OPTIMIZATION

301

5.3.1 Baseline and Single-objective Solutions

As a baseline, we compute the optimization solution

that only ensures feasibility by minimizing the total

under-delivery penalty, but does not explicitly opti-

mize for the other objectives. The result for this base-

line solution is shown in the ﬁrst row of Table 1 and is

used as the basis for normalization. We then optimize

for each single objective separately and report the nor-

malized solutions in the same table, were NGD refers

to non-guaranteed revenue, and GD refers to guaran-

teed representativeness. It can be seen that while op-

timizing a single objective may signiﬁcantly improve

that objective, it has a potentially signiﬁcant impact

on the other objectives.

Table 1: Baseline and single-objective solutions.

Objective NGD Click NGD+ GD

Click GD

Baseline 1 1 1 -1

NGD 1.0165 1.0905 1.0229 -0.9836

Click 1.0062 2.9136 1.1722 -2.2214

NGD+Click 1.0131 2.9013 1.1774 -1.7440

GD 0.9968 0.9226 0.9903 -0.0027

5.3.2 Two-stage Programming

We run the two-stage programming algorithm (Sec-

tion 4.4) with 100 different values of the ψ parameter.

Table 2 shows the objectives in normalized scale for a

subset of the generated efﬁcient solutions. The whole

efﬁcient frontier by using all the 100 points is de-

picted in Figure 3, which shows the trade-off between

the monetary objective (non-guaranteed revenue plus

click value) and the non-monetary objective (repre-

sentativeness).

Table 2: Two-stage programming results.

ψ NGD Click NGD+ GD

Click

0.8411 0.9968 0.9226 0.9903 -0.0027

0.8570 0.9978 1.1269 1.0090 -0.0028

0.8729 0.9993 1.3260 1.0277 -0.0034

0.8888 1.0016 1.5171 1.0464 -0.0046

0.9047 1.0047 1.6990 1.0651 -0.0069

0.9205 1.0079 1.8810 1.0838 -0.0109

0.9364 1.0094 2.0801 1.1026 -0.0181

0.9523 1.0110 2.2782 1.1213 -0.0328

0.9682 1.0127 2.4763 1.1340 -0.0660

0.9841 1.0131 2.6861 1.1587 -0.1474

0.9999 1.0131 2.9013 1.1774 -1.7440

Figure 3 also shows the baseline and single-

objective solutions as different symbols. The baseline

solution and most of the single-objective solutions are

located in the interior of the feasible solution region

Figure 3: Efﬁcient frontier of two-stage programming.

and thus dominated by efﬁcient solutions on the fron-

tier. Further, the efﬁcient frontier shows that a very

small loss in one objective can lead to a signiﬁcant

gain in the other objective, thereby enabling a better

combined trade-off as compared to single-objective

solutions.

5.3.3 Three-stage Programming

We run the three-stage programming algorithm (Sec-

tion 4.5) with 100 different combinations of the η and

ω parameters. Table 3 shows the objectives in nor-

malized scale for a subset of the generated efﬁcient

solutions. The efﬁcient frontier for the tri-objective

optimization problem is a surface in a 3D space. One

way to visualize the efﬁcient frontier is to project it

to a 2D space by ﬁxing the level in the third dimen-

sion. Figure 4 shows three such contours in the space

of click value and GD representativeness for evenly-

spaced NGD revenues. The trade-off among the three

objectives can be observed by comparing points on

the same contour and between different contours.

Table 3: Three-stage programming results.

η ω NGD Click NGD+ GD

Click

0.9961 0.3812 1.0125 1.1075 1.0208 -0.0084

0.9961 0.6906 1.0125 2.0067 1.0990 -0.0180

0.9961 1.0000 1.0125 2.9058 1.1772 -1.7272

0.9981 0.4073 1.0145 1.1740 1.0284 -0.0129

0.9981 0.7037 1.0145 2.0281 1.1027 -0.0232

0.9981 1.0000 1.0145 2.8823 1.1770 -1.7225

0.9999 0.6967 1.0165 1.1209 1.0255 -0.3264

0.9999 0.8483 1.0165 1.3649 1.0468 -0.3280

0.9999 0.9999 1.0165 1.6090 1.0680 -0.5039

5.4 Discussion

The results above and especially the efﬁcient frontier

give us a global picture of the trade-off among dif-

ICORES 2012 - 1st International Conference on Operations Research and Enterprise Systems

302

Figure 4: Efﬁcient frontier of three-stage programming.

ferent objectives. It reveals what percentage of one

objective can be gained at the cost of one percent of

another objective and how the trade-off rate changes

with the location of the solution, thereby providing

valuable insight in setting the right parameters in a

real production system to truly reﬂect the business pri-

ority. Perhaps more importantly, it demonstrates the

signiﬁcant beneﬁt of a combined optimization model

for multiple objectives, as opposed to optimizing for

just a single objective.

6 CONCLUSIONS

In this paper we have shown that multi-objective opti-

mization provides an efﬁcient and ﬂexible framework

for the allocation of user visits to guaranteed and non-

guaranteed campaigns. The proposed models also in-

corporate a very ﬂexible means of taking into account

revenue derived from clicks, as well as non-monetary

objectives, in particular, “representativeness” or “fair-

ness”, in the allocation of eligible user visits to cam-

paigns. We are able to do this using off-the-shelf soft-

ware, such as a commercial scale optimization system

for large scale quadratic programming, or specialized

network optimization codes for some steps.

We believe that the proposed models can be ex-

tended to other objectives of interest such as ad rele-

vance. As part of future research, we are exploring ex-

tensions to the model to include stochastic elements,

such as uncertainty in supply and demand, and non-

linear pricing.

ACKNOWLEDGEMENTS

We gratefully acknowledge the assistance of Sumanth

Jagannath and Wenjing Ma in preparing the data for

our experiments, and Jianchang Mao for managing

much of the click model development.

REFERENCES

Aggarwal, G., Goel, A., and Motwani, R. (2006). Truthful

auctions for pricing search keywords. In Proc. of the

7th ACM Conf. on Electronic Commerce.

Aleai, S., Arcaute, E., Khuller, S., Ma, W., Malekian, A.,

and Tomlin, J. (2009). Online allocation of display

advertisements subject to advanced sales contracts. In

Proc. of the 3rd Int. Workshop on Data Mining and

Audience Intelligence for Advertising (ADKDD).

Bertsekas, D. (1998). Network Optimization: Continuous

and Discrete Models. Athena Scientiﬁc Press.

Bollapragada, S., Chen, H., Phillips, M., Garbiras, M., Sc-

holes, M., Gibbs, T., and Humphreville, M. (2002).

NBC’s optimization systems increase revenues and

productivity. Interfaces, 32(1):47 – 60.

Broder, A. Z. (2008). Computational advertising and rec-

ommender systems. In Proceedings of the 2008 ACM

conference on Recommender systems.

Broder, A. Z., Fontoura, M., Josifovski, V., and Riedel, L.

(2007). A semantic approach to contextual advertis-

ing. In Proc. ACM SIGIR.

Devanur, N. and Hayes, T. (2009). The adwords problem:

Online keyword matching with budgeted bidders un-

der random permutations. Presented at EC.

Easterly, A. (2009). Revenue management in online ad-

vertising: Challenges and opportunities. Presented at

INFORMS.

Feige, U., Immorlica, N., Mirrokni, V., and Nazerzadeh,

H. (2008). A combinatorial allocation mechanism

with penalties for banner advertising. Presented at IN-

FORMS.

Feldman, J., Mehta, A., Mirrokni, V., and Muthukrishnan,

S. (2009). Online stochastic matching: Beating 1-1/e.

Presented at FOCS.

FICO (2010). Xpress—Optimizer Reference Manual.

Ghosh, A., McAfee, R., Papineni, K., and Vassilvitskii,

S. (2009). Bidding for representative allocations for

display advertising. In Proc. of the 4th interna-

tional Workshop on Internet and Network Economics

(WINE).

Han, P. (2009). Yield optimization in display ad networks.

Presented at INFORMS.

Langheinrich, M., Nakamura, A., Abe, N., Kamba, T., and

Koseki, Y. (1999). Unintrusive optimization tech-

niques for web advertising. In Proc. of World Wide

Web Conf. (WWW1999).

Nakamura, A. and Abe, N. (2005). Improvements to the lin-

ear programming based scheduling of web advertise-

ments. J. Electronic Commerce Research, 5:75–98.

Radovanovic, A. and Zeevi, A. (2009). Revenue maximiza-

tion in reservation-based online advertising. Presented

at INFORMS.

Richardson, M., Dominowska, E., and Ragno, R. (2007).

Predicting clicks: Estimating the click-through rate

INVENTORY ALLOCATION FOR ONLINE GRAPHICAL DISPLAY ADVERTISING USING MULTI-OBJECTIVE

OPTIMIZATION

303

for new ads. In Proc. of World Wide Web Conf.

(WWW2007).

Roels, G. and Fridgeirsdottir, K. (2009). Dynamic revenue

management for online display advertising. Journal

of Revenue and Pricing Management, 8(5):452–466.

Shaparenko, B., C¸ etin, O., and Iyer, R. (2009). Data-driven

text features for sponsored search click prediction. In

Proc. of the 3rd Int. Workshop on Data Mining and

Audience Intelligence for Advertising (ADKDD).

Shumway, R. and Stoffer, D. (2007). Time Series Analysis

and Its Applications. Springer.

Steuer, R. (1986). Multiple criteria optimization: theory,

computation, and application. Wiley, New York.

Tomlin, J. (2000). An entropy approach to unintrusive tar-

geted advertising on the web. In Proc. of World Wide

Web Conf. (WWW2000).

Vee, E., Vassilvitskii, S., and Shanmugasundarum, J.

(2009). Optimal online assignment with forecasts. Ya-

hoo! Labs research report YL- 2009-005.

Wilson, A. (1970). Entropy in Urban and Regional Mod-

elling. Pion Press, London.

Yang, J. (2009). Multi-objective optimization for online

advertising inventory allocation - an extension. Pre-

sented at INFORMS.

Yang, J. (2010). Inventory allocation for online advertising

with malleable supply. Presented at INFORMS.

Yang, J. and Tomlin, J. (2008). Advertising inventory al-

location based on multi-objective optimization. Pre-

sented at INFORMS.

ICORES 2012 - 1st International Conference on Operations Research and Enterprise Systems

304