
ROBUST FACE RECOGNITION USING WAVELET AND DCT
BASED LIGHTING NORMALIZATION, AND SHIFTING-MEAN LDA
I. Gede Pasek Suta Wijaya
1,2
, Keiichi Uchimura
1
, Gou Koutaki
1
and Cuicui Zhang
3
1
Electrical Engineering and Computer Science Dept., Kumamoto University, Kurokami 2-39-1, Kumamoto Shi, Japan
2
Electrical Engineering Dept., Mataram University, Jl. Majapahit 62, Mataram, Indonesia
3
Department of Intelligence Science and Technology, Graduate School of Informatics, Kyoto University, Kyoto, Japan
Keywords:
Frequency analysis, Lighting normalization, Incremental LDA, Holistic features, Face recognition.
Abstract:
This paper presents an integration of Wavelet and Discrete Cosine Transform (DCT) based lighting normal-
ization, and shifting-mean Linear Discriminant Analysis (LDA) based face classifiers for face recognition.
The aims are to provide robust recognition rate against large face variability due to lighting variations and to
avoid retraining problem of the classical LDA for incremental data. In addition, the compact holistic features
is employed for dimensional reduction of the raw face image. From the experimental results, the proposed
method gives sufficient and robust achievement in terms of recognition rate and requires short computational
time.
1 INTRODUCTION
The existing face recognition methods (Zhao et al.,
2003; Chen et al., 2005; Yu and Yang, 2001; Wi-
jaya et al., 2010; Pang et al., 2005; Zhao and Yuen,
2008) still leave several problems such as low perfor-
mance for large face variability due to large lighting
variations and requiring long computational time for
retraining of incremental data.
In terms of large face variability due to large
lighting variations, a comparative study of different
pre-processing approach to illumination compensa-
tion has been proposed for solving this problem (del
Solar and Quinteros, 2008). In addition, robust pre-
processing for illumination compensation of face im-
age which was based on low-pass filter has been pro-
posed and it provided robust achievements over the
SQI (Kurita and Tomikawa, 2010). However, it still
has the difficulty to determine the type of low-pass fil-
ter that is suitable for those algorithms. An alternative
method which was based on the local mean has been
proposed for overcome this problem and works well
for data from YaleB database (Wijaya et al., 2010).
However,the performances of mentioned methods are
not optimum yet especially for data which contain
large illumination.
Regarding to retraining problem, several methods
have been proposed (Pang et al., 2005; Zhao and
Yuen, 2008; Wijaya et al., 2010). An algorithm called
as incremental LDA (ILDA) was presented to avoid
this problem (Pang et al., 2005) which is redefined the
within-class scatter (S
w
) formulation, made simplifi-
cation of calculating the global mean, and determined
the projection matrix (W) using singular valuedecom-
position (SVD). An improvement of ILDA strategy
was proposed called as generalized SVD incremental
LDA (GSVD-ILDA) which determined W of incre-
mental data using generalized SVD(Zhao and Yuen,
2008). The GSVD-ILDA needed less computation
time than that of ILDA. Another strategy was pro-
posed to solve the retraining problem using the con-
stant global mean for all data samples to obtain the
between class scatter, S
b
(Wijaya et al., 2010). It
also implemented compact holistic features (HF) for
dimensional reduction of the raw image which com-
pressed the original size of image into 90%. The HF
could provide good enough achievements in terms of
recognition rate and required short processing time.
The sufficient spanning sets ILDA (Kim et al., 2011)
also has been presented to overcome retraining prob-
lem of incremental data which works using sufficient
spanning sets for converting the large eigen problem
of classical LDA into a smaller eigen problem. Fur-
thermore, a new incremental LDA which was based
on least square solution to LDA called as LS-ILDA
was presented to avoid the eigen analysis bottleneck
on conventional LDA (Liu et al., 2009). However,
they requires less computational complexity when the
input data size (n) is much larger than the total data
classes (L) and the LS-ILDA determined the optimum
343
Gede Pasek Suta Wijaya I., Uchimura K., Koutaki G. and Zhang C. (2012).
ROBUST FACE RECOGNITION USING WAVELET AND DCT BASED LIGHTING NORMALIZATION, AND SHIFTING-MEAN LDA.
In Proceedings of the 1st International Conference on Pattern Recognition Applications and Methods, pages 343-350
DOI: 10.5220/0003753303430350
Copyright
c
SciTePress

DCT and
DWT
Analysis
f
t
(x,y)=
(I(x,y)/L(x,y)).
α
αα
α
Normalized Face
0 100 200
0
200
400
600
Input Image I(x,y)
Low Freq. L(x,y)
Histogram of
Normalized Face
Figure 1: Lighting normalization process.
W just from total scatter matrix and the updating pro-
cess has to be done by inserting one sample.
In this paper, we present an integration of discrete
wavelet transforms (DWT) and DCT based lighting
normalization with shifting-mean LDA (SM-LDA)-
based face classifiers for robust face recognition. The
DCT and Wavelet based lighting normalization which
are simple and fast lighting normalization are pro-
posed for solving the remaining problem of large face
variability due to lighting variations. Next, the SM-
LDA which is a new approach for avoiding to recal-
culate the S
w
and S
b
for each incremental data is pro-
posed for solving retraining problem of conventional
LDA. In this research, to solve eigen analysis bottle-
neck on conventional LDA, the compact holistic fea-
tures is implemented as dimensional reduction of raw
face image. In this case, the dimensional of the raw
face image is reduced into 53 coefficients from 16384
coefficients.
2 DWT AND DCT BASED
LIGHTING NORMALIZATION
The existing methods for lighting normalization still
does not work well yet for large face variability due to
lighting variations especially for data which contain
large illumination such as sub-set 4 of YaleB database
(face images set which the angles of the light source
direction are up to 77
0
from the camera).
To solve this problem, we develop simple lighting
normalization algorithm as shown in Fig.1, which is
based on the frequency transformation analysis. The
main goal is to improve recent existing methods such
as modified local binary pattern (mLBP) and local
mean methods. This idea comes from the descrip-
tion of low-pass filter-based algorithm (Kurita and
Tomikawa, 2010) which explains that the illumina-
tion information of the image is placed on the low
frequency component of the face image. As known
that the DCT and DWT have good capability to ex-
tract the frequency content of the image which have
much energy compactness.
Suppose the original image is I(x,y), the illumi-
nant component is L(x, y), and the normalized image
is defined as f
t
(x,y). The lighting normalization starts
from the YCbCr transformation because the RGB is
not required and the lighting just affects the contrast
and brightness of the image, which is placed in the
intensity (Y) component. Next, from the Y compo-
nent, the illuminant component is extracted by both
DCT and multi-resolution DWT using the following
procedures:
• Performing the DCT and multi-resolution DWT
of the Y component then select small m coeffi-
cients, which contain 99% of total energy.
• Reconstructing the image from the selected co-
efficients using inverse DCT and multi-resolution
DWT algorithm.
Next, dividing the original image (I(x,y)) that rep-
resents the input stimulus with the low frequency
extraction output (L(x,y)) that represent the illumi-
nant or perception using: f
t
(x,y) = I(x,y)/L(x,y).α,
where the α is constant coefficient for making cen-
tring the image intensity. Finally, stretching the
f
t
(x,y) to get the uniform contrast and brightness, as
shown in Fig. 2(b and c) for DCT and DWT based
lighting normalization, respectively.
The DCT and DWT can work for lighting nor-
malization because the most of the illuminant com-
ponents are well extracted, as shown in the Fig. 3(a
and b). From those images, we can see that the illu-
mination part of the input images is exactly extracted
by the DCT and DWT-based methods. From the out-
put of the lighting normalization (see Fig. 2(b and
c)) show that all of the images have almost the same
brightness and contrast, which is shown by almost
identical histogram data for DCT-based and multi-
resolution DWT-based algorithms, respectively. In
addition, these methods still leave clear facial features
such as eyes, mouth, nose, face outline, and face tex-
ture. It means the proposed lighting normalization
tend to overcome the large variations of face images
due to the lighting variations. In other words, the
proposed methods tend to provide and better and ro-
bust achievements in terms of recognition rate than
the previous methods because the most significant
discriminant information such as local facial features
still exist after normalization.
3 SHIFTING-MEAN LDA
Briefly, the LDA methods works as follows: suppose
we have data set which have L classes and each class
ICPRAM 2012 - International Conference on Pattern Recognition Applications and Methods
344

w
time S
b
) and then select m orthonormal ei
(d) DWT based illumination definition
0 100 200
0
100
200
0 100 200
0
100
200
0 100 200
0
100
200
(a) Input images
0 100 200
0
100
200
0 100 200
0
100
200
0 100 200
0
100
200
(b) DCT-based method
0 100 200
0
100
200
0 100 200
0
100
200
0 100 200
0
100
200
(c) Multi-resolution DWT-based method
Figure 2: The input and output of lighting normalization and their histogram.
(k-th) has N
k
samples. From the data set, the opti-
mum W, which has to satisfy the Fisher criterion (Eq.
1), can be determined by eigen analysis of inverse S
w
time S
b
and then select m orthonormal eigenvectors
corresponding to the largest eigenvalues (i.e. m < n),
where n is the dimensional of input vector, x
k
i
.
J
LDA
(W) = argmax
W
| W
T
S
b
W |
| W
T
S
w
W |
(1)
Where both of the S
w
=
1
N
∑
L
k=1
∑
N
k
i=1
(x
k
i
− µ
k
)(x
k
i
−
µ
k
)
T
and S
b
=
∑
L
k=1
P(x
k
)(µ
k
− µ
a
)(µ
k
− µ
a
)
T
with
P(x
k
) = N
k
/N, N =
∑
L
k=1
N
k
, µ
k
=
1
N
k
∑
N
k
i=1
x
k
i
, and
µ
a
=
1
N
∑
L
k=1
N
k
µ
k
.
(a) DCT-based
(b) MR-DWT-based
Figure 3: Low frequency extraction outputs.
By using this LDA algorithm for face recognition,
good and stable recognition rate for both small and
large sample size data (Chen et al., 2005; Yu and
Yang, 2001) can be achieved. However, it need re-
training process for incremental data. To avoid the
retraining problem and to decrease its computational
load, we can simplify the S
b
using the shifting-mean
algorithm as follows.
S
b
=
1
N
L
∑
k=1
N
k
(µ
k
− µ
a
)(µ
k
− µ
a
)
T
=
1
N
L
∑
k=1
N
k
µ
k
µ
T
k
+ αµ
a
µ
T
a
− rµ
T
a
− µ
a
r
T
=
Θ
N
− µ
a
µ
T
a
(2)
where, Θ =
∑
L
k=1
N
k
µ
k
µ
T
k
, α = N, r =
∑
L
k=1
N
k
µ
k
, and
µ
a
=
1
N
∑
L
k=1
N
k
µ
k
=
r
N
. If a new class, x
new
, comes
into the system, the S
b
can be updated as follows.
S
u
b
=
1
L+ N
new
Θ+ N
new
µ
new
µ
T
new
− µ
u
a
(µ
u
a
)
T
=
1
L+ N
new
(Θ
old
+ Θ
new
) − µ
u
a
(µ
u
a
)
T
(3)
where Θ
old
= Θ, Θ
new
= N
new
µ
new
µ
T
new
, and
µ
u
a
=
1
L+ N
new
(Lµ
a
+ N
new
µ
new
). (4)
By using this simplification, the updated S
b
has
exactly the same scatter as the original. In detail, to
update the S
b
using Eq. 3, we just need to calculate
the Θ
new
, µ
u
a
, and µ
u
a
(µ
u
a
)
T
which require (2n
2
) multi-
plication operations and (n
2
+ n) additions. However,
the original one requires (L+1)n
2
multiplications and
(L+ 1)n
2
additions.
In addition, the S
w
, which does not depend on the
global mean, can be redefined as follows:
S
u
w
=
1
N + N
L+1
(
L
∑
k=1
S
k
w
+ S
L+1
w
)
=
1
N + N
L+1
n
S
old
w
+ S
new
w
o
, (5)
where S
k
w
=
∑
N
k
i=1
(x
k
i
− µ
k
)(x
k
i
− µ
k
)
T
, S
old
w
=
∑
L
k=1
S
k
w
,
and S
new
w
= S
L+1
w
.
Finally, the optimum W is obtained by substitut-
ing the S
u
b
and the S
u
w
of LDA eigen analysis and then
select several large eigen vectors which correspond to
the largest eigen values. This optimum W is called
as shifting mean LDA projection matrix (W
SM−LDA
).
The projected features of the both training and query-
ing data set can be performed using the W
SM−LDA
as
done by the original LDA.
4 THE FACE RECOGNITION
ALGORITHM
In order to know the effectiveness of the proposed
methods, we integrated both of them for face recog-
nition which consists of two main components: face
pre processing and feature extraction and classifica-
tion, as shown in Fig. 4.
The algorithm starts from localizing of face loca-
tion, next detecting the eyes coordinates from the lo-
calized face image, and finally cropping the face im-
age which is done by respecting to the detected eyes
ROBUST FACE RECOGNITION USING WAVELET AND DCT BASED LIGHTING NORMALIZATION, AND
SHIFTING-MEAN LDA
345

Training Set
Training Set
Query Face
Query Face
Pre
Pre
-
-
Processing
Processing
HF Extraction
HF Extraction
Face Likeness
Face Likeness
Do Projection
Do Projection
Updating
Updating
Sw
Sw
,
,
Sb
Sb
.
.
Using
Using
Eq
Eq
. 3 and 6
. 3 and 6
Determine
Determine
W
W
and Do
and Do
the projection
the projection
Save
Save
upadated
upadated
Sw
Sw
and
and
Sb
Sb
.
.
W,
W,
and
and
Y
Y
pp
Matrixes
Matrixes
Pre
Pre
-
-
Processing
Processing
HF Extraction
HF Extraction
Norm
Norm
-
-
based
based
Classification
Classification
Decision Rule
Decision Rule
W
W
Yp
Yp
Figure 4: The block diagram of the proposed face recogni-
tion.
coordinates. Next, the cropped face images is normal-
ized using the mentioned algorithm (Section 2) to re-
move non-uniform lighting effect on face image. Fi-
nally, a compact holistic feature (HF) of face image
that is based on frequency and moment analysis of en-
tire face is implemented as dimensional reduction of
raw face image. The HF consists of the dominant fre-
quency content of the face image extracting by DCT
and moment information that provides invariant mea-
sure of face images shape. The HF with considering
the invariant moment set provides higher discrimina-
tory power than without moment information (Wijaya
et al., 2010).
The face classification consists of training and
recognition process. In the training process, the sys-
tem defines the optimum W using shifting-mean LDA
based algorithm as described in section 3 with the HF
as the raw input. Then, the extracted HF and the de-
termined optimum W are saved into database for the
next process.
In the recognition process, the Euclidean distance
based on nearest neighbour rule is implemented for
face classification. In this case, the negative samples
(non-training faces and non-face images) are used to
define the threshold for face verification. If the min-
imum score is less than the defined threshold the in-
put data is verified as known face (registered ID) and
other wise is concluded as negative face or unknown
face.
In order to get better recognition rate, score fu-
sion mechanism is implemented for face verification
as follows.
S
f
= αS
1
+ βS
2
+ γS
3
(6)
where, S
f
is the final score, S
1
, S
2
, and S
3
are the
matching score between the three kind of features
vector (Y, Cb, and Cr components) of the querying
and training of the face images. The Cb and Cr com-
ponents are considered in order to cover the skin color
information of the face image. The weight coeffi-
cients (α, β, and γ) are determined using the following
equation. The main aim of this equation is to balance
the contribution of three kinds of features vectors in
face verification.
w
n
i
= (w
i
− min(⌊w
1
⌋,⌊w
2
⌋,...,⌊w
j
⌋))
2
(7)
where w
i
is the i-th feature vector score, j is number
feature vectors of each face image, and finally the α =
w
1
, β = w
2
, and γ = w
3
.
5 EXPERIMENTS AND RESULTS
The first experiment was carried out on the YaleB
database (Lee et al., 2005) to investigate the perfor-
mance of the proposed lighting normalization against
to any variations of lighting condition and to compare
its achievementswith some established methods, such
as histogram equalization (HE), modified Local Bi-
nary Pattern (mLBP(del Solar and Quinteros, 2008)),
and Local Mean(Wijaya et al., 2010). The Yale-B
database was divided into four different sub-sets ac-
cording to the angle of the light source direction forms
with the camera axis. In detail, the sub-set 1, 2, 3 , and
4 are the face images set which the angles of the light
source direction are up to 12
0
, up to 30
0
, up to 60
0
,
and up to 77
0
, respectively from the camera. An ex-
ample of face variability due to lighting variation of
YaleB database can be seen in Fig. 5. In this test, the
subset 1 was chosen as training data and the remain-
ing sub-sets were selected as testing data.
(a) Sub-Set 1
(b) Sub-Set 2
(c) Sub-Set 3 (d) Sub-Set 4
Figure 5: Example of face with large lighting variations of
Yale database.
The experimental results show that the proposed
lighting normalization can improve significantly the
existed methods, such as mLBP and Local Mean as
shown in Table 1. The significant improvement of
recognition rate is given by sub-set 4, because face
images of this sub-set contains large lighting varia-
tions such as large illumination. It can be achieved
because the DCT and multi-resolution DWT-based
ICPRAM 2012 - International Conference on Pattern Recognition Applications and Methods
346
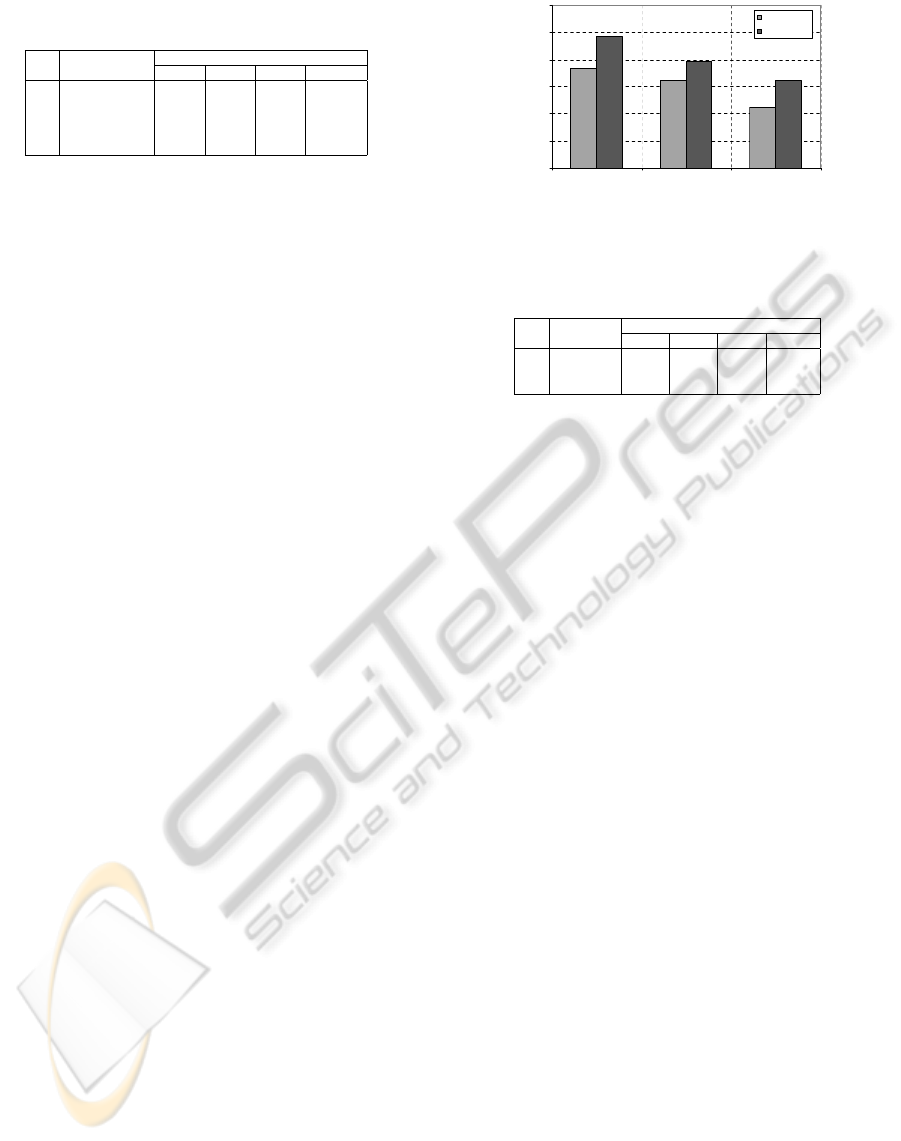
Table 1: The effect of lighting normalization on the recog-
nition rate for YaleB database.
No
Methods of Recognition Rate (%)
Normalization 1 vs 2 1 vs 3 1 vs 4 Average
1 HE 95.39 60.13 13.69 56.39
2 mLBP 100 100 78.71 92.90
4 Local Mean 100 100 80.40 93.47
5 DCT-Based 100 100 87.71 95.90
6 DWT-Based 100 100 95.71 98.57
note:i vs j means sub-set i versus sub-set j
lighting compensation can remove most of the illumi-
nant information of the input image, which is placed
in low frequency component. Between the DCT and
DWT, the multi-resolution DWT provide better im-
provement because the wavelet analysis has good fre-
quency resolution and poor time resolution at low fre-
quencies analysis. Therefore, it can extract well the
illuminant component which is mostly placed low fre-
quency component, as shown in Fig. 3. It means
any lighting condition of face images are normalized
into almost the same contrast and brightness by the
proposed lighting normalization method. Based on
this experimental result, we will implement the DWT-
based lighting normalization for pre-processing of the
face images in the all next experiments.
In addition, the integration of DWT-based light-
ing normalization and SM-LDA provide robust re-
sult over the previous methods (see Fig. 6) when the
experiment was done in three challenges databases:
ITS- Lab. Kumamoto University(Wijaya et al., 2010),
INDIA(Jain and Mukherjee, 2002) databases repre-
senting small size database and FERET(Philips et al.,
2000) database representing large size database. This
experiment is done to support the previous result as
presented Table 1. The result showsthat, the proposed
lighting condition can improve the previous lighting
normalization, by about 1% of the baseline method
(local mean). It can be achieved because two reasons:
• the DWT-based normalization can perfectly ex-
tracted the non uniform lighting effect on the face
images because the DWT works as filter-bank to
remove the low frequency component, and
• the DWT can extracted not only the low frequency
component but also where is the frequency ex-
ist. It means the DWT work as time window fast
Fourier transforms. Therefore, it is better to used
for extracting the non uniform lighting effect on
the face images than that of the local mean method
because the local mean extracts lighting compo-
nent in the blocking image which depends on the
block size and the block size is not always cover
all of the illumination part.
The third experiment was carried out using data
from ITS- Lab., INDIA, and FERET databases. From
these data, half of the samples were selected as the
training sample and remaining as test samples. In
94
95
96
97
98
99
100
ITS LAB INDIA FERET
Database
Recognition Rate (%)
Local Mean
DWT-Based
Figure 6: The robust recognition rate of our approach com-
pared to that of base line on several databases.
Table 2: The effect of the score fusion on the recognition
rate of the integration proposed face recognition.
No
Databases Recognition Rate (%) of
Y Cr Cb Fusion
1 ITS 98.31 96.27 94.93 98.84
2 INDIA 90.96 93.41 93.03 97.93
3 FERET 91.27 92.53 91.96 96.85
this test, we investigate the effectiveness of the score
fusion to improve the recognition rate of the single
features-based face recognition method. The experi-
mental result shows that the score fusion of three fea-
tures (Y, Cb, and Cr) can improve significantly the
recognition rate for all tested database, as shown in
Table 2. It means that the score fusion make the sys-
tem consider much more discriminant information for
face verification than that of the without fusion. In
addition, by fusing the chrominant (Cb and Cr) com-
ponents of the face image means that the system in-
cludes the skin information in the face classification.
In order to show that the SM-LDA can solve the
retraining problem, the next experiments were done to
investigated the effect of processing time of S
b
recal-
culation to the processing time of entire LDA. In this
experiment, we determined the time ratio between the
processing time of S
b
recalculation and the processing
time of entire LDA.
The time ratio as function of number of incremen-
tal data was determined using combined data from
all mentioned databases. From this data, 100 classes
were selected for initial training set and 1900 classes
were selected for incremental data which was in-
serted into the system step by step (each step was 100
classes). The S
b
and S
w
recalculation time and entire
training time of CLDA were determined the same as
done in previous one. The results shows that time ra-
tio of CLDA increases significantly while that of our
the proposed method is almost constant for each in-
cremental data, as shown in Fig. 7. It means the SM-
LDA requires very short computation time for S
b
and
S
w
recalculation when new classes are added into the
system.
From this achievement, the S
b
and S
w
recalcula-
tion of CLDA greatly affect the entire LDA process-
ing time while that of our proposed method does not
ROBUST FACE RECOGNITION USING WAVELET AND DCT BASED LIGHTING NORMALIZATION, AND
SHIFTING-MEAN LDA
347

0
5
10
15
20
25
30
35
40
45
50
10 0 300 500 700 90 0 1100 1300 1500 1700 1900
Number of Classes
Computation Time Ratio (%)
CLDA
SM LD A
Figure 7: The time ratio as function of inserted data.
affect the entire LDA processing time at all. In this
case, the eigen analysis does not create a bottleneck
for the computational cost of LDA, because the size
of features vector is much less then total data sam-
ples (the features vector size is 53 elements while
M > 1000 images). It can be achieved because the
S
b
recalculation process of our proposed method just
contains summation of the Θ
old
and the Θ
new
, and
vector multiplication (µ
u
a
(µ
u
a
)
T
) as shown in Eq. 3.
In addition, the S
b
recalculation is just summation of
both S
old
w
and S
new
w
. Based on this experimental result,
our proposed method could solve the retraining prob-
lem of CLDA.
In order to show that the integration of the pro-
posed lighting normalization provides robust recog-
nition rate than that of recent sub-space methods for
incremental data (GSVD-ILDA, SP-ILDA, and LS-
ILDA methods), the next experiment was performed.
It was done in FERET face database with face features
of 53 elements and the training was performed grad-
ually: firstly, it was trained 208 face classes and then
added gradually 20 new face classes to the system
until 508 face classes. In addition, the DWT-based
lighting normalization and the score fusion were im-
plemented in this test. In order to know the retrain-
ing time, the experiment was done using data from
all mentioned databases (consist of 2000 classes) with
face features of 53 elements and the training was per-
formed gradually: firstly, 100 face classes was setup
as initial training and then 100 classes is inserted for
each step until reaching 2000 classes
In term of recognition rate, the SM-LDA provides
higher stable recognition rate than that of the recent
subspace methods for incremental data, as shown in
Fig. 8(a). This result supports our previous achieve-
ments, which provesthat our proposed method has the
same structure as conventional CLDA but they have
simpler computational complexity. This approach is
an alternative algorithm for features cluster of large
sample size databases, which requires much retrain
processing such as for incremental data. In addition,
the recent establish methods haveless recognition rate
than our proposed method because the optimum W of
86
88
90
92
94
96
98
208 248 288 328 368 408 448 488
Incre mental data (step by 20 data)
Recognition Rate (%)
GSVD-ILDA SP-ILDA
LS-ILDA SM-LDA
(a)
0
0.5
1
1.5
2
2.5
3
3.5
4
4.5
100 300 500 700 900 1100 1300 1500 1700 1900
Incre me ntal data (step by 100 data)
Retraining Time (s)
GSVD- ILDA
SP-ILDA
SMLDA
(b)
Figure 8: The robust recognition rate and retraining time of
the proposed method compared to two established methods
for incremental data.
GSVD-ILDA is provided by computing the best rank
k-th approximation of the matrix X = [A,B] for each
incremental data B; the W of LS-ILDA is just deter-
mined from total scatter matrix without considering
the S
b
at all; and W of SP-ILDA is also defined from
the total scatter and S
b
. The total scatter matrix repre-
sents the global covariance matrix of the training set
which provides the same information as that of the
PCA and the S
b
provides the null space information.
Therefore, the recognition rate of SP-ILDA is better
than GSVD-ILDA and LS-ILDA.
In term of retraining process, our proposed
method provides much the same retraining time as
SP-ILDA and less than GSVD-ILDA, as shown in
Fig. 8(b). It can be achieved because the GSVD-
ILDA requires higher time complexity than SP-ILDA
and our proposed method. The GSVD-ILDA needs
O(nqk + n(L + M)t + q
2
n + k
3
), where t and k are
number of selected leading principle sub matrix of
SVD decomposition, as detail described in the ILDA
algorithms(Zhao and Yuen, 2008), while the SP-
ILDA requires O(d
3
T,1
t + d
3
B,1
+ nd
T,3
d
b,3
), where the
d
T,1
, d
T,3
, and d
B,1
are equal to n and the d
B,3
< n,
and our proposed method require O(n
3
). Even though
our proposed method time complexity is greatly af-
fected by the eigen analysis time complexity (O(n
3
)
but the dimensional size of data input (n) is much less
than total data samples (M). Therefore, the computa-
tional time of our proposed method (0.13 second) is
much the same as that of SP-ILDA (0.16 second) for
n ≪L≪M. In other words, the eigen analysis does not
ICPRAM 2012 - International Conference on Pattern Recognition Applications and Methods
348

create a bottleneck for the computational time of the
SM-LDA method, because the size of HF vector is
much less then total data samples. In this test, the size
of n is 53 elements, the L is 2000 and the M is 10000
images.
The retraining time of LS-ILDA can not be com-
pared with that of GSVD-ILDA, SP-ILDA, and our
proposed method because the retraining was done
by insert a block of data consisting of 100 classes
and each class consisting of 5 face images. In case
of retraining experiment using 1 face image inser-
tion, the LS-ILDA requires almost the same retrain-
ing time as that of GSVD-ILDA, SP-ILDA, and SM-
LDA for 200 data classes data training initial which
each class consists of 5 face images (the M is 1000,
L is 200, and n is 53). For one sample insertion, the
retraining time of LS-ILDA is 0.19 second while the
GSVD-ILDA, SP-ILDA, and SM-LDA just require
0.31, 0.17, and 0.13 second, respectively. As our
evaluation of the LS-ILDA, it has computationalcom-
plexity O(min(M,n)×n)+O(M×L×n) for each up-
dating W when training data have M ≫ Ł ≫ n. If the
retraining is done by inserting a block data consist-
ing of q samples (q ≫ n) into the LS-ILDA method, it
requires much longer time complexity than SM-LDA
(q{O(min(M,n) × n) + O(M × L × n)} > O(n
3
) for
updating the W. Suppose q = 500 and n = 53, time
complexity of LS-LDA becomes almost 500 times of
our proposed method.
6 CONCLUSIONS AND FUTURE
WORKS
From the experimental result, we can conclude as fol-
lows. Firstly, the proposed lighting normalization is
an alternative solution for large face image variability
due to lighting variations. Secondly, the face recogni-
tion, which considers much more features, tends to
provide better achievement than that of single fea-
tures. Thirdly, the SM-LDA based classifier can solve
the retraining problem of CLDA on incremental data
which provides stable recognition rate over recent
ILDA methods. Finally, the integration of the pro-
posed lighting compensation and shifting-mean LDA
classifier as well as fusion score for face recogni-
tion give sufficient and robust enough achievement in
terms of recognition rate and it also requires short pro-
cessing time.
In future, the research will be continued for avoid-
ing the eigen analysis in determining the optimum
projection matrix and finding another strategy to solve
retraining problem on incremental data which belong
to known class (old data). Furthermore, more experi-
ments are required to know the robustness of the pro-
posed lighting normalization against to large variabil-
ity face due to lighting variations, such as the test us-
ing data from FRGC data set.
ACKNOWLEDGEMENTS
I would like to send my great thank and appreciation
to the owner of YALE, INDIA, and FERET face
databases, to Image Media Laboratory of Kumamoto
University for supporting this research, and to the re-
viewers who have given some helpful comments and
suggestions for improving the paper presentation.
REFERENCES
Chen, W., Meng, J.-E., and Wu, S. (2005). PCA and
LDA in DCT Domain. Pattern Recognition Letter,
3(26):2474–2482.
del Solar, J. R. and Quinteros, J. (2008). Illumination com-
pensation and normalization in eigenspace-based face
recognition: A comparative study of different pre-
processing approaches. Pattern Recognition Letter,
29(14):1966–1979.
Hisada, M., Ozawa, S., Zhang, K., Pang, S., and Kasabov,
N. (2009). A novel incremental linear discriminant
analysis for multitask pattern recognition problems.
Advances in Neuro-Information Processing Lecture
Notes in Computer Science, 5506.
Jain, V. and Mukherjee, A. (2002). The indian face
database.
Kim, T.-K., Stenger, B., Kittler, J., and Cipolla, R. (2011).
Incremental linear discriminant analysis using suffi-
cient spanning sets and its applications. International
Journal of Computer Vision, 91(2):216–232.
Kurita, S. and Tomikawa, T. (2010). Study On Robust Pre-
Processing For Face Recognition Under Illumination
Variations. In the Workshop of Image Electronics and
Visual Computing 2010, Nice France (CD-ROM).
Lee, K., Ho, J., and Kriegman, D. (2005). Acquiring linear
subspaces for face recognition under variable light-
ing. IEEE Trans. Pattern Anal. Mach. Intelligence,
27(5):684–698.
Liu, L.-P., Jiang, Y., and Zhou, Z.-H. (2009). Least Square
Incremental Linear Discriminant Analysis. In pro-
ceedings of the Ninth IEEE International Conference
on Data Mining, pages 298–3061.
Pang, S., Ozawa, S., and Kasabov, N. (2005). Incremen-
tal Linear Discriminant Analysis for Classification of
Data Streams. IEEE Transactions on Systems, Man,
and Cybernetics-Part B: Cybernetics, 35(5):905–914.
Philips, P. J., Moon, H., Risvi, S. A., and Rauss, P. J.
(2000). The FERET Evaluation Methodology for Face
Recognition Algorithms. IEEE Transactions on Pat-
tern Analysis and Machine Intelligence, 22(10):1090–
1104.
ROBUST FACE RECOGNITION USING WAVELET AND DCT BASED LIGHTING NORMALIZATION, AND
SHIFTING-MEAN LDA
349

Wijaya, I., Uchimura, K., and Hu, Z. (2010). Improving the
PDLDA based face recognition using lighting com-
pensation. In the Workshop of Image Electronics and
Visual Computing 2010, Nice France (CD-ROM).
Yu, H. and Yang, J. (2001). A Direct LDA algorithm
for High-Dimensional Data-with Application to Face
Recognition. Pattern Recognition, 34:2067–2070.
Zhao, H. and Yuen, P. (2008). Incremental linear discrimi-
nant analysis for face recognition. IEEE Transactions
on Systems, Man, and Cybernetics-Part B: Cybernet-
ics, 38(1):210–221.
Zhao, W., Chellappa, R., and Rosenfeld, A. (2003). Face
recognition: A literature survey. ACMComputing Sur-
veys, 35:399–458.
ICPRAM 2012 - International Conference on Pattern Recognition Applications and Methods
350
