
F
o
F
1
-ATPase STATOR REGULATION STUDIED
WITH A RESONANCE MODEL
Yao-Gen Shu and Zhong-Can Ou-Yang
Institute of Theoretical Physics, Chinese Academy of Sciences, Beijing 100190, China
Keywords:
Molecular motor, F
o
F
1
-ATPase, Stator regulation, Binding change mechanism, Resonance model.
Abstract:
The F
o
F
1
-ATPase activity was regulated through external links on the exposed stator. The regulation tendency
of synthesis was the same with that of hydrolysis. A resonance model has been proposed to illustrate these
regulation phenomena. The novel model not only has deepened our understanding of the “binding change
mechanism”, but also was very useful to develop the rotary motor into a biosensor.
1 INTRODUCTION
F
o
F
1
-ATPase is the ubiquitous rotary motor that uses
the transmembrane electrochemical potential to syn-
thesize ATP in bacteria, chloroplasts and mitochon-
dria. The holoenzyme is a complex of two rotary
motors, F
o
and F
1
, which are mechanically coupled
by a common central stalk (“rotor”), c
n
-ε-γ. The
membrane embedded F
o
unit converts the proton mo-
tive force(p.m.f) into mechanical rotation of the “ro-
tor”, thereby causing cyclic conformational change of
α
3
β
3
crown (“stator”) in F
1
and driving ATP synthe-
sis. A striking characteristic of this motor is its re-
versibility. It may rotate in the reverse direction for
ATP hydrolysis and utilize the excess energy to pump
protons across the membrane. In F
1
motor, the eccen-
tric rotation of γ subunit and the cyclic conformational
change of α
3
β
3
crown, are mechanically coupled at
near 100% efficiency(Boyer,1997; Leslie and Walker,
2000; Weber and Senior, 2003; Kinosita et al., 2004;
Junge, 2004; Wilkens, 2005; Nakamoto et al., 2008;
Ballmoos et al., 2008; Yasuda et al., 1998; Shu et al.,
2010).
In the proof-of-principle demonstrations, the
holoenzyme activity was regulated by changing of the
transmembrane gradient of proton(P¨anke and Rum-
berg, 1996; Turina et al., 2003; Diez et al., 2004;
Steigmiller et al., 2008). Moreover, the F
1
activ-
ity was studied in detail through an actin filament
or a bead on the “rotor”(Yasuda et al., 1998; Itoh
et al., 2004). On the other hand, several pioneering
investigations(Boyer, 1993; Abrahams et al., 1994;
Noji et al., 1997; Nishizaka et al., 2004) have re-
vealed that the cyclic conformational change of α
3
β
3
crown “stator” is tightly coupled with the rotation of
γ “rotor”. A fascinating question arises: can we reg-
ulate the holoenzyme activity through a convenient
method? Yue Group’s recent experiments(Cheng
et al., 2010) about virus detection have demonstrated
that the holoenzyme activity can be regulated by the
external links on the exposed α (or β) subunits. The
external links not only inhibit the enzyme but also ac-
tivate it, and the regulation tendency of synthesis is
the same with that of hydrolysis. However, what is
the implied mechanism?
It is impossible for the two movements to transfer
energy at near 100% efficiency(Yasuda et al., 1998)
unless they work in a resonance fashion through
an elastic element. Actually, Boyer’s “binding
change mechanism”(Boyer, 1993), Walker’s struc-
ture(Abrahams et al., 1994) and Oster’s hinge bend-
ing model(Wang and Oster, 1998) have partly implied
that F
1
-ATPase works in a fashion of driven oscilla-
tion(Kargovsky et al., 2009; W¨achter et al., 2011).
The driving force is supplied by the eccentric rotation
of γ subunit for synthase or by the binding of ATP
for hydrolase, whereas the passive oscillation is the
cyclic conformational change of α
3
β
3
crown, whose
frequency is the driving frequency. If we regard α
or β subunit as a harmonic oscillator, α and β sub-
units will vibrate at its natural frequency. Once the
driving frequency matches the natural frequency, res-
onance occurs. At resonancefrequency, the amplitude
of steady state response is the biggest in proportion to
the amount of driving force, which is the most conve-
nient for binding of substrates and releasing of prod-
ucts. The driving force is essentially just pumping en-
ergy back into the system to compensate for the loss
132
Shu Y. and Ou-Yang Z..
FoF1-ATPase STATOR REGULATION STUDIED WITH A RESONANCE MODEL.
DOI: 10.5220/0003753401320137
In Proceedings of the International Conference on Biomedical Electronics and Devices (BIODEVICES-2012), pages 132-137
ISBN: 978-989-8425-91-1
Copyright
c
2012 SCITEPRESS (Science and Technology Publications, Lda.)
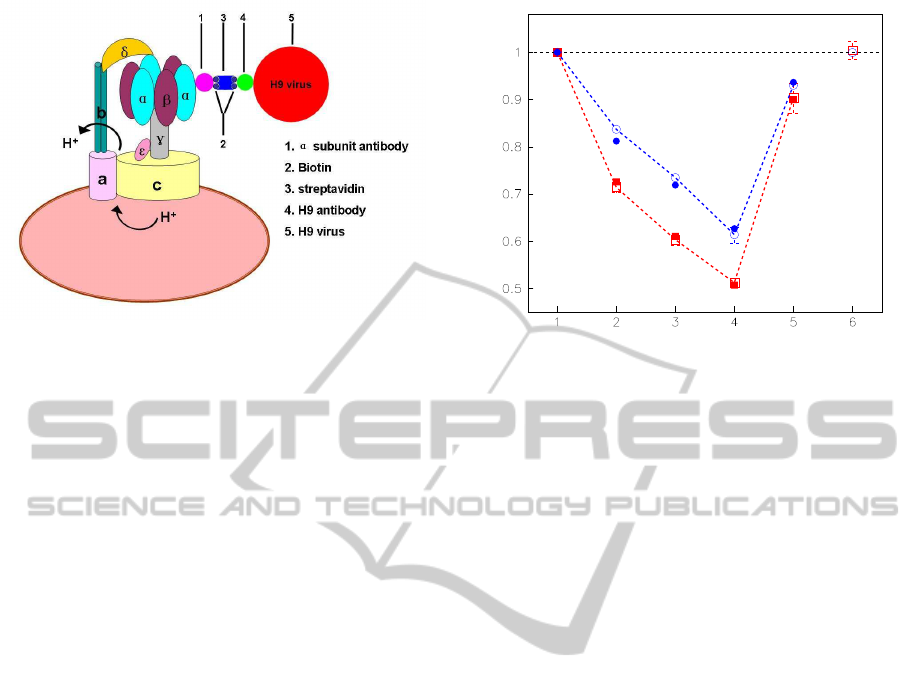
Figure 1: The schematic illustration of the activity regu-
lation assay, showing the experimental geometry (not to
scale). The other two same links are not painted. All the
external links, α antibody, streptavidin, H9 antibody and
H9 virus, are regarded as harmonic oscillators as shown in
Fig.3.
of energy due to ATP synthesis or protons pumping
as well as damping, which is the most efficient way
for motor to work. The rotary speed of motor, which
corresponds to the measurable holoenzyme synthesis
activity, is equal to the resonance frequency of “sta-
tor”.
2 EXPERIMENTAL RESULTS
A series of harmonic oscillators have been designed
to link to the exposed α subunits. The schematic il-
lustration of this activity regulation assay is shown in
Fig.1. F
o
F
1
-ATPase is embedded in a chromatophore,
in which the transmembrane p.m.f is stored. The first
external harmonic oscillator is the α antibody, the sec-
ond one is the streptavidin, the third one is H9 avian
influenza virus (hereafter called H9 virus) antibody
and the fourth one is the H9 virus.
The holoenzyme activity with different links has
been measured as follows: Firstly, each α subunit was
bound by an α antibody, the holoenzyme was inhib-
ited, and the relative synthesis and hydrolysis activity
decreased to 0.71 and 0.84 respectively. Secondly,
the streptavidin was linked to α antibody through a
small biotin, the enzyme was inhibited continuously,
and the relative activities of synthesis and hydroly-
sis declined to 0.60 and 0.73 respectively. Thirdly,
H9 antibody was linked to streptavidin through biotin,
the holoenzyme was inhibited again, and the relative
activities of synthesis and hydrolysis dropped to 0.51
and 0.61 respectively. However,when H9 virus bound
to its antibody finally, the modified enzyme was acti-
vated, and its relative activities jumped to 0.90 and
Relative synthesis /hydrolysis activity
❍: hydrolysis
❑: synthesis
●, ■: Theoretical data
Figure 2: Different activities of enzyme with different links
on α subunit shown in Fig.3. The statistical value (mean ±
s.e.m.) of each system was computed by 50∼60 samples.
The experiment has been repeated independently more than
five times. The native F
o
F
1
-ATPase activity was taken as a
control and others were expressed in proportion to the con-
trol. The solid dots are calculated by Eq.(4).
0.93 respectively. It is very amazing that the activity
of the modified holoenzyme, in which a series of ex-
ternal proteins and virus are linking on “stator”, can
resume to a nativelevel. These results are correspond-
ingly indicated in Fig.2 No. 2, 3, 4 and 5. The activ-
ity of No. 5 is about two times that of No. 4, which
means that the No. 4 complex is a sensitive biosensor
of virus detecting.
To identify whether H9 virus affects F
o
F
1
-ATPase
activity directly, we measured the activity of native
buffer incubated with H9 virus. The result shown in
Fig.2 No.6 has proved that the H9 virus doesn’t have
any direct effect on the holoenzyme activity no matter
the enzyme functions as a synthase or hydrolase.
F
1
hydrolysis activity can be expectably regu-
lated by varying the load on the “rotor”(Yasuda et al.,
1998). With increasing of the length of filament at-
tached on the “rotor”, the damping force will increase,
thereby inhibiting the F
1
hydrolysis activity, which
has been approvingly interpreted by traditional mod-
els(Sun et al., 2004; Xing et al., 2005; Jonathan et al.,
2006). Our experiment has revealed that the holoen-
zyme activity also can be regulated by the external
links on the “stator”. The regulation tendency of syn-
thesis is the same with that of hydrolysis. However, it
is very difficulty for us to understand this regulation
mechanism using traditional model. Here, we intro-
duce the resonance mechanism to statistically illus-
trate these phenomena.
FoF1-ATPase STATOR REGULATION STUDIED WITH A RESONANCE MODEL
133

Figure 3: Resonance model. m
0
, m
1
, m
2
, m
3
and m
4
repre-
sent the inertial mass(Dalton molecular weight ) of α sub-
unit, α antibody, streptavidin, H9 antibody and H9 virus re-
spectively. k
i
is the elastic coefficient of corresponded har-
monic oscillator.
3 RESONANCE MODEL
The “stator” of F
1
motor is a crown with alternat-
ing α and β subunits. Each catalytic site located in
β subunit is at different stage of the enzyme kinetic
cycle: one binds ATP, another binds ADP, and the
third keeps empty. All three sites coordinate for the
next 120
◦
step. The different stage of catalytic site is
tightly coupled to the different conformation of β and
α subunit(Nishizaka et al., 2004; Diez et al., 2004;
Itoh et al., 2004). We define the cyclic conformational
change of α
3
β
3
crown as an oscillation. The oscil-
lations of three α subunits are identical with the ex-
ception of 120
◦
phase. Hence, the activity regulation
assay may be simply cartooned in Fig.3 with one α
subunit. Each link, including α subunit, functions as a
spring with its inertial mass, and is simply regarded as
a harmonic oscillator. Five harmonic oscillators have
constructed five systems. Each harmonic oscillator is
a damped, driven harmonic oscillator. The dynamic
equation of the ith system is
M
¨
X+ KX+ Λ
˙
X = F+ Γ (1)
where
M = I
m
0
.
.
.
m
i
, X =
x
0
.
.
.
x
i
,
K =
k
0
+ k
1
−k
1
0 .. . .. .
−k
1
k
1
+ k
2
−k
2
0
.
.
.
0
.
.
.
.
.
.
.
.
.
0
.
.
. .. . −k
i−1
k
i−1
+ k
i
−k
i
0 .. . .. . −k
i
k
i
,
and
Λ = I
λ
0
.
.
.
λ
i
,F =
f
0
(t)
.
.
.
f
i
(t)
,Γ =
Γ
0
(t)
.
.
.
Γ
i
(t)
.
I is an identity matrix. M
¨
X is the inertial force and
is usually ignored in linear motors motility study due
to overdamping. i = 0,1,2, 3,4 represents α subunit,
α subunit antibody, streptavidin, H9 antibody and H9
virus respectively, the inertial mass, m
i
, is in propor-
tion to its Dalton molecular weight, that is, m
i
∝ 55,
170, 60, 170 and ∞ (KD) for i =0, 1, 2, 3, and 4 re-
spectively, x
i
is the displacement of the ith oscillator.
KX is the restoring force. Λ
˙
X is the damping force.
F is the driving force ( f
i
(t) = 0 for i ≥ 1). Γ is the
random force characterized by a Gaussian distribu-
tion with zero mean (hΓi = 0). The general solution
of Eq.(1) is a sum of a transient solution that depends
on initial conditions, and a steady state one that de-
pends only on driving frequency,driving force, restor-
ing force and damping force. Of course, we only dis-
cuss the latter.
F
o
F
1
motor consists of two rotary motors acting in
opposition: F
1
motor generates a mechanical torque
using the hydrolysis energy of ATP, while F
o
motor
generates a rotary torque in the opposite direction us-
ing a transmembrane p.m.f. When the motor func-
tions as a synthase, the driving force of α subunit,
f
γ
+ (t), is generated by the eccentric rotation of γ sub-
unit that is impelled by the transmembraneproton flux
of chromatophore, whereas the incurred counterforce,
f
Tr
(t), comes of the releasing of ATP in β subunit, the
net driving force then f
0
(t) = f
γ
+ (t) − f
Tr
(t). When
the motor functions as a hydrolase, the driving force
of α subunit, f
Tb
(t), is generated by the binding of
ATP in β subunit, whereas the incurred counterforce,
f
γ
− (t), comes of the transmembrane protons pump-
ing, the net driving force then f
0
(t) = f
Tb
(t)− f
γ
− (t).
At steady state, F
o
F
1
-ATPase converts directly chemi-
cal energy at nearly 100% efficiency(Oster and Wang,
2000; Kinosita et al., 2000) between p.m.f and energy
currency, ATP, which means that motor doesn’t out-
put any mechanical work and dissipates hardly heat
in medium, hence, the net driving force f
0
(t) ≈ 0.
Resonance is the tendency of a system to oscil-
late with the maximum amplitude at a certain fre-
BIODEVICES 2012 - International Conference on Biomedical Electronics and Devices
134

k
1
/k
–
0
P
G
(k
1
)
k
2
/k
–
0
P
G
(k
2
)
k
3
/k
–
0
P
G
(k
3
)
k
4
/k
–
0
P
G
(k
4
)
<ω
1
>=0.73
<ω
0
>=1.0
P
0
(<ω
0
>)
<ω
0/1
>
P
1
(<ω
1
>)
<ω
2
>=0.61
<ω
2
>
P
2
(<ω
2
>)
<ω
3
>=0.51
<ω
3
>
P
3
(<ω
3
>)
<ω
4
>=0.90
<ω
4
>
P
4
(<ω
4
>)
Figure 4: Right: Distribution of time average resonance fre-
quency. The ensemble statistic average value is calculated
by Eq.(3).Left: Distribution of elastic coefficient. All of
them are assumed Gaussian distribution. The fitted aver-
age values k
i
/
¯
k
0
= 0.35, 0.13, 0.06 and 8 for i = 1,2,3,4
respectively. The standard deviation, σ
i
, is not sensitive
to the average value. Here, σ
i
/
¯
k
0
=0.1, 0.04, 0.02 and 0.3
for i = 1,2,3,4 respectively, and σ
0
/
hω
0
i=0.3 for P
0
(hω
0
i).
¯
k
0
≡ m
0
hω
0
i
2
.
quency. At this resonance frequency, even small pe-
riodic driving force can produce large amplitude vi-
bration because the system stores vibrational energy.
When damping is small, the resonance frequency is
approximately equal to the natural frequency of the
system(Ogata, 2004). So, if we only consider the
time average resonance frequency of the ith system
at steady state for small damping, Eq.(1) may be sim-
plified into
Mh
¨
Xi = −KhXi (2)
where h·i means time average value. Eq.(2) can be
used to determine the distribution of the time average
resonance frequency of ith system, P
i
(hω
i
i), if that of
native holoenzyme, P
0
(hω
0
i), has been given. Con-
sidering the diversity of motors and external links, we
assume hω
0
i and all k
i
(i ≥ 1) are Gaussian distribu-
tion as inserted in right top and shown in the left row
of Fig.4. The right row of Fig.4 is the corresponding
P
i
(hω
i
i). The system that comprises n harmonic oscil-
lators in series possesses n natural frequencies, that is,
motor has n frequencies to match for resonance. The
frequency spectrum indicated in Fig.4 can be directly
tested by a mass of single molecule experiments. The
ensemble averageresonance frequency of α
3
β
3
crown
is equal to the average holoenzyme activity. For sim-
plest, we consider that motor equiprobably matches
every resonance frequency, the ensemble statistic time
average resonance frequency of ith system can be cal-
culated statistically by
hω
i
i =
Z
...
Z Z
P
i
(hω
i
i)hω
i
idhω
i
idk
1
...dk
i
(3)
Systematic kinetics study of F
o
F
1
-ATPase(Shu
and Lai, 2008) has derived the formula of saturated
rotary speed. The rates of ATP synthesis and hydrol-
ysis have been given by
v
s
i
= 3k
−
i,T
, v
h
i
=
3k
−
i,D
k
−
i,P
k
−
i,D
+ k
−
i,P
respectively, where k
−
i,
is the releasing rate of corre-
sponding product, and T, D and P represent ATP, ADP
and phosphate respectively. Because phosphate is too
small to be blocked in the catalytic cleft, we consider
that the releasing rate of phosphate, k
−
i,P
, doesn’t rely
on the conformation of β subunit and is constant, k
−
P
.
The releasing of ATP(ADP) is tightly coupled to the
conformational change of β subunit because the size
of ATP(ADP) can be compared with the size of cat-
alytic cleft, that is, k
−
i,T
(k
−
i,D
) =
hω
i
i/2π. The relative
synthesis and hydrolysis activities are defined as
ρ
s
i
≡
v
s
i
v
s
0
=
hω
i
i
hω
0
i
, ρ
h
i
≡
v
h
i
v
h
0
= ρ
s
i
1+ b
ρ
s
i
+ b
(4)
respectively, where b ≡ k
−
P
/(
hω
0
i/2π). Eq.(4) pre-
dicts that ρ
h
i
> ρ
s
i
if ρ
s
i
< 1 as indicated in Fig.2, oth-
erwise, ρ
h
i
< ρ
s
i
which has also been demonstrated by
our recent experiment with links on β subunit. The
fitted b = 1.58, a reasonable value.
4 DISCUSSIONS
Different from previous activity regulation as-
says(Yasuda et al., 1998; P¨anke and Rumberg, 1996;
Turina et al., 2003; Diez et al., 2004; Steigmiller et al.,
2008; Itoh et al., 2004), our regulation based on the
stator links. The external links not only inhibit the en-
zyme but also resume it, and the regulation tendency
of synthesis is the same with that of hydrolysis. It is
very difficulty for power stroke model(Wang and Os-
ter, 1998) to interpret this regulation mechanism. The
FoF1-ATPase STATOR REGULATION STUDIED WITH A RESONANCE MODEL
135

resonance mechanism, however, has satisfactorily il-
lustrated these phenomena. Each external link serves
as a harmonic oscillator. The more oscillators are
linked in series, the more resonance frequencies may
be selected. If the system does in a resonance fash-
ion, the motor works in a most efficient way. Here,
we consider that motor will equiprobably match ev-
ery resonance frequency. The average resonance fre-
quency is statistically equal to the ensemble experi-
mental activity. Actually, the lowest resonance fre-
quency will be closer and closer to zero with adding
of oscillator or the increasing of inertial mass. How-
ever, it is impossible for F
1
motor to stop in virtue
of the driving of F
o
or binding of ATP. This lowest
frequency that is close to zero has to be cancelled in
statistics and the average resonance frequency then
will jump. This is one of reasons that the value of
No.5 is higher than that of No.4 in Fig.2. The criti-
cal lowest resonance frequency is waiting to be deter-
mined by further experiments. Our novel resonance
model together with systematic kinetics study(Shu
and Lai, 2008) has predicted that the relative activity
of hydrolysis is higher(lower) than that of synthesis if
the latter is less(higher) than 1, which has been exper-
imentally demonstrated.
The frequencyspectrum indicated in Fig.4 is wait-
ing to be tested by a mass of single molecule experi-
ments. If there is enough single molecule experimen-
tal data, we can firstly confirm whether the distribu-
tion of activity of single motor is the same with that of
our model. Secondly, we can affirm whether the mo-
tor equiprobably matches every resonance frequency
or not. Finally, we can estimate the standard devia-
tion, σ
i
, for each Gaussian distribution. Here, for sim-
plest, we consider that motor equiprobably matches
every resonance frequency. The fitted elastic coeffi-
cient can be used to estimate the elasticity of linking
protein. It seems reasonable that k
4
is much higher
than others in view of the stiff capsid of H9 virus.
The fitted rate of P
i
releasing is also logical because
it is higher than
hω
0
i/2π.
It is clear that the mechanical movement of F
1
comprises the eccentric rotation of γ subunit and the
conformational change of the α
3
β
3
crown, and they
are tightly coupled with each other. However, pre-
vious theoretical study only focus on the rotation of
γ subunit. In fact, the conformational change of the
α
3
β
3
crown is very important for the entire motor,
and plays an active role in hydrolysis. On the other
hand, the role that α subunit plays in the conforma-
tional change of the α
3
β
3
crown has not been studied
although the structure of α subunit resembles that of β
subunit with the exception of catalytic site. This work
is try to investigate what α subunit functions in the
rotary motor and has expanded the “binding change
mechanism”.
In contrast with Langevin equation that ignores
the inertial force due to overdamping, our resonance
model does neglect the damping force because the en-
tire motor doesn’t output any mechanical work and
dissipates hardly heat in medium. Additionally, the
scale of conformational change of the α
3
β
3
crown is
very small, thereby the average velocity of oscilla-
tion is so low that λ
i
h ˙x
i
i ≪ m
i
h ¨x
i
i, which is possi-
ble although the values have not been estimated. It
should be noted that the elastic coefficient is indepen-
dent of the additional links. Although the elastic co-
efficient can in fact depend on the additional links due
to electrostatic interaction, in the simplest version of
the model, we assume that all elastic coefficients are
links-independent.
ACKNOWLEDGEMENTS
This work is partially supported by the NSFC grant
No.91027045 and No.11075015, and the National
Basic Research Program of China (973 Program) un-
der the grant No. 2007CB935903.
REFERENCES
Abrahams, J. P., Leslie, A. G. W., Lutter, R., and Walker,
J. E. (1994). Structure at 2.8˚a resolution of F
1
-
ATPase from bovine heart mitochondria. Nature,
370:621–628.
Ballmoos, C. V., Cook, G. M., and Dimroth, P. (2008).
Unique rotary ATP synthase and its biological diver-
sity. Annu. Rev. Biophys., 37:43–64.
Boyer, P. D. (1993). The binding change mechanism
for ATP synthase-some probabilities and possibilities.
Biochim. Biophys. Acta., 1140:215–250.
Boyer, P. D. (1997). The ATP synthase-a splendid molecu-
lar machine. Annu. Rev. Biochem., 66:717–749.
Cheng, J., Zhang, X. A., Shu, Y. G., and Yue, J. C. (2010).
F
o
F
1
-ATPase activity regulated by external links on β
subunits. Biochem. Biophys. Res. Commun., 391:182–
186.
Diez, M., Zimmermann, B., B¨orsch, M., K¨onig, M.,
Schweinberger, E., Steigmiller, S., Reuter, R.,
Felekyan, S., Kudryavtsev, V., Seidel, C. A. M., and
Gr¨aber, P. (2004). Proton-powered subunit rotation
in single membrane-bound F
o
F
1
-ATP synthase. Nat.
Struct. Mol. Biol., 11:135–141.
Itoh, H., Takahashi, A., Adachi, K., Noji, H., Yasuda,
R., Yoshida, M., and Jr, K. K. (2004). Mechani-
cally driven ATP synthesis by F
1
-ATPase. Nature,
427:465–468.
BIODEVICES 2012 - International Conference on Biomedical Electronics and Devices
136

Jonathan, L. E., Chakraborty, A. K., and Oster, G. (2006).
Simple models for extracting mechanical work from
the ATP hydrolysis cycle. Biophys. J., 90:4281–4294.
Junge, W. (2004). Protons, proteins and ATP. Photosynthe-
sis Res., 80:197–221.
Kargovsky, A. V., Romanovsky, Y. M., and Tikhonov, A. N.
(2009). F
1
-ATPase as an auto-oscillatory system. Bio-
physics, 54:1–7.
Kinosita, J. K., Yasuda, R., Noji, H., and Adachi, K. (2000).
A rotary molecular motor that can work at near 100%
efficiency. Phil. Trans. R. Soc. Lond. B, 355:473–489.
Kinosita, K. J., Adachi, K., and Itoh, H. (2004). Rotation
of F
1
-ATPase: How an ATP-driven molecular ma-
chine may work. Annu. Rev. Biophys. Biomol. Struct.,
33:245–268.
Leslie, A. G. W. and Walker, J. E. (2000). Structural model
of F
1
-ATPase and the implications for rotary catalysis.
Phil. Trans. R. Soc. Lond. B, 355:465–472.
Nakamoto, R. K., Scanlon, J. A. B., and Al-Shawi, M. K.
(2008). The rotary mechanism of the ATP synthase.
Arch. Biochem. Biophys., 476:43–50.
Nishizaka, T., Oiwa, K., Noji, H., Kimura, S., Muneyuki,
E., Yoshida, M., and Jr, K. K. (2004). Chemomechan-
ical coupling in F
1
-ATPase revealed by simultaneous
observation of nucleotide kinetics and rotation. Nat.
Struct. Mol. Biol., 11:142–148.
Noji, H., Yasuda, R., Yoshida, M., and Kinosita, K. (1997).
Direct observation of the rotation of F
1
-ATPase. Na-
ture, 386:299–302.
Ogata, K. (2004). System Dynamics. University of Min-
nesota, Minnesota, 4th edition.
Oster, G. and Wang, H. (2000). Why is the efficiency of
the F
1
ATPase so high? J. Bioenerg. Biomembr.,
332:459–469.
P¨anke, O. and Rumberg, B. (1996). Kinetic modelling of
the proton translocating CF
o
CF
1
-ATP synthase from
spinach. FEBS Lett., 383:196–200.
Shu, Y. G. and Lai, P. Y. (2008). Systematic kinetics study
of F
o
F
1
-ATPase. J. Phys. Chem. B, 112:13453–13459.
Shu, Y. G., Yue, J. C., and Ou-Yang, Z. C. (2010). F
o
F
1
-
ATPase, rotary motor and biosensor. Nanoscale,
2:1284–1293.
Steigmiller, S., Turina, P., and Gr¨aber, P. (2008). The ther-
modynamic H
+
/ATP ratios of the H
+
-ATPsynthases
from chloroplasts and Escherichia coli. Proc. Natl.
Acad. Sci. USA, 105:3745–3750.
Sun, S. X., Wang, H., and Oster, G. (2004). Asymmetry
in the F
1
-ATPas and its implications for the rotational
cycle. Biophys. J., 86:1373–1384.
Turina, P., Samoray, D., and Gr¨aber, P. (2003). H
+
/ATP
ratio of proton transport-coupled ATP synthesis and
hydrolysis catalysed by CF
o
CF
1
-liposomes. EMBO
J., 22:418–426.
W¨achter, A., Bi, Y. M., Dunn, S. D., Cain, B. D., Sielaff,
H., Wintermann, F., Engelbrecht, S., and Junge, W.
(2011). Two rotary motors in F-ATP synthase are
elastically coupled by a flexible rotor and a stiff sta-
tor stalk. Proc. Natl. Acad. Sci. USA, 108:3924–3929.
Wang, H. and Oster, G. (1998). Energy transduction in the
F
1
motor of ATP synthase. Nature, 396:279–282.
Weber, J. and Senior, A. E. (2003). ATP synthesis driven by
proton transport in F
1
F
0
-ATP synthase. FEBS Lett.,
545:61–70.
Wilkens, S. (2005). Rotary molecular motors. Adv. Protein
Chem., 71:345–382.
Xing, J., Liao, J. C., and Oster, G. (2005). Making ATP.
Proc. Natl. Acad. Sci. USA, 102:16539–16546.
Yasuda, Y., Noji, H., Kinosita, K., and Yoshida, M. (1998).
F
1
-ATPase is a highly efficient molecular motor that
rotates with discrete 120
◦
steps. Cell, 93:1117–1124.
FoF1-ATPase STATOR REGULATION STUDIED WITH A RESONANCE MODEL
137
