SEEKING AND AVOIDING COLLISIONS

A Biologically Plausible Approach

M. A. J. Bourassa and N. Abdellaoui

Defence Research and Development Canada Ottawa, 3701 Carling Ave., Ottawa, Ontario, K1A 0Z4, Canada

Keywords:

Agent models, Collision avoidance, Proportional navigation.

Abstract:

The success of an agent model that incorporates a hierarchical structure of needs, required that the needs

trigger human-like actions such as collision avoidance. This paper demonstrates a minimalist, “rule-of-thumb”

collision avoidance approach that performs well in dynamic, obstacle-cluttered domains. The algorithm relies

only on the range, range rate, bearing, and bearing rate of a target perceived by an agent. Computation is

minimal and the approach yields a natural behaviour suitable for robotic or computer generated agents in

games.

1 INTRODUCTION

An agent architecture based on Maslow’s Hierar-

chy of Needs (Maslow, 1943), was introduced by

Bourassa et al.(Bourassa et al., 2011) as a possible ap-

proach to obtaining more human-like behaviour from

computer-generated characters. The approach was in-

spired by the belief that purely reactive agents that

populate many games cannot display human like be-

haviour because they lack a basic human trait: moti-

vation.

To varying degrees, human behaviour is modu-

lated by motivating factors other than a stated goal or

rules. An agent model should therefore incorporate

some aspect of motivation.

Maslow proposed a theory of human motiva-

tion (Maslow, 1943) that was human-centered and

founded on the integrated wholeness of the organism

and goals as opposed to drives. It was postulated that

humans possessed a hierarchy of needs. The most ba-

sic needs were physiological: food, drink, rest, etc.

As these needs are satisﬁed, other needs emerge suc-

cessively: safety, love, esteem, and self-actualisation.

Figure 1 illustrates a proposed agent model incorpo-

rating Maslow’s Hierarchy of Needs. A more detailed

illustration of the concept of agent needs is provided

in Figure 2. A one-to-one correspondence must be

established between the needs in Maslow’s Hierarchy

and equivalents for a generic agent hierarchy with the

nature of the agent being the guiding factor. For ex-

ample, human hunger and thirst may correspond to

fuel and lubricant levels in a robotic agent but to “en-

Figure 1: A proposed agent model based on Maslow’s Hi-

erarchy of Needs. The agent has sensors and a world model

for two environments: internal and external. The agent’s

actions are decided upon by the fulﬁllment of its needs (see

text).

ergy level” in a computer generated character in a

video game.

Each level in the hierarchy is comprised of several

individual needs. Each need is represented by a goal

and utility. Goals are common to all needs and levels,

and map a need to an action. Utilities are unique to

each need and provide a model of a need that maps

to a level of satisfaction that, in turn, modulates the

action mapped to a goal.

In the simplest implementation of the preceding

agent model, any action taken is in response to the

lowest unsatisﬁed need. The model provides human-

like decisions. The actions themselves, however,must

be human-like if a credible semblance of human be-

haviour is desired. This paper therefore focuses on

creating human-like behaviour for one action. This

240

A. J. Bourassa M. and Abdellaoui N..

SEEKING AND AVOIDING COLLISIONS - A Biologically Plausible Approach.

DOI: 10.5220/0003753602400245

In Proceedings of the 4th International Conference on Agents and Artiﬁcial Intelligence (ICAART-2012), pages 240-245

ISBN: 978-989-8425-96-6

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

Figure 2: The proposed Agent’s Hierarchy of Needs. The

lowest unmet needs in the pyramid are the highest motiva-

tors. Each need is associated with a goal and utility.

paper addresses one aspect of the lowest level of

Maslow’s Hierarchy, the Physiological Needs invok-

ing the action of collision avoidance. The implemen-

tation of collision avoidance is fundamental to artiﬁ-

cial organisms such as non-player characters (NPC’s)

in computer games and simulations. Collision avoid-

ance is currently implemented either by using exten-

sive geometric algorithms or very simplistic and ﬁxed

sets of rules (Millington, 2006). The result is colli-

sion avoidance at the cost of predictable, mechanistic

behaviour.

In this paper, an algorithm for collision avoidance

for mobile autonomous agents is deﬁned based on

principles known to be employed in nature. A known

biological technique for collision avoidance, Constant

Bearing Decreasing Range (CBDR) is explored to

fulﬁl two purposes: collision avoidance and its con-

verse, intercept. Taking a theoretical approach cen-

tred on the agent instead of the more traditional abso-

lute reference system (Shneydor, 1998), gives insight

into rules-of-thumbfor both interception and collision

avoidance. The rules-of-thumb yield a simply imple-

mented natural behaviour, not necessarily an optimal

solution. The goal is for error-tolerant, not error-free,

behaviour. The rules do not depend on assumptions

of predictable behaviour by the targets or obstacles,

making them ideal for dynamic environments.

2 PROPORTIONAL NAVIGATION

The principle of CBDR states that a collision will oc-

cur with any object that: remains on a steady bearing

relative to one’s own direction of motion and has a

range that is decreasing. The principle is the founda-

tion of parallel, or proportional, navigation (PN). PN

Figure 3: Guided by an observer at O, The agent begins at

O and attempts to intercept T by maintaining a course along

the LOS (dashed line).

is used in missile guidance, by predators in the animal

world (Ghose et al., 2009), and by humans for driving

or catching balls (Shneydor, 1998).

Figure 3 shows a common representation of the in-

tercept problem. Assume a planar engagement where

a moving missile (agent or robot), A, seeks to inter-

cept a moving target (or goal), T. The angle, λ, is the

line-of-sight (LOS) between the agent and target mea-

sured with respect to the reference. θ is known as the

lead angle of the agent, while δ is the path angle of

the target.

Simplifying assumptions to facilitate an intercept

solution are that the target moves at constant speed in

a known direction. Successful interception can only

occur when the agent adjusts course to remain on the

LOS and overtakes the target. Naturally, as the target

moves, λ changes and so the agent must adjust its path

angle, θ+ λ, in order to remain on the LOS.

LOS navigation is applicable in a situation where

robot guidance is remotely provided by an observer.

In this sense, it is a “three-point” guidance scheme ap-

propriate for, say, radio controlled robots. The agents

of interest for this paper react autonomously to their

sensor inputs. In this sense, they have a “two-point”

guidance scheme.

An autonomous agent does not have third-party

guidance so the relative motion between the agent and

an object with which it may collide, is the most im-

portant measure. One reason why a self-referential

view is more valid for an autonomous agent is that an

absolute reference may not always be available nor

relevant. For example, a third-party observer may

not have complete information of both agent and tar-

get due to an obstruction. Second, agent sensors op-

erate relative to the agent and so inherently provide

such information. The translation of the principles of

LOS guidance to a two-point guidance scheme is de-

picted in Figure 4. An agent “A” (green) and a target

SEEKING AND AVOIDING COLLISIONS - A Biologically Plausible Approach

241

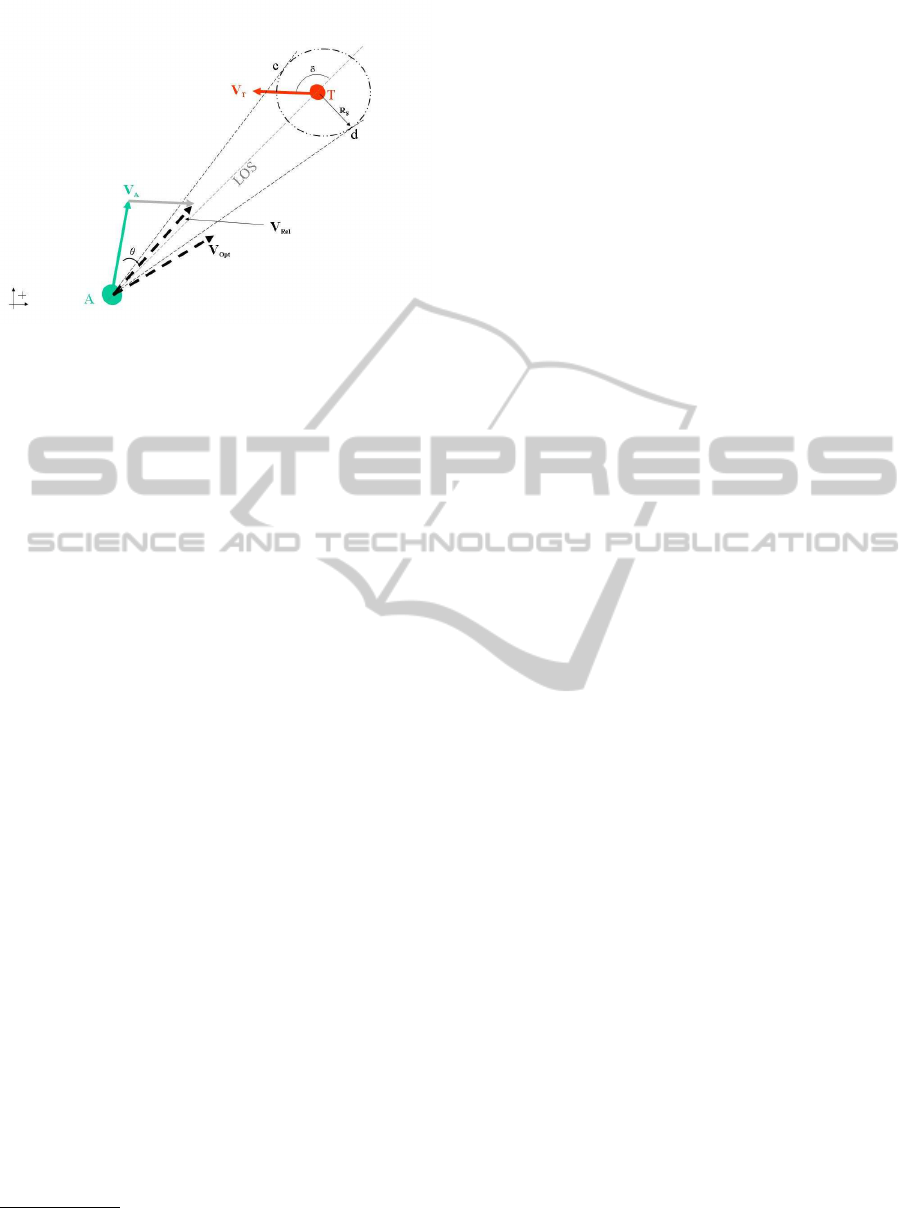
Figure 4: A simple system of typical variables for a col-

lision avoidance or interception in a rotating frame of co-

ordinates. For Proportional Navigation, all variables are

assumed to be known hence it is possible to calculate the

relative velocity, V

Rel

, and seek an optimal desired velocity,

Opt

,that lies outside the collision cone (△

Acd

“T” (red) are shown in an arbitrary dynamic relation-

ship similar to that of Figure 3. The agent is moving

with velocity V

and the target with velocity V

. The

agent attempts to maintain the LOS at an angle θ to

achieve interception of the target. An optimal solu-

tion is possible under the assumption of perfect infor-

mation.(Shneydor,1998)

Collision avoidance is the opposite of interception

where a change of θ is induced in order to avoid in-

terception. The relative velocity is determined and,

if it lies within the “collision cone”

, a lateral accel-

eration is provided to redirect the vector outside the

cone, V

Opt

The “proportional” in PN is that to effect a change

of relative velocity, the agent induces a lateral ac-

celeration proportional to the rate of change of θ.

Therefore the classical solution for PN guidance (also

known as True PN (Shneydor, 1998)) is:

= −KV

θ (1)

where K is the navigation constant. Explicit values

for K can be found when constraints are put on target

manoeuvrability and velocity, otherwise one can con-

sider it an arbitrary constant. There are several slight

variants on the equation.(Shneydor, 1998; Zarchan,

1994)

3 PROBLEM OUTLINE

PN can be applied to collision avoidance by revers-

The collision cone is a triangle deﬁned by the position

of the agent (vertex) and the points of intersection of two

lines tangent to a circle representing a “safe” radius, R

about the target.

ing the guidance laws that apply for intercept, that

is, inducing

θ to generate a miss. It is typically as-

sumed an agent/robot will be in an intercept (some-

times referred to as “navigation”) mode while pro-

ceeding to a goal and then will switch to a collision

avoidance mode in the presence of obstacles meeting

some criteria. The principal challenges in using PN

have been: dynamic and/or multiple obstacles/targets

and high computational demands.

With the exception of Menon’s work on missile

guidance using fuzzy PN (Menon and Iragavarapu,

1998), approaches to robotic navigation assume: that

precise information is available to the agent, that com-

putational demands can be met, and/or that simplify-

ing assumptions of target motion are valid. These are

reasonable assumptions for aircraft (manned or oth-

erwise) with sophisticated sensor suites, but not for

small or more poorly equipped vehicles. Biological

organisms are unlikely to have such perfect knowl-

edge of targets. In this paper the following assump-

tions are made:

• target range, bearing, range rate (V

), and the

bearing rate (

θ) are known within an error;

• target aspect and velocity are unknown and no as-

sumptions are made on either; and

• lateral acceleration is not applied explicitly but

indirectly through either a change in velocity or

bearing.

These assumptions are biologically plausible and

sufﬁcient to allow a robust version of proportional

navigation.

4 RULES-OF-THUMB

In Figure 5, the geometry of the guidance problem is

recast to a purely agent-centric point of view. In such

a framework, proportional navigation distills to bal-

ancing the velocities of the agent and the target that

are perpendicular to the LOS (essentially the intent

of True Proportional Navigation or TPN (Shneydor,

1998)). Additionally, no assumptions are made, or re-

quired, about target behaviour, orientation, or veloc-

ities. Since the velocities perpendicular to the LOS

of the agent and target must remain equal for inter-

ception to occur, the agent must ﬁrst detect when the

velocities are not equal and then apply some means

of compensation. The challenge is that V

, and hence

T⊥

, is not known.

In the ﬁrst case, the agent needs to assess whether

there is a change in bearing angle,

θ > 0, or range,

> 0. This mandates that the agent have at least

two consecutive “looks” at the target to obtain rate

ICAART 2012 - International Conference on Agents and Artificial Intelligence

242

Figure 5: In this simple system, guidance is considered

within a agent-centric frame of reference. A line-of-sight

(LOS) between an agent (A) and target (T) is deﬁned with

respect to an agent’s heading. From this point-of-view, a

collision will occur if the velocity components perpendic-

ular to the LOS remain equal and the parallel components

sum to a positive value.

information. This will provide instantaneous rates of

change for both bearing and range.

In the second case, one must identify what options

there are for an agent to effect a change in V

A⊥

. The

following expresses the rate of change of the perpen-

dicular velocity in terms of agent heading and veloc-

ity.

A⊥

= V

· sinθ

A⊥

· sinθ+ V

· cosθ·

θ (2)

Changes to V

A⊥

can be effected by varying agent ve-

locity or applying a change of heading. The equation

(2) highlights the inﬂuence of the magnitude of θ. At

θ ∼ 90 degrees, the sinθ term dominates, while at an-

gles nearer to 0 or 180 degrees, the cosθ term domi-

nates. This implies that at times, changes in V

have

more effect on V

A⊥

while at others, changes in head-

ing have a greater effect. When combined with PN

principles, this insight yields simple rules-of-thumb

that can be used by an agent to produce a very natural

behaviour for collision avoidance and interception.

A ﬁrst rule-of-thumb is the CBDR:

• A constant LOS bearing and closing velocity

indicate a collision is imminent.

This rule is the one that precipitates one of two

courses of action. In a collision avoidance mode, this

rule will signal that inducing a change in LOS bearing

is required. If the desired action is interception, then

this rule signals that no further changes are required

to the agent’s current state.

Other rules-of-thumb derived from Equation 2

are:

• If the LOS bearing is changing, and the

instantaneous LOS bearing is small (0

◦

≤

θ << 45

◦

), compensate by changing head-

ing.

• If the LOS bearing is changing, and the in-

stantaneous LOS bearing is large (45

◦

θ ≤ 90

◦

), compensate by changing velocity.

• If the LOS bearing is changing, and the in-

stantaneous LOS bearing is approximately

◦

, either a change in heading or change

in bearing will sufﬁce. The deciding factor

would be whether the agent has the energy

or ability to increase V

A less obvious rule that governs which direction to

turn to change heading is:

• For intercept: adjust heading in the same di-

rection as the bearing rate change. Do the

opposite for collision avoidance.

This means that for interception an agent will steer

in direction to minimize

θ while for collision avoid-

ance, the intent is the opposite. This appears counter-

intuitive as it will mean that collision avoidance will

require possibly brieﬂy steering towards the target’s

general direction.

In all cases, Equation 1to determine the magnitude

of bearing and velocity changes is used.

5 IMPLEMENTATION AND

RESULTS

The agent model (Figure 1) is destined to be used

in the OneSAF (Systems, 1998) and other Computer

Generated Forces (CGF) environments (Bourassa

et al., 2011). A simpler platform was used for algo-

rithm development consisting of Netlogo (Tisue and

Wilensky, 2004) and the R Programming Language

(R Development Core Team, 2011).

Netlogo is a 2-D, multi-agent, programmable

modeling platform used to create agents, render the

agent environment, and run simulations. It provides,

and manages, agent sensors and agent interactions.

Netlogo does not have a full suite of computational

libraries and so, in anticipation of future work, the R

Programming Language was coupled to Netlogo via

an extension (Thiele and Grimm, 2010). The rules

were then coded in R scripts and called by the agents

in the Netlogo environment.

A multi-agent environment was created with 2-30

agents each with a different initial course and speed.

The agents were divided into two groups with each

group having a goal that ensured that the groups must

SEEKING AND AVOIDING COLLISIONS - A Biologically Plausible Approach

243

cross paths enroute to their respective goals as well as

avoid ﬁxed obstacles. Each agent was programmed:

• to proceed towards its goal (intercept using equa-

tion 1) unless there were other agents or obstacles

within sensor range;

• if other agents or obstacles were within sensor

range, assess whether the nearest represented a

collision danger; and

• apply rules for collision avoidance (the negative

of equations 1).

The assessment of collision danger followed the ﬁrst

rule of thumb. The nature of the Netlogo environ-

ment meant that bearing rates of zero could not oc-

cur. Implementation of the rule was done with vari-

ous threshold values for bearing rate over a range of

±0.2− 1.0.

Each agent had a “vision cone” and val-

ues of ±10

◦

to ±90

◦

were tried. These values were

chosen as roughly comparable to human vision. Ad-

ditionally, 10% Gaussian noise was added to all mea-

surements meaning that all agents operated with im-

perfect information as might be expected in a biologi-

cal organism. Finally, each agent had a maximum im-

posed on speed, acceleration, and bearing rate. These

substituted for factors such as turning-rate or vehicle

dynamics.

Figure 6 illustrates a simple collision scenario in-

volving six agents. Each of the maneuvering agents

has altered course to steer behind an oncoming agent.

Note that this involved no path planning nor was any

perfect information available to any agent about other

agents. The agents were further challenged with less

linear motion by introducing ﬁxed obstacles. This

caused agent movement to be nonlinear and unpre-

dictable. Figure 7 shows agents threading their way

past obstacles and other agents while proceeding to

goals far above and far to the right of the screen cap-

ture. The algorithm called for intercept of the goal

in the absence of obstacles thus the agents altered be-

tween goal-seeking and collision avoidance. Finally,

a more congested view shown in Figure 8 shows more

intricate manoeuvering as well as the challenges of a

simulated environment. Here fourteen agents pursue

distant goals. The centre-most agent has threaded its

way effectively past an obstacle and a green agent.

The top, left-most agent has collided with a ﬁxed ob-

stacle but this was an artifact of the way the environ-

ment is implemented in Netlogo.

This was one of several “tweaks” of the algorithm im-

posed by the nature of the simulation environment used.

Another was that the division of the “world” in to patches

introduces artifacts into sensor performance.

Figure 6: Netlogo screen capture of six agents exercising

pure collision avoidance. Each of the maneuvering agents

altered course to steer behind an oncoming agent. No path

planning was involved. No information of the interfering

agents was provided except noisy range and bearing (see

text).

Figure 7: Netlogo screen capture of six agents exercising

collision avoidance while proceeding to intercept goals far

to the right and above the screen capture. Again no path

planning was involved and no perfect information was avail-

able. Agent vision was restricted to a 180

◦

cone centred on

the agents heading, with a radius of 15 patches.

6 DISCUSSION AND INSIGHTS

The results of the experiments were successful. De-

spite the simplicity of the algorithms, the behaviour of

the agents was natural. For example, agents slowed

down at times to allow others to pass, or steered

around agents that they overtook. Success with de-

graded sensor information highlighted that the algo-

rithm is not dependent on high quality or perfect in-

formation.

Collisions did occur but this should be viewed

in perspective. In the biological world, there are no

guarantees of interception nor collision avoidance. A

cheetah, for instance, is successful in chasing down

prey only 50% of the time (O’Brien et al., 1986) de-

spite an often signiﬁcant speed advantage; a manoeu-

vering target is a difﬁcult intercept challenge. Sim-

ICAART 2012 - International Conference on Agents and Artificial Intelligence

244

Figure 8: Netlogo screen capture of fourteen agents exercis-

ing collision avoidance while proceeding to intercept goals

far to the right and above the screen capture. Note the com-

plex manoeuvering of the centre-most red agent.

ilarly, despite rigorous control of airspace and ship-

ping lanes, collisions do occur. The strength of the

algorithm is in: its simplicity, its applicability without

assumptions or excessive computation, and its robust-

ness to noise.

Target range and bearing rates can be combined

with known agent information to derive information

about the sensed environment, with simple sensors,

and without requiring global knowledge. For exam-

ple, if T were a stationary object and A were on a

ﬁxed course and speed for severaltime iterations, then

T’s motion is entirely predictable, that is: it will pro-

ceed on a course parallel to A’s heading, and it’s range

rate will behave according to −V

cosθ. An even sim-

pler characterization, useful for formation movement,

is that any target maintaining the same distance and

bearing,

θ = 0 andV

= 0, is moving at the same speed

and heading as the agent.

7 CONCLUSIONS

To satisfy the requirements for an agent model based

on motivation, a collision avoidance and interception

algorithm was developed using principles known to

be used by biological organisms. The algorithm used

basic target information obtainable by simple sensors:

range, bearing, range rate, and bearing rate. The

strength of the approach is that it is simple, robust

to noise, computationally undemanding, and biologi-

cally plausible. Its implementation is feasible in real

time, for real-world platforms with simple sensors.

An additional useful insight was the use of range rate

and bearing rate to characterize objects detected in the

environment.

This work is considered a proof-of-concept and

follow-on work in progress includes: using fuzzy

logic for rule implementation, implementation in the

OneSAF CGF, and an implementation in a mobile

robotic platform.

REFERENCES

Bourassa, M., Abdellaoui, N., and Parkinson, G. (2011).

Agent-based computer-generated-forces’ behaviour

improvement. In ICAART (2), pages 273–280.

Ghose, K., Triblehorn, J. D., Bohn, K., Yager, D. D., and

Moss, C. F. (2009). Behavioral responses of big brown

bats to dives by praying mantises. Journal of Experi-

mental Biology, 212:693–703.

Maslow, A. (1943). A theory of human motivation. Psy-

chological Review, 50:370–396.

Menon, P. and Iragavarapu, V. (1998). Blended hom-

ing guidance law using fuzzy logic. In AIAA Guid-

ance, Navigation and Control Conference, pages 1–

13, Boston, MA.

Millington, I. (2006). Artiﬁcial Intelligence for Games (The

Morgan Kaufmann Series in Interactive 3D Technol-

ogy). Morgan Kaufmann Publishers Inc., San Fran-

cisco, CA, USA.

O’Brien, S., Wildt, D., and Bush, M. (1986). The cheetah

in genetic peril. Scientiﬁc American, 254:6876.

R Development Core Team (2011). R: A Language and

Environment for Statistical Computing. R Foundation

for Statistical Computing, Vienna, Austria. ISBN 3-

900051-07-0.

Shneydor, N. (1998). Missile Guidance and Pursuit: Kine-

matics, Dynamics and Control. Horwood Series

in Engineering Science. Horwood Publishing Chich-

ester.

Systems, L. M. I. (1998). One-saf testbed baseline assess-

ment: Final report. Advanced distributed simulation

technology ii, Lockeed Martin Corporation. Commis-

sioned Report for NAWCTSD/STRICOM ADST-II-

CDRL-ONESAF-9800101.

Thiele, J. and Grimm, V. (2010). Netlogo meets r: Linking

agent-based models with a toolbox for their analysis.

Environmental Modelling and Software, 25(8):972 –

974.

Tisue, S. and Wilensky, U. (2004). Netlogo: A simple envi-

ronment for modeling complexity. In in International

Conference on Complex Systems, pages 16–21.

Zarchan, P. (1994). Tactical and Strategic Missile Guid-

ance, volume 157 - Progress in Astronautics and

Aeronautics of AIAA Tactical Misslie Series. Amer-

ican Institute of Aeronautics and Astronautics, Inc.,

2nd edition.

SEEKING AND AVOIDING COLLISIONS - A Biologically Plausible Approach

245