STRATEGIES FOR CHALLENGING TWO-PLAYER GAMES

Some Lessons from Iterated Traveler’s Dilemma

Predrag T. To

and Philip C. Dasler

1,2

Department of Computer Science, University of Houston, Houston, Texas, U.S.A.

Department of Computer Science, University of Maryland, College Park, Maryland, U.S.A.

Keywords:

Algorithmic game theory, Economic models of individual rationality, Strategic multi-agent encounters,

Non-zero-sum two-player games, Iterated games, tournaments, Performance analysis.

Abstract:

We study the iterated version of the Traveler’s Dilemma (TD). TD is a two-player, non-zero sum game that

offers plenty of incentives for cooperation. Our goal is to gain deeper understanding of iterated two-player

games whose structures are far from zero-sum. Our experimental study and analysis of Iterated TD is based on

a round-robin tournament we have recently designed, implemented and analyzed. This tournament involves 38

distinct participating strategies, and is motivated by the seminal work by Axelrod et al. on Iterated Prisoners

Dilemma. We ﬁrst motivate and deﬁne the strategies competing in our tournament, followed by a summary

of the tournament results with respect to individual strategies. We then extend the performance comparison-

and-contrast of individual strategies in the tournament, and carefully analyze how groups of closely related

strategies perform when each such group is viewed as a “team”. We draw some interesting lessons from the

analyzes of individual and team performances, and outline some promising directions for future work.

1 INTRODUCTION

Game theory is important to AI and multi-agent

systems research communities because it provides

mathematical foundations for modeling interactions

among self-interested rational agents that may need

to combine competition and cooperation with each

other in order to meet their individual objectives (Par-

sons and Wooldridge, 2002; Rosenschein and Zlotkin,

1994; Wooldridge, 2009). An example of such inter-

actions is the iterated Prisoner’s Dilemma (PD) (Ax-

elrod, 1980; Axelrod, 1981), a classical two-person

non-zero-sum game that has been extensively studied

by psychologists, sociologists, economists, political

scientists, applied mathematicians and computer sci-

entists.

We study an interesting and rather complex 2-

player non-zero sum game, the (Iterated) Traveler’s

Dilemma (Becker et al., 2005; Capra et al., 1999;

Land et al., 2008; Pace, 2009). In TD, each player has

a large number of possible actions or moves. In the

iterated context, many possible actions per round im-

ply, for games of many rounds, an astronomic number

of possible strategies overall. We are interested in the

Iterated TD because its structure deﬁes the usual pre-

scriptions of the classical game theory insofar as what

constitutes good or “optimal” play. We attempt to

gain a deeper understanding into what general types

of strategies can be expected to do well in an Iter-

ated TD setting via an experimental, simulation-based

study of several broad classes of strategies matched

against each other, that is, via a tournament. More-

over, we do so in a manner that, we argue, minimizes

the impact of individual parameter choices in those

strategies, thus enabling us to draw some broader,

more general conclusions.

The paper is organized as follows. We ﬁrst deﬁne

the Traveler’s Dilemma, motivate its signiﬁcance and

summarize the most relevant prior art. We then pur-

sue a detailed analysis of the “baseline” variant of the

game. Our analysis is based on a round-robin, many-

round tournament that we have recently designed, im-

plemented and run. We ﬁrst summarize our main

ﬁndings on the relative performances of various in-

dividual strategies with respect to the “bottom line”

metric (which is, essentially, the appropriately nor-

malized total dollar amount won). We subsequently

focus on team performances of several carefully se-

lected groups of closely related strategies. We draw

a number of interesting conclusions based on our ex-

tensive experimentation and analyzes of the individ-

ual and team performances. Finally, we outline some

T. Toši

c P. and C. Dasler P..

STRATEGIES FOR CHALLENGING TWO-PLAYER GAMES - Some Lessons from Iterated Traveler’s Dilemma.

DOI: 10.5220/0003753900720082

In Proceedings of the 4th International Conference on Agents and Artiﬁcial Intelligence (ICAART-2012), pages 72-82

ISBN: 978-989-8425-96-6

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

promising ways forward in this quest for deeper in-

sights into what we have informally dubbed the “far-

from-zero-sum” iterated two-player games.

2 TRAVELER’S DILEMMA

Traveler’s Dilemma was originally introduced in

(Basu, 1994). The motivation behind the game was

to expose some fundamental limitations of the classi-

cal game theory (Neumann and Morgenstern, 1944),

and in particular the notions of individual rational-

ity that stem from game-theoretic notions of “optimal

play” based on Nash equilibria (Basu, 1994; Basu,

2007; Wooldridge, 2009). The original version of

TD, which we will treat as the “default” variant of

this game, is deﬁned as follows:

An airline loses two suitcases belonging to two

different travelers. Both suitcases happen to be iden-

tical and contain identical items. The airline is li-

able for a maximum of $100 per suitcase. The two

travelers are separated so that they cannot communi-

cate with each other, and asked to declare the value

of their lost suitcase and write down (i.e., bid) a value

between $2 and $100. If both claim the same value,

the airline will reimburse each traveler the declared

amount. However, if one traveler declares a smaller

value than the other, this smaller number will be taken

as the true dollar valuation, and each traveler will

receive that amount along with a bonus/malus: $2

extra will be paid to the traveler who declared the

lower value and a $2 deduction will be taken from the

person who bid the higher amount. So, what value

should a rational traveler (who wants to maximize the

amount she is reimbursed) declare?

A tacit assumption in the default formulation of

TD is that the bids have to be integers. That is, the

bid granularity is $1, as this amount is the smallest

possible difference between two non-equal bids.

This default TD game has some very interest-

ing properties. The game’s unique Nash equilibrium

(NE), the action pair (p, q) = ($2, $2), is actually

rather bad for both players, under the usual assump-

tion that the level of the players’ well-being is propor-

tional to the dollar amount they individually receive.

The choice of actions corresponding to NE results in

a very low payoff for each player. The NE actions

also minimize social welfare, which for us is simply

the sum of the two players’ individual payoffs. How-

ever, it has been argued (Basu, 1994; Capra et al.,

1999; Goeree and Holt, 2001) that a perfectly ratio-

nal player, according to classical game theory, would

“reason through” and converge to choosing the low-

est possible value, $2. Given that the TD game is

symmetric, each player would reason along the same

lines and, once selecting $2, would not deviate from it

(since unilaterally deviating from a Nash equilibrium

presumably can be expected to result in decreasing

one’s own payoff). In contrast, the non-equilibrium

pair of strategies ($100, $100) results in each player

earning $100, very near the best possible individual

payoff for each player. Hence, the early studies of TD

concluded that this game demonstrates a woeful inad-

equacy of the classical game theory, based on Nash

(or similar notions of) equilibria (Basu, 2007). Inter-

estingly, it has been experimentally shown that hu-

mans (both game theory experts and laymen) tend

to play far from the TD’s only equilibrium, at or

close to the maximum possible bid, and therefore fare

much better than if they followed the classical game-

theoretic approach (Becker et al., 2005).

We note that adopting one of the alternative con-

cepts of game equilibria found in the “mainstream”

literature does not appear to help, either. For example,

it is argued in (Land et al., 2008) that the action pair

($2, $2) is also the game’s only evolutionary equilib-

rium. Similarly, seeking sub-game perfect equilibria

(SGPE) (Osborne, 2004) of Iterated TD also isn’t par-

ticularly promising, since the set of a game’s SGPEs

is a subset of that game’s full set of Nash equilibria in

the mixed strategies.

We also note that the game’s only stable strategy

pair is nowhere close to being Pareto optimal: there

are many obvious ways of making both players much

better off than if they play the NE strategies. In par-

ticular, while neither stable nor an equilibrium in any

sense of those terms, ($100, $100) is the unique strat-

egy pair that maximizes social welfare and is, in par-

ticular, Pareto optimal.

3 ITERATED TD TOURNAMENT

Our Iterated Traveler’s Dilemma tournament has been

inspired by, and is in form similar to, Axelrod’s

Iterated Prisoner’s Dilemma tournament (Axelrod,

2006). In particular, it is a round-robin tournament

where each strategy plays against every other strategy

as follows: each agent plays N matches against each

other agent, incl. one’s own “twin”. A match con-

sists of T rounds. The agents do not know T or N and

cannot tweak their strategies with respect to the dura-

tion of the encounter. Similarly, the strategies are not

allowed to use any other assumptions (such as, e.g.,

the general or speciﬁc nature of the opponent they are

playing against in a given match). Indeed, the only

data available to the learning and adaptable strate-

gies in our “pool” of tournament participants (see be-

STRATEGIES FOR CHALLENGING TWO-PLAYER GAMES - Some Lessons from Iterated Traveler's Dilemma

low) is what they can learn and infer about the future

rounds, against a given opponent, based on the bids

and outcomes of the prior rounds of the current match

against that opponent.

In order to have statistically signiﬁcant results

(esp. given that many of our strategies involve ran-

domization in various ways), we have selected N =

100 and T = 1000.

In every round, each agent must select a valid bid.

Thus, the action space of an agent in the tournament

is A = {2, 3, . . . , 100}. The method in which an agent

chooses its next action for all possible histories of pre-

vious rounds is known as a strategy. A valid strategy

is a function S that maps some set of inputs to an ac-

tion, S : · → A. Let C denote the set of strategies that

play one-against-one matches with each other, that is,

the set of agents competing in the tournament.

The agents’ actions are deﬁned as follows: x

the bid traveler x makes on round t; and x

n,t

= the

bid traveler x makes on round t of match n.

Reward per round, R : A × A → Z ∈ [0, 101], for

action α against action β, where α, β ∈ A, is deﬁned

as R(α, β) = min(α, β)+2·sgn(β−α), where sgn(x)

is the usual sign function. Therefore, the total reward

M : S × S → R received by agent x in a match against

y is deﬁned as

M(x, y) =

∑

t=1

R(x

, y

The reward received by agent x in the n

match

against agent y is denoted as M

(x, y).

In order to make a reasonable baseline compari-

son, we use the same classes of strategies as in (Dasler

and Tosic, 2010), ranging from rather simplistic to

moderately complex. We remark that no strategy in

the tournament is allowed to use any kind of meta-

knowledge, such as what is the number of rounds or

matches to be played against a given opponent, what

“strategy type” an opponent belongs to (for exam-

ple, if a learning-based strategy knows it is matched

against a TFT-based strategy, such meta-knowledge

can be exploited by the learner), or similar. All that is

available to a strategy are the plays and outcomes of

the previous rounds within a given match.

Assuming each agent knows the evaluation met-

ric, the outcomes (i.e., rewards) can be always

uniquely recovered from one’s own play and that of

the opponent; however, the opponent’s play in a given

round, in general, cannot be uniquely recovered from

just knowing one’s own action and the received re-

ward in that round. Consistently with most of the

existing tournament-based game theory literature, we

therefore assume that, at the end of each round, each

agent gets to see the bid of the other agent. We

remark that the incomplete information alternative,

where each agent knows its reward but not the op-

ponent’s bid, is rather interesting and even more chal-

lenging than the complete information scenario that

we assume throughout this paper.

Summary of the strategy classes follows; for a

more detailed description, see (Dasler and Tosic,

2010).

The “Randoms”. The ﬁrst, and simplest, class of

strategies play a random value, uniformly distributed

across a given interval. We have implemented two

instances using the following intervals: {2, 3, ..., 100}

and {99, 100}.

The “Simpletons”. The second extremely simple

class of strategies which choose the exact same dol-

lar value in every round. The values we used in the

tournament were x

= 2 (the lowest possible), x

= 51

(“median”), x

= 99 (slightly below maximal possi-

ble; would result in maximal individual payoff should

the opponent consistently play the highest possible

action, which is $100), and x

= 100 (the highest pos-

sible).

Tit-for-Tat-in-spirit. The next class of strategies

are those that can be viewed as Tit-for-Tat-in-spirit,

where Tit-for-Tat is the famous name for a very sim-

ple, yet very effective, strategy for the iterated pris-

oner’s dilemma (Axelrod, 1980; Axelrod, 1981; Ax-

elrod, 2006; Rapoport and Chammah, 1965). The

idea behind Tit-for-Tat (TFT) is simple: cooperate on

the ﬁrst round, then “do to thy neighbor” (that is, op-

ponent) exactly what he did to you on the previous

round. We note that the baseline PD can be viewed

as a special case of our TD, when the action space of

each agent in the latter game is reduced to just two

actions: {BidLow, BidHigh}. However, unlike iter-

ated PD, even in the baseline version iterated TD as

deﬁned above, each agent has many actions at his dis-

posal. In general, bidding high values in ITD can be

viewed as an approximation of “cooperating” in IPD,

whereas playing low values is an approximation of

“defecting”. We deﬁne several Tit-for-Tat-like strate-

gies for ITD. These strategies can be roughly grouped

into two categories. One are the simple TFT strategies

bid value ε below the bid made by the opponent in the

last round, where we restricted ε ∈ {1, 2}. The second

category are the predictive TFT strategies that com-

pare whether their last bid was lower than, equal to, or

higher than that of the other agent. Then a bid is made

similar to the simple TFT strategies, i.e. some value ε

below the bid made by competitor c in the last round,

where c ∈ {x, y} and ε ∈ {1, 2}. The key distinction

is that a bid can be made relative to either the oppo-

nent’s last bid or the bid made by the agent strate-

gizing along the TFT lines himself. In essence, the

ICAART 2012 - International Conference on Agents and Artificial Intelligence

complex TFT strategies are attempting to predict the

opponent’s next bid based on the bids in the previous

round and, given that prediction, they attempt to out-

smart the opponent. A variant of TFT was the overall

winner of a similar (but much smaller and simpler) it-

erated prisoner’s dilemma round-robin tournament in

(Axelrod, 1980). Given the differences between the

Traveler’s Dilemma and the Prisoner’s Dilemma, we

were very curious to see how well various TFT-based

strategies would do in the iterated TD context.

“Mixed”. The mixed strategies combine up to three

pure strategies. For each mixed strategy, a pure strat-

egy σ ∈ C is selected from one of the other strategies

deﬁned in the competition for each round according

to a speciﬁed probability distribution (see Table 1).

Once a strategy has been selected, the value that σ

would bid at time step t is bid. We chose to use only

mixtures of the TFT, Simpleton, and Random strate-

gies. This allows for greater transparency when at-

tempting to decipher the causes of a particular strat-

egy’s performance.

The notation in Table 1 (see Appendix) is Mixed

followed by up to three (Strategy, Probability) pairs,

where each such pair represents a strategy and the

probability that that strategy is selected for any given

round. Simpleton strategies are represented simply

by their bid, e.g. (100, 20%). Random strategies are

represented by the letter R followed by their range,

e.g. (R[99, 100], 20%). TFT strategies come in two

varieties: simple and complex. In Mixed strategies,

a Simple TFT used in the “mix” is represented by

T FT (y −n), where n is the value to bid below the op-

ponent’s bid (that is, the value of y). Complex TFTs

used in a given “mix” are represented with L, E, and H

indicators (denoting Lower, Equal and Higher), fol-

lowed by the bid policy. Bid policies are based on

either the opponent’s previous bid (y) or this agent’s

own previous bid (x). Details can be found in (Dasler

and Tosic, 2010). An example (see Table 1) will hope-

fully clarify this somewhat cumbersome notation:

Mixed: (L(y − g)E(x − g)H(x −

g), 80%); (100, 10%); (2, 10%) denotes a complex

mixed strategy according to which an agent:

• plays a complex TFT strategy 80% of the time, in

which it bids: (i) the opponent’s last bid minus

the granularity if this strategy’s last bid was lower

than its opponent’s; (ii) this strategy’s last bid mi-

nus the granularity if this strategy’s last bid was

equal to its opponent’s; and (iii) this strategy’s last

bid minus the granularity if this strategy’s last bid

was higher than its opponent’s;

• 10% of the time simply bids $100, that is, plays

the Simpleton $100 strategy;

• the remaining 10% of the time bids $2 (i.e., plays

the Simpleton $2 strategy).

In the version of ITD reported in this paper, the value

of bid granularity is g = 1 throughout.

Buckets – Deterministic. These strategies keep

a count of each bid by the opponent in an array of

buckets. The bucket that is most full (i.e., the value

that has been bid most often) is used as the predicted

value, with ties being broken by one of the following

methods: the highest valued bucket wins, the lowest

valued bucket wins, a random bucket wins, and the

most recent tied-for-the-lead bucket wins. The strat-

egy then bids the highest possible value strictly below

the predicted opponent’s bid. (If the opponent bids

the lowest possible value, which in our baseline ver-

sion of TD is $2, then the deterministic bucket agent

bids that lowest value, as well.) An instance of each

tie breaking method above competed as a different

bucket-based strategy in the tournament.

Buckets – Probability Mass Function based. As

with deterministic buckets, this strategy class counts

instances of the opponent’s bids and uses them to pre-

dict the opponent’s next bid. Rather than picking the

value most often bid, the buckets are used to deﬁne a

probability mass function from which a prediction is

randomly selected. Values in the buckets decay over

time in order to assign greater weights to the more

recent data than to the older data; we’ve selected a re-

tention rate (0 ≤ γ ≤ 1) to specify the speed of mem-

ory decay. We have entered into our tournament sev-

eral instances of this strategy using the following rate

of retention values γ: 1.0, 0.8, 0.5, and 0.2. The strat-

egy bids the largest value strictly below the predicted

value of the opponent’s next bid (so, in the default

version, it is the “one under” the predicted opponent’s

bid). We note that the “bucket” strategies based on

probability mass buckets are quite similar to a learn-

ing model in (Capra et al., 1999).

Simple Trending. This strategy looks at the previous

k time steps, creates a line of best ﬁt on the rewards

earned, and compares its slope to a threshold θ. If

the trend has a positive slope greater than θ, then the

agent will continue to play the same bid it has been

as the rewards are increasing. If the slope is negative

and |slope| > θ, then the system is trending toward the

Nash Equilibrium and, thus, the smaller rewards. In

this case, the agent will attempt to entice the opponent

to collaborate and will start playing $100. Otherwise,

the system of bidding and payouts is relatively sta-

ble and the agent will play the adversarial“one under”

strategy that attempts to outsmart the other player. We

have implemented instances of this strategy with an

arbitrary θ of 0.5 and the following values of k: 3,

STRATEGIES FOR CHALLENGING TWO-PLAYER GAMES - Some Lessons from Iterated Traveler's Dilemma

10, and 25, where larger values of k mean trending

is determined over a longer time-window. In partic-

ular, we have incorporated a simple explicit mech-

anism to push the player away from the “bad” NE:

“simple trenders” share the adversarial philosophy of

TFT as long as the rewards are high, but unilaterally

move into collaboration-inviting, high-bidding behav-

ior when the rewards are low (presumably, hoping that

an adaptable opponent would follow suit in the subse-

quent rounds).

Q-learning. This strategy uses a learning rate α

to emphasize new information and a discount rate γ

to emphasize future gains. In particular, the learn-

ers in our tournament are simple implementations of

Q-learning (Watkins and Dayan, 1992) as a way of

predicting the best action at time (t + 1) based on the

action selections and payoffs at times [1, ...,t]. This

is similar to the Friend-or-Foe Q-learning method

(Littman, 2001), without the limitation of having to

classify the allegiance of one’s opponent. Due to scal-

ing issues, our implementation of Q-learning does not

capture the entire state/action space but rather divides

it into a handful of meaningful classes based on just

three states and three actions, as follows:

State: The opponent played higher, lower, or

equal to our last bid.

Action: We play one higher than, one lower than,

or equal to our previous bid.

Recall that actions are deﬁned for just a single

time-step. The actual implementation treats the state

as a collection of moves by the opponent over the last

k rounds. We have decided to use k = 5 as an in-

tuitively reasonable (but admittedly fairly arbitrary)

value for k as it allows us to capture some history

without data sizes becoming unmanageable. We are

implementing this basic Q-learning algorithm with

the learning rates of 0.8, 0.5 and 0.2.

Zeuthen Strategies. A Zeuthen Strategy (Zeuthen,

1967) calculates the level of risk of each agent, and

makes concessions accordingly. Risk is the ratio of

loss from accepting the opponent’s proposal vs. the

loss of forcing the conﬂict deal (the deal made when

no acceptable proposal can be found). While ITD

is strictly speaking not a negotiation (originally, a

Zeuthen strategy is a negotiation strategy), one can

still treat each bid (i.e. x

and y

) to be a proposal: if

= i, then agent x is proposing to agent y the pair

(i, i + 1) as the next action pair. For TD, we consider

the conﬂict deal (the outcome in the event that the

negotiators can not come to an agreement) to be the

N.E. at ($2, $2). Given the proposals of each agent,

a risk comparison is done. An agent continues mak-

ing the same bid as long as its risk is greater than or

equal its opponent’s. Otherwise, the agent will make

the minimal sufﬁcient concession: the agent adjusts its

proposal so that (i) its risk is higher than opponent’s

risk and (ii) the opponent’s utility increases as little

as possible. Due to the peculiar structure of TD, it is

possible that a “concession” actually leads to a loss of

utility for the opponent. This, however, goes against

the very notion of making a concession. Thus, we

have implemented two Zeuthen strategies: one that

allows counter-intuitive negative concessions and one

that does not.

The metric that we use to evaluate relative perfor-

mances of various strategies is essentially “the bottom

line”, that is, appropriately normalized dollar amounts

that a player would win if she engaged in the pre-

scribed number of plays against a particular (ﬁxed)

opponent. More speciﬁcally, the metric U

below is

the sum of all payoffs gained by an agent, normalized

by the total number of rounds played and the maxi-

mum allowable reward:

(x) =

|C|

∑

j∈C

· N · T

∑

n=1

(x, j)

where R

is the maximum possible reward given in

one round, N is the number of matches played be-

tween each pair of competitors, T is the number of

rounds per each match, and |C| is the number of com-

petitors in the tournament. In experiments discussed

in this paper, R

= $101, N = 100, T = 1000 and

|C| = 38.

We note that some other candidate metrics for

measuring performance in ITD, and analyzes of per-

formances of various strategies w.r.t. those alternative

metrics, can be found in (Dasler and Tosic, 2011).

4 TOURNAMENT RESULTS FOR

INDIVIDUAL STRATEGIES

The Traveler’s Dilemma Tournament with which we

have experimented involves a total of 38 competitors

(i.e., distinct strategies), playing 100 head-to-head

matches per opponent, made of 1000 rounds each.

The ﬁnal rankings with respect to the (normalized)

“bottom-line” metric U

are given in Table 1 in the

Appendix.

We brieﬂy summarize our main ﬁndings. First,

the top three performers in our tournament turn out to

be three “dumb” strategies that always bid high val-

ues. These three strategies are greedy in a very literal,

simplistic sense, and are all utterly oblivious to what

their opponents do – yet they outperform, and by a rel-

atively considerable margin, the adaptable strategies

ICAART 2012 - International Conference on Agents and Artificial Intelligence

such as the Q-learners and the “buckets”. The strategy

which always bids the maximum possible value ($100

in our case) and the strategy which always bids “one

under” the maximum possible value are both outper-

formed by the strategy which randomly alternates be-

tween the two: “Random{99, 100}” picks to bid ei-

ther $99 or $100 with equal probabilities, and without

any consideration for the opponent’s bids or previous

outcomes.

The Zeuthen strategy that does not allow for neg-

ative “concessions” performs quite well, and is the

highest performer among all “smart” and adaptable

strategies in the tournament. The ﬁrst work (as far as

we are aware) that proposed the use of negotiation-

inspired Zeuthen strategies in the game strategy for

ITD context (see (Dasler and Tosic, 2010)) encoun-

tered some stern criticism on the grounds that play-

ing an ITD-like game has little or nothing in com-

mon with multi-agent negotiation. However, ITD is

a game ripe for collaboration among self-interested

yet adaptable agents, and the excellent performance

of a strategy such as Zeuthen-Positive, that is will-

ing to sacriﬁce its short-term payoff in order to en-

tice the other agent into being more collaborative (i.e.,

systematic higher bidding) in the subsequent rounds,

validates our initial argument that highly collabora-

tive, non-greedy (insofar as “outsmarting” the oppo-

nent) adaptable strategies should actually be expected

to do quite well against a broad pool of other adapt-

able strategies.

We ﬁnd it rather interesting that (i) TFT-based

strategies, in general, do fairly poorly, and (ii) their

performances vary considerably depending on the ex-

act details of the bid prediction method. In (Dasler

and Tosic, 2010), it is reported that a relatively com-

plex TFT-based strategy that, in particular, (a) makes

a nontrivial model of the other agent’s behavior and

(b) “mixes in” some randomization, is among the top

performers, whereas other TFT-based strategies ex-

hibit mediocre (or worse) performance. In our anal-

ysis of individual performances, the top pure TFT

based performer, which bids “one under” the oppo-

nent if the opponent made a lower bid than our TFT

agent on the previous round, and lowers its own bid

in the previous round in other scenarios, shows a

mediocre performance with respect to the rest of the

tournament participants. The best simple TFT strat-

egy simply always bids “two below” the opponent’s

bid on the previous round. All other pure TFT-based

strategies, simple and complex (i.e., predictive) alike,

perform poorly, and some of the sophisticated predic-

tive TFT strategies are among the very worst perform-

ers among all adaptable strategies in the tournament.

This is in stark contrast to Axelrod’s famous IPD tour-

nament, where the original TFT strategy ended up the

overall winner (Axelrod, 1980; Axelrod, 1981).

Beside Zeuthen-Positive, the adaptable strategies

that tend to do well overall are the ones based on lin-

ear extrapolation of the (recent) past (these strategies

we generically refer to as simple trenders) and the

strategies that make probabilistic or deterministic pre-

diction of the opponent’s next move based on all past

moves with some pre-speciﬁed rate of decay (that is,

the deterministic and probabilistic “buckets”).

We observe that the probabilistic bucket strategies

perform decently overall, as long as the retention rate

is strictly less than 1; with the retention rate of 1,

guessing the opponent’s bid turns out to be abysmally

poor and is by far the worst adaptable strategy in the

tournament. We have therefore restricted our further

analysis only to the bucket strategies with γ < 1 (and

have eliminated the latter from the tournament table

and further analysis). We also note that, for the given

pool of opponents, probabilistic bucket strategies con-

siderably outperform their deterministic counterparts

(as long as the retention rate γ < 1).

Another general ﬁnding, fairly surprising to us, is

the relative mediocrity of the learning based strate-

gies: Q-learning based strategies perform decently,

but do not excel – not even if the performance is

measured with respect to the late(r) rounds alone (not

shown in the table for space constraint reasons). On

the other hand, the adaptability of Q-learning based

strategies, combined with relative simplicity (and, in

many cases, stationarity) of the selected “pool” of op-

ponents, ensure that Q-learners do not do badly, ei-

ther. Furthermore, the choice of the learning rate

α seems to make a fairly small difference: all Q-

learning based strategies show similar performance,

and, hence, end up ranked close to each other.

Last but not least, the single worst performer w.r.t.

the normalized dollar-amount metric is the always-

bid-lowest-possible strategy. This strategy can be

viewed as the ultimate adversarial strategy that tries to

always underbid, and hence outperform, the opponent

– regardless of the actual payoff earned. (By bidding

the lowest possible value, one indeed ensures to never

be out-earned by the opponent; while such reasoning

in most situations would not be considered common

sense, there are certainly quite a few real-world exam-

ples of such behavior in for example politics and eco-

nomics.) “Always bid $2” happens to be the unique

NE strategy for the default TD that, according to the

classical, Nash Equilibrium based game theory, a ra-

tional agent that assumes a rational opponent should

actually make this strategy his strategy of choice.

How are relative performances of various indi-

vidual strategies affected as the ratio of the game’s

STRATEGIES FOR CHALLENGING TWO-PLAYER GAMES - Some Lessons from Iterated Traveler's Dilemma

two main parameters – namely, the bonus and the bid

granularity – is varied, is analyzed in detail in (Tosic

and Dasler, 2011). We now turn our attention to team

performances of closely related groups of strategies

in the default Iterated TD as described in Section 2.

5 TEAM PERFORMANCE

ANALYSIS

Perhaps the greatest conceptual problem with an ex-

perimental study of iterated games based on a round-

robin tournament is the sensitivity of results with re-

spect to the choice of participants in the tournament.

While our choice of the ﬁnal 38 competing strate-

gies was made after a great deal of deliberation and

careful surveying of prior art, we are aware that both

absolute and relative performances of various strate-

gies in the tournament might have been rather differ-

ent had those strategies encountered a different set of

opponents. The types of strategies we implemented

(the Randoms, the Simpletons, Simple Trenders, Tit-

For-Tat, Q-learners, etc.) have been extensively stud-

ied in the literature, and are arguably fairly “rep-

resentative” of various relatively cognitively simple

(and hence requiring only a modest computational ef-

fort) approaches to playing iterated PD, iterated TD

and similar games. Within the selected classes of

strategies, we admittedly made several fairly arbitrary

choices of the critical parameters (such as, e.g., the

learning rates in Q-learning). It is therefore highly de-

sirable to be able to claim robustness of our ﬁndings

irrespective of the exact parameter values in various

parameterized types of strategies.

The team performance study summarized in this

section has been undertaken for two main reasons.

One, we’d like to reduce as much as possible the ef-

fects of some fairly arbitrary choices of particular pa-

rameter values for types of strategies. Two, given the

opportunities for collaboration that Iterated TD offers,

yet the complex structure of this game, we would like

to see which pairs of strategy types, when matched

against each other, mutually reinforce and therefore

beneﬁt each other; this analysis also applies to “self-

reinforcement” as strategies of the same type are also

matched up “against” each other. For example, we

want to investigate how well the Q-learners get to

do, with time, if playing Iterated TD “against” them-

selves.

Figure 1 summarizes relative performances of

each strategy class against a given type of oppo-

nent, with the U

score against the uniformly ran-

dom strategy Random[2...100] used as the yardstick

(hence normalized to 1). For each given “team”,

the contributions of individual strategies within the

team all count equally. The plot in Figure 1 is read

as follows: consider the second leftmost cluster of

twelve adjacent bars, corresponding to 12 groups of

strategies. The very leftmost one is the performance

against the random strategy (in this particular case,

it’s the mix made of two Randoms vs. itself); the

bar indicates that “mixed randoms vs. mixed ran-

doms” score about 35% higher than against the yard-

stick, which is deﬁned as the normalized score against

Random[2...100] alone. The next bar (2nd from the

left) in the same group shows that the same mix of

random strategies scores about 36% higher against the

“mix” or team of four different “always bid the same

value” strategies (see previous section) than against

the yardstick Random[2...100]. The highest bar in this

cluster shows that the mix of random strategies scores

against the complex, predictive TFTs nearly two and

a half times higher than against the uniformly random

“yardstick” opponent, etc. The bar next to it captures

(in a normalized fashion) how well the bucket-based

strategies, viewed as a team, do against the random

strategy. The next (middle) bar in this ﬁve-bar cluster

captures how Q-learners, viewed as a team, perform

against the random strategy, and so on.

We summarize the main ﬁndings for this particu-

lar set of strategy classes. Overall, Simple Trending

seems to be the best general strategy against the given

pool of opponents. The simple trenders are overall the

most consistent group of adaptable strategies: each of

them performs quite well individually (see again Ta-

ble 1). Therefore, after the simplistic “always bid very

high”, the simple trenders offer the best tradeoff be-

tween simplicity and underlying computational effort

on one hand, and performance, on the other. Among

the simple trenders, a longer “memory window” of

the previous runs leads to relatively poorer perfor-

mance. One possible explanation is that, with a fairly

long-term memory (such as for K = 25), the “uphill”

and ”downhill” trends tend to average out, resulting

in smaller slopes (in the absolute value) of the linear

trend approximator, and thus, slower adjustments in

the simple trenders’ bidding.

Essentially adversarial in a game that is far from

zero-sum and generally rewards cooperation, pre-

dictive TFT strategies “bury themselves into the

ground”: their performance against themselves is

among the worst of all team performance pairs, and

is the “safest” way of getting to and then staying

at the Nash equilibrium ($2, $2). In stark contrast,

however, TFT-based strategies and Zeuthen strategies

work well together; that is, Zeuthen’s initial “generos-

ity” in order to encourage the opponent to move to-

ward higher bids, in the long run, beneﬁts TFT-based

ICAART 2012 - International Conference on Agents and Artificial Intelligence

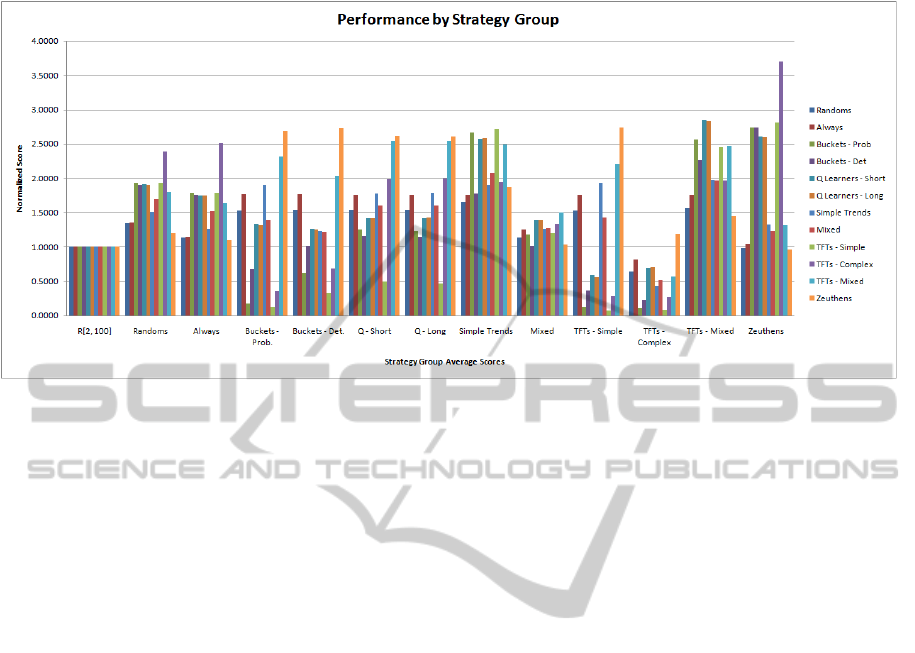
Figure 1: Relative group performances for the selected classes of strategies.

strategies when matched against the Zeuthens. An-

other interesting result about TFT strategies: when

some randomization is added to a TFT-based strategy,

esp. of a kind where very high bids are made in ran-

domly selected rounds, the overall performance im-

proves dramatically, as evidenced by the high scores

of the group TFT-Mixed in comparison to both sim-

ple and complex “pure” TFT strategies. In fact, the

mixed TFT strategies (that do include some random-

ization) are, together with simple trenders, the best

“team” overall. In particular, mixed TFTs do very

well when matched against any adaptable opponent

in our tournament. In contrast, the predictive com-

plex TFTs that don’t use any randomization are by far

the worst “team” of strategies overall.

Q-learners handle TFT based strategies quite well.

Furthermore, Q-Learners and Simple Trenders rather

nicely reinforce each other, i.e., when matched up

“against” each other, both end up doing quite well.

Similar mutual reinforcement of rewarding collabora-

tive play can be observed when buckets (both proba-

bilistic and deterministic) are matched up with Ran-

domized TFTs and Zeuthens. One very striking in-

stance of mutual reinforcement is what Zeuthens do

for complex predictive TFTs (the variants without

random bids), and in the process also for themselves,

when matched against predictive TFTs.

In contrast to these examples of mutual rein-

forcement, neither short- nor long-term memory Q-

learners perform particularly impressively against

themselves. We suspect that this in part is due to

high sensitivity to the bid choices in the initial round;

this sensitivity to initial behavior warrants further in-

vestigation. Moreover (see also Table 1), choice of

the learning rate α seems to make a fairly small dif-

ference: all Q-learning based strategies show similar

performances to each other against most types of op-

ponents.

6 CONCLUSIONS AND FUTURE

DIRECTIONS

We study the Iterated Traveler’s Dilemma, an inter-

esting and rather complex two-player non-zero sum

game. We investigate what kind of strategies tend to

do well in this game by designing, implementing and

analyzing a round-robin tournament with 38 partici-

pating strategies. Our study of relative performances

of various strategies with respect to the “bottom-line”

metric has corroborated that, for an iterated game

whose structure is far from zero-sum, the traditional

game-theoretic notions of individual rationality, based

on the concept(s) of Nash (or similar kinds of) equi-

libria, are rather unsatisfactory.

While we have been using the phrase “far from

zero-sum” rather informally (indeed, as far as we

know, there is no game-theoretic formal deﬁnition of

how far a game is from being zero-sum), the basic in-

tuition is that there is no reason to assume that the

solution concepts (i.e., what it means to play well

and, by extension, to act rationally in certain types

of strategic encounters) that originate from studying

strictly competitive, zero-sum or close to zero-sum

games, would be applicable and provide satisfactory

notions of individual rationality for encounters that

are much closer to the cooperative than strictly com-

petitive end of the spectrum. Indeed, most of clas-

sical game solutions and equilibrium concepts, such

as those of Nash equilibria and evolutionary equilib-

STRATEGIES FOR CHALLENGING TWO-PLAYER GAMES - Some Lessons from Iterated Traveler's Dilemma

ria, originated from studying competitive encounters.

The insights from what kinds of strategies tend to

do well in Iterated Traveler’s Dilemma do not point

out a paradox, like K. Basu and some other early re-

searchers of TD claimed. Rather, in our opinion, they

expose a fundamental deﬁciency in applying notions

of rationality that are appropriate in strictly compet-

itive contexts to strategic encounters where both in-

tuition and mathematics suggest that being coopera-

tive is the best way to ensure high individual payoff

in the long run. We point out that some other, newer

notions of game solutions, such as that of regret equi-

libria (Halpern and Pass, 2009), may turn out to pro-

vide a satisfactory notion of individual rationality for

cooperation-rewarding games such as TD; further dis-

cussion of these novel concepts, however, is beyond

our current scope.

We brieﬂy outline some other lessons learned

from detailed analysis of individual and team per-

formances in our round-robin Iterated TD tourna-

ment. These lessons include that (i) common-sense

unselﬁsh greedy behavior (“bid high”) generally tends

to be rewarded in ITD, (ii) not all adaptable/learning

strategies are necessarily successful, even against

simple opponents, (iii) more complex models of an

opponent’s behavior may but need not result in better

performance, (iv) exact choices of critical parameters

may have a great impact on performance (such as with

various bucket-based strategies) or hardly any impact

at all (e.g., the learning rate in Q-learners), and (v)

collaboration via mutual reinforcement between con-

siderably different adaptable strategies appears to of-

ten be much better rewarded than self-reinforcement

between strategies that are very much alike.

Our analysis also raises several interesting ques-

tions, among which we are particularly keen to further

investigate (i) to what extent other variations of cog-

nitively simple models of learning can be expected to

help performance, (ii) to what extent complex mod-

els of the other agent really help an agent increase

its payoff in the iterated play, and (iii) assuming that

this phenomenon occurs more broadly than what we

have investigated so far, what general lessons can be

learned from the observed higher rewards for hetero-

geneous mutual reinforcement than for homogeneous

self-reinforcement?

Last but not least, in order to be able to draw gen-

eral conclusions less dependent on the selection of

strategies in a tournament, we are also pursuing evolv-

ing a population of strategies similar to the approach

found in (Beauﬁls et al., 1998). We hope to report

new results along those lines in the near future.

REFERENCES

Axelrod, R. (1980). Effective choice in the prisoner’s

dilemma. Journal of Conﬂict Resolution, 24(1):3 –25.

Axelrod, R. (1981). The evolution of cooperation. Science,

211(4489):1390–1396.

Axelrod, R. (2006). The evolution of cooperation. Basic

Books.

Basu, K. (1994). The traveler’s dilemma: Paradoxes of ra-

tionality in game theory. The American Economic Re-

view, 84(2):391–395.

Basu, K. (2007). The traveler’s dilemma. Scientiﬁc Ameri-

can Magazine.

Beauﬁls, B., Delahaye, J.-P., and Mathieu, P. (1998). Com-

plete classes of strategies for the classical iterated pris-

oner’s dilemma. In Evolutionary Programming, pages

33–41.

Becker, T., Carter, M., and Naeve, J. (2005). Experts play-

ing the traveler’s dilemma. Technical report, Depart-

ment of Economics, University of Hohenheim, Ger-

many.

Capra, C. M., Goeree, J. K., Gmez, R., and Holt, C. A.

(1999). Anomalous behavior in a traveler’s dilemma?

The American Economic Review, 89(3):678–690.

Dasler, P. and Tosic, P. (2010). The iterated traveler’s

dilemma: Finding good strategies in games with

“bad” structure: Preliminary results and analysis. In

Proc of the 8th Euro. Workshop on Multi-Agent Sys-

tems, EUMAS’10.

Dasler, P. and Tosic, P. (2011). Playing challenging iterated

two-person games well: A case study on iterated trav-

elers dilemma. In Proc. of WorldComp Foundations

of Computer Science FCS’11; to appear.

Goeree, J. K. and Holt, C. A. (2001). Ten little treasures

of game theory and ten intuitive contradictions. The

American Economic Review, 91(5):1402–1422.

Halpern, J. Y. and Pass, R. (2009). Iterated regret mini-

mization: a new solution concept. In Proceedings of

the 21st international jont conference on Artiﬁcal in-

telligence, IJCAI’09, pages 153–158, San Francisco,

CA, USA. Morgan Kaufmann Publishers Inc.

Land, S., van Neerbos, J., and Havinga, T. (2008). An-

alyzing the traveler’s dilemma Multi-Agent systems

project.

Littman, M. L. (2001). Friend-or-Foe q-learning in General-

Sum games. In Proc. of the 18th Int’l Conf. on Ma-

chine Learning, pages 322–328. Morgan Kaufmann

Publishers Inc.

Neumann, J. V. and Morgenstern, O. (1944). Theory of

games and economic behavior. Princeton Univ. Press.

Osborne, M. (2004). An introduction to game theory. Ox-

ford University Press, New York.

Pace, M. (2009). How a genetic algorithm learns to play

traveler’s dilemma by choosing dominated strategies

to achieve greater payoffs. In Proc. of the 5th interna-

tional conference on Computational Intelligence and

Games, pages 194–200.

Parsons, S. and Wooldridge, M. (2002). Game theory and

decision theory in Multi-Agent systems. Autonomous

Agents and Multi-Agent Systems, 5:243–254.

ICAART 2012 - International Conference on Agents and Artificial Intelligence

Rapoport, A. and Chammah, A. M. (1965). Prisoner’s

Dilemma. Univ. of Michigan Press.

Rosenschein, J. S. and Zlotkin, G. (1994). Rules of en-

counter: designing conventions for automated nego-

tiation among computers. MIT Press.

Tosic, P. and Dasler, P. (2011). How to play well in non-zero

sum games: Some lessons from generalized traveler’s

dilemma. In Zhong, N., Callaghan, V., Ghorbani, A.,

and Hu, B., editors, Active Media Technology, volume

6890 of Lecture Notes in Computer Science, pages

300–311. Springer Berlin / Heidelberg.

Watkins, C. and Dayan, P. (1992). Q-learning. Machine

Learning, 8(3-4):279–292.

Wooldridge, M. (2009). An Introduction to MultiAgent Sys-

tems. John Wiley and Sons.

Zeuthen, F. F. (1967). Problems of monopoly and economic

warfare / by F. Zeuthen ; with a preface by Joseph A.

Schumpeter. Routledge and K. Paul, London. First

published 1930 by George Routledge & Sons Ltd.

APPENDIX

Below are Table 1 and Table 2 as referenced in the

main text.

Table 1 contains the scores for all classes of strate-

gies based on the U

metric, i.e. they are ranked ac-

cording to a normalized total dollar amount. These

scores are normalized additionally by the perfor-

mance of a purely random strategy.

Table 2 contains the sorted ranking for all individ-

ual strategies based on the U

metric, i.e. they are

ranked according to a normalized total dollar amount.

STRATEGIES FOR CHALLENGING TWO-PLAYER GAMES - Some Lessons from Iterated Traveler's Dilemma

Table 1: Final rankings of teams or classes of closely related strategies w.r.t. metric U

Table 2: Final ranking of the individual strategies w.r.t. metric U

0.760787 Random [99, 100]

0.758874 Always 100

0.754229 Always 99

0.754138 Zeuthen Strategy - Positive

0.744326 Mixed - L(y-g) E(x-g) H(x-g), 80%); (100, 20%)

0.703589 Simple Trend - K = 3, Eps = 0.5

0.681784 Mixed - TFT (y-g), 80%); (R[99, 100], 20%)

0.666224 Simple Trend - K = 10, Eps = 0.5

0.639572 Simple Trend - K = 25, Eps = 0.5

0.637088 Mixed - L(x) E(x) H(y-g), 80%); (100, 20%)

0.534378 Mixed - L(y-g) E(x-g) H(x-g), 80%); (100, 10%); (2, 10%)

0.498134 Q Learn - alpha= 0.2, discount= 0.0

0.497121 Q Learn - alpha= 0.5, discount= 0.0

0.496878 Q Learn - alpha= 0.5, discount= 0.9

0.495956 Q Learn - alpha= 0.2, discount= 0.9

0.493640 Q Learn - alpha= 0.8, discount= 0.0

0.493639 Buckets - (Fullest, Highest)

0.493300 Q Learn - alpha= 0.8, discount= 0.9

0.492662 TFT - Low(y-g) Equal(x-g) High(x-g)

0.452596 Zeuthen Strategy - Negative

0.413992 Buckets - PD, Retention = 0.5

0.413249 Always 51

0.412834 Buckets - PD, Retention = 0.2

0.408751 Buckets - PD, Retention = 0.8

0.406273 Buckets - (Fullest, Random)

0.390303 TFT - Simple (y-g)

0.387105 Buckets - (Fullest, Newest)

0.334967 Buckets - (Fullest, Lowest)

0.329227 TFT - Simple (y-2g)

0.316201 Random [2, 100]

0.232063 Mixed - L(y-g) E(x-g) H(x-g), 80%); (2, 20%)

0.164531 Mixed - L(x) E(x) H(y-g), 80%); (100, 10%); (2, 10%)

0.136013 TFT - Low(x) Equal(x) High(y-g)

0.135321 TFT - Low(x) Equal(x-2g) High(y-g)

0.030905 TFT - Low(x-2g) Equal(x) High(y-g)

0.030182 TFT - Low(x-2g) Equal(x-2g) High(y-g)

0.026784 Mixed - L(x) E(x) H(y-g), 80%); (2, 20%)

0.024322 Always 2

ICAART 2012 - International Conference on Agents and Artificial Intelligence