EFFICIENT COMPUTATION OF VORONOI NEIGHBORS BASED

ON POLYTOPE SEARCH IN PATTERN RECOGNITION

Juan Mendez

and Javier Lorenzo

Dept. Informatica y Sistemas, Univ. Las Palmas de Gran Canaria, Las Palmas, Spain

IUSIANI, Univ. Las Palmas de Gran Canaria, Las Palmas, Spain

Keywords:

Pattern Recognition, Machine Learning, Nearest Neighbors, Voronoi adjacency, Linear programming.

Abstract:

Some algorithms in Pattern Recognition and Machine Learning as neighborhood-based classiﬁcation and

dataset condensation can be improved with the use of Voronoi tessellation. The paper shows the weakness

of some existing algorithms of tessellation to deal with high dimensional datasets. The use of linear pro-

gramming can improve the tessellation procedures by focusing in Voronoi adjacency. It will be shown that

the adjacency test based on linear programming is a version of the polytope search. However, the polytope

search procedure provides more information than a simple Boolean test. The paper proposes a strategy to use

the additional information contained in the basis of the linear programming algorithm to obtain other tests.

The theoretical results are applied to tessellate several random datasets, and also for much-used datasets in

Machine Learning repositories.

1 INTRODUCTION

Pattern Recognition(PR) and Machine Learning (ML)

are disciplines where the knowledge about the spa-

tial organization of the data can improve the perfor-

mance of the learning and classiﬁcation procedures.

Voronoi and Delaunay tessellations provide partitions

of some representation spaces useful in applications

concerning the spatial organization of data collec-

tions. The tessellation process makes a partition of

the space in disjunct regions or cells called Delaunay

or Voronoi polytopes/polyhedra. Unfortunately De-

launay/Voronoi based approaches have not been very

successful in PR and ML (if compared with Statis-

tical one) because the computational complexity of

these methods. When the attributes that deﬁne each

instance of the dataset are deﬁned in R, every instance

can be represented as a point in R

, where n is the di-

mensionality of the problem. Thus, the processing of

datasets with real attributes can exploit their geomet-

rical equivalence and take advantage of many well-

founded geometrical procedures.

Many PR procedures, for example Neighborhood-

based Classiﬁcation or Dataset Condensation, only

need the adjacency relations between instances in-

stead of full details of Voronoi or Delaunay tessel-

lations. The Voronoi adjacency deals with the prob-

lem of checking if a pair of training instances have a

common boundary, that is if both are neighbors in the

Voronoi tessellation.

The Nearest Neighbor (NN) and k-NN are the

most used algorithms in the family of neighborhood-

based procedures. Voronoi based is only a category of

search procedures in spaces that are coded by means

data structures, as Delaunay/Voronoi or other spatial

related threes (Navarro, 2002). The k parameter in k-

NN is usually chosen by means of a cross-validation

process over the training samples (Duda et al., 2001).

Instead of using a ﬁx k value for the whole dataset,

it will be useful to deﬁne a neighborhood that lo-

cally adapts to the data without the need for cross-

validation (Gupta et al., 2008; Chin et al., 2007). The

natural neighbors for a test point q can be deﬁned

from the Voronoi tessellation of the training set as the

set of training instances p

whose Voronoi cell con-

tains (or are adjacent to the cell containing) q. This

deﬁnition follows the previously introduced by Sib-

son (Sibson, 1981) and Gupta et alt (Gupta et al.,

2008). The natural neighbors are in a subset of in-

stances that encloses or surrounds the test point.

Procedures of dataset editing, pruning or con-

densing are useful in ML applications where mas-

sive dataset are used to train practical classiﬁers, eg.

SVM or Neural Networks. In such cases volumes of

the training sets are drastically reduced with low or

null loss in the information. The condensation pro-

357

Mendez J. and Lorenzo J. (2012).

EFFICIENT COMPUTATION OF VORONOI NEIGHBORS BASED ON POLYTOPE SEARCH IN PATTERN RECOGNITION.

In Proceedings of the 1st International Conference on Pattern Recognition Applications and Methods, pages 357-364

DOI: 10.5220/0003755703570364

 SciTePress

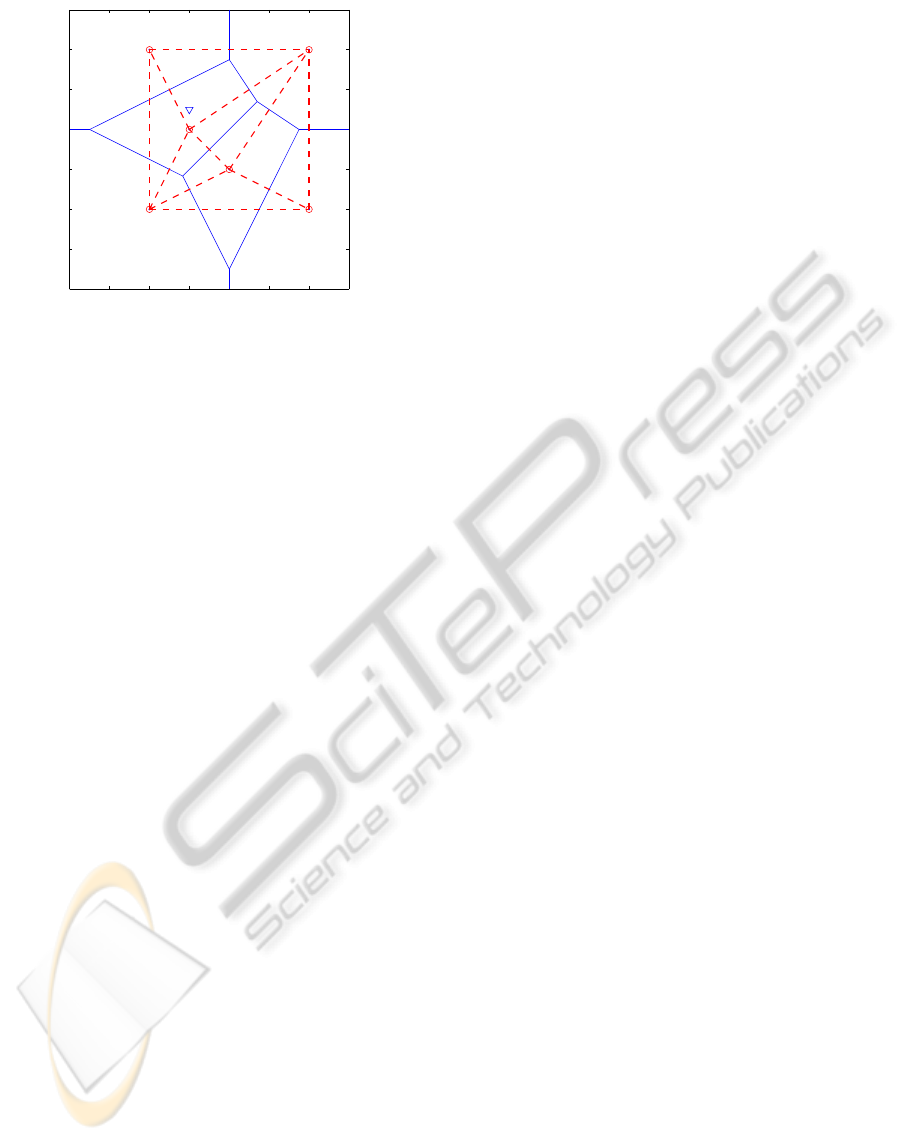
−2 −1 0 1 2 3 4 5

−2

−1

Figure 1: A simple dataset(Fukuda, 2004),

P = {(0,0),(2,1),(1,2),(4,0),(0,4),(4,4)}, showing

the Voronoi polyhedra as well as the Delaunay polytopes.

The nearest neighbor of point q is p

and its natural

neighbors are: {p

cedures that are decision-boundary consistent (Bhat-

tacharya et al., 1992; Duda et al., 2001) based on

Voronoi adjacency do not modify the boundary be-

tween classes. Therefore, any improvement in the

computation of the Voronoi tesselation will imply a

reduction in the computational cost of any procedure

that can be obtained from this tesselation as the k-

NN. In this approach of using spatial information

provided by Dlaunay/Vornoy methods is clustering

method(Koivistoinen et al., 2006) is an agglomera-

tive clustering algorithm which access density infor-

mation by constructing a Voronoi diagram for the in-

put samples.

The Voronoi tessellation procedure uses the met-

ric distance to deﬁne the boundary planes between

regions or cells. Metric distance, as well as vector

norm, only can be used on spaces with a metric struc-

ture. However, many applications in ML deal with

data collections without such a level of structured do-

mains. One way to transform the experimental raw

space in a metric space is to use the statistical Ma-

halanobis distance (Web, 2002). An equivalent ap-

proach is the use of an orthonormal linear transforma-

tion as performed in the Karhunen-Loewe (KL) trans-

formation (Web, 2002). In this case, the Euclidean

distance in the transformed space is equivalent to the

Mahalanobis distance in the experimental space.

There are several methods to compute the Voronoi

and its dual the Delaunay tessellations (Watson, 1981;

Bowyer, 1981; Ramasubramanian and Paliwal, 1997).

Perhaps one of the more successful approaches is

the one based on representation in an extended space

by mapping the instances in R

n+1

, and attempting to

search their convex hull. The projection of the so-

lution in R

generates the tessellation. The greatest

problem with the computation of Voronoi tessella-

tion is the computational complexity. For a dataset

with m instances it is in O(mlogm) for 2D cases,

and for a space with dimension n, it is in O(m

n/2

)

in the general case (Gupta et al., 2008; Barber et al.,

1996), which is clearly exponential with the problem

dimensionality. Figure 2 shows the results of the pro-

gram qvoronoi, a member of the qhull package (Bar-

ber et al., 1996), for some UCI datasets(Asuncion and

Newman, 2007). It is highly efﬁcient in computing

low dimensional datasets, but can not tessellate high

dimension datasets.

The computational complexity of Voronoi tes-

sellations can be reduced with the use of Grabriel

graphs(Gabriel and Sokal, 1969), which have been

used as lower cost alternatives for Voronoi adja-

cency (Aupetit, 2003; Aupetit and Catz, 2005). How-

ever, Gabriel graphs are subsets of Voronoi graphs

and do not provide the full information about neigh-

boring relations.

Computing the Voronoi or Delaunay tessellation

in higher dimensional spaces can become unpracti-

cal. However, computing only the Voronoi adjacency

can be done very efﬁciently by using Linear Pro-

gramming(LP)(Fukuda, 2004). The relationship be-

tween Voronoi and LP problems has a sound theoret-

ical background (Agrell, 1993; Kalai, 1997; Fukuda

et al., 1997; Avis and Fukuda, 1992; Bremner et al.,

1997) and can be continually improved with the ad-

vances in computer hardware because Linear Pro-

gramming (LP) can be efﬁciently programmed in ma-

trix processors as GPUs(Greeff, 2005) and multipro-

cessor systems(Yarmish and van Slyke, 2001).

As it was stated above, any reduction in the com-

putation of the Voronoi adjacency will imply an im-

provement in methods like the k-NN and condensa-

tion techniques. The aim of this paper is to present

a method for an efﬁcient computation of the Voronoi

adjacency graph. This computation is based on Lin-

ear Programming and it introduces some innovations

over papers previously referenced. The ﬁrst one is

the modiﬁcation of the Voronoi adjacency test pro-

posed by Fukuda (Fukuda, 2004) by showing that it

can be reduced to the polytope search procedure. The

second innovation is to show that the use of the dual

problem (Winston, 1994; Bazaraa et al., 1990) of the

adjacency test brings computational advantages. And

last innovation, but not least, the proposal of an ad-

jacency search strategy without backtracking. This

strategy assures the computation of the correct value

for all adjacency pairs without needing the computa-

tion of adjacency test for all the pairs.

The paper is structured as follows, ﬁrstly, the adja-

cency test for an instance pair is formulated, modiﬁed

ICPRAM 2012 - International Conference on Pattern Recognition Applications and Methods

358

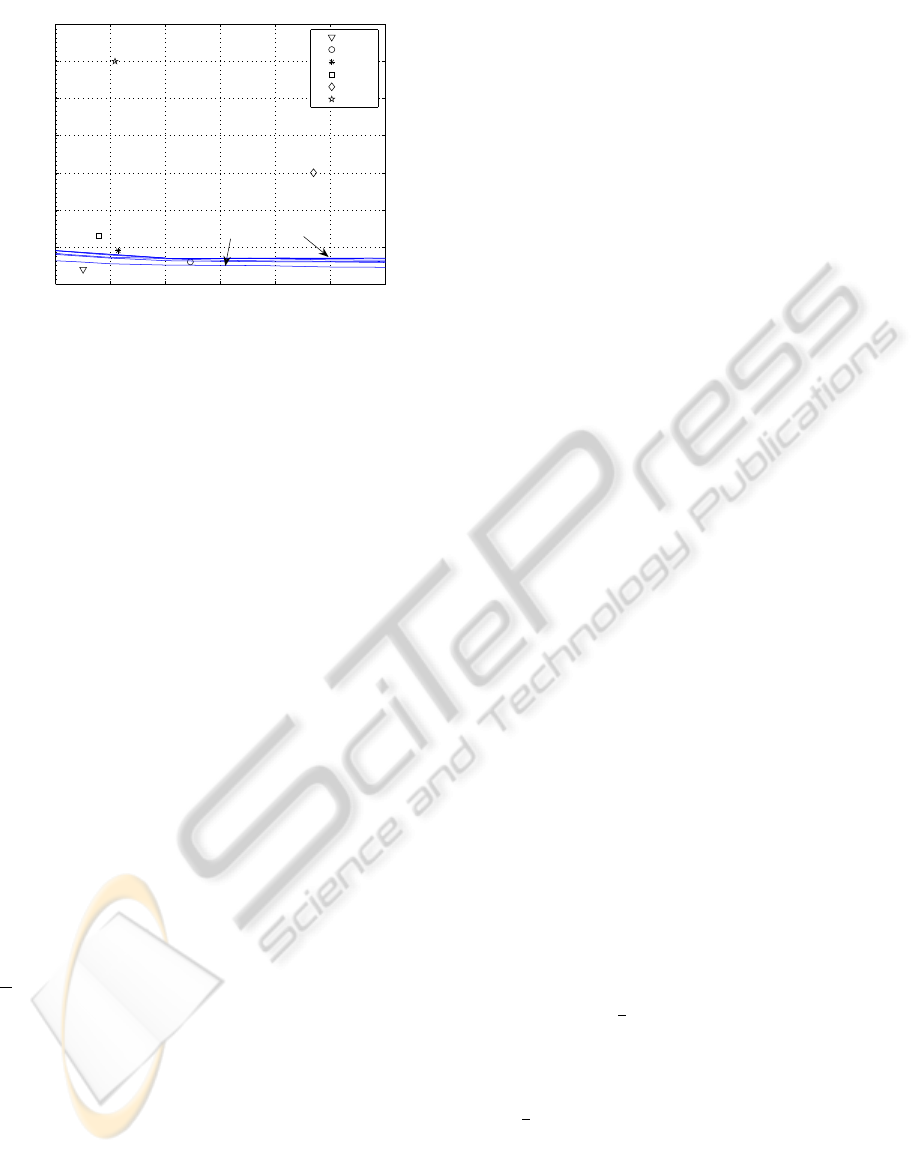
100 200 300 400 500 600 700

m (instance number)

n (space dimension)

iris

bupa

glass

wine

wdbc

sonar

qvoronoi: [1,10,20,50,100,200] secs.

Figure 2: Efﬁciency area of qvoronoi and its relation with

some of most used datasets in ML. It is very efﬁcient, but

only for low dimensionality problems.

and transformed to its dual form. Then, the proce-

dure of polytopesearch is formulated and transformed

to its dual form. It will be shown that the adjacency

test is a version of the polytope search. However, the

polytope search procedure provides more information

than a simple Boolean test. The paper proposes a

strategy to use the additional information contained in

the basis of the linear programming algorithm to ob-

tain other tests. The experiments were realized with

both artiﬁcial and real datasets. Real datasets with nu-

merical features were taken from the UCI repository

to allow comparisons with the results presented in this

work.

2 EFFICIENT COMPUTATION OF

VORONOI ADJACENCIES

One way to compute the Voronoi polyhedron of a

dataset P = {p

,...,p

} in R

is based on the con-

struction of an extended paraboloid representation in

n+1

. If x ∈ R

, the n + 1 paraboloid coordinate is:

n+1

∑

+,··· ,+x

= kxk

. If p

are the co-

ordinate values of p

, its extended representation is:

= (p

,..., p

,kp

). The set of tangent (n + 1)-

planes in every instance of the dataset generates a

polyhedron whose projection in R

is the Voronoi di-

agram (Fukuda, 2004). The polyhedron is deﬁned by

the following set of linear equations:

∑

j=1

− x

n+1

≤ kp

i = 1,...,m (1)

The adjacency of two instances p

and p

is ver-

iﬁed if they have a common separating plane in R

therefore, the tangent planes in R

n+1

in each instance

have an intersection and a common edge. This con-

dition is veriﬁed if a solution exits for the following

linear system:

∑

j=1

− x

n+1

≤ kp

i 6= a,b

∑

j=1

− x

n+1

= kp

∑

j=1

− x

n+1

= kp

(2)

This feasibility test of this linear system is related

to the solution of the following problem of linear pro-

gramming, where f() is an objective function subject

to the following constraints:

maximize f(x

,...,x

n+1

)

∑

j=1

− x

n+1

≤ kp

i 6= a,b

∑

j=1

− x

n+1

= kp

∑

j=1

− x

n+1

= kp

(3)

This problem can be solved by introducing slack

and surplus variables and using the Two-Phase

Method(Winston, 1994). The feasibility of this prob-

lem is obtained in the ﬁrst phase by solving the next

linear problem, whose goal is the minimization of the

sum of all the surplus variables:

minimize Z = s

+ s

∑

j=1

− x

n+1

+ s

= kp

i = 1,...,m

≥ 0 i = 1,...,m

(4)

The feasibility test for the original problem of

Equation (2) is that the optimal solution become null,

∗

= 0, equivalent to: s

∗

= s

∗

= 0. This problem can

be modiﬁed as:

minimize Z

′

∑

j=1

+ p

− x

n+1

∑

j=1

− x

n+1

≤ kp

i = 1,...,m

(5)

Where −Z = 2Z

′

− kp

, and the slack

and surplus variables have been hidden. The linear

programming dual of this problem is:

minimize Z

′′

∑

i=1

∑

i=1

+ p

) j = 1,...,n

∑

i=1

= 1

≥ 0 i = 1,...,m

(6)

The optimal solution of the dual must be: Z

′′∗

′∗

(kp

+ kp

2.1 Polytope Search

Voronoi polyhedra can be unbound, but a bounded

polyhedron is called a polytope. Delaunay poly-

topes are the dual of Voronoi polyhedra. The test

EFFICIENT COMPUTATION OF VORONOI NEIGHBORS BASED ON POLYTOPE SEARCH IN PATTERN

RECOGNITION

359

for Voronoi adjacency, as deﬁned in Equation (6), is

related to the problem of the polytope search. This

problem is related to ﬁnd the Delaunay polytope that

encloses a test point q ∈ R

: more precisely, in obtain-

ing the subset of the dataset instances which deﬁne

the polytope enclosing the test point. The polytope

degree ranges from 1 to n + 1 depending on the num-

ber of instances included, or the degree of degeneracy

of the polytope. Unfortunately, not all the polytopes

found are of the biggest degree of (n+ 1), however, a

lower degree provides valuable information because a

k-polytope includes k(k − 1)/2 Voronoi adjacencies.

If we are trying to ﬁnd the enclosing polytope of a

point q, the problem can be solved by using linear

programming and ﬁnding the solution for y

∈ R and

y ∈ R

verifying(Fukuda, 2004):

minimize Z = y

∑

j=1

−y

−

∑

j=1

≤ kp

i = 1,...,m

(7)

The Delaunay polytope containing the test point is

the one whose corresponding inequalities are satisﬁed

as equality when the problem reaches optimal. That

is, whose dual variables are not null. This linear pro-

gramming algorithm has two different stop states. In

the ﬁrst, the enclosing polytope is found if the prob-

lem reaches the optimality. In the second one, the

problem gets unbound and no solution is provided be-

cause the test point is outside the convex hull of the

dataset instances. If the solution is optimal but degen-

erate, a k-polytope is obtained with 1 ≤ k ≤ n+1. The

enclosing polytope can be obtained easily by solving

the dual of the Equation (7):

minimize W =

∑

i=1

∑

i=1

= q

∑

i=1

= 1

≥ 0 i = 1,...,m

(8)

If the test point is outside the convex hull, the

problem in Equation (7) becomes unbound, while its

dual in Equation (8) becomes unfeasible. If the prob-

lem is not degenerate, the number of non-null prob-

lem variables z ∈ R

is n+ 1 that deﬁne the enclosing

Delaunay polytope. If the problem is degenerate the

number of non-null variables is lower. However the

number of problem variables in the ﬁnal basis pro-

vides some additional information: if a problem vari-

able is null but is included in the ﬁnal basis, we can in-

fer that the k-polytope is a subset of a (k+1)-polytope

deﬁned by k non-null variables and this null one that

also is included in the basis. Therefore, knowledge of

the ﬁnal basis provides extra information in cases of

degeneracy.

For computational purposes the polytope search

procedure can be express as: B ← POLYTOPE(P,q).

Where B is the set of instances in P included in the

basis of the linear programming. The scalar K =

card(B) is an upper bound of the polytope degree, it

veriﬁes: 1 ≤ k ≤ K ≤ n+1. When the test point is out-

side the convex hull, we get K = 0 for computational

purpose. The Voronoi adjacencytest for two instances

in a dataset in Equation (6) corresponds to the poly-

tope search procedure in Equation (8) by testing the

middle point between the pair: q =

+ p

). This

test point is always within the convex hull, therefore

the unfeasible solution is not possible.

A Voronoi adjacency graph is constructed by tak-

ing each dataset instance as a node and the Boolean

link v

∈ {0, 1} as the value of the adjacency test be-

tween instances p

and p

. The test for every middle

point assures knowledge of the v

value, but in ev-

ery test also other v

link values are also obtained

depending on the cardinality of B. In the best case,

a number of: n(n+ 1)/2+ 1 links of the Voronoi ad-

jacency graph are obtained. In the worst case only a

link value is obtained: it occurs when the middle point

of two instances p

and p

is just another instance of

the dataset q = p

. The best case happens when the

middle point is within a Delaunay polytope that does

not include the test pair. In this case K = n+ 1, there-

fore, n(n+ 1)/2 links with true values are obtained as

well as a false one: v

= 0. The Algorithm 1 shows

the proposed procedure. It initialize all the links to

false values and only positive adjacencies are added

throughout the following steps. Table 1 contains a

trace of the computed pairs for dataset in Figure1,

where the values for the basis variables are shown.

2.2 Gabriel Adjacency

Gabriel adjacency is a subset of Voronoi adjacency,

its deﬁnition resembles the general deﬁnition of De-

launay polytope. A set of (n + 1) instances deﬁnes a

Delaunay polytope if the n-sphere that they describe

has no instance into. While, two instances are Gabriel

neighbors (Devroye et al., 1996) if no other instance

is included in the n-sphere that is centered in the mid-

dle point:

+ p

) and has a radius:

− p

that is:

−

+ p

)k ≥

− p

k ∀i 6= a,b (9)

Based on: ku− vk

= kuk

+ kvk

− 2u· v, it can

be simpliﬁed as:

· p

− p

· p

− p

· p

+ p

· p

≥ 0 ∀i 6= a,b (10)

The Delaunay test, which involves n+ 1 instances

to deﬁne the sphere, is more expensive than the

ICPRAM 2012 - International Conference on Pattern Recognition Applications and Methods

360

Algorithm 1: Computes the Voronoi adjacency graph. The input is the dataset instances, P = p

,. .., p

, and the output the

graph, V = {v

procedure ADJACENCY1(P = p

,. .. ,p

,V = {v

})

Initialize: ∀

← 0

for i ← 1,m− 1 do

for j ← i+ 1,m do ⊲ only the upper triangular

if v

= 0 then

q ←

+ p

) ⊲ the middle point between p

and p

B ←POLYTOPE(P,q) ⊲ gets the basis of the polytope

K ← card(B) ⊲ by solving Equation (8)

if K ≥ 2 then ⊲ if degeneracy: 1 ≤ K ≤ n+ 1

for h ← 1,K − 1 do

c ← B

for l ← h+ 1,K do

d ← B

← 1 ⊲ p

and p

are Voronoi neighbors

← 1 ⊲ and the symmetrical

Gabriel adjacency, which uses two instance to deﬁne a

smaller sphere. If an instance pair veriﬁes the Gabriel

test, it also veriﬁes the Voronoi neighbor test, but not

the converse. This property can be used to introduce

a cheaper but incomplete pre-test of adjacency.

The Gabriel test is advantageous if compared to

the general Delaunay test, but this advantage is un-

clear when compared with Voronoi adjacency ob-

tained with LP, because it provides only a link value

in every test. To increase the performance of the

polytope-based adjacency test, one algorithm is pro-

posed that use the cheaper Gabriel test. The Boolean

procedure GABRIEL(P, i, j) is used to test for the ad-

jacency of the instances p

and p

. In the Algorithm 2,

prior to the polytope test, a pre-test is included for

every instance. If the ﬁrst test fails, the second one

computes the pairs values.

3 RESULTS

A systematic test have been performed to show the

strength and weakness of existing tessellation proce-

dures. One of the more used and faster packages is the

before mentioned qhull(Barber et al., 1996). To solve

several problems in computational geometry in R

, it

uses the computation of the convex hull in R

n+1

as the

kernel procedure. The family of programs based on

qhull are very fast for problems with low dimension-

ality. However, they suffer the curse of dimensional-

ity when applied in high dimension problems such as

those used in ML.

The test uses several random datasets whose in-

stances are within the unit cube centered at the origin.

The dimension used are: n = 2,3, . . . , 9, 10,20, . . .,70

and te number of instances is: m = 100,200, . . ., 700.

The computation time were taken from the program

qvoronoi, a member of the qhull package. To illus-

trate the obtained results for these datasets a contour

plot was generated as shown in Figure 2. Some val-

ues from 1 to 200 seconds are plot to illustrate the

efﬁciency area of the procedure efﬁciency. The num-

ber of dimensions and instances of some of the most

used dataset in the UCI Machine Learning Repos-

itory(Asuncion and Newman, 2007) as iris, bupa,

glass, wine, wdbc and sonar are also plotted. The

Figure shows that while bupa dataset (345 instances

and dimension 6) can be effectively tessellated in 5.76

sec. on a test computer (Intel Pentium M, 1.6 Ghz and

1 GB of RAM), the glass dataset (214 instances and

dimension 9) took several hours to complete. A prac-

tical conclusion were obtained, namely, that datasets

with a dimension greater than eight can not be tessel-

lated effectively with this procedure.

The Algorithm 1 deﬁnes how to compute the

Voronoi adjacencies, which are coded as a graph. The

Boolean links v

∈ {0, 1} are symmetric: v

= v

therefore, only the upper triangular is computed. The

Algorithm was implemented in C++ using double pre-

cision real numbers. The same systematic test that

had been conducted for the qvoronoi was performed

for the implementation of the Algorithm 1. The con-

tour plot of the efﬁciency is shown in Figure 3. The

entire range of the UCI datasets is covered in the

range of 200 seconds in this test computer. The efﬁ-

ciency area seems to covera more extended area in the

n vs. m plane, which allows to cover a wide-range of

practical ML applications. In low dimension datasets,

qhull signiﬁcatively outperforms the proposed imple-

mentation, but for n ≥ 8, it is outperformed.

A performance factor is deﬁned about how many

middle point tests are required to obtain all the ad-

jacency links of a dataset. The factor is deﬁned as:

γ = 2N

test

/m(m− 1), where N

test

is the number of

EFFICIENT COMPUTATION OF VORONOI NEIGHBORS BASED ON POLYTOPE SEARCH IN PATTERN

RECOGNITION

361

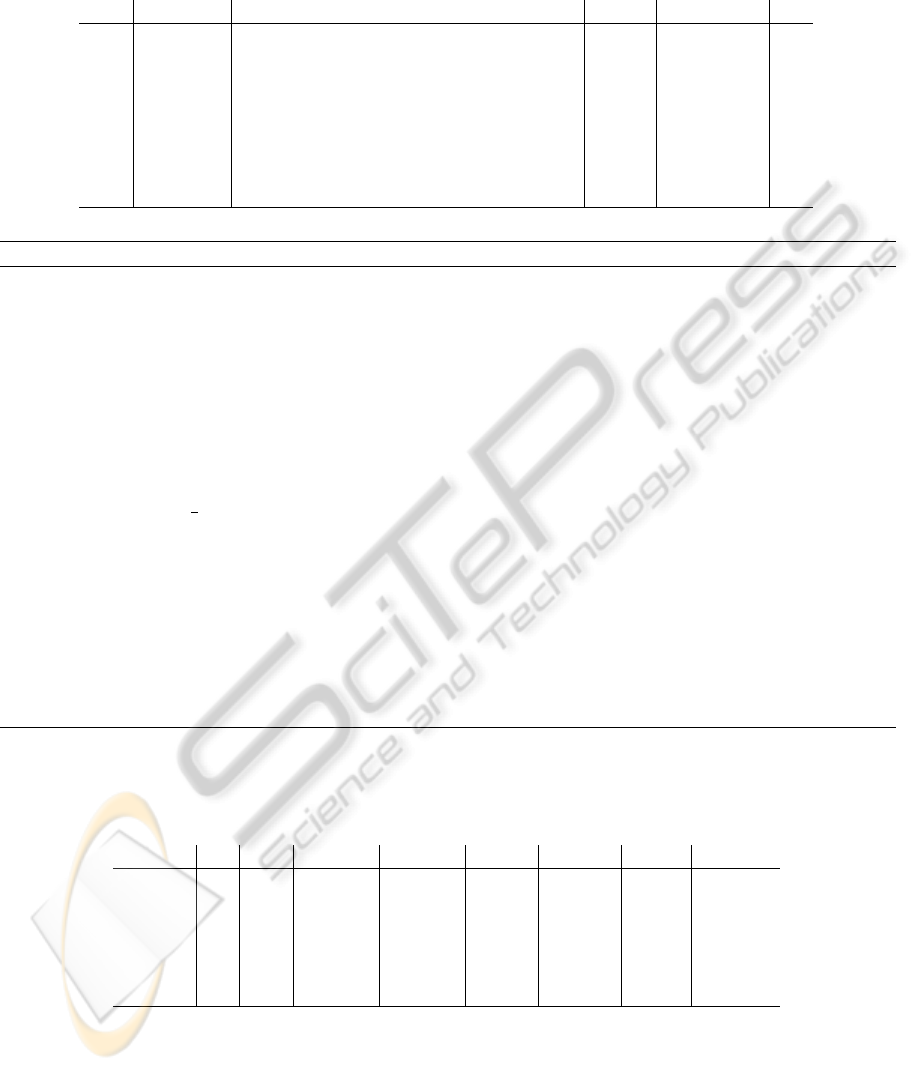
Table 1: Computation of Voronoi neighbors for the dataset in Figure 1. The Algorithm 1 takes 8 test to compute the 15

adjacent pairs, and used N

= 24 iterations of Simplex Dual algorithm. The k parameter is the polytope degree, whereas K is

the number of z variables in the basis. The ﬁlled-in z variables are those in the basis.

pair q z

k K links N

1,2 1.0 0.5 0.50 0.50 2 2 v

1,3 0.5 1.0 0.50 0.50 2 2 v

1,4 2.0 0.0 0.50 0.00 0.50 2 3 v

1,5 0.0 2.0 0.50 0.00 0.50 2 3 v

1,6 2.0 2.0 0.40 0.40 0.20 3 3 v

2,5 1.0 2.5 0.75 0.19 0.06 3 3 v

3,4 2.5 1.0 0.75 0.19 0.06 3 3 v

4,5 2.0 2.0 0.40 0.40 0.20 3 3 v

Algorithm 2: A modiﬁcation of Algorithm 1 that computes all the Grabriel pre-tests previously to the polytope ones.

procedure ADJACENCY2(P = p

,. .. ,p

,V = {v

})

Initialize: ∀

← 0

for i ← 1,m− 1 do

for j ← i+ 1,m do

if GABRIEL(P, i, j) then ⊲ tries Gabriel adjacency

= 1

for i ← 1,m− 1 do

for j ← i+ 1,m do ⊲ only the upper triangular

if v

= 0 then

q ←

+ p

) ⊲ the middle point between p

and p

B ←POLYTOPE(P,q) ⊲ gets the basis of the polytope

K ← card(B) ⊲ by solving Equation (8)

if K ≥ 2 then ⊲ if degeneracy: 1 ≤ K ≤ n+ 1

for h ← 1,K − 1 do

c ← B

for l ← h+ 1,K do

d ← B

← 1 ⊲ p

and p

are Voronoi neighbors

← 1 ⊲ and the symmetrical

Table 2: Tessellation results for several datasets coded in normalized coordinates after the KL transformation: T

the com-

putational time used by qvoronoi, T

the used by the proposed Algorithm 1, N

test

the number of middle points tested, N

the

number of Simplex iterations used to tessellate the whole dataset, and γ the performance factor. The T

column contains the

computational time for the Algoritm 2

Dataset n m T

(sec.) T

(sec.) N

test

γ T

(sec.)

iris 4 150 0.04 0.503 9349 96844 0.837 0.515

bupa 6 345 6.71 10.136 45891 783100 0.773 10.162

glass 9 214 n/a 2.708 9262 256613 0.406 2.733

wine 13 178 n/a 0.863 3082 69167 0.196 0.898

wdbc 30 569 n/a 58.886 18109 664385 0.112 61.358

sonar 60 208 n/a 6.003 5237 46555 0.243 6.752

tested pairs necessary to achieved the computation of

all Voronoi adjacencies. It depends of each dataset,

and in general would have a general dependence on m

an n. Low factor values are equivalent to high tessel-

lation performance, because its inverse provides the

average number of adjacency relations obtained for

each test. The tessellation cost not only depends on

the size of dataset m and n, it also depends on the dis-

tribution of instances. The Table 2 contains the com-

putation time for the ML Repository datasets, as well

as the N

test

and the Simplex iterations used. Normal-

ized coordinates are used after the KL transformation

because raw data coordinates are meaningless when

used in a metric distance.

ICPRAM 2012 - International Conference on Pattern Recognition Applications and Methods

362

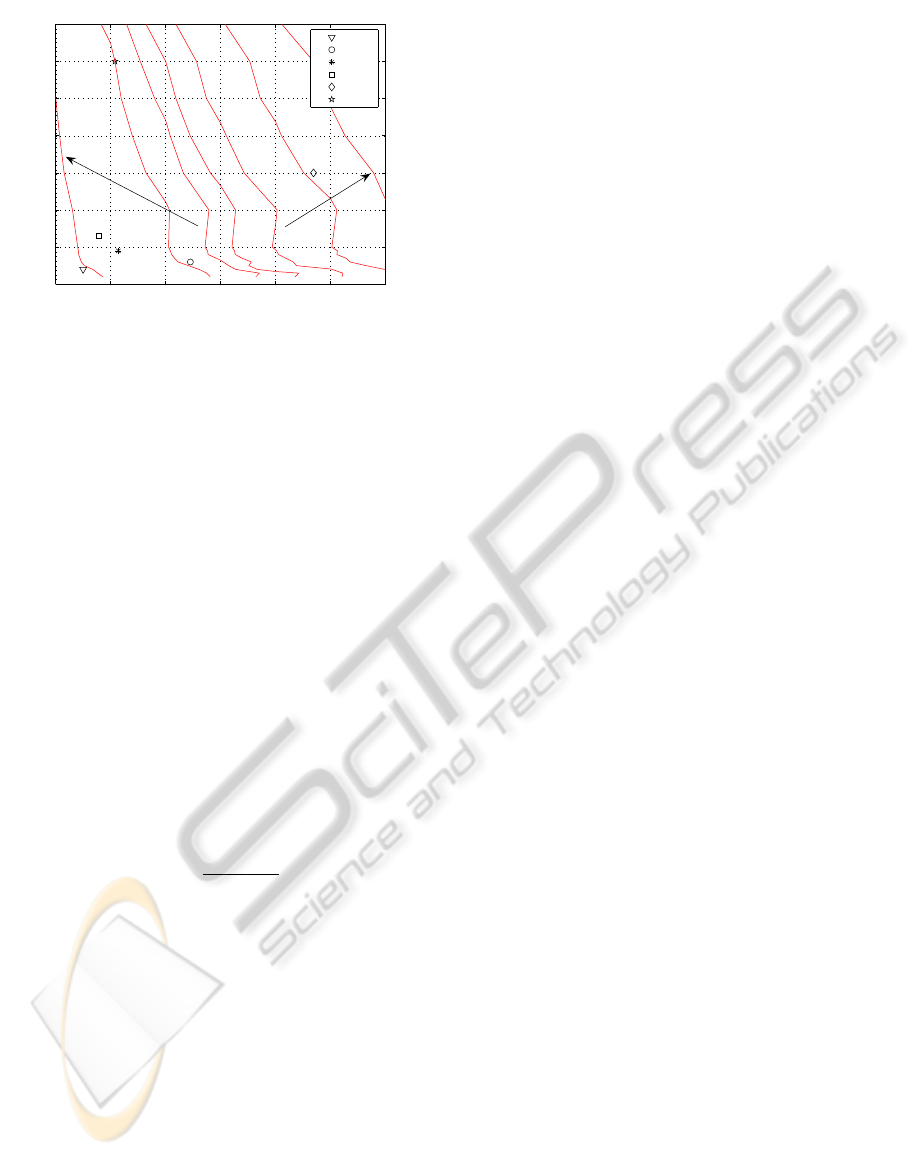
100 200 300 400 500 600 700

m (instance number)

n (space dimension)

iris

bupa

glass

wine

wdbc

sonar

[1,10,20,30,50,100,200] secs.

Figure 3: Efﬁciency area of the tessellation procedure based

on polytope search. The covered area is more extensive that

the covered by qhull and includes the datasets. However, for

low dimensional problems qhull signiﬁcatively outperforms

it.

It should be mentioned that the plotted points of

each of the ML Repository dataset in the Figure 3

are only qualitative because the plotted background

data are related to random datasets. No qvoronoi val-

ues are available for glass dataset and larger, because

these tests had not ﬁnished after several hours of com-

putation. Therefore, they are not comparable for prac-

tical purposes. These data are computed on an In-

tel Xeon, 3.06 Ghz, 512K in L2 cache and 1.5GB of

RAM. The last column contains the T

computed for

the Algorithm 2, only slight differences are detected

between the two Algorithms.

The cost analysis of proposed procedure depends

on the analysis cost of the LP problem for ﬁnding a

Polytope enclosing a point. The cost to obtain all the

Voronoi adjacencies C

AllAd

(n,m) is:

AllAd

(n,m) = γ(n,m)

m(m− 1)

Poly

(n,m) (11)

Where γ(n,m) is the fraction of the m(m − 1)/2

pairs that that are tested. It runs, in the considered

cases of the dataset in UCI, from 0.837 for iris dataset

to 0.112 for wdbc dataset. In general it would have

a general dependence on m and n that future works

could clarify. We think that it depend for every spe-

ciﬁc dataset, and that a general dependence as γ(n,m)

is only valid as an average for random datasets.

The cost to obtain a polytope, C

Poly

(n,m), is the

cost to solve a LP problem. Although we have used

in practice the Simplex Dual Algorithm for practi-

cal proposes, any of the available LP Algorithms can

be used. This algorithm choice is no central of our

proposal; such as future works will test the rela-

tive efﬁciency of other choices (Simplex based vari-

ants as well as interior methods). A founded opin-

ion (Dantzig and Thapa, 2003) is that the efﬁciency of

good implementations of simplex-based methods and

interior point methods are similar for practical appli-

cations of linear programming. However, for speciﬁc

types of LP problems, it may be that one type of algo-

rithm is better than another, but it cannot be decided

without an exhaustive test.

Is very difﬁcult to deﬁne the theoretical cost of

a LP Algorithm because we have to decide between

the cost for worst-case and the cost for average-case

in the deﬁned application. Although the worst-case

complexity of the Simplex Algorithm is exponential

in the problem dimension, it was widely known that

in practice it is probably a polynomial-time (Wright,

2004), that is in practice the Simplex method almost

always convergeson real-world problems in a number

of iterations that is polynomial in the problem dimen-

sion.

If the average cost of LP problem for poly-

tope ﬁnding is on the class of O( f(m)g(n), where

f(m) and g(n) are polynomial, so we can conclude

that the practical cost C

AllAd j

(n,m) falls in the class

O(m

f(m)g(n)) also polinomial. That is very advan-

tageous to qhull based approaches (which are in ex-

ponential O(m

n/2

) class) for large values of the space

dimensionality n, but unadvantageous for small ones.

4 CONCLUSIONS

Machine Learning applications impose unattainable

goals on traditional tessellation techniques, while lin-

ear programming provides alternative approaches to

perform the tessellation of high dimensional datasets.

Linear programming provides a sound theoretical

background for the tessellation problem as well as an

inspirational source for efﬁcient implementations. A

modiﬁcation of the Voronoi adjacency test had shown

that it is basically the polytope search procedure, en-

abling the implementation of a more efﬁcient algo-

rithm for high dimensional datasets. It is more ef-

ﬁcient that a single adjacency test because in each

trial it provides a polytope, that is many adjacency

values. These perform best if focusing on theγ pa-

rameter, which is related to the fraction of all the all-

to-all needed test. The reason for this is that, the

higher dimensionality the greater the number of in-

stances included in each polytope. This is the coun-

terpart of the curse of the dimensionality. Perhaps this

would be the reason why it permits a relative good

performance at high dimensionality. The qhull-based

and the linear programming-based implementations

are complementary because each is good in differ-

ent domains. A suitable use of both algorithms can

EFFICIENT COMPUTATION OF VORONOI NEIGHBORS BASED ON POLYTOPE SEARCH IN PATTERN

RECOGNITION

363

efﬁciently tessellate many massive datasets in Ma-

chine Learning. The use of a pre-test based on the

Gabriel adjacency, which provides a faster but incom-

plete graph of neighboring relations, does not signi-

ﬁcatively increase performance because, while it is

fast, it provides only one link value while the poly-

tope provides several link values in each test.

REFERENCES

Agrell, E. (1993). A method for examining vector quan-

tizer structures. In Proceeding of IEEE International

Symposium on Information Theory, page 394.

Asuncion, A. and Newman, D. (2007). UCI machine learn-

ing repository.

Aupetit, M. (2003). High-dimensional labeled data analy-

sis with gabriel graphs. In European Symposium on

Artiﬁcial Neuron Networks, pages 21–26.

Aupetit, M. and Catz, T. (2005). High-dimensional labeled

data analysis with topology representating graphs.

Neurocomputing, 63:139–169.

Avis, D. and Fukuda, K. (1992). A pivoting algorithm for

convex hulls and vertex enumeration of arrangements

and polyhedra. Discrete Comput. Geom., 8(3):295–

313.

Barber, C. B., Dobkin, D. P., and Huhdanpaa, H. (1996).

The quickhull algorithm for convex hulls. ACM Trans-

actions on Mathematical Software, 22(4):469–483.

Bazaraa, M. S., Jarvis, J. J., and Sherali, H. S. (1990). Lin-

near Programming and Networks Flows. Wiley.

Bhattacharya, B., Poulsen, R., and Toussaint, G. (1992).

Application of proximity graphs to editing nearest

neighbor decision rules. Technical Report SOCS

92.19, School of Computer Science, McGill Univer-

sity.

Bowyer, A. (1981). Computing Dirichlet tessellations. The

Computer Journal, 24(2):162–166.

Bremner, D., Fukuda, K., and Marzetta, A. (1997). Primal-

dual methods for vertex and facet enumeration. In

SCG ’97: Proceedings of the thirteenth annual sympo-

sium on Computational geometry, pages 49–56, New

York, NY, USA. ACM.

Chin, E., Garcia, E. K., and Gupta, M. R. (2007). Color

management of printers by regression over enclosing

neighborhoods. In IEEE International Conference on

Image Processing. ICIP 2007, volume 2, pages 161–

164.

Dantzig, G. B. and Thapa, M. N. (2003). Linear Program-

ming 2: Theory and Extensions. Springer Verlag.

Devroye, L., Gyorﬁ, L., and Lugosi, G. (1996). A Proba-

bilistic Theory of Pattern Recognition.

Duda, R., Hart, P., and Stork, D. (2001). Pattern Classiﬁca-

tion. John Wiley.

Fukuda, K. (2004). Frecuently asked questions in polyhe-

dral computation. Technical report, Swiss Federal In-

stitute of Technology, Lausanne, Switzerland.

Fukuda, K., Liebling, T. M., and Margot, F. (1997). Analy-

sis of backtrak algoritms for listing all vertices and all

faces of convex polyhedron. Computational Geome-

try, 8:1–12.

Gabriel, K. R. and Sokal, R. R. (1969). A new stattistical

approach to geographic variation analysis. Systematic

Zoology, 18:259–270.

Greeff, G. (2005). The revised simplex algorithm on a GPU.

Technical report, Dept. of Computer Science, Univer-

sity of Stellenbosch.

Gupta, M. R., Garcia, E. K., and Chin, E. (2008). Adaptive

local linear regression with application to printer color

management. IEEE Trans. on Image Processing.

Kalai, G. (1997). Linear programming, the simplex algo-

rithm and simple polytopes. Math. Program., 79:217–

233.

Koivistoinen, H., Ruuska, M., and Elomaa, T. (2006). A

voronoi diagram approach to autonomous clustering.

Lecture Notes in Computer Science, (4265):149–160.

Navarro, G. (2002). Searching in metric spaces by spatial

approximation. The VLDB Journal, 11:28–46.

Ramasubramanian, V. and Paliwal, K. (1997). Voronoi

projection-based fast nearest-neighbor search algo-

rithms: Box-search and mapping table-based search

techniques. Digital Signal Processing, 7:260–277.

Sibson, R. (1981). Interpreting multivariate data, chapter

A brief description of natural neighbour interpolation,

pages 21–36. John Wiley.

Watson, D. F. (1981). Computing the n-dimensional tes-

sellation with application to voronoi polytopes. The

Computer Journal, 24(2):167–172.

Web, A. (2002). Statistical Pattern Recognition. John Wi-

ley, 2nd edition.

Winston, W. L. (1994). Operations Research Applications

and Algorithms. Wadsworth.

Wright, M. H. (2004). The interior-point revolution in op-

timization: History, recent developments,nnd lasting

consequences. Bull. of AMS, 42(1):39–56.

Yarmish, G. and van Slyke, R. (2001). retroLP, an imple-

mentation of the standard Simplex method. Technical

report, Dept. of Computer and Information Science,

Brooklyn College.

ICPRAM 2012 - International Conference on Pattern Recognition Applications and Methods

364