
NON-PARAMETRIC SEGMENTATION OF REGIME-SWITCHING
TIME SERIES WITH OBLIQUE SWITCHING TREES
Alexei Bocharov and Bo Thiesson
Microsoft Research, One Microsoft Way, Redmond, WA 98052, U.S.A.
Keywords:
Regime-switching time series, Spectral clustering, Regression tree, Oblique split, Financial markets.
Abstract:
We introduce a non-parametric approach for the segmentation in regime-switching time-series models. The
approach is based on spectral clustering of target-regressor tuples and derives a switching regression tree,
where regime switches are modeled by oblique splits. Our segmentation method is very parsimonious in the
number of splits evaluated during the construction process of the tree–for a candidate node, the method only
proposes one oblique split on regressors and a few targeted splits on time. The regime-switching model can
therefore be learned efficiently from data. We use the class of ART time series models to serve as illustration,
but because of the non-parametric nature of our segmentation approach, it readily generalizes to a wide range
of time-series models that go beyond the Gaussian error assumption in ART models. Experimental results on
S&P 1500 financial trading data demonstrates dramatically improved predictive accuracy for the exemplifying
ART models.
1 INTRODUCTION
The analysis of time-series data is an important area
of research with applications in areas such as natu-
ral sciences, economics, and financial trading to men-
tion a few. Consequently, a wide range of time-series
models and algorithms can be found in the literature.
Many time series exhibit non-stationarity due to
regime switching, and proper detection and modeling
of this switching is a major challenge in time-series
analysis. In regime-switching models, the parame-
ters of the model change between regimes from time
to time in order to reflect changes in the underlying
conditions for the time series. As a simple exam-
ple, the volatility or the basic trading value of a stock
may change according to events such as earnings re-
ports or analysts’ upgrades or downgrades. Patterns
may repeat and, as such, it is possible that the model
switches back to a previous regime.
A wide variety of standard mixture modeling ap-
proaches have over the years been adapted to model
regime-switching time series. In Markov-switching
models (see, e.g., Hamilton, 1989, 1990) a Markov
evolving hidden state indirectly partitions the time-
series data to fit local auto-regressive models in the
mixture components. Another large body of work
(see, e.g., Waterhouse and Robinson, 1995; Weigend
et al., 1995) have adapted the hierarchical mixtures
of experts (Jordan and Jacobs, 1994) to regime-
switching time-series models. In these models–also
denoted as gated experts–the hierarchical gates ex-
plicitly operate on the data in order to define a parti-
tion into local regimes. In both the Markov-switching
and the gated expert models, the determination of the
partition and the local regimes are tightly integrated
in the learning algorithm and demands an iterative ap-
proach, such as the EM algorithm. Furthermore, the
learned partitions have ”soft” boundaries, in the sense
that multiple regimes may contribute to the explana-
tion of data at any point in time.
In this paper, we focus on a more simplistic di-
rection for adapting mixture modeling to regime-
switching time series, which will more easily lend it-
self to explanatory analysis. In that respect, it con-
trasts the above work in the following ways: 1) a
modular separation of the partition and the regime
learning makes it easy to experiment with different
types of models in the local regimes, potentially using
out-of-the-box implementations for the learning, and
2) a direct and deterministic dependence on data in
the switching conditions makes the regime-switching
models easier to interpret.
We model the actual switching conditions in a
regime-switching model in the form of a regression
tree and call it the switching tree. Typically, the con-
struction of a regression tree is a stagewise process
116
Bocharov A. and Thiesson B. (2012).
NON-PARAMETRIC SEGMENTATION OF REGIME-SWITCHING TIME SERIES WITH OBLIQUE SWITCHING TREES.
In Proceedings of the 1st International Conference on Pattern Recognition Applications and Methods, pages 116-125
DOI: 10.5220/0003758601160125
Copyright
c
SciTePress

that involves three ingredients: 1) a split proposer that
creates split candidates to consider for a given (leaf)
node in the tree, 2) one or more scoring criteria for
evaluating the benefit of a split candidate, and 3) a
search strategy that decides which nodes to consider
and which scoring criterion to apply at any state dur-
ing the construction of the tree. Since the seminal
paper (Breiman et al., 1984) popularized the classic
classification and regression tree (CART) algorithm,
the research community has given a lot of attention
to both types of decision trees. Many different algo-
rithms have been proposed in the literature by varying
specifics for the three ingredients in the construction
process mentioned above.
Although there has been much research on learn-
ing regression trees, we know of only one setting,
where these models have been used as switching trees
in regime-switching time series models–namely the
class of auto-regressive tree (ART) models (Meek
et al., 2002). The ART models is a generaliza-
tion of the well-known auto-regressive (AR) mod-
els (e.g.,(Hamilton, 1994)) that is the foundation of
many time-series analyses. The ART models gen-
eralize these models by having a regression tree de-
fine the switching between the different AR models
in the leafs. As such, the well-known threshold auto-
regressive (TAR) models (Tong and Lim, 1980; Tong,
1983) can also be considered as a specialization of an
ART model with the regression tree limited to a sin-
gle split variable. We offer a different approach to
building the switching tree than (Meek et al., 2002),
but we will throughout the paper use the ART models
to both exemplify our approach and at the same time
emphasize the differences with our work.
In particular, we propose a novel improvement to
the way ART creates the candidate splits during the
switching tree construction. A split defines a predi-
cate, which, given the values of regressor variables,
decides on which side of the split a data case should
belong.
1
A predicate may be as simple as checking
if the value of a regressor is below some threshold or
not. We will refer to this kind of split as an axial split,
and it is in fact the only type of splits allowed in the
original ART models. Importantly, we show that for a
broad class of time series, the best split is not likely to
be axial, and we therefore extend the switching trees
to allow for so-called oblique splits. The predicate in
an oblique split tests if a linear combination of values
for the regressors is less than a threshold value.
It may sometimes be possible to consider and eval-
uate the efficacy of all feasible axial splits for the
1
For clarity of presentation, we will focus on binary
splits only. It is a trivial exercise to extend our proposed
method to allow for n-ary splits.
data associated with a node in the tree, but for com-
binatorial reasons, oblique splitting rarely enjoys this
luxury. We therefore need a split proposer, which is
more careful about the candidate splits it proposes. In
fact, our approach is extreme in that respect by only
proposing a single oblique split to be considered for
any given node during the construction of the tree.
Our oblique split proposer involves a simple two step
procedure. In the first step, we use a spectral clus-
tering method to separate the data in a node into two
classes. Having separated the data, the second step
now proceeds as a simple classification problem, by
using a linear discriminant method to create the best
separating hyperplane for the two data classes. Any
discriminant method can be used, and there is in prin-
ciple no restriction on it being linear, if more compli-
cated splits are sought.
Oblique splitting has enjoyed significant attention
for the classification tree setting. See, e.g., (Breiman
et al., 1984; Murthy et al., 1994; Brodley and Ut-
goff, 1995; Gama, 1997; Iyengar, 1999). Less atten-
tion has been given to the regression tree setting, but
still a number of methods has come out of the statis-
tics and machine learning communities. See, e.g.,
(Dobra and Gehrke, 2002; Li et al., 2000; Chaud-
huri et al., 1994) to mention a few. Setting aside the
time-series context for our switching trees, the work
in (Dobra and Gehrke, 2002) is in style the most sim-
ilar to the oblique splitting approach that we propose
in this paper. In (Dobra and Gehrke, 2002), the EM
algorithm for Gaussian mixtures is used to cluster the
data. Having committed to Gaussian clusters it now
makes sense to determine a separating hyperplane via
a quadratic discriminant analysis for a projection of
the data onto a vector that ensures maximum separa-
tion of the Gaussians. This vector is found by mini-
mizing Fisher’s separability criterion.
We will in our method do without the dependence
on parametric models when creating an oblique split
candidate for the following two reasons. First of all,
we consider the class of ART models for the pur-
pose of illustration only. Without the dependence
on specific parametric assumptions, our approach can
be readily generalized to a wide range of time-series
models that go beyond the limit of the Gaussian er-
ror assumption in these models. For example, long-
tailed, skewed, or other non-Gaussian errors, as of-
ten encountered in finance (see, e.g., Mandelbrot and
Hudson, 2006; Mandelbrot, 1966). Second, it is a
common claim in the literature that spectral cluster-
ing often outperforms traditional parametric cluster-
ing methods, and it has become a popular geometric
clustering tool in many areas of research (see, e.g.,
von Luxburg, 2007).
NON-PARAMETRIC SEGMENTATION OF REGIME-SWITCHING TIME SERIES WITH OBLIQUE SWITCHING
TREES
117

Spectral clustering dates back to the work in (Do-
nath and Hoffman, 1973; Fiedler, 1973) that sug-
gest to use the method for graph partitionings. Vari-
ations of spectral clustering have later been popu-
larized in the machine learning community (Shi and
Malik, 2000; Meil
˘
a and Shi, 2001; Ng et al., 2002),
and, importantly, very good progress has been made
in improving an otherwise computationally expensive
eigenvector computation for these methods (White
and Smyth, 2005). We use a simple variation of the
method in (Ng et al., 2002) to create a spectral clus-
tering for the time series data in a node. Given this
clustering, we then use a simple perceptron learning
algorithm (e.g., (Bishop, 1995)) to find a hyperplane
that defines a good oblique split predicate for the au-
toregressors in the model.
Let us now turn to the possibility of splitting on
the time feature in a time series. Due to the special
nature of time, it does not make sense to involve this
feature as an extra dimension in the spectral cluster-
ing; it would not add any discriminating power to the
method. Instead, we propose a procedure for time
splits, which uses the spectral clustering in another
way. The procedure identifies specific points in time,
where succeeding data elements in the series cross the
cluster boundary, and proposes time splits at those
points. Our split proposer will in this way use the
spectral clustering to produce both the oblique split
candidate for the regressors, and a few very targeted
(axial) split candidates for the time dimension.
The rest of the paper is organized as follows. In
Section 2, we briefly review the ART models that
we use to exemplify our work, and we define and
motivate the extension that allows for oblique splits.
Section 3 reviews the general learning framework for
ART models. Section 4 contains the details for both
aspects of our proposed spectral splitting method–
the oblique splitting and the time splitting. In Sec-
tions 5 and 6 we describe experiments and provide ex-
perimental evidence demonstrating that our proposed
spectral splitting method dramatically improves the
quality of the learned ART models over the current
approach. We will conclude in Section 7.
2 STANDARD AND OBLIQUE
ART MODELS
We begin by introducing some notation. We de-
note a temporal sequence of variables by X =
(X
1
,X
2
,...,X
T
), and we denote a sub-sequence con-
sisting of the i’th through the j’th element by X
j
i
=
(X
i
,X
i+1
,...,X
j
), i < j. Time-series data is a se-
quence of values for these variables denoted by x =
(x
1
,x
2
,...,x
T
). We assume continuous values, ob-
tained at discrete, equispaced intervals of time.
An autoregressive (AR) model of length p, is sim-
ply a p-order Markov model that imposes a linear re-
gression for the current value of the time series given
the immediate past of p previous values. That is,
p(x
t
|x
t−1
1
) = p(x
t
|x
t−1
t−p
) ∼ N (m +
p
∑
j=1
b
j
x
t−j
,σ
2
)
where N (µ,σ
2
) is a conditional normal distri-
bution with mean µ and variance σ
2
, and θ =
(m,b
1
,...,b
p
,σ
2
) are the model parameters (?,
e.g.,)page 55]DeGroot:1970.
The ART models is a regime-switching general-
ization of the AR models, where a switching regres-
sion tree determines which AR model to apply at each
time step. The autoregressors therefore have two pur-
poses: as input for a classification that determines a
particular regime, and as predictor variables in the
linear regression for the specific AR model in that
regime.
As a second generalization
2
, ART models may al-
low exogenous variables, such as past observations
from related time series, as regressors in the model.
Time (or time-step) is a special exogenous variable,
only allowed in a split condition, and is therefore only
used for modeling change points in the series.
2.1 Axial and Oblique Splits
Different types of switching regression trees can be
characterized by the kind of predicates they allow for
splits in the tree. The ART models allow only a simple
form of binary splits, where a predicate tests the value
of a single regressor. The models handle continuous
variables, and a split predicate is therefore of the form
X
i
≤ c
where c is a constant value and X
i
is any one of the re-
gressors in the model or a variable representing time.
A simple split of this type is also called axial, because
the predicate that splits the data at a node can be con-
sidered as a hyperplane that is orthogonal to the axis
for one of the regressor variables or the time variable.
The best split for a node in the tree can be learned
by considering all possible partitionings of the data
according to each of the individual regressors in the
model, and then picking the highest scoring split for
these candidates according to some criterion. It can,
2
The class of ART models with exogenous variables has
not been documented in any paper. We have learned about
this generalization from communications with the authors
of (Meek et al., 2002).
ICPRAM 2012 - International Conference on Pattern Recognition Applications and Methods
118

however, be computationally demanding to evaluate
scores for that many split candidates, and for that rea-
son, (Chickering et al., 2001) investigated a Gaussian
quantile approach that proposes only 15 split points
for each regressor. They found that this approach
is competitive to the more exhaustive approach. A
commercial implementation for ART models uses the
Gaussian quantile approach and we will compare our
alternative to this approach.
We propose a solution, which will only produce
a single split candidate to be considered for the en-
tire set of regressors. In this solution we extend the
class of ART models to allow for a more general split
predicate of the form
∑
i
a
i
X
i
≤ c (1)
where the sum is over all the regressors in the model
and a
i
are corresponding coefficients. Splits of this
type are in (Murthy et al., 1994) called oblique due to
the fact that a hyperplane that splits data according to
the linear predicate is oblique with respect to the re-
gressor axes. We will in Section 4 describe the details
behind the method that we use to produce an oblique
split candidate.
2.2 Motivation for Oblique Splits
There are general statistical reasons why, in many sit-
uations, oblique splits are preferable over axial splits.
In fact, for a broad class of time series, the best
splitting hyperplane turns out to be approximately or-
thogonal to the principal diagonal d = (
1
√
p
,...,
1
√
p
).
To qualify this fact, consider two pre-defined classes
of segments x
(c)
,c = 1, 2 for the time-series data x.
Let µ
(c)
and Σ
(c)
denote the mean vector and covari-
ance matrix for the sample joint distribution of X
t−1
t−p
,
computed for observations on p regressors for targets
x
t
∈ x
(c)
.
Let us define the moving average A
t
=
1
p
∑
p
i=1
X
t−i
.
We show in the Appendix that in the context where
X
t−i
−A
t
is weakly correlated with A
t
, while its vari-
ance is comparable with that of A
t
, the angle between
the principal diagonal and one of the principal axes
of Σ
(c)
,c = 1,2 is small. This would certainly be the
case with a broad range of financial data, where in-
crements in price curves have notoriously low corre-
lations with price values (Samuelson, 1965; Mandel-
brot, 1966), while seldom overwhelming the averages
in magnitude. With one of the principal axes being
approximately aligned with the principal diagonal d
for both Σ
(1)
and Σ
(2)
it is unlikely that a cut orthogo-
nal to either of the coordinate axes X
t−1
,...,X
t−p
can
provide optimal separation of the two classes. (The
argument depends on all eigenvalues for Σ
(c)
being
distinct; a somewhat different argument involving the
geometry of mean vectors µ
(c)
is needed in the special
case, where the eigenvalues are not distinct.)
3 THE LEARNING PROCEDURE
An ART model is typically learned in a stagewise
fashion. The learning process starts from the trivial
model without any regressors and then greedily adds
regressors one at a time until the learned model does
not improve a chosen scoring criterion. The candi-
date regressors considered at any given stage in this
process consist of the autoregressor one step further
back in time than currently accepted in the model and
possibly a preselected set of exogenous variables from
related cross-predicting time series.
The task of learning a specific autoregressive
model considered at any stage in this process can be
cast into a standard task of learning a linear regres-
sion tree. It is done by a trivial transformation of
the time-series data into multivariate data cases for
the regressor and target variables in the model. For
example, when learning an ART model of length p
with an exogenous regressor, say z
t−q
, from a re-
lated time series, the transformation creates the set of
T − max(p, q) cases of the type (x
t
t−p
,z
t−q
), where
max(p,q) + 1 < t ≤ T . We will in the following de-
note this transformation as the phase view, due to a
vague analogy to the phase trajectory in the theory of
dynamical systems.
Most regression tree learning algorithms construct
a tree in two stages (see, e.g., Breiman et al., 1984):
First, in a growing stage, the learning algorithm will
maximize a scoring criterion by recursively trying to
replace leaf nodes by better scoring splits. A least-
squares deviation criterion is often used for scoring
splits in a regression tree. Typically the chosen crite-
rion will cause the selection of an overly large tree
with poor generalization. In a pruning stage, the
tree is therefore pruned back by greedily eliminating
leaves using a second criterion–such as the holdout
score on a validation data set–with the goal of mini-
mizing the error on unseen data.
In contrast, (Meek et al., 2002) suggests a learn-
ing algorithm that uses a Bayesian scoring criterion,
described in detail in that paper. This criterion avoids
over-fitting by penalizing for the complexity of the
model, and consequently, the pruning stage is not
needed. We use this Bayesian criterion in our experi-
mental section.
In the next section, we describe the details of the
algorithm we propose for producing the candidate
NON-PARAMETRIC SEGMENTATION OF REGIME-SWITCHING TIME SERIES WITH OBLIQUE SWITCHING
TREES
119

splits that are considered during the recursive con-
struction of a regression tree. Going from axial to
oblique splits adds complexity to the proposal of can-
didate splits. However, our split proposer dramati-
cally reduces the number of proposed split candidates
for the nodes evaluated during the construction of the
tree, and by virtue of that fact spends much less time
evaluating scores of the candidates.
4 SPECTRAL SPLITTING
This section will start with a brief description of spec-
tral clustering, followed by details about how we ap-
ply this method to produce candidate splits for an
ART time-series model. A good tutorial treatment
and an extensive list of references for spectral clus-
tering can be found in (von Luxburg, 2007).
The spectral splitting method that we propose
constructs two types of split candidates–oblique and
time–both relying on spectral clustering. Based on
this clustering, the method applies two different views
on the data–phase and trace–according to the type of
splits we want to accomplish. The algorithm will only
propose a single oblique split candidate and possibly a
few time split candidates for any node evaluated dur-
ing the construction of the regression tree.
4.1 Spectral Clustering
Given a set of n multi-dimensional data points
(x
1
,...,x
n
), we let a
i j
= a(x
i
,x
j
) denote the affin-
ity between the i’th and j’th data point, accord-
ing to some symmetric and non-negative measure.
The corresponding affinity matrix is denoted byA =
(a
i j
)
i, j=1,...,n
, and we let D denote the diagonal matrix
with values
∑
n
j=1
a
i j
, i = 1,...,n on the diagonal.
Spectral clustering is a non-parametric clustering
method that uses the pairwise affinities between data
points to formulate a criterion that the clustering must
optimize. The trick in spectral clustering is to en-
hance the cluster properties in the data by changing
the representation of the multi-dimensional data into
a (possibly one-dimensional) representation based on
eigenvalues for the so-called Laplacian.
L = D −A
Two different normalizations for the Laplacian have
been proposed in (Shi and Malik, 2000) and (Ng et al.,
2002), leading to two slightly different spectral clus-
tering algorithms. We will follow a simplified version
of the latter. Let I denote the identity matrix. We
will cluster the data according to the second small-
est eigenvector–the so-called Fiedler vector (Fiedler,
1973)–of the normalized Laplacian
L
norm
= D
−1/2
LD
−1/2
= I −D
−1/2
AD
−1/2
The algorithm is illustrated in Figure 1. Notice that
we replace L
norm
with
L
0
norm
= I −L
norm
which changes eigenvalues from λ
i
to 1 − λ
i
and
leaves eigenvectors unchanged. We therefore find the
eigenvector for the second-largest and not the second-
smallest eigenvector. We prefer this interpretation of
the algorithm for reasons that become clear when we
discuss iterative methods for finding eigenvalues in
Section 4.2.
1. Construct the matrix L
0
norm
.
2. Find the second-largest eigenvector e =
(e
1
,...,e
n
) of L
0
norm
.
3. Cluster the elements in the eigenvector (e.g.
by the largest gap in values).
4. Assign the original data point x
i
to the clus-
ter assigned to e
i
.
Figure 1: Simple normalized spectral clustering algorithm.
Readers familiar with the original algorithm in
(Ng et al., 2002) may notice the following simplifi-
cations: First, we only consider a binary clustering
problem, and second, we only use the two largest
eigenvectors for the clustering, and not the k largest
eigenvectors in their algorithm. (The elements in the
first eigenvector always have the same value and will
therefore not contribute to the clustering.) Due to
the second simplification, the step in their algorithm
that normalizes rows of stacked eigenvectors can be
avoided, because the constant nature of the first eigen-
vector leaves the transformation of the second eigen-
vector monotone.
4.2 Oblique Splits
Oblique splits are based on a particular view of the
time series data that we call the phase view, as de-
fined in Section 3. Importantly, a data case in the
phase view involves values for both the target and re-
gressors, which imply that our oblique split proposals
may capture regression structures that show up in the
data–as opposed to many standard methods for axial
splits that are ignorant to the target when determining
split candidates for the regressors.
It should also be noted that because the phase view
has no notion of time, similar patterns from entirely
different segments of time may end up on the same
side of an oblique split. This property can at times
ICPRAM 2012 - International Conference on Pattern Recognition Applications and Methods
120

result in a great advantage over splitting the time se-
ries into chronological segments. First of all, splitting
on time imposes a severe constraint on predictions,
because splits in time restrict the prediction model to
information from the segment latest in time. Informa-
tion from similar segments earlier in the time series
are not integrated into the prediction model in this
case. Second, we may need multiple time splits to
mimic the segments of one oblique split, which may
not be obtainable due to the degradation of the statis-
tical power from the smaller segments of data. Fig-
ure 2(d) shows an example, where a single oblique
split separates the regime with the less upward trend-
ing and slightly more volatile first and third data seg-
ments of the time series from the regime consisting of
the less volatile and more upward trending second and
fourth segments. In contrast, we would have needed
three time splits to properly divide the segments and
these splits would therefore have resulted in four dif-
ferent regimes.
Our split proposer produces a single oblique split
candidate in a two step procedure. In the first step, we
strive to separate two modes that relates the target and
regressors for the model in the best possible way. To
accomplish this task, we apply the affinity based spec-
tral clustering algorithm, described in Section 4.1, to
the phase view of the time series data. For the exper-
iments reported later in this paper, we use an affinity
measure proportional to
1
1 + ||p
1
−p
2
||
2
where ||p
1
− p
2
||
2
is the L2-norm between two
phases. We do not consider exogenous regressors
from related time series in these experiments. All
variables in the phase view are therefore on the same
scale, making the inverse distance a good measure
of proximity. With exogenous regressors, more care
should be taken with respect to the scaling of variables
in the proximity measure, or the time series should be
standardized. Figure 2(b) demonstrates the spectral
clustering for the phase view of the time-series data
in Figure 2(a), where this phase view has been con-
structed for an ART model with two autoregressors.
The oblique split predicate in (1) defines an in-
equality that only involves the regressors in the
model. The second step of the oblique split pro-
poser therefore projects the clustering of the phase
view data to the space of the regressors, where the
hyperplane separating the clusters is now constructed.
While this can be done with a variety of linear dis-
crimination methods, we decided to use a simple
single-layer perceptron optimizing the total misclas-
sification count. Such perceptron will be relatively
insensitive to outliers, compared to, for example,
Fisher’s linear discriminant.
The computational complexity of an oblique split
proposal is dominated by the cost of computing the
full affinity matrix, the second largest eigenvector for
the normalized Laplacian, and finding the separating
hyperplane for the spectral clusters. Recall that n de-
notes the number of cases in the phase view of the
data. The cost of computing the full affinity matrix is
therefore O(n
2
) affinity computations. Direct meth-
ods for computing the second largest eigenvector is
O(n
3
). A complexity of O(n
3
) may be prohibitive
for series of substantial length. Fortunately, there are
approximate iterative methods, which in practice are
much faster with tolerant error. For example, the Im-
plicitly Restarted Lanczos Method (IRLM) has com-
plexity O(mh + nh), where m is the number of non-
zero affinities in the affinity matrix and h is the num-
ber of iterations required until convergence (White
and Smyth, 2005). With a full affinity matrix m = n
2
,
but a significant speedup can be accomplished by only
recording affinities above a certain threshold in the
affinity matrix. Finally, the perceptron algorithm has
complexity O(nh).
4.3 Time Splits
A simple but computationally expensive way of de-
termining a good time split is to let the split pro-
poser nominate all possible splits in time for the fur-
ther evaluation. The commercial implementation of
the ART models relies on an approximation to this
approach that proposes a smaller set of equispaced
points on the time axis.
We suggest a data driven approximation, which
will more precisely target the change points in the
time series. Our approach is based on another view
of the time series data that we call the trace view. In
the trace view we use the additional time information
to label the phase view data in the spectral clustering.
The trace view, now traces the clustered data through
time and proposes a split point each time the trace
jumps across clusters. The rationale behind our ap-
proach is that data in the same cluster will behave in a
similar way, and we can therefore significantly reduce
the number of time-split proposals by only proposing
the cluster jumps. As an example, the thin lines or-
thogonal to the time axis in Figure 2(d) shows the few
time splits proposed by our approach. Getting close
to a good approximation for the equispaced approach
would have demanded far more proposed split points.
Turning now to the computational complexity.
Assuming that spectral clustering has already been
performed for the oblique split proposal, the addi-
tional overhead for the trace through data is O(n).
NON-PARAMETRIC SEGMENTATION OF REGIME-SWITCHING TIME SERIES WITH OBLIQUE SWITCHING
TREES
121
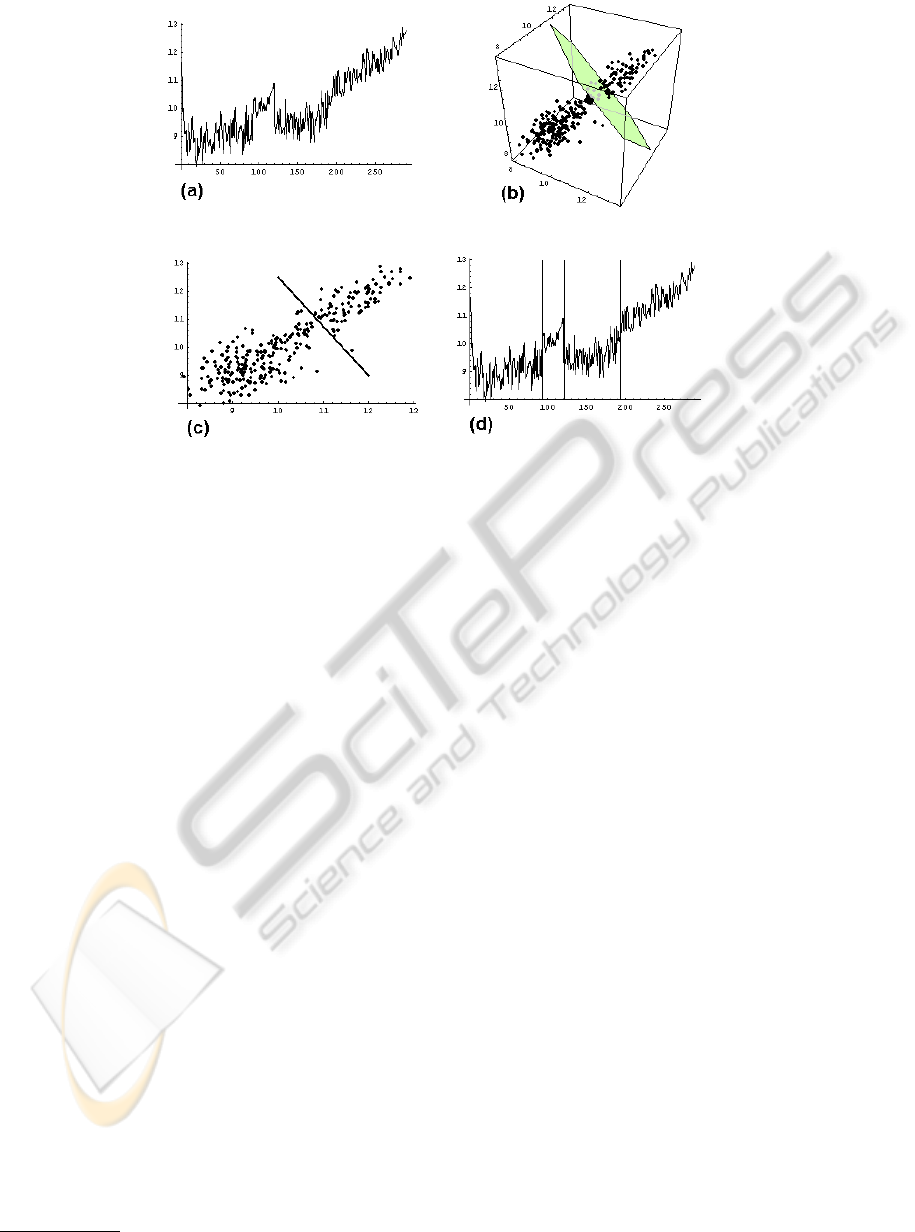
Figure 2: Oblique split candidate for ART model with two autoregressors. (a) The original time series. (b) The spectral
clustering of phase-view data. The polygon separating the upper and lower parts is a segment of a separating hyperplane for
the spectral clusters (c) The phase view projection to regressor plane and the separating hyperplane learned by the perceptron
algorithm. (d) The effect of the oblique split on the original time series: a regime consisting of the slightly less upward
trending and more volatile first and third data segments is separated from the regime with more upward trending and less
volatile second and fourth segments.
5 EVALUATION
In this section, we provide an empirical evaluation for
our spectral splitting methods. We use a large collec-
tion of financial trading data. The collection contains
the daily closing prices for 1495 stocks from Standard
& Poor’s 1500 index
3
as of January 1, 2008. Each
time series spans across approximately 150 trading
days ending on February 1, 2008. (Rotation of stocks
in the S&P 1500 lead to the exclusion of 5 stocks with
insuffient data.) The historic price data is available
from Yahoo!, and can be downloaded with queries of
format http://finance.yahoo.com/q/hp?s=SYMBOL,
where SYMBOL is the symbol for the stock in the
index. We divide each data set into a training set,
used as input to the learning method, and a holdout
set, used to evaluate the models. We use the last five
observations as the holdout set, knowing that the data
are daily with trading weeks of five days.
In our experiments, we learn ART models with an
arbitrary number of autoregressors and we allow time
as an exogenous split variable. We do not complicate
the experiments with the use of exogenous regressors
from related time series, as this complication is irrele-
vant to the objective for this paper. For all the models
that we learn, we use the same Bayesian scoring cri-
3
standardandpoors.com
terion, the same greedy search strategy for finding the
number of autoregressors, and the same method for
constructing a regression tree – except that different
alternative split candidates are considered for the dif-
ferent splitting algorithms that we consider.
We evaluate two different types of splitting with
respect to the autoregressors in the model: Axial-
Gaussian and ObliqueSpectral. The AxialGaussian
method is the standard method used to propose mul-
tiple axial candidates for each split in an ART model,
as described in Section 2.1. The ObliqueSpectral
method is our proposed method, which for a split con-
siders only a single oblique candidate involving all re-
gressors. In combination with the two split proposer
methods for autoregressors, we also evaluate three
types of time splitting: NoSplit, Fixed, and Time-
Spectral. The NoSplit method does not allow any
time splits. The Fixed method is the simple standard
method for learning splits on time in an ART model,
as described in Section 4.3. The TimeSpectral method
is our spectral clustering-based alternative. In order
to provide context for the numbers in the evaluation
of these methods, we will also evaluate a very weak
baseline, namely the method not allowing any splits.
We call this method the Baseline method.
We evaluate the quality of a learned model by
computing the sequential predictive score for the
ICPRAM 2012 - International Conference on Pattern Recognition Applications and Methods
122

holdout data set corresponding to the training data
from which the model was learned. The sequential
predictive score for a model is simply the average log-
likelihood obtained by a one-step forecast for each of
the observations in the holdout set. To evaluate the
quality of a learning method, we compute the average
of the sequential predictive scores obtained for each
of the time series in the collection. Note that the use
of the log-likelihood to measure performance simul-
taneously evaluates both the accuracy of the estimate
and the accuracy of the uncertainty of the estimate.
Finally, we use a (one-sided) sign test to evaluate if
one method is significantly better than another. To
form the sign test, we count the number of times one
method improves the predictive score over the other
for each individual time series in the collection. Ex-
cluding ties, we seek to reject the hypothesis of equal-
ity, where the test statistic for the sign test follows a
binomial distribution with probability parameter 0.5.
6 RESULTS
To make sure that the results reported here are not
an artifact of sub-optimal axial splitting for the Ax-
ialGaussian method, we first verified the claim from
(Chickering et al., 2001) that the Gaussian quantiles
is a sufficient substitute for the exhaustive set of pos-
sible axial splits. We compared the sequential predic-
tive scores on 10% of the time series in our collection
and did not find a significant difference.
Table 1 shows the average sequential predictive
scores across the series in our collection for each
combination of autoregressor and time-split proposer
methods. First of all, for splits on autoregressors, we
see a large improvement in score with our Oblique-
Spectral method over the standard AxialGaussian
method. Even with the weak baseline–namely the
method not allowing any splits–the relative improve-
ment from AxialGaussian to ObliqueSpectral over the
improvement from the baseline to AxialGaussian is
still above 20%, which is quite impressive.
The fractions in Table 2 report the number of times
one method has higher score than another method for
all the time series in our collection. Notice that the
numbers in a fraction do not necessarily sum to 1495,
because we are not counting ties. We particularly no-
tice that the ObliqueSpectral method is significantly
better than the standard AxialGaussian method for all
three combinations with time-split proposer methods.
In fact, the sign test rejects the hypothesis of equality
at a significance level < 10
−5
in all cases. Combin-
ing the results from Tables 1 and 2, we can conclude
that the large improvement in the sequential predic-
Table 1: Average sequential predictive scores for each com-
bination of autoregressor and time split proposer methods.
Regressor splits Time splits Ave. score
Baseline Baseline -3.07
AxialGaussian NoSplit -1.73
AxialGaussian Fixed -1.72
AxialGaussian TimeSpectral -1.74
ObliqueSpectral NoSplit -1.45
ObliqueSpectral Fixed -1.46
ObliqueSpectral TimeSpectral -1.44
Table 2: Pairwise comparisons of sequential predictive
scores. The fractions show the number of time series, where
one method has higher score than the other. The column
labels denote the autoregressor split proposers being com-
pared.
Baseline / Baseline / AxialGaussian /
AxialGaussian ObliqueSpectral ObliqueSpectral
NoSplit 118 / 959 74 / 1168 462 / 615
Fixed 114 / 990 79 / 1182 226 / 418
SpectralTime 122 / 955 71 / 1171 473 / 604
tive scores for our ObliqueSpectral method over the
standard AxialGaussian method is due to a general
trend in scores across individual time series, and not
just a few outliers.
We now turn to the surprising observation that
adding time-split proposals to either of the Axial-
Gaussian and the ObliqueSpectral autoregressor pro-
posals does not improve the quality over models
learned without time splits–neither for the Fixed nor
the TimeSpectral method. Apparently, the axial and
oblique splitting on autoregressors are flexible enough
to cover the time splits in our analysis. We do not
necessarily expect this finding to generalize beyond
series that behave like stock data, due to the fact that
it is a relatively easy exercise to construct an artificial
example that will challenge this finding.
Finally, the oblique splits proposed by our method
involve all regressors in a model, and therefore rely
on our spectral splitting method to be smart enough to
ignore noise that might be introduced by irrelevant re-
gressors. Although efficient, such parsimonious split
proposal may appear overly restrictive compared to
the possibility of proposing split candidates for all
possible subsets of regressors. However, an additional
set of experiments have shown that the exhaustive ap-
proach in general only leads to insignificant improve-
ments in predictive scores. We conjecture that the
NON-PARAMETRIC SEGMENTATION OF REGIME-SWITCHING TIME SERIES WITH OBLIQUE SWITCHING
TREES
123

stagewise inclusion of regressors in the overall learn-
ing procedure for an ART model (see Section 3) is a
main reason for irrelevant regressors to not pose much
of a problem for our approach.
7 CONCLUSIONS AND FUTURE
WORK
We have presented a spectral splitting method that
improves segmentation in regime-switching time se-
ries, and use the segmentation in the process of cre-
ating a switching regression tree for the regimes in
the model. We have exemplified our approach by
an extension to the ART models–the only type of
models that to our knowledge applies switching trees
in regime-switching models. However, the spectral
splitting method does not rely on specific paramet-
ric assumptions, which allows for our approach to
be readily generalized to a wide range of regime-
switching time-series models that go beyond the limit
of the Gaussian error assumption in the ART mod-
els. Our proposed method is very parsimonious in
the number of split predicates it proposes for candi-
date split nodes in the tree. It only proposes a single
oblique split candidate for the regressors in the model
and possibly a few very targeted time-split candidates,
thus keeping computational complexity of the over-
all algorithm under control. Both types of split can-
didates rely on a spectral clustering, where different
views–phase and trace–on the time-series data give
rise to the two different types of candidates.
Finally, we have given experimental evidence that
our approach, when applied for the exemplifying ART
models, dramatically improves predictive accuracy
over the current approach. Regarding time splits,
we hope to be able to find–and are actively looking
for–real-world time series for future experiments that
will allow us to factor out and compare the quality of
our spectral time-split proposer method to the current
ART approach.
The focus in this paper has been on learning
regime-switching time-series models that will easily
lend themselves to explanatory analysis and interpre-
tation. In future experiments we also plan to evaluate
the potential tradeoff in modularity, interpretability,
and computational efficiency with forecast precision
for our simple learning approach compared to more
complicated approaches that integrates learning of
soft regime switching and the local regimes the mod-
els, such as the learning of Markov-switching (e.g.
Hamilton, 1989, 1990) and gated expert (e.g. Wa-
terhouse and Robinson, 1995; Weigend et al., 1995)
models.
REFERENCES
Bishop, C. M. (1995). Neural Networks for Pattern Recog-
nition. Oxford University Press, Oxford.
Breiman, L., Friedman, J. H., Olshen, R. A., and Stone,
C. J. (1984). Classification and Regression Trees.
Wadsworth International Group, Belmont, California.
Brodley, C. E. and Utgoff, P. E. (1995). Multivariate deci-
sion trees. Machine Learning, 19(1):45–77.
Chaudhuri, P., Huang, M. C., Loh, W.-Y., and Yao, R.
(1994). Piecewise polynomial regression trees. Sta-
tistica Sinica, 4:143–167.
Chickering, D., Meek, C., and Rounthwaite, R. (2001).
Efficient determination of dynamic split points in a
decision tree. In Proc. of the 2001 IEEE Inter-
national Conference on Data Mining, pages 91–98.
IEEE Computer Society.
DeGroot, M. (1970). Optimal Statistical Decisions.
McGraw-Hill, New York.
Dobra, A. and Gehrke, J. (2002). Secret: A scalable lin-
ear regression tree algorithm. In Proc. of the 8th
ACM SIGKDD International Conference on Knowl-
edge Discovery and Data Mining, pages 481–487.
ACM Press.
Donath, W. E. and Hoffman, A. J. (1973). Lower bounds for
the partitioning of graphs. IBM Journal of Research
and Development, 17:420–425.
Fiedler, M. (1973). Algebraic connectivity of graphs.
Czechoslovak Mathematical Journal, 23:298–305.
Gama, J. (1997). Oblique linear tree. In Proc. of the Second
International Symposium on Intelligent Data Analy-
sis, pages 187–198.
Hamilton, J. (1994). Time Series Analysis. Princeton Uni-
versity Press, Princeton, New Jersey.
Hamilton, J. D. (1989). A new approach to the economic
analysis of nonstationary time series and the business
cycle. Econometrica, 57(2):357–84.
Hamilton, J. D. (1990). Analysis of time series subject to
changes in regime. Journal of Econometrics, 45:39–
70.
Iyengar, V. S. (1999). Hot: Heuristics for oblique trees. In
Proc. of the 11th IEEE International Conference on
Tools with Artificial Intelligence, pages 91–98, Wash-
ington, DC. IEEE Computer Society.
Jordan, M. I. and Jacobs, R. A. (1994). Hierarchical mix-
tures of experts and the EM algorithm. Neural Com-
putation, 6:181–214.
Li, K. C., Lue, H. H., and Chen, C. H. (2000). Interactive
tree-structured regression via principal Hessian direc-
tions. Journal of the American Statistical Association,
95:547–560.
Mandelbrot, B. (1966). Forecasts of future prices, unbiased
markets, and martingale models. Journal of Business,
39:242–255.
Mandelbrot, B. B. and Hudson, R. L. (2006). The
(mis)Behavior of Markets: A Fractal View of Risk,
Ruin And Reward. Perseus Books Group, New York.
Meek, C., Chickering, D. M., and Heckerman, D. (2002).
Autoregressive tree models for time-series analysis. In
Proc. of the Second International SIAM Conference
on Data Mining, pages 229–244. SIAM.
ICPRAM 2012 - International Conference on Pattern Recognition Applications and Methods
124

Meil
˘
a, M. and Shi, J. (2001). Learning segmentation by ran-
dom walks. In Advances in Neural Information Pro-
cessing Systems 13, pages 873–879. MIT Press.
Murthy, S. K., Kasif, S., and Salzberg, S. (1994). A sys-
tem for induction of oblique decision trees. Journal of
Artificial Intelligence Research, 2:1–32.
Ng, A. Y., Jordan, M. I., and Weiss, Y. (2002). On spectral
clustering: Analysis and an algorithm. In Advances
in Neural Information Processing Systems 14, pages
849–856. MIT Press.
Samuelson, P. (1965). Proof that properly anticipated prices
fluctuate randomly. In Industrial Management Re-
view, volume 6, pages 41–49.
Shi, J. and Malik, J. (2000). Normalized cuts and image
segmentation. IEEE Transactions on Pattern Analysis
and Machine Intelligence, 22(8):888–905.
Tong, H. (1983). Threshold models in non-linear time se-
ries analysis. In Lecture notes in statistics, No. 21.
Springer-Verlag.
Tong, H. and Lim, K. S. (1980). Threshold autoregres-
sion, limit cycles and cyclical data- with discussion.
Journal of the Royal Statistical Society, Series B,
42(3):245–292.
von Luxburg, U. (2007). A tutorial on spectral clustering.
Statistics and Computing, 17(4):395–416.
Waterhouse, S. and Robinson, A. (1995). Non-linear pre-
diction of acoustic vectors using hierarchical mixtures
of experts. In Advances in Neural Information Pro-
cessing Systems 7, pages 835–842. MIT Press.
Weigend, A. S., Mangeas, M., and Srivastava, A. N. (1995).
Nonlinear gated experts for time series: Discovering
regimes and avoiding overfitting. International Jour-
nal of Neural Systems, 6(4):373–399.
White, S. and Smyth, P. (2005). A spectral clustering ap-
proach to finding communities in graphs. In Proc. of
the 5th SIAM International Conference on Data Min-
ing. SIAM.
APPENDIX
Lemma 1. Let Σ be a non-singular sample auto-
covariance matrix for X
t−1
t−p
defined on the p-
dimensional space with principal diagonal direction
d = (
1
√
p
,...,
1
√
p
), and let A
t
=
1
p
∑
p
i=1
X
t−i
. Then
sin
2
(Σd,d) =
∑
p
i=1
cov(X
t−i
−A
t
,A
t
)
2
∑
p
i=1
cov(X
t−i
,A
t
)
2
. (2)
Proof. Introduce S
t
=
∑
p
i=1
X
t−i
. As per bi-linear
property of covariance, (Σd)
i
=
1
√
p
cov(X
t−i
,S
t
),i =
1,..., p and (Σd)d =
1
p
∑
p
i=1
cov(X
t−i
,S
t
) =
cov(A
t
,S
t
). Non-singularity of Σ implies that
the vector Σd 6= 0. Hence, |Σd|
2
6= 0 and
cos
2
(Σd,d) =
((Σd)d)
2
|(Σd)|
2
=
p cov(A
t
,S
t
)
2
∑
p
i=1
cov(X
t−i
,S
t
)
2
.
It follows that
sin
2
(Σd,d)
= 1 −cos
2
(Σd,d)
=
p
1
p
∑
p
i=1
cov(X
t−i
,S
t
)
2
−cov(A
t
,S
t
)
2
∑
p
i=1
cov(X
t−i
,S
t
)
2
=
∑
p
i=1
cov(X
t−i
−A
t
,S
t
)
2
∑
p
i=1
cov(X
t−i
,S
t
)
2
Dividing the numerator and denominator of the last
fraction by p
2
amounts to replacing S
t
by A
t
, which
concludes the proof. 2
Corollary 1. When X
t−i
−A
t
and A
t
are weakly cor-
related, and the variance of X
t−i
−A
t
is comparable
to that of A
t
, i = 1,..., p, then sin
2
(Σd,d) is small.
Specifically, let σ and ρ denote respectively stan-
dard deviation and correlation, and introduce ∆
i
=
cov(X
t−i
−A
t
,A
t
)
σ(A
t
)
= ρ(X
t−i
− A
t
,A
t
)σ(X
t−i
− A
t
). We
quantify both assumptions in Corollary 1 by positing
that |∆
i
|< εσ(A
t
),i = 1,..., p, where 0 < ε 1. Easy
algebra on Equation (2) yields
sin
2
(Σd,d) =
Σ∆
2
i
Σ(σ(A
t
) + ∆
i
)
2
<
pε
2
σ(A
t
)
2
p(1 −ε)
2
σ(A
t
)
2
=
ε
2
(1 −ε)
2
(3)
Under the assumptions of Corollary 1, we can now
show that d is geometrically close to an eigenvector of
Σ. Indeed, by inserting (3) into the Pythagorean iden-
tity we derive that |cos(Σd,d)| >
√
1−2ε
1−ε
and close to
1. Now, given a vector v for which |v|= 1, |cos(Σv,v)|
reaches the maximum of 1 iff v is an eigenvector of Σ.
When the eigenvalues of Σ are distinct, d must there-
fore be at a small angle with one of the p principal
axes for Σ.
NON-PARAMETRIC SEGMENTATION OF REGIME-SWITCHING TIME SERIES WITH OBLIQUE SWITCHING
TREES
125
