LANE DETECTION IN PEDESTRIAN MOTION AND
ENTROPY-BASED ORDER INDEX
Olivier Chabiron
1
, J´erˆome Fehrenbach
1
, Pierre Degond
1
, Mehdi Moussa¨ıd
2,3
, Julien Pettr´e
4
and Samuel Lemercier
4
1
Toulouse Mathematics Institute, Paul Sabatier University
118 route de Narbonne, Toulouse, France
2
Centre de Recherches sur la Cognition Animale, UMR-CNRS 5169, Universit´e Paul Sabatier, Bˆat 4R3, 118 Route de
Narbonne, 31062 Toulouse cedex 9, France.
3
CNRS, Centre de Recherches sur la Cognition Animale, F-31062 Toulouse, France
4
INRIA Rennes - Bretagne Atlantique, Campus de Beaulieu, F-35042 Rennes, France
Keywords:
Clustering, Classification, Motion and tracking, Detection, Graphs, Entropy, Complex systems.
Abstract:
This paper proposes a distance measurement between pedestrian trajectories. This distance is used in a clus-
tering method aiming to detect lanes of pedestrians in experimental data. The main ingredient is to take full
advantage of the time sequence available. A study of the sensitivity of the clustering to the parameters shows it
is possible to choose a stable set of parameters. We also define an order index based on the concept of entropy.
The potential of this index is illustrated in the case of pedestrian lane detection.
1 INTRODUCTION
Human crowd is a complex system that exhibits the
emergence of self-organized patterns. Several studies
deal about the social and biological aspects of these
phenomenons (Helbing and Molnar, 1995; Helbing
et al., 2001; Helbing et al., 2005; Moussa¨ıd et al.,
2011; Sumpter, 2010; Couzin and Krause, 2003).
A particular aspect of pedestrian traffic is the self-
segregation into two or more lanes of opposite direc-
tion (Older, 1968; Yamori, 1998; Kretz et al., 2006).
The formation of lanes can also be observed in other
complex systems, like ants (Casellas et al., 2008) or
charged particles (Rex and Lwen, 2007).
The present study addresses the quantitative as-
pects of lane formation, which were studied in army
ants by (Couzin and Franks, 2003). This work
proposes tools to process motion data in pedestrian
crowds, these tools are general and the ideas pre-
sented here can also be applied to other data (e.g. ants,
particles). The first objective of this work is to pro-
pose a robust method to detect lanes. The novelty of
this method is the use of the temporal aspect of the
data. The second objective is to define an order index
that allows to quantify the orderliness of a pedestrian
crowd. The index we propose is based on the notion
of entropy. The lane detection algorithm and the order
index are tested on experimental data of pedestrians
walking in a ring-shaped arena.
2 PEDESTRIAN DATA
ACQUISITION
Experimental Setup. Controlled experiments were
conducted in May 2009 by INRIA in Rennes, France.
A total of 119 participants took part in the study,
which conformed to the Declaration of Helsinki.
Pedestrians are walking in a ring-shaped arena, of in-
ner radius 2 m and outer radius 4.5 m. Some are
instructed to walk the arena clockwise, the others
counter-clockwise. They are forbidden to change di-
rection in the course of the session.
Participants wore 4 reflexive markers, one on the
forehead, one on the left acromion, and two on the
right acromion to easily distinguish the left shoulder
from right one. Markers motion was reconstructed
using Vicon IQ software. Participants motion was fi-
nally modeled as the one of the barycenter of the 4
markers projected onto the horizontal plane. The mo-
tion was recorded at the frequency of 10 pictures per
second. Several configurations were experimented: 8
pedestrians, 10 pedestrians, 18 pedestrians, 30 pedes-
trians, 50 pedestrians and 60 pedestrians in the arena.
192
Chabiron O., Fehrenbach J., Degond P., Moussaïd M., Pettré J. and Lemercier S. (2012).
LANE DETECTION IN PEDESTRIAN MOTION AND ENTROPY-BASED ORDER INDEX.
In Proceedings of the 1st International Conference on Pattern Recognition Applications and Methods, pages 192-197
DOI: 10.5220/0003762901920197
Copyright
c
 SciTePress

Figure 1: Experimental setup.
Post-processing. Pedestrians trajectories are ex-
tracted from the recordings. Trajectory data consists
in every pedestrian’s position and velocity at each
capture time (i.e every 0.1 s). Positions are computed
in a Cartesian coordinate system which origin is the
center of the ring. In the end, for each session, we
have access to:
• The number N of pedestrians taking part in the
session.
• Their position in the arena plane. We denote by
(X
i
(t),Y
i
(t)) the coordinates of pedestrian number
i at time t.
• The direction each of them is walking in. The di-
rection η
i
takes a value of 1 for ”clockwise” and
−1 for ”counter-clockwise”.
3 LANE DETECTION
The technique that we propose here to detect pedes-
trian lanes is based on the definition of a distance be-
tween pedestrians and a graph-based clustering tech-
nique.
Qualitative Lane Definition
The first and most decisive step of our clustering
method consists in defining a distance, which will be
the one used in the computation of the distance matrix
related to the pedestrians graph. This distance should
give a measure of how far one pedestrian is from an-
other, in terms of lane affiliation. Of course, taking
only the physical (euclidean) distance on R
2
into ac-
count is not sufficient to achieve lane detection. For
this purpose, several things have been taken into ac-
count:
• A lane should contain only pedestrians follow-
ing each other. Their positions should be close
enough.
• Pedestrians walking in opposite directions should
not be in the same lane, even if they are very close
to one another.
• A pedestrian walking through a lane while going
in the opposite direction should break that lane.
• A pedestrian’s trajectory over the next few mo-
ments should be taken into account to determine
its affiliation to a lane.
This last rule is the pillar and the main novelty
upon which the method is built. By introducing a time
dependency, we hope to achieve a better accuracy in
the detection of the formation and breaking of lanes.
The principle applied is as follows: if a pedestrian
is following another, then he will walk right in the
other’s footsteps in the next second or so.
Non-alignment Penalization
In order to make sure that two pedestrians walking in
opposite directions do not belong to the same lane,
we define the following penalization term. This term
depends on the sign of the product between the pedes-
trians direction.
Let i and j be two pedestrians. let us denote η
i
the direction of i and η
j
that of j. For every pedes-
trian, η is a constant and takes a value of 1 for ”clock-
wise” and −1 for ”counter-clockwise”. The penaliza-
tion term P
i, j
between pedestrians i and j at time t is:
P
i, j
=

0 if η
i
η
j
= 1
∞ if η
i
η
j
= −1
(1)
Distance Definition
Since we are working with recorded data, the com-
plete trajectory of every pedestrian is available. We
take advantage of this information to detect if a pedes-
trian is following another. Let us denote by d
i, j
(t
′
,t)
the distance between i at time t
′
and j at time t. If we
stop time at t for every pedestrian except one, let it be
pedestrian number i, does i walk straight into the spot
where pedestrian number j is standing (i.e was stand-
ing at time t)? This principle is illustrated in Figure
2.
Figure 2: Trajectory alignment.
The procedure is as follows: We define τ a small
time interval, that represent a pedestrian’s ”follow”
LANE DETECTION IN PEDESTRIAN MOTION AND ENTROPY-BASED ORDER INDEX
193

time. At time t, we compute d
i, j
(t,t
′
) for each time
t
′
∈ [t, t + τ].
d
i, j
(t
′
,t) =
q
(X
i
(t
′
)−X
j
(t))
2
+ (Y
i
(t
′
)−Y
j
(t))
2
+

0 if η
i
η
j
= 1
∞ if η
i
η
j
= −1
(2)
Then, we select the minimum distance over the
interval as the distance between i and j :
d
min
i, j
(t) = min
t≤t
′
≤t+τ
(d
i, j
(t
′
,t)) (3)
The ”follow” time τ has been set to one second, which
appeared to us as a good measure of the time needed
for a ”follower” pedestrian to literally follow in the
footsteps of a ”leader” pedestrian. Parameter explo-
ration has shown this is an adequate value for τ (see
section 4).
Distance Symmetrization
The definition in Equation (3) results in a non-
symmetrical distance d
min
i, j
(t). In order to define
lanes of pedestrians we define a symmetrical distance
D
i, j
(t). We use a minimum-based symmetrization,
and the N × N matrix D(t) is defined by:
D
ij
(t) = min(d
i, j
(t),d
j,i
(t)) (4)
Connected Components
At this step of the procedure we dispose of a full dis-
tance matrix. In order to define clusters we define an
adjacency graph G in the network of pedestrians. Two
pedestrians are connected in G if their distance is be-
low a given threshold δ. The adjacency matrix (G
i, j
)
of the graph G is defined by:
G
ij
=

0 if D
ij
≥ δ
1 if D
ij
< δ
(5)
The lanes of pedestrians are the connected com-
ponents of the graph G.
To summarize this section, we present the algo-
rithm that is used to compute the adjacency matrix
(G
i, j
) of the clustering graph.
4 PARAMETER SENSITIVITY
STUDY
Parameters for Pedestrians
Through parameter exploration, we set δ to 0.7m,
because this value gives consistent results for every
experimental configuration, i.e from eight to sixty
pedestrians. There is also a biological justification for
Algorithm 1: Lane clustering algorithm.
Input:
N: number of pedestrians;
X(t),Y(t)
0≤t≤T
: positions of the pedestrians;
η
i
: walking directions of the pedestrians;
δ,τ: space and time thresholds;
Output:
G(t): clustering matrix at every time t.
begin
for t ∈ [0..T − τ] do
for i, j = 1..N do
define d
i, j
(t) by Equation (3) ;
end
for i, j = 1..N do
define
G
i, j
(t) := 0 if d
i, j
≥ δ and d
j,i
≥ δ
1 otherwise;
end
end
end
this value, which we can see if we note that the dis-
tance between two pedestrians walking in the same
direction is actually euclidean. Then, 0.7 meters
roughly correspond to the width of two bodies side
to side. This value is relevant when a suitable time
parameter τ is chosen. Indeed, both parameters to-
gether build this space-time corridor which selects
only pedestrians who are ”following footsteps”. Fig-
ure 3 shows an example of lane detection accom-
plished with Algorithm 1 for a 60-pedestrianssession.
The values chosen for our parameters, δ and τ,
have been set mainly by biological considerations,
data we possessed concerning the systems studied.
However, one might not always dispose of such data,
or might need improved stability. That is why a
parametric sensitivity study is crucial to gather infor-
mation about eventual ranges of parameter values of
lesser sensitivity.
Parameter Range and Indicator
The study was performed for τ ∈ [0,2] (in seconds)
and δ ∈ [0, 1.25] (in meters, the data used being that
of the pedestrian motion). The number of lanes was
used as the main indicator. In order to be able to com-
pare one value for each {τ, δ} couple, we compute a
mean of the indicator over the ”meaningful” time of
all experimental recordings with the same number of
pedestrians. That is to say, from 5 seconds after the
pedestrians start walking to 50 seconds later. We write
N
K
L
(τ,δ) the mean number of lanes for the ensemble
of all K-pedestrians experiments.
Graphical Study in the τ,δ Plane
Figure 4 shows the surfaces drawn by N
50
L
(τ,δ) and
ICPRAM 2012 - International Conference on Pattern Recognition Applications and Methods
194

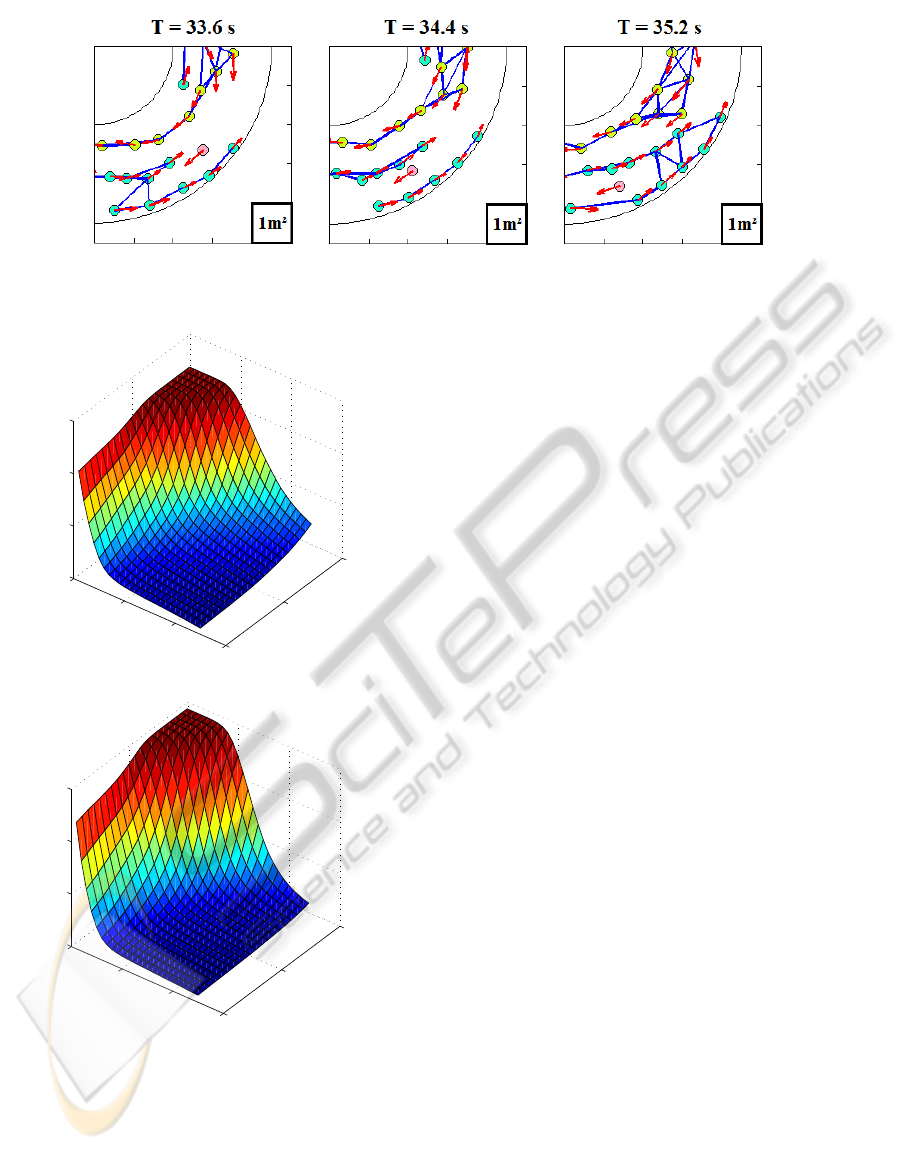
Figure 3: Example of lane detection with N = 60. We can see the pink pedestrian beginning to cross the cyan lane (left
picture), forcing cyan pedestrians to evade him thus breaking the lane (center picture), before the lane reforms (right picture).
0
1
2
0
0.5
1
1.5
0
20
40
60
Tau
Delta
Mean Number of Lanes
0
1
2
0
0.5
1
1.5
0
20
40
60
Tau
Delta
Mean Number of Lanes
Figure 4: Surface plot of the mean number of lanes detected
for 50 pedestrians experiments (top) and 60 pedestrians ex-
periments (bottom).
N
60
L
(τ,δ). Since the study for small numbers of pedes-
trians shows abrupt variations, we focused our at-
tention to the experiments with N = 50 and N = 60
pedestrians, those showing far smoother variations.
Lesser Sensitivity Window
Though this parametric study doesn’t yield an ideal,
universal set of values that would minimize param-
eter sensitivity for every kind of experiment, it does
indicates that the values of both τ and δ must be high
enough to ensure a low sensitivity. Very low values
also show low sensitivity but the detection would be
meaningless.
In the N = 60 pedestrians case, we observe a flat
band in the τ,δ plane. In the N = 50 pedestrians
case, this flat band is also relatively flat, though not as
much. This result suggest that any set of parameters
chosen in this area will yield a similar N
L
function,
which seems to be the case after testing.
However, more than minimizing parameter sensi-
tivity, we need our detection of lanes to make sense.
That is why we define a lesser sensitivity window that
combines a low sensitivity to τ and δ and a somewhat
realistic range of values for these same parameters.
This is the following window:
1 ≤ τ ≤ 1.6 (6)
0.7 ≤ δ ≤ 1.0 (7)
Inside this window, the relative variation of N
60
L
with both τ and δ does not exceed 7% and that of
N
50
L
do not exceed 10%. Though the choice of this
window takes experiments with less pedestrians into
account, these are more parameter-sensitive. Indeed,
fewer agents naturally results in greater relative dif-
ferences in clustering when parameters are changed.
5 ENTROPY-BASED ORDER
INDEX
When studying complex systems, it is vital to be
equipped with a trusted order index that should be
both stable and efficient (relatively to some criteria).
LANE DETECTION IN PEDESTRIAN MOTION AND ENTROPY-BASED ORDER INDEX
195

Besides, an order index is rarely transferable to differ-
ent systems. For these reasons, we worked on design-
ing a new index, which should respect the following
constraints:
• The index should not over-penalize a well-ordered
system because of a few isolated agents.
• The index should present relatively smooth varia-
tions.
• The index should be transferable to a large panel
of studies.
What is Entropy?
Entropy originates in thermodynamics and was in-
troduced by Rudolph Clausius in the middle of the
nineteenth century, but its significance was only high-
lighted around 1870 by Ludwig Boltzmann. It was
first introduced in the complex systems field by (Wol-
fram, 1984). The entropy of a system is a function
of the system’s states which ”measures its disorder”.
Let {Ω,X, p} be a finite state space, |Ω| = M. Let
p(x) denote the probability that the system is in state
x. Then the statistical entropy is given by:
S = −k
∑
x∈X

p(x) ln p(x) if p(x) 6= 0
0 if p(x) = 0
(8)
where k usually is a physical constant. An interpre-
tation of this function consists in saying that entropy
measures the logarithm of the number of states actu-
ally accessible for the system. To illustrate this, let us
look at two opposite cases.
If a state x
0
is attained with certainty, i.e
p(x
0
) = 1, p(x 6= x
0
) = 0 , then:
S = S
min
= 0 (9)
If all states are equally likely, i.e
p(x) = 1/M ∀x , then:
S = S
max
= −kM
1
M
ln
1
M
= k lnM. (10)
Definition of the β Index. In order to adapt the
concept of entropy to build an order index, we need
to define a state space and write a normalized func-
tion based on Equation (8). Thanks to the clustering,
we dispose of all the data concerning the lanes (their
number, their sizes, and the identification number of
the pedestrians who form them).
If we think of the arena as a box (an isolated sys-
tem) containing a certain number of particles (pedes-
trians), we are close to describing the experiment as a
thermodynamic system. The different states accessi-
ble to the system are the different kinds of particle ag-
gregation, i.e each possible configuration of the lanes.
The probability of being in a state-lane L, of size x
L
, is
replaced by the actual ratio of the number of pedestri-
ans forming the lane over the total number of pedes-
trians, i.e x
L
/N.
This allows us to define β
tmp
a temporary index
which measures disorder:
β
tmp
= −
N
L
∑
L=1

x
L
N
ln
x
L
N
if x
L
6= 0
0 if x
L
= 0
(11)
In this formula, N
L
denotes the total number of
lanes. This number is obviously time-dependent, as is
the size of each lane. Together these numbers rule the
variations of the index.
Then, in the case of N lanes, each with a single
pedestrian, the number of state-lanes accessible by the
system is maximum and equal to N. In this configu-
ration, all state-lanes of the system are of equal size.
This corresponds to a maximum disorder situation.
In order to have an index that is normalized be-
tween 0 (no order at all) and 1 (perfectly ordered sit-
uation) an affine transformation is applied. This leads
to define the β index by:
β = 1−
β
tmp
ln(N)
(12)
Application to Pedestrian Traffic: Directional Or-
der Index
In order to illustrate the capabilities of the β index, we
show in Figure 5 an example where the order mea-
surement is segregated. Indeed, in our experimen-
tal conditions, it is of interest to know if clockwise-
walking pedestrians are as well ordered as counter-
clockwise-walking pedestrians. If we compute a β
index for each subsystem, we can transform visual
insight into quantitative measurement. For this pur-
pose, we define β
c
the clockwise order index and β
cc
its counter-clockwise counterpart.
Sensitivity of β to the Parameters
We conducted the same parametric study as in section
4, this time using a mean value of β. In the previously
defined window (see (6) and (7)), the relative varia-
tion of the mean index does not exceed 2% (for 60
pedestrians) and 5% (for 50 pedestrians).
6 CONCLUSIONS
We have developed an effective clustering technique
which realizes the detection of lanes in pedestrian
crowds using only two parameters: a distance scale,
ICPRAM 2012 - International Conference on Pattern Recognition Applications and Methods
196

Figure 5: Comparison between two situations occurring
within the same experimental session (N = 30 pedestrians).
The first situation (left graph) is clearly asymmetric in its or-
derliness: counter-clockwise pedestrians are all in the same
lane but one, whereas clockwise pedestrians form several
small lanes. At this moment β
c
= 0.38 and β
cc
= 0.91. The
second situation (right graph) is more balanced: β
c
= 0.73
and β
cc
= 0.70.
and a time scale. Indeed, its originality lies in tak-
ing time into account to detect the formation and the
break-up of lanes. Moreover, sensitivity studies show
that the method is robust to parameter variations as
long as their values are high enough.
In addition, we designed a universal order index
which can prove to be very useful in both experimen-
tal and numerical data of complex systems. Being
based on the concept of statistical entropy, it ensures
a measure of order in a very general sense, and is eas-
ily transferable to different contexts and studies in the
complex systems field.
Future work will include the application of these
tools to systems with a large number of agents,
namely trail formation in simulated and experimental
ant colonies.
ACKNOWLEDGEMENTS
This study was supported by a research grant from the
PEDIGREE project funded by the French National
Research Agency (Grant No ANR-08-SYSC-015).
REFERENCES
Casellas, E., Gautrais, J., Fournier, R., Blanco, S., Combe,
M., Fourcassi, V., Theraulaz, G., and Jost, C. (2008).
From individual to collective displacements in het-
erogenous environments. Journal of Theoretical Bi-
ology, 250: 424-434.
Couzin, I. and Franks, N. (2003). Self-organized lane for-
mation and optimized traffic flow in army ants. Pro-
ceedings of the Royal Society B: Biological Sciences
270(1511):139-146.
Couzin, I. and Krause, J. (2003). Self-organization and col-
lective behavior in vertebrates. Advances in the Study
of Behavior 32:1-75.
Helbing, D., Buzna, L., Johansson, A., and Werner, T.
(2005). Self-organized pedestrian crowd dynam-
ics: Experiments, simulations, and design solutions.
Transportation Science 39(1):1-24.
Helbing, D. and Molnar, P. (1995). Social force model for
pedestrian dynamics. Physical Review E. 51(5):4282-
4286.
Helbing, D., Molnar, P., Farkas, I., and Bolay, K. (2001).
Self-organizing pedestrian movement. Environment
and Planning B: Planning and Design 28:361-383.
Kretz, T., Gr¨unebohm, A., Kaufman, M., Mazur, F., and
Schreckenberg, M. (2006). Experimental study of
pedestrian counterflow in a corridor. Journal of Sta-
tistical Mechanics: Theory and Experiments P10001.
Moussa¨ıd, M., Helbing, D., and Theraulaz, G. (2011). How
simple rules determine pedestrian behavior and crowd
disasters. Proceedings of the National Academy of
Sciences 108(17):6884-6888.
Older, S. (1968). Movement of pedestrians on footways
in shopping streets. Traffic Engineering and Control
10:160-163.
Rex, M. and Lwen, H. (2007). Lane formation in oppositely
charged colloids driven by an electric field: Chaining
and two-dimensional crystallization. Physical Review
E (Statistical, Nonlinear, and Soft Matter Physics) 75.
Sumpter, D. (2010). Collective animal behavior. Princeton
University Press.
Wolfram, S. (1984). Universality and complexity in cellular
automata. Physica 10D, 1-35.
Yamori, K. (1998). Going with the flow: micro-macro dy-
namics in the macrobehavioral patterns of pedestrian
crowds. Psychological Review, Vol. 105, No.3, 530-
557.
LANE DETECTION IN PEDESTRIAN MOTION AND ENTROPY-BASED ORDER INDEX
197