APPLICATION OF A GTEM CELL TO DETERMINE RF INDUCED

CURRENTS IN ELECTRODES OF MEDICAL IMPLANTS

An Alternative to Measurements in MRI Birdcages

Karin M

ortlbauer, Daniel Zemann and Erwin Hochmair

Institute of Ion Physics and Applied Physics, University of Innsbruck, Technikerstrasse 25, 6020 Innsbruck, Austria

Keywords:

VNA, GTEM cell, Transmission line, Scattering parameter, Medical-Implant, MRI.

Abstract:

RF induced currents in elongated electrodes of medical implants can cause hazardous tissue heating during

MRI scans. In this paper we introduce an experimental setup to investigate the inﬂuence of the geometri-

cal electrode design on the magnitude of the RF induced current. A Vector Network Analyser (VNA) was

connected to a Gigahertz Transverse Electromagnetic (GTEM) cell containing the electrode under test. The

forward power gain (S

scattering parameter) was measured by the VNA, whereof the magnitude of the cur-

rent at the electrode tip could be derived. Furthermore, calculations via transmission line theory were done

to describe the present mechanism of current induction. These calculations show good agreement with the

results of the performed measurements.

1 INTRODUCTION

Medical implants used to electrically stimulate nerves

or muscles (e.g. cardiac pacemakers, cochlear im-

plants or deep brain stimulation) ﬁnd widespread ap-

plication in therapeutic medicine. Some of these im-

plants are contraindicated with magnetic resonance

imaging (MRI). If these implants contain compara-

tively long metallic electrode leads, these electrodes

couple with the radiofrequency ﬁeld of the MRI scan-

ner, which can cause serious burns of tissue specif-

ically in the vicinity of the electrode contacts (Nitz

et al., 2001). A current is induced along the axis of

the electrode lead, which is prone to create a high cur-

rent density in the tissue at the electrode contact. The

electrical energy is absorbed and converted into ther-

mal energy in the tissue, which has a much higher

speciﬁc ohmic resistance than the electrode material.

Therefore the amount of heating depends on the in-

duced current, which in turn depends on the geo-

metric design of the electrode. Other authors have,

for instance, investigated tissue heating of different

solenoidal electrode designs (Gray et al., 2005). Such

changes in the electrode geometry may be capable of

avoiding hazardous tissue heating.

In this paper we present an experimental setup to

investigate the inﬂuence of electrode design on tis-

sue heating. Instead of a temperature measurement of

the tissue in a MRI birdcage, however, measurements

of scattering parameters were performed by a Vector

Network Analyser (VNA), connected to a Gigahertz

Transverse Electromagnetic (GTEM) cell containing

the electrode.

It is important to mention that the exciting elec-

tromagnetic ﬁeld in the GTEM cell differs from the

one in the MRI birdcage. Therefore, the presented

GTEM setup is not proper for safety measurements

of certain electrodes, but allows comparative investi-

gations of induced RF currents in differently designed

electrodes.

2 METHOD

The different electrode geometries were investigated

under two different circumstances: with an alignment

of the electrode perpendicular to the electric ﬁeld and

parallel to it. The experimental setup and the trans-

mission line theory for the former alignment are de-

scribed in the following paragraphs. The latter situa-

tion, which is more realistic in comparison to the sit-

uation in the MRI birdcage, will be subject of future

experiments.

2.1 Experimental Setup

A LA19-13-02 3GHz VNA (LA Techniques, UK)

315

Mörtlbauer K., Zemann D. and Hochmair E..

APPLICATION OF A GTEM CELL TO DETERMINE RF INDUCED CURRENTS IN ELECTRODES OF MEDICAL IMPLANTS - An Alternative to

Measurements in MRI Birdcages.

DOI: 10.5220/0003763103150318

In Proceedings of the International Conference on Biomedical Electronics and Devices (BIODEVICES-2012), pages 315-318

ISBN: 978-989-8425-91-1

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

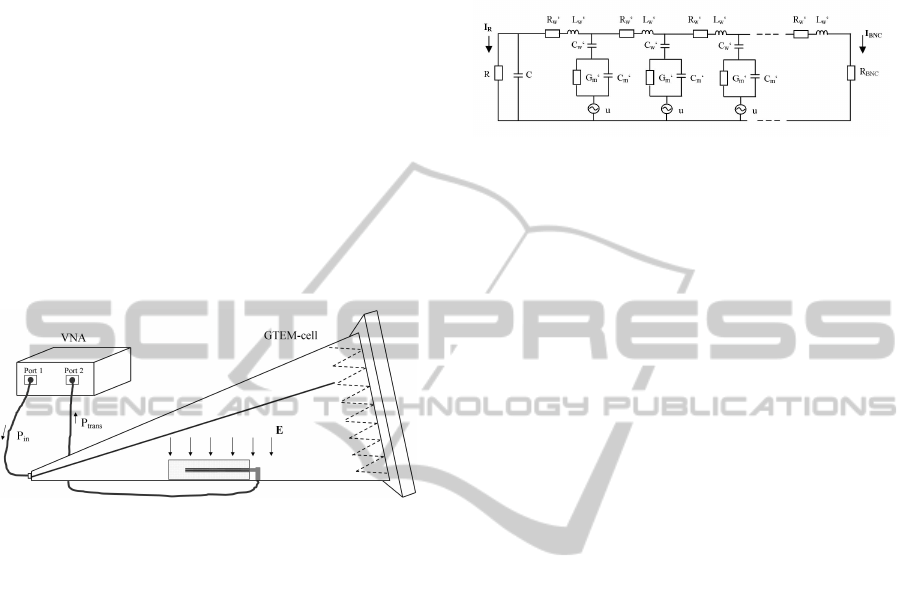
was connected to a GTEM cell (Model 5402, ETS-

Lindgren, USA) as it is shown in Figure 1. The

output power of the VNA from port 1 was used to

generate a homogeneous transverse electromagnetic

ﬁeld inside the GTEM cell. The electrode was posi-

tioned inside a medium and connected to port 2 via a

BNC-connector at one end and left in contact to the

medium on the other end. Several different media

were investigated: air, silicone and a phantom mus-

cle. The latter was a mixture of the gelling agent

TX151 (Brunschwig Chemie, Netherlands), distilled

water and sodium chloride (Chou et al., 1995). The

electrode axis was in a horizontal orientation and thus

perpendicular to the electric ﬁeld, which is vertically

aligned. The electric ﬁeld was measured with an elec-

tric ﬁeld probe (D.A.R.E.!! Instruments, RadiSense,

LP1001A, Netherlands).

Figure 1: Connection of the VNA and the GTEM cell.

The electrode under test is horizontally positioned and sur-

rounded by a medium.

The Network Analyser measures the amplitude

and phase of the four scattering parameters in a fre-

quency range from 3 MHz to 300 MHz. Only the

reverse (S

) or forward (S

) power gain – both are

equal (reciprocity theorem) – are relevant in our in-

vestigation. The S

-parameter is deﬁned as the ratio

of the transmitted power at the matched port 2 to the

input power at port 1. We compared the amplitudes

of the S

-parameter of different electrode geometries

(straight wires, completely and partially solenoidal

wires) over the complete frequency range in air and

silicone and at 64 MHz and 128 MHz in the phantom

material, which are the RF frequencies for the 1.5 T

and 3 T MRI-scanners, respectively.

The electrodes tested in viscous materials (e.g. sil-

icone) were moulded into these materials to provide a

perfect contact between the tip of the electrode and

the medium.

2.2 Transmission Line Theory

A part of the equivalent circuit of the electrode be-

ing excited by the electric ﬁeld of the GTEM cell is

shown in ﬁgure 2. It is important to note that a the-

oretical description of the electrode as a transmission

line must include environmental parameters in addi-

tion to intrinsic parameters of the electrode (Konings

et al., 2000). In the presented setup, the electrode is

Figure 2: The equivalent circuit of the electrode in a per-

pendicular electric ﬁeld inside the GTEM cell.

considered to be the inner conductor and the housing

of the GTEM cell the outer conductor of the trans-

mission line. The ﬁeld perpendicular to the electrode

axis induces a voltage u between the electrode and

the GTEM housing. The equivalent circuit is a cas-

cade connection of n consecutive quadripoles (three

of them are shown in ﬁgure 2). Each quadripole

is characterized by two complex impedances, one

along the wire, consisting of a resistance R

in se-

ries with an inductance L

, another between the in-

ner and outer conductor, consisting of C

in series

with a parallel connection of G

and C

. R

and

are the resistance and inductance of the wire per

quadripole length, respectively, C

is the capacitance

along the insulation layer between wire and medium

per quadripole length, G

and C

are the conductance

and capacitance between the surface of the insulation

and the outer conductor per quadripole length. R

BNC

is the resistance of the BNC-connection (=50Ω). For

simplicity, the lead tip is described as a hemisphere,

with surface area of the lead tip’s real contact area,

and thus representing the capacitance C of a hemi-

sphere and an analogous resistance R. The total resis-

tance and capacitance of the wire were also calculated

by geometric considerations and checked by low fre-

quency measurements and then divided by the num-

ber of quadripoles to yield the values per quadripole

length. A calculation of R

and C

is trivial for any

wire with concentric insulation. L

was estimated via

well known inductance formulas for solenoids and

straight wires. To determine G

and C

we consid-

ered the transmission line to be a coaxial line, with the

radius of the outer conductor being equal to the dis-

tance between electrode and cell housing, while the

radius of the inner conductor is equal to the wire ra-

dius for straight wires and equal to the coil radius for

solenoid wires.

The equivalent circuit is a linear network with n

voltage sources and described by 3n+2 independent

ﬁrst-order differential equations. They can be written

in state space representation:

BIODEVICES 2012 - International Conference on Biomedical Electronics and Devices

316

˙x(t) = A · x(t) + B · u(t), (1)

where A and x(t) are the state matrix and state vector,

B and u(t) are the source matrix and source vector, re-

spectively. In the case of harmonic time dependence

jωt

, the equation simpliﬁes such that x(t) can be eas-

ily calculated from u(t) within parts of a second using

a commercial mathematical tool even for networks of

40 quadripoles and more. The vector x(t) contains the

current and voltage along every element of the equiv-

alent circuit including I

BNC

. The power absorbed in

BNC

is P

trans

= I

BNC

· R

BNC

. The amplitude of the

-parameter is then given by:

| =

trans

, (2)

where P

= 1mW .

For in vivo experiments the amount of tissue heat-

ing is most appropriately characterized by the speciﬁc

absorption rate (SAR) (Yeung and Atalar, 2001). The

SAR value can be derived from the current density by

SAR = J

/(ρ · σ), where ρ and σ are the mass density

and electric conductivity of the tissue, respectively. In

our model the current density is maximal at the elec-

trode contact, where it is equal to I

divided by the

area of the electrode contact.

3 PRELIMINARY RESULTS

The model was checked by a rough comparison over

the whole frequency range of measured and calcu-

lated S

-parameters of solenoidal and straight cop-

per wires with a diameter of 0.77mm. Figures 3 and

4 show good qualitative agreement of measurement

and calculation of these electrodes in media with dif-

ferent relative permittivity ε

, which was air (ε

= 1)

and silicone (ε

= 3), respectively. A comparison of

our model and a measurement of the electrode in the

phantom muscle were not yet possible; a better deﬁ-

nition of the relative permittivity and conductivity of

the phantom material over the whole frequency range

is required.

Excessive heating effects at the electrode contacts

occur due to resonating RF waves (Konings et al.,

2000), which depend strongly on the length of an

electrode and the surrounding medium. The latter

makes it difﬁcult to exactly predict resonances, which

is important for MRI safety aspects, however.

4 DISCUSSION & OUTLOOK

The presented experimental setup provides a possibil-

ity to determine currents induced in electrodes by RF

Figure 3: Comparison of the amplitude of the measured

(dashed lines) and calculated (solid lines) S

-parameter of

a solenoid (blue) and a straight wire (magenta) in air. The

parameters of the solenoid were: #turns = 54, pitch = 2mm,

solenoid radius = 2.5mm, length of the solenoid = 0.1m.

The length of the straight wire also was 0.1m.

Figure 4: Comparison of the amplitude of the measured

(dashed lines) and calculated (solid lines) S

-parameter of

a solenoid (blue) and a straight wire (magenta) in silicone.

The parameters of the solenoid and the straight wire were

the same as in ﬁgure 3.

ﬁelds. It measures the power received by the elec-

trode, which represents an antenna, and veriﬁes the

validity of the equivalent circuit by comparison of the

-parameter over a wide frequency range. The cur-

rent along the electrode as well as the current density

at the electrode tip (which is relevant for SAR and

thus the temperature rise estimation) can be derived

by a state space analysis of the equivalent circuit. It

has not escaped our attention that this approach con-

tains uncertainties. The correct determination of the

induced currents relies strongly on the accuracy of a

theoretically derived equivalent circuit. Furthermore,

the equivalent circuit correctly describing the situa-

tion of the electrode in the MRI birdcage differs from

the one in the GTEM cell. Thus it is questionable

to what extent one can conclude from the results in

the presented setup to tissue heating in a MRI bird-

cage. The validity of such a conclusion must be con-

ﬁrmed experimentally and theoretically. This can be

APPLICATION OF A GTEM CELL TO DETERMINE RF INDUCED CURRENTS IN ELECTRODES OF MEDICAL

IMPLANTS - An Alternative to Measurements in MRI Birdcages

317

achieved by comparing results of our setup to results

of temperature measurements in a MRI birdcage or

verifying the equivalent circuit via numerical com-

puter simulation techniques. This will be a future

challenge.

Nevertheless, already at the present stage the setup

allows fast and uncomplicated measurements over a

wide frequency range including several RF frequen-

cies of present commercial MRI scanners. Such a

broadband current measurement allows a better in-

sight in the mechanism of RF induced currents in

electrodes than temperature measurements at a single

frequency in MRI scanners.

Further work will be done to investigate differ-

ent electrode geometries and materials with electrode

axis parallel to the electric ﬁeld.

ACKNOWLEDGEMENTS

This research has been supported by MED-EL corp.

in Innsbruck, Austria.

REFERENCES

Chou, C. K., McDougall, J. A., and Chan, K. W. (1995).

Absence of radiofrequency heating from auditory im-

plants during magnetic resonance imaging. Bioelec-

tromagnetics, 16(5):307–316.

Gray, R. W., Bibens, W. T., and Shellock, F. G. (2005).

Simple design changes to wires to substantially re-

duce MRI-induced heating at 1.5 T: implications

for implanted leads. Magnetic Resonance Imaging,

23(8):887–891.

Konings, M. K., Bartels, L. W., Smits, H. F., and Bakker, C.

J. G. (2000). Heating around intravascular guidewires

by resonating RF waves. Journal of Magnetic Reso-

nance Imaging, 12(1):79–85.

Nitz, W. R., Oppelt, A., Renz, W., Manke, C., Lenhart, M.,

and Link, J. (2001). On the heating of linear conduc-

tive structures as guide wires and catheters in interven-

tional MRI. Journal of Magnetic Resonance Imaging,

13(1):105–114.

Yeung, C. J. and Atalar, E. (2001). A green’s function ap-

proach to local rf heating in interventional MRI. Med-

ical Physics, 28(5):826–832.

BIODEVICES 2012 - International Conference on Biomedical Electronics and Devices

318