
IRIS RECOGNITION IN VISIBLE LIGHT DOMAIN
Daniel Riccio
1
and Maria De Marsico
2
1
Biometric and Image Processing Laboratory, University of Salerno, via Ponte don Melillo, 84084, Fisciano, Italy
2
Dipartimento di Informatica, Sapienza Università di Roma, via Salaria 113, 00198, Rome, Italy
Keywords: Iris Recognition, Linear Binary Pattern, BLOB.
Abstract: Present iris recognition techniques allow very high recognition performances in controlled settings and with
cooperating users; this makes iris a real competitor to other biometric traits like fingerprints, with the further
advantage of requiring a contactless acquisition. Moreover, most of the existing approaches are designed for
Near Infrared or Hyperspectral images, which are less affected by changes in illumination conditions.
Current research is focusing on designing new techniques aiming to ensure high accuracy even on images
acquired in visible light and in adverse conditions. This paper deals with an approach to iris matching based
on the combination of local features: Linear Binary Patterns (LBP) and discriminable textons (BLOBs).
Both these technique have been readapted in order to deal with images captured in variable visible light
conditions, and affected by noise due to distance/resolution or to scarce user collaboration (blurring, off-axis
iris, occlusion by eyelashes and eyelids). The obtained results are quite convincing and strongly motivate
the addition of more local features.
1 INTRODUCTION
In controlled settings and with cooperative users, iris
provides comparable or even higher accuracy than
other biometric traits like fingerprints. Therefore,
present research trend is towards focusing on the
possibility of relaxing some of the strong constraints
for subject cooperation and the quality of the
acquired image. An iris based recognition system
working in every-day applications has to deal with
several kinds of distortions, such as blurring, off-
axis, occlusions and reflections. As a matter of fact,
in a semi-controlled setting, due either to lower
user's cooperation, or to limited performances of the
capture device, the system must work over noisy iris
images, which are often partially compromised.
Literature offers a wide spread of iris based
techniques for automatic personal identification
(Bowyer, 2008). The first, significant work about
iris recognition was presented in 1993 by J.
Daugman (Daugman, 1993), whose approach relied
on an integro-differential filter to locate the useful
region, and on 2D Gabor filters to extract relevant
features. Wildes’ (Wildes, 1997) proposal was quite
different: an edge detection filter during
segmentation, and then Hough transform to detect
circular regions. The feature extraction process
constructs a Laplacian pyramid by iteratively
applying a Gaussian lowpass filter and decimation
operator to the iris image. The similarity between
new samples and stored templates is computed using
the normalized correlation. Both these systems
(Daugman and Wildes) require a strict image quality
control to guarantee a high identification accuracy,
as they are heavily influenced by illumination and
position changes.
In (Sung, 2002) the authors discuss potential
issues to be overcome in order to make an iris
identification algorithm working in uncontrolled
settings. They specifically address the off-angle and
defocused images problems by proposing ad hoc
correction algorithms, while the illumination
problem is considered insurmountable, unless input
images are acquired with special lighting
equipments. In (Du, 2005), Du et al. investigated
about the use of three different kinds of partial iris
recognition (left-to-right, outside-to-inside, inside-
to-outside). In their experiments, the authors
concluded that only the inner part of the iris is really
discriminating. In (Dorairaj, 2005), Dorairaj et al.
described a strategy to correct off-angle images
before extracting the biometric features. They start
with the estimation of the gaze direction and then
apply a projective transformation bringing the
captured iris image to frontal view. Recently, other
55
Riccio D. and De Marsico M. (2012).
IRIS RECOGNITION IN VISIBLE LIGHT DOMAIN.
In Proceedings of the 1st International Conference on Pattern Recognition Applications and Methods, pages 55-62
DOI: 10.5220/0003763500550062
Copyright
c
SciTePress
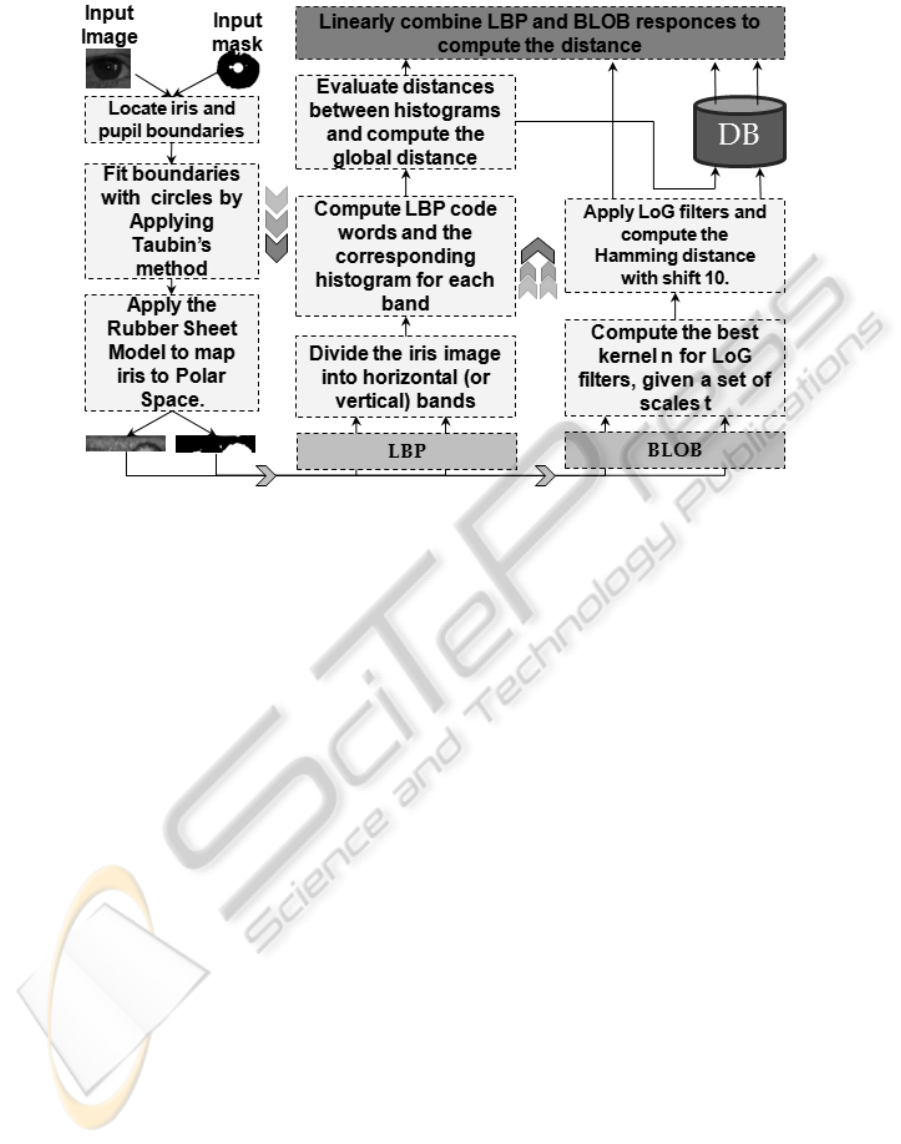
Figure 1: The architecture of N-IRIS.
researchers including (Proença, 2007) and (Bowyer,
2008) have contributed new methods to decrease the
effects of lighting conditions and low quality
captured images. Despite this, most of them expect a
cooperative behaviour from the user. This implicit
assumption represents a strong limitation for all
those settings not guaranteeing this requirement. In
present research non-cooperative iris recognition is
still a great challenge.
Many approaches try to solve these problems by
working locally, by analyzing separate iris sub-
regions independently. Along this line, a Noisy Iris
Recognition Integrated Scheme (N-IRIS) is
proposed in this paper (Figure 1).
It adopts and combines two local feature
extraction techniques, Linear Binary Patterns (LBP)
and extraction of discriminable textons (BLOBs),
which differently and independently characterize
relevant regions of iris.
In order to be effectively applied to iris
recognition, the proposed local operators must
provide a low computational cost. Iris recognition
systems often acquire high resolution images or have
to work in real time. The LBP descriptor meets this
requirement, although providing a discriminating
local texture descriptor, since it seems to be the best-
able for quite regular patterns. However, the
uniqueness of the iris texture is also characterized by
the irregular distribution of local feature blocks such
as furrows, crypts and freckles or spots. Such
features can be considered as blobs: a group of
image pixels which form a structure which can be
darker or lighter than the surrounding region. The
extraction of the blobs from an iris image is obtained
through different LoG (Laplacian of Gaussian) filter
banks. This technique will be referred as BLOB.
Both LBP and BLOB have been adapted to the
case at hand. Further, their combination has also
been investigated. The fusion between the two
approaches is performed at score level by exploiting
a weighted mean of matching scores. Experimental
results show that such combination of the LBP and
BLOB, though not particularly complex, overcomes
both single strategies in terms of accuracy. This
suggests that different kinds of iris features may call
for different suited codings for a better matching.
Possible future studies will focus on the combination
of more kinds of features, as well as the design of
more sophisticated schemes for the integration of
different information.
2 IMAGE SEGMENTATION
Typically an iris identification system starts with the
location and segmentation of the iris sample. The
precision of the separation between the useful region
for identification and those that can be considered as
noise elements (reflections, eyelids, eyelashes)
heavily influence subsequent steps. The higher such
precision, the more informative the obtained iris
code, and therefore the better the expected
ICPRAM 2012 - International Conference on Pattern Recognition Applications and Methods
56

recognition result.
The collarette separates the two main parts of the
iris that are the pupillary and ciliary regions. The
former is the innermost one and determines the
pupil's contour, while the latter is the outermost one
and surrounds the pupillary region. Sclera, eyelids
and eyelashes represents further important elements,
which are taken into account during segmentation as
well as coding. As a matter of fact, eyelids and
eyelashes may often hinder a correct segmentation,
and may lead to a poor coding if they are included in
the pupil code. On the other hand, useful structures
for recognition are crypts, circular and radial
furrows, freckles and spots with various extent.
Though strictly correlated, according to the
preceding considerations, segmentation and
matching represent two well distinguishable steps.
International challenges like NICE also performed
such kind of distinction, since NICE I explicitly and
uniquely addressed the problem of noisy iris
segmentation, while NICE II focused on the problem
o matching noisy iris images. However, methods
participating to the NICE II competition have been
provided with segmentation mask produced by the
best performing segmentation algorithm (Tan, 2010)
in previous NICE I (Figure 2 shows some
examples). N-IRIS exploits such segmentation mask
to refine and transform the iris region into a
rectangular region, from which features are then
extracted.
N-IRIS starts by approximating iris and pupil
boundary by circumferences (centre and radius) as
accurately as possible, so as to allow the mapping
from the image Cartesian space to the iris region
polar space. Possible distortion introduced in this
phase invalidate all the following steps. In a naïve
solution both circumferences are approximated by
solving an ellipse fitting problem. However, Figure
2 (b) shows some cases in which such approach fails
to retrieve the desired circumferences. This happens
because the ellipse fitting algorithm is too sensible
to discontinuities introduced in the iris and pupil
contours by occlusions due to reflections or eyelids.
In practice, curves resulting from contour
approximation tend to get completely deformed just
to precisely adhere to the available boundary
portion. A further problem arises in all those cases
which are similar to the irises in the third row of
Figure 2: the black region contour represents a
single object without discontinuities. This makes it
difficult to distinguish pupil frontier points from iris
contour ones.
A more articulated solution is then needed to cope
with problems caused by images like that in the third
row of figure 2. The segmentation algorithm
implemented in N-IRIS locates the pupil contour
first, and proceeds by separating the pupil from the
iris region. The mask is scanned row by row from
top to bottom. Each row is scanned from the first to
the last column, by marking the first and the last
black pixels. These pixels represent the iris frontier.
Frontier points are inputted to the Taubin’s
algorithm that approximates planar curves through
implicit equations (more details on this method are
discussed in (Taubin, 1991)) and outputs the centre
and radius of the circumference representing the iris.
A new circle centred in the iris centre, but with a
radius length of 1/5 of the iris radius is considered
(pupil will most likely fall inside this zone) and all
image pixels which fall outside such circle are
deleted. The centre and the radius of the
circumference approximating the pupil are
determined by repeating the procedure of circle
fitting on this new image, after inverting it.
Since the iris often undergoes several kinds of
distortions due to the illumination conditions, to the
acquisition distance or to partial occlusions, before
proceeding to actual feature extraction, one needs to
transform the iris region in a suitable form, also
considering future matching operations. Capture
distance represents a potential issue, as the iris
diameter may not be constant and the iris shape
influences matching results. Therefore, this
dimension must be normalized, yet avoiding to lose
details or to introduce "ghost" information and also
taking into account possible translations and
rotations. Furthermore, illumination conditions
cause dilation/contraction and small displacements
of the pupil that is seldom exactly located at the
center of the iris. Therefore N-IRIS transforms the
iris so that the iris representation is constant in
dimensions and that relevant features are
approximately located in the same points. To this
aim the Rubber Sheet Model by Daugman
(Daugman, 1993, Daugman, 2004) is exploited. This
model maps the iris in radial coordinates while
fixing the final dimensions of the obtained
(rectangular) image. Due to anticipated scarce
resolution of iris images at hand, N-IRIS adopts a
radial resolution (number of pixels along a radial
line) of 40 pixels, and an angular resolution (number
of radial lines around the iris region) of 360 pixels.
The same normalization is separately performed on
the segmentation mask associated to each image
(Figure 3). The mask is such that M(x,y)=1 if I(x,y)
is a pixel of noise, and M(x,y)=0 otherwise, so that
only information in relevant iris regions is coded.
IRIS RECOGNITION IN VISIBLE LIGHT DOMAIN
57

Figure 2: Column (a) shows, from top to bottom, iris
masks of increasing difficulty; column (b) shows mask
processing by ellipse fitting; column (c) shows mask
processing by N-IRIS.
3 FEATURE EXTRACTION
The feature extraction process aims to generate a
discriminating code for the iris annulus after that
noisy elements (e.g. eyelashes, which occupy
different positions and extent in different captures of
the same subject) have been discarded by the
segmentation algorithm. The quite rich structure of
the iris texture suggests to adopt different local
operators to capture different kinds of salient
information, while a subsequent fusion algorithm
merges their matching results at the score level. The
present work only exploits binary patterns to record
textural regularities present in the iris, and blob
identification for coding lighter or darker spots
inside the iris region (Figure 3). However, future
developments will investigate the addition of
appropriate versions of further local operators.
In particular, the first attempts were aimed at
investigating the usefulness of local texture analysis
based on Local Binary Pattern (LBP) (Ojala, 2002,
Mäenpää, 2000). In particular, the solution in (Sun,
2006) has been evaluated, before devising a
proprietary version, based on experimental evidence
on the best strategy to be adopted. In order to further
enhance the obtained results, this ad hoc
implementation of the LBP was combined with a
blob identification strategy (Chenhong, 2008),
namely BLOB. The BLOB algorithm has been
further enhanced to extract discriminable textons,
representing image regions which are lighter or
darker than the surrounding zone. Then, N-IRIS
merges the matching criteria stemming from the two
techniques, to exploit the respective strengths.
Figure 3: Feature extraction and coding based on
normalized iris image and segmentation mask.
3.1 Linear Binary Pattern
The Local Binary Pattern (LBP) is a local operator
introduced by Ojala (Ojala, 2002) to analyze image
texture. In its basic version, the operator evaluates
the 3×3 square region surrounding a pixel (eight
neighbours). Each neighbour has a corresponding
position in a 8 bits string, so that if the central pixel
has a lower value than one of its neighbours, a 1 is
recorded in the string for such neighbour, and a 0
otherwise (Figure 4). A variation is presented by
(Ojala, 2002), where the basic operator is extended
to process pixel neighbourhoods of variable
dimension, and to be invariant to rotations. The
circular neighbourhood of a pixel is exploited, and
sample points are identified by interpolation. The
resulting operator is called LBP
P,R
where P is the
number of sample points, and R is the radius of the
neighbourhood.
Sun et al. re-adapted LBP for iris recognition
(Sun, 2006). Their approach divides the normalized
iris image into blocks (Figure 5 (a)) and computes an
histogram for each of them. N-IRIS further improves
Sun’s method with a less computationally expensive
solution. N-IRIS splits the normalized iris image
into horizontal (or vertical) bands b
j
(Figure 5 (b)
and (c)) and computes the histogram H
j
of LBP
values for each of them. The overall iris code C is
built up by concatenating all histograms H
j
and the
noise mask M: C=(H
1
, H
2
, …, H
bands
, M).
N-IRIS assumes that the mask M is provided by
the segmentation algorithm. The mask M is used
ICPRAM 2012 - International Conference on Pattern Recognition Applications and Methods
58

Figure 4: Computation of LBP (a) and LBP
P,R
(b).
during matching to take into account the amount of
noise which is present within the compared bands.
The higher the number of noise pixels in the
matched bands, the less reliable the similarity
measure between the histograms.
Given two codings C
1
=(H
1
, H
2
, …, H
bands
, M)
and C
2
=(K
1
, K
2
, …, K
bands
, N), and any histogram
similarity measure δ (e.g. correlation, intersection or
Bhattacharyya), matching is performed by
computing the mean of the following values:
},,2,1{,1),( bandsb
totpixel
noise
KH
b
bb
K∈∀
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−⋅
δ
(1)
where
b
noise
represents the mean number of
noise pixels in the b-th band of masks M and N.
Bands specialize blocks: a generic block is m
(rows)×n (columns) pixels, an horizontal band is a
1×n block and a vertical band is a m×1 block. Once
blocks are ordered row-first, formula (1) always
holds.
Section 4 reports the most significant
experiments with LBP on the UBIRIS.v2, which
were aimed to testing both different types (block,
vertical, horizontal) and numbers of bands. Results
suggested that five horizontal bands represent the
best choice, which mostly depends on the
normalization parameters. It is also interesting to
notice that the most accurate solution in terms of
type of bands is also the most bound to anatomical
features, since horizontal bands in the polar image
correspond to circular bands in the original image,
and therefore are expected to be quite significant in
coding iris features.
Figure 5: Division in (a) blocks, (b) horizontal bands, or
(c) vertical bands.
3.2 BLOB
What we call BLOB is a differential operator
combining a Laplacian operator (a good contour
detector, but very sensible to noise) with a Gaussian
filter (to preliminarily smooth the image). It is very
effective in identifying lighter or darker regions in
the iris (Figure 6). N-IRIS improves the basic BLOB
method in (Chenhong, 2008) with a better blob
setting off, due to increased size of the Gaussian
filter. In that work blobs are modelled by a Gaussian
2-dimensional non-symmetric function, with length
features
1
t
and
2
t
:
21
22
221121
2
),(),(),(
2
2
2
1
2
1
tt
e
txgtxgxxf
t
x
t
x
π
+
==
(2)
To identify blobs of different sizes, the
IRIS RECOGNITION IN VISIBLE LIGHT DOMAIN
59

representation must be given both in space and in
scale. For the semi-group property of Gaussian
kernels g(⋅;t
A
)*g(⋅;t
B
) = g(⋅;t
A
+t
B
) the authors derive:
);();(
2211
ttxgttxgL ++=
(3)
If an image undergoes a space-scale smoothing,
values of spatial derivatives generally decrease with
scale. Then a normalized differential operator ∇
2
norm
must be used. The authors show that the normalized
response of a blob detector at scale t is:
)(
22
LtL
norm
∇=∇
(4)
The solution by (Chenhong, 2008) to extract and
code blob features is: fix the different scales,
compute ∇
2
norm
L for each scale and fuse the results
by taking, for each pixel, the maximum value among
all scales. Popular computational tricks allow to fuse
Gaussian and Laplacian in a single LoG operator.
Here the sizes of the convolution kernels at different
scales were found using cross-validation, e.g.
regression.
N-IRIS computes a matrix with real coefficients,
where positive values correspond to dark spots,
while negative values represent light ones. A
threshold operation is applied to binarize those
values: negative values are set to 0, while positive
ones are mapped on 1. Matching between two binary
codes can be performed by Hamming distance,
weighted by the segmentation masks, as discussed
by (Daugman, 1993). In order to account for rotation
variations, N-IRIS also considers shifts of 10 pixels
and returns as the final distance, the one computed
on the alignment returning the maximum match. A
further improvement has been attempted by chaining
the separate scale (binary) codings in a longer code,
instead of fusing them. Matching was performed by
comparing codes at the same scale and taking the
mean of obtained values as distance. This modality
will be referred as chain, as opposed to the original
one (fusion). It seemed to rely on more
discriminative information, but this did not produce
the expected improvements.
3.3 Combining LBP and BLOB
LBP and BLOB methods have been combined
according to a parallel protocol. This results in a
multi-classifier approach referred to as LBP-BLOB.
The iris biometric key is made up by chaining LBP
and BLOB codes. When two iris biometric keys
have to be matched, LBP and BLOB work
separately and fusion is performed at score level.
Given I a normalized iris image and M its
Figure 6: Some examples of blobs that are local features
such as furrows, crypts and freckles or spots.
normalized segmentation mask, N-IRIS computes
c
LBP
and c
BLOB
, the LBP and BLOB coding of the
couple (I, M) respectively (actually, coding is only
performed on the I element). Thus, the final method
for coding and matching is:
• Coding of the pair (I, M) is c={c
LBP
, c
BLOB
}
• Matching between codings c
1
and c
2
is given by:
),,()1(
),(),(
,2,1
,2,121
BLOBBLOBBLOB
LBPLBPLBP
cc
cccc
δλ
λδ
δ
−+
=
(5)
where the value 0.5 for
λ
was found experimentally.
The adopted fusion strategy was assessed by
experiments on a large set of iris images. On this
sufficiently substantial test bed, it was observed that
LBP and BLOB show a quite uncorrelated behaviour
in terms of ability to discriminate between genuine
and impostor matches.
Though this is not a formal proof of the actual
lack of correlation between the two techniques, it is
an expected result considered that they rely on
different theoretical frameworks, aiming to capture
different relevant characteristics (texture regularity
and the presence of significant "hot spots"). In future
research lines, a related study represents a core
point. For the time being, the previous observations
can explain, in the present setting, why the simple
sum of the two scores improves the performances of
the single classifiers, as confirmed by experimental
results.
ICPRAM 2012 - International Conference on Pattern Recognition Applications and Methods
60
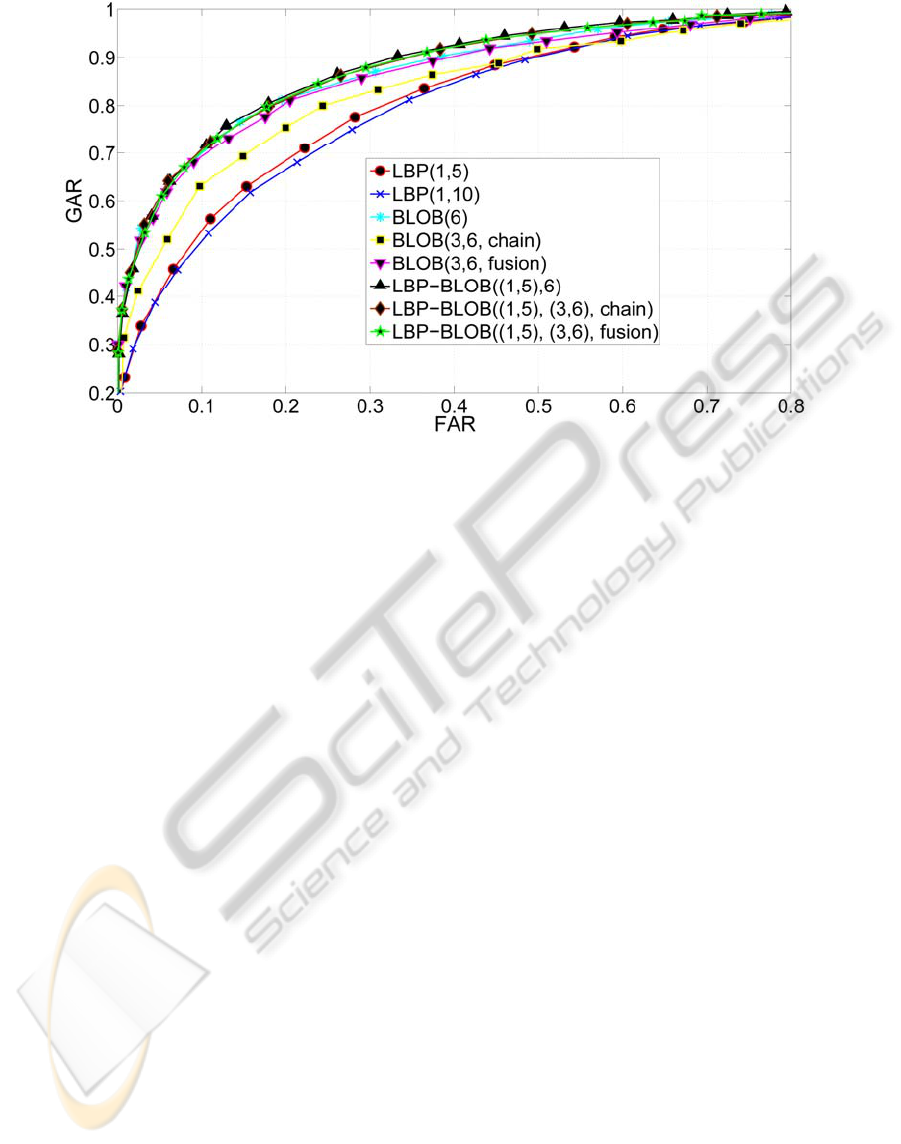
Figure 7: Results from LBP, BLOB and LBP-BLOB with different configurations on NICE II tuning database.
4 EXPERIMENTAL RESULTS
The experiments to assess N-IRIS performances
were performed on the database of 1000 images and
corresponding segmentation masks provided for
tuning purposes by NICE II program committee to
challenge participants, together with a dedicated
JAVA platform. The results were measured in terms
of the classical accuracy "figure of merit" Receiving
Operating Curve (ROC).
All color images were converted in gray scale by
assigning each pixel the weighted mean of the three
primary channels of its RGB color. LBP was tested
by dividing the images in horizontal or vertical
bands and in blocks. LBP(n,m) will denote LBP
execution on an image subdivided in n columns and
m rows. BLOB was run in single scale
configuration, with fusion of different scale results,
and with chaining (see Section 3.2). Scale t varied in
the set T={2,4,6,8,12,16,24}. In fusion and chain
modes, pairs (t
1
, t
2
) and triplets (t
1
, t
2
, t
3
) of scales
from T have been considered. BLOB(t
1
) will denote
single scale execution of BLOB at scale t
1
, BLOB(t
1
,
t
2
, mode) will denote the execution of BLOB in
mode mode∈{chain, fusion} for the pair of scales
(t
1
, t
2
) and BLOB(t
1
, t
2
, t
2
, mode) will denote the
execution of BLOB in mode mode∈{chain, fusion}
for the triplet of scales (t
1
, t
2
, t
3
). A configuration for
LBP-BLOB combines single configurations for LBP
and BLOB: LBP-BLOB(n, m, t
1
), LBP-BLOB(n, m,
t
1
, t
2
, mode) and LBP-BLOB(n, m, t
1
, t
2
, t
3
, mode).
Figure 7 shows the ROC curves from LBP and
BLOB with different configurations, as well as
different combinations of such configurations, on
UBIRIS v2. The subdivision in five horizontal bands
seems an optimal LBP configuration for this
databases. BLOB in fusion mode (the original one)
provides better results than BLOB in chain mode.
Moreover, BLOB works better with a single scale on
UBIRIS.v2. Though sounding strange, this is a
consequence of the scarce clearness of most images
in this database. For such images, using more scales
provides poor benefit. BLOB seems to perform
better than LBP, but this trend is reversed on low
resolution images. This underlines a better ability by
LBP to extract relevant features in these cases. It is
worth noticing that normalization fails in some
critical situations, were the useful iris region is
especially scarce and, at the same time, iris and pupil
boundaries are not well separated as in the last row
of Figure 2. Matching problems encountered with
LBP are related to excessive blurring, since the
histogram undergoes a substantial alteration, while
BLOB problems are related to irises with high off-
axis angles which significantly alter blobs shape.
Figure 7 also shows that the LBP-BLOB
performs better than the single methods. The
performances of the combined method were also
measured in terms of decidability value. Decidability
is defined as a function of mean and variance of
intra- and inter-class scores. The higher the index,
the better the discrimination ability of the system. If
D
I
and D
E
denote the set of similarities resulting
from intra- and inter-class matches,
μ
(D
I
) and
μ
(D
E
)
IRIS RECOGNITION IN VISIBLE LIGHT DOMAIN
61

the respective mean values, and
σ
(D
I
) and
σ
(D
E
) the
standard deviations, the decidability index is:
))()((5.0
)()(
22 EI
EI
DD
DD
d
σσ
μμ
−
−
=
(6)
On the given dataset, the method achieved a
decidability value of 1.4825. N-IRIS was then tested
by the NICE II evaluation commission on new
images and masks, never provided before. The
obtained result is very close to the decidability
reported here. It has been submitted to NICE II
international competition and has been awarded as
one of the best 6 iris segmentation and recognition
algorithms (Nice II, 2011).
5 CONCLUSIONS
This work presents an approach for matching irises
captured in the visible light spectrum and in
uncontrolled settings. Linear Binary Patterns (LBP)
and BLOB have been adapted and combined in an
original and specific way, to address the difficult
operational conditions due to the strongly relaxed
capture constraints. The obtained results are quite
satisfactory both in terms of ROC and of
decidability value, most of all against the present
research scenario, as the independent tests
performed by NICE II program committee have
demonstrated. This is a strong motivation to further
improve performances. A very promising research
line is the use of more local features, able to set off
different iris peculiarities, as for example the
directionality of extracted patterns.
REFERENCES
Bowyer K. W., Hollingsworth K., Flynn P. J., 2008. Image
Understanding for Iris Biometrics: A Survey, vol. 110,
no. 2, pp. 281–307.
Chenhong L., Zhaoyang L., 2008. Local feature extraction
for iris recognition with automatic scale selection.
Image and Vision Computing, vol. 26, no. 7, pp. 935–
940.
Daugman J., 2004. How Iris Recognition Works, IEEE
Transactions on Circuits and Systems for Video
Technology, vol. 14, no. 1, pp. 21–30.
Daugman, J., 1993. High confidence visual recognition of
persons by a test of statistical independence. IEEE
Transactions Pattern Analysis and Machine
Intelligence vol. 15, no. 11, pp. 1148-1161.
Dorairaj V., Schmid N., Fahmy G., 2005. Performance
evaluation of non-ideal iris based recognition system
implementing global ICA encoding. In Proceedings of
the IEEE International Conference on Imag
Processing (ICIP 2005), pp. 285–288.
Du Y., Bonney B., Ives R., Etter D., Schultz R., 2005.
Analysis of partial iris recognition using a 1-d
approach. In Proceedings of the IEEE International
Conference on Acoustics, Speech and Signal
Processing (ICASSP’05), pp. 961–964.
Ojala T., Pietikäinen M., Mäenpää T., 2002.
Multiresolution gray-scale and rotation invariant
texture classification with local binary patterns. IEEE
Transactions on Pattern Analysis and Machine
Intelligence, vol. 24, no. 7, pp. 971–987.
Proença H., Alexandre L. A., 2007. Toward non-
cooperative iris recognition: A classification approach
using multiple signatures,” IEEE Transactions on
Pattern Analysis and Machine Inteligence, vol. 9,
no.4, pp. 607–612.
Proença H., Filipe S., Santos R., Oliveira J., Alexandre L.
A., 2010. The UBIRIS.v2: A Database of Visible
Wavelength Images Captured On-The-Move and At-
A-Distance, IEEE Transactions on Pattern Analysis
and Machine Intelligence, vol. 32, no. 8, pp. 1529–
1535.
Sun Z., Tan T., Qiu X., 2006. Graph Matching Iris Image
Blocks with Local Binary Pattern. In Proceedings of
the International Conference on Biometrics, pp.366–
372
Sung E., Chen. Xilin, Yang J., 2002. Towards non-
cooperative iris recognition systems. In Proceedings of
the seventh International Conference on Control,
Automation, Robotics and Vision, pp. 990–995.
Tan T., Hea Z., Sun Z., 2010. Segmentation of Visible
Wavelength Iris Images Captured At-a-distance and
On-the-move, Image and Vision Computing, vol. 28,
no. 2, pp. 223–230.
Taubin G., 1991. Estimation Of Planar Curves, Surfaces
And Nonplanar Space Curves Defined By Implicit
Equations, With Applications To Edge And Range
Image Segmentation. IEEE Transaction on Patterna
Analysis and Machine Intelligence, vol. 13, pp. 1115–
1138.
Mäenpää T., Ojala T., Pietikäinen M., Soriano M., 2000.
Robust Texture Classification by Subsets of Local
Binary Patterns. 15-th International Conference on
Pattern Recognition, pp. 947–950.
Wildes R., 1997. Iris recognition: an emerging biometric
technology. Proceedings of the IEEE, vol. 85, no. 9,
1997.
NICE II, nice2.di.ubi.pt. Last visit on November 06 2011.
ICPRAM 2012 - International Conference on Pattern Recognition Applications and Methods
62
