A 0.45NW, 0.5V, 59-DB DR, G

-C LOW-PASS FILTER

FOR PORTABLE ECG RECORDING

Chutham Sawigun, Senad Hiseni and Wouter A. Serdijn

Biomedical Electronics Group, Electronics Laboratory, Delft University of Technology,

Mekelweg 4, 2628 CD, Delft, The Netherlands

Keywords: Analog Circuit, G

-C Filter, Low-Pass Filter, Sub-Threshold CMOS, Ultra Low-Power, Weak Inversion.

Abstract: This paper presents the design of a sub-threshold CMOS G

-C low-pass filter in a portable ECG detection

system. The proposed filter is formed by cascading 6 stages of identical 1

-order low-pass sections. With a

minimum number of active components in the 1

-order section, the noise contribution of the circuit can be

kept low while minimizing the size of transistors and capacitors. The filter cut-off frequency is designed to

be adjustable over the range from 100Hz to 250Hz by changing the bias current. Circuit simulations, using

AMS’ 0.18µm CMOS technology and operating from a 0.5V supply voltage, show that, for a cut-off

frequency of 150Hz, the filter draws 0.9nA of current. An input referred noise of 88µV

rms

is obtained while

for 1% total harmonic distortion, the voltage swing can be as high as 0.23Vpp.

1 INTRODUCTION

As a consequence of the heart activity,

electrocardiograms (ECGs) can be recorded by skin

electrodes (Webster, 1995). By measuring the ECG

signal, the heart condition can be diagnosed and

monitored. In a portable ECG detection system a

low-pass filter (LPF) is required to impede high

frequency electrical signals from non-cardiac

muscles (muscle noise or artifact) (Garcia-Niebla

and Serra-Autonell, 2009) and to avoid aliasing in

the sampling process of an analog to digital

converter (ADC) (Lee and Cheng, 2009).

In order to minimize power consumption of the

LPF in the portable ECG detector, weak inversion

operation of CMOS devices is the first condition to

handle for a design using very little bias current.

Nonlinearity, noise and mismatch of this operating

region are, however, more severe than that of its

strong inversion counterpart. Recently, the

systematic design of an ECG filter optimizing those

non-idealities within a linearized G

-C filter

structure has been reported (Lee and Cheng, 2009).

A very good figure-of-merit (FoM) was obtained at

a power consumption of only 453nW.

To further reduce the power consumption, this

paper proposes a LPF design technique that does not

require a linear G

. Instead of trying to linearize the

cell to obtain a good performance before

substituting it into a passive prototype LC filter, a

nonlinear G

with feedback is used to create a 1

order LPF cell before forming the higher order filter

by cascading the identical 1

-order cells. This

approach can reduce a lot of power while other

performances remain the same (or become even

better) in the pass-band of the LPF. To demonstrate

this idea, we exploit a follower integrator (FI)

(Mead, 1989) as the fundamental element of our

ECG filter, which subsequently is realized by

cascading 6 FI stages. Simulation results, using

Cadence with AMS’ 0.18µm CMOS model

parameters, confirm that for comparable

performance, the proposed ECG filter’s power

consumption is three orders of magnitude lower than

that of the LPF in (Lee and Cheng, 2009).

The remaining sections of the paper are

organized as follows. In Sec. II, a brief description

of the ECG portable detector is shown. The basic

concept of the 1

-order FI based filter is described

and a 6

-order Bessel LPF is presented in Sec. III.

Next, Sec. IV presents the simulation results. The

conclusions will be drawn in the last section.

2 LOW-PASS FILTER DESIGN

ISSUES IN ECG DETECTOR

Fig. 1 illustrates a portable ECG detection device.

324

Sawigun C., Hiseni S. and A. Serdijn W..

A 0.45NW, 0.5V, 59-DB DR, GM-C LOW-PASS FILTER FOR PORTABLE ECG RECORDING.

DOI: 10.5220/0003764103240328

In Proceedings of the International Conference on Biomedical Electronics and Devices (BIODEVICES-2012), pages 324-328

ISBN: 978-989-8425-91-1

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

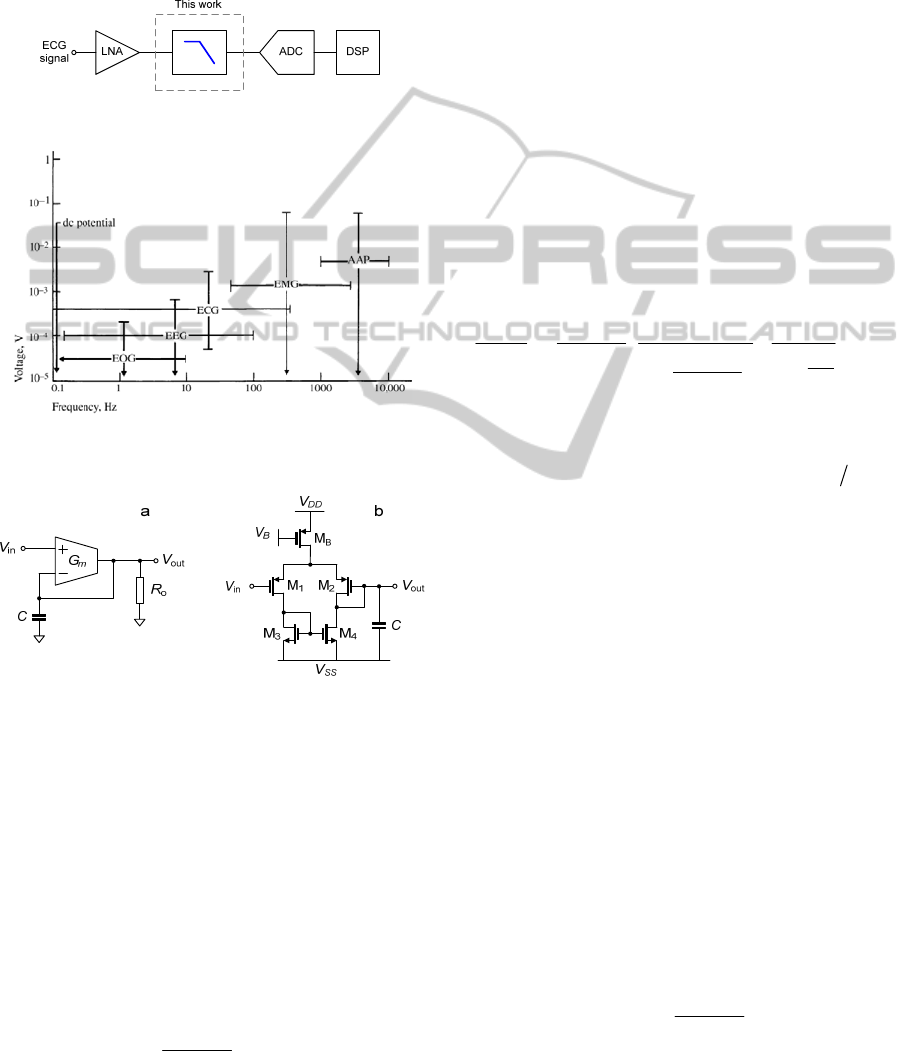
First, a low noise amplifier is used to amplify the

very weak ECG signal. Depending on the electrodes

used, ECG signal amplitudes can range from around

50µV to approximately 4 mV (see Fig. 2) (Webster,

1995). Next, high frequency components of the ECG

signal are filtered out to decrease the out-of-band

noise. Herein, the recommended low-pass cut off

Figure 1: Portable ECG detection.

Figure 2: Different biopotential voltages versus frequency

spectrum (Webster, 1995).

Figure 3: Follower integrator a) macro-model b) transistor

level circuit.

frequencies are 150Hz and 250Hz in case of adults

and children, respectively (Kligfield et al., 2007)

(Rijnbeek et al., 2001). Afterwards, an ADC is

utilized in which the analog input signal is quantized

and converted into digital values as needed for the

subsequent digital signal processing (DSP).

Since there is a large variation on the expected

amplitude of the input signal, the amplifier and filter

are required to have a minimal Dynamic Range

(DR), according to (Lee and Cheng, 2009) (Luo and

Johnston, 2010), of

max

min

20log 44dB

ECG

⎛⎞

=≅

⎜⎟

⎝⎠

(1)

To avoid aliasing, the filter should provide sufficient

attenuation in the stop-band. In (Lee and Cheng,

2009), for a sampling frequency (f

) of 1kS/s, 29dB

attenuation at 500Hz (f

/2) was found. In this work,

we target the same numbers of attenuation and

sampling rate. Besides, to minimize phase distortion,

a constant group delay over the pass-band response

of the filter should be obtained (Hejjel and Kellenyi,

2005).

3 FOLLOWER INTEGRATOR

BASED LOW-PASS FILTER

The FI is conceptually shown in Fig. 3a. It

comprises a transconductor and a grounded

capacitor connected in a negative-feedback fashion.

Resistor R

represents the output resistance of the

transconductor to ground (which is usually many

times larger than

−

). We then find that

out

()

() 1

Vs GR

sCR

⎛⎞

=≅

⎜⎟

⎛⎞

⎝⎠

⎜⎟

⎝⎠

(2)

As one can see from (2), the FI provides a low-pass

frequency response with a pass-band gain and cut-

off frequency of

K ≅ 1 and f

= 2

repectively.

According to this characteristic,

out

is following

closely for input signal frequencies below f

. In

other words, the differential input voltage of the

is kept small, which helps the filter to suffer less

from nonlinearity of the

itself. Benefitting from

the fact mentioned above, high dynamic range low-

pass filters realized from nonlinearized

s have

been successfully implemented in (Python, 1999)

and (D’Amico et al., 2006). Hence, without

linearization, the

s can be made compact and low

noise and low-power consumption can be expected

while a good linearity can be achieved due to the

large loop-gain at low frequencies.

The FI can be simply formed by the circuit

shown in Fig. 3b (Mead, 1989). It comprises a

simple differential pair M1-M2 biased by current

source MB with a current mirror active load, M3-

M4, and a grounded capacitor,

Neglecting channel length modulation, the

capacitance current can be found to be

in out

tanh

⎛⎞

−

⎜⎟

⎝⎠

(3)

The nonlinear relation in (3) is shown here to give

A 0.45NW, 0.5V, 59-DB DR, GM-C LOW-PASS FILTER FOR PORTABLE ECG RECORDING

325

an intuitive understanding that at low frequencies I

≅ 0 and consequently, V

and V

out

are forced to be

equal. The hyperbolic tangent function will not

produce any distortion in this case. But for higher

frequencies, the phase difference between

≅ V

out

becomes greater and more distortion will be

produced.

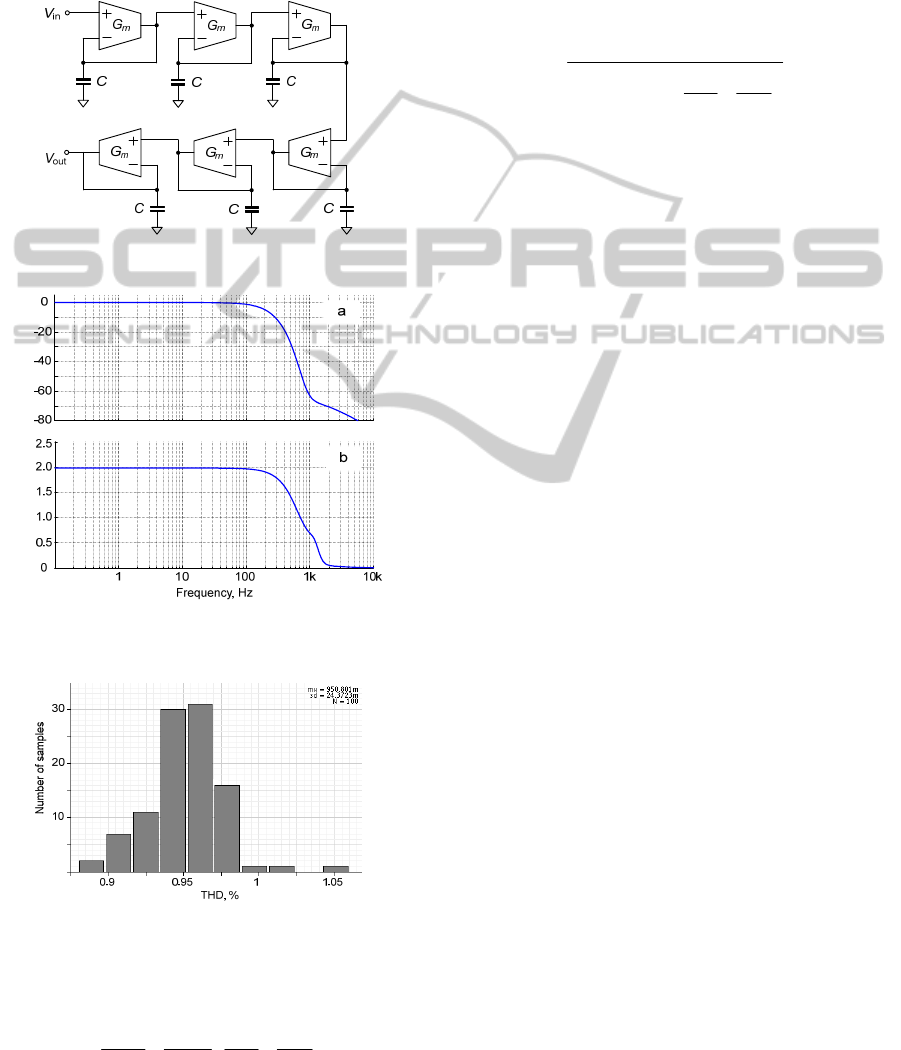
Figure 4: FI based 6

order LPF.

Magnitude, dBGroup delay, ms

Figure 5: Frequency response of the proposed filter

a) magnitude response b) group delay.

Figure 6: Monte-Carlo simulation.

The power spectral density of the output noise

voltage can be found to be (at low frequencies)

811

()

vno

mOX

nkT

GCfWLWL

⎛⎞

=+ +

⎜⎟

⎝⎠

(4)

where

is a flicker noise parameter, all the other

symbols have their usual meanings,

WL WL

and G

/2nU

For our application that deals with input

frequencies below a few hundred hertz, the majority

of the noise power is not only contributed by the

thermal noise but also by 1/

f noise. From (4) the

noise corner frequency can be found as

()

corner

qI K

nkT C

WL WL

⎛⎞

⎜⎟

⎝⎠

(5)

We can see from (5) that to keep

corner

low, the

FI requires large transistor sizes and low bias

current.

The requirements of the filter mentioned in

Section II can be simply met by cascading 6

identical FI stages as shown in Fig. 4. Formed by

identical circuit elements this structure provides a

Bessel transfer function. All the

s are realized by

the transconductor in Fig. 3b. The advantages of this

filter topology are pointed out in the following list:

• As a consequence of the use of identical

components in a modular structure, the

filter’s sensitivity to capacitance and

transconductance variations is low.

• The linearity of the filter is less susceptible

to mismatch due to the unity gain feedback

in each 1

-order section.

• The internal node voltage swings are all

identical in the pass-band. Hence, the filter

distortionless output swing is maximized

(Groenewold, 1992).

• The contributions of all

stages to the

overall output noise are almost equal.

Hence, the filter output noise is minimized

(Groenewold, 1992).

• Constant group delay can be expected in

the pass-band frequency range.

The drawback is that the transition band roll-off

is less steep compared to other filter types.

For a cutoff frequency of 150Hz, realizing this

filter circuit within an acceptable chip area and

obtaining very low power consumption to achieve a

pass-band gain of 0dB and sufficient magnitude

attenuation at

/2 = 500Hz are feasible.

4 CIRCUIT SIMULATIONS

The LPF circuit has been designed to be

BIODEVICES 2012 - International Conference on Biomedical Electronics and Devices

326

implemented in AMS’ 0.18

μm CMOS process

technology. The bias current of each FI circuit is set

= 0.15nA. The total bias current for the filter

core equals 0.9nA. Operated from a 0.5V supply,

this results in 0.45nW static power. Dimensions of

the MOS transistors used are listed in Table. I. The

transistors are largely sized to reduce the transistor’s

flicker noise and mismatch. The total capacitance

equals 6pF (1pF per stage).

Table 1: Transistor Dimensions.

MOSFET W [µm] L [µm]

, M

: M

15:8:12 2.5:8:6

Table 2: Performance Summary and Comparison.

Lee and Cheng,

2009

(Measurement)

This work

(Simulation)

Approx. type Butterworth Bessel

CMOS Tech. 0.18µm 0.18µm

1V 0.5V

P 453nW 0.45nW

order, N 5 6

Total cap. 5.76pF 6pF

Pass-band gain –10.5dB 0dB

–3dB

250Hz 150Hz

/2 attenuation –29dB* –28dB

IRN 340µV

rms

88µV

rms

DR@THD

(50Hz f

)

40.3dB@-48.6dB

59.3dB@-40dB,

52.1dB@-48.4dB

FoM 8.99×10

-12

8.43×10

-15

9.6×10

-15

* From the simulated frequency response

Fig. 5 shows the simulated magnitude response

and the group delay of the proposed filter. The

–3dB

cut-off frequency is found at 150Hz and a magnitude

attenuation of –28dB is obtained at 500Hz. The

group delay of 2ms remains constant over the range

of DC to 100Hz. At 250Hz a 0.6ms delay deviation

from 2ms is found.

For a more realistic estimation of the circuit

linearity, we also performed a statistical analysis.

The effect of transistor mismatch is verified through

a Monte-Carlo simulation for the condition of a

0.11V input amplitude. For 100 runs, the obtained

result is very satisfying as can be seen from the

histogram in Fig. 6. The mean value of the THD

obtained is 0.95% with a standard deviation of

0.024%.

Table II shows a performance comparison

between the proposed LPF and the measured results

from the recently reported ECG LPF (Lee and

Cheng, 2009) that relies on a linearized

composed of several transistors and a filter structure

that does not contain local unity-gain feedback

loops. Hence, high amounts of noise and mismatch

induced nonlinearity cannot be avoided. Due to the

compact

circuit and the local negative feedback

in the FI structure, our proposed filter outperforms

the previous ECG filter on most of its performance

except the transition band attenuation and the value

of the capacitance while the power consumption of

our design is 1000 times lower. Considering the

FoM (Vittoz and Tsividis, 2002) defined by

()

3dB

PNf DR

−

×× ×

, where, N is the filter order and

P is the power consumption, the proposed LPF also

improves the FoM by approximately three orders of

magnitude.

5 CONCLUSIONS

The design of a 6

-order G

-C low-pass filter using

nonlinear CMOS transconductors operating in their

sub-threshold region has been presented. The

presented filter features good linearity in the pass-

band and mismatch insensitivity due to its embedded

negative feedback within each fundamental FI cell.

Low noise and low-power consumption are achieved

from the compactness of the ordinary

transconductors that we employ. The obtained

simulation results confirm that our design fits

portable ECG detection requirements well.

REFERENCES

D’Amico S., Conta M., Baschirotto A. 2006. A 4.1mW

10MHz fourth-order source-follower-based conti-

nuous-time filter with 79-dB DR, IEEE J. Solid-State

Circuits, pp. 2713-2719.

Garcia-Niebla J., Serra-Autonell G., 2009. Effects of

inadequate low-pass filter application, Journal of

Electrocardiography, vol. 42, pp. 303-304.

Groenewold G., 1992, Optimal dynamic range integrators,

IEEE Trans. Circuits Syst. I, vol. 39, p.614 .

Hejjel L., Kellenyi L., 2005. The corner frequencies of the

ECG amplifier for heart rate variability analysis,

Physiological Measurement, vol. 26, pp. 39–47.

Kligfield P., Gettes L. S., Bailey J. J., et al., 2007.

Recommendations for the standardization and

interpretation of the electrocardiogram, J. Am. Coll

Cardiol, vol. 49, no. 10, pp 1109–1127.

Lee S. Y., Cheng C. J., 2009. Systematic design and

modeling of a OTA-C filter for portable ECG

detection, IEEE Trans. Biomed. Circuits Syst., vol. 3,

no. 1, pp. 53-64.

Luo S., Johnston P., 2010. A review of electrocardiogram

filtering, Journal of Electrocardiology, vol. 43, no 6,

pp 486 – 496.

A 0.45NW, 0.5V, 59-DB DR, GM-C LOW-PASS FILTER FOR PORTABLE ECG RECORDING

327

Mead C. A., 1989 Analog VLSI and Neural Systems.

Addison-Wesley Publishing Co., Reading, MA, 1989.

Python D., Porret A. S., Enz C., 1999. A 1V 5

-order

Bessel filter dedicated to digital standard proceses,

Proc. IEEE CICC, pp. 505-508.

Rijnbeek P. R., Kors J. A., 2001. Witsenburg M.,

Minimum bandwidth requirements for recording of

pediatric electrocardiograms, Circulation, vol. 104, pp

3087-3090.

Vittoz E., Tsividis Y., 2002 Frequency-dynamic range-

power, in Trade-Offs in Analog Circuit Design, C.

Toumazou, G. S. Moschytz, and B. Gilbert, Eds.

Boston, MA: Kluwer, ch. 10.

Webster, J. G., 1995. Medical Instrumentations:

Application and Design, New York: Wiley.

BIODEVICES 2012 - International Conference on Biomedical Electronics and Devices

328