SUPPORT VECTOR DATA DESCRIPTION FOR SPOKEN DIGIT

RECOGNITION

Amirhossein Tavanaei

, Alireza Ghasemi

, Mohammad Tavanaei

, Hossein Sameti

and Mohammad T. Manzuri

Department of Computer Engineering, Sharif University of Technology, Azadi Street, Tehran, Iran

Department of Computer Engineering, École Polytechnique Fédérale de Lausanne, Lausanne, Switzerland

Department of Control and Signal Processing, SAIPA Company, Karaj Street, Tehran, Iran

Keywords: Speech recognition, Machine learning, Pattern recognition, Mel frequency discrete wavelet transform, One-

class learning, Support vector data description.

Abstract: A classifier based on Support Vector Data Description (SVDD) is proposed for spoken digit recognition.

We use the Mel Frequency Discrete Wavelet Coefficients (MFDWC) and the Mel Frequency cepstral

Coefficients (MFCC) as the feature vectors. The proposed classifier is compared to the HMM and results

are promising and we show the HMM and SVDD classifiers have equal accuracy rates. The performance of

the proposed features and SVDD classifier with several kernel functions are evaluated and compared in

clean and noisy speech. Because of multi resolution and localization of the Wavelet Transform (WT) and

using SVDD, experiments on the spoken digit recognition systems based on MFDWC features and SVDD

with weighted polynomial kernel function give better results than the other methods.

1 INTRODUCTION

Speech recognition and digit recognition as a part of

it have been studied for many years. Several feature

extraction methods are used for speech recognition.

The Mel Frequency Cepstral Coefficients (MFCC)

feature vector is widely used in many popular

speech recognition systems. The Mel Frequency

Discrete Wavelet Coefficients (MFDWC) feature

vector has been used for these purposes recently

(Bresolin, 2008) and (Gowdy and Tufekci, 2000).

The HMM is the most frequent classifier used in

speech recognition applications (Rabiner and Juang,

1986) and (Rabiner, 1989). Another classifier that is

useful for speech recognition is the Support Vector

Machine (SVM). The use of SVM classifiers in

speech recognition by improving their kernel

functions have resulted in very good performances.

In (Bresolin, 2008) SVM is used for classifying

Brazilian Portuguese spoken digits with polynomial

kernel function. Several studies in speech

recognition are based on combination of SVM and

HMM for modelling the speech signals

(Ganapathiraju, 2004) and (Sonkamble, 2008).

Another approach that is used for improving both

the generality and learning ability in SVM classifier

for speech recognition is the convex combination of

polynomial and Gaussian kernels (Bai, 2008).

Spoken digit recognition is a multi-class

classification problem, whereas SVM is best suited

for binary, i.e. two-class problems. The difficulty

arises when one tries to solve a multi-class problem

using SVM by the so-called one-against-all

approach. In addition to imbalance between target

class and outlier class (which is composed of

samples from all other classes except the target),

another problem is that, unlike the target class, the

outliers can not be easily identified as a uniform

class (Figure 1). The outlier class is composed of

many different classes which, summed together, do

not form a uniform class. To solve such a problem,

the so-called one-class learning approach is used

(Khan, 2009), which assumes that samples of only

one class are available and a model is constructed

using for each class these samples. After that, the

likelihood of every test sample is evaluated in each

model and samples are ranked according to their

likelihood. The number of targets in top k samples

(assuming it is known a priori that k targets are

present in test data) is the measure used to evaluate

the model.

Tavanaei A., Ghasemi A., Tavanaei M., Sameti H. and T. Manzuri M..

SUPPORT VECTOR DATA DESCRIPTION FOR SPOKEN DIGIT RECOGNITION.

DOI: 10.5220/0003764400320037

In Proceedings of the International Conference on Bio-inspired Systems and Signal Processing (BIOSIGNALS-2012), pages 32-37

ISBN: 978-989-8425-89-8

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

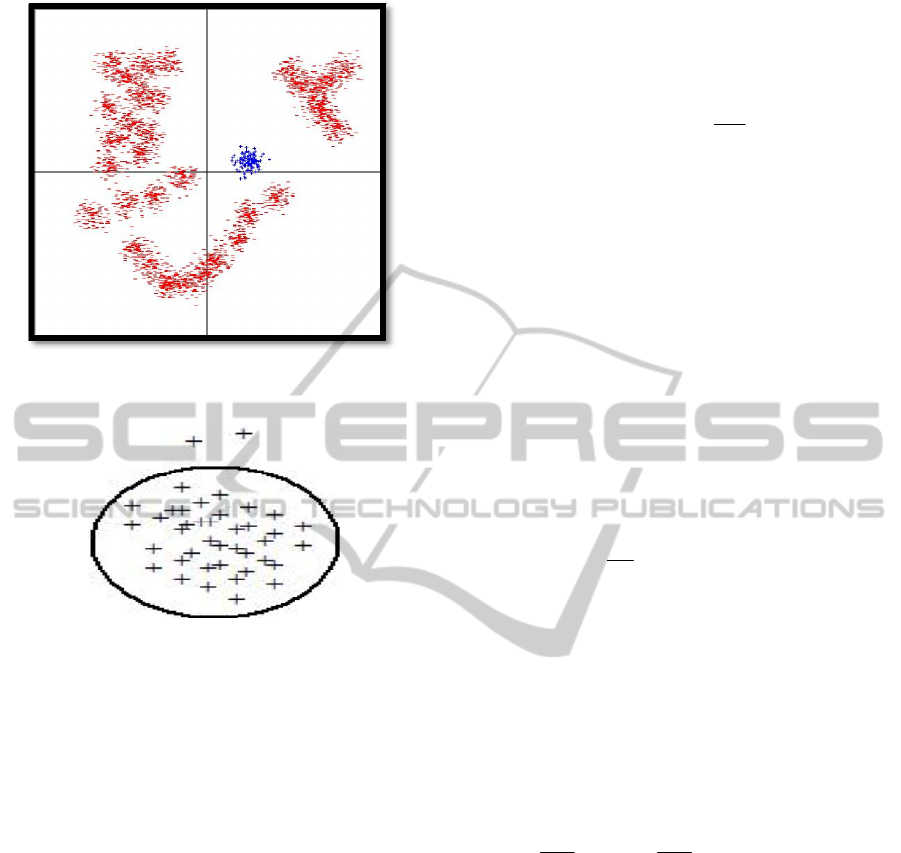
Figure 1: A Sample database suitable for one-class

learning.

Figure 2: Support vector data description.

2 THE DATA DESCRIPTION

APPROACH

We propose a one-class learning approach for

solving the problem of spoken digit recognition. The

goal is to train a classifier for each digit that can

separate that digit from all others. We achieve this

by using the Support Vector Data Description

(SVDD) approach to one-class learning (DeMenthon

and Doermann, 2008). We mention SVDD briefly in

the rest of this section. For a more detailed

explanation, refer to the seminal work of Tax and

(Tax and Duin, 2004). Functionality of the SVDD is

depicted in Figure 2.

Suppose we are given a dataset {x

, x

, ... x

}. It

constitutes the training set. The main idea of support

vector data description is to draw a hyper sphere in

the feature space containing as many training

samples as possible while having minimum possible

volume. The sphere is characterized by its centre c

and radius R > 0. The minimization of the sphere

volume is achieved by minimizing its square radius

. Data samples outside the hyper sphere are

penalized in the objective function. To count for

these, slack variables





are introduced and the

optimization problem is formulated as

min

RCF













(1)

Such that

|| || 0

iii

xC R and



  

(2)

The parameter “u” controls the trade-off between the

hyper sphere volume and the proportion of samples

in the hyper sphere. If x

is within the sphere or on

the boundary, there is no error and the corresponding



equals to zero. Otherwise,



> 0 is the squared

distance from x

to the boundary of the sphere.

Introducing Lagrangian multipliers to account for

constraints, we obtain the following dual problem:

min ( , ) ( , )

iji j iii

ij i

xx xx



 





(3)

Such that

and



 



(4)

Solving the dual optimization problem yields



. If

is within the sphere, the inequality constraint

|| ||

xc R





is satisfied and the

corresponding Lagrangian multiplier,



, is zero.

Otherwise, for x

on the sphere (



= 0) or beyond

the sphere (



> 0), the equality constraint

|| ||

xc R





has to be enforced and the

Lagrangian multipliers will become non-zero, i.e.,

Nu Nu



 

. Samples x

with

positive



are called Support Vectors of the SVDD.

Given a new sample z, we compare its distance

to the centre of the sphere with the radius of the

sphere R. If z lies inside the hyper sphere, it belongs

to the target class; otherwise, z is classified as an

outlier.

Another notable property of the SVDD is the

kernel trick. To count for cases in which support of

data does not have a spherical shape, we may

transform the data into a higher dimensional space in

which the data lie in a spherically-shaped support.

Note that in the dual optimization problem, samples

only appear in the form of inner products with other

points; Hence, we only need to express the inner

product in new space as a function of samples in the

original space. The kernel is stated as:

SUPPORT VECTOR DATA DESCRIPTION FOR SPOKEN DIGIT RECOGNITION

(, ) ((),( ))

ij i j

kx x x x





(5)

In which



is the transformation function.

3 EXPERIMENTS AND RESULTS

3.1 Implementation Details

In this section we describe the implementation

details of our approach. After discussing the process

of feature extraction and features used, we describe

the kernels and parameters used, as well as tuning

strategies for kernel parameters.

Dynamic windowing (Fixed number of frames):

Spoken digits have different durations, so fixed-

length frames don’t seem appropriate for recognition

of them. For every digit we can extract 76 frames

and duration of each frame is determined by total

duration of utterance. Using this approach, feature

vectors of equal dimension are obtained for each

spoken digits.

Mel Frequency Cepstral Coefficients: The MFCCs

are obtained by applying a logarithmic scale similar

to the human auditory systems called Mel scale to

spectrum coefficients. After computing the energy of

each sub band in Mel frequency, then feature vectors

are obtained by applying a Discrete Cosine

Transform (DCT) on them. Equation (6) shows the

cepstral coefficients formula.

cos( ( ))

Cmj









(6)

where N is the number of log-spectrum coefficients

each denoted by m

and L is the number of cepstral

coefficients. We use 15 coefficients for feature

vector of each frame in digit recognition.

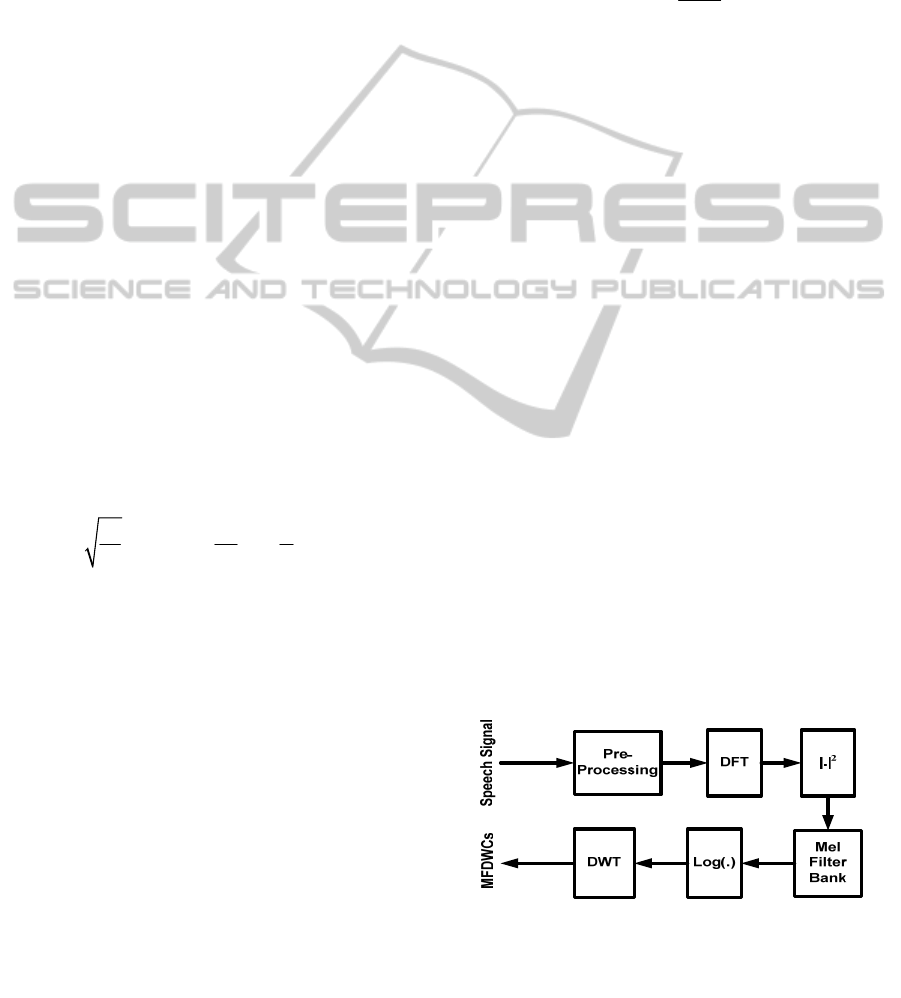
Mel Frequency Discrete Wavelet Transform: The

MFDWCs are obtained by applying the discrete

wavelet transform to the Mel-scale log filter bank

energies of a speech frame. For this purpose we use

32 filter banks and 4 scales of Daubechies 6 wavelet

function. So each frame has 15 coefficients as the

feature vector. Figure 3 depicts the process of

MFDWT feature extraction.

Kernel Selection and Tuning: There are many

different kernels available to use (Taylor and

Cristianini, 2004). We tried to use the most

prevalent kernels and tune their parameters to

achieve the best performance.

The most popular kernel used in machine learning

research is the Gaussian or radial basis kernel. This

popularity is mostly due to the flexibility of

Gaussian kernel which is achieved by tuning

bandwidth parameter to different values and hence

deriving different support shapes. The bandwidth

parameter of kernel was selected using ten-fold

cross-validation and exponential modifying.

|| ||

(, )

kxy e







(7)

In which



is the bandwidth parameter.

However, the main problem with Gaussian

kernel is that it treats all dimension of the feature

vector with the same significance. In our

experiments, however, the lower coefficients

extracted from each frame are more important and

probably more discriminative. Hence, they should be

given more significance in the process of computing

the kernel. The Gaussian kernel does not allow easy

assignment of different weights to features. In order

to assign different weights to feature dimensions, we

used the polynomial kernel which has already been

applied successfully to certain problems in speech

recognition. Traditional Unweighted Polynomial

kernel is expressed as

(, ) (. 1) ( . 1)

kxy xy x y



 



(8)

where d is the degree of the polynomial.

In our experiments we used different degrees of

2, 5 and 10 by using cross validation to select the

best parameter, just in the same manner as the

Gaussian kernel.

As mentioned above, the main reason we used

polynomial kernel in our experiments was that it

enabled us to weigh features differently for

similarity measurement. The weighted polynomial

kernel may be expressed in the form below:

Figure 3: MFDWT feature extraction.

(, ) ( . . 1)

iii

kxy w x y







(9)

BIOSIGNALS 2012 - International Conference on Bio-inspired Systems and Signal Processing

where w

s are weights for different features. As

mentioned in the feature extraction section, we

extract 15 features for each frame and 76 frames for

each utterance. Hence we have a feature vector of

length 1140. To weigh features, we notice that

among 15 coefficients extracted from each frame,

the lower ones are more important than the higher

coefficients, hence we must assign bigger weights to

them. To accomplish this, we assign weights to each

feature according to its index in the feature vector

modulo 15. For a linear weighting we have

( 1) mod15

wi

(10)

And for exponentially increasing weight, we have

1 mod 15i





(11)

We experimented both weighting schemes and

concluded that linear weighting outperforms the

other scheme.

3.2 Experimental Setup

In this paper, the database we used was the set of

digits of the TIMIT. The TIMIT contains broadband

recordings of 630 speakers of eight major dialect

regions of American English. We use 2700 digits (0

to 9) of this database. Depicted in Figure 4 is a two-

dimensional visualization of TIMIT dataset using

Principal Component Analysis.

For extracting the feature vectors of spoken

digits, the MFCC and the MFDWC are used. Every

frame of each digit has 15 features. First the MFCC

feature vectors are used to train and test the HMM-

based and SVDD-based digit recognition. Then, the

MFDWC feature vectors are used. The MFDWCs

consist of 15 coefficients obtained by DWT with

scales of 1, 2, 4 and 8. By this arrangement of

coefficients, the lower coefficients are more

important than the higher ones. For this purpose we

use feature vectors consisting of 15 coefficients and

5 lower coefficients. If we use 15 coefficients, we

obtained the 1140-dimensions digit feature vector

sequence and if we use 5 coefficients, dimension of

feature vector is 380.

In SVM classification the ”one-against-all”

approach is used. So 10 classes of digits are

obtained. We use Weighted Polynomial and

Exponentially Weighted Polynomial kernel

functions by using the first 5 and all 15 coefficients

as the feature vectors. We use Simple Polynomial

and Gaussian kernel functions by using all 15

coefficients as the feature vector.

The digit recognition systems are tested on noisy

environment speech (SNR=5dB and Noisy Speech is

obtained by Speech Signal + White Noise). This

kind of noise on speech data can severely deteriorate

the performance of speech recognition. The accuracy

rates of HMM-based digit recognition are shown in

Table 1. The result of the HMM-based and SVDD-

based digit recognition using MFDWC is better than

the MFCC feature vectors. It’s because of

localization and multi resolution characteristics of

the Wavelet Transform (WT). In Table 2 the

accuracy rates of SVDD-based digit recognition

separately (for each digit) and using MFDWCs are

shown for each class of digits (zero to nine spoken

data). The resulted accuracy rates show that

Weighted Polynomial kernel functions are better

than the other kernel functions. When the Weighted

Polynomial kernel functions are used, appropriate

coefficients can be applied for each feature

(Equation 9). By comparing between 5-dimensions

feature vectors and 15-dimentions feature vectors,

it’s inference that we can use 5-dimensions feature

vectors with improved learning, because the time

and space complexity of 5-dimensions feature

vectors are about much less than 15-dimensions.

Table 3 represents accuracy rates of the SVDD-

based digit recognition using MFCC feature vector.

Comparing Tables 1 with Table 2 and Table 3, it

is inferred that the HMM-based digit recognition are

better than the SVDD-based on the MFCC feature

vectors but the SVDD can compete with the HMM

classifier in speech recognition on the MFDWC

feature vectors.

Figure 4: A 2-D visualization of TIMIT dataset using

PCA.

Comparing Tables 1 with Table 4, showing

accuracy rates of the SVDD-based digit recognition

on noisy (SNR=5dB) test data on the MFDWC

feature vector, it is observed that the SVDD can

handle the noisy environments in the speech

recognition better than HMM classifier.

SUPPORT VECTOR DATA DESCRIPTION FOR SPOKEN DIGIT RECOGNITION

Table 1: Accuracy rate of HMM-based digit recognition.

Feature vector Acc. Noisy Acc. (SNR=5dB)

MFCC 92.00 37.70

MFDWC 92.25 49.18

4 CONCLUSIONS

In this paper we used the MFCC and the MFDWC

as the feature vectors for spoken digits recognition.

After experiments on the HMM-based digit

recognition it is exhibited that performance of the

MFDWC feature vectors is better than the MFCC. In

this paper we presented a new approach to learning

of digit recognition system. For learning of each

digit, we used SVDD classifier. Simple Polynomial,

Weighted Polynomial, Exponentially Weighted

Polynomial and Gaussian kernel functions were tried

to train the system. The experiment results were

presented to compare the digit recognition accuracy

using the HMM and SVDD with different kernel

functions; the results showed that the SVDD-based

approach with weighted polynomial kernel function

method had better performance than the other

methods for digit recognition.

Table 2: Accuracy rate of SVDD-based digit recognition using MFDWT with different kernels. LW=Linearly Weighted,

UW=Unweighted, EW=Exponentially Weighted, P=Polynomial Kernel, G=Gaussian Kernel, 5 and 15=Number of features

extracted for each frame.

Digit LWP5 UWP5 EWP5 LWP15 UWP15 EWP15 G15

0 91.06 91.06 69.11 86.18 69.11 70.73 72.36

1 90.32 91.13 54.84 91.13 72.58 56.45 76.61

2 90.40 90.40 51.20 91.20 67.20 56.00 63.20

3 91.13 91.13 70.97 92.74 81.45 72.58 85.48

4 91.87 92.68 60.98 93.50 78.86 63.41 81.30

5 92.80 92.80 66.40 93.60 83.20 68.00 84.00

6 92.62 93.44 69.67 94.26 86.89 71.31 84.07

7 91.74 91.74 64.46 93.39 72.73 65.29 66.12

8 94.26 94.26 64.75 92.62 85.25 67.21 87.70

9 92.00 92.80 65.60 92.80 72.80 67.20 76.80

Average 91.82 92.144 63.798 92.142 77.007 65.818 77.764

Table 3: Accuracy rate of SVDD-based digit recognition using MFCC features with different kernels. LW=Linearly

Weighted, UW=Unweighted,EW=Exponentially Weighted, P=Polynomial Kernel, G=Gaussian Kernel, 5 and 15=Number

of features extracted for each frame.

Digit LWP5 UWP5 EWP5 LWP15 UWP15 EWP15 G15

0 53.66 53.66 63.41 52.58 34.96 63.41 86.18

1 70.16 69.35 69.35 58.06 45.97 69.35 71.58

2 45.60 46.40 47.20 70.40 51.20 46.40 72.00

3 68.55 66.13 73.39 57.26 51.61 73.39 66.13

4 66.67 65.85 66.67 43.09 53.66 68.29 68.29

5 79.20 79.20 76.00 79.20 23.20 76.80 68.80

6 77.05 76.23 77.87 82.79 68.85 77.05 95.90

7 71.90 70.25 71.07 78.51 49.59 71.07 85.95

8 71.31 71.31 69.67 73.77 65.57 69.67 82.79

9 68.80 68.00 72.80 75.20 24.80 72.80 57.60

Average 67.29 66.638 68.743 67.086 46.941 68.823 75.522

Table 4: Accuracy rate of SVDD-based digit recognition on noisy test data using MFDWT and LWP5.

Digit 0 1 2 3 4 5 6 7 8 9

LWP5(%) 58.31 42.31 46.67 59.26 53.33 47.83 61.54 50.00 58.33 44.00

Average 52.16 %

BIOSIGNALS 2012 - International Conference on Bio-inspired Systems and Signal Processing

REFERENCES

Bresolin A. et. al., "Digit recognition using wavelet and

SVM in Brazilian Portuguese". ICASSP 2008, pp.

J. N. Gowdy and Z. Tufekci, "Mel-scaled discrete wavelet

coefficients for speech recognition", ICASSP 2000, pp.

1351:1354, Istanbul 2000.

Rabiner L. and Juang B., "An introduction to hidden

Markov models", IEEE ASSP, 3(1):4-16, 1986.

Rabiner L., "A tutorial on Hidden Markov Models and

selected applications in speech recognition".

Proceedings of the IEEE 77 (2): 257286, 1989.

Ganapathiraju A. et. al., "Applications of Support Vector

Machines to Speech Recognition", IEEE Transactions

on Signal Processing, 52(8):2348-2355, 2004.

Sonkamble B. A et. al., "An Overview of Speech

Recognition System based on the Support Vector

Machines", ICCCE 2008, pp. 768-771 Kuala Lumpur

2008.

Bai J. et. al., "Speech Recognition Based on A Compound

Kernel Support Vector Machine", ICCT 2008, pp.

696-699 China 2008.

Khan S. S.,A, "Survey of Recent Trends in One Class

Classification". AICS 2009, pp. 188-197, Ireland 2009.

DeMenthon Y. X. and Doermann D. S., "Support Vector

Data Description for image categorization from

Internet images". ICPR 2008, pp. 1-4, Florida U.S.A

2008.

Tax D. and Duin. R., "Support Vector Data Description,

Machine Learning", 54(1):45-66, 2004.

Taylor J. S. and Cristianini. N., “Kernel Methods for

Pattern Analysis” Cambridge University Press, 2004.

SUPPORT VECTOR DATA DESCRIPTION FOR SPOKEN DIGIT RECOGNITION