A n

RNA SECONDARY STRUCTURE PREDICTION ALGORITHM

Markus E. Nebel and Anika Scheid

∗

Department of Computer Science, University of Kaiserslautern, P.O. Box 3049, D-67653 Kaiserslautern, Germany

Keywords:

RNA folding, RNA secondary structure, Computational prediction, Probabilistic modeling, Stochastic

context-free grammars, Statistical sampling, Inside-outside calculation, Heuristic approximation.

Abstract:

Several state-of-the-art tools for predicting RNA secondary structures have worst-case time and space require-

ments of O(n

) and O(n

) for sequence length n, limiting their applicability for practical purposes. Accord-

ingly, biologists are interested in getting results faster, where a moderate loss of accuracy would willingly be

tolerated. For this reason, we propose a novel algorithm for structure prediction that reduces the time com-

plexity by a linear factor to O(n

), while still being able to produce high quality results. Basically, our method

relies on a probabilistic sampling approach based on an appropriate stochastic context-free grammar (SCFG):

using a well-known or a newly introduced sampling strategy it generates a random set of candidate structures

(from the ensemble of all feasible foldings) according to a “noisy” distribution (obtained by heuristically ap-

proximating the inside-outside values) for a given sequence, such that ﬁnally a corresponding prediction can

be efﬁciently derived. Sampling can easily be parallelized. Furthermore, it can be done in-place, i.e. only

the best (most probable) candidate structure generated so far needs to be stored and ﬁnally communicated.

Together, this allows to efﬁciently handle increased sample sizes necessary to achieve competitive prediction

accuracy in connection with the noisy distribution.

1 INTRODUCTION

Over the past years, several new approaches towards

the prediction of RNA secondary structures from a

single sequence have been invented which are based

on generating statistically representative and repro-

ducible samples of the entire ensemble of feasible

structures for the given sequence. For example, the

popular Sfold software (Ding and Lawrence, 2003;

Ding et al., 2004) employs a sampling extension

of the partition function (PF) approach (McCaskill,

1990) to produce statistically representative subsets

of the Boltzmann-weighted ensemble. More recently,

a corresponding probabilistic method has been stud-

ied (Nebel and Scheid, 2011) which actually sam-

ples the possible foldings from a distribution implied

by a sophisticated stochastic context-free grammar

(SCFG).

Notably, both sampling methods can be extended

for predicting secondary structures in O(n

) time and

with O(n

) space requirements, respectively. These

worst-case complexities are actually identical to those

of modern state-of-the-art tools for computational

∗

Corresponding author. The research of this author has

been supported by the Carl-Zeiss-Stiftung.

structure prediction from a single sequence, for in-

stance the commonly used minimum free energy

(MFE) based Mfold (Zuker, 1989; Zuker, 2003) and

Vienna RNA (Hofacker et al., 1994; Hofacker, 2003)

packages or the popular SCFG based Pfold soft-

ware (Knudsen and Hein, 1999; Knudsen and Hein,

2003). Furthermore, applications to structure predic-

tion showed that neither of the two competing sam-

pling approaches (SCFG and PF based method) gen-

erally outperforms the other and consequently, it is

not obvious which one should rather be preferred in

practice. This somehow contradicts the fact that the

best physics-based prediction methods still generally

perform signiﬁcantly better than the best probabilis-

tic approaches. In principle, only if the computa-

tional effort of one particular variant could be im-

proved without signiﬁcant losses in quality (that is if

one of them required considerably less time than the

others while it sacriﬁced only little predictive accu-

racy), then the corresponding method would be un-

doubtably the number one choice for practical appli-

cations, indeed outperforming all other modern com-

putational tools for predicting the secondary structure

of RNA sequences. This, by the way, due to the of-

ten quite large sizes of native RNA molecules consid-

E. Nebel M. and Scheid A..

A n2 RNA SECONDARY STRUCTURE PREDICTION ALGORITHM.

DOI: 10.5220/0003764600660075

In Proceedings of the International Conference on Bioinformatics Models, Methods and Algorithms (BIOINFORMATICS-2012), pages 66-75

ISBN: 978-989-8425-90-4

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

ered in practice, meets exactly the demands imposed

by biologists on computational prediction procedures:

rather getting moderately less accurate (but still good

quality) results in less time than needing signiﬁcantly

more time for obtaining results that are expectedly not

considerably more accurate.

Note that recently, there already have been sev-

eral practical heuristic speedups (Wexler et al., 2007;

Backofen et al., 2011). Particularly, the approach

of (Wexler et al., 2007) for folding single RNA se-

quences manages to speed up the standard dynamic

programming algorithms without sacriﬁcing the opti-

mality of the results, yielding an expected time com-

plexity of O(n

· ψ(n)), where ψ(n) is shown to be

constant on average under standard polymer fold-

ing models; in (Backofen et al., 2011), it is shown

how to reduce those average-case time and space

complexities in the sparse case. Furthermore, the

practical technique from (Frid and Gusﬁeld, 2010)

achieves an improved worst-case time complexity of

O(n

/log(n)), and with the (MFE and SCFG based)

algorithms from (Akutsu, 1999), a slight worst-case

speedup of O(n

· log(log(n))

1/2

/log(n)

1/2

) time can

be reached (whose practicality is unlikely and un-

established).

In this article, we present a new way to reduce the

worst-case time complexity of SCFG based statisti-

cal sampling by a linear factor, making it possible

to predict for instance the most probable (MP) struc-

ture among all feasible foldings for a given input se-

quence of length n (in direct analogy to conventional

structure prediction via SCFGs) with only O(n

) time

and space requirements. This complexity improve-

ment is basically realized by employing an appropri-

ate heuristic instead of the corresponding exact algo-

rithm for preprocessing the input sequence, i.e. for

deriving a “noisy” distribution (induced by heuristic

approximations of the corresponding inside and out-

side probabilities) on the entire structure ensemble

for the input sequence. From this distribution candi-

date structures can be efﬁciently sampled.

Moreover,

we will consider two different sampling strategies: (a

slight modiﬁcation of) the widely known sampling

procedure from (Ding and Lawrence, 2003; Nebel

and Scheid, 2011) which basically generates a ran-

dom structure from outside to inside, and a novel al-

ternative strategy that obeys to contrary principles and

employs a reverse course of action (from inside to out-

side) but manages to take more advantage of the ap-

With purposive proof-of-concept implementations (in

Wolfram Mathematica 7.0), for instance the overall prepro-

cessing time for E.coli tRNA

Ala

(of length n = 76) could be

reduced from 49.0 (traditional cubic algorithm) to only 3.7

(new quadratic strategy) seconds.

proximative preprocessing.

As we will see, even building on our new heuris-

tic preprocessing step, both sampling strategies can

be applied to obtain MP structure predictions of re-

spectable accuracy. In principle, for sufﬁciently large

sample sizes we obtain a similar high predictive accu-

racy as in the case of exact calculations

. The seem-

ingly sole pitfall is that due to the noisy ensemble dis-

tribution resulting from approximative computations,

the resulting samples are no longer guaranteed to pri-

marily contain rather likely structures (with respect to

the exact distribution of feasible foldings for a given

input sequence), such that we usually have to gen-

erate more candidate structures (i.e., consider larger

sample sizes) in oder to ensure reproducible structure

predictions. However, this is quite unproblematic in

practice: ﬁrstly, we can generate the candidate struc-

tures in-place (only the so far most probable structure

needs to be stored), such that large sample sizes give

no rise to memory consumption and secondly, gen-

erating samples can easily be parallelized on modern

multi-core architectures or grids.

2 PRELIMINARIES

In the sequel, given an RNA molecule r consisting of

n nucleotides, we denote the corresponding sequence

fragment from position i to position j, 1 ≤ i ≤ j ≤ n,

by R

i, j

= r

i+1

...r

j−1

. Accordingly, S

i, j

denotes a

feasible secondary structure on R

i, j

2.1 Sampling based on SCFG Model

Brieﬂy, probabilistic sampling based on a suitable

SCFG G

with sets I

and R

of intermediate sym-

bols and productions, respectively, and axiom S ∈ I

(that models the class of all feasible secondary struc-

tures) has two basic steps: In the ﬁrst step (prepro-

cessing), all inside probabilities

(i, j) := Pr(X ⇒

∗

...r

) (1)

and all outside probabilities

(i, j) := Pr(S ⇒

∗

...r

i−1

X r

j+1

...r

) (2)

for a sequence r of size n, X ∈ I

and 1 ≤ i, j ≤ n, are

computed. According to (Nebel and Scheid, 2011),

this can be done with a special variant of an Earley-

style parser (such that the considered grammar does

not need to be in Chomsky normal form (CNF)),

For E.coli tRNA

Ala

, we for instance observed the same

sensitivity and speciﬁcity values of 1.0 and 0.91, respec-

tively, with a particular application of our heuristic method

and the corresponding exact variant.

A n2 RNA SECONDARY STRUCTURE PREDICTION ALGORITHM

where the grammar parameters (trained beforehand

on a suitable RNA structure database) are splitted into

a set of transition probabilities Pr

(rule) for rule ∈

and two sets of emission probabilities Pr

(·) for

the 4 unpaired bases and the 16 possible base pairings.

For any such SCFG G

, there results O(n

) time com-

plexity and O(n

) memory requirement for this pre-

processing step. Note that in this work, we will use

the sophisticated grammar from (Nebel and Scheid,

2011) which has been parameterized to impose two

relevant restrictions on the class of all feasible struc-

tures, namely a minimum length of min

for hairpin

loops and a minimum number of min

hel

consecutive

base pairs for helices.

The second step takes the form of a recursive sam-

pling algorithm to randomly draw a complete sec-

ondary structure by consecutively sampling substruc-

tures (deﬁned by base pairs and unpaired bases). No-

tably, different sampling strategies may be employed

for realizing this step; two contrary variants that will

be considered within this work are described in detail

in Section 4. In general, for any sampling decision

(for example choice of a new base pair), the strategy

considers the respective set of all possible choices that

might actually be formed on the currently considered

fragment of the input sequence. Any of these sets con-

tains exactly the mutually and exclusive cases as de-

ﬁned by the alternative productions (of a particular in-

termediate symbol) of the underlying grammar. The

corresponding random choice is then drawn accord-

ing to the resulting conditional sampling distribution

(for the considered sequence fragment). This means

that the respective sampling distributions are deﬁned

by the inside and outside values derived in step one

(providing information on the distribution of all pos-

sible choices according to the actual input sequence)

and the grammar parameters (transition probabilities).

Since every of the before mentioned conditional

distributions needed for randomly drawing one of the

respective possible choices can be derived in linear

time (during the sampling process), any valid

base

pair can be sampled in time O(n). Thus, since any

structure of size n can have at most b

n−min

c base

pairs, a random candidate structure for the given input

sequence can be generated in O(n

) time.

Thus, one straightforward approach for improving

the performance of the overall sampling algorithm in

the worst-case is to reduce the O(n

) time complex-

One may for example consider only the 6 different

most stable canonical pairs as valid ones (like usually done

in physics-based approaches due to missing thermodynam-

ics parameters for non-canonical pairs). However, we de-

cided to drop this restriction, considering all possible non-

crossing base pairings to be valid.

ity required for the preprocessing step at least to the

quadratic time of the sampling strategy. To us, this

means we might be able to save a signiﬁcant amount

of time by replacing the exact inside-outside calcula-

tions with a corresponding heuristic method yielding

only approximative inside-outside values for a given

input sequence. To see if this might actually be suc-

cessful, we next want to determine to which extend

the inside and outside probabilities react to different

types and degrees of disturbances in order the get evi-

dence if it could actually be possible to ﬁnd an appro-

priate heuristic.

2.2 Disturbance Types and Levels

We decided to disturb the exact inside and outside

probabilities for a given input sequence r of length n

in the following ways: For each X ∈ I

and 1 ≤ i, j ≤

n, redeﬁne the corresponding inside value according

(i, j) := max(min(α

(i, j) + α

err

,1),0), (3)

where α

err

is randomly chosen from the following in-

terval or set:

[−max

ErrPerc

(i, j),+max

ErrPerc

(i, j)] or

{−ﬁx

ErrPerc

(i, j),+ﬁx

ErrPerc

(i, j)}

(relative errors), with max

ErrPerc

,ﬁx

ErrPerc

∈ (0, 1]

deﬁning percentages, or else,

[−max

ErrVal

,+max

ErrVal

] or {−ﬁx

ErrVal

,+ﬁx

ErrVal

}

(absolute errors), with max

ErrVal

,ﬁx

ErrVal

∈ (0,1] be-

ing ﬁxed values. Random errors on all outside values

(i, j), X ∈ I

and 1 ≤ i, j ≤ n, can be generated in

the same way.

The needed conditional sampling distributions (as

considered by a particular strategy) are then derived

from the exact grammar parameters and the disturbed

inside-outside probabilities for the input sequence.

This might create the need to (slightly) modify a par-

ticularly employed sampling strategy for being capa-

ble of dealing with these skewed distributions, as we

will see in Section 4.1.

2.3 Analysis of Disturbance Inﬂuence

To get a ﬁrst impression on the inﬂuence of distur-

bances (in the ensemble distribution for a given input

sequence) on the quality of generated sample sets, we

opted for the potentially most intuitive application in

this context, namely probability proﬁling for unpaired

bases within particular loop types (see, e.g., (Ding and

Lawrence, 2003)). In principle, for each nucleotide

position i, 1 ≤ i ≤ n, of a given sequence of length

BIOINFORMATICS 2012 - International Conference on Bioinformatics Models, Methods and Algorithms

0.0

0.2

0.4

0.6

0.8

1.0

Nucleotide Position

Probability

Hplot

Figure 1: Hairpin loop proﬁle and MP prediction obtained

for E.coli tRNA

Ala

. All results have been derived from sam-

ples of size 1,000, generated with min

hel

= 2 and min

3. Errors were produced with max

ErrPerc

= 0.99 (thick

gray lines) and ﬁx

ErrPerc

= 0.99 (thick dotted darker gray

lines).The proﬁles also display the respective exact results

(thin black lines) and the native folding of E.coli tRNA

Ala

(black points).

0.0

0.2

0.4

0.6

0.8

1.0

Nucleotide Position

Probability

Hplot

Figure 2: Sampling results for E.coli tRNA

Ala

correspond-

ing to those presented in Figure 1, where max

ErrVal

= 10

−9

(thick gray lines) and ﬁx

ErrVal

= 10

−9

(thick dotted darker

gray lines) have been chosen for generating the distur-

bances.

n, one computes the probabilities that i is an unpaired

base within a speciﬁc loop type. These probabilities

are given by the observed frequencies in a represen-

tative statistical sample of the complete ensemble (of

all possible secondary structures) for the given input

sequence.

Furthermore, in order to investigate to what ex-

tend the accuracy of predicted foldings changes when

different dimensions of relative disturbances are in-

corporated into the needed sampling probabilities, we

will additionally derive the most probable (MP) struc-

ture in the generated samples, respectively, as predic-

tion. Note that for our examinations, we will exem-

plarily consider a well-known trusted tRNA structure,

Escherichia coli tRNA

Ala

, since this molecule folds

into the typical cloverleaf structure, making it very

easy to judge the accuracy of the resulting proﬁles and

predictions.

Figure 1 indicates that even in the case of large

relative errors, the sampled structures still exhibit

the typical cloverleaf structure of tRNAs, especially

for the extenuated disturbance variant according to

max

ErrPerc

which seems to have practically no effect

on the resulting sampling quality and prediction ac-

curacy. However, Figure 2 perfectly demonstrates

that if the disturbances have been created by gener-

ating absolute errors on all inside values, then – even

for rather small values – the resulting samples (and

corresponding predictions as well) seem to be use-

less. Nevertheless, it seems reasonable to believe that

the inside and outside probabilities do not necessarily

have to be computed in the exact way, but it may prob-

ably sufﬁce to only (adequately) approximate them.

3 HEURISTIC PREPROCESSING

According to the previous discussion, the proclaimed

aim of this section is to lower the O(n

) time com-

plexity for preliminary inside-outside calculations to

O(n

), such that the preprocessing has the same

worst-case time requirements as the subsequent sam-

pling process (for constructing a constant number of

random secondary structure of size n).

3.1 Basic Idea

The main idea for reaching this time complexity re-

duction by a factor n in the worst-case is actually

quite simple: Instead of deriving the inside values

(i, j) (and the corresponding outside probabilities

(i, j)), X ∈ I

, for any combination of start po-

sition i and end position j, 1 ≤ i, j ≤ n, we abstract

from the actual position of subword R

i, j

= r

...r

in the input sequence and consider only its length

d = |r

...r

|. Thus, for any X ∈ I

, we do not need

to calculate O(n

) values α

(i, j) (and β

(i, j)) for

1 ≤ i, j ≤ n, but only O(n) values α

(d) (and β

(d))

for 0 ≤ d ≤ n. However, the problem with this ap-

proach is that distance d alone may be associated with

any of the strings in {r

...r

| j −i+1 = d}, i.e. with-

out using positions i and j we are inevitably forced to

additionally abstract from the actual input sequence r.

Note that it is also possible to combine both alter-

natives, that is we can ﬁrst use the traditional algo-

rithms to calculate exact values α

(i, j) (and β

(i, j))

within a window of ﬁxed size W

exact

, i.e. for j − i +

1 ≤ W

exact

(and j −i+1 ≥ n−W

exact

), and afterwards

derive the remaining values for W

exact

< d ≤ n (and

0 ≤ d < n −W

exact

) in an approximate fashion by em-

ploying the time-reduced variant for obtaining α

(d)

(and β

(d)) for each X ∈ I

. Since W

exact

is con-

stant, this effectively yields an improvement in the

time complexity of the corresponding complete inside

computation, which is then given by O(n

· W

exact

However, even for ﬁx W

exact

the time requirements

for such a mixed outside computation are O(n

3.2 Approximative Emission Terms

Due to the unavoidable abstraction from sequence, we

have to determine some approximated terms for the

A n2 RNA SECONDARY STRUCTURE PREDICTION ALGORITHM

emissions of unpaired bases and base pairs, respec-

tively, that

• do not depend on the positions of subwords within

the overall input word, but

• should at least depend on the lengths of the corre-

sponding subwords,

where it is strongly recommended to make sure that

as much information on the composition of the actual

input sequence as possible is incorporated into these

approximated terms.

Therefore, we decided to use the following

emission terms that incorporate relative frequencies

,i − i + 1) and rf

, j − i + 1) for unpaired

bases and base pairs, respectively, that can be efﬁ-

ciently derived from the actual input sequence:

(1) :=

∑

u∈Σ

(u) · rf

(u,1), (4)

(d) :=

∑

∈Σ

) · rf

,d). (5)

3.3 (Improved) Approximated

Sampling Probabilities

Fortunately, during the complete sampling process,

not only the start and end positions of the currently

considered sequence fragment R

i, j

, 1 ≤ i, j ≤ n, but

also the actual input sequence r are always known.

Thus, we can in certain cases easily remove some ap-

proximate factors in the corresponding approximated

inside and outside probabilities and replace them with

the respective correct terms (depending on i, j and r)

in order to obtain more reliable values.

Therefore, for any sampling strategy, the sampling

probabilities from which the respective (conditional)

distributions for possible choices are inferred should

be deﬁned by using such improved inside and out-

side probabilities (instead of the corresponding uncor-

rected precomputed ones). For example, if X ∈ I

generates hairpin loops, we should use

(i, j) :=

(

(i, j), if ( j − i + 1) ≤ W

exact

( j − i + 1) · c

(i, j), else,

(6)

and

(i, j) :=











(i, j), if ( j − i + 1) ≥ n − W

exact

( j − i + 1)×

(i − min

hel

, j + min

hel

,min

hel

), else,

(7)

where

(s,e) :=

∏

k=s

)

(1)

e−s+1

(8)

and

(i, j,l) :=

∏

l−1

k=0

i+k

j−k

)

∏

l−1

k=0

(( j − k) − (i + k) + 1)

. (9)

4 CONSIDERED SAMPLING

STRATEGIES

For the subsequent examinations, we will employ two

different sampling strategies, which are introduced

now.

4.1 Well–Established Strategy

Let us ﬁrst consider a slightly modiﬁed variant of the

rather simple and widely known sampling strategy

from (Ding and Lawrence, 2003; Nebel and Scheid,

2011). Brieﬂy, this well-established strategy samples

a complete secondary structure S

1,n

for a given input

sequence r of length n in the following recursive way:

Start with the entire RNA sequence R

1,n

and con-

secutively compute the adjacent substructures (single-

stranded regions and paired substructures) of the ex-

terior loop (from left to right). Any (paired) substruc-

ture on fragment R

i, j

, 1 ≤ i < j ≤ n, is folded by recur-

sively constructing substructures (hairpins, stacked

pairs, bulges, interior and multibranched loops) on

smaller fragments R

l,h

, i ≤ l < h ≤ j. That is, frag-

ments are sampled in an outside-to-inside fashion.

Notably, without disturbances of the underlying

probabilistic model, it is guaranteed that any sam-

pled loop type for a considered sequence fragment

can be successfully generated (otherwise its probabil-

ity would have been 0). As this must not hold in dis-

turbed cases (like e.g. those of Section 2.3), the most

straightforward modiﬁcation to solve this problem is

that in any such case where the chosen substructure

type can not be successfully generated, the strategy

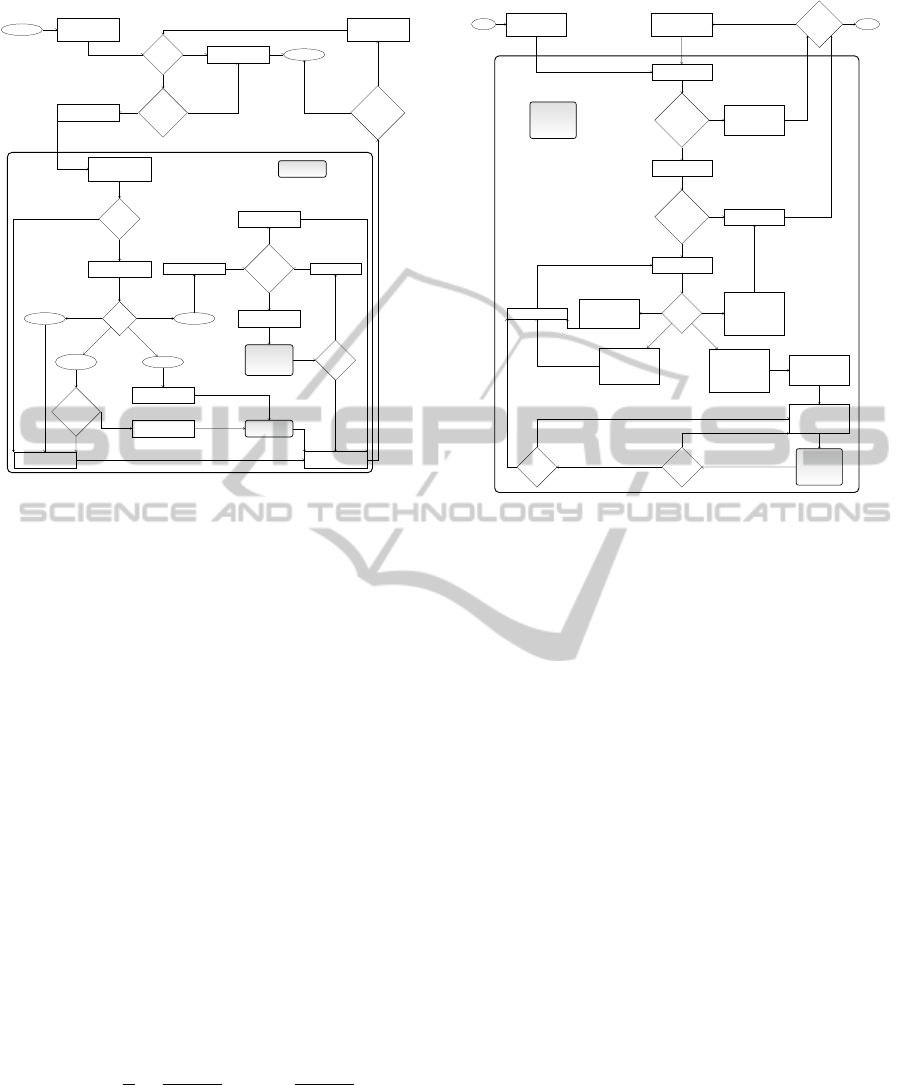
returns the partially formed substructure. Figure 3

gives a schematic overview on this inherently con-

trolled sampling strategy.

As regards this particular sampling strategy, the out-

side values can easily be omitted from the correspond-

ing formulae for deﬁning the needed sampling prob-

abilities, since in any case they contribute the same

multiplicative factor to the distinct sampling proba-

bilities for mutually exclusive and exhaustive cases,

such that they ﬁnally do not inﬂuence the sampling

decision at all.

The correctness of this simpliﬁcation can easily be

veriﬁed by considering a particular set ac

(i, j) of all

choices for (valid) derivations of intermediate symbol

BIOINFORMATICS 2012 - International Conference on Bioinformatics Models, Methods and Algorithms

Start folding of

i+1,j−1

:= R

h+1,l−1

(by adding pair i.j)

i.j could

close loop?

Sample loop type

closed by i.j

Type

Hairpin

Stacking

Take consecutive pair

h.l := (i + 1).(j − 1)

Bulge or

interior

Helix

possible on

i+1,j−1

Sample accessible pair

h.l (ﬁrst h, then l)

Multiloop

Set k := 1 and l := i

kth helix

possible on

l+1,j−1

remains

single-stranded

Sample kth accessible

pair h.l (ﬁrst h, then l)

Recursively

fold the kth

multiloop

substructure S

h,l

Further

helix?

Set k := k + 1

i+1,j−1

becomes

single-strand

Recursively fold

substructure S

h,l

Finish folding of R

i,j

is now complete)

Helix

possible on

i,j

Sample free pair h.l

(ﬁrst h, then l)

Further

helix?

Consider entire

input sequence

i,j

:= R

1,n

Start

i,j

becomes

single-strand

End

Overall

structure

1,n

folded?

Consider remaining

sequence fragment

i,j

:= R

j+1,n

yes

Recursively fold

substructure S

h,l

Figure 3: Flowchart for recursive sampling of an RNA sec-

ondary structure S

1,n

for a given input sequence r of length

n according to an inherently controlled strategy with pre-

determined order, similar to that of (Ding and Lawrence,

2003; Nebel and Scheid, 2011)).

X ∈ I

on sequence fragment R

i, j

, 1 ≤ i < j ≤ n,

which actually correspond to possible substructures

on R

i, j

. Under the assumption that the alternatives for

intermediate symbol X are X → Y and X → VW , the

(valid) mutually exclusive and exhaustive cases are

deﬁned by:

acX(i, j) := acX

(i, j) ∪ acX

(i, j), (10)

where

acX

(i, j) := {{0, p} | p 6= 0 for

p = β

(i, j) · α

(i, j) · Pr

(X → Y )} (11)

and

acX

(i, j) := {{k, p} | i ≤ k ≤ j and p 6= 0 for

p = β

(i, j) · α

(i,k)α

(k + 1, j) · Pr

(X → VW )}.

(12)

We then sample from the probability distribution in-

duced by acX(i, j) (conditioned on fragment R

i, j

which implies

1 =

∑

p∈acX(i, j)

(i, j)

∑

p∈acX(i, j)

(i, j)

(13)

for z :=

∑

p∈acX(i, j)

p, since β

(i, j) 6= 0 due to the def-

inition of acX(i, j).

4.2 Alternative Strategy

Unfortunately, the common sampling strategy from

Start folding of

start,end

(Further)

hairpin

possible on

start,end

Finish folding of

start,end

(unfolded positions

become unpaired)

Sample hairpin loop

ii,jj

on R

start,end

ii,jj

extendable

start,end

Finish folding of

substructure S

ii,jj

Sample extension of

ii,jj

on R

start,end

Extension

type

Stacking:

ii,jj

is extended by

adding enclosing base

pair(s)

Bulge or interior:

ii,jj

is extended by

adding a preceding or

a following

single-strand (or both)

Substructure of

multiple loop:

ii,jj

is extended by

adding a preceding

single-strand of

arbitrary length

Substructure of

exterior lo op:

ii,jj

is extended by

adding a preceding

single-strand of

arbitrary length

Update ii and jj

Update end

(must be indeed the

last position of the

multiloop)

Update start

(not necessarily the

ﬁrst position of the

multiloop)

Recursively fold

new (paired)

substructure

ii,jj

start,end

Structure

type

Multiloop

complete?

Still exist

unfolded

fragments?

End

Take one of the

unfolded fragments

start,end

Take sole unfolded

fragment

start,end

:= R

1,n

Start

yes

substructure of exterior loop

substructure of multiple loop

yes

Recursively fold

new (paired)

substructure

ii,jj

start,end

Figure 4: Flowchart for recursive sampling of an RNA sec-

ondary structure S

1,n

for a given input sequence r of length

n according to a less restrictive strategy with extensively

more freedom (that requires dynamic validation of possible

random choices during the sampling process).

Section 4.1 lacks the ability to take full advan-

tage of the exact inside values

(i, j) = α

(i, j), for

X ∈ I

and j −i+1 ≤ W

exact

, obtained by employing

a particular mixed preprocessing variant according to

0 ≤ W

exact

< n. Particularly, the strategy in general

inevitably has to sample the ﬁrst base pairs from cor-

responding conditional probability distributions for

rather large fragments R

i, j

with j − i + 1 > W

exact

which are indeed induced by approximated sampling

probabilities rather than exact ones. Therefore, we

worked out an alternative to this well-established

sampling strategy that obeys to contrary principles,

resulting in a reverse sampling direction.

Basically, a complete secondary structure S

1,n

for

a given input sequence r of length n can alternatively

albeit unconventionally be sampled in the following

(deliberately less controlled) way: Start with the en-

tire RNA sequence R

start,end

= R

1,n

and randomly

construct adjacent substructures (paired substructures

preceeded by potentially empty single-stranded re-

gions) of the exterior loop on the considered sequence

fragment R

start,end

(where the construction does not

follow a particular order, e.g. does not sample from

left to right), as long as no further paired substructure

can be folded. Any (paired) substructure on fragment

start,end

, 1 ≤ start ≤ end ≤ n, is created by sampling

a random hairpin loop (with closing base pair i. j, for

start < i < j < end) – here we can take advantage of

A n2 RNA SECONDARY STRUCTURE PREDICTION ALGORITHM

Table 1: Comparsion of the considered sampling strategies (for an arbitrary input sequence of length n).

Aspect Conventional Strategy Alternative Strategy

Preprocessing time O(n

) for exact calculations,

O(n

) for approximate variant,

O(n

) with constant W

exact

≥ 0

O(n

) for exact calculations,

O(n

) for approximate variant,

O(n

) with constant W

exact

≥ 0

Constraints None Constant max

hairpin

, max

bulge

and max

strand

Characteristics and

course of action

Inherently controlled, ordered:

- substructures from left to right,

- sampling proceeds “inwards”:

construction of substructure S

i, j

starts

by considering R

i, j

and ends by gener-

ating an unpaired region (usually a hair-

pin loop)

Extensively more freedom, less restrictive:

- substructures in arbitrary order,

- sampling proceeds “outwards”:

construction of new substructure on unfolded frag-

ment R

start,end

starts with random hairpin loop

which is extended to a complete and valid (paired)

substructure S

i, j

on R

start,end

Beneﬁts of sam-

pling direction

(Sub)structures are folded in accor-

dance with the generation of the cor-

responding (unique leftmost) derivation

(sub)tree by the underlying SCFG

Takes more advantage of inside probabilities for

shorter fragments containing less approximated

terms and thus less inaccuracies (although this po-

tential is narrowed by the outside values for which

the contrary holds)

Function of outside

values

Not considered (do not inﬂuence sam-

pling distributions)

1) “Normalize” sampling probabilities

2) Ensure valid extensions

Identiﬁcation of

valid choices

Not required (all possible choices are

principally valid)

Dynamic checking required (due to dependence on

previously folded substructures)

Folding time O(n

) O(n

) with larger constants

Overall time com-

plexity for MP pre-

dictions

O(n

) with exact variant,

O(n

) with constant W

exact

≥ 0 or in

completely approximated case

O(n

) in case of exact computations or mixed vari-

ants according to W

exact

≥ 0,

O(n

) only in completely approximated case

exact inside values from a mixed preprocessing since

most likely i and j are close – and extending it (to-

wards the ends of R

start,end

) by successively drawing

closing base pairs. During this extension, basically all

known substructures (stacked pairs, bulges, interior

and multibranched loops, that obey to certain restric-

tions which will be discussed later) may be folded,

where each substructure (e.g. multiloop) has to be

completed before its closing base pair is added and the

corresponding helix can actually be further extended.

The process of folding a particular paired substructure

ends with a complete and valid paired structure (of the

currently folding multiloop or of the exterior loop), ei-

ther with or without a directly preceeding unpaired re-

gion, both on the considered fragment R

start,end

. Fig-

ure 4 gives a schematic overview on this inside-out

fashion sampling strategy.

Note that in order to ensure that all sampled sub-

structures can be successfully folded, especially in

the case of multiloops, we have to take care that at

any point, the strategy may only draw such random

choices that do not make it impossible to success-

fully ﬁnish the currently running construction process

(of a particular loop). As this strongly depends on

the actual positions and types of all previously folded

paired substructures, the algorithm obviously needs to

dynamically determine the respective set of all valid

choices (during the sampling process itself) before

a corresponding probability distribution (needed for

drawing a particular random choice) can be derived.

This, however, may cause severe problems as re-

gards the time complexity for randomly sampling the

next extension (or base pair). Nevertheless, in or-

der to guarantee that the worst-case time complex-

ity for drawing any random choice remains in O(n),

we only need to impose a few restrictions concerning

the lengths of single-stranded regions in some types

of loops. In detail, we have to consider a maximum

allowed number of nucleotides in unpaired regions

of hairpin loops (max

hairpin

), bulge or interior loops

(max

bulge

), and multiloops (max

strand

)

For example, if X ∈ I

generates hairpin loops,

then the set of all possible hairpin loops that can be

validly folded on sequence fragment R

start,end

is given

pcHL(start, end) :=



{i, j, p} |

start + min

hel

≤ i ≤ j ≤ end − min

hel

and

i + min

− 1 ≤ j ≤ i + max

hairpin

− 1 and

i−min

hel

, j+min

hel

not folded and

p =

(i, j) ·

(i, j) 6= 0



. (14)

Obviously, max

hairpin

indeed ensures that

Note that these restrictions are not as severe as it may

seem, since for example choosing the constant value 30 (as

also done by many MFE based prediction algorithms) for all

three parameters can be expected to hardly have a negative

impact on the resulting sampling quality.

BIOINFORMATICS 2012 - International Conference on Bioinformatics Models, Methods and Algorithms

pcHL(start, end) can be computed in O(n) time.

Finally, it should be noted that this sampling strategy

needs to additionally consider outside probabilities,

for two reasons: First, for “normalizing” the result-

ing sampling probabilities. This is due to the fact that

the different possible choices {i, j, p} usually imply

substructures S

i, j

of different lengths j − i + 1, such

that only p =

(i, j) ·

(i, j) ensures that the prob-

abilities of all possible choices are of the same order

of magnitude and hence imply a reasonable probabil-

ity distribution for drawing a random choice. Sec-

ond, the outside values are required for guaranteeing

that sampled substructures can be validly extended.

This means that only such hairpin loops and exten-

sions (implying a surrounding base pair i. j) may be

sampled that can actually lead to the generation of a

corresponding valid helix.

We conclude this section by referring to Table 1

that summarizes the main differences of both sam-

pling variants.

5 APPLICATIONS

First, the sampling results shown in Figure 5 indicate

that for the common sampling strategy, considering

a window of constant size W

exact

(chosen to cover

the size of hairpin-loops) with a mixed preprocess-

ing variant, actually yields a slight improvement of

the resulting sampling quality, where the same time

requirements are needed for generating the respective

sample sets.

Contrary to this observation, Figure 6 demon-

strates that when employing our alternative sampling

strategy, the corresponding results are not signiﬁ-

cantly different for the completely approximate pre-

processing variant and for a mixed version on the ba-

sis of a constant value for W

exact

. Thus, to our surprise

it does not matter if we consider a constant window

for exact calculations or simply approximate all in-

side and outside values, which is not only an interest-

ing observation itself, but also fortunately prevents us

from having to deal with an undesirable trade-off be-

tween reducing the worst-case time complexity (by a

linear factor) and sacriﬁcing less of the resulting sam-

pling quality. In fact, this means we may (without re-

sulting signiﬁcant quality losses) always use the more

efﬁcient approximative preprocessing variant in order

to reduce the worst-case time complexity of the over-

all sampling algorithm.

However, all proﬁles perfectly demonstrate that

due to the noisy ensemble distribution caused by ap-

proximating the highly relevant sequence-dependent

0.0

0.2

0.4

0.6

0.8

1.0

Nucleotide Position

Probability

Hplot

Figure 5: Sampling results for E.coli tRNA

Ala

, derived with

the common strategy (under the assumption of min

hel

2 and min

= 3), where we used sample size 100,000,

10,000 and 1,000 for W

exact

= −1 (no window, thick gray

lines), W

exact

= 30 (moderate window, thick dotted darker

gray lines) and W

exact

= +∞ (complete window, thin black

lines), respectively.

0.0

0.2

0.4

0.6

0.8

1.0

Nucleotide Position

Probability

Hplot

Figure 6: Sampling results corresponding to those of Fig-

ure 5, obtained by employing the alternative sampling strat-

egy.

emission probabilities, the resulting sample sets usu-

ally contain many foldings that are rather unlikely ac-

cording to the exact distribution for the considered in-

put sequence. For this reason, it can not be recom-

mended to employ one of the following otherwise rea-

sonable construction schemes for deriving predictions

according to the entire sample set: we should rather

neither predict γ-MEA nor γ-centroid structures of the

generated sample set as deﬁned in (Nebel and Scheid,

2011), since those effectively reﬂect the overall be-

havior of the sample set. Those predictions must any-

way be considered inappropriate choices in our case,

since their computation requires O(n

) time, which

would inevitably undo the time reduction reached by

approximating. Nevertheless, we can without signif-

icant losses in performance (without increasing the

worst-case time complexity of the overall algorithm)

identify the MP structure of the generated sample

, in

strong analogy to traditional SCFG approaches. Since

for this selection principle, we can actually rely on the

exact distribution of feasible structures

, this seems to

The probability of each structure can either be deter-

mined on the ﬂy while sampling, multiplying the probabili-

ties of the production rules which correspond to the respec-

tive sampling decisions, and otherwise – since the under-

lying SCFG from (Nebel and Scheid, 2011) is unambigu-

ous – are computable in O(n

) time making use, e.g., of an

Earley-style parser.

Note that the probability for a particular folding of a

given RNA sequence is equal to a product of (different pow-

A n2 RNA SECONDARY STRUCTURE PREDICTION ALGORITHM

be the right choice indeed.

On the basis of a series of experiments, we observed

that stability in resulting predictions and a competi-

tive prediction accuracy can only be reached by in-

creasing the sample size, especially in the case of

complete approximation for the preprocessing step

and sampling according to the alternative strategy in-

troduced in Section 4.2. That is, more candidate struc-

tures ought to be generated for guaranteeing that the

resulting MP predictions are reproducible (by inde-

pendent runs for the same input sequence) and of

hight quality. This negative effect is considerably

lowered by using (larger) constant values of W

exact

≥

0, and is actually less recognizable when employing

the conventional sampling strategy recapped in Sec-

tion 4.1.

20000

40000

60000

80000

100000

0.5

0.6

0.7

0.8

0.9

1.0

Sample Size

Sensitivity

20000

40000

60000

80000

100000

0.5

0.6

0.7

0.8

0.9

1.0

Sample Size

Specificity

20000

40000

60000

80000

100000

0.5

0.6

0.7

0.8

0.9

1.0

Sample Size

Sensitivity

20000

40000

60000

80000

100000

0.5

0.6

0.7

0.8

0.9

1.0

Sample Size

Specificity

Figure 7: Sensitivity and speciﬁcity of predictions as a func-

tion of sample size derived for E.coli tRNA

Ala

. Top (bot-

tom) lines show the common (alternative) sampling strat-

egy.

Figure 7 shows the averaged sensitivities and

speciﬁcities obtained for 50 independent runs of con-

tinuously sampling secondary structures taking the so

far most probable one as the actual prediction (which

determines sensitivity and speciﬁcity for the actual

sample size). We observe that when making use of

approximate probabilities sample sizes about 40 to

50 times as large as for a precise preprocessing are

needed to generate competitive predictions. Thus, for

ers of the diverse) transition and emission probabilities (ac-

cording to the corresponding derivation tree), which means

it depends only on the exact trained parameter values of the

underlying SCFG.

a naive implementation the speedup gained by ap-

proximation may partly be lost. However, unlike pre-

diction algorithms using dynamic programming, sam-

pling can easily be parallelized. Making use of a grid

environment where today one may assume a proces-

sor to have about 8 cores, a grid of size 5 or 6 com-

puters is sufﬁcient to compensate the increased sam-

ple size. Furthermore, since we only make use of

the most probable sampled structure for our predic-

tion, sampling can be done in-place, storing in each

core only the best structure seen so far. This re-

duces the memory requirements and keeps the com-

munication costs rather moderate since it is ﬁnally

only necessary to gather m structures from m cores

and select the best. We performed a series of exper-

iments, making use of Mathematica’s parallel com-

putation features, which proved that the overall pro-

cess scales linearly in the number of cores used with

a non-measurable communication overhead. This ﬁ-

nally proves the applicability of our approach provid-

ing a factor n speedup compared to established predic-

tion tools but still maintaining the limits implied by a

quadratic memory consumption (in our case used to

store parameter values).

6 CONCLUSIONS

The major advantage of the presented approximative

method is that it is more efﬁcient than all other mod-

ern prediction algorithms (implemented in popular

tools like Mfold (Zuker, 2003), Vienna RNA (Ho-

facker, 2003), Pfold (Knudsen and Hein, 2003),

Sfold (Ding et al., 2004) or CONTRAfold (Do et al.,

2006)), reducing the worst-case time complexity by

a linear factor, such that the time and space require-

ments are both bounded by O(n

). However, a poten-

tial drawback lies in the observation that the overall

quality of generated samples decreases (as indicated

by probability proﬁling for speciﬁc loop types), which

is due to the approximated ensemble distribution. As

a consequence, we usually need to use larger sample

sizes for obtaining a competitive prediction accuracy

and stable predictions, i.e., more candidate structures

for a given input sequence have to be generated to

ensure that the approximation method outputs rather

identical predictions in independent runs for that se-

quence. According to our experiments, an efﬁcient

implementation that really takes advantage of the ac-

celerated preprocessing (3.7 compared to 49 seconds

for our proof-of-concept implementation in Wolfram

Mathematica) but handles large sample sizes can be

obtained by parallelization.

Note that all results presented in this article have been

BIOINFORMATICS 2012 - International Conference on Bioinformatics Models, Methods and Algorithms

derived with a purposive proof-of-concept implemen-

tation of the described methods. A more sophisti-

cated tool will be realized in the future, hoping that

the proposed prediction approach proves capable of

yielding acceptable accuracies even for such types of

RNAs whose molecules imply a great variety of struc-

tural features (due to large sequence lengths). In fact,

we here only considered exemplary applications for

one particular tRNA molecule in order to get positive

feedback that (at least) the MP predictions obtained

via approximated SCFG based sampling can be of

high quality. Accordingly, more general experiments

are needed, e.g., in connection with RNA molecules

of sizes n = 3000 − 30000 (for which the memory

constraints of our approach are not restrictive assum-

ing 1GB of memory for each core) and where long

distance base pairs in a global folding are of interest.

In such a scenario the proposed algorithm could be

the method of choice provided it performs similarly

well.

This line of research is work in progress, but we

found the ﬁrst impressions presented within this note

so motivating that we wanted to share them with the

scientiﬁc community already at this point, primarily

because this work leaves a number of open questions

that may be inspiration for further research of other

groups. For instance, recall that we used a sophis-

ticated SCFG (representing a formal language coun-

terpart to the thermodynamic model applied in the

Sfold program) as probabilistic basis for the consid-

ered sampling strategies. However, it would also be

possible to employ other SCFG designs, for example

one of the commonly known lightweight grammars

from (Dowell and Eddy, 2004). This might of course

yield at least noticeable if not signiﬁcant changes in

the resulting sampling quality, which could be an in-

teresting subject to be explored.

It should also be noted that a similar approxima-

tive approach could potentially be considered when

attempting to reduce the worst-case time complexity

of the sampling extension of the PF approach. In fact,

since sequence information is incorporated into the

used (equilibrium) PFs and corresponding sampling

probabilities only in the form of particular sequence-

dependent free energy contributions, it seems reason-

able to believe that the time complexity for the for-

ward step (preprocessing) could possibly be reduced

by a linear factor to O(n

) when using some sort

of approximated (averaged) free energy contributions

that do not depend on the actual sequence (but con-

tain as much sequence information as possible), in

analogy to the approximated preprocessing step (in-

side and outside calculations) considered in this work,

where we eventually only had to use averaged emis-

sion terms instead of the exact emission probabilities

in order to save time.

REFERENCES

Akutsu, T. (1999). Approximation and exact algorithms for

RNA secondary structure prediction and recognition

of stochastic context-free languages. J. Comb. Optim.,

3(2–3):321–336.

Backofen, R., Tsur, D., Zakov, S., and Ziv-Ukelson, M.

(2011). Sparse RNA folding: Time and space efﬁcient

algorithms. Journal of Discrete Algorithms, 9:12–31.

Ding, Y., Chan, C. Y., and Lawrence, C. E. (2004). Sfold

web server for statistical folding and rational design

of nucleic acids. Nucleic Acids Research, 32:W135–

W141.

Ding, Y. and Lawrence, C. E. (2003). A statistical sam-

pling algorithm for RNA secondary structure predic-

tion. Nucleic Acids Research, 31(24):7280–7301.

Do, C. B., Woods, D. A., and Batzoglou, S. (2006).

CONTRAfold: RNA secondary structure predic-

tion without physics-based models. Bioinformatics,

22(14):e90–e98.

Dowell, R. D. and Eddy, S. R. (2004). Evaluation of sev-

eral lightweight stochastic context-free grammars for

RNA secondary structure prediction. BMC Bioinfor-

matics, 5:71.

Frid, Y. and Gusﬁeld, D. (2010). A simple, practical and

complete O(n

/log(n))-time algorithm for RNA fold-

ing using the Four-Russians speedup. Algorithms for

Molecular Biology, 5(1):5–13.

Hofacker, I., Fontana, W., Stadler, P., Bonhoeffer, S.,

Tacker, M., and Schuster, P. (1994). Fast folding and

comparison of rna secondary structures (the Vienna

RNA package). Monatsh Chem., 125(2):167–188.

Hofacker, I. L. (2003). The vienna RNA secondary structure

server. Nucleic Acids Research, 31(13):3429–3431.

Knudsen, B. and Hein, J. (1999). RNA secondary structure

prediction using stochastic context-free grammars and

evolutionary history. Bioinformatics, 15(6):446–454.

Knudsen, B. and Hein, J. (2003). Pfold: RNA sec-

ondary structure prediction using stochastic context-

free grammars. Nucleic Acids Research, 31(13):3423–

3428.

McCaskill, J. S. (1990). The equilibrium partition function

and base pair binding probabilities for RNA secondary

structure. Biopolymers, 29:1105–1119.

Nebel, M. E. and Scheid, A. (2011). Evaluation of a so-

phisticated SCFG design for RNA secondary structure

prediction. Submitted.

Wexler, Y., Zilberstein, C., and Ziv-Ukelson, M. (2007). A

study of accessible motifs and RNA folding complex-

ity. Journal of Computational Biology, 14(6):856–

872.

Zuker, M. (1989). On ﬁnding all suboptimal foldings of an

RNA molecule. Science, 244:48–52.

Zuker, M. (2003). Mfold web server for nucleic acid fold-

ing and hybridization prediction. Nucleic Acids Res.,

31(13):3406–3415.

A n2 RNA SECONDARY STRUCTURE PREDICTION ALGORITHM