A VACCINATION CONTROL LAW BASED ON FEEDBACK
LINEARIZATION TECHNIQUES FOR SEIR EPIDEMIC
MODELS
S. Alonso-Quesada
1
, M. De la Sen
1
and A. Ibeas
2
1
Department of Electricity and Electronics, Faculty of Science and Technology, University of the Basque Country
Campus of Leioa, 48940-Leioa, Bizkaia, Spain
2
Departamento de Telecomunicación e Ingeniería de Sistemas, Escuela Técnica Superior de Ingeniería
Universitat Autònoma, Barcelona, Spain
Keywords: SEIR epidemic models, Vaccination, Nonlinear control, Stability, Positivity.
Abstract: This paper presents a vaccination strategy for fighting against the propagation of epidemic diseases. The
disease propagation is described by a SEIR (susceptible plus infected plus infectious plus removed by
immunity populations) epidemic model. The model takes into account the total population amounts as a
refrain for the illness transmission since its increase makes more difficult contacts among susceptible and
infected. The vaccination strategy is based on a continuous-time nonlinear control law synthesized via an
exact feedback input-output linearization approach. The control objective is to asymptotically eradicate the
infection. Moreover, the positivity and stability properties of the controlled system are investigated.
1 INTRODUCTION
A relevant area in the mathematical theory of
epidemiology is the development of models for
studying the propagation of epidemic diseases in a
host population. The epidemic mathematical models
analysed include the most basic ones (De la Sen and
Alonso-Quesada, 2010); (Keeling and Rohani,
2008); (Li et al., 1999); (Makinde, 2007); (Mollison,
2003), namely: (i) SI models where only susceptible
and infected populations are assumed to be present
in the model, (ii) SIR models which include
susceptible plus infected plus removed-by-immunity
populations and (iii) SEIR models where the
infected population is split into two ones, namely,
the “infected” (or “exposed”) which incubate the
disease but they do not still have any disease
symptoms and the “infectious” (or “infective”)
which do have the external disease symptoms. Those
models can be divided in two main classes, namely,
the so-called “pseudo-mass action models”, where
the total population is not taken into account as a
relevant disease contagious factor and the so-called
“true-mass action models”, where the total
population is more realistically considered as an
inverse factor of the disease transmission rates.
There are many variants of the above models as,
for instance, the SVEIR epidemic models which
incorporate the dynamics of a vaccinated population
in comparison with the SEIR models (De la Sen et
al., 2011); (Song et al., 2009), the SEIQR-SIS model
which adds a quarantine population (Jumpen et al.,
2011) and the model proposed in (Safi and Gumel,
2011) which incorporates vaccinated, quarantine and
hospitalized populations. Other variant consists of
the generalization of such models by incorporating
point and/or distributed delays (De la Sen et al.,
2010); (Zhang et al., 2009). Another one is
concerned with the inclusion of a saturated disease
transmission incidence rate for taking into account
the inhibition effect from the behavioural change of
susceptible individuals when the infectious
individual number increases (Xu et al., 2010).
The analysis of the existence of equilibrium
points, relative to either the persistence or extinction
of the epidemics, the conditions for the existence of
a backward bifurcation where both equilibrium
points co-exist and the constraints for guaranteeing
the positivity and the boundedness of the solutions
of such models have been some of the main
objectives in the aforementioned papers. Also, the
conditions that generate an oscillatory behaviour in
such solutions has been dealt with in the literature
76
Alonso-Quesada S., De la Sen M. and Ibeas A..
A VACCINATION CONTROL LAW BASED ON FEEDBACK LINEARIZATION TECHNIQUES FOR SEIR EPIDEMIC MODELS.
DOI: 10.5220/0003764900760085
In Proceedings of the International Conference on Bioinformatics Models, Methods and Algorithms (BIOINFORMATICS-2012), pages 76-85
ISBN: 978-989-8425-90-4
Copyright
c
 2012 SCITEPRESS (Science and Technology Publications, Lda.)

about epidemic mathematical models
(Mukhopadhyay and Bhattacharyya, 2007). Other
important aim is that relative to the design of control
strategies in order to eradicate the persistence of the
infection in the host population (De la Sen and
Alonso-Quesada, 2010); (De la Sen et al., 2011);
(Makinde, 2007); (Safi and Gumel, 2011). In this
context, an explicit vaccination function of many
different kinds may be considered, namely: constant,
continuous-time, impulsive, mixed
constant/impulsive, mixed continuous-
time/impulsive, discrete-time and so on.
In this paper, a SEIR epidemic model is
considered. The dynamics of susceptible (S) and
immune (R) populations are directly affected by a
vaccination function
V(t) , which also has indirectly
influence in the time evolution of infected or
exposed (E) and infectious (I) populations. In fact,
such a vaccination function has to be suitably
designed in order to eradicate the infection from the
population. This model has been already studied in
(De la Sen and Alonso-Quesada, 2010) from the
viewpoint of equilibrium points in the controlled and
free-vaccination cases. A vaccination auxiliary
control law being proportional to the susceptible
population was proposed in order to achieve the
whole population be asymptotically immune. Such
an approach assumed that the SEIR model was of
the aforementioned true-mass action type, its
parameters were known and the illness transmission
was not critical. Moreover, some important issues of
positivity, stability and tracking of the SEIR model
were discussed. The present paper proposes an
alternative method to obtain the vaccination control
law to asymptotically eradicate the epidemic
disease. Namely, the vaccination function is
synthesized by means of an input-output exact
feedback linearization technique. Such a
linearization control strategy constitutes the main
contribution of the paper. Moreover, mathematical
proofs about the epidemics eradication based on
such a controlled SEIR while maintaining the non-
negativity of all the partial populations for all time
are issued. The exact feedback linearization can be
implemented by using a proper nonlinear coordinate
transformation and a static-state feedback control.
The use of such a linearization strategy is motivated
by three main facts, namely: (i) it is a power tool for
controlling nonlinear systems which is based on
well-established technical principles (Isidori, 1995),
(ii) the given SEIR model is highly nonlinear and
(iii) such a control strategy has not been yet applied
in epidemic models.
2 SEIR EPIDEMIC MODEL
Let S(t) , E(t) , I(t) and R(t) be, respectively, the
susceptible, infected (or exposed), infectious and
removed-by-immunity populations at time
t .
Consider a time-invariant true-mass action type
SEIR epidemic model given by:

S(t)I(t)
S(t) S(t) R(t) N 1 V(t)
N
    

(1)
S(t)I(t)
E(t) ( )E(t)
N
 

(2)
I(t) ( )I(t) E(t) 

(3)
R(t) ( )R(t) I(t) NV(t)  

(4)
subject to initial conditions
S(0) 0 , E(0) 0 ,
I(0) 0 and R(0) 0 under a vaccination function
00
V:


, with


0
0,

 
. In the above
SEIR model,
N
0 is the total population at any
time instant
0
t


 , 0

 is the rate of deaths and
births from causes unrelated to the infection,
0


is the rate of losing immunity,
0 is the
transmission constant (with the total number of
infections per unity of time at time
t being
S(t)I(t) N

) and,
1
0


 and
1
0


 are,
respectively, the average durations of the latent and
infective periods. The total population dynamics can
be obtained by summing-up (1)-(4) yielding:
N(t) S(t) E(t) I(t) R(t) 0

 


(5)
so that the total population
N
(t)N(0)N
is
constant
0
t


 
. Then, this model is suitable for
epidemic diseases with very small mortality
incidence caused by infection and for populations
with equal birth and death rates so that the total
population may be considered constant for all time.
3 VACCINATION STRATEGY
An ideal control objective is that the removed-by-
immunity population asymptotically tracks the whole
population
. In this way, the joint infected plus
infectious population asymptotically tends to zero as
t , so the infection is eradicated from the
population. A vaccination control law based on a
static-state feedback linearization strategy is
developed for achieving such a control objective.
This technique requires a nonlinear coordinate
A VACCINATION CONTROL LAW BASED ON FEEDBACK LINEARIZATION TECHNIQUES FOR SEIR
EPIDEMIC MODELS
77

transformation, based on the Lie derivatives Theory
(Isidori, 1995), in the system representation.
The dynamics equations (1)-(3) of the SEIR
model can be equivalently written as the following
nonlinear control affine system:


x(t) f x(t) g x(t) u(t)
y(t) h x(t)
 




(6)
where
0
y(t) I(t)

 ,
0
u(t) V(t)

 and

T
3
0
x(t) I(t) E(t) S(t)

 are, respectively,
considered as the output signal, the input signal and
the state vector of the system
0
t

 and
R(t) N S(t) E(t) I(t)   has been used, with:





3
1
1
T
3
00
( )I(t) E(t)
f x(t) ( )E(t) I(t)S(t)
I(t)E(t)()NS(t)I(t)S(t)
g x(t) 0 0 N ; h x(t) I(t)

 
 
     
 






(7)
where
1
N



and


0
, 0

  
. The first
step to apply a coordinate transformation based on
the Lie derivation is to determine the relative degree
of the system. For such a purpose, the following
definitions are taken into account: (i)





k1
f
k
f
Lhx(t)
Lh x(t) f x(t)
x




is the kth-order
Lie derivative of

hx(t) along

fx(t) with

0
f
Lh x(t) h x(t) and (ii) the relative degree r
of the system is the number of times that the output
must be differentiated to obtain the input explicitly,
i.e., the number
r so that

k
gf
LLh x(t) 0

for
kr1 and

r1
gf
LL h x(t) 0

 .
From (7),
 
ggf
Lh x(t) LLh x(t) 0


while

2
gf
L L h x(t) I(t) , so the relative degree of
the system is 3 in


T
3
0
DxIES I0


,
i.e.,
3
0
x

 except in the singular surface I0

of the state space where the relative degree is not
well-defined. Since the relative degree of the system
is exactly equal to the dimension of the state space
for any
xD
, the nonlinear coordinate change







0
f
f
2
f
2
1
I (t) L h x(t) I(t)
E(t) L h x(t) 1 0 0 f x(t) ( )I(t) E(t)
S(t) L h x(t) ( ) 0 f x(t)
( ) I(t) (2 )E(t) I(t)S(t)

 

   
(8)
allows to represent the model in the called normal
form in a neighbourhood of any
xD . Namely:

 

x(t) f x(t) g x(t) u(t)
y(t) h x(t)






(9)
where
T
x(t) I(t) E(t) S(t)





and:
 







T
T
2
1
1
f x(t) E(t) S(t) x(t)
g x(t) 0 0 I (t) ; h x(t) I (t)
x(t) ( ) ( )( ) I (t)
( )(2 )E(t) (3 )S(t)
( ) ( )( ) I (t)
(2 ) I (t)E(t)

 
     
    
    
  
1
2
I (t)S(t)
E(t)S(t) E (t)
+ (2 )
I(t) I(t)


(10)
The following result being relative to the input-
output linearization of the system is established.
Theorem 1: The state feedback control law
   

3 2
f01f2f
2
gf
u(t)
Lhx(t) hx(t) Lhx(t) Lhx(t)
LLh x(t)

 
(11)
where
i

, for

 i0, 1, 2
, are the controller tuning
parameters, induces the linear closed-loop dynamics
210
y(t) y(t) y(t) y(t) 0


  
(12)
around any point xD

.
Proof: The state equation for the closed-loop system
 
3
f 012
I(t)
E(t)
E(t) S(t)
S(t)
x(t) L h x(t) I (t) E(t) S(t)

    















(13)
is obtained by introducing the control law (11) in (9)
and taking into account the fact that


2
gf
L L h x(t) I(t) I(t) 0

    xD
and the coordinate transformation (8). Moreover, it
follows by direct calculations that:





33
f
2
2
11
22
11
Lh x(t) ( ) ( ) I(t)
( ) (2 )( ) E(t)
I(t) I(t) E(t) E(t)S(t)
(4 2 )I(t)S(t) I (t)S(t)

    
   
   
(14)
One may express


3
f
Lh x(t) in the state space
defined by
x(t) via the application of the reverse
coordinate transformation to that in (8). Then, it
follows directly that

 
3
f
L h x(t) x(t) . Thus, the
state equation of the closed-loop system in the state
space defined by
x(t) can be written as:
BIOINFORMATICS 2012 - International Conference on Bioinformatics Models, Methods and Algorithms
78

x(t) Ax(t)

with
012
010
A001











(15)
Furthermore, the output equation of the closed-loop
system is
y(t) Cx(t) with


C100 since
y(t) I(t) I(t) . From (15) and the closed-loop
output equation, it follows that:
() At
y(t) CAex(0)

for
 0, 1, 2, 3
(16)
with
 denoting the order of the differentiation of
y(t) . Finally, the dynamics of the closed-loop
system (12) is directly obtained from (16).
Remarks 1: (i) The controller parameters
i

, for
 i0, 1, 2
, will be adjusted such that the roots of
the closed-loop system characteristic polynomial


3123
P(s) Det sI A (s r )(s r )(s r )
, with
33
3
I


denoting the identity matrix, be located at prescribed
positions. i.e.,
iij
(r)
for
 i0, 1, 2 and
 j1, 2, 3
, with
j
(r) denoting the desired roots
of P(s) . If one of the control objectives is to
guarantee the exponential stability of the closed-loop
system then

j
Re r 0 for all
 j1, 2, 3
. Then,
the values
0123
rrr 0  ,
1121323
rr rr r r 0   
and
2123
rrr 0    for the controller parameters
have to be chosen in order to achieve such a stability
result. It implies that the strictly positivity of the
controller parameters is a necessary condition for the
exponential stability of the closed-loop system.
(ii) The control (11) may be rewritten as:

32
01 2
2
2
12
2
( )() ()()
u(t)
(3 2 )
I(t) E(t) S(t)
NN
()(2 )( ) (2 )
E(t)
I(t)
E(t)S(t)
I(t)S(t)
NI(t)
N
      


 



      






(17)
by using (8) and (14).
(iii) The control law (11) is well-defined for all
3
0
x

 
except in the surface
I0 . However, the
infection may be considered eradicated from the
population once the infectious population strictly
exceeds zero while it is smaller than one individual,
so the vaccination strategy may be switched off
when
0I(t) 1. This fact implies that the
singularity in the control law is not reached. i.e.,
such a control law is well-defined by the nature of
the system. In this sense, the control law
f
p
f
u(t) for 0 t t
u(t)
0 for t t






(18)
may be used instead of (11) in a practical situation.
The signal
u(t) in (18) is given by the linearizing
control law (11) while
f
t denotes the eventual time
instant after which the infection propagation may be
assumed ended. Formally, such a time instant is


f0f
tMint I(t) for some 0 1


 
(19)
Then, the control action is maintained active while
the infection persists in the population and it is
switched off once the epidemics is eradicated.
3.1 Control Parameters Choice
The application of the control law (11), obtained
from the exact input-output linearization strategy,
makes the closed-loop dynamics of the infectious
population be given by (12). Such a dynamics
depends on the control parameters
i
 , for

 i0, 1, 2 . Such parameters have to be
appropriately chosen in order to guarantee the
following suitable properties: (i) the stability of the
controlled SEIR model, (ii) the eradication of the
infection, i.e., the asymptotic convergence of
I(t)
and
E(t) to zero as time tends to infinity and (iii)
the positivity property of the controlled SEIR model
under a vaccination based on such a control strategy.
The following theorems related to the choice of the
controller tuning parameter in order to meet such
properties are proven.
Theorem 2: Assume that the initial condition

T
3
0
x(0) I(0) E(0) S(0)

 is bounded and all
roots
j
(r)

for

 j1, 2, 3 of the characteristic
polynomial
P(s) associated with the closed-loop
dynamics (12) are of strictly negative real part via an
appropriate choice of the free-design controller
parameters
i
0

 , for  i0, 1, 2 . Then, the
control law (11) guarantees the exponential stability
of the transformed controlled SEIR model (6)-(10)
while achieving the eradication of the infection from
the host population as
t . Moreover, the SEIR
model (1)-(4) has the following properties:
E(t) ,
I(t) , S(t)I(t) and


S(t) R(t) N E(t) I(t)
are
A VACCINATION CONTROL LAW BASED ON FEEDBACK LINEARIZATION TECHNIQUES FOR SEIR
EPIDEMIC MODELS
79

bounded for all time, E(t) 0 , I(t) 0 ,
S(t) R(t) N and S(t)I(t) 0 exponentially as
t , and

I(t) o 1 S(t) .
Proof: The dynamics of the controlled SEIR model
(12) can be equivalently rewritten with the state
equation (15) and the output equation
y(t) Cx(t)

,
where


C100 , by taking into account that
y(t) I(t) , y(t) E(t)

and y(t) S(t)

. The initial
condition
T
x(0) I (0) E(0) S(0)



in such a
realization is bounded since it is related to
x(0) via
the coordinate transformation (8) and
x(0) is
assumed to be bounded. The controlled SEIR model
is exponentially stable since the eigenvalues of the
matrix
A are the roots
j
r0

 for  j1, 2, 3 of
P(s) which are assumed to be in the open left-half
plane. Then, the state vector
x(t) exponentially
converges to zero as
t  while being bounded
for all time. Moreover,
I(t) and E(t) are also
bounded and converge exponentially to zero as
t  from the boundedness and exponential
convergence to zero of
x(t) as t  according to
the first and second equations of the coordinate
transformation (8). Then, the infection is eradicated
from the host population. Furthermore, the
boundedness of
S(t) R(t) follows from that of
E(t) and I(t) , and the fact that the total population
is constant for all time. Also, the exponentially
convergence of
S(t) R(t) to the total population as
t  is derived from the exponential convergence
to zero of
I(t) and E(t) as t , and the fact that
S(t) E(t) I(t) R(t) N 
0
t

 . Finally, from
the third equation of (8), it follows that
S(t)I(t) is
bounded and it converges exponentially to zero as
t  from the boundedness and convergence to
zero of
I(t) , E(t) and x(t) as t . The facts
that
I(t) 0 and S(t)I(t) 0 as t  imply
directly that

I(t) o 1 S(t) .
Remark 2: Theorem 2 implies the existence of a
finite time instant
f
t after which the epidemics is
eradicated when the vaccination control law (18) is
used instead of (11). Concretely, such an existence
derives from the fact that
I(t) 0 as t  via the
application of the control law (11).
Theorem 3: Assume an initial condition for the
SEIR model satisfying
R(0) 0 ,
3
0
x(0)

  , i.e.,
I(0) 0 , E(0) 0 and S(0) 0 , and the constraint
S(0) E(0) I(0) R(0) N

 . Assume also that
some strictly positive real numbers
j
r for

 j1, 2, 3 are chosen such that:
(a)


1
0r Min ,





,
2
r  and


3
rMax,    , so that
321
rrr0
(b)
1
r and
3
r satisfy the inequalities:
13
2
13 1 3
313
rr 2
rr ( )(r r )+( )(2 ) ( )
(r r )(r )



      




Then:
(i) the application of the control law (11) to the
SEIR model guarantees that the epidemics is
asymptotically eradicated from the population while
I(t) 0 , E(t) 0 and S(t) 0
0
t

 , and
(ii) the application of the control law (18) guarantees
the epidemics eradication after a finite time
f
t , the
positivity of the controlled SEIR epidemic model


f
t0, t and that u(t) V(t) 1




f
t0, t so
that
u(t) 0
0
t


  , provided that the controller
tuning parameters
i

,

 i0, 1, 2 , are chosen so
that
j
(r)

,

 j1, 2, 3 , be the roots of the
characteristic polynomial
P(s) associated with the
closed loop dynamics (12).
Proof: (i) On one hand, the epidemics asymptotic
eradication is proved by following the same
reasoning that in
Theorem 2. On the other hand, the
dynamics (12) of the controlled SEIR model can be
written in the state space defined by
T
x(t) I(t) E(t) S(t)





as in (15). From such a
realization and taking into account the first equation
in (8) and that
j
(r)

for  j1, 2, 3 are the
eigenvalues of
A , it follows that:
3
12
rt
rt r t
12 3
I(t) I(t) y(t) c e c e c e


  
(20)
0
t


  for some constants
j
c for  j1, 2, 3
being dependent on the initial conditions y(0) , y(0)

and
y(0)

. In turn, such initial conditions are related
to the initial conditions of the SEIR model in its
original realization, i.e., in the state space defined by

T
x(t) I(t) E(t) S(t) via (8). The constants
j
c
BIOINFORMATICS 2012 - International Conference on Bioinformatics Models, Methods and Algorithms
80

for
 j1, 2, 3 can be obtained by solving the
following set of linear equations:
123
11 2 2 3 3
222
11 2 2 3 3
2
1
I (0) y(0) c c c I(0)
E(0) y(0) (c r c r c r ) ( )I(0) E(0)
S(0) y(0) c r c r c r
( ) I(0) (2 )E(0) I(0)S(0)



   


(21)
where (8) and (20) have been used. Such equations
can be compactly written as
p
RKM
where:
1
p123 2
222
123 3
2
1
111 c
R r r r , K c and
rrr c
I(0)
M()I(0)E(0)
( ) I(0) (2 )E(0) I(0)S(0)


   










(22)
Then, once the desired roots of the characteristic
equation of the closed-loop dynamics have been
prefixed the constants
j
c
for
 j1, 2, 3 of the
time-evolution of
I(t) are obtained from
1
p
KRM


since
p
R
is a non-singular matrix, i.e., an invertible
matrix. In this sense, note that
p213132
Det(R ) (r r )(r r )(r r ) 0   since
p
R is a
Vandermonde matrix (Fulton and Harris, 1991) and
the roots
j
(r) for
 j1, 2, 3
have been chosen
different among them. Namely:




 
 
23 23 1
2131
1
13 13 1
2
2132
3
12 12 1
313 2
F r , r I(0) G r , r E(0) I(0)S(0)
(r r )(r r )
c
F r , r I(0) G r , r E(0) I(0)S(0)
c
(r r )(r r )
c
F r , r I(0) G r , r E(0) I(0)S(0)
(r r )(r r )
 

 


 















(23)
where
2
F:

 and
2
G:

 are defined as:
2
F(v,w) vw ( )(v w) ( )
G(v,w) v w (2 )
  



(24)
Note that
31
1
13 1
(r )E(0) I(0)S(0)
c0
(r)(rr)
 

 
since
I(0) 0 , E(0) 0 , S(0) 0 ,

23
Fr,r 0

,

23 3
Gr,r r 0,
1
r0  and
31
rr0 by taking into account the constraints in
(a). On one hand,
I(t) 0
0
t

 is proved
directly from (20) as follows. One ‘a priori’ knows
that
1
c0 . However, the sign of both
2
c and
3
c
may not be ‘a priori’ determined from the initial
conditions and constraints in (a). The following four
cases may be possible: (i)
2
c0 and
3
c0 , (ii)
2
c0 and
3
c0

, (iii)
2
c0 and
3
c0 , and (iv)
2
c0

and
3
c0

. For the cases (i) and (ii), i.e., if
2
c0 , it follows from (20) that:


3
12
33312
rt
rt rt
12 12
rt rt rtrt r t
12
I(t) c e c e I(0) c c e
c e e c e e I(0)e 0



 

  
(25)
0
t


 where the facts that
123
I(0) c c c 0
and,
3
1
rt
rt
ee0



 and
3
2
rt
rt
ee0



0
t

 since
123
rrr

 have been taken into account. For the case
(iii), i.e., if
2
c0

and
3
c0 , it follows that:




3
12
3121
rtrt r t
23 2 3
rt
rt rt rt
32 3
I(t) I(0) c c e c e c e
I(0) c e c e e c e 0



  

 
(26)
0
t


  by taking into account that
123
I(0) c c c

,
21
rt rt
ee0



0
t

 since
12
rr

and the fact that:

3
313 1 1
313
I(0) c
(r r )(r ) S(0) I(0) ( r )E(0)
0
(r r )(r )

   


(27)
where (23), (24),

12 1
Gr,r r 0,


12
Fr,r 0

and the constraints in (a) and (b) have
been used. In particular, the coefficient multiplying
to
I(0) in (27) is non-negative if
1
r and
3
r satisfy
the third inequality of the constraints (b) by taking
into account
1
S(0) S(0) N

  and
S(0) N

. This later inequality is directly implied by
I(0) 0 , E(0) 0 , S(0) 0 , R(0) 0 and
N
I(0) E(0) S(0) R(0)

 . Finally, for the case
(iv), i.e., if
2
c0

and
3
c0

, it follows that:

 
3
12
3
121 1
rt
rt rt
23 2 3
rt
rt rt rt rt
23
I(t) I(0) c c e c e c e
I(0)e c e e c e e 0



 
  


(28)
0
t


  , where
21
rt rt
ee0



and
3
1
rt
rt
ee0


,
since
123
rr r

 , and
123
I(0) c c c 0 have
been taken into account. In summary,
I(t) 0
0
t


  if all partial populations are initially non-
negative and the roots
j
(r)

, for  j1, 2, 3 , of the
closed-loop characteristic polynomial satisfy the
constraints in (a) and (b). On the other hand, one
A VACCINATION CONTROL LAW BASED ON FEEDBACK LINEARIZATION TECHNIQUES FOR SEIR
EPIDEMIC MODELS
81

obtains from the reverse coordinate transformation
to (8) and (20) that:


j
j
3
rt
jj
j1
1
3
rt
2
jj j
j1
1
11
E(t) E(t) ( ) I (t) c ( r )e
S(t) ( )( ) I (t) (2 )E(t)
S(t)
I(t)
cr (2 )r ( )( )e
I(t)






    


    




(29)
from the facts that E(t) I(t)

and S(t) I(t)

. If
one fixes the parameter
2
r

 then:



3
1
1
3
rtrt
113 3
rt
2
11 1
rt
2
1
33 3
1
E(t) c ( r )e c ( r )e
c r (2 )r ( )( ) e
1
S(t)
I(t)
cr (2 )r ( )( )e





    


     



(30)
where the function H:

 defined as:
2
H(v) v (2 )v ( )( )










(31)
is zero for
2
vr has been used. From the
first equation in (30), it follows that
33 11
c( r) E(0) c( r)    and then:

331
rt rtrt
11
c( r) e e E(0)e
E(t) 0

  


(32)
0
t

 by applying such a relation between
1
c
and
3
c in (30) and by taking into account that
11
c( r) 0  , E(0) 0 and
3
1
rt
rt
ee 0




0
t

 since
13
rr . In this way, the non-
negativity of
E(t) has been proven. From the
second equation in (30), it follows that
33 1 11
c H(r ) I(0)S(0) c H(r )  and then:

331
rt rtrt
11 1
1
c H(r ) e e I(0)S(0)e
S(t) 0
I(t)




(33)
0
t

 by applying such a relation between
1
c
and
3
c in (30) and by taking into account that
11
cH(r) 0 since

1
rMin,    , I(0) 0 ,
S(0) 0 , I(t) 0 and
3
1
rt
rt
ee 0



0
t


 
since
13
rr . In this way, the non-negativity of S(t)
has been proven. Note that the function
H(v)
defined in (31) is an upper-open parabola zero-
valued for
1
v  and
2
v  so
1
H(r ) 0
from the assumption that

1
rMin, 



.
(ii) On one hand, if the control law (18) is used
instead of that in (11) then the time evolution of the
infectious population is also given by (20) while the
control action is active. Thus,
I(t) 0 as t  in
(20) implies directly the existence of a finite time
instant
f
t at which the control (18) switches off.
Obviously, the non-negativity of
I(t) , E(t) and
S(t)


f
t0, t is proved by following the same
reasoning used in the part (i) of the current theorem.
The non-negativity of
R(t)


f
t0, t is proven
by using continuity arguments. In this sense, if R(t)
reaches negative values for some


f
t0, t starting
from an initial condition R(0) 0 then R(t) passes
through zero, i.e., there exists at least a time instant


0f
t0, t such that
0
R(t ) 0 . Then, it follows
from (4) that:
00 0
23
01 2
0
00
20 00
0
2
012
0
R(t) I(t) NV(t)
()()()
I(t ) N
E(t)S(t)
( 3 2)S(t) I(t)S(t)
I(t ) N
E(t )()(2 )( ) (2 )
N
I(t )
 
      
 


      
      



(34)
by introducing the control law (18), taking into
account that
V(t) u(t)

and where the fact that
000
I(t) E(t) S(t) N

, since
0
R(t ) 0 , has been
used. Moreover, the non-negativity of
I(t) , E(t)
and
S(t)


f
t0, t
as it has been previously
proven, implies that
0
I(t ) N ,
0
E(t ) N and
0
S(t ) N

. Also,
0
I(t ) 0 since
0f
tt and
from the definition of
f
t in (19). Then, one obtains:
23
01 2
00
00
20
0
2
0
12
0
()()()
R(t) I(t) N
E(t)S(t)
(32)S(t)
I(t )
E(t )
()(2 )( ) (2 )
N
I(t )
      
 

   
      



(35)
from (34). The controller tuning parameter
i

for

 i0, 1, 2 are related to the roots
j
(r)
, for

 j1, 2, 3 , of the closed-loop characteristic
polynomial
P(s) , see Remark 1 (i), by:
01231121323 2123
rrr ; rr rr +r r ; r r r

 
(36)
The assignment of
j
r for  j1, 2, 3 such that the
BIOINFORMATICS 2012 - International Conference on Bioinformatics Models, Methods and Algorithms
82

constraints (a) and (b) are fulfilled implies that:
2
2
12
23
01 2
320
()(2 )( ) (2 )0
()()() 0

       
       
(37)
Then,
0
R(t ) 0

by taking into account (37) in (35).
The facts that
R(t) 0


0
t0, t ,
0
R(t ) 0

and
0
R(t ) 0

imply that R(t) 0


f
t0, t via
complete induction.
On the other hand, from (17) and (18), it follows:
32
01 2
2
2
2
12
() ()()
u(t) + R(t)
N
(3 2 )
E(t)S(t)
S(t) I(t)S(t)
NNI(t)
N
()(2 )( ) (2 )
E(t)
I(t)
      


 
 




      


(38)


f
t0, t
by taking into account that
S(t) E(t) I(t) R(t) N . Moreover:

32
01 2
2
12
2
f
() ()()
u(t)
()(2 )( ) (2 )
E(t)
I(t)
32
+ S(t) t 0, t
N
                


      





(39)
where the facts that 0I(t)N

  , E(t) 0 ,
S(t) 0 and R(t) 0


f
t0, t have been used.
If the roots of the polynomial
P(s) satisfy the
conditions in (a) and (b), it follows from (39) that:
2
2
12
32
u(t) 1 S(t)
N
()(2 )( ) (2 )
E(t)
1
I(t)



      


(40)


f
t0, t by taking into account the third
equation in (37) and the non-negativity of
S(t) ,
E(t) and I(t)


f
t0, t . Finally, it follows that
u(t) 0
0
t

 from (18) and (40).
4 SIMULATION RESULTS
An example based on an outbreak of influenza in a
British boarding school in early 1978 (Keeling and
Rohani, 2008) is used to illustrate the theoretical
results presented. Such an epidemic can be described
by the SEIR mathematical model (1)-(4) with
1
70 years 25550 days

  , 1.66 per day ,
11
2.2 days

 and
1
15 days

 . A total
population of
N
1000 boys

is considered with the
initial conditions
S(0) 800 boys

, E(0) 100 boys ,
I(0) 60 boys

and R(0) 40 boys

. Two sets of
simulation results are presented to compare the
evolution of the SEIR mathematical model
populations in two different situations, namely:
when no vaccination control actions are applied and
if a control action based on the feedback input-
output linearization approach is applied.
4.1 Epidemic Evolution without
Vaccination
The time evolution of the respective populations is
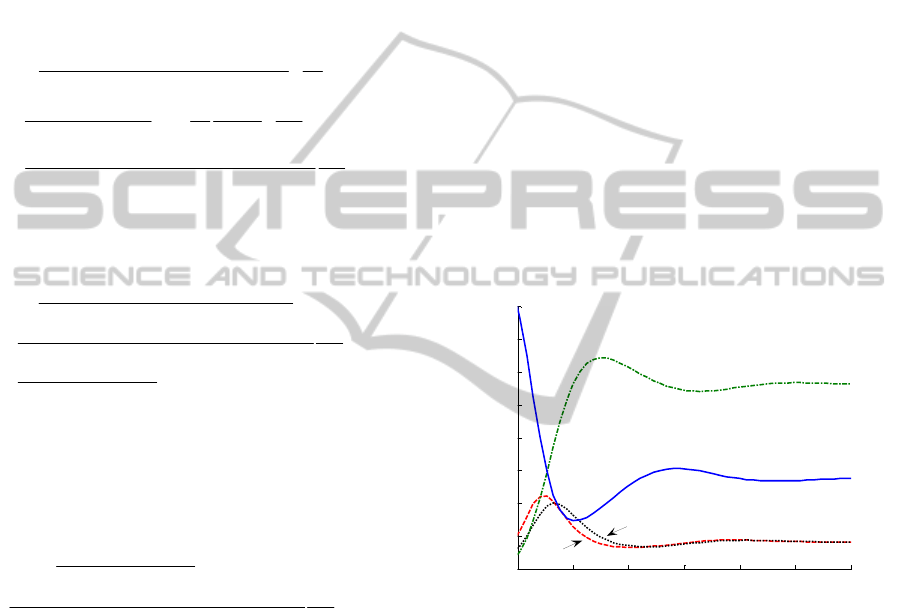
displayed in Figure 1. The model tends to its
endemic equilibrium point as time tends to infinity.
There are susceptible, infected and infectious
populations at such an equilibrium point. As a
consequence, a vaccination control action has to be
applied in order to eradicate the epidemics.
0 10 20 30 40 50 60
0
100
200
300
400
500
600
700
800
Time (days)
Partial populations
R(t)
I(t)
S(t)
E(t)
Figure 1: Time evolution of the individual populations
without vaccination.
4.2 Epidemic Evolution with a
Feedback Control Law
The control law given by (18)-(19) is applied with
0.001

 and the free-design controller parameters
i

, for

 i0, 1, 2
, being chosen so that the roots of
the characteristic polynomial
P(s) associated with
the closed-loop dynamics (12) are
1
r,
2
r()

 and
3
r(2)

  . Such values for
i

are obtained from (36). The time evolution of the
respective populations is displayed in Figure 2 and
the vaccination function in Figure 3.
A VACCINATION CONTROL LAW BASED ON FEEDBACK LINEARIZATION TECHNIQUES FOR SEIR
EPIDEMIC MODELS
83

0 5 10 15 20 25 30
0
100
200
300
400
500
600
700
800
900
1000
Time (day s )
Partial populations
S(t)
E(t)
I(t)
R(t)
Figure 2: Time evolution of the individual populations
with the vaccination control action.
0 5 10 15 20 25 30
0
2000
4000
6000
8000
10000
12000
14000
Time (days)
Vacci nation f unc t ion V(t
)
Figure 3: Time evolution of the vaccination function.
The vaccination control action achieves the
control objectives as it is seen in Figure 2. The
infection is eradicated from the population since
both infectious and infected populations converge
rapidly to zero. Also, the susceptible population
converges to zero while the removed-by-immunity
population tracks asymptotically the whole
population as time tends to infinity. Such a result is
coherent with the result proved in
Theorem 3.
Moreover, the positivity of the system is maintained
for all time as it can be seen from such figures. Such
a property is satisfied although all constraints of the
assumption (b) of
Theorem 3 are not fulfilled by the
system parameters and the chosen control
parameters. However, such a result is coherent since
such constraints are sufficient but not necessary to
prove the positivity of the system. The switched off
time instant for the vaccination is
f
t30 days .
The time evolution of the respective partial
populations under the application of the developed
control strategy is similar to that obtained under the
use of other vaccination strategies proposed in other
papers by our research group, for instance, in (De la
Sen and Alonso-Quesada, 2010). The purpose of the
paper is to present an alternative method to obtain a
vaccination control law from linearization
techniques in the SEIR epidemic model.
5 CONCLUSIONS
A vaccination control strategy based on feedback
input-output linearization techniques has been
proposed to fight against the propagation of
epidemic diseases. A SEIR model with known
parameters is used to describe the propagation of the
disease. The stability and the positivity properties of
the closed-loop system as well as the eradication of
the epidemics have been proved.
Such a strategy has
a main drawback, namely, the control law needs the
knowledge of the true values of the susceptible,
infected and infectious populations at all time
instants which may not be available in certain real
situations. Future researches are going to deal with
alternative approaches useful to overcome such a
drawback. For instance, an observer may be added
to estimate online all the partial populations
. Also,
the application of the current approach and similar
non-linear techniques to other disease propagation
models can be considered.
ACKNOWLEDGEMENTS
The authors thank to the Spanish Ministry of
Education by its support of this work through Grant
DPI2009-07197 and to the Basque Government by
its support through Grants IT378-10, SAIOTEK
SPE07UN04 and SAIOTEK SPE09UN12.
REFERENCES
De la Sen, M., Agarwal, R. P., Ibeas, A., Alonso-Quesada,
S., 2010. On a generalized time-varying SEIR
epidemic model with mixed point and distributed
time-varying delays and combined regular and
impulsive vaccination controls.
Advances in
Difference Equations 2010, Article ID 281612,
42
pages, doi:10.1155/2010/281612.
De la Sen, M., Agarwal, R. P., Ibeas, A., Alonso-Quesada,
S., 2011. On the existence of equilibrium points,
boundedness, oscillating behavior and positivity of a
SVEIRS epidemic model under constant and
impulsive vaccination.
Advances in Difference
Equations 2011, Article ID 748608,
32 pages,
doi:10.1155/2011/748608.
De la Sen, M., Alonso-Quesada, S., 2010. On vaccination
control tools for a general SEIR-epidemic model. In
18th Mediterranean Conference on Control &
BIOINFORMATICS 2012 - International Conference on Bioinformatics Models, Methods and Algorithms
84

Automation (MED’10), pp. 1322-1328,
doi:10.1109/MED.2010.5547865.
Fulton, W., Harris, J. D., 1991. Representation Theory,
S
pringer, New York.
Isidori, A., 1995. Nonlinear Control Systems,
Springer-
Verlag
, London.
Jumpen, W., Orankitjaroen, S., Boonkrong, P.,
Wiwatanapataphee, B., 2011. SEIQR-SIS epidemic
network model and its stability.
International Journal
of Mathematics and Computers in Simulation 5, pp.
326-333.
Keeling, M. J., Rohani, P., 2008.
Modeling Infectious
Diseases in Humans and Animals
, Princeton
University Press, Princeton and Oxford.
Li, M. Y., Graef, J. R., Wang, L., Karsai, J., 1999. Global
dynamics of a SEIR model with varying total
population size.
Mathematical Biosciences 160, pp.
191-213
.
Makinde, O. D., 2007. Adomian decomposition approach
to a SIR epidemic model with constant vaccination
strategy.
Applied Mathematics and Computation 184,
pp. 842-848.
Mollison, D., 2003.
Epidemic Models: Their Structure and
Relation to Data
, Publications of the Newton Institute,
Cambridge University Press.
Mukhopadhyay, B., Bhattacharyya, R., 2007. Existence of
epidemic waves in a disease transmission model with
two-habitat population.
International Journal of
Systems Science
38, pp. 699-707.
Safi, M. A., Gumel, A. B., 2011. Mathematical analysis of
a disease transmission model with quarantine,
isolation and an imperfect vaccine.
Computers and
Mathematics with Applications
61, pp. 3044-3070.
Song, X. Y., Jiang, Y., Wei, H. M., 2009. Analysis of a
saturation incidence SVEIRS epidemic model with
pulse and two time delays.
Applied Mathematics and
Computation
214, pp. 381-390.
Xu, R., Ma, Z., Wang, Z., 2010. Global stability of a
delayed SIRS epidemic model with saturation
incidence and temporary immunity.
Computers and
Mathematics with Applications
59, pp. 3211-3221.
Zhang, T. L., Liu, J. L., Teng, Z. D., 2009. Dynamic
behaviour for a nonautonomous SIRS epidemic model
with distributed delays.
Applied Mathematics and
Computation
214, pp. 624-631.
A VACCINATION CONTROL LAW BASED ON FEEDBACK LINEARIZATION TECHNIQUES FOR SEIR
EPIDEMIC MODELS
85