
IMPROVING ELECTRIC FRAUD DETECTION
USING CLASS IMBALANCE STRATEGIES
Mat´ıas Di Martino, Federico Decia, Juan Molinelli and Alicia Fern´andez
Instituto de Ingenier´ıa El´ectrica, Facultad de Ingenier´ıa Universidad de la Rep´ublica Montevideo, Montevideo, Uruguay
Keywords:
Electricity theft, Support vector machine, Optimum path forest, Unbalance class problem, Combining
classifier, UTE.
Abstract:
Improving nontechnical loss detection is a huge challenge for electric companies. The great number of clients
and the diversity of the different types of fraud makes this a very complex task. In this paper we present a
fraud detection strategy based on class imbalance research. An automatic detection tool combining classifi-
cation strategies is proposed. Individual classifiers such as One Class SVM, Cost Sensitive SVM (CS-SVM),
Optimum Path Forest (OPF) and C4.5 Tree, and combination functions are designed taken special care in the
data’s class imbalance nature. Analysis over consumers historical kWh load profile data from Uruguayan Elec-
tric Company (UTE) shows that using combination and balancing techniques improves automatic detection
performance.
1 INTRODUCTION
Nontechnical losses represent a very high cost to
power supply companies, who aims to improve fraud
detection in order to reduce this losses. Research in
pattern classification field has been made to tackle this
problem (Ramos et al., 2010), (Nagi and Mohamad,
2010), (Muniz et al., 2009), (Jiang et al., 2000)
In Uruguay the national electric power company
(henceforth call UTE) faces the problem by manually
monitoring a group of customers. A group of experts
looks at the monthly consumption curve of each cus-
tomer and indicates those with some kind of suspi-
cious behavior. This set of customers, initially clas-
sified as suspects are then analyzed taking into ac-
count other factors (such as fraud history, counter type
etc.). Finally a subset of customers is selected to be
inspected by an UTE employee, who confirms (or not)
the irregularity. The procedure described before, has
major drawbacks, mainly, the number of costumers
that can be manually controlled is small compared
with the total amount of costumer (around 500.000
only in Montevideo). To improve the efficiency of
fraud detection and resource utilization, we imple-
mented a tool that automatically detects suspicious
behavior analyzing customers historical consumption
curve. Thus, UTE’s experts only need to look to a re-
duced number of costumers and then select those who
need to be inspected.
Due to the applications nature there is a great
imbalance between “normal” and “fraud/suspicious”
classes. The class imbalance problem in general and
fraud detection in particular have received consider-
able attention in recent years. Garcia et al. and Guo
and Zhou review main topics in the field of the class
imbalance problem (Garcia et al., 2007), (Guo and
Zhou, 2008). These include: resampling methods for
balancing data sets (Batista et al., 2004),(Barandela
and Garcia, 2003), (Chawla et al., 2002), (Chawla
et al., 2003), (Kolez et al., 2003), feature extrac-
tion and selection techniques -wrapper (Dash and Liu,
1997), and choose of F-value as performance mea-
sure.
In addition, it is generally accepted that combina-
tion of diverse classifiers can improveperformance. A
difficult task is to choose the combination strategy for
a diverse set of classifiers. Kuncheva found the opti-
mum set of weights for the majority weight vote com-
biner when the performance metrics is accuracy and
with independent base classifiers (Kuncheva, 2004).
Further analysis has been done on the relationship be-
tween diversity and the majority rules performance
(Brown and Kuncheva, 2010), (Wang and Yao, 2009),
(Chawla and Sylvester, 2007). In this paper we pro-
pose a combination function adapted to the imbalance
between classes, using F-value as the performance
measurement and some well-known pattern recogni-
tion techniques such as SVM (Support Vector Ma-
135
Di Martino M., Decia F., Molinelli J. and Fernández A. (2012).
IMPROVING ELECTRIC FRAUD DETECTION USING CLASS IMBALANCE STRATEGIES.
In Proceedings of the 1st International Conference on Pattern Recognition Applications and Methods, pages 135-141
DOI: 10.5220/0003768401350141
Copyright
c
SciTePress

chine) (Vapnik, 1998), (Scholkopf and Smola, 2002),
Tree classifiers and more recent algorithms such as
Optimum Path Forest (Papa and Falcao, 2010),(Papa
et al., 2007) as base classifiers.
Performance evaluation using test dataset shows
very good results on suspicious profiles selection.
Also, on field evaluation of fraud detection using our
automatic system shows similar results to manual ex-
perts’ method.
The paper is organized as follows. Section 2 de-
scribes general aspects of the class imbalance prob-
lem, section 3 describes different strategies proposed,
section 4 presents the results obtained, and, finally,
section 5 concludes the work.
2 THE CLASS IMBALANCE
PROBLEM
When working on the fraud detection problem, one
can not assume that the number of people who com-
mit fraud are the same than those who do not, usually
there are fewers elements from the class who com-
mit fraud. This situation is known as the problem of
class imbalance, and it is particularly important in real
world applicationswhere it is costly to misclassify ex-
amples from the minority class. In this cases, stan-
dard classifiers tend to be overwhelmed by the major-
ity class and ignore the minority class, hence obtain-
ing suboptimal classification performance. Having to
confront this type of problem, we decided to use three
different strategies on different levels, changing class
distribution by resampling, manipulating classifiers,
and on the ensemble of them.
The first consists mainly in resampling techniques
such as under-sampling the majority class or over-
sampling the minority one. Random under-sampling
aims at balancing the data set through random re-
moval of majority class examples. The major prob-
lem of this technique is that it can discard poten-
tially important data for the classification process. On
the other hand, the simplest over-sampling method is
to increase the size of the minority class by random
replication of those samples. The main drawback of
over-sampling is the likelihood of over-fitting, since
it makes exact copies of the minority class instances
As a way of facing the problems of resampling tech-
niques discussed before, different proposals address
the imbalance problem by adapting existing algo-
rithms to the special characteristics of the imbalanced
data sets. One approach is one-class classifiers, which
tries to describe one class of objects (target class) and
distinguish it from all other objects (outliers). In this
paper, the performance of One-Class SVM, adapta-
tion of the popular SVM algorithm, will be analyzed.
Another technique is cost-sensitive learning, where
the cost of a particular kind of error can be different
from others, for example by assigning a high cost to
mislabeling a sample from the minority class.
Another problem which arises when working with
imbalanced classes is that the most widely used met-
rics for measuring the performance of learning sys-
tems, such as accuracy and error rate, are not appro-
priate because they do not take into account misclas-
sification costs, since they are strongly biased to fa-
vor the majority class. In the past few years, sev-
eral new metrics which measure the classification per-
formance on majority and minority classes indepen-
dently, hence taking into account the class imbalance,
have been proposed (Manning et al., 2009).
• Recall
p
=
TP
TP+ FN
• Recall
n
=
TN
TN + FP
• Precision =
TP
TP+ FP
• F
value
=
(1+ β
2
)Recall
p
× Precision
β
2
Recall
p
+ Precision
Table 1: Confusion matrix.
Labeled as
Positive Negative
Positive TP (True Positive) FN (False Negative)
Negative FP (False Positive) TN (True Negative)
Recall
p
is the percentage of correctly classified
positive instances, in this case, the fraud samples.
Precision is defined as the proportion of labeled as
positive instances that are actually positive. The com-
bination of this two measurements, the F-value, rep-
resents the geometric mean between them, weighted
by the parameter β. Depending on the value of β we
can prioritize Recall or Precision. For example, if we
have few resources to perform inspections, it can be
useful to prioritize Precision, so the set of samples la-
beled as positive has high density of true positive.
3 STRATEGY PROPOSED
The system presented consists of basically on three
modules: Pre-Processing and Normalization, Feature
selection and extraction and, finally, Classification.
Figure 1 shows the system configuration. The sys-
tem input corresponds to the last three years of the
monthly consumption curve of each costumer, here
ICPRAM 2012 - International Conference on Pattern Recognition Applications and Methods
136

Figure 1: Block Diagram.
called X
m
= {x
m
1
, ... x
m
n
}, where x
m
i
is the con-
sumption of the m costumer during the i-th month.
The first module called Pre-Processing and Normal-
ization, normalizes the input data so that they all have
unitary mean and implements some filters to avoid
peaks from billing errors.
The proposed methodology was developed as GUI
software in Matlab using PRTOOLS (Duin, 2000), Li-
bOPF (Papa et al., 2008) and LibSVM (Chang and
Lin, 2001).
3.1 Attributes
A feature set was proposed taking into account UTEs
technician experts in fraud detection by manual in-
spection and recent papers on non technical loss de-
tection (Alcetegaray and Kosut, 2008), (Muniz et al.,
2009), (Nagi and Mohamad, 2010). Below a list of
some of the proposed features:
• Consumption ratio for the last 3, 6 and 12 months
and the average consumption.
• Norm of the difference between the expected con-
sumption and the actual consumption.
• Difference between Fourier coefficients from the
last and previous years.
• Difference between Wavelet coefficients from the
last and previous years.
• Difference in the coefficients of the polynomial
that best fits the consumption curve.
• Variance of the consumption curve.
• Slope of the straight line that fits the consumption
curve.
It is well known that when thinking about the fea-
tures to use, large number of attributes do not imply
better performances. The important thing is their rel-
evance and the relationship between the number of
these and the number of elements. This is why we
implemented a feature selection stage. We imple-
mented several algorithms for feature selection, and
concluded that for each classifier algorithms it is best
to use a different feature set.
3.2 Classifiers
SVM is an algorithm frequently used in pattern recog-
nition and fraud detection. The main purpose of the
binary SVM algorithm is to construct an optimal de-
cision function f(x) that predicts unseen data into two
classes and minimizes the classification error. In or-
der to obtain this, one looks to maximize the sep-
aration margin between the two classes and hence
classify correctly unseen data (Nagi and Mohamad,
2010). This can be formulated as a quadratic pro-
gramming optimization problem
Φ(ω,ζ
i
) = min
(
1
2
kωk
2
+C
n
∑
i=1
ζ
i
)
(1)
subjected to the constraint that all the training samples
are correctly classified, that is
y
i
(hω,xi + b) ≥ 1− ζ
i
, i = 1, 2,...,n (2)
where ζ
i
for i = 1,2,..., n are nonnegative slack vari-
ables. C is a regularization parameter and is selected
to be the tradeoff between the two terms in 1.
3.2.1 CS-SVM and One-class SVM
Two different approaches where introduced when de-
scribing the class imbalance problem, one-class clas-
sifiers and cost-sensitive learning. When applying this
two approaches on SVM, we talk about One-Class
SVM and CS-SVM.
In One-Class SVM equation 1 becomes,
min
ω∈H ,ζ
i
∈R,ρ∈R
1
2
kωk
2
+
1
νl
n
∑
i=1
ζ
i
− ρ (3)
while in CS-SVM it becomes:
Φ(ω,ζ
i
) = min
(
1
2
kωk
2
+
∑
i/y
i
=1
C
+
ζ
i
+
∑
i/y
i
=−1
C
−
ζ
i
)
(4)
Both the kernel parameter K and the values of C
+
,
C
−
and ω are often chosen using cross validation. The
method consists in splitting the data set into p parts of
equal size, and perform p training runs. Each time,
leaving out one of the p parts and use it as an inde-
pendent validation set for optimizing the parameters.
IMPROVING ELECTRIC FRAUD DETECTION USING CLASS IMBALANCE STRATEGIES
137

Usually, the parameters which work best on average
over the p runs are chosen. Finally, these average pa-
rameters are used to train the complete training set.
There are some problems with this, as can be seen on
(Scholkopf and Smola, 2002).
Having said this, the method used to determine the
optimum parameters for CS-SVM was:
1. Determine sets C = [C
1
,C
2
,...,C
n
] and γ =
[γ
1
,γ
2
,..., γ
m
].
2. Select C
i
∈ C and γ
j
∈ γ, split the training set into
p parts of equal size and perform p training runs.
Each set is called B
i
with i = {1,2,..., p}.
3. Use B
te
= B
1
as the test set and B
tr
= B
2
∪ B
3
∪
... ∪B
p
as the training set.
4. Determine a classifier model for B
tr
, C
i
and γ
j
.
As the ratio between the two classes is unbal-
anced, when determining the CS-SVM classifier
two parameters are defined, C
+
and C
−
using
class weights defined by calculating the sample
ratio for each class. This was achieved by dividing
the total number of classifier samples with the in-
dividual class samples. In addition, class weights
were multiplied by a factor of 100 to achieve satis-
factory weight ratios (Nagi and Mohamad, 2010).
5. Classify the samples from the training set B
te
and compare the results with the labels predeter-
mined. From these comparison, obtain the esti-
mated F
value
for C
i
and γ
j
called F
value
1
(C
i
,γ
j
).
6. Repeat these procedure for B
te
= B
2
and the
combination of the reaming sets as B
tr
getting
e
2
(C
i
,γ
j
), then for B
te
= B
3
and so on until com-
pleting the p iterations.
7. For each pair of (C
i
,γ
j
) there’s an estimation of
the classification error for each cross validation.
The classification error for this pair (C
i
,γ
j
) is the
average value of the classification errors obtained
in each cross validation, e(C
i
,γ
j
) =
1
p
∑
e
l
(C
i
,γ
j
).
8. This method is repeated combining all the values
from the sets C and γ.
9. The values of C
opt
and γ
opt
are the ones for which
the smallest classification error is obtained.
The metric used for measuring the classification
error for this method was the F
value
. For One-Class
SVM, the method was the same but with the main ob-
jective of finding σ ∈ S = { σ
1
,σ
2
.....σ
l
}.
3.2.2 OPF
In (Ramos et al., 2010) a new approach, Optimum
Path Forest (OPF), is applied to fraud detection in
electricity consumption. The work shows good re-
sults in a problem similar to the targeted. OPF creates
a graph with training dataset elements. A cost is as-
sociated to each path between two elements, based on
the distance of the intermediate elements belonging
to the path. It is assumed, that elements of the same
class will have a lower path cost, than elements of dif-
ferent classes. The next step is to choose representa-
tives from each class, called prototypes. Classifying a
new element implies to find the prototype with lowest
path cost. Since OPF is very sensitive to class im-
balance, we under-sampled the majority class. Best
performance was obtained while using a training data
set with 40% of the elements from the minority class.
3.2.3 C4.5
The fourth classifier used is a decision tree proposed
by Ross Quinlan: C4.5. Trees are a method widely
used in pattern recognition problems due to its sim-
plicity and good results. To classify, a sequence of
simple questions is done. It begins with an initial
question, and depending on the answer, the procedure
continues until reaching a conclusion about the label
to be assigned. The disadvantage of these methods is
that they are very unstable and highly dependent on
the training set. To fix this, in C4.5 a later stage of
AdaBoost was implemented. It generates multiple in-
stances of the tree with different portions of the train-
ing set and then combines them achieving a more ro-
bust result. As in OPF, sensitivity to class imbalance
has led to sub-sampling the majority class. Again, we
found that the best results was obtained while using
a training data set with 40% of the elements from the
minority class.
3.3 Combining Classifiers
The next step after selecting feature sets and adjust-
ing classification algorithms to the training set, is to
decide how to combine the information provided by
each classifier. There are several reasons to combine
classifiers, for example, to obtain a more robust and
general solution and improve the final performance
(Dietterich, 2000).
After labels have been assigned by each individual
classifier, a decision rule is build as:
g
p
(x) = λ
p
O−SVM
d
p
O−SVM
+ λ
p
CS−SVM
d
p
CS−SVM
+λ
p
OPF
d
p
OPF
+ λ
p
Tree
d
p
Tree
(5)
g
n
(x) = λ
n
O−SVM
d
n
O−SVM
+ λ
n
CS−SVM
d
n
CS−SVM
+λ
n
OPF
d
n
OPF
+ λ
n
Tree
d
n
Tree
(6)
ICPRAM 2012 - International Conference on Pattern Recognition Applications and Methods
138

where d
i
j
(x) = 1 if the classifier j labels the sample as
i and 0 otherwise. Then if g
p
(x) > g
n
(x) the sample
is assigned to the positive class, if g
n
(x) > g
p
(x) the
sample is assigned to the negative class.
In (Kuncheva, 2004), the weighted majority vote
rule is analyzed and optimum weights are found for
maximum overall accuracy, assuming independence
between classifiers: λ
i
j
= log
Accuracy
j
1−Accuracy
j
, where
Accuracy
j
represents the ratio of correctly classified
samples for the classifier j, (in (Kuncheva, 2004) pri-
ors are also consider on the g
{p,n}
(x) construction
adding log(P(ω
{p,n}
)))
Inspired in this result, but taking into account that
we want to find a solution with good balance between
Recall and Precision, several weights λ
p,n
j
were pro-
posed:
• λ
i
j
= log
Recall
p
j
+1
Recall
p
j
−1
• λ
i
j
= log
F
value
j
+1
F
value
j
−1
• λ
i
j
= log
Accuracy
j
1−Accuracy
j
• λ
p
j
= Recall
n
j
and λ
n
j
= Recall
p
j
Also the optimal multipliers were found by ex-
haustive search over a predefined grid, looking
for those which maximize the classification F
value
.
Search was made by looking for all the possibilities
with λ
i
j
∈ [0 : 0.05 : 1] and was evaluated with a 10-
fold cross validation.
All of the proposed combined classifiers improved
individual classifiers performance. In Table 2 we
present the performance results using optimal multi-
pliers, found by exhaustive search.
4 RESULTS
4.1 Data
For this paper we used a data set of 1504 indus-
trial profiles (October 2004- September 2009) ob-
tained from the Uruguayan electric power company
(DATASET 1). Each profile is represented by the cus-
tomers monthly consumption. UTE technicians make
random profile selection and data labeling. Train-
ing and performance evaluation shown in Table 2 was
done with DATASET 1. Another independent dataset
(DATASET 2) of 3338 industrial profiles with con-
temporary data (January 2008-2011) was used for on
field evaluation.
4.2 Labeling Results
Table 2 shows performance for individual classifiers
and for the combination of them, results shown here
were achieved by using a 10-fold cross validation us-
ing DATASET1. CS-SVM presented the best F
value
,
followed by One class SVM. We saw that combina-
tion improved performance achieving better results
than those of the the best individual classifier.
Table 2: Data Set 1 labeling results.
Description Acc. Rec
p
. Pre. Fval.
(%) (%) (%) (%)[β = 1]
O-SVM 84,9 54,9 50,8 52,8
CS-SVM 84,5 62,8 49,7 55,5
OPF 80,1 62,2 40,5 49
Tree (C4.5) 79 64,6 39 48,6
Combination 86,2 64 54,4 58,8
4.3 On Field Results
After all the proposed alternatives were evaluated (on
DATASET 1), comparing automatic labelling with
manual labelling performed by UTE’s experts, we
tested data labels with on field evaluation.
This test were done in the following way:
1. Train the classification algorithm using
DATASET 1.
2. Classify samples from DATASET 2. Lets call
DATASET 2P the samples of DATASET 2 la-
belled as positive (associated to abnormal con-
sumption behaviour).
3. Inspect customers on DATASET 2P
560 samples of DATASET 2 were labelled as pos-
itive, from those, 340 were randomly selected (due to
human resource issues) to perform inspections. The
inspections yielded 11 irregular situations and 4 sus-
pect situations (being analyzed). This results show
that the automatic framework has a hit rate of be-
tween 3.3% and 4.4%. Manual fraud detection per-
formed by UTE’s experts during 2010 had a hit rate
of about 4%, so results are promising. Specially tak-
ing into account that manual detection considers more
information than just the consumption curve, such
as fraud history, surface dimension and contracted
power, among others.
Figures 2, 3 and 4 show some examples of cus-
tomers classified as suspicious by our automatic sys-
tem. Once inspected, illegal activities were detected
in these cases.
IMPROVING ELECTRIC FRAUD DETECTION USING CLASS IMBALANCE STRATEGIES
139
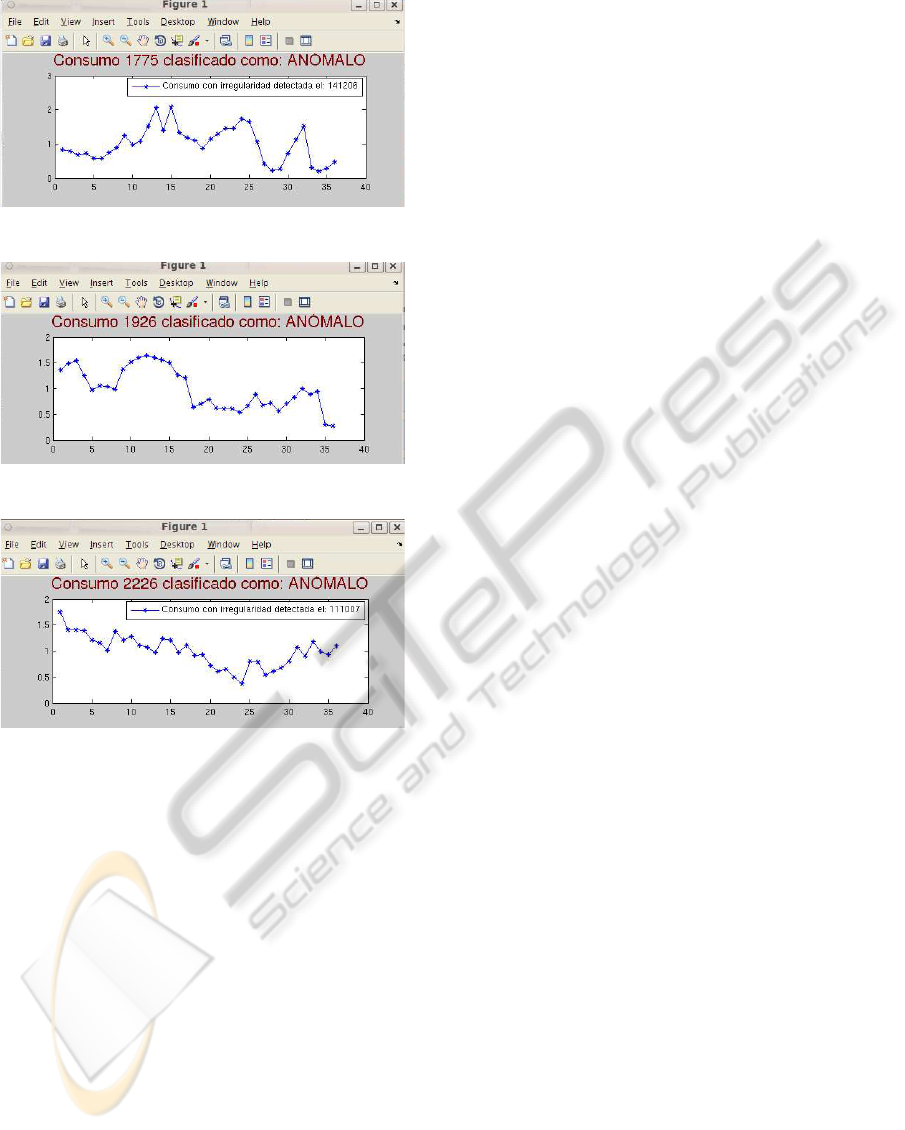
Figure 2
Figure 3
Figure 4
5 CONCLUSIONS
We developed a framework able to detect customers
whose consumption behaviour show some kind of ir-
regularities. UTE is beginning to incorporate the sys-
tem proposed and first results showed that it is use-
ful and can lead to important savings, both time and
money. We will continue working with UTE’s collab-
oration, focusing our investigation on the lines of:
• Improving final performance and monitor bigger
customer sets aiming to reach all customers in
Montevideo (Uruguayan capital city).
• Analyze existence of data clusters.
• Add more features to our learning algorithm, such
as: counter type (digital or analog), customer type
(dwelling or industrial) and contracted power,
among others.
We introduce different classifiers suitable for this
type of problems (with unbalanced classes), compar-
ing performance results for each of them. Innovative
combination strategies are also proposed, all of them
showing better results (using F-value as performance
measurement) than the best individual classifier.
ACKNOWLEDGEMENTS
The authors would like to thank UTE, especially Juan
Pablo Kosut, for providing datasets and share fraud
detection expertise. We also want to thank Pablo
Muse, Pablo Cancela and Martin Rocamora for useful
advice.
REFERENCES
Alcetegaray, D. and Kosut, J. (2008). One class svm para
la detecci´on de fraudes en el uso de energ´ıa el´ectrica.
Trabajo Final Curso de Reconocimiento de Patrones,
Dictado por el IIE- Facultad de Ingenier´ıa- UdelaR.
Barandela, R. and Garcia, V. (2003). Strategies for learn-
ing in class imbalance problems. Pattern Recognition,
pages 849–851.
Batista, G., Pratti, R., and Monard, M. (2004). A study of
the behavior of several methods for balancing machine
learning training data. SIGKDD Explorations 6, pages
20–29.
Brown, G. and Kuncheva, L. (2010). ”good” and ”bad” di-
versity in majority vote ensembles. In Multiple Clas-
sifier Systems. Springer Berlin Heidelberg.
Chang, C. and Lin, C. (2001). LIBSVM: a library for sup-
port vector machines.
Chawla, N., Bowyer, K., and Hall, L. (2002). Smote: syn-
thetic minority over-sampling technique. Journal of
Artificial Intelligence Research.
Chawla, N., Lazarevic, A., and Hall, L. (2003). Smote-
boost: impoving prediction of the minority class in
boosting. European Conf. ok Principles and Practice
of Knowledge Discovery in Databases.
Chawla, N. and Sylvester, J. (2007). Exploiting diversity
in ensembles: Improving the performance on unbal-
anced datasets. Departament of Computer Science
and Engineering.
Dash, M. and Liu, H. (1997). Feature selection for classifi-
cation. Intelligent Data Analysis, 1:131–156.
Dietterich, T. (2000). Ensemble methods in machine learn-
ing. Multiple Classifier Systems, volume 1857 of Lec-
ture Notes in Computer Science.
Duin, R. (2000). PRTools Version 3.0: A Matlab Toolbox
for Pattern Recognition.
Garcia, V., Sanchez, J., Mollineda, R., Alejo, R., and So-
toca, J. (2007). The class imbalance problem in pat-
tern classification and learning. In Congreso Espaol
de Informtica, Spain.
ICPRAM 2012 - International Conference on Pattern Recognition Applications and Methods
140

Guo, X. and Zhou, G. (2008). On the class imbalance prob-
lem. IIE - Computer Society, 1:192.
Jiang, R., Tagaris, H., and Laschusz, A. (2000). Wavelets
based feature extraction and multiple cassifiers for
electricity fraud detection.
Kolez, A., Chowdhury, A., and Alspector, J. (2003). Data
duplication: an imbalance problem? Proc. Proc. Intl.
Conf. on Machine Learning, Workshop on Learning
with Imbalanced Data Sets II.
Kuncheva, L. (2004). Combining Pattern Classifiers: Meth-
ods and Algorithms. Wiley-Interscience.
Manning, C., Raghavan, P., and Schutze, H. (2009). An
Introduction to Information Retrival. Cambridge Uni-
versity Press, Cambridge, England, 1 edition.
Muniz, C., Vellasco, M., Tanscheit, R., and Figueiredo, K.
(2009). Ifsa-eusflat 2009 a neuro-fuzzy system for
fraud detection in electricity distribution.
Nagi, J. and Mohamad, M. (2010). Nontechnical loss de-
tection for metered customers in power utility using
support vector machines. IEEE TRANSACTIONS ON
POWER DELIVERY, VOL. 25, NO. 2.
Papa, J. and Falcao, A. (2010). Optimum-path forest: A
novel and powerful framework for supervised graph-
based pattern recognition techniques. Institute of
Computing University of Campinas.
Papa, J., Falcao, A., and C.Suzuki (2008). LibOPF: a li-
brary for Opthimum Path Forets.
Papa, J., Falcao, A., Miranda, P., Suzuki, C., and Mas-
carenhas, N. (2007). Design of robust pattern clas-
sifiers based on optimum-path forests. 8th Interna-
tional Symposium on Mathematical Morphology Rio
de Janeiro Brazil Oct, pages 337–348.
Ramos, C., de Sousa, A. N., Papa, J., and Falcao, A.
(2010). A new approach for nontechnical losses de-
tection based on optimum-path forest. IEEE TRANS-
ACTIONS ON POWER SYSTEMS.
Scholkopf, B. and Smola, A. (2002). Learning with Kernels.
The MIT Press, London, 2. edition.
Vapnik, V. (1998). Statistical Learning Theory. New York:
Wiley.
Wang, S. and Yao, X. (2009). Theoretical study of the rela-
tionship between diversity and single-class measures
for class imbalance learning.
IMPROVING ELECTRIC FRAUD DETECTION USING CLASS IMBALANCE STRATEGIES
141
