
PREDICTION OF PROTEIN INTERACTIONS ON HIV-1–HUMAN
PPI DATA USING A NOVEL CLOSURE-BASED INTEGRATED
APPROACH
Kartick C. Mondal
1
, Nicolas Pasquier
1
, Anirban Mukhopadhyay
2
, C´elia da Costa Pereira
1
Ujjwal Maulik
3
and Andrea G. B. Tettamanzi
4
1
Laboratoire I3S (CNRS UMR-6070), Universit´e de Nice Sophia Antipolis, Nice, France
2
Department of Computer Science and Engineering, University of Kalyani, Kalyani, India
3
Department of Computer Science and Engineering, Jadavpur University, Kolkata, India
4
Information Technology Department, Universit`a degli Studi di Milano, Milan, Italy
Keywords:
Frequent closed itemsets, Association rules, Bi-clustering, HIV-1-Human Protein-Protein interactions.
Abstract:
Discovering Protein-Protein Interactions (PPI) is a new interesting challenge in computational biology. Iden-
tifying interactions among proteins was shown to be useful for finding new drugs and preventing several kinds
of diseases. The identification of interactions between HIV-1 proteins and Human proteins is a particular PPI
problem whose study might lead to the discovery of drugs and important interactions responsible for AIDS.
We present the FIST algorithm for extracting hierarchical bi-clusters and minimal covers of association rules
in one process. This algorithm is based on the frequent closed itemsets framework to efficiently generate a
hierarchy of conceptual clusters and non-redundant sets of association rules with supporting object lists. Ex-
periments conducted on a HIV-1 and Human proteins interaction dataset show that the approach efficiently
identifies interactions previously predicted in the literature and can be used to predict new interactions based
on previous biological knowledge.
1 INTRODUCTION
Acquired Immune Deficiency Syndrome (AIDS) is
the last stage of HIV infection. At this stage, the hu-
man immune system fails to protect the body from
infections, and this eventually leads to death. HIV is
a member of the retrovirus family (lentivirus) which
infects important cells in the human immune system.
This kind of infection is due to the interaction be-
tween proteins of both the virus and the human host in
the human cells. Predicting such interactions is an im-
portant goal of PPI research. In particular, analyzing
well-known interactions and finding new interactions
can provide useful information to find new drugs and
discover the reasons and mechanisms of this kind of
viral disease (Arkin and Wells, 2004).
PPI databases contain information about the fact
that proteins can interact if they come into contact.
The absence of such information does not imply that
they cannot interact with each other as there is no in-
formation about non-interacting proteins. The HIV-1-
Human PPI dataset is a database containing possible
viral and human protein interactions. As stated above,
only positive interactions are shown.
Several approaches for predicting interactions
have been studied in the literature. These approaches
are based on Bayesian networks (Jansen et al., 2003),
random forest classifiers (Lin et al., 2004), mixture-
of-feature-expert classifiers (Qi et al., 2007), kernel
methods (Yamanishi et al., 2004; Ben-Hur and Noble,
2005), or decision trees (Zhang et al., 2004). Most of
them have been used to find interactions within a sin-
gle organism, like yeast or human (intra-species in-
teractions). Recently, two approaches have been pro-
posed to predict the set of interactions between HIV-1
and human host cellular proteins (Tastan et al., 2009;
Mukhopadhyay et al., 2010). In particular, in (Tas-
tan et al., 2009) the authors proposed a supervised
learning framework that integrates heterogeneous bi-
ological information to predict inter-species interac-
tions. However,this approach solves the classification
problem using the random forest classifier which, like
most of the above mentioned approaches, needs both
positive and negative samples of PPIs. Negative sam-
ples here are pairs of human and HIV proteins known
not to interact, but such “negative interactions” (or,
better, proven absence of interactions) are not known
in the current state of knowledge in the PPI prob-
164
C. Mondal K., Pasquier N., Mukhopadhyay A., da Costa Pereira C., Maulik U. and G. B. Tettamanzi A..
PREDICTION OF PROTEIN INTERACTIONS ON HIV-1–HUMAN PPI DATA USING A NOVEL CLOSURE-BASED INTEGRATED APPROACH.
DOI: 10.5220/0003769001640173
In Proceedings of the International Conference on Bioinformatics Models, Methods and Algorithms (BIOINFORMATICS-2012), pages 164-173
ISBN: 978-989-8425-90-4
Copyright
c
2012 SCITEPRESS (Science and Technology Publications, Lda.)

lem studied here. Negative samples have then to be
prepared, for example by randomly selecting protein
pairs that are not present in the database, thus leading
to a high dependency between the classifier perfor-
mance and the choice of the negative samples. The
approach proposed in (Mukhopadhyay et al., 2010)
uses the well-known Apriori algorithm for mining as-
sociation rules. The particularity of such an approach
is that only information based on positive samples is
used to predict viral-human interactions (inter-species
interactions). This is also the case for the approach
proposed here.
In this paper, we present FIST, a novel approach
to integrated bi-clustering and association rule min-
ing, whose aim is threefold: in a single process, (i) to
efficiently mine frequent closed itemsets and gener-
ators, (ii) to generate minimal non-redundant covers
of association rules, (iii) to generate hierarchical con-
ceptual bi-clusters. Moreover, compared to classical
association rule mining methods, the list of rows of
the dataset supporting each association rule is gener-
ated. From the viewpoint of bi-clustering (Madeira
and Oliveira, 2004), the generated clusters form a hi-
erarchical lattice structure and can overlap, allowing
an object to belong to several bi-clusters, if relevant.
Another important aim of the FIST approach is to find
out interactions between proteins and features in order
to extract relationships between annotations (biologi-
cal and publication) and interactions.
FIST was validated by applying it to HIV-1-
Human PPI data for finding interactions between vi-
ral and host proteins. Most existing approaches ex-
tract relationships in a single organism (Mukhopad-
hyay et al., 2010) whereas FIST extracts bi-clusters
and association rules showing relationships involving
viral proteins, host proteins, or both at the same time.
The paper is organized as follows. The integrated
frequent closed itemset based approach is presented
in Section 2 and the FIST algorithm is described in
Section 3. In Section 4, we present and discuss exper-
imental results and Section 5 concludes the paper.
2 PRELIMINARIES
Early approaches to association rule mining showed
that the problem can be divided into two parts: first,
find frequent itemsets with their supports, which is the
most time-consuming part, and then generate associ-
ation rules from these itemsets (Agrawal et al., 1996).
Then, the frequent closed itemsets (FCIs) framework
was defined to improve the efficiency of the mining in
case of non-sparse data (Pasquier et al., 1999; Zaki,
2000). The frequent closed itemsets, defined using the
Galois closure (Ganter and Wille, 1999), are a sub-
order of the subset lattice. This framework was later
used to define minimal covers, or bases, of associa-
tion rules (Bastide et al., 2000; Pasquier et al., 2005;
Zaki, 2004). This approach relies on the property that
the frequent closed itemsets with supports constitute a
non-redundant minimal representation of the frequent
itemsets and their supports. It was experimentally
shown that the set of frequent closed itemsets is on
average much smaller for real-life datasets, thus mak-
ing this process faster than directly mining frequent
itemsets. Association rules, or association rule bases,
are then directly generated from the frequent closed
itemsets. See (Ceglar and Roddick, 2006) for a com-
prehensive survey on association rule mining.
The FIST approach aims at providing the user
with a minimal set of knowledge patterns represent-
ing relationships between data values in the dataset,
without information loss. For this task, two types of
patterns are generated: informative bases for associa-
tion rules and hierarchical conceptual clusters. These
compact sets of patterns can then be searched for
specific information such as intra- and inter-species
protein interactions, or relationships between protein
interactions and features (biological annotations and
characteristics, publications, etc.).
Extracted patterns depict relationships between
proteins, which are viral or host proteins, or both.
Let V = {v
1
,...,v
N
} be the set of viral proteins and
H = {h
1
,...,h
M
} the set of human host proteins. We
consider three possible kinds of patterns:
• r
1
: v
1
,v
2
,...,v
n
⇐⇒ h
1
,h
2
,...,h
m
where v
i
∈ V,
h
j
∈ H;
• r
2
: v
1
,v
2
,...,v
n
=⇒ v
n+1
,v
n+2
,...,v
n+ p
where
{v
1
,v
2
,...,v
n
} ∩ {v
n+1
,v
n+2
,...,v
n+ p
} =
/
0 and
v
i
∈ V;
• r
3
: h
1
,h
2
,...,h
m
=⇒ h
m+1
,h
m+2
,...,h
m+q
where
{h
1
,h
2
,...,h
m
}∩{h
m+1
,h
m+2
,...,h
m+q
} =
/
0 and
h
j
∈ H.
Type r
1
relationships capture interactions between
some viral proteins and some host proteins (inter-
species PPI). Identifying such rules is similar to the
problem of bi-clustering, that is, in the context of
FIST, finding frequent closed itemsets with related
object identifiers. Type r
2
and r
3
relationships are as-
sociation rule patterns showing implications among
viral proteins and host proteins respectively (intra-
species PPI). Classification methods usually need
both positive and negative examples of the predicted
class, e.g., interacting and non-interacting protein
pairs, in order to achieve an optimal supervised clas-
sification. However,in the case of HIV-1-Human PPI,
information on non-interacting pairs of proteins is not
PREDICTION OF PROTEIN INTERACTIONS ON HIV-1-HUMAN PPI DATA USING A NOVEL CLOSURE-BASED
INTEGRATED APPROACH
165

available (Fu et al., 2009; Ptak et al., 2008). Hence,
descriptive methods, such as unsupervised classifica-
tion (clustering) and association rule extraction, seem
better suited to this PPI problem.
FIST was designed both to extract in one process
different kinds of knowledge patterns, bi-clusters and
association rules, and to extract additional informa-
tion for each of these patterns compared to classi-
cal approaches. It can process discrete numerical,
boolean, textualand nominal data. As for the majority
of similar methods, in the case of continuous numeri-
cal data, a discretization method has to be applied be-
fore processing the data with FIST. This is for exam-
ple the case for numerical gene expression data where
numerical values must be discretized to identify “up-
regulated”, “unchanged” and “down-regulated” genes
(rows) for each experimental biological conditions
(columns). See (Yang et al., 2010) for a recent discus-
sion on discretization methods used in data mining.
Consider the example dataset D
1
in Table 1 where
H
1
to H
6
are human proteins, V
1
to V
5
are viral
proteins and Annot columns represent annotations of
human proteins extracted from biological knowledge
bases (Gene Ontology, KEGG, etc.) and publication
bases (Pubmed, Reactome pathways, etc.). These an-
notations, represented as nominal data, describe bio-
logical knowledge on human proteins such as biolog-
ical functions or characteristics (F
n
) or bibliographic
citation references (B
m
). A “1” in column V
i
for row
H
j
means that there is a positive (i.e., experimen-
tally verified) interaction between H
j
and V
i
, while
“-” means that no interaction has been reported. For
example, we can state that there is a positive interac-
tion between human protein H
1
and viral proteins V
1
,
V
3
and V
4
, while no interaction between H
1
, V
2
and
V
5
has been reported. Besides, we can also state that
H
1
is annotated by biological annotations F
1
and F
2
and referenced by bibliographical annotation B
1
.
Table 1: Example dataset D
1
.
OID V
1
V
2
V
3
V
4
V
5
Annot Annot Annot
H
1
1 - 1 1 - F
1
F
2
B
1
H
2
1 - 1 - - F
2
B
1
B
2
H
3
- - 1 - 1 B
3
- -
H
4
1 - 1 1 - F
2
F
3
B
1
H
5
- 1 - - - F
4
- -
H
6
1 - 1 1 1 F
2
B
1
B
3
Conceptual bi-clusters extracted by FIST form a
hierarchical structure and both HIV and Human pro-
teins can participate to several bi-clusters according
to their co-occurrences in the data. In the context
of HIV-1-Human PPI, each conceptual cluster asso-
ciates a list of HIV proteins and a list of Human pro-
teins that interact. FIST bi-clusters also associate to
each bi-cluster the minimal set of common properties,
called generators, required to construct it (Hamrouni
et al., 2006; Pasquier et al., 1999). Moreover, un-
like most clustering methods, conceptual clustering
does not need to define the number of clusters before
the process as data are grouped according to their co-
occurrences in the dataset. The Hasse diagram of the
lattice structure of the four bi-clusters extracted from
D
1
for minsupport = 2/6 is shown in Figure 1. The
top bi-cluster in this figure is irrelevant from the view-
point of informativenessand is not generated by FIST;
it is represented here for completeness of the lattice.
Examining the rightmost bi-cluster, we can see in this
lattice that human proteins H
3
and H
6
both interact
with viral proteins V
3
and V
5
and are cited in biblio-
graphical reference B
3
. The leftmost bi-clusters show
that human proteins H
1
, H
2
, H
4
, and H
6
all interact
with viral proteins V
1
and V
3
, are all annotated with
F
2
, and are cited in bibliographical reference B
1
and
that human proteins H
1
, H
4
, and H
6
all interact with
viral proteins V
1
, V
3
, and V
4
, are all annotated with
F
2
, and are cited in bibliographical reference B
1
. We
can also see that the viral protein that interacts with
the greatest number of human proteins is V
3
, which
interacts with H
1
, H
2
, H
3
, H
4
, and H
6
, and that this
interaction is the only property common to these five
human proteins. It should be noted that for this min-
support value, there are 4 frequent closed itemsets,
whereas there are 37 frequent itemsets for dataset D
1
.
These frequent closed itemsets are represented in the
left element of the bi-clusters.
Figure 1: Hierarchical bi-clusters for minsupport = 2/6.
Association rules are implication rules of the
form: {r: antecedent =⇒ consequent, support(r),
confidence(r)} where antecedent and consequent are
sets of data values, support(r) is the number of ob-
jects (rows of the dataset) supporting the rule and
confidence(r) is the proportion of rows verifying the
rule in the dataset. FIST aims at improving the pro-
cess compared to frequent itemsets based approaches.
BIOINFORMATICS 2012 - International Conference on Bioinformatics Models, Methods and Algorithms
166

First, the number of extracted rules can be reduced
by a significant proportion as redundant rules can
represent the majority of extracted rules (Bastide
et al., 2000; Zaki, 2000). Association rules ex-
tracted by FIST are constructed using generators, as
antecedents, and frequent closed itemsets, as conse-
quents. These rules, also called min-max association
rules, constitute the informative base of association
rules (Pasquier et al., 2005). FIST extracts rules in
two distinct sets: exact association rules that have
confidence = 1, i.e., with no counter example in the
dataset, and approximate association rules, having
confidence < 1. It also extends the association rules
by adding information to each rule: The list of objects
(rows) supporting each one is also generated, allow-
ing the user to see which objects verify this rule in the
dataset as shown in Table 2. We can see that for min-
support = 2/6 and minconfidence = 2/6, 6 exact and
6 approximate min-max association rules are gener-
ated by FIST from dataset D
1
whereas 192 association
rules (117 exact and 75 approximate) are generated by
classical Apriori-like approaches.
Table 2: Minimal non-redundant association rules.
Association rule supp conf Objects
B
1
=⇒ V
1
, V
3
, F
2
4 1 H
1
, H
2
, H
4
, H
6
F
2
=⇒ V
1
, V
3
, B
1
4 1 H
1
, H
2
, H
4
, H
6
V
1
=⇒ V
3
, F
2
, B
1
4 1 H
1
, H
2
, H
4
, H
6
V
4
=⇒ V
1
, V
3
, F
2
, B
1
3 1 H
1
, H
4
, H
6
B
3
=⇒ V
3
, V
5
2 1 H
3
, H
6
V
5
=⇒ V
3
, B
3
2 1 H
3
, H
6
V
3
=⇒ V
1
, F
2
, B
1
4 0.80 H
1
, H
2
, H
4
, H
6
B
1
=⇒ V
1
, V
3
, V
4
, F
2
3 0.75 H
1
, H
4
, H
6
F
2
=⇒ V
1
, V
3
, V
4
, B
1
3 0.75 H
1
, H
4
, H
6
V
1
=⇒ V
3
, V
4
, F
2
, B
1
3 0.75 H
1
, H
4
, H
6
V
3
=⇒ V
1
, V
4
, F
2
, B
1
3 0.60 H
1
, H
4
, H
6
V
3
=⇒ V
5
, B
3
2 0.40 H
3
, H
6
3 FIST ALGORITHM
The FIST (Frequent Itemset mining using Suffix-
Trees) algorithm is a three-phase process: (1) pre-
processing the dataset, (2) extracting frequent closed
itemsets, (3) finding bases for association rules and
hierarchical conceptual bi-clusters. Its general flow
is shown in Algorithm 1. Its input is a dataset rep-
resented as a data matrix in which rows are called
objects and columns are called attributes. Each dis-
tinct value of an attribute constitutes an item. FIST
performs one scan of the input dataset to generate a
compressed database that is scanned once for gener-
ating frequent closed itemsets, generators, bases for
association rules, and conceptual bi-clusters.
Algorithm 1: FIST algorithm.
Input: Dataset, minsupport value, minconfidence value
Output: Frequent closed itemsets, generators, conceptual
clusters, association rules
/* Phase 1: Preparing the database */
1: Generate Item Table
2: Generate Sorted Frequent Database
/* Phase 2: Mining frequent closed itemsets */
3: Create frequent Generalized Itemset Suffix-Tree
4: Find frequent closed itemsets
/* Phase 3: Generating knowledge patterns */
5: Find generators of each frequent closed itemsets
6: Find conceptual bi-clusters
7: Generate basis of exact association rules
8: Generate basis of approximate association rules
3.1 Phase 1: Preparing the Database
The first phase of FIST consists in the preparation of
the Item Table (IT) and the Sorted Frequent Database
(SFD) data structures used in the following phases of
the algorithm. These data structures are stored in sec-
ondary memory for re-use. In the SFD database, each
row is the list of items, each one representing an at-
tribute value, contained in the corresponding row of
the original dataset. An example source dataset D
2
containing 5 attributes and 5 objects is given in Ta-
ble 3. This preprocessing phase, which aims at op-
timizing the efficiency of the extraction and data ac-
cesses, is performed in two steps.
Table 3: Example dataset D
2
.
OID C
1
C
2
C
3
A A
O
1
- v
2
- v
5
-
O
2
v
1
v
2
v
3
v
5
-
O
3
v
1
- v
3
v
4
-
O
4
- v
2
v
3
v
5
-
O
5
v
1
v
2
v
3
v
5
v
6
The first step consists in constructing the IT ta-
ble by mapping attribute values in the dataset, which
can be booleans, numerics, nominals or textuals, to
items represented as discrete numbers. This data rep-
resentation aims at optimizing the memory space re-
quired for data storage and the efficiency of compar-
ison operations. This operation, which is performed
only once and requires only one read of the dataset,
can be omitted if the dataset contains uniquely dis-
crete numbers. To create this table, a unique number
is created for each pair {attribute, value} usinga map-
ping function. During this operation, the support of
each item in the dataset, corresponding to its number
of occurrences, is counted. Then, using the minimum
support threshold value minsupport provided by the
user, the infrequent items, i.e., those with support less
than the minsupport value, are discarded. Finally, the
PREDICTION OF PROTEIN INTERACTIONS ON HIV-1-HUMAN PPI DATA USING A NOVEL CLOSURE-BASED
INTEGRATED APPROACH
167

remaining frequent items are sorted in ascending or-
der of their supports to optimize the size of the data
structure used in the second phase of the algorithm.
During the second step, the SFD database is cre-
ated to reflect the occurrences of frequent items in
rows of the original dataset. Rows of the original
dataset containing only infrequent items are not rep-
resented in the SFD database. The example SFD
database and the corresponding IT table for dataset
D and minsupport = 2/5 are given in Figure 2. In this
example, data values A = v
4
and A = v
6
with support
1/5 are infrequent and, given their support values, fre-
quent items are ordered as: {C
1
= v
1
, C
2
= v
2
, A = v
5
,
C
3
= v
3
}. Notice that these frequent items are ordered
first on the support and then in order of appearance in
the rows of the dataset. For example, C
1
= v
1
is in the
first position in the IT table because it has a lower sup-
port (3), while A = v
5
appears before C
3
= v
3
because
it is the second in order of appearence while C
3
= v
3
appears in the fifth place.
(A) IT TABLE
Data Support Item
C
1
= v
1
3 1
C
2
= v
2
4 2
A = v
5
4 3
C
3
= v
3
4 4
(B) SFD DATABASE
Items
2 3
1 2 3 4
1 4
2 3 4
1 2 3 4
Figure 2: IT table and SFD database for minsupport=2/5.
3.2 Phase 2: Mining FCIs
During the second phase, which is the core of the
FIST algorithm, the frequent closed itemsets are
mined from the SFD database. This phase is carried
out in two steps. The first step is the generation of
the frequent Generalized Itemset Suffix-Tree (fGIST),
which is a main memory data structure specific to the
FIST algorithm. In the fGIST tree, each internal node
represents an item, each branch from the root to a leaf
represents an itemset, and each leaf node represents
the list of numbers of objects (rows) containing this
itemset. The second step is the extraction of the fre-
quent closed itemsets from the fGIST tree. This ex-
traction is based on inclusion and intersection opera-
tions performed on the branches and the sub-branches
of the fGIST tree.
Creating fGIST Tree. To create the fGIST data
structure, each row of the SFD database is accessed
once from the first to the last. Each row read is rep-
resented as a vector of items associated with the iden-
tifier number of the row in the SFD database. Since
items were ordered in ascending order of their sup-
ports during the construction of the SFD database,
they are also sorted in this order in the vector. This
vector is then inserted into the fGIST tree as a branch,
starting from the root, with a leaf containing the iden-
tifier number of the row. If this vector of items is al-
ready represented as a branch in the tree, that is if an
identical row was read before, then only the leaf is
updated by adding the identifier number of the row.
Then, this process is repeated for all suffixes of the
vector of items that are sub-vectors obtained by delet-
ing successively one item from the first to the last.
In our example, the first branch to be inserted is {2,
3}, then the branch corresponding to its unique suffix
{3}. The third branch to be inserted into the tree is
{1, 2, 3, 4}, and then the ones corresponding to its
suffixes {2, 3, 4}, {3, 4}, and {4}, and so on. The
fGIST tree for database SFD is given in Figure 3.
The insertion of a vector of items in the fGIST tree
is a recursive procedure starting from the root node.
Each item of the vector is processed sequentially from
first to last. For each item, we test if there is a sub-
node of the current node representing this item. If this
is the case, then we go to this node and repeat the pro-
cess for the next item of the vector. Otherwise, a new
sub-node is created to represent this item as a child
of the current node. When the last item of the vector
was processed, we test if there is a leaf sub-node of
the current node. If this is the case, the row number
corresponding to the vector processed is added to the
list of row numbers in this leaf. Otherwise, a new leaf
sub-node is created with a list of row numbers initial-
ized with the row number corresponding to the vector.
Figure 3: Frequent Generalized Itemset Suffix-Tree.
During this process, the whole SFD database is
accessed only once. At the end of the process, the
fGIST tree contains a condensed representation of the
frequent itemsets in the dataset. This data structure is
optimized for the following phases of the process as
the most frequent itemsets resulting of intersections
of dataset rows, which are in majority closed itemsets,
are represented as branches. This property is ensured
BIOINFORMATICS 2012 - International Conference on Bioinformatics Models, Methods and Algorithms
168

by the fact that items are ordered in ascending order
of their supports.
Creating FCI Table. The second step consists in
extracting the FCIs, with the list of objects containing
each of them, from the fGIST tree. Each entry in the
FCI table contains two elements: A list of items and
the list of numbers of objects containing that itemset
in the database.
First, each branch of the fGIST tree from the root
to a leaf is traversed and a new entry in the FCI table
is created for the itemset correspondingto that branch.
The associated list of numbers of objects is initialized
using the leaf node of that branch. The size of this
object list corresponds to the support of the itemset in
the database.
Then, the non-closed itemsets in the FCI table are
identified using associated object lists as follows. If
an itemset is included in another itemset and both
have identical object lists, then the included itemset
is not closed and is deleted from the table.
Finally, the frequent closed itemsets not already
found are identified by performing intersections be-
tween two closed itemsets in the FCI table and ver-
ifying if the resulting itemset is not infrequent or al-
ready present in the table. If this is not the case, that
itemset is a new FCI and it is inserted into the table.
The associated object list is the result of the union of
the object lists of the two intersected itemsets. If at
least one new frequent closed itemset is generated in
such a way, then the process is repeated for the new
generated itemsets. This iterative process ends when
no new frequent closed itemset is generated. At the
end, the FCI table contains all frequent closed item-
sets with associated list of objects containing each of
them as shown in Table 4.
Table 4: FCI Table for SFD database.
Itemset Object list
{4} {2, 3, 4, 5}
{1, 4} {2, 3, 4}
{2, 3} {1, 2, 4, 5}
{2, 3, 4} {2, 4, 5}
{1, 2, 3, 4} {2, 4}
3.3 Phase 3: Generating Patterns
During the third phase, the conceptual bi-clusters, the
generators of frequent closed itemsets and the associ-
ation rules are extracted from the FCI table. The asso-
ciation rules are generated in two distinct sets: a min-
imal cover for exact association rules and a minimal
cover for approximate association rules. These mini-
mal covers, or bases, contain, respectively, the non-
redundant exact and approximate association rules
with minimal antecedent (predictor itemset) and max-
imal consequent (predicted items) (Pasquier et al.,
2005). Minimality is defined here according to the
inclusion relation. The pseudo-code of the extraction
of these knowledge patterns is given in Algorithm 2.
First, rows in the FCI table are sorted in increas-
ing order of itemset sizes (step 1) and output sets BIC,
GEN, and AR are initialized with the empty set (step
2). Then, each entry FCI[i] in the FCI table is pro-
cessed successively (steps 3 to 25) for creating hi-
erarchical bi-clusters (step 4) and identifying gener-
ators and association rules (steps 6 to 24) as follows.
All subsets S of itemset FCI[i].Itemset are generated,
sorted in increasing order of their sizes (steps 7 and
8) and processed one by one (steps 10 to 22). For
instance, for itemset {2, 3, 4}, the generated sub-
sets are {2}, {3}, {4}, {2, 3}, {2, 4} and {3, 4}.
The algorithm first determines if S is a generator of
FCI[i].Itemset (steps 11 to 13). Then, all association
rules with S as antecedent are generated if their con-
fidence is greater than or equal to the minconfidence
threshold (steps 14 to 21). Considering itemset {2, 3,
4}, generators {2, 4} and {3, 4} are identified, as they
are the only minimal itemsets contained in exactly the
same objects as {2, 3, 4}. From these itemsets, rules
{2, 4}=⇒{3} and {3, 4}=⇒{2} are generated. Fi-
nally, knowledge patterns in the BIC, GEN, and AR
sets are mapped to data values using the Item Table,
and object numbers are mapped to object identifiers
(e.g., gene or protein names) if the source dataset con-
tained such information, in order to simplify their in-
terpretation by the end-user (step 26).
4 EXPERIMENTAL RESULTS
The FIST algorithm was implemented in Java for
portability. Experiments were conducted on a PC
with an Intel Core 2 Duo T5670 processor at 1.80
GHz and 4 GB of RAM, running under the 32
bits Windows 7 Professional Edition operating
system. The PPI dataset used for performance
experiments was constructed from the HIV-1-Human
Protein Protein Interaction Database of the NI-
AID (Fu et al., 2009; Ptak et al., 2008) available at
http://www.ncbi.nlm.nih.gov/RefSeq/HIVInteractions/.
This dataset is a matrix of 19 columns corresponding
to the different HIV-1 proteins and 1433 rows cor-
responding to the human proteins. Each cell of the
matrix contains a 1 if there is a positive interaction
between the corresponding pair of proteins and a
question mark if no interaction is reported. To assess
the scalability of FIST when the number of columns
increases, a second dataset was constructed
PREDICTION OF PROTEIN INTERACTIONS ON HIV-1-HUMAN PPI DATA USING A NOVEL CLOSURE-BASED
INTEGRATED APPROACH
169
Algorithm 2: Generating knowledge patterns.
Input: FCI table, minconfidence value, IT table
Output: Bi-clusters (BIC), generators (GEN), association
rules (AR)
1: sort FCI in increasing size of itemsets
2: GEN, BIC, AR ←
/
0
3: for all row FCI[i] in FCI do
4: BIC ← {FCI[i].Itemset, FCI[i].Object list}
5: M ← FCI[i].Itemset.size()
6: if (M ≥ 2) then
7: SUB ← list of subsets of FCI[i].Itemset
8: sort SUB in increasing size of subsets
9: K ← SUB.size()
10: for all subset S in SUB do
11: if (S /∈ GEN) and (S /∈ FCI.Itemset) then
12: GEN[i] ← S
13: end if
14: for j = 1 to K do
15: if (S.size() + SUB[j].size() = M) and
(S 6= SUB[j]) then
16: create rule R : {S =⇒ SUB[j]}
17: if (confidence(R) ≥ minconfidence) and
(R /∈ AR) then
18: AR ← {R, support(R), confidence(R),
FCI[i].Object list}
19: end if
20: end if
21: end for
22: end for
23: SUB ←
/
0
24: end if
25: end for
26: map patterns in BIC, GEN, AR to dataset values in IT
by integrating biological and bibliographical annota-
tions of human proteins with these interaction data.
These two datasets can be downloaded at http://
keia.i3s.unice.fr/.
4.1 Algorithmic Performance
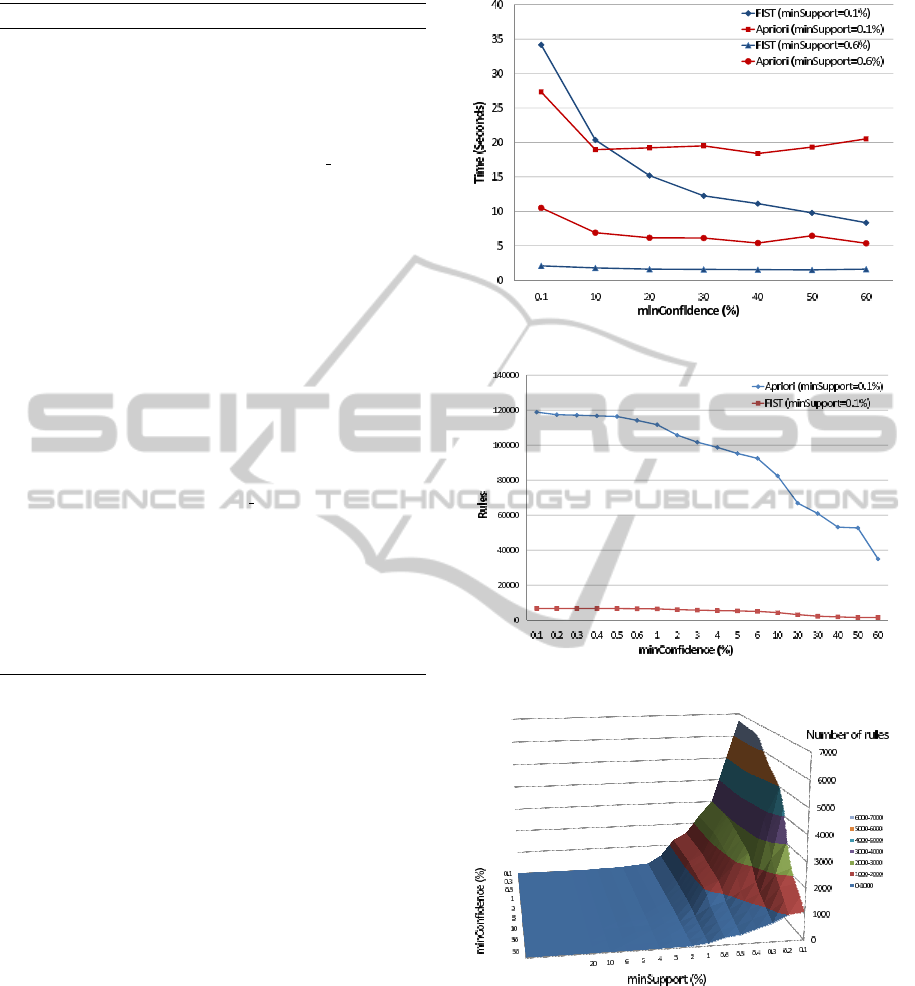
Figure 4 compares the execution times of FIST (blue
curves) and the Java implementation of Apriori (red
curves) in WEKA (Hall et al., 2009). Two minsup-
port values (0.1% and 0.6 %), were used and min-
confidence was varied between 0.1% and 60%. We
can see that except for minsupport=0.1% and min-
confidence=0.1%, execution times of FIST are always
smaller than those of Apriori. It should be noted that
FIST generates more information than Apriori: bi-
clusters and object lists supporting each association
rule are also generated by FIST, bringing to the end-
user more information on extracted relationship pat-
terns. With object lists supporting each association
rule, the end-user can see precisely the list of objects
(human proteins) concerned by the rule.
The number of association rules generated by
Apriori and FIST is shown in Figure 5. We can see
Figure 4: Execution times.
Figure 5: Number of association rules.
Figure 6: Number of minimal non-redundant rules.
that FIST reduces this number by a factor up to sev-
eral tens, allowing the end-user to concentrate on the
most relevant rules. In Figure 6, the number of asso-
ciation rules generated by FIST for different minsup-
port and minconfidence values is shown. The number
of bi-clusters extracted by FIST for minsupport values
ranging from 0.1% to 50% is shown in Table 5.
BIOINFORMATICS 2012 - International Conference on Bioinformatics Models, Methods and Algorithms
170

Table 5: Number of bi-clusters extracted by FIST.
minsupport (%) 0.1 0.5 1 5 10 20 30 40 50
Bi-clusters 342 187 104 22 7 2 2 1 1
4.2 Scalability
To assess the scalability of FIST when the number
of attributes increases, a second dataset integrating
biological annotations and related publications
for human proteins was constructed. GO bi-
ological annotations of human proteins from
the UniProtKB-GOA (GO Annotation@EBI)
database were collected from the Gene Ontol-
ogy web site at http://www.geneontology.org/
GO.downloads.annotations.shtml and GO annota-
tions with evidence code TAS, i.e., annotations man-
ually validated by biologists and cited in a published
biological reference that are the most reliable biolog-
ical annotations, were integrated in the data. Pub-
lication annotations were collected from the NCBI
web site at http://www.ncbi.nlm.nih.gov/sites/entrez
and Pubmed and Reactome publications related to
the GO biological annotations of human proteins
were also integrated in the dataset as new attributes
(columns). This dataset contains overall 1149 dis-
tinct GO annotations and 2670 distinct publication
annotations, and up to 40 GO annotations and 88
publication annotations for each protein. We were
unable to run Apriori on this dataset, even for
minsupport and minconfidence values as high as 90%
and with a maximum java heap size parameter set to
its maximal value, that is 1.5 GB, due to the memory
consumption of the approach that requires to identify
all frequent itemsets and not only frequent closed
itemsets. Execution times of the execution of FIST
on this second dataset for minsupport values 10%,
1% and 0.6% and for minconfidence varying between
0.1% and 60% are depicted in Figure 7. We can see
that even for this very large dataset, execution times
remain reasonable for all threshold values, ranging
from a few seconds to a few minutes. We can also
see slight execution time variations for different
minconfidence values due to other running operating
system processes.
4.3 Discussion
It is interesting to compare our results to the results
obtained by Tastan et al. (Tastan et al., 2009), which
are the most comprehensive HIV-Human PPI results
available to date. We focus on the results gener-
ated by FIST for minsupport = 0.1% and minconfi-
dence = 0.1%, which are the lowest threshold values
tested and thus contain maximal information.
Figure 7: Execution times for integrated dataset.
For each protein pair interaction predicted in (Tas-
tan et al., 2009), we counted the number of FCIs (and
association rules) generated by FIST covering it. Of
the 3372 interactions predicted in (Tastan et al., 2009)
by a random forest classifier, 895 are covered by at
least one FCI generated by FIST. This is 26.5% of
their predicted pairs.
Now, the random forest classifier is reported to
achieve a mean average precision (MAP) of 0.23 on
this problem, meaning that around 23% of the pre-
dicted interacting pairs should be expected to be true
positives. This is just a little below the percentage of
predicted pairs that are “confirmed” by FIST. Since
the random forest classifier has little in common with
FIST, we believe the two techniques should be re-
garded as complementary to one another. By the same
argument, there are good chances that the interacting
pairs predicted by (Tastan et al., 2009) and confirmed
by FIST are indeed true interactions.
In general, it appears that proteins pairs predicted
by the random forest classifier with a high score are
mostly confirmed by a large number of FCIs, al-
though exceptionsexist, like the novel high-score pre-
dicted pair henv gp120,CALM1i, which is not cov-
ered by any FCI, indicating perhaps that it is a false
positive. Likewise, most low-score predictions are
not confirmed by FIST with some exceptions, like
henv gp120,EP300i which, however, were known to
be indirectly interacting (the human gene is reported
in the siRNA screen in (Konig et al., 2008)). All in all,
exceedingly few (28) of the 2100 novel predictions by
(Tastan et al., 2009), or 1.3%, are confirmed by FIST.
An exhaustive list thereof is given in Table 6, along
with the number of covering FCIs, approximate, and
exact rules. For rules, two separate counts are pro-
vided for rules that have the viral protein in the an-
tecedent (IF part) and in the consequent (THEN part).
On the other hand, FIST finds 451 protein pairs
that are covered by at least one FCI among those not
PREDICTION OF PROTEIN INTERACTIONS ON HIV-1-HUMAN PPI DATA USING A NOVEL CLOSURE-BASED
INTEGRATED APPROACH
171

Table 6: New predicted interacting pairs confirmed by FIST.
HIV-1 Human #FCI #approx rules #exact rules
IF THEN IF THEN
ENV GP160 APOBEC3G 1 0 0 0 0
REV CXCR4 4 5 5 0 0
ENV GP120 FURIN 1 0 0 0 0
VPR MAPK3 34 186 197 7 0
ENV GP120 PAK1 1 0 0 0 0
TAT PAK2 2 1 1 0 0
NEF PIK3R2 8 19 19 0 0
TAT PPARG 1 0 0 0 0
NEF PRKCD 34 275 300 17 5
NEF PRKCG 34 275 300 17 5
NEF PRKCZ 18 77 83 4 0
TAT RAF1 3 2 2 0 0
VPR RAF1 3 2 2 0 0
ENV GP120 RAN 2 1 1 0 0
TAT RPA2 4 5 5 0 0
TAT SDCBP 2 1 1 0 0
GAG PR55 SHC1 1 0 0 0 0
ENV GP120 SLC3A2 1 0 0 0 0
TAT SREBF2 2 1 1 0 0
NEF STAT5A 4 5 5 0 0
NEF SUMO1 1 0 0 0 0
TAT TCEB1 1 0 0 0 0
ENV GP120 TUBB1 1 0 0 0 0
ENV GP120 UBB 2 1 1 0 0
NEF UBB 2 1 1 0 0
TAT UBE2I 1 0 0 0 0
TAT WT1 1 0 0 0 0
REV XRCC5 3 2 2 0 0
included in (Tastan et al., 2009), i.e., for which no
explicit indication of possible interaction was pointed
out. This is 2.2% of the pairs not included in (Tastan
et al., 2009).
The most covered of these protein pairs is
hNEF,IFNGi, covered by 70 FCIs. The NEF protein
occurs in the antecedent of 755 approximate rules, in
the consequent of 779 approximate rules, in the an-
tecedent of 28 exact rules and in the consequent of
30 exact rules. Lagging far behind this pair, we find
the four pairs hTAT, ACTG1i, covered by 45 FCIs.
hNEF,IL6i, covered by 45 FCIs, hTAT,IL2i, cov-
ered by 44 FCIs, and hTAT,IL6i, covered by 44 FCIs.
There are a number of other pairs covered by 35 or
fewer FCIs.
The hNEF,IFNGi pair, to begin by the most cov-
ered novel suggestion, although not previously sig-
naled, looks like a promising candidate for further in-
vestigation: NEF is the viral negative regulatory fac-
tor, associated with the early stages of HIV infection,
and the IFNG gene encodes for the interferon-γ pro-
tein, an important immune response stimulator and
modulator; the suggestion of some kind of relation-
ships between these two proteins may be corroborated
by recent research on HIV vaccines (Gahery et al.,
2007).
The same negative regulatory factor is involved
in the hNEF, IL6i pair: IL6 is the gene encoding for
interleukin-6, a pro-inflammatory cytokine secreted
by T-cells and macrophages to stimulate immune re-
sponse. Indeed, the interaction between NEF and
interleukin-6 has been recognized quite early in the
study of AIDS (Chirmule et al., 1994).
Other two novel pairs suggested by FIST, namely
hTAT,IL2i and hTAT,IL6i, involve interleukins. IL2
is the gene of interleukin-2, a signaling molecule nor-
mally produced during an immune response: an anti-
gen binding to a T-cell receptor stimulates the se-
cretion of interleukin-2, which in turn stimulates the
growth of antigen-selected cytotoxic T-cells. TAT,
for trans-activator of transcription, is a key protein of
HIV-1, the first to be transcribed, causing the sub-
sequent massive increase in the transcription levels
of the HIV dsRNA. Both interactions are mentioned
in the literature: the interaction between TAT and
interleukin-6 in (Scala, 1994) and the one between
TAT and interleukin-2 in (Westendorp et al., 1994).
As for pair hTAT,ACTG1i suggested by FIST, we
are not aware of any work in the literature mention-
ing it. However, the suggestion does not look com-
pletely implausible, for TAT functions also as a cell-
penetrating peptide that acts as a toxine, causing the
apoptosis of uninfected T-cells, and the γ-actin 1, en-
coded for by gene ACTG1, is a component of the cy-
toskeleton of T-cells.
5 CONCLUSIONS
We presented the new FIST algorithm for mining as-
sociation rules and conceptual bi-clusters that is based
on the concept of closure. The main advantages of
FIST are that it generates:
• A minimal non-redundant cover for association
rules, from which all rules generated by Apriori
can be deduced if required, that is much smaller;
• For each association rule, the list of objects (rows)
supporting the rule instead of the support of the
rule (number of these rows) only;
• The bi-clusters, which are concepts (intension and
extension) and form a dual lattice structure de-
fined by inclusion relation;
• For each frequent closed itemset, the generators,
which are the minimal sets of properties required
to construct the closed itemset.
The method was validated by applying it for pre-
dicting HIV-1-Human protein interactions. Besides
proving faster than Apriori-like mining methods, the
results obtained by FIST confirm and improvethe pre-
BIOINFORMATICS 2012 - International Conference on Bioinformatics Models, Methods and Algorithms
172

dictions by existing methods, and suggest new possi-
ble interactions to be further investigated.
In the future, we plan to apply the FIST method
to data integrating additional information about pro-
teins, like structural and sequential similarities, with
protein-protein interactions to improve the results. In-
deed, the integration of different kinds of biologi-
cal information is an essential consideration to fully
understand the underlying biological processes (Bell
et al., 2011).
REFERENCES
Agrawal, R., Mannila, H., Srikant, R., Toivonen, H., and
Verkamo, A. I. (1996). Fast discovery of association
rules. In Advances in Knowledge Discovery and Data
Mining, pages 307–328. AAAI/MIT Press.
Arkin, M. R. and Wells, J. A. (2004). Small-molecule in-
hibitors of protein-protein interactions: Progressing
towards the dream. Nat. Rev. Drug Discov., 3:301–
317.
Bastide, Y., Pasquier, N., Taouil, R., Stumme, G., and
Lakhal, L. (2000). Mining minimal non-redundant as-
sociation rules using frequent closed itemsets. InProc.
CL, pages 972–986.
Bell, L., Chowdhary, R., Liu, J. S., Niu, X., and Zhang, J.
(2011). Integrated bio-entity network: A system for
biological knowledge discovery. PLoS ONE, 6.
Ben-Hur, A. and Noble, W. S. (2005). Kernel methods for
predicting protein-protein interactions. Bioinformat-
ics, 21(1):38–46.
Ceglar, A. and Roddick, J. (2006). Association mining.
ACM Comput. Surv., 2(38).
Chirmule, N., Oyaizu, N., Saxinger, C., and Pahwa, S.
(1994). Nef protein of hiv-1 has b-cell stimulatory
activity. AIDS, 6(8):733–4.
Fu, W., Sanders-Beer, B. E., Katz, K. S., Maglott, D. R.,
Pruitt, K. D., and Ptak, R. G. (2009). Human im-
munodeficiency virus type 1, human protein interac-
tion database at ncbi. Nucl. Acids Res., 37:417–422.
Gahery, H., Figueiredo, S., Texier, C., and et al. (2007).
Hla-dr-restricted peptides identified in the nef pro-
tein can induce hiv type 1-specific il-2/ifn-gamma-
secreting cd4+ and cd4+ /cd8+ t cells in humans after
lipopeptide vaccination. AIDS Res. and Hum. Retro-
viruses, 3(23):427–37.
Ganter, B. and Wille, R. (1999). Formal Concept Analysis:
Mathematical foundations. Springer.
Hall, M., Frank, E., Holmes, G., Pfahringer, B., Reutemann,
P., and Witten, I. H. (2009). The WEKA data mining
software: An update. SIGKDD Expl., 1(11).
Hamrouni, T., Yahia, S. B., and Nguifo, E. M. (2006). Suc-
cinct system of minimal generators: A thorough study,
limitations and new definitions. In Proc. CLA, pages
80–95.
Jansen, R., H. Yu, D. G., Kluger, Y., Krogan, N. J., Chung,
S., Emili, A., Snyder, M., Greenblatt, J. F., and Ger-
stein, M. (2003). A bayesian networks approach for
predicting protein-protein interactions from genomic
data. Science, 302:449–453.
Konig, R., Zhou, Y., Elleder, D., and et al. (2008). Global
analysis of host-pathogen interactions that regulate
early-stage hiv-1 replication. Cell, 135:49–60.
Lin, N., Wu, B., Jansen, R., Gerstein, M., and Zhao, H.
(2004). Information assessment on predicting protein-
protein interactions. BMC Bioinformatics, 5(154).
Madeira, S. C. and Oliveira, A. L. (2004). Bicluster-
ing algorithms for biological data analysis: A survey.
IEEE/ACM Trans. Comput. Biol. Bioinform., 1:24–45.
Mukhopadhyay, A., Maulik, U., Bandyopadhyay, S., and
Eils, R. (2010). Mining association rules from hiv-
human protein interaction. In Proc. ICSMB, pages
344–348.
Pasquier, N., Bastide, Y., Taouil, R., and Lakhal, L. (1999).
Efficient mining of association rules using closed
itemset lattices. Inform. Systems, 1(24):25–46.
Pasquier, N., Taouil, R., Bastide, Y., Stumme, G., and
Lakhal, L. (2005). Generating a condensed repre-
sentation for association rules. J. Intell. Inf. Syst.,
1(24):29–60.
Ptak, R. G., Fu, W., Sanders-Beer, B. E., Dickerson, J. E.,
Pinney, J. W., Robertson, D. L., Rozanov, M. N., Katz,
K. S., Maglott, D. R., Pruitt, K. D., and Dieffenbach,
C. W. (2008). Cataloguing the hiv-1 human protein
interaction network. AIDS Res. and Hum. Retrov.,
4(12):1497–1502.
Qi, Y., Klein-Seetharaman, J., and Bar-Joseph, Z. (2007).
A mixture of feature experts approach for protein-
protein interaction prediction. BMC Bioinform., 8.
Scala, G. (1994). The expression of the interleukin 6 gene
is induced by the human immunodeficiency virus 1 tat
protein. J. Exp. Medicine, 3(179):961–971.
Tastan, O., Qi, Y., Carbonell, J., and Klein-Seetharaman, J.
(2009). Prediction of interactions between hiv-1 and
human proteins by information integration. In Proc.
PSB, pages 516–527.
Westendorp, M. O., Li-Weber, M., Frank, R. W., and Kram-
mer, P. H. (1994). Human immunodeficiency virus
type 1 tat upregulates interleukin-2 secretion in acti-
vated t cells. J. of Virology, 7(68):4177–4185.
Yamanishi, Y., Vert, J. P., and Kanehisa, M. (2004). Pro-
tein network inference from multiple genomic data: A
supervised approach. Bioinformatics, 20:363–370.
Yang, Y., Webb, G., and Wu, X. (2010). Discretization
methods. In Data Mining and Knowledge Discovery
Handbook, Part 1, pages 101–116.
Zaki, M. J. (2000). Generating non-redundant association
rules. In Proc. KDD, pages 34–43.
Zaki, M. J. (2004). Mining non-redundant association rules.
Data Min. Knowl. Disc., 9(23):223–248.
Zhang, L., Wong, S., King, O., and Roth, F. (2004). Pre-
dicting co-complexed protein pairs using genomic and
proteomic data integration. BMC Bioinform., 5(38).
PREDICTION OF PROTEIN INTERACTIONS ON HIV-1-HUMAN PPI DATA USING A NOVEL CLOSURE-BASED
INTEGRATED APPROACH
173
