EXTRACTION OF BLOOD DROPLET FLIGHT TRAJECTORIES

FROM VIDEOS FOR FORENSIC ANALYSIS

L. A. Zarrabeitia, D. A. Aruliah and F. Z. Qureshi

Faculty of Science, University of Ontario Institute of Technology, Oshawa, ON, Canada

Keywords:

Stereo reconstruction, Tracking, Droplets, Blood ﬂight, Multi-target tracking.

Abstract:

We present a method for extracting three-dimensional ﬂight trajectories of liquid droplets from video data.

A high-speed stereo camera pair records videos of experimental reconstructions of projectile impacts and

ensuing droplet scattering. After background removal and segmentation of individual droplets in each video

frame, we introduce a model-based matching technique to accumulate image paths for individual droplets. Our

motion detection algorithm is designed to deal gracefully with the lack of feature points, with the similarity of

droplets in shape, size, and color, and with incomplete droplet paths due to noise, occlusions, etc. The ﬁnal

reconstruction algorithm pairs two-dimensional paths accumulated from each of the two cameras’ videos to

reconstruct trajectories in three dimensions. The reconstructed droplet trajectories constitute a starting point

for a physically accurate model of blood droplet ﬂight for forensic bloodstain pattern analysis.

1 INTRODUCTION

Bloodstain pattern analysis (BPA) comprises tech-

niques for inferring spatial locations of bloodletting

events from bloodstains found at crime scenes (Bevel

and Gardner, 2008; Buck et al., 2011). At present,

BPA, to a large extent, is a qualitative sub-discipline

of forensic science. Our present goal is to im-

prove computational models for bloodletting events

and bloodstain pattern formation. These models, we

believe, will be of immense value to forensic inves-

tigators and BPA specialists for reasoning accurately

from images of bloodstain patterns at crime scenes.

Furthermore, such models are required to develop the

next generation of BPA software for inference and as-

sessing uncertainties in BPA.

Stringing (Buck et al., 2011) is a common method

for locating the bloodletting event responsible for a

particular bloodstain pattern. This method relies on

the assumption that blood droplets move in straight

lines, ignoring the effects of gravity and aerodynamic

drag. Stringing can provide reasonable approximate

locations projected onto a horizontal plane. At short

distances, stringing may also provide estimates for the

height of the bloodletting event. More accurate bal-

listic models that incorporate viscous drag forces and

gravity, are only used when the stringing method pro-

duces unreasonable locations or speeds (Buck et al.,

2011). Our results suggest that the effects of gravity

and drag are noticeable, even over the short distances

and time scales recorded in our experiments.

The present work is concerned with reconstruct-

ing 3D trajectories of blood droplets from high-speed

video data. We have developed a stereo vision sys-

tem capable of tracking individual blood droplets in

high-speed videos (1300 frames per second) and auto-

matically reconstructing their three-dimensional (3D)

ﬂight trajectories. In each experiment, the stereo cam-

era pair captures a high-speed video of the impact of a

BB pellet with a ballistic gel encasing transfer blood

(i.e., approximating human ﬂesh); this scenario is in-

tended to simulate a penetrating trauma (e.g., a gun-

shot wound). Upon impact, the ballistic gel is punc-

tured and expels its contents at high speeds. Blood

droplets then ﬂy through the air hitting nearby sur-

faces to create bloodstain patterns. Our video record-

ings of these simulated bloddletting events allow us

to study the effects of gravity and aerodynamic drag

on blood droplet trajectories (see Figure 1). We also

photograph the resulting bloodstain patterns.

Estimation of individual blood droplet trajectories

from recorded videos comprises three stages:

1. subtracting the background and connected-

component analysis to identify images of

individual blood droplets in each video frame;

2. tracking of individual blood droplets between

video frames to generate 2D droplet in each cam-

era’s view; and

3. estimating three-dimensional trajectories by link-

142

A. Zarrabeitia L., A. Aruliah D. and Z. Qureshi F. (2012).

EXTRACTION OF BLOOD DROPLET FLIGHT TRAJECTORIES FROM VIDEOS FOR FORENSIC ANALYSIS.

In Proceedings of the 1st International Conference on Pattern Recognition Applications and Methods, pages 142-153

DOI: 10.5220/0003770201420153

 SciTePress

(a) (b) (c)

Figure 1: (a) BB pellet impacting ballistic gel containing transfer blood. (b) Tracking individual blood droplets in high-speed

video (1300 frames per second). (c) Reconstructed blood droplet trajectories. Notice the effects of gravity and viscous drag

forces even for short trajectories.

ing image paths from each camera’s view.

We present a model-based approach to tackle this

challenging problem.

The long-term goal that motivates the present

study is to develop accurate physics-based models of

blood ﬂight to reconstruct impact conditions in blood-

stain pattern analysis. As a ﬁrst step, then, we record

and compare ﬂight patterns with models traditionally

used in this ﬁeld. Thus, we automate the extraction

and synthesis of 3D trajectories of individual droplets

from video recordings.

1.1 Related Work

While object-tracking has been studied extensively

within the computer vision community (see, e.g.,

(Yilmaz et al., 2006)), tracking ﬂight paths of liq-

uid droplets across a large number of frames of video

presents considerable challenges. In particular, track-

ing individual blood droplets involves identifying

hundreds of semi-transparent, quasi-deformable ob-

jects of very similar sizes and appearances. Tracking

can be formulated by establishing correspondences

between detected objects represented by points (or

targets) across frames. Point correspondence is a

complicated problem, especially in the presence of

occlusions, misdetections, and objects entering or

leaving the ﬁeld of view. The most obvious difﬁ-

culty in our problem arises from the similarity be-

tween blood droplets; tracking techniques based on

detection of feature points (such as in (Yilmaz et al.,

2006)) are not effective in this context. We apply

an approach similar to that followed in (Balch et al.,

2001) to detect individual blood droplets in each of

the video frames captured by each camera. The prob-

lem in this earlier work is similar to ours, albeit with

fewer targets and greater information in each frame.

A core requirement of tracking algorithms is solv-

ing assignment problems to match objects between

successive video frames. The Kuhn-Munkres Al-

gorithm (also known as the Hungarian algorithm

(Kuhn, 1955; Munkres, 1957)) was proposed in the

mid-1950s to solve linear assignment problems in

polynomial time. Bourgeois and Lassalle extended

the Kuhn-Muhnkres algorithm to handle rectangular

problems in 1971 (Bourgeois and Lassalle, 1971). A

more recent effort, in addressing the sailor assign-

ment problem, produced a variant of the rectangu-

lar method for sparse graphs and multiobjective prob-

lems (Dasgupta et al., 2008). For more recent surveys

of rectangular assignment problems in the context of

multiple target tracking and in general, see (Poore

and Gadaleta, 2006) and (Bijsterbosch and Volgenant,

2010).

Among algorithms proposed to solve the problem

of multi-target tracking are MHT (Reid, 1979) and

Greedy Optimal Assignment (Veenman et al., 2001).

The latter is used in (Betke et al., 2007) to track a large

number of bats. A similar strategy is used in (Balch

et al., 2001) for tracking the behaviour of live insects.

In (Khan et al., 2003) and (Khan et al., 2005a), the au-

thors propose a particle ﬁlter for tracking the motion

of insects. Both of these studies involve applying a

Markov ﬁeld to model insect interactions and assum-

ing that the targets actively avoid collisions. (Khan

et al., 2005b) extends these works to deal with split

and merged measurements. A problem similar to ours

is studied in (Grover et al., 2008) and (Straw et al.,

2011). They succeed in reconstructing the 3D trajec-

tories of multiple targets — in these instances, ﬂies

— from a multi-camera setup. The movements of in-

sects are arguably harder to predict than the ballistic

trajectory of blood droplets. On the other hand, the

insect-tracking problem is less sensitive to errors in

prediction as there are fewer targets moving at lower

speeds and the number of targets does not change (as

compared to ﬂying droplets that can split and merge).

2 BACKGROUND REMOVAL AND

SEGMENTATION

The cameras detect minute lighting ﬂuctuations be-

EXTRACTION OF BLOOD DROPLET FLIGHT TRAJECTORIES FROM VIDEOS FOR FORENSIC ANALYSIS

143

tween frames due to the high frame-rate even under

carefully controlled conditions. As such, we employ

a dynamic background model (Balch et al., 2001) to

identify pixels corresponding to blood droplets. Once

the background is subtracted, a binary mask is super-

imposed to identify target clusters of pixels that os-

tensibly correspond to ﬂuid droplets.

2.1 Identifying the Background

Our proposed dynamic background model success-

fully compensates for noticeable ﬂuctuations in over-

all image intensity between successive frames. Let

(k)

denote the image intensity in the k

video frame

and let B

(k)

denote the corresponding background

model. Both and I

(k)

and B

(k)

are matrices with real-

valued entries between 0.0 and 1.0. We also con-

struct the corresponding binary mask F

(k)

(i.e., a ma-

trix with 0-or-1 entries) to indicate pixels in frame k

associated with blood droplets (see Figure 2).

(a) (b)

Figure 2: Blood droplet segmentation: (a) Original image

intensity I

(k)

. (b) Background model B

(k)

. (c) Deviation

from the background model



(k)

− B

(k)



. (d) Foreground

mask F

(k)

The aforementioned lighting ﬂuctuations preclude

using a constant background model B

(k)

= B

(0)

= I

(0)

in all frames. Instead, we apply the dynamic linear

model

(0)

= I

(0)

, (1a)

(k+1)

= (1 − α)B

(k)

+ αI

(k)

, α ∈ [0,1]. (1b)

The coefﬁcient α in (1b) controls how quickly the

background model adapts to the changes in the back-

ground (e.g., newly formed bloodstains on the back

wall). Small values of α imply a slow learning speed.

For example, when α = 0, the result is a constant

background model; such a model is incapable of deal-

ing with changes in illumination or in the background.

Conversely, large values of α may cause the moving

droplets to be considered part of the background; this

leads to a ghosting effect where droplets are detected

twice in each frame. More sophisticated techniques

(e.g., random Markov ﬁelds) could alternatively be

used for background subtraction; however, in this ap-

plication context, such models unnecessarily intro-

duce additional complexity without signiﬁcant gain.

Having determined the background model B

(k)

the k

frame, the binary mask F

(k)

is computed pixel-

wise by the rule

(k)

(u,v) =

(

1 if



(k)

(u,v)− B

(k)

(u,v)



> ε

0 otherwise.

(2)

The preselected threshold value ε

∈ [0,1] in (2) has

to be chosen carefully. The challenge is to ensure cap-

turing droplets ﬂying over darker regions of the back-

ground, while ignoring intensity ﬂuctuations between

frames.

Suitable values of α and ε

cannot generally be

determined a priori; they depend on ambient exper-

imental conditions indiscernible by the naked eye.

This problem can be alleviated, but not completely

solved, by previewing a few frames taken at high

speed prior to the experiment. Previewing a few

frames allows us to relocate the lights to maximize

contrast and reduce shadows.

2.2 Segmentation of Individual Droplets

The process of background removal yields a sequence

of binary masks

(k)

frames

k=0

. From the binary mask

(k)

of the k

video frame, the clusters of pixels in the

connected components of F

(k)

correspond to individ-

ual foreground objects. Some of these clusters corre-

spond to genuine blood droplets, but some others are

false positives (e.g., the projectile, falling gelatin, and

noise or illumination artifacts). False positives are ﬁl-

tered out by discarding clusters that are either too big

or too small. We refer to the pixel clusters associated

with blood droplets as targets and we denote the set

of all targets accepted in frame k by T

(k)

Each target t ∈ T

(k)

has a number of properties

that are recorded. For instance, the target t has an area

a (in pixels) and associated raw moments M

, M

and M

(see, e.g., the documentation of OPENCV

(Bradski, 2000) for appropriate deﬁnitions). The mo-

ments of t are required to compute the image coordi-

nates of the target’s centroid (u,v) which is consid-

ered the location of the blood droplet associated with

the target. These properties are recorded for each tar-

get in each frame and are used to match targets in suc-

cessive frames for motion tracking.

ICPRAM 2012 - International Conference on Pattern Recognition Applications and Methods

144

3 TRACKING TARGET PATHS IN

IMAGES

Tracking the motion of an object using video data en-

tails identifying images of the same points (targets)

in a sequence of successive frames. When dealing

with small numbers of easily distinguishable rigid ob-

jects (e.g., when colour and shape are clearly distinct

or when obvious feature points are available), associ-

ating targets from frame to frame is straightforward.

However, when trying to track large collections of

very similar objects, more sophisticated measures are

needed to assess the credibility of the reconstructed

motion of individual targets.

3.1 Limitations of Tracking Targets

Strictly Frame-by-frame

To state the tracking problem in concrete terms, re-

call that T

(k)

denotes the set of all targets (images of

droplets) detected in frame k. Each target in t

(k)

∈

(k)

can be thought of as a pair t

(k)



(k)



of pixel coordinates (given by the target’s centre of

mass). Targets have additional properties other than

their centroids (e.g., areas, moments, etc.) that can be

used in tracking. Many tracking algorithms (e.g., in

(Balch et al., 2001)) are based on linking targets in

(k)

(i.e., from frame k) directly to targets in T

(k+1)

(i.e., from frame k + 1).

Such approaches work well when the cardinality

of the target sets does not vary signiﬁcantly between

frames. For the droplet tracking problem, this as-

sumption breaks down in a number of ways:

1. a false target t

(k)

is spuriously detected in frame

k, i.e., pixels contaminated by noise are mistaken

for a legitimate physical object in the scene;

2. a true target t

(k)

is not detected by the camera in

frame k + 1;

3. a true target t

(k)

is temporarily occluded by an-

other object in frame k + 1;

4. a target t

(k)

temporarily leaves the ﬁeld of view

between frames k and k + 1;

5. a target t

(k+1)

returns to the ﬁeld of view between

frames k and k + 1;

6. a target t

(k)

permanently leaves the ﬁeld of view

between frames k and k + 1; and

7. a target t

(k+1)

initially enters the ﬁeld of view be-

tween frames k and k + 1.

These modes of failure are the norm rather than ex-

ceptions. In case (1), it is necessary to handle spuri-

ous detections gracefully. The cases (2), (3), and (4)

are temporary failures; it is best not to match the tar-

get t

(k)

∈ T

(k)

with any target in T

(k+1)

. Similarly,

in case (5) when the target t

(k+1)

is detected again in

frame k + 1, it should be paired with a candidate from

a frame prior to frame k (i.e., the most recent frame

in which the corresponding droplet was detected). Fi-

nally, the situations (6) and (7) should be considered

only when there is no suitable candidate target in any

later or earlier frames respectively.

3.2 Assignment Problems for Tracking

We modify the formulation of the tracking problem

to allow for the difﬁculties outlined in Section 3.1.

The key problem that needs to be solved at each stage

is an assignment problem. Assignment or matching

problems constitute a fundamental class of problems

in combinatorial optimization. In speciﬁc language,

let A and B be ﬁnite sets (i.e., vertices of a bipartite

graph), let cost : A×B → R be a cost function associ-

ated edges between A and B, and let M ⊂ P (A × B)

be a proper subset of the power set P (A × B). The

Assignment Problem (AP) is to construct a matching

M ⊂ A × B such that the total cost summed over all

edges in M is minimized, i.e.,

min

M∈M

∑

(a,b)∈M

cost(a,b). (3)

are equal and M consists of all pos-

sible matchings that cover both A and B, the problem

(AP) is called a Linear Assignment Problem (LAP). If

, and M consists of all matchings that cover

the smaller set, the problem (AP) is called a Rectan-

gular Linear Assignment Problem (RLAP). Observe

that the constraint M on the set of possible match-

ings is necessary; otherwise, for many cases, the min-

imizer would simply be the empty matching M =

Assuming for the moment that the constraint M ⊂

P (A × B) is known, we shall assume henceforth that

“M = SolveAP(A,B,cost, M )” (4)

means “Solve (AP) by computing the matching

M ∈ M that minimizes the sum in (3).” We implicitly

assume that a solution of (AP) exists as does a rea-

sonable algorithm for computing it. For all practical

purposes, we use the techniques in (Dasgupta et al.,

2008) to compute M in (4).

In some cases of (AP), not all edges are present

in the bipartite graph, i.e., some of the elements of

A are not connected to elements of B. This as-

signment problem can still be solved using a variant

of the Kuhn-Munkres algorithm that assigns (prac-

tically) inﬁnite cost to absent edges (see (Dasgupta

et al., 2008)). The missing edges also introduce the

constraint M ⊂ P (A × B).

EXTRACTION OF BLOOD DROPLET FLIGHT TRAJECTORIES FROM VIDEOS FOR FORENSIC ANALYSIS

145

As an example of an assignment problem in track-

ing, the approach followed by (Balch et al., 2001) is

to ﬁnd, at step k, a matching

(k)

= SolveAP(T

(k)

(k+1)

,dist,M ), (5)

where M consists of all matchings that cover either

(k)

or T

(k+1)

and

dist



(k)

(k+1)





(k)

− t

(k+1)



. (6)

There is no problem computing the cost for any edge

since it is merely the Euclidean distance.

In our formulation, we solve an assignment prob-

lem (3) where “A” is a set of paths and “B” are tar-

gets (rather than targets and targets as in (Balch et al.,

2001)). To the best of our knowledge, this formula-

tion differs from previous tracking work that matches

targets strictly between subsequent frames. Speciﬁ-

cally, a path is an ordered list of one or more targets

)

,...,t

)

] occurring in a strictly increasing

sequence of frames (i.e., so that k

< k

< ·· · < k

Notice that we do not require that successive targets

in a given path occur in successive video frames (i.e.,

that t

(k)

∈ T

(k)

absolutely must be followed by some

(k+1)

∈ T

(k+1)

) as we wish to deal with situations

enumerated in Section 3.1 gracefully. With this ter-

minology, we consider a set P

(k)

of paths linking tar-

gets in a strictly increasing subsequence drawn from

the 0

frame up to and including the k

frame.

Our multi-target tracking problem can then be ex-

pressed recursively using the solution of an assign-

ment problem at each step. In particular, the desired

matching is

(k)

= SolveAP(P

(k)

(k+1)

dist,

M ), (7)

where

dist is deﬁned using a path-based predictive

model described in Section 3.3. The set

M is a lit-

tle harder to describe; it consists of matchings M with

the property that, if

dist(p,t) < ∞, then M covers at

least one of p or t (but not necessarily both).

3.3 A Model-based Distance Metric

We do not solve the assignment problem by minimiz-

ing a sum of Euclidean distances between targets in

successive frames as in (6). Instead, we track tar-

get motion by minimizing the distances between tar-

gets in the next frame and targets predicted using the

paths. Predictive algorithms usually include a step

in which a model for each target’s motion is learned

(e.g., by a Bayesian network (Nillius et al., 2006) or a

Kalman Filter (Iwase and Saito, 2004)). In the present

context, we exploit basic models of droplet motion.

Projectiles follow simple parabolic trajectories

(with constant horizontal speeds and constant vertical

acceleration g ' 9.81ms

−2

) in the absence of aerody-

namic drag forces. The projection of such ballistic

trajectories in the image plane are similarly quadratic

curves. Even accounting for viscous drag effects,

over sufﬁciently short time intervals (as is the case

for high-speed video), quadratic polynomials provide

robust approximations.

Thus, given a path p ∈ P

(k)

corresponding to some

droplet’s partial motion up to and including frame k,

the estimated image coordinates of the target in frame

k + 1 are given by

(k+1)

ˆu

(k+1)

ˆv

(k+1)



k+1

+ b

k+1

+ c

k+1

+ b

k+1

+ c



, (8)

where τ

k+1

is the time corresponding to frame k + 1.

The coefﬁcients a

, a

, b

, c

, and c

are deter-

mined using standard polynomial least-squares ﬁtting

based on the targets in the path p. In the ﬁrst few

frames, if a least-squares quadratic cannot be used to

ﬁt targets in path p, polynomials of degree 0 or 1 are

generated to predict

(k+1)

instead.

Given a path p ∈ P

(k)

, the predicted target

(k+1)

from (8) is used to deﬁne the modiﬁed cost function

dist in (7) for match p to targets in T

(k+1)

. To evaluate

a proposed matching M

(k)

⊆ P

(k)

× T

(k+1)

, the cost

function is given by

dist



p,t

(k+1)





(k+1)

−

(k+1)



. (9)

That is, when comparing different assignments of

paths p ∈ P

(k)

to candidate targets t

(k+1)

∈ T

(k+1)

, this

cost function penalizes targets that deviate too much

(in Euclidean distance) from the prediction

(k+1)

3.4 A Predictive Tracking Algorithm

With an explicit speciﬁcation of the prediction strat-

egy (8) and the cost function (9), we can now provide

a high-level description of our approach to tracking

targets through the video data in Algorithm 1.

Observe that, rather than keeping track of in-

dividual collections of paths P

(k)

, all the paths are

simply accumulated into a single set. The loop at

line 4 accumulates a set of candidate matches for p

in S; corresponding edges are added to E

(k)

in line 7.

The purpose of accumulating E

(k)

is for various

performance enhancements exploiting sparsity for

solving (7) for the matching M

(k)

at line 8 (as in

(Dasgupta et al., 2008)). The ﬁnal loop at line 9

extends the paths p covered by M

(k)

once the matched

targets t

(k+1)

∈ T

(k+1)

have been determined. Finally,

ICPRAM 2012 - International Conference on Pattern Recognition Applications and Methods

146

Algorithm 1: Tracking and assembling image paths.

Input: Set of targets in each frame {T

(k)

}

frames

k=0

Output: Set P of (possibly incomplete) paths

1: P ←



(0)

] | t

(0)

∈ T

(0)



{singleton lists}

2: for k = 0 : N

frames

− 1 do

3: E

(k)

←

4: for each path p ∈ P do

5: Predict

(k+1)

from p using (8)

6: Find S ⊆ T

(k+1)

within ε

track

(k+1)

7: E

(k)

← E

(k)

∪ {(p,t

(k+1)

) | t

(k+1)

∈ S }

8: M

(k)

= SolveAP(P

(k)

(k+1)

dist,

M ) with

M as in (7) and

dist as in (9)

9: for each edge (p, t

(k+1)

) ∈ M

(k)

10: Replace p ∈ P by p with t

(k+1)

appended

11: Remove t

(k+1)

from T

(k+1)

12: P ← P ∪ {[t

(k)

] | t

(k)

∈ T

(k)

}

at line 12, the set of paths P is extended with new

paths containing singleton paths

(k+1)

of targets in

(k+1)

not covered by M

(k)

4 RECONSTRUCTION OF 3D

TRAJECTORIES

Each camera in our studies accumulates a collection

of paths in image coordinates as outlined in Section 3.

The problem, then, is to match image paths captured

by each camera to produce three-dimensional trajec-

tories. For convenience, we refer to the two cameras

as Camera I and Camera II and we refer to the asso-

ciated sets of image paths produced by Algorithm 1

as P

and P

respectively. The cameras are calibrated

so that their intrinsic and extrinsic parameters, includ-

ing the location and orientation of Camera II relative

to Camera I, are known. The calibration process is

discussed in section 5.1. We sketch the essential pro-

cedure in Algorithm 2 and ﬁll in the details in Sec-

tions 4.1 and 4.2.

The result of Algorithm 2 is a set C of curved tra-

jectories consisting of three-dimensional world coor-

dinates of points. Actually, since each point on the

trajectory is matched to a particular video frame k,

we store the image frame k and a measure of error

(k)

with the world coordinates r

(k)

of each point in

the computed trajectory.

4.1 Reconstructing World Coordinates

Given a pixel (u

) in image coordinates captured

by Camera I, it is straightforward to determine a line

Algorithm 2: Reconstructing trajectories in 3D.

Input: Collections of image paths P

and P

captured

by Camera I and Camera II respectively

Output: Set C of trajectories in three dimensions

1: C ←

2: for p

∈ P

3: for p

∈ P

4: K ← set of common frames of p

and p

5: if

> K

min

then

6: c ←

7: for k ∈ K do

8: Select t

(k)

from p

, t

(k)

from p

9: Back-project t

(k)

onto line `

(k)

10: Back-project t

(k)

onto line `

(k)

11: Find distance d

(k)

between `

(k)

& `

(k)

12: Find midpoint r

(k)

∈ R

13: Append tuple (k, r

(k)

) onto c

14: C ← C ∪{c}

15: Deﬁne dist(p

, p

) =average of d

(k)

16: M = SolveAP(P

,dist,M ) with

M as in (7) and dist as above

⊆ R

for which every point in the line is projected

onto the pixel (u

) by Camera I. The details re-

quired to compute a representation of `

involve ho-

mogeneous coordinates and Camera I’s intrinsic and

extrinsic parameters; see, e.g., (Hartley and Zisser-

man, 2004) for more details. The computation is iden-

tical for Camera II, so, lines 9 and 10 of Algorithm 2

simply refer to this procedure as “back-projecting”

the pixels t

(k)

and t

(k)

onto the spatial lines `

(k)

and

(k)

respectively.

Given representations of the lines `

(k)

and `

(k)

, it is

elementary to ﬁnd the shortest distance d

(k)

between

the two lines. We refer to the world coordinates of the

midpoint of the corresponding line segment between

the two closest points on either line as r

(k)

. Presum-

ably, if two back-projected lines actually intersect, the

computed error d

(k)

would be zero; as such, the dis-

tance d

(k)

is a reasonable proxy for the error in using

(k)

as the supposed spatial point that corresponds to

image points t

(k)

and t

(k)

simultaneously.

The tentative curves in world coordinates are ac-

cumulated in line 13 of Algorithm 2. These curves

consist of the midpoints r

(k)

as described above. The

frame coordinate k and the length d

(k)

are stored also

(the latter providing a measure of pointwise error).

4.2 Matching Image Paths to Space

Curves

After the space curves are built up in Algorithm 2, it

EXTRACTION OF BLOOD DROPLET FLIGHT TRAJECTORIES FROM VIDEOS FOR FORENSIC ANALYSIS

147

remains to ﬁgure out which paths in P

and P

actu-

ally do correspond to a physically reasonable curve c

in 3D. The construction of a distance function dist at

line 15 can be used to set up another assignment prob-

lem. The function dist(p

, p

) computes the average

value d

(k)

, i.e.,

d =

∑

k∈K

(k)

, (10)

where K is the set of common frames of p

and p

For paths p

and p

deemed obviously incompatible,

dist(p

, p

) = ∞.

The metric deﬁned in (10) allows us to solve an-

other ﬁnal assignment problem to ﬁgure ﬁnd a match-

ing of paths from either camera (and hence the desired

three-dimensional trajectories). Again, rather than as-

sume that one of the sets P

or P

must be covered,

the set M ⊂ P (P

× P

) has a more subtle deﬁnition.

Any matching M ∈ M has the property that, for any

edges (p

, p

) such that dist(p

, p

) < ∞, one of p

is covered by M (as in (7)).

5 EXPERMIENTS AND ANALYSIS

Our experimental apparatus consists of two video

cameras because real-world coordinates of the ﬂight

paths cannot be obtained by a single camera. How-

ever, the two-dimensional images provided by a sin-

gle camera still provide useful qualitative informa-

tion. For instance, it is plainly visible that grav-

ity plays an important role in blood droplets’ curved

trajectories even at small distances. This observa-

tion brings into question the validity of the string-

ing method for inferring the location of the blood-

letting event. Furthermore, we can later combine

the two-dimensional information from both cameras

to build accurate three-dimensional trajectories with

real-world measurements.

5.1 Experimental Setup

Figure 3 shows our experimental setup. The exper-

iments are set up on a steel table with dimensions

roughly 0.9 × 3.0 m. Plywood boards with a white

vinyl ﬁnish are placed along the two edges opposite

to the stereo camera pair. These boards act as walls

to contain the splatter and to provide a uniform back-

ground for the experiments

. The target is a thin latex

packet containing 20 ml of transfer blood encased in

Different surfaces can be clamped onto the walls to

study blood-surface interaction responsible for bloodstain

pattern formation. We plan to study this issue in the future.

Figure 3: Experimental setup showing ballistic gel contain-

ing transfer blood. Experiments are captured using a stereo

camera pair capable of recording high-speed video.

gelatin designed to approximate human ﬂesh. The tar-

get is raised off the table with a lab jack. The paintball

gun sits directly behind the target.

Two high-speed cameras, protected by sheets of

Plexiglas, record the experimental setup from two

viewpoints, capturing videos necessary to reconstruct

the blood droplets’ trajectories in 3D. In the follow-

ing discussion, we will refer to them as the frontal

and lateral cameras, in reference to their position

around the experiment table. Fourteen 500 W work

lights illuminate the scene, allowing cameras to cap-

ture videos at 1300 frames per second. A triggering

mechanism controls the two cameras to capture syn-

chronized videos. Each experiment begins by record-

ing the calibration rig—a ﬂat checkerboard pattern—

moving through the cameras’ ﬁelds of view. These

calibration videos are used to compute each individ-

ual cameras’ intrinsic and extrinsic parameters (Hart-

ley and Zisserman, 2004). Once calibrated, the cam-

eras are conﬁgured to record the experimental area at

high speed and the gun is ﬁred. Upon impact with

the target, the latex container breaks, causing the gel

and the liquid to escape and leaving “bloodstains”

on the wall. The process typically takes anywhere

from 0.6 to 1.3 seconds, producing up to 1690 grey-

scale frames from each camera. Video resolution is

1280 × 800 pixels.

Our system has a very low threshold for errors,

so we devised the following calibration scheme. We

point a laser at the scene and record a pair of videos

showing the laser dot moving through the scene. The

position of the laser dot in each video frame can then

be used to verify the camera pair calibration (see Fig-

ure 4). A modiﬁed version of the segmentation proce-

dure from Section 2.2 is used to detect the laser dot;

only the brightest region is kept if the segmentation

ﬁnds more than one connected component. We as-

sume that the location and direction of the cameras

do not change during the course of the experiment,

i.e, that the extrinsic parameters computed during the

calibration process do not change. The laser veriﬁca-

ICPRAM 2012 - International Conference on Pattern Recognition Applications and Methods

148

tion procedure described above is repeated after each

experiment to validate the preceding assumption.

A failure in the second laser veriﬁcation signals

that at least one of the cameras moved during the ex-

periment, This could happen due to kinetic energy be-

ing transferred to the walls or the camera base by re-

coil from the gun or the bullet bouncing off the walls.

In either case, the experiment is discarded as we can-

not use visual cues from the experiment table to com-

pensate for this movement.

Figure 4: Calibration veriﬁcation by shining a laser at the

observed region. In these ﬁgures, thin blue circles depict the

laser dot, blue lines represent the epipolar line correspond-

ing to the the laser dot in the other camera, and the thick

red circles show the re-projection of the 3D reconstruction

of the laser dot. The left image shows a successful calibra-

tion. Here, the epipolar line crosses the laser dot and the

re-projection coincides with the original location. The right

image shows an inaccurate calibration. One of the cameras

has moved, perhaps due to the vibrations generated by the

recoil of the gun.

A few pictures of the bloodstains are captured be-

fore cleaning up the lab and preparing for the next

experiment. These pictures are taken using similar

equipment and techniques available to a forensic in-

vestigator capturing photographic evidence of blood-

stains at a crime scene. 48 successful experiments

were conducted.

5.2 Validation by Visual Inspection

A single video from an experiment yields hundreds

of image paths from each camera. It is infeasible to

track more than a few trajectories manually, far fewer

than would required to obtain a statistically represen-

tative sample of the entire set of trajectories. Fur-

thermore, correlating trajectories tracked by hand to

ones tracked automatically by our system would re-

quire a scheme to account for quantitative differences

between clusters of pixels identiﬁed subjectively by

a human operator versus those segmented automati-

cally by the scheme outlined in Section 2.2. Thus, we

need a way to allow the operator to quickly track and

compare hundreds of tracks simultaneously, sacriﬁc-

ing the quantitative measure of how many paths and

how many false paths were found.

We have developed a tool that allows a user to

explore tracking performance visually. The video is

played back at a lower frame-rate, overlaid with par-

tial trajectories (see the middle image of Figure 1).

Only the currently active trajectories—those that have

started but have not yet ended in the current frame—

are shown, and only the path segments up to the cur-

rent frame. The overall effect is that the trajecto-

ries appear to be following the droplets, allowing the

operator to focus the attention on a group of mov-

ing droplets and evaluate the correctness of the paths.

This tool was improved to show the predicted position

and search window in subsequent frames as an aid to

evaluate the accuracy of the predictions.

5.3 Validation by Counting Matches

Ideally, the process described in sections 2.1 to 3.3

should return the paths of all droplets and no spurious

or erroneous paths. In this event, every image path de-

tected by the frontal camera corresponds to an image

path detected by the lateral camera. In actual experi-

ments, some droplets are not detected by one or both

cameras, one or both cameras may register image tar-

gets that are false positives, and some droplets may be

visible by only one of the cameras in some frames. In

all of these cases, the matching algorithm should not

match image paths between the cameras’ respective

videos.

Table 1: Number of matching paths for three of the exper-

iments and cumulative result for the 48 experiments con-

ducted.

N. Frontal Lateral Matches Accuracy

1 368 281 233 82.9 %

2 416 327 235 71.9 %

3 598 270 203 75.2 %

T 25542 9769 8534 87.4 %

The ﬁrst three rows of Table 1 show the match-

ing results for three experiments. The ﬁrst column

simply labels the experiments; the last row being a

summary over all 48 experiments conducted. The Ac-

curacy column is computed as the ratio between the

number of paths detected by the camera that found

the least amount of tracks (in these cases, the lateral

camera) and the number of matches.

Figure 5 images with paths overlaid from the least

accurate experiment from Table 1. As the front-facing

camera detected more paths than the lateral camera

(which suggests that it has a better view of the exper-

EXTRACTION OF BLOOD DROPLET FLIGHT TRAJECTORIES FROM VIDEOS FOR FORENSIC ANALYSIS

149

Figure 5: 3D matching. Left column: lateral camera. Right column: front-facing camera. Top row: all paths. Middle row:

matched paths. Bottom row: discarded paths. The paths were drawn on top of the ﬁrst video frame to give an idea of the

relative location and orientation of the cameras.

iment), we necessarily discarded more paths from the

front view than from the lateral view. Of the paths

discarded from the lateral view (bottom row of Fig-

ure 5), most were travelling backwards or downwards

from the initial position of the target, i.e., toward re-

gions outside the view of the frontal camera. There-

fore, the apparent poor matching in this particular ex-

periment from Table 1 can be accounted for by paths

partially hidden from one of the cameras. It is also

worth noting that some of the discarded paths match

very closely to their own shadows (this can be seen in

the short path near the centre of the lower left image).

Figure 6 shows the reconstruction errors for all

points and paths obtained in the 48 experiments. The

left histogram plots the error (in cm) on the horizon-

tal axis against the number of points on the vertical

axis. The right-hand histogram shows the same pa-

rameters again, but with maximimum errors for each

path versus the number of paths. For most of the re-

constructed points, the reconstruction error is lower

than 5mm. Figure 7 shows the 3D reconstructions for

Experiments 1 and 2.

5.4 Validation by Inferring Parameters

If we assume constant acceleration, the position of a

droplet at time τ is given by

p(τ) =





(τ)





= p(0) + v(0)τ +

. (11)

This model is not completely accurate as it ignores

viscous effects. However, (11) can still be used to

compute a rough estimate of the gravitational constant

ICPRAM 2012 - International Conference on Pattern Recognition Applications and Methods

150

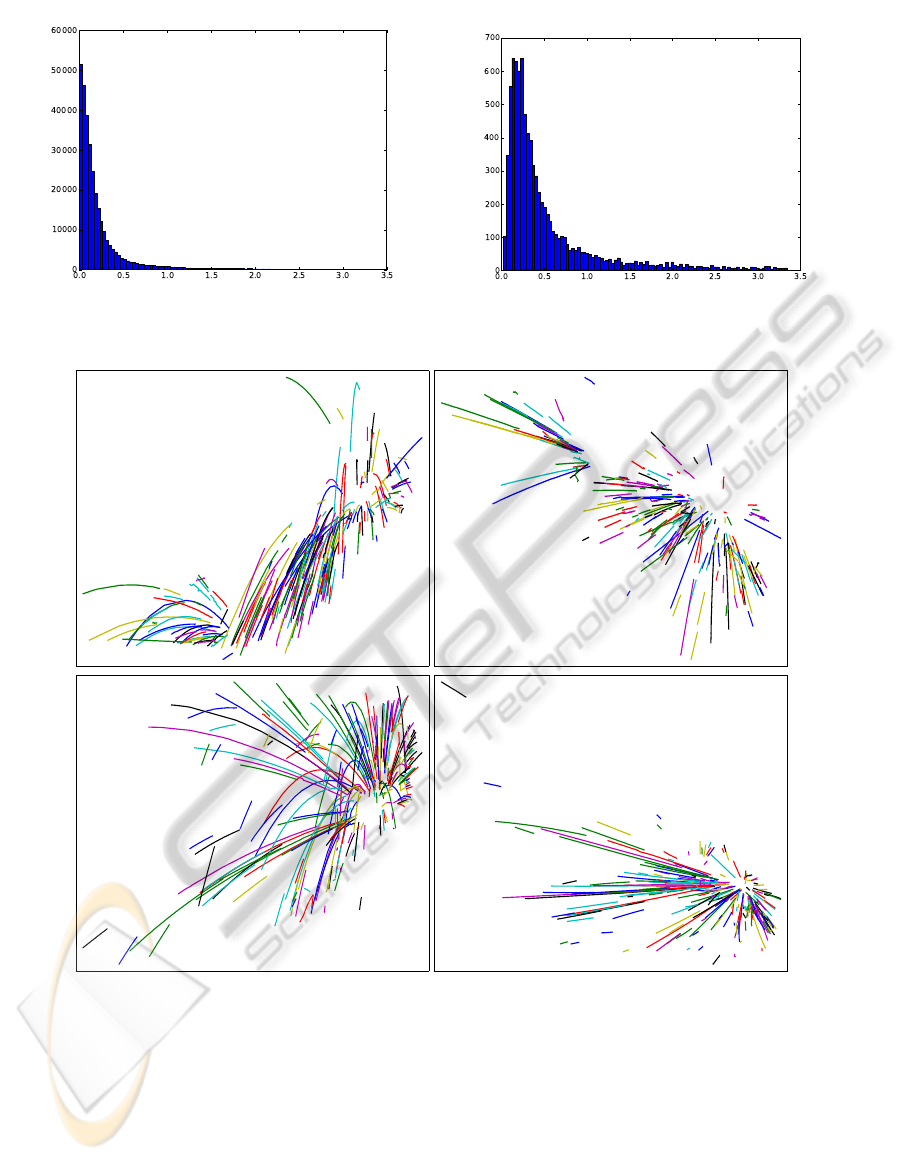
Figure 6: Error histograms. Left: Error in cm (horizontal axis) vs. the number of points (vertical axis). Right: Number of

paths (vertical axis) vs. maximum error in these paths.

Figure 7: 3D reconstruction of experiments 1 (top) and 2 (bottom). Left: lateral view. Right: top view.

g ≈ 9.8 m/s

. Notice we that we cannot use g directly

in our model-based prediction of image paths because

the parabolic paths constructed using Algorithm 1 be-

cause the paths constructed there are in image coordi-

nates.

From the frame-rate and our tracking data, we

know the locations p(τ) and times τ. Similarly as in

Section 3.3, we can ﬁt each component of the data

points p(τ) with a parabola:

p(τ) ≈ d + e τ + f τ

. (12)

From (11) and (12), we can estimate the accelera-

tions as a ≈ 2f. When a droplet is ascending, both the

force of gravity and the drag force point downward.

Conversely, when a droplet is descending, the force

of gravity opposes the drag force. Thus, if we com-

pute the accelerations independently for upward and

downward portions of the trajectories, we should ob-

tain a greater magnitude for the vertical components

of acceleration in the ﬁrst case than in the second.

Table 2 summarizes the mean vertical accelera-

EXTRACTION OF BLOOD DROPLET FLIGHT TRAJECTORIES FROM VIDEOS FOR FORENSIC ANALYSIS

151

100

150

200

250

300

350

400

450

100

150

200

250

300

100

200

300

400

500

600

Figure 8: Accelerations (in m/s

) computed from the 3D reconstruction. Left: using only the upwards portions of the paths.

Right: using only the downwards portions of the paths.

Table 2: Estimated value of g inferred from the paths, using

only the upwards portions, the downwards portions, and all

the points in the path, respectively. A constant acceleration

was assumed. Only sections of paths with at least 30 mea-

surements are used to compute these values. The number of

paths that had more than 30 measurements in each direction

are indicated in parentheses.

N. (up / down / all) Up Down Total

1 (19 / 111 / 120) 9.09 9.03 9.08

2 (69 /62 / 124) 10.41 9.13 9.85

3 (37 / 31 / 69) 9.93 7.84 9.04

T (1214 / 2486 / 3545) 10.36 10.24 10.36

tions obtained from the three experiments. Note that

the value is consistently greater in the upwards por-

tions than in the downwards portions, as expected.

Figure 8 is a histogram of the acceleration com-

ponents associated with each path extracted by the

experiments. Despite having obtained a good approx-

imation of g in the second row, the variance of the

computed values for the three axis shows that the ef-

fect of drag forces is not negligible and should be

taken into account when analyzing bloodstain pat-

terns in crime scenes.

6 CONCLUSIONS

We apply computer vision techniques to estimate pa-

rameters needed to describe blood droplet ﬂight paths

caused by a violent event accurately. This paper rep-

resents the ﬁrst step toward that goal: estimating 3D

trajectories of blood droplets using a stereo camera

setup. The system described here uses model-based

tracking to estimate trajectories of image features cap-

tured by individual cameras. The 2D image trajecto-

ries are then matched across the two cameras to re-

construct 3D trajectories in world coordinates. In a

given experiment, any proposed system needs to track

hundreds of droplets simultaneously; therefore, man-

ual annotation of ground truth to determine the per-

formance of the proposed algorithm is infeasible. In-

stead, we have developed three novel strategies for

indirectly measuring the performance of our system.

The initial results appear promising.

Several extensions of this work are currently in

progress. From our results, it is obvious that air resis-

tance and gravity play a signiﬁcant role in how blood

droplets move through the air even at short distances.

We are currently developing physics-based models in-

corporating the inﬂuence of gravity and aerodynamic

drag to describe blood droplet trajectories. The data

acquired by the system described here can validate

putative physic-based motion models under devel-

opment and determine the relative magitude of the

forces ignored in stringing-based methods. Beyond

modelling droplet ﬂight, it is necessary to investigate

robust methods based on a validated model for back-

tracking from a bloodstain to the original source.

REFERENCES

Balch, T., Khan, Z., and Veloso, M. (2001). Automati-

cally tracking and analyzing the behavior of live insect

colonies. In AGENTS ’01, pages 521–528. ACM.

Betke, M., Hirsh, D. E., Bagchi, A., Hristov, N. I., Makris,

N. C., and Kunz, T. H. (2007). Tracking large variable

numbers of objects in clutter. In CVPR ’07, pages 1–8.

IEEE.

Bevel, T. and Gardner, R. M. (2008). Bloodstain Pattern

Analysis With an Introduction to Crimescene Recon-

struction. CRC Press, 3

edition.

ICPRAM 2012 - International Conference on Pattern Recognition Applications and Methods

152

Bijsterbosch, J. and Volgenant, A. (2010). Solving the rect-

angular assignment problem and applications. Ann.

Oper. Res., 181:443–462.

Bourgeois, F. and Lassalle, J.-C. (1971). An extension of

the Munkres algorithm for the assignment problem to

rectangular matrices. Commun. ACM, 14:802–804.

Bradski, G. (2000). The OpenCV Library. Dr. Dobbs J.

Buck, U., Kneubuehl, B., N

ather, S., Albertini, N., Schmidt,

L., and Thali, M. (2011). 3D bloodstain pattern analy-

sis: Ballistic reconstruction of the trajectories of blood

drops and determination of the centres of origin of the

bloodstains. Forensic Sci. Int., 206(1-3):22–28.

Dasgupta, D., Hernandez, G., Garrett, D., Vejandla, P. K.,

Kaushal, A., Yerneni, R., and Simien, J. (2008). A

comparison of multiobjective evolutionary algorithms

with informed initialization and Kuhn-Munkres algo-

rithm for the sailor assignment problem. In GECCO

’08, pages 2129–2134. ACM.

Grover, D., Tower, J., and Tavar

e, S. (2008). O ﬂy, where

art thou? J. Roy. Soc. Interface, 5(27):1181–1191.

Hartley, R. and Zisserman, A. (2004). Multiple view geom-

etry in computer vision. Cambridge University Press,

edition.

Iwase, S. and Saito, H. (2004). Parallel tracking of all soccer

players by integrating detected positions in multiple

view images. In ICPR 2004, volume 4, pages 751–

754. IEEE.

Khan, Z., Balch, T., and Dellaert, F. (2003). Efﬁcient parti-

cle ﬁlter-based tracking of multiple interacting targets

using an MRF-based motion model. In IROS 2003,

volume 1, pages 254–259. IEEE.

Khan, Z., Balch, T., and Dellaert, F. (2005a). MCMC-Based

Particle Filtering for Tracking a Variable Number of

Interacting Targets. IEEE Trans. Pattern Anal. Mach.

Intell., 27(11):1805–1918.

Khan, Z., Balch, T., and Dellaert, F. (2005b). Multitar-

get tracking with split and merged measurements. In

CVPR ’05, volume 1, pages 605–610. IEEE.

Kuhn, H. (1955). The Hungarian Method for the assignment

problem. Nav. Res. Logist., 2(1-2):83–97.

Munkres, J. (1957). Algorithms for the Assignment and

Transportation Problems. SIAM J. Appl. Math.,

5(1):32–38.

Nillius, P., Sullivan, J., and Carlsson, S. (2006). Multi-

Target Tracking–Linking Identities using Bayesian

Network Inference. In CVPR ’06, volume 2, pages

2187–2194.

Poore, A. B. and Gadaleta, S. (2006). Some assignment

problems arising from multiple target tracking. Math.

Comput. Model., 43(9-10):1074–1091.

Reid, D. (1979). An algorithm for tracking multiple targets.

IEEE Trans. Autom. Control, 24(6):843–854.

Straw, A. D., Branson, K., Neumann, T. R., and Dick-

inson, M. H. (2011). Multi-camera real-time three-

dimensional tracking of multiple ﬂying animals. J.

Roy. Soc. Interface, 8(56):395–409.

Veenman, C., Reinders, M., and Backer, E. (2001). Resolv-

ing motion correspondence for densely moving points.

IEEE Trans. Pattern Anal. Mach. Intell., 23(1):54–72.

Yilmaz, A., Javed, O., and Shah, M. (2006). Object track-

ing: A survey. ACM Comput. Surv., 38(4).

EXTRACTION OF BLOOD DROPLET FLIGHT TRAJECTORIES FROM VIDEOS FOR FORENSIC ANALYSIS

153