1-D MATHEMATICAL MORPHOLOGY FOR WATER

REMOVAL IN

H MR SPECTROSCOPY TOOL

Juan José Fuertes

, Valery Naranjo

, Jesús Angulo

and Mariano Alcañiz

1,3

Instituto Interuniversitario de Investigación en Bioingeniería y Tecnología Orientada al Ser Humano (I3BH),

Universitat Politècnica de València, I3BH/LabHuman, Camino de Vera s/n, 46022 Valencia, Spain

Centre de Morphologie Mathématique, Mathématiques et Systèmes, MINES Paristech, Paris, France

Ciber, Fisiopatología de Obesidad y Nutrición, CB06/03 Instituto de Salud Carlos III, Madrid, Spain

Keywords: Magnetic Resonance Spectroscopy, Signal Processing, Brain Cancer Detection, Multivoxel, Magnetic

Resonance Imaging.

Abstract: This work shows the basics and performance of a new morphological signal method for 1-D water signal

removal included in a simple and interactive multivoxel spectroscopy tool to help surgeons detect brain

cancer. It consists of mathematical morphology usually applied in 2D images to filter 1D spectroscopic

signals. 1D water signal reconstruction from the original data is performed in frequency domain through the

use of an elementary operation: geodesic dilation. Then, the water signal is subtracted from the original

signals due to the large amount of water which exists in the brain compared to the rest of molecules, making

possible quantitation procces. The goal of this paper is to present this new morphological method commonly

used in 2D domain for 1D water removal, spreading its use to several processing methods as quantitation.

1 INTRODUCTION

Many spectroscopic algorithms have been developed

to solve the problem of quantifying signals in

MRS data in the last 20 years, being them included

in the most popular software tools, such as the

jMRUI software package (Stefan, Di Cesare,

Andrasescu, Popa, Lazariev, Vescovo, Strbak,

Williams, Starcuk, Cabanas, Van Ormondt and

Graveron-Demilly, 2009) and the AQSES software

(Simonetti, Poullet, Sima, De Neuter, Vanhamme,

Lemmerling and Van Huffel, 2006). One of the most

important algorithms in

H MRS is the water

suppression from original signals, in order to

eliminate the large amount of water which exists in

the brain compared to the rest of molecules. The so-

called blackbox methods based on singular value

decomposition (SVD) such as HSVD (De Beer and

Van Ormondt, 1992), HLSVD (Pijnappel, Van den

Boogaart, De Beer and Van Ormondt, 1992) and

HTLS (Van Huffel, Chen, Decanniere and Van

Hecke, 1994), have been successful in

reconstructing the signal as a sum of Lorentzians,

but the influence that the users have when the

estimated parameters are chosen could reduce the

quality of the signal fitting. Another important

method is the maximum-phase Finite Impulse

Response (MP-FIR) which has been shown to be

one of the most accurate and efficient technique for

quantifying MRS spectra (Sundin, Vanhamme, Van

Hecke, Dologlou, and Van Huffel, 1999). In

addition, MP-FIR allows the inclusion of prior

knowledge that may be taken into account during

quantitation; however the drawback of these filters is

that they are linear phase filters which generate

distortion due to the fact that the signals are

composed of exponentially damped sinusoids and

not pure sinusoids, and this distortion cannot be

totally neglected. Other techniques as Wavelets

(Günther, Ludwig, and Rüterjans, 2002) or Gabor

transforms (Coron, Vanhamme, Antoine, Hecke, and

Van Huffel, 2001) have also used for water removal

but with lower accuracy than the other ones. These

methods are compared in a filtering review to solve

suppression in MRS (Coron et al., 2001): the MP-

FIR method was the most accurate and efficient

technique. The water suppression method presented

in this paper belongs to a general process where the

main steps included in most of spectroscopy

software tools are illustrated in Figure 1:

381

Fuertes J., Naranjo V., Angulo J. and Alcañiz M..

1-D MATHEMATICAL MORPHOLOGY FOR WATER REMOVAL IN 1H MR SPECTROSCOPY TOOL.

DOI: 10.5220/0003770403810384

In Proceedings of the International Conference on Bio-inspired Systems and Signal Processing (BIOSIGNALS-2012), pages 381-384

ISBN: 978-989-8425-89-8

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

Figure 1: Block diagram for

H MR spectroscopy

analysis.

In this work we are focusing on the dominant

signals removal, specifically in the water

suppression algorithm. This method is included in a

software tool (See Figure 2) which also incorporates

the main algorithms to process data, performs the

registration between spectroscopic data and MR

images, and generates the metabolite maps. In short,

the aim of this paper is to provide researchers with a

new morphological method for water suppression,

introducing it for a future use in quantitation

metabolite signals.

This paper is set up as follows: section 2

reminds some basics of morphology and the main

characteristics of mathematical algorithms: dilation,

erosion, opening and closing. In section 3, the water

removal algorithm based on mathematical operations

is shown. Section 4 explains the experiments and

finally, a brief conclusion is given in section 5

together with the future work.

Figure 2: Main window of the

H MR Spectroscopy tool.

2 MATHEMATICAL

MORPHOLOGY

Mathematical morphology is a non-linear

image/signal processing methodology based on

minimum and maximum operations (Serra, 1982), in

order to extract relevant components of an

image/signal respectively. In the last years, this

technique has been commonly used in 2D images,

but its use for 1D signal processing is also possible.

Let f be a signal which is defined as:





: → (1)

where 



∈  is the time sample. In the case of

discrete valued signals, =







,



1,…





is an ordered set of amplitude-levels.

Furthermore, let 



 be a sub-set of  called

structuring element (shape probe) centred at

point



. The size of the structuring element (SE) is

usually chosen according to some a priori

knowledge about the geometry of the relevant and

irrelevant signal components. The two basic

morphological operators are:

• Dilation:



















=

∈















• Erosion:



















=

∈















Those elementary operations can be combined to

obtain a new set of operators or basic filters given

by:

• Opening: 









=









• Closing: 









=









There are other complex filters derived from the

basic operator based on geodesic transformations of

a signal f (marker) and a second signal g (reference):

• Geodesic reconstruction:

















=





















with 















=









⋀



• Opening by reconstruction:









=











with









 = 









.

A combination of these operators can be used if

we want to reconstruct the water signal and subtract

it from the original signals as it has been introduced

in section 1. In next section the basic morphological

operation will be illustrated.

3 WATER SIGNAL SUPPRESSION

In order to perform water removal, many algorithms

have been proposed since 1990 in the time and

Patient’s Brain

MR Imaging

uisition

Signal

uisitions

Quantitation

Phase Correction

nal Enhancement

Water Removal Parameter Estimation

BIOSIGNALS 2012 - International Conference on Bio-inspired Systems and Signal Processing

382

frequency domain (Vanhamme, Sundin, Hecke and

Huffel, (2001); Poullet, Sima and Huffel, (2008)),

but nowadays only some of them are really used in

multivoxel spectroscopy imaging. Ideally, the FID

signal obtained with the MRS machine is noiseless

and results from the addition of K exponentially

damped sinusoids which are characterized by

frequencies f

, amplitudes A

in arbitrary units (a.u.),

phases φ

, damping factors α

, length of the FID N, i

the square root of -1 and Δt the sampling interval, as:



=

∑

























n= 0,...,N-1. (2)

In order to remove the water signal, the

exponentially damped sinusoids whose frequencies

appear in the water region are estimated and

subtracted from the original FID. For example,

Hankel Lanczos Singular Value Decomposition

(HLSVD-PRO) algorithm (Laudadio, Mastronardi,

Vanhamme, Van Hecke and Van Huffel, 2002),

estimates the whole set of model parameters making

full use of mathematical model functions,

reconstructing the water signal and subtracting it

from the original signals.

Figure 3: Imperfect reconstruction of water contribution to

subtract it from the original signal. In blue and in red the

original and the reconstructed signal respectively.

The main problem of this method lies in the

accurate reconstruction of the water contribution to

subtract it from the original signal (Figure 3);

sometimes the water peak is not well reconstructed,

other times the base of a signal has imperfections

and it is so difficult to fit the parameters. For this

reason, the method proposed in this work uses the

geodesic reconstruction by means of a delta centred

on the maximum value of the original signal as

marker, and the original signal as reference signal,

allowing us to perform the water reconstruction

accurately in frequency domain without affecting

other signals. In figures 4, 5, and 6, the full process

of water suppression is illustrated.

Figure 4: The original spectroscopic signal.

Figure 5: In blue, the delta used as marker. In red, the

reconstructed signal after using geodesic reconstruction.

Figure 6: Residue after performing the process.

4 EXPERIMENTS AND RESULTS

As it was told in section 2, the introduction of

mathematical morphology for 1D signal processing

could help us when we want to suppress water signal

or calculate metabolite quantitation. In Figure 7 the

original spectroscopic signal in black and the water

reconstruction in red using the geodesic

reconstruction are observed together. Then, the red

signal is subtracted from the original one in time

domain, eliminating the large amount of the water.

Figure 7:

H MR original spectroscopy (black) and water

reconstruction (red) signals.

480 490 500 510 520 530 540 550 560

0.5

1.5

2.5

3.5

x 10

0 50 100 150 200 250 300 350 400 450

x 10

O riginal

0 50 100 150 200 250 300 350 400 450

x 10

M arcador (azul) y Reconstruida (rojo)

0 50 100 150 200 250 300 350 400 450

100

200

300

400

500

600

Solo el residuo original-reconstruida (verde)

470 480 490 500 510 520 53 0 540

0.5

1.5

2.5

x 10

original

reconstructed

f (points)

Amplitude (a.u.)

f (points)

Amplitude (a.u.)

1-D MATHEMATICAL MORPHOLOGY FOR WATER REMOVAL IN 1H MR SPECTROSCOPY TOOL

383

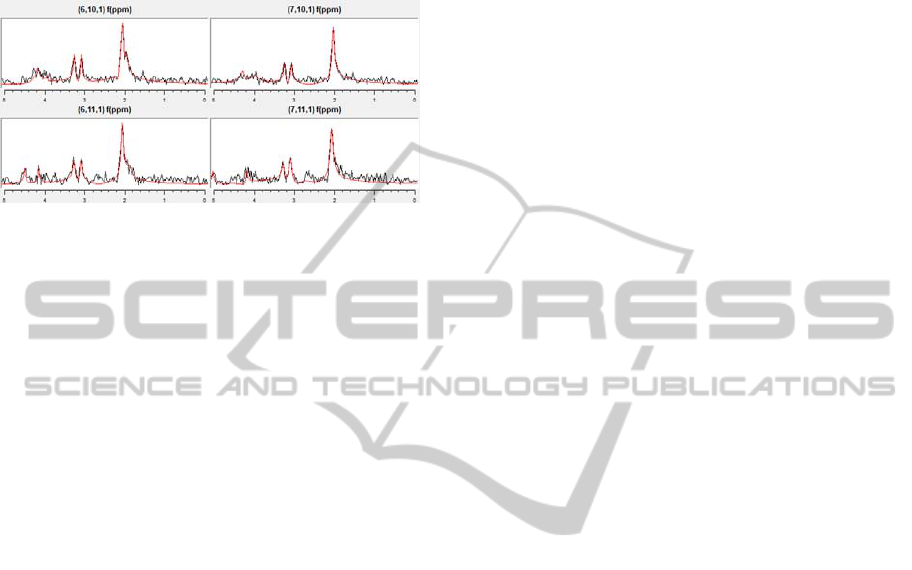
Other processing algorithms as phase correction,

apodize funtions or SNR improvement can be

applied. Figure 8 shows the result after signal

filtering, SNR improvement and HLSVD

quantitation for several spectroscopic signals.

Figure 8: Signal processing for metabolite quantitation.

5 CONCLUSIONS AND FUTURE

WORK

In this paper, we have introduced the use of 1D

mathematical morphology in a software tool to help

surgeons detect brain cancer through the use of the

magnetic resonance spectroscopy. This method is

appropriate for water removal when the metabolite

signals are not overlapped with the water

contribution; otherwise, methods as HLSVD are

recommended in order to avoid a bad suppression.

However, a depth study about the use of

morphological methods in overlapped signals must

be done since an appropriate family of filters can

obtain the desired signal. Coming soon experiments

are focused on the comparison of the proposed

algorithm with other filtering methods to verify its

efficiency and in the study of new quantification

methods based on non-linear filters (1D

mathematical morphology) for its use in MRS.

ACKNOWLEDGEMENTS

This work has been supported by Centro para el

Desarrollo Tecnológico Industrial (CDTI) under the

project ONCOTIC (IDI-20101153), and partially by

projects Consolider-C (SEJ2006-14301/PSIC),

“CIBER of Physiopathology of Obesity and

Nutrition, an initiative of ISCIII” and Excellence

Research Program PROMETEO (Generalitat

Valenciana. Conselleria de Educación, 2008-157).

We would like to express our deep gratitude to the

Hospital Clínica Benidorm for its participation in

this project. The work of Juan José Fuertes has been

supported by a FPI grant from “Programa de Ayudas

de Investigación y Desarrollo (PAID)” of UPV.

REFERENCES

Coron, A., Vanhamme, L., Antoine, J. P., Hecke, P. V.

and Van Huffel, S. (2001). The filtering approach to

solvent peak suppression. Journal of Magnetic

Resonance. 152(1):26-40.

De Beer, R. and Van Ormondt, D. (1992). Analysis of

NMR data using time domain fitting procedures. NMR

Basic Principles and Progress. 26:202-48.

Günther, U. L., Ludwig, C. H., and Rüterjans, H. (2002).

WAVEWAT-improved solvent suppression in NMR

spectra employing wavelet transforms. Journal of

Magnetic Resonance. 156(1):19-25.

Laudadio, T., Mastronardi, N., Vanhamme, L., Van

Hecke, P. and Van Huffel, S. (2002). Improved

Lanczos algorithms for blackbox MRS data

quantitation. Journal of Magnetic Resonance.

157:292-297.

Pijnappel, W. W. F., Van den Boogaart, A., De Beer, R.,

and Van Ormondt, D. (1992). SVD-based

quantiffication of magnetic resonance signals. Journal

of Magnetic Resonance. 97(1):122-134.

Poullet, J. B, Sima, D. M., and Van Huffel, S. (2008).

MRS signal quantitaion: a review of time- and

frewuency-domain methods. Journal of Magnetic

Resonance. 195(2):134-144.

Serra, J. (1982). Image Analysis and Mathematical

Morphology, volume I. Ac. Press, London.

Simonetti, A. W., Poullet, J-B., Sima, D. M., De Neuter,

B., Vanhamme, L., Lemmerling, P., and Van Huffel S.

(2006). An open source short echo time MR

quantitation software solution: AQSES.

Stefan, D., Di Cesare, F., Andrasescu, A., Popa, E.,

Lazariev, A., Vescovo, E., Strbak, O., Williams, S.,

Starcuk, Z., Cabanas, M., Van Ormondt, D., and

Graveron-Demilly, D. (2009). Quantitation of

magnetic resonance spectroscopy signals: the jMRUI

software package. Measurement Science and

Technology, volume 20.

Sundin, T., Vanhamme, L., Van Hecke, P., Dologlou, I.,

and Van Huffel, S. (1999). Accurate quantification of

1H spectra: From infinite impulse response filter

design for solvent suppression to parameter

estimation. Journal of Magnetic Resonance.

139(2):189-204.

Van Huffel, S., Chen, H., Decanniere, C., and Van Hecke,

P. (1994) Algorithm for time-domain NMR data

fitting based on total least squares. Journal of

Magnetic Resonance. 110:228-237.

Vanhamme, L., Sundin, T., Hecke, P. V., and Huffel, S.

V. (2001). MR Spectroscopic Quantitation: a Review

of Time-Domain Methods. NMR in Biomedicine.

14:233-246.

NAA

Cho

BIOSIGNALS 2012 - International Conference on Bio-inspired Systems and Signal Processing

384