
BENEFITS OF GENETIC ALGORITHM FEATURE-BASED
RESAMPLING FOR PROTEIN STRUCTURE PREDICTION
Trent Higgs
1
, Bela Stantic
1
, Tamjidul Hoque
2
and Abdul Sattar
1,3
1
Institute for Integrated and Intelligent Systems (IIIS), Griffith University, Nathan, Australia
2
School of Informatics, Indiana Center for Computational Biology and Bioinformatics
Indiana University Purdue University Indianapolis (IUPUI), Indianapolis, U.S.A.
3
NICTA Queensland Research Laboratory, Nathan, Australia
Keywords:
Genetic algorithms, Protein structure prediction, Feature-based resampling.
Abstract:
Protein structure prediction (PSP) is an important task as the three-dimensional structure of a protein dic-
tates what function it performs. PSP can be modelled on computers by searching for the global free energy
minimum based on Afinsen’s ‘Thermodynamic Hypothesis’. To explore this free energy landscape Monte
Carlo (MC) based search algorithms have been heavily utilised in the literature. However, evolutionary search
approaches, like Genetic Algorithms (GA), have shown a lot of potential in low-resolution models to pro-
duce more accurate predictions. In this paper we have evaluated a GA feature-based resampling approach,
which uses a heavy-atom based model, by selecting 17 random CASP 8 sequences and evaluating it against
two different MC approaches. Our results indicate that our GA improves both its root mean square deviation
(RMSD) and template modelling score (TM-Score). From our analysis we can conclude that by combining
feature-based resampling with Genetic Algorithms we can create structures with more native-like features due
to the use of crossover and mutation operators, which is supported by the low RMSD values we obtained.
1 INTRODUCTION
Critical Assessment of Techniques for Protein Struc-
ture Prediction (CASP) is a worldwide experiment
that was developed to determine the capabilities and
limitations of current protein structure prediction
(PSP) approaches. There have been numerous CASP
experiments starting in 1994 through to 2010, with a
2 year interval between each (Kryshtafovych et al.,
2009). PSP methods are evaluated by performing a
large amount of blind predictions on soon to be re-
leased protein structures.
In PSP numerous search algorithms have been
utilised (Bornberg-Bauer, 1997), (Simons and et al.,
2001), (Shmygelska and Hoos, 2005). Two of the
most popular methods are: Monte Carlo based algo-
rithms (MC) (Simons and et al., 2001) and Genetic
Algorithms (GA) (Hoque et al., 2007). GAs pro-
vide a way of constructing a generalised search ap-
proach, which alleviates the need to change its main
search operators for separate sequences. A tech-
nique that can be easily applied to the GA search
process is feature-based resampling. The intuition
behind feature-based resampling is that various PSP
approaches generate large amounts of local minima,
which may contain features that when combined to-
gether create structures that are more uniformly low
in free energy (Blum, 2008), (Higgs et al., 2010). A
simplistic example of this would be given a predicted
protein structure with one domain wrong, by inter-
mixing this with a protein that has the other domain
correct a structure that is closer to the native confor-
mation is created.
In this paper we compare a Genetic Algorithm
feature-based resampling PSP method (Higgs et al.,
2010) against state-of-the-art benchmark sequences
used in CASP 8, and demonstrate the potential evo-
lutionary algorithms have over other popular search
algorithms like Monte Carlo (MC) based methods. To
do this we have picked 17 random CASP 8 sequences
and have conducted simulations using Rosetta, our
feature-based resampling GA, and a Monte Carlo ap-
proach. This MC method was implemented using
similar move sets, energy calculations, and scoring
methods to allow for a fair comparison.
On average our method performed better than the
MC approach by creating more native-like structures.
It also, in general, did better than Rosetta by obtaining
188
Higgs T., Stantic B., Hoque T. and Sattar A..
BENEFITS OF GENETIC ALGORITHM FEATURE-BASED RESAMPLING FOR PROTEIN STRUCTURE PREDICTION.
DOI: 10.5220/0003770801880194
In Proceedings of the International Conference on Bioinformatics Models, Methods and Algorithms (BIOINFORMATICS-2012), pages 188-194
ISBN: 978-989-8425-90-4
Copyright
c
2012 SCITEPRESS (Science and Technology Publications, Lda.)

an average 10.72% RMSD improvement and 7.76%
TM-Score improvement after resampling. From this
we observed that the overall topology of the protein
formed due to the larger feature-space provided by the
GAs population, and the crossover and mutation op-
erators, which allow to easily and efficiently search
this feature-space.
The rest of this paper is organised as follows. In
Section II we discuss the general background, Sec-
tion III we will outline our methodology, Section IV
presents and analyses the results we gained from our
experimentation, and finally in Section V we draw our
conclusions and mention possible future work.
2 BACKGROUND
Computational PSP methods have been historically
broken up into three categories: comparative mod-
elling (Sali and Blundell, 1993), threading (Zhang
and Skolnick, 2004a), and ab initio. Out of these three
methods ab initio (Simons and et al., 2001) is proba-
bly the most difficult as the target protein usually has
no structurally related protein in the PDB library.
Two popular search algorithms that have been
extensively used in the literature for threading and
ab initio PSP are Monte Carlo based algorithms
(Baker, 2006), (Zhang, 2007), and Genetic Algo-
rithms (Hoque et al., 2009). MC algorithms for PSP
problems work by conducting a random walk of the
energy landscape, using a set of random move sets
(e.g. protein fragment replacement). It only accepts a
new state if the energy is lower than the current state
(i.e. gradient descent) (Brunette and Brock, 2005).
GAs, on the other hand, belong to a specific class
of evolutionary algorithms that are bio-inspired. It
starts off with a large pool of genetic traits, which by
use of genetic operators are reproduced, sometimes
with random mutations, and are subjected to natu-
ral selection (i.e. the fittest survives). In PSP GAs
have proven to be a very successful way of sampling
the free-energy conformational landscape (Unger and
Moult, 1993), (Pedersen and Moult, 1997), (Jiang
et al., 2003), (Arunachalam et al., 2006), (Hoque
et al., 2007), (Hoque et al., 2009), (Higgs et al., 2010).
3 METHODOLOGY
In this publication we apply a GA feature-based re-
sampling algorithm (Higgs et al., 2010) to 17 se-
quences that were used in CASP 8 for our predic-
tions. To gauge the validity of using a GA approach
we will also compare our algorithm against a Monte
Carlo method, which uses a similar approach as our
GA to make it a fair comparison. Both of these meth-
ods will be explained briefly in the next two sections.
3.1 Genetic Algorithm Feature-based
Resampling Approach
A technique that can be applied to the GA search pro-
cess is feature-based resampling. Feature-based re-
sampling is concerned with native-like features from
the previous sampling round. If no models from the
previous round of sampling produces a structure close
enough with the native structure, they still may con-
tain various native-like features, which can be recom-
bined to create new structures that are closer to the
native conformation.
Taking this idea of feature-based resampling we
applied it to a GA based search, which utilises genetic
operators designed for low-resolution lattice models.
Our feature-based resampling GA works by taking
the initial predicted structures from a complete run
of a protein structure prediction (PSP) software us-
ing an arbitrary target protein. These initial structures
are then used as input into our GA for refinement.
The PSP software that we use to create these struc-
tures is Rosetta (Simons and et al., 2001). The rea-
sons for this is two fold: (1) in Critical Assessment of
Techniques for Protein Structure Prediction (CASP)
(Bradley et al., 2003) Rosetta outperformed numer-
ous other PSP software suites in high-resolution struc-
ture prediction, and (2) Rosetta is open source making
it easy to modify and integrate into our GA. For the
same reasons we use Rosetta’s energy function for fit-
ness calculations.
In regards to our GA search operators we use a
roulette wheel procedure for selection. Crossover is
carried out by splicing together protein fragments,
that have native-like features according to the fit-
ness function f , contained within the current popu-
lation. This is done by using a single point crossover
technique that randomly selects a crossover point (n)
where n ∈ Cα(S), Cα(S) refers to the set of Cα atoms
contained within the structure S. Let p1 be parent 1,
and p2 be parent two everything from n onwards in p1
is replaced with everything from n onwards in p2, and
vice versa. This process will produce two offsprings.
Mutation is performed by using a random pivot
rotation move on either the x, y, or z axis. Pivot
rotations work by translating all points to a cho-
sen pivot (n) where n ∈ Cα(S) and rotating the sub-
structure around that pivot point (n + 1 to m). The
sub-structure, in this case, refers to all the points in
a protein structure from n + 1 to the end of the struc-
ture (m). Finally scoring the output of our algorithm
BENEFITS OF GENETIC ALGORITHM FEATURE-BASED RESAMPLING FOR PROTEIN STRUCTURE
PREDICTION
189

Table 1: GA and MC Resampled Results.
Protein
GA MC
RMSD T M RMSD% TM% RMSD T M RMSD% TM%
t0389 11.816
˚
A 0.2733 6.18 23.00 15.74
˚
A 0.1976 7.51 -0.05
t0390 12.913
˚
A 0.1667 10.20 -0.12 18.111
˚
A 0.1237 18.82 14.01
t0392 6.994
˚
A 0.2941 19.78 -10.66 14.57
˚
A 0.1988 4.23 6.37
t0393-D1 10.484
˚
A 0.4149 12.43 38.58 14.951
˚
A 0.247 33.96 11.66
t0395 15.248
˚
A 0.1715 4.07 -7.94 19.818
˚
A 0.1544 6.19 6.93
t0397-D1 7.999
˚
A 0.2067 23.62 9.22 9.16
˚
A 0.2978 14.75 19.98
t0398-D1 12.757
˚
A 0.1847 3.88 17.49 13.47
˚
A 0.1554 17.18 13.51
t0399 12.694
˚
A 0.2213 11.05 14.19 17.535
˚
A 0.1628 4.34 -2.28
t0404 4.674
˚
A 0.4185 6.69 -4.67 5.021
˚
A 0.4024 11.07 7.68
t0405-D1 3.58
˚
A 0.5665 33.67 40.54 6.831
˚
A 0.3171 22.48 3.42
t0405-D2 13.945
˚
A 0.2728 8.77 8.69 15.15
˚
A 0.2274 15.94 -4.33
t0406 9.871
˚
A 0.3457 -7.03 5.85 17.44
˚
A 0.2185 5.49 -19.79
t0407-D1 15.537
˚
A 0.2169 6.93 5.75 19.999
˚
A 0.1894 10.02 13.82
t0407-D2 12.684
˚
A 0.2053 0.03 -4.33 14.214
˚
A 0.2066 27.61 15.74
t0409-D2 9.759
˚
A 0.2874 8.86 -22.19 12.689
˚
A 0.3449 14.24 -5.27
t0411 7.742
˚
A 0.405 4.04 18.08 14.271
˚
A 0.2518 9.07 0.92
t0415 6.523
˚
A 0.3606 29.05 0.47 9.616
˚
A 0.3616 18.09 6.86
is taken care of by two structural measures: root mean
square deviation (RMSD), and template modelling
score (TM-Score) (Zhang and Skolnick, 2004b).
3.2 Monte Carlo Approach
Most Monte Carlo (MC) approaches (Metropolis and
Ulam, 1949) apply random variance to improve a so-
lution. It starts with a random conformation S
1
with
energy E
1
. It then applies some random change to the
conformation to make a new solution S
2
, which has
energy E
2
. If the energy improves (E
2
< E
1
) then ac-
cept the change, otherwise the metropolis criterion is
applied to decide whether or not to accept the change.
In our approach we have used similar techniques
that were applied in our GAs mutation operator to
allow for a fair comparison of the two algorithms.
Therefore, the random change in the MC algorithm
will be conducted by using rotational move sets.
4 RESULTS AND DISCUSSION
For all of our experiments 17 CASP 8 sequences were
chosen to test our algorithms on. Our GA used a 70%
crossover rate, 10% mutation rate, twin removal of
>= 80% similarity, and the algorithm was run for
100 generations. Output from the GA was saved in
10 generation increments (10, 20, 30, ·· · , 100). For
each sequence the structure that had the lowest RMSD
out of all the structures saved was chosen as a repre-
sentative for that sequence.
Our MC algorithm was run for 16000 steps, and
had a temperature value of 2, which is steadily cooled
each step to reach convergence. Starting points for the
MC simulations were also decoys created by Rosetta
to allow for a fair comparison between our GA ap-
proach.
4.1 Empirical Results
A summarisation of our results can be found in Ta-
ble 1. This table contains the protein’s CASP iden-
tification, GA resampled RMSD, GA resampled TM-
Score, GA resampled RMSD and TM-Score improve-
ment in percent over the best Rosetta model in the
initial population, MC resampled RMSD, MC resam-
pled TM-Score, MC resampled RMSD and TM-Score
improvement in percent over the starting point created
with Rosetta. Improvement is measured the same way
as described in (Higgs et al., 2010).
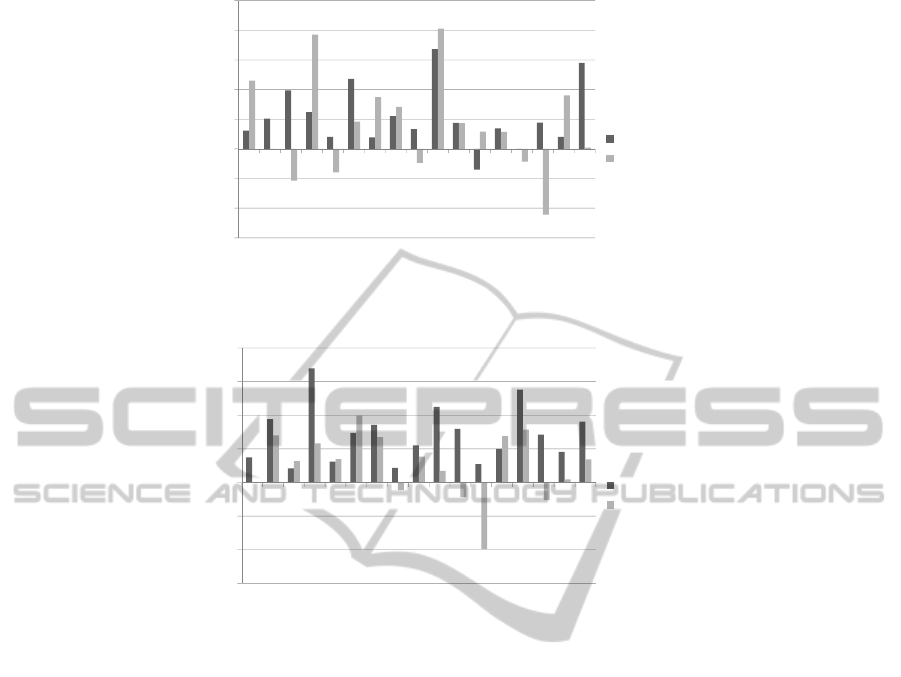
Figures 1(a) and 1(b) show the RMSD and TM-
score improvement in percent over the initial starting
point/s for our GA and MC algorithms. In Figures
1(a) and 1(b) the x axis is the protein’s CASP identi-
fication, and the y axis is the improvement percentage
over the best Rosetta models used in the GA/MC sim-
ulations. We have also depicted a direct comparison
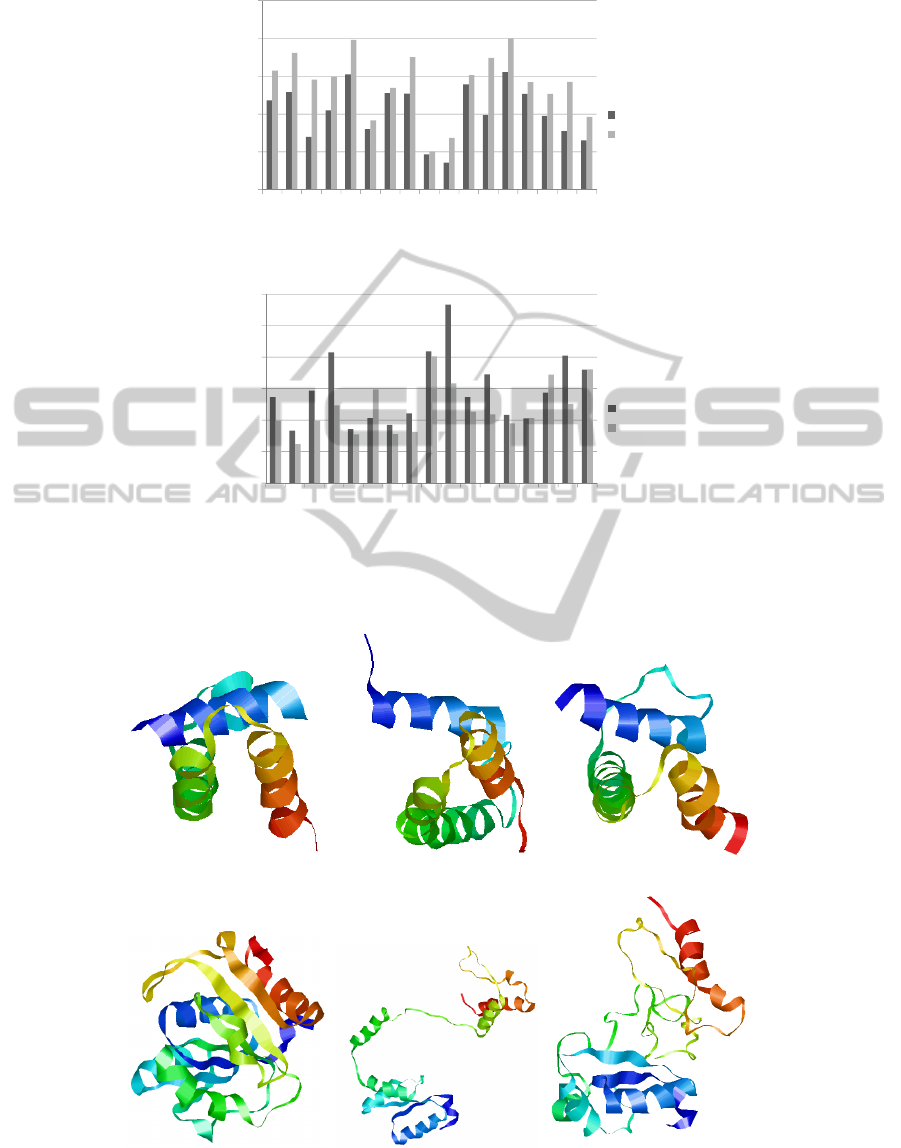
of RMSD and TM-score measures between the two
algorithms in Figures 2(a) and 2(b). In Figures 2(a)
and 2(b) the x axis is the protein’s CASP identifica-
tion, and the y axis is the RMSD/TM-Score value.
And finally in Figure 3 we visually depict our im-
provements for t0405-D1 using our GA approach, and
t0393-D1 using our MC approach.
BIOINFORMATICS 2012 - International Conference on Bioinformatics Models, Methods and Algorithms
190
10
20
30
40
50
RMSD
-30
-20
-10
0
t0389
t0390
t0392
t0393
-
D1
t0395
t0397
-
D1
t0398
-
D2
t0399
t0404
t0405
-
D1
t0405
-
D2
t0406
t0407
-
D1
t0407
-
D2
t0409
-
D2
t0411
t0415
RMSD
TM
t0393
t0397
t0398
t0405
t0405
t0407
t0407
t0409
(a) Genetic Algorithm Approach
0
10
20
30
40
RMSD
-30
-20
-10
0
t0389
t0390
t0392
t0393
-
D1
t0395
t0397
-
D1
t0398
-
D2
t0399
t0404
t0405
-
D1
t0405
-
D2
t0406
t0407
-
D1
t0407
-
D2
t0409
-
D2
t0411
t0415
RMSD
TM
t0393
t0397
t0398
t0405
t0405
t0407
t0407
t0409
(b) Monte Carlo Approach
Figure 1: RMSD and TM-Score improvements over the initial starting points.
4.2 Analysis of Results
First of all we will discuss the results and perfor-
mance of our GA approach in regards to its resam-
pling improvement. From Table 1, and Figure 1(a)
you can see that the resampled structures on average
improve in either RMSD, TM-Score or both, when
compared to the best Rosetta model in the initial pop-
ulation. Over the complete data set we had an aver-
age RMSD improvement of 10.72%, and an average
7.76% TM-Score improvement. The lower average
TM-Score is attributed to a few structures having an
improved RMSD value, but worse TM-Score, which
can be seen in Figure 1(a). Out of the 17 sequences
we used we had 16/17 improvements in RMSD, and
11/17 improvements in TM-Score. The main reason
why it appears that the TM-Score is poor would be
due to the formula we use to calculate improvement.
As the scale of TM-Score is 0 to 1, 1 being exactly
the same as native, the improvement calculation can
make simple changes from 0.3 to 0.2 look like a large
deterioration (i.e. -50%). Finally, to visually demon-
strate the benefits of our GA approach Figure 3 (a)-(c)
demonstrates the structural improvements for one of
our best predicted structures: t0405-D1.
In comparison to our GA, our MC approach per-
formed about on par at resampling Rosetta starting
points (see Table 1, and Figure 1(b)). Out of the 17
sequences we used we had an average 14.18% RMSD
improvement, and an average 5.25% TM-Score im-
provement. Our MC approach had 17/17 structures
with RMSD improvements, and 12/17 structures with
TM-Score improvements. These results provided us
with a similar conclusion as our GA results in re-
gards to the TM-Score deteriorating in some struc-
tures when the RMSD improves. This can also be
blamed on the bias imposed by the improvement mea-
sure we are using. In Figure 3 we show our most im-
proved MC resampled structure (f) compared to its
Rosetta starting point (e), and native conformation
(d).
It is obvious from our results that both algo-
rithms perform quite well at resampling structures
from Rosetta. However, the major difference between
BENEFITS OF GENETIC ALGORITHM FEATURE-BASED RESAMPLING FOR PROTEIN STRUCTURE
PREDICTION
191
10
15
20
25
GA
MC
0
5
t0389
t0390
t0392
t0393
-
D1
t0395
t0397
-
D1
t0398
-
D2
t0399
t0404
t0405
-
D1
t0405
-
D2
t0406
t0407
-
D1
t0407
-
D2
t0409
-
D2
t0411
t0415
MC
(a) RMSD
0.2
0.3
0.4
0.5
0.6
GA
MC
0
0.1
t0389
t0390
t0392
t0393
-
D1
t0395
t0397
-
D1
t0398
-
D2
t0399
t0404
t0405
-
D1
t0405
-
D2
t0406
t0407
-
D1
t0407
-
D2
t0409
-
D2
t0411
t0415
MC
(b) TM-Score
Figure 2: Comparison of RMSD and TM measured values between GA and MC algorithms.
(a) Native (b) Rosetta (c) FBR GA
(d) Native (e) Rosetta (f) FBR MC
Figure 3: In (a)-(c) we compare our GA to Rosetta using protein t0405-D1, and in (d)-(f) we compare our MC implementation
to Rosetta using protein t0405-D1. All proteins were generated with the visualisation program Rasmol (Sayle, 2009).
BIOINFORMATICS 2012 - International Conference on Bioinformatics Models, Methods and Algorithms
192

the two algorithms can be seen in Figures 2(a) and
2(b). In Figure 2(a) we show the RMSD values of our
resampled structures for each algorithm. All of our
GA resampled structures have a lower RMSD value
than our MC resampled structures. In Figure 2(b) our
GA approach has 13 structures with better TM-Score
values, and two that are on par with our MC approach.
The lower the RMSD the closer the structure is to the
native-conformation, and likewise the higher the TM-
Score value is the closer the structure is to the native.
This means that our GA approach, on average, is cre-
ating structures that are closer to the native conforma-
tion. The main reason for this is that it has a larger
feature-space to work with due to the GAs ability to
contain a library of low energy features in its popula-
tion, and by using crossover and mutation operators a
lot more of the conformational landscape can be ex-
plored. In contrast our MC algorithm only uses one
Rosetta decoy as a starting point, and therefore it has
less features at its disposal. This means it is highly
unlikely to find structures that are < 15
˚
A to the native
conformation.
Based on the above analysis we have shown that
using an evolutionary approach can give better re-
sults than other popular algorithms like the Monte
Carlo (MC) method. It also indicated that combining
feature-based resampling with Genetic Algorithms
can create structures with more native-like features,
which is supported by the lower RMSD values we ob-
tained when compared to our MC approach. Due to
this we can infer that more correct features are being
added to the search space, and thus guiding our search
to more accurate structures.
5 CONCLUSIONS
Critical Assessment of Techniques for Protein Struc-
ture Prediction (CASP) is a good way to accurately
indicate how far we have come in solving the protein
prediction problem. In this paper by randomly select-
ing 17 CASP 8 sequences we have demonstrated the
capabilities of our GA feature-resampling approach.
We have also compared it to Rosetta, a state-of-the-
art PSP suite, and another MC algorithm which we
developed to demonstrate the potential evolutionary
algorithms have over other non-deterministic search
algorithms.
Both algorithms were run on a set of 17 randomly
chosen sequences, which were used in the CASP 8
experiment. Our results showed that our GA per-
formed well overall, obtaining good improvements in
both RMSD and TM-Score. This indicated that most
of the overall topology of the protein was forming
throughout our GA search. We have also shown that
evolutionary algorithms have the potential to be more
successful than other non-deterministic search algo-
rithms like MC approaches. Our GA performed very
similar in resampling Rosetta starting points as our
MC approach, however due to having a larger feature-
space our GA approach produced more accurate pre-
dictions than our MC method.
In regards to future work it would be interesting
to look at modelling energy preferences in the fitness
function to enforce a bias on certain features or ar-
rangement of features that are observed in native con-
formations. This could increase the accuracy of our
search, and hence produce better predictions.
REFERENCES
Arunachalam, J., Kanagasabai, V., and Gautham, N. (2006).
Protein structure prediction using mutually orthogonal
latin squares and a genetic algorithm. Biochemical
and Biophysical Research Communications, 342:424–
433.
Baker, D. (2006). Prediction and design of macromolecular
structures and interactions. Philosphical Transactions
of the Royal Society B, 361:459–463.
Blum, B. (2008). Resampling Methods for Protein Structure
Prediction. PhD thesis, Electrical Engineering and
Computer Sciences University of California at Berke-
ley.
Bornberg-Bauer, E. (1997). Chain growth algorithms for
HP-type lattice proteins. In Research in Computa-
tional Molecular Biology RECOMB, pages 47–55.
Bradley, P., Chivian, D., Meiler, J., Misura, K., Rohl,
C., Schief, W., Wedemeyer, W., Scueler-Furman, O.,
Murphy, P., Schonbrun, J., Strauss, C., and Baker, D.
(2003). Rosetta predictions in CASP5: Success, fail-
ure, and prospects for complete automation. PRO-
TEINS: Structure, Function, and Genetics, 53:457–
468.
Brunette, T. and Brock, O. (2005). Improving protein struc-
ture prediction with model-based search. Bioinformat-
ics, 21 (Suppl. 1):i66–i74.
Higgs, T., Stantic, B., Hoque, T., and Sattar, A. (2010).
Genetic algorithm feature-based resampling for pro-
tein structure prediction. In IEEE World Congress on
Computational Intelligence, pages 2665–2672.
Hoque, T., Chetty, M., and Sattar, A. (2007). Protein folding
prediction in 3D FCC HP lattice model using genetic
algorithm. In IEEE Congress on Evolutionary Com-
putation, pages 4138–4145.
Hoque, T., Chetty, M., and Sattar, A. (2009). Extended
HP model for protein structure prediction. Journal of
Computational Biology, 16:85–103.
Jiang, T., Cui, Q., Shi, G., and Ma, S. (2003). Protein fold-
ing simulations of hydrophobic-hydrophilic model by
combining tabu search with genetic algorithms. Jour-
nal of Chemical Physics, 119(8):4592–4596.
BENEFITS OF GENETIC ALGORITHM FEATURE-BASED RESAMPLING FOR PROTEIN STRUCTURE
PREDICTION
193

Kryshtafovych, A., Krzysztof, F., and Moult, J. (2009).
CASP8 results in context of previous experiments.
Proteins: Structure, Function, and Bioinformatics,
77(S9):217–228.
Metropolis, N. and Ulam, S. (1949). The monte carlo
method. Journal of the American Statistical Associ-
ation, 44:335–341.
Pedersen, J. and Moult, J. (1997). Protein folding simula-
tions with genetic algorithms and a detailed molecular
description. Journal of Molecular Biology, 269:240–
259.
Sali, A. and Blundell, T. (1993). Comparative protein mod-
elling by satisfaction of spatial restraints. Journal of
Molecular Biology, 234(3):779–815.
Sayle, R. (2009). Molecular visualization freeware and
rasmol classic site. http://www.umass.edu/microbio/
rasmol/index2.htm.
Shmygelska, A. and Hoos, H. (2005). An ant colony op-
timisation algorithm for the 2D and 3D hydrophobic
polar protein folding problem. BMC Bioinformatics,
6(30).
Simons, K. and et al. (2001). Prospects for ab initio protein
structural genomics. Journal of Moleculer Biology,
306:1191–1199.
Unger, R. and Moult, J. (1993). Genetic algorithms for 3D
protein folding simulations. Journal of Molecular Bi-
ology, 231:75–81.
Zhang, Y. (2007). Template-based modeling and free mod-
eling by I-TASSER in CASP7. Proteins, 8:108–117.
Zhang, Y. and Skolnick, J. (2004a). Automated structure
prediction of weakly homologous proteins on a ge-
nomic scale. PNAS, 101(20):7594–7599.
Zhang, Y. and Skolnick, J. (2004b). Scoring function for au-
tomated assessment of protein structure template qual-
ity. PROTEINS: Structure, Function, and Bioinfor-
matics, 57:702–710.
BIOINFORMATICS 2012 - International Conference on Bioinformatics Models, Methods and Algorithms
194
