
ESTIMATION OF THE COMMON OSCILLATION
FOR PHASE LOCKED MATRIX FACTORIZATION
Miguel Almeida
1,2
, Ricardo Vig´ario
2
and Jos´e Bioucas-Dias
1
1
Institute of Telecommunications, Instituto Superior T´ecnico, Lisbon, Portugal
2
Adaptive Informatics Research Centre, Aalto University School of Science, Finland
Keywords:
Matrix factorization, Phase synchrony, Phase-locking, Independent component analysis, Blind source
separation, Convex optimization.
Abstract:
Phase Locked Matrix Factorization (PLMF) is an algorithm to perform separation of synchronous sources.
Such a problem cannot be addressed by orthodox methods such as Independent Component Analysis, because
synchronous sources are highly mutually dependent. PLMF separates available data into the mixing matrix
and the sources; the sources are then decomposed into amplitude and phase components. Previously, PLMF
was applicable only if the oscillatory component, common to all synchronized sources, was known, which
is clearly a restrictive assumption. The main goal of this paper is to present a version of PLMF where this
assumption is no longer needed – the oscillatory component can be estimated alongside all the other variables,
thus making PLMF much more applicable to real-world data. Furthermore, the optimization procedures in
the original PLMF are improved. Results on simulated data illustrate that this new approach successfully
estimates the oscillatory component, together with the remaining variables, showing that the general problem
of separation of synchronous sources can now be tackled.
1 INTRODUCTION
Synchrony is an increasingly studied topic in modern
science. On one hand, there is an elegant yet deep
mathematical framework which is applicable to many
domains where synchrony is present, including laser
interferometry, the gravitational pull of stellar objects,
and the human brain (Pikovsky et al., 2001).
It is believed that synchrony plays an important
role in the way different sections of human brain in-
teract. For example, when humans perform a motor
task, several brain regions oscillate coherently with
the muscle’s electromyogram (EMG) (Palva et al.,
2005; Schoffelen et al., 2008). Also, processes such
as memorization and learning have been associated
with synchrony; several pathologies such as autism,
Alzheimer’s and Parkinson’s are associated with a
disruption in the synchronization profile of the brain;
and epilepsy is associated with an anomalous increase
in synchrony (Uhlhaas and Singer, 2006).
To infer knowledge on the synchrony of the net-
works present in the brain or in other real-world sys-
tems, one must have access to the dynamics of the
individual oscillators (which we will call “sources”).
Usually, in the brain electroencephalogram (EEG)
and magnetoencephalogram (MEG), and other real-
world situations, individual oscillator signals are not
directly measurable; one has only access to a superpo-
sition of the sources.
1
In fact, EEG and MEG signals
measured in one sensor contain components coming
from severalbrain regions (Nunez et al., 1997). In this
case, spurious synchrony occurs, as has been shown
both empirically and theoretically in previous works
(Almeida et al., 2011a). We briefly review this evi-
dence in Section 2.3.
Undoing this superposition is usually called a
blind source separation (BSS) problem. Typically,
one assumes that the mixing is linear and instanta-
neous, which is a valid and common approximation
in brain signals (Vig´ario et al., 2000) and other ap-
plications. In this case, if the vector of sources is
denoted by s(t) and the vector of measurements by
x(t), they are related through x(t) = Ms(t) where
M is a real matrix called the mixing matrix. Even
with this assumption, the BSS problem is ill-posed:
1
In EEG and MEG, the sources are not individual neu-
rons, whose oscillations are too weak to be detected from
outside the scalp even with no superposition. In this case,
the sources are populations of closely located neurons os-
cillating together.
78
Almeida M., Vigário R. and Bioucas-Dias J. (2012).
ESTIMATION OF THE COMMON OSCILLATION FOR PHASE LOCKED MATRIX FACTORIZATION.
In Proceedings of the 1st International Conference on Pattern Recognition Applications and Methods, pages 78-85
DOI: 10.5220/0003774300780085
Copyright
c
SciTePress

there are infinitely many solutions. Thus, one must
also make some assumptions on the sources, such as
statistical independence in Independent Component
Analysis (ICA) (Hyv¨arinen et al., 2001). However,
in the case discussed in this paper, independence of
the sources is not a valid assumption, because syn-
chronous sources are highly dependent. In this paper
we address the problem of how to separate these de-
pendent sources, a problem we name Separation of
Synchronous Sources, or Synchronous Source Sepa-
ration (SSS). Although many possible formal models
for synchrony exist (see, e.g., (Pikovsky et al., 2001)
and references therein), in this paper we use a simple
yet popular measure of synchrony: the Phase Lock-
ing Factor (PLF), or Phase Locking Value (PLV). The
PLF between two signals is 1 if they are perfectly syn-
chronized. Thus, in this paper we tackle the problem
of source separation where all pairs of sources have a
PLF of 1.
A more general problem has also been addressed,
where the sources are organized in subspaces, with
sources in the same subspace having strong syn-
chrony and sources in different subspaces having
weak synchrony. This general problem was tackled
with a two-stage algorithm called Independent Phase
Analysis (IPA) which performed well in the noiseless
case (Almeida et al., 2010) and with moderate lev-
els of added Gaussian white noise (Almeida et al.,
2011a). In short, IPA uses TDSEP (Ziehe and M¨uller,
1998) to separate the subspaces from one another.
Then, each subspace is a separate SSS problem; IPA
uses an optimization procedure to complete the intra-
subspace separation. Although IPA performs well for
the noiseless case, and for various types of sources
and subspace structures, and can even tolerate moder-
ate amounts of noise, its performance for higher noise
levels is unsatisfactory. Also, in its current form, IPA
is limited to square mixing matrices, i.e., to a num-
ber of measurements equal to the number of sources.
It may as well return singular solutions, where two
or more estimated sources are (almost) identical. On
the other hand, IPA can deal with subspaces of phase-
locked sources and with sources that are not perfectly
phase-locked (Almeida et al., 2011a).
In this paper we address an alternative technique,
named Phase Locked Matrix Factorization (PLMF).
PLMF was originally introduced in (Almeida et al.,
2011b), using a very restrictive assumption, of prior
knowledge of the oscillation common to all the
sources. The goal of this paper is to remove this re-
strictive assumption, and to improve the optimization
of the problem.
Unlike IPA, PLMF can deal with higher amounts
of noise and with non-square mixing matrices (more
measurements than sources). Furthermore, it only
uses variables directly related with the data model,
and is immune to singular solutions. PLMF is in-
spired on the well-known Non-negative Matrix Fac-
torization (NMF) approach (Lee and Seung, 2001),
which is not applicable directly to the SSS problem,
because some factors in the factorization are not pos-
itive, as will be made clear below. For simplicity, we
will restrict ourselves to the case where the sources
are perfectly synchronized.
One should not consider PLMF as a replacement
for IPA, but rather as a different approach to a similar
problem: PLMF is a model-drivenalgorithm, whereas
IPA is data-driven. As we will show, PLMF has ad-
vantages and disadvantages relative to IPA.
This paper is organized as follows. In Sec. 2 we
introduce the Phase Locking Factor (PLF) quantity
which measures the degree of synchronization of two
signals, and show that full synchronization between
two signals has a very simple mathematical character-
ization. Sec. 3 describes the PLMF algorithm in de-
tail. In Sec. 4 we explain how the simulated data was
generated and show the results obtained by PLMF. Di-
rections for future work are discussed in Sec. 5. Con-
clusions are drawn in Sec. 6.
2 PHASE SYNCHRONY
2.1 Phase of a Real-valued Signal
In this paper we tackle the problem of Separation
of Synchronous Sources (SSS). The sources are as-
sumed to be synchronous, or phase-locked: thus, one
must be able to extract the phase of a given signal.
In many real-world applications, such as brain EEG
or MEG, the set of measurements available is real-
valued. In those cases, to obtain the phase of such
measurements, it is usually convenient to construct
a set of complex-valued data from them. Two ap-
proaches have been used in the literature: complex
wavelet transforms (Torrence and Compo, 1998) and
the Hilbert transform (Gold et al., 1973).
In this paper we present only results on simulated
data, which is directly generated as complex-valued,
thus curcumventing this issue.
2.2 Phase-locking Factor
Let φ
j
(t) and φ
k
(t), for t = 1,..., T, be the time-
dependent phases of signals j and k. The real-valued
2
2
“Real-valued” is used here to distinguish from other pa-
pers, where the absolute value operator is dropped, hence
ESTIMATION OF THE COMMON OSCILLATION FOR PHASE LOCKED MATRIX FACTORIZATION
79

Phase Locking Factor (PLF) between those two sig-
nals is defined as
ρ
jk
≡
1
T
T
∑
t=1
e
i
[
φ
j
(t)−φ
k
(t)
]
=
D
e
i
(
φ
j
−φ
k
)
E
, (1)
where h·i is the time average operator, and i =
√
−1.
Note that 0 ≤ ρ
jk
≤1. The value ρ
jk
= 1 corresponds
to two signals that are fully synchronized: their phase
lag, defined as φ
j
(t) −φ
k
(t), is constant. The value
ρ
jk
= 0 is attained if the two phases are not corre-
lated, as long as the observation period T is suffi-
ciently long. Values between 0 and 1 represent par-
tial synchrony. Typically, the PLF values are stored
in a PLF matrix Q such that Q( j, k) ≡ ρ
jk
. Note that
a signal’s PLF with itself is trivially equal to 1: thus,
for all j, ρ
j j
= 1.
2.3 Effect of Mixing on the PLF
The effect of a linear mixing operation on a set of
sources which have all pairwise PLFs equal to 1 is
now discussed. This effect has a simple mathemati-
cal characterization: if s(t) is a set of such sources,
and we define x(t) ≡ Ms(t), with det(M) 6= 0, then
the only possibility for the observations x to have all
pairwise PLFs equal to 1 is if M is a permutation of
a diagonal matrix (Almeida et al., 2011a). Equiva-
lently, the only possibility for that is if x = s up to
permutation and scaling, a typical non-restrictive in-
determinancy in source separation problems.
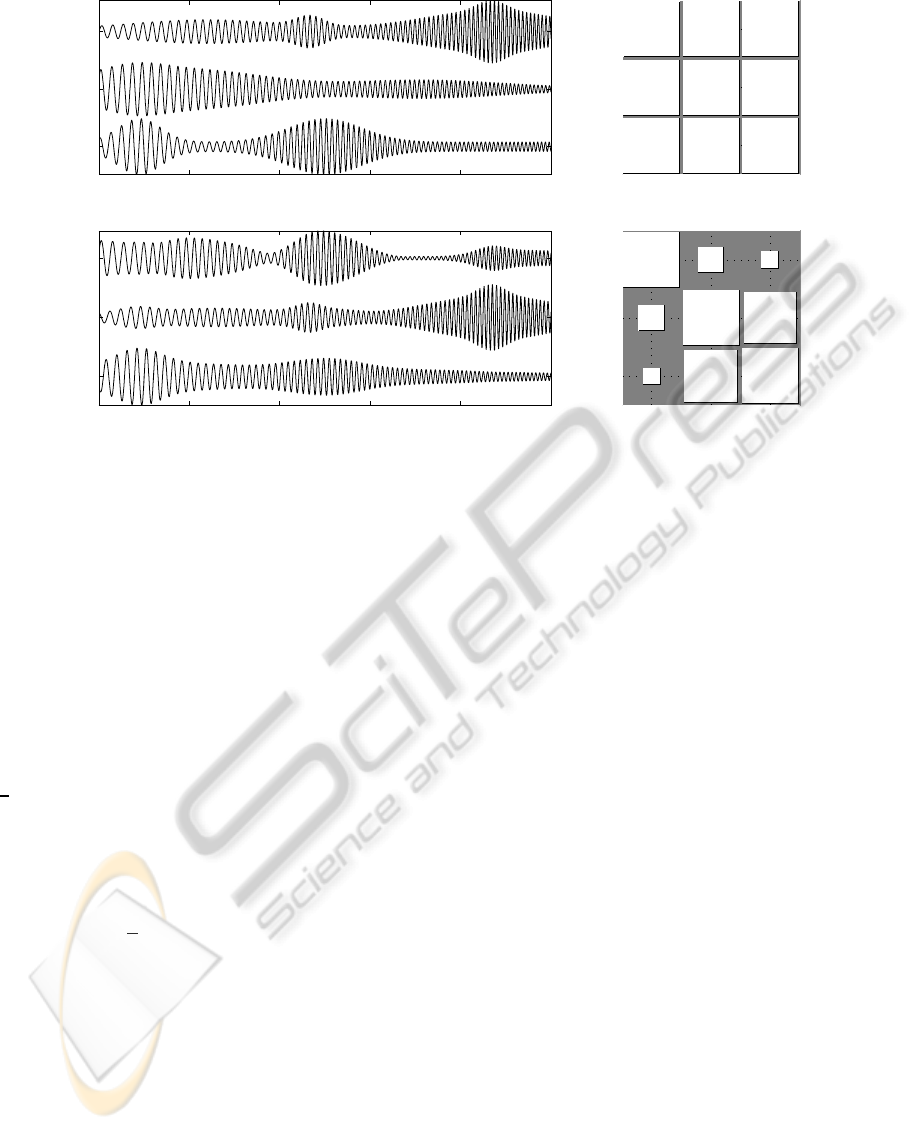
This effect is illustrated in Figure 1, which shows
a set of three perfectly synchronized sources and their
PLFs. That figure also depicts three signals obtained
througha linear mixing of the sources, and their PLFs.
These mixtures have PLFs lower than 1, in accor-
dance with the result stated in the previous paragraph
(even though the PLF between sources 2 and 3 hap-
pens to be rather high, but still not 1).
This property illustrates that separation of these
sources is necessary to make any type of inference
about their synchrony, as measured through the PLF.
If they are not properly separated, the synchrony val-
ues measured will not be accurate. On the other
hand, established BSS methods such as Independent
Component Analysis (ICA) are not adequate for this
task, since phase-locked sources are not independent
(Almeida et al., 2011a). PLMF is a source separation
algorithm tailored specifically for this problem, and it
is presented in the next section.
making the PLF a complex quantity (Almeida et al., 2011a).
3 ALGORITHM
We begin with a summary of the notation and defini-
tions used in this section; we then formulate the opti-
mization problem for PLMF and present a table of the
algorithm at the end.
3.1 Assumptions and General
Formulation
We assume that we have a set of N complex-valued
sources s
j
(t) for j = 1,.. .,N and t = 1,... , T. We
assume also that N is known. Denote by S a N
by T complex-valued matrix whose ( j,t)-th entry is
s
j
(t). One can easily separate the amplitude and
phase components of the sources through S = A⊙Φ,
where ⊙ is the elementwise (or Hadamard) product,
A is a real-valued N by T matrix with its ( j,t) ele-
ment defined as a
j
(t) ≡ |s
j
(t)|, and Φ is a N by T
complex-valued matrix with its ( j,t) element defined
as Φ
j
(t) ≡ e
i(angle(s
j
(t)))
≡ e
iφ
j
(t)
.
The representation of S in amplitude and phase is,
thus far, completely general: it merely represents S in
polar coordinates. We place no constraints on A other
than non-negativity, since it its elements are absolute
values of complex numbers. This is consistent with
the use of the PLF as a measure of synchrony: the
PLF uses no information from the signal amplitudes.
We assume that the sources are perfectly synchro-
nized; as discussed in Section 2.2, in this situation,
∆φ
jk
(t) = φ
j
(t) −φ
k
(t) is constant for all t, for any j
and k. Thus, Φ can be decomposed as
Φ ≡ zf
T
, (2)
where z is a complex-valued column vector of size
N containing the relative phase lags of each source,
and f is a complex-valued column vector of size T
containing the common oscillation. In simpler terms,
if the sources are phase-locked, then rank(Φ) = 1,
and the above decomposition is always possible, even
though it is not unique. Then, the time evolution of
each source’s phase is given by φ
j
(t) = angle(z
j
) +
angle( f
t
), where z
j
and f
t
are the j-th entry of z and
the t-th element of f, respectively.
Although one can conceive complex-valued
sources where the rows of A and the vector f vary
rapidly with time, in real-world systems we expect
them to vary smoothly; for this reason, as will be seen
below, we chose to softly enforce the smoothness of
these two variables in PLMF.
We also assume that we only have access to P
measurements (P ≥ N) that result from a linear mix-
ing of the sources, as is customary in source separa-
tion problems:
X ≡ MS+ N,
ICPRAM 2012 - International Conference on Pattern Recognition Applications and Methods
80
1 2 3
1
2
3
0 1000 2000 3000 4000 5000
3
2
1
1 2 3
1
2
3
0 1000 2000 3000 4000 5000
3
2
1
Figure 1: (Top row) Three sources (left) and PLFs between them (right). (Bottom row) Three mixed signals (left) and PLFs
between them (right). On the right column, the area of the square in position (i, j) is proportional to the PLF between the
signals i and j. Therefore, large squares represent PLFs close to 1, while small squares represent values close to zero.
where X is a P by T matrix containing the measure-
ments, M is a P by N real-valued mixing matrix and
N is a P by T complex-valued matrix of noise. Our
assumption of a real mixing matrix is appropriate in
the case of linear and instantaneous mixing, as mo-
tivated earlier. We will deal only with the noiseless
model, where N = 0, although we then also test how
it copes with noisy data.
The goal of PLMF is to recover S and M us-
ing only X. A simple way to do this is to find
M and S such that the data misfit, defined as
1
2
X−M
A⊙(zf
T
)
2
F
, where k·k
F
is the Frobe-
nius norm, is as small as possible. As mentioned
above, we also want the estimates of A and f to be
smooth. Thus, the minimization problem to be solved
is given by
min
M,A,z,f
1
2
X−M
A⊙(zf
T
)
2
F
+
+ λ
A
kAD
A
k
2
F
+ λ
f
kD
f
fk
2
2
, (3)
s.t.: 1) All elements of M must lie between -1 and +1.
2) All elements of A must be non-negative.
3) All elements of z and f must have
unit absolute value.
where D
A
and D
f
are the first-order difference oper-
ators of appropriate size, such that the entry ( j,t) of
AD
A
is given by a
j
(t) −a
j
(t + 1), and the k-th en-
try of D
f
f is given by f
k
− f
(k+1)
. The first term di-
rectly measures the misfit between the real data and
the product of the estimated mixing matrix and the es-
timated sources. The second and third terms enforce
smoothness of the rows of A and of the vector f, re-
spectively. These two terms allow for better estimates
for A and f under additive white noise, since enforc-
ing smoothness is likely to filter the high-frequency
components of that noise.
Constraint 2 ensures that A represents amplitudes,
whereas Constraint 3 ensures that z and f represent
phases. Constraint 1 prevents the mixing matrix M
from exploding to infinity while A goes to zero. Note
that we also penalize indirectly the opposite indeter-
minancy, where M goes to zero while A goes to in-
finity: that would increase the value of the second
term while keeping the other terms constant, as long
as the rows of A do not haveall elements equal to each
other. Thus, the solution for M lies on the boundary
of the feasible set for M; using this constraint instead
of forcing the L
1
norm of each row to be exactly 1, as
was done in (Almeida et al., 2011b), makes the sub-
problem for M convex, with all the known advantages
that this brings (Boyd and Vandenberghe, 2004).
3.2 Optimization
The minimization problem presented in Eq. (3) de-
pends on the four variables M, A, z, and f. Although
the minimization problem is not globally convex, it
is convex in A and M individually, while keeping the
other variables fixed. For simplicity, we chose to op-
timize Eq. (3) in each variable at a time, by first op-
ESTIMATION OF THE COMMON OSCILLATION FOR PHASE LOCKED MATRIX FACTORIZATION
81

timizing on M while keeping A, z and f constant;
then doing the same for A, followed by z, and then
f. This cycle is repeated until convergence. From our
experience with the method, the particular order in
which the variables are optimized is not critical. Al-
though this algorithm is not guaranteed to converge
to a global minimum, we have experienced very few
cases of local optima.
In the following, we show that the minimiza-
tion problem above can be translated into well-known
forms (constrained least squares problems) for each
of the four variables. We also detail the optimiza-
tion procedure for each of the four sub-problems. For
brevity, we do not distinguish the real variables such
as M from their estimates
ˆ
M throughout this section:
in each sub-problem, only one variable is being esti-
mated, while all the others are kept fixed and equal to
their current estimates.
3.2.1 Optimization on M
If we define m ≡ vec(M) and x ≡ vec(X)
3
, then the
minimization sub-problem for M, while keeping all
other variables fixed, is equivalent to the following
constrained least-squares problem:
min
m
1
2
R (x)
I (x)
−
R (R)
I (R)
m
2
2
(4)
s.t.: −1 ≤m ≤ +1,
where R (.) and I (.) are the real and imaginary parts,
I
P
is the P by P identity matrix, and R ≡ [S
T
⊗I
P
],
with ⊗ denoting the Kronecker product and k·k
2
de-
noting the Euclidean norm. Here, and throughout
this paper, all inequalities should be understood in the
componentwise sense, i.e., every entry of M is con-
strained to be between -1 and +1. For convenience,
we used the least-squares solver implemented in the
MATLAB Optimization Toolbox to solve this prob-
lem, although many other solvers exist.
The main advantage of using the constraint −1 ≤
M ≤ +1 is now clear: it is very simply translated
into −1 ≤ m ≤ +1 after applying the vec(.) opera-
tor, remaining a convex constraint, whereas other con-
straints would be harder to apply.
3.2.2 Optimization on A
The optimization in A can also be reformulated as a
least-squares problem. If a ≡ vec(A), the minimiza-
tion on A is equivalent to
min
a
1
2
R (x)
I (x)
0
(N
2
−N)
−
R (K)
I (K)
√
λ
A
D
A
⊗I
N
a
2
2
(5)
3
The vec(.) operator stacks the columns of a matrix into
a column vector.
s.t.: a ≥0,
where K ≡[(Diag(f)⊗M)Diag(z
0
)], 0
(N
2
−N)
is a col-
umn vector of size (N
2
−N), filled with zeros, and
Diag(.) is a square diagonal matrix of appropriate di-
mension having the input vector on the main diagonal.
We again use the built-in MATLAB solver to solve
this sub-problem.
3.2.3 Optimization on z
The minimization problem in z with no constraints is
equivalent to:
min
z
1
2
kOz−xk
2
2
with O =
f
1
M Diag(a(1))
f
2
M Diag(a(2)))
.
.
.
f
T
M Diag(a(T))
,
(6)
where f
t
is the t-th entry of f, and a(t) is the t-th col-
umn of A. Usually, the solution of this system will
not obey the unit absolute value constraint. To cir-
cumvent this, we solve this unconstrained linear sys-
tem and afterwards normalize z for all sources j and
time instants t, by transferring its absolute value onto
variable A:
a
j
(t) ← |z
j
|a
j
(t) and z
j
← z
j
/|z
j
|.
It is easy to see that the new z obtained after this nor-
malization is still a global minimizer of (6) (where the
new value of A should be used).
3.2.4 Optimization on f
Let
˜
x ≡vec(X
T
). The minimization problem in f with
no constraints can be shown to be equivalent to
min
f
1
2
P
√
λ
f
D
f
f−
˜
x
0
(N−1)
2
2
(7)
with P =
∑
j
m
1j
z
j
Diag(a
j
)
∑
j
m
2j
z
j
Diag(a
j
)
.
.
.
∑
j
m
Pj
z
j
Diag(a
j
)
,
where f
t
is the t-th entry of f, m
ij
is the (i, j) entry of
M, z
j
is the j-th entry of z, and a
j
is the j-th row of
A.
As in the sub-problemfor z, in general the solution
of this system will not obey the unit absolute value
constraint. Thus, we perform a similar normalization,
given by
a
j
(t) ← |f
t
|a
j
(t) and f
t
← f
t
/|f
t
|. (8)
Note that unlike the previous case of the optimization
for z, this normalization changes the cost function, in
ICPRAM 2012 - International Conference on Pattern Recognition Applications and Methods
82
particular the term λ
f
kD
f
fk
2
2
. Therefore, there is no
guarantee that after this normalization we have found
a global minimum for f.
For this reason, we construct a vector of angles
β ≡ angle(f) and minimize the cost function (3) as
a function of β, using 20 iterations of Newton’s al-
gorithm. Although infinitely many values of β cor-
respond to a given f, any of those values is suitable.
The advantage of using this new variable is that there
are no constraints in β, so the Newton algorithm can
be used freely. Thus, the normalized solution of the
linear system in (7) can be considered simply as an
initialization for the Newton algorithm on β, which in
most conditions can find a local minimum.
On the first time that the Newton algorithm is run,
it is initialized using the unconstrained problem (7)
and the ensuing normalization (8). On the second and
following times that it is run, the result of the previous
minimization on f is used as initial value.
3.2.5 Phase Locked Matrix Factorization
The consecutive cycling of optimizations on M, A, z
and f constitutes the Phase Locked Matrix Factoriza-
tion (PLMF) algorithm. A summary of this algorithm
is presented below.
PHASE LOCKED MATRIX FACTORIZATION
1: Input data X
2: Input random initializations
ˆ
M,
ˆ
A,
ˆ
z,
ˆ
f
3: for iter ∈ {1,2,...,MaxIter}, do
4: Solve the constrained problem in Eq. (4)
5: Solve the constrained problem in Eq. (5)
6: Solve the unconstrained system in Eq. (6)
7: a
j
(t) ← |z
j
|a
j
(t) and z
j
← z
j
/|z
j
|, j = 1, ... ,N
8: if iter = 1
9: Solve the unconstrained system in Eq. (7)
10: a
j
(t) ← |f
t
|a
j
(t) and f
t
← f
t
/|f
t
|, t = 1, ... ,T
11: Optimize β ≡angle(f) with Newton algorithm
(use result of step 10 as initialization)
12: else
13: Optimize β ≡angle(f) with Newton algorithm
(use Newton algorithm from (iter-1) as init.)
14: end for
4 SIMULATION AND RESULTS
In this section we show results on small simulated
datasets, demonstrating that PLMF can correctly fac-
tor the data X into a mixing matrix M, amplitudes
A, and phases z and f. Despite deriving PLMF for
the noiseless case, we will also test its robustness to a
small noisy perturbation.
4.1 Data Generation
We generate the data directly from the model X =
MS, with S = A⊙Φ = A⊙(zf
T
), taking N = 2 and
P = 4. The number of time samples is T = 100. M
is taken as a random matrix with entries uniformly
distributed between -1 and +1. We then normalize
M so that the entry with the largest absolute value is
±1. Each row of A (i.e. each source’s amplitude) is
generated as a sum of a constant baseline and 2 to 5
Gaussians with random mean and random variance.
z is generated by uniformly spacing the N sources in
the interval
0,
2π
3
.
4
f is generated as a complex si-
nusoid with angular frequency 0.06 in the first half
of the observation period, and angular frequency 0.04
in its second half, in a way that f has no discontinu-
ities. X is then generated according to the data model:
X = M(A⊙(zf
T
)).
The initial values for the estimated variables are
all random: elements of
ˆ
M and
ˆ
A are drawn from the
Uniform([0,1]) distribution (
ˆ
M is then normalized in
the same way as M), while the elements of
ˆ
z are of
the form e
iα
with α taken from the Uniform
0,
π
2
distribution. The elements of f are also of the form
e
iβ
, with β uniformly distributed between 0 and 2π.
We generate 100 datasets of each of two types of
datasets with the following features:
• Dataset 1: 2 sources, 4 sensors, 100 time points,
no noise.
• Dataset 2: exactly the same data as dataset 1, plus
complex Gaussian noise with standard deviation
0.1, added after the mixture (additive noise).
4.2 Quality Measures
ˆ
M can be compared with M through the gain matrix
G ≡
ˆ
M
+
M, where
ˆ
M
+
is the Moore-Penrose pseudo-
inverse of
ˆ
M (Ben-Israel and Greville, 2003). This is
the same as
ˆ
M
−1
M if the number of sensors is equal
to the number of sources. If the estimation is well
done, the gain matrix should be close to a permutation
of the identity matrix. After manually compensating
a possible permutation of the estimated sources, we
compare the sum of the squares of the diagonal el-
ements of G with the sum of the squares of its off-
diagonal elements. This is a criterion not unlike the
well-known Signal-to-Interference Ratio (SIR), but
our criterion depends only on the true and estimated
mixing matrices. Since this criterion is inspired on the
SIR, we call this criterion pseudo-SIR, or pSIR.
4
This choice of z is done to ensure that the sources never
have phase lags close to 0 or π, which violate the mild as-
sumptions mentioned in Section 2.3 (Almeida et al., 2011a).
ESTIMATION OF THE COMMON OSCILLATION FOR PHASE LOCKED MATRIX FACTORIZATION
83

Table 1: Comparison of the estimated mixing matrix
ˆ
M
with the true mixing matrix M through the pseudo-SIR of
the gain matrix G ≡
ˆ
M
+
M. For zero noise (dataset 1), the
estimation is quite good, and the performance hit due to the
presence of noise (dataset 2) is minimal.
Data pSIR (dB)
Dataset 1 21.2 ± 11.3
Dataset 2 20.7 ± 11.7
Also,
ˆ
A will be compared to A through visual in-
spection for one dataset with a pSIR close to the aver-
age pSIR of the 100 datasets.
4.3 Results
We did not implement a convergence criterion; we
simply do 400 cycles of the optimization on M, A, z
and f using λ
A
= 3 and λ
f
= 1. The mean and standard
deviation of the pSIR criterion are presented in Ta-
ble 1. Figure 2 shows the results of the estimation of
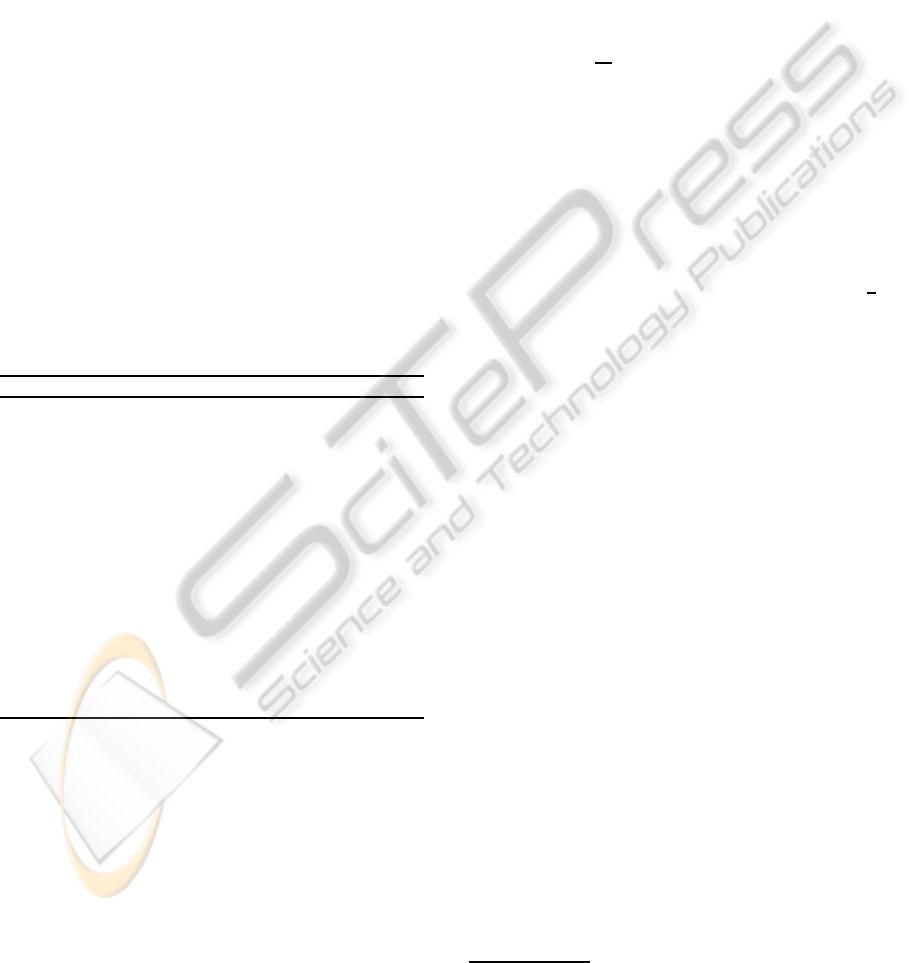
the source amplitudes for one representative dataset,
showing that
ˆ
A is quite close to the real A for both the
noiseless and the noisy datasets. Note that if noise is
present, it is impossible to recreate the original ampli-
tudes as they are only present in the data corrupted by
noise: one can thus only estimate the corrupted am-
plitudes. If desired, a simple low-pass filtering proce-
dure can closely recreate the original amplitudes.
These results illustrate that PLMF can separate
phase-locked sources in both the noiseless and the
noisy condition. Furthermore, they show that the per-
formance hit due to the presence of a small amount
of noise is minimal, suggesting that PLMF has good
robustness against small perturbations.
5 DISCUSSION
The above results show that this approach has a
high potential, although some limitations must be ad-
dressed to turn this algorithm practical for real-world
applications.
The values of the parameters that we chose were
somewhat ad hoc. Nevertheless, it is likely that
knowledge of the covariance of the additive noise al-
lows one to choose the values of these parameters op-
timally.
One incomplete aspect of PLMF is its lack of a
stopping criterion; in fact, the results shown in Table
1 could be considerably improved if the number of it-
erations is increased to, say, 1000, although that is not
the case for all of the 100 datasets. We did not tackle
this aspect due to lack of time; however, the data mis-
0 10 20 30 40 50 60 70 80 90 100
0.4
0.6
0.8
1
1.2
1.4
1.6
1.8
0 10 20 30 40 50 60 70 80 90 100
0.4
0.6
0.8
1
1.2
1.4
1.6
1.8
Figure 2: Visual comparison of the estimated amplitudes
ˆ
A
(dashed lines) with the true amplitudes A (solid lines), for
a representative dataset, after both are normalized so that
they have unit means over the observation period. (Top) Re-
sults for dataset 1: the two estimated amplitudes are close
to the true values. (Bottom) Results for dataset 2: due to
the presence of noise, it is impossible for the two estimated
amplitudes to coincide perfectly with the true ones, but nev-
ertheless the estimated amplitudes follow the real ones very
closely.
fit (first term of the cost function) can probably be
used to design a decent criterion.
If the sources are not perfectly phase-locked, their
pairwise phase differences ∆φ
ij
are not constant in
time and therefore one cannot represent the source
phases by a single vector of phase lags z and a single
vector f with a common oscillation. In other words, Φ
will have a rank higher than 1 (in most cases, it will
have the maximum possible rank, which is N), which
makes a representation Φ = zf
T
impossible. We are
investigating a way to estimate the “most common”
phase oscillation f from the data X, after which PLMF
can be used to initialize a more general algorithm that
estimates the full Φ. We are currently testing also
a more general algorithm, which optimizes Φ with a
gradient descent algorithm. Yet, it is somewhat prone
to local minima, as one would expect for optimizing
variables of size NT = 200. A good initialization is
likely to alleviate this problem.
Another limitation of PLMF is the indetermina-
ICPRAM 2012 - International Conference on Pattern Recognition Applications and Methods
84

tion that arises if two sources have ∆φ
ij
= 0 or π. In
that case, the problem becomes ill-posed, as was al-
ready the case in IPA (Almeida et al., 2011a). In fact,
using sources with ∆φ
ij
<
π
10
starts to deteriorate the
results of PLMF, even with zero noise.
One further aspect which warrants discussion is
PLMF’s identifiability. If we find two factorizations
such that X = M
1
A
1
⊙(z
1
f
T
1
)
= M
2
A
2
⊙(z
2
f
T
2
)
(i.e., two factorizations which perfectly describe the
same data X), does that imply that M
1
= M
2
, and
similar equalities for the other variables? It is quite
clear that the answer is negative: the usual indeter-
minancies of BSS apply to PLMF as well, namely
the indeterminancies of permutation, scaling, and sign
of the estimated sources. There is at least one fur-
ther indeterminancy: starting from a given solution
X = M
1
A
1
⊙(z
1
f
T
1
)
, one can always construct a
new one by defining z
2
≡ e
iψ
z
1
and f
2
≡ e
−iψ
f
1
,
while keeping M
2
≡ M
1
and A
2
≡ A
1
. Note that
S
1
= A
1
⊙(z
1
f
T
1
) = A
2
⊙(z
2
f
T
2
) = S
2
, thus the esti-
mated sources are exactly the same.
6 CONCLUSIONS
We presented an improved version of Phase Locked
Matrix Factorization (PLMF), an algorithm that di-
rectly tries to reconstruct a set of measured signals as
a linear mixing of phase-locked sources, by factoriz-
ing the data into a product of four variables: the mix-
ing matrix, the source amplitudes, their phase lags,
and a common oscillation.
PLMF is now able to estimate the sources even
when their common oscillation is unknown – an ad-
vantage which greatly increases the applicability of
the algorithm. Furthermore, the sub-problem for M
is now convex, and the sub-problems for z and f are
tackled in a more appropriate manner which should
find local minima. The results show good perfor-
mance for the noiseless case and good robustness to
small amounts of noise. The results show as well that
the proposed algorithm is accurate and can deal with
low amounts of noise, under the assumption that the
sources are fully phase-locked, even if the common
oscillation is unknown. This generalization brings us
considerably closer to being able to solve the Separa-
tion of Synchronous Sources (SSS) problem in real-
world data.
ACKNOWLEDGEMENTS
This work was partially funded by the DECA-Bio
project of the Institute of Telecommunications, and
by the Academy of Finland through its Centres of Ex-
cellence Program 2006-2011.
REFERENCES
Almeida, M., Bioucas-Dias, J., and Vig´ario, R. (2010). In-
dependent phase analysis: Separating phase-locked
subspaces. In Proceedings of the Latent Variable
Analysis Conference.
Almeida, M., Schleimer, J.-H., Bioucas-Dias, J., and
Vig´ario, R. (2011a). Source separation and cluster-
ing of phase-locked subspaces. IEEE Transactions on
Neural Networks, 22(9):1419–1434.
Almeida, M., Vigario, R., and Bioucas-Dias, J. (2011b).
Phase locked matrix factorization. In Proc. of the EU-
SIPCO conference.
Ben-Israel, A. and Greville, T. (2003). Generalized in-
verses: theory and applications. Springer-Verlag.
Boyd, S. and Vandenberghe, L. (2004). Convex Optimiza-
tion. Cambridge University Press.
Gold, B., Oppenheim, A. V., and Rader, C. M. (1973). The-
ory and implementation of the discrete hilbert trans-
form. Discrete Signal Processing.
Hyv¨arinen, A., Karhunen, J., and Oja, E. (2001). Indepen-
dent Component Analysis. John Wiley & Sons.
Lee, D. and Seung, H. (2001). Algorithms for non-negative
matrix factorization. In Advances in Neural Informa-
tion Processing Systems, volume 13, pages 556–562.
Nunez, P. L., Srinivasan, R., Westdorp, A. F., Wijesinghe,
R. S., Tucker, D. M., Silberstein, R. B., and Cadusch,
P. J. (1997). EEG coherency I: statistics, refer-
ence electrode, volume conduction, laplacians, cor-
tical imaging, and interpretation at multiple scales.
Electroencephalography and clinical Neurophysiol-
ogy, 103:499–515.
Palva, J. M., Palva, S., and Kaila, K. (2005). Phase syn-
chrony among neuronal oscillations in the human cor-
tex. Journal of Neuroscience, 25(15):3962–3972.
Pikovsky, A., Rosenblum, M., and Kurths, J. (2001). Syn-
chronization: A universal concept in nonlinear sci-
ences. Cambridge Nonlinear Science Series. Cam-
bridge University Press.
Schoffelen, J.-M., Oostenveld, R., and Fries, P. (2008).
Imaging the human motor system’s beta-band syn-
chronization during isometric contraction. NeuroIm-
age, 41:437–447.
Torrence, C. and Compo, G. P. (1998). A practical guide
to wavelet analysis. Bull. of the Am. Meteorological
Society, 79:61–78.
Uhlhaas, P. J. and Singer, W. (2006). Neural synchrony in
brain disorders: Relevance for cognitive dysfunctions
and pathophysiology. Neuron, 52:155–168.
Vig´ario, R., S¨arel¨a, J., Jousm¨aki, V., H¨am¨al¨ainen, M., and
Oja, E. (2000). Independent component approach to
the analysis of EEG and MEG recordings. IEEE
Trans. On Biom. Eng., 47(5):589–593.
Ziehe, A. and M¨uller, K.-R. (1998). TDSEP - an effi-
cient algorithm for blind separation using time struc-
ture. In International Conference on Artificial Neural
Networks, pages 675–680.
ESTIMATION OF THE COMMON OSCILLATION FOR PHASE LOCKED MATRIX FACTORIZATION
85
