
NONINVASIVE CARDIOVASCULAR SYSTEM
IDENTIFICATION USING PULSE WAVE TRANSIT TIME
Sérgio Okida
1,2
, Pedro Giassi Júnior
2
, João Fernando Refosco Baggio
2
, Raimes Moraes
2
,
Maurício Gonçalves de Oliveira
3
and Gastão Fernandes Duval Neto
4
1
Electronics Coordination, Federal University of Technology of Paraná, Ponta Grossa, PR, Brazil
2
Electrical Engineering Department, Federal University of Santa Catarina, Florianópolis, SC, Brazil
3
Medical School Hospital, Federal University of Santa Catarina, Florianópolis, SC, Brazil
4
Faculty of Medicine, Federal University of Pelotas, Pelotas, RS, Brazil
Keywords: Heart Rate Variability, Autonomic Nervous System, System Identification, Autoregressive Moving Average
Model, Pulse Wave Transit Time.
Abstract: This work shows that it is possible to model the heart rate autonomic control from samples of ECG, PPG
and respiratory flow waveform (RFW). Usually, such modelling is carried out with physiological signals
that are more difficult to acquire during the clinical exams: ECG, arterial blood pressure and instantaneous
lung volume. In this work, the ECG, PPG and RFW were recorded with a portable system from volunteers
at two different postures: supine and standing. The ECG, PPG and RFW were processed off line in order to
obtain the RR, the inverse of the pulse wave transit time (IPWTT) and the RFW series. These series were
used as input for ARMA models and the obtained results were compared to the ones available in the
literature. The qualitative and quantitative comparisons of the results reveal very similar performance.
1 INTRODUCTION
The power spectral density (PSD) analysis of the
heart rate variability (HRV) is widely used for the
non-invasive assessment of the autonomic nervous
system (ANS). The higher frequency (HF)
components of the HRV (0.15 to 0.4 Hz) are related
to the breathing rate (Respiratory Sinus Arrhythmia -
RSA) and mediated by the parasympathetic system
(Pagani et al., 1986; Berntson et al., 1997). The
lower frequency components (LF: 0.04 to 0.15 Hz)
comprise the Mayer waves (around 0.1Hz) and
contain oscillations due to the interactions between
the heart rate (HR) and the blood pressure (BP). The
LF power is affected by both sympathetic and
parasympathetic systems. The LF/HF power ratio is
often used as an index of the sympathovagal balance
(Pagani et al., 1986; Task Force, 1996).
Although the spectral analysis contributes to the
understanding of the heart rate autonomic control, it
characterizes the output and not the system itself.
Modelling allows the system characterization, i.e., to
obtain the transfer functions between each input and
the output and their impulse responses (Xiao et al.,
2005).
The cardiovascular system neural control has
been modelled by a multi-input/single-output
(MISO) system, using as inputs, the arterial blood
pressure (ABP) and the instantaneous lung volume
(ILV) and, as output, the HRV (Perrott and Cohen,
1996). Systolic blood pressure (SBP) series obtained
from the ABP waveform has also been used as input
to discrete models instead of ABP samples (e.g.,
Baselli et al., 1997).
The instantaneous ABP is registered by a
catheter inserted into an artery or non-invasively,
using commercial systems such as the Finapress
(Ohmeda Inc). The ILV is usually measured using
chest-abdomen inductance plethysmography.
Research on the cardiovascular models has
provided useful data to characterize patients’ clinical
condition (Xiao et al., 2005; Faes et al., 2006).
Nevertheless, the acquisition of the ILV and ABP as
described above may hamper the broad use of
models to obtain diagnosis indexes. The chest-
abdomen inductance plethysmograph is cumbersome
in procedures during which cardiac arrest may
occur. The Finapress is not available in many
clinical facilities and it is susceptible to movement
artefacts. Besides, it is also difficult to synchronize
232
Okida S., Giassi Júnior P., Fernando Refosco Baggio J., Moraes R., Gonçalves de Oliveira M. and Duval Neto G..
NONINVASIVE CARDIOVASCULAR SYSTEM IDENTIFICATION USING PULSE WAVE TRANSIT TIME.
DOI: 10.5220/0003775402320237
In Proceedings of the International Conference on Bio-inspired Systems and Signal Processing (BIOSIGNALS-2012), pages 232-237
ISBN: 978-989-8425-89-8
Copyright
c
2012 SCITEPRESS (Science and Technology Publications, Lda.)

signals acquired from different commercial systems
since no information is usually provided on their
processing (time delay).
As alternatives to the use of the SBP and ILV as
model inputs, the pulse wave transit time (PWTT)
and respiratory flow waveforms (RFW) are here
investigated.
The PWTT, usually defined as the interval
between the ECG R-wave
and the base of the
leading photoplethysmography (PPG) deflection
within a same cardiac cycle (Figure 1), has been
shown to be significantly correlated to the systolic
blood pressure (SBP). The SBP is inversely
proportional to the PWTT (Lass et al., 2004; Teng
and Zhang, 2006).
Figure 1: The PWTT is the interval between the ECG R-
wave peak and the base of the leading edge of the PPG.
The RR series is a measurements set of the time interval
between consecutive ECG R-waves.
Eckberg (2003) suggests that the mechanical
stretch of pulmonary and thoracic receptors has
small contribution to the RSA, pointing out that the
RSA is mainly generated by the central respiratory
motoneurone activity. Therefore, the breathing rate
obtained from the inspired and expired flow
waveform (acquired by nasal thermometry) may
convey information on the respiratory motoneurone
discharges that affect the HRV.
This work investigates the feasibility of using the
PWTT series and the RFW samples as inputs for the
cardiovascular system neural control modelling.
These signals can be acquired with a simple system,
barely disturbing the usual clinical exams.
Therefore, their use circumvents practical
difficulties to obtain useful indexes from models in
order to help assessing patients’ health.
2 MATERIALS AND METHODS
This section describes the acquisition of the
physiological signals from healthy volunteers and
the methods used to model the HRV.
2.1 Subjects
Five volunteers (4 males; 1 female; age: 22-46
years; ASA1) took part of the study. The protocol
(Project 529/10) was approved by the Research
Ethics Committee of the Federal University of Santa
Catarina (UFSC). These subjects were informed
about the protocol and gave their written consent.
The experiments were carried out at the Medical
School Hospital of the UFSC.
2.2 Protocol
The experimental data were recorded from
volunteers at two different postures: supine and
standing. After changing the posture, five minutes
were waited for hemodynamic stabilization before
the data acquisition.
At each position, the subjects breathed according
to two different patterns guided by a metronome.
The first pattern corresponds to a broadband
respiratory signal (Poisson distribution) necessary as
input to generate a reliable autonomic heart rate
control model (Berger et al., 1989). This pattern
consists of breathing cycles ranging from 1 to 15s
(mean=5s) during 6 minutes.
The second pattern is paced breathing at the rate
of 12 breaths/min. This pattern was recorded for
each subject during 2 minutes.
2.3 Signal Acquisition and
Discrete–time Signal Processing
A portable device developed in our laboratory was
employed to acquire the required waveforms: RFW
by nasal thermometry, EGC and PPG. The RFW,
ECG and PPG were filtered by band-pass second
order Butterworth filters to limit their bandwidths to
0-6Hz, 0.5-100Hz and 0.8-10Hz, respectively. The
filtered waveforms were sampled at the rate of 1
kSPS and converted to 12-bit words. The sampled
waveforms were transmitted via Bluetooth to a
laptop computer where they were stored into
separated files (16 bits Intel PCM format). More
information on the developed system can be found
elsewhere (Giassi Jr. et al., 2011).
The sampled waveforms were processed off line
in order to obtain the inputs series for the models.
NONINVASIVE CARDIOVASCULAR SYSTEM IDENTIFICATION USING PULSE WAVE TRANSIT TIME
233

The ECG, PPG and RFW were further filtered by
digital FIR filters in order to attenuate interfering
signals. The ECG, PPG and RFW bandwidths were
limited to 0.5-40Hz, 0.26-15Hz and 0-0.75Hz,
respectively.
The R-wave peaks of the ECG were detected
using continuous wavelet transform (CWT) as
proposed by Ghaffari et al. [9]. According to these
authors, the algorithm achieved a sensitivity of
99.91% and a predictivity of 99.72% when applied
to signals of the MIT/BIH database. The RR series is
the measurements set of the time interval between
consecutive R-waves of the ECG. As it corresponds
to an irregularly sampled waveform, the RR series
was linearly interpolated to achieve the sampling
rate of 1.5 SPS. The HR consists of the inverse
interpolated RR series.
The ECG and the PPG are used to obtain the
PWTT series. The Figure 1 shows a PWTT
measurement for a cardiac cycle. The PWTT is the
time interval between the R-wave peak and the base
point within the same cardiac cycle. Following Chiu
et al. (1991), the base marker corresponds to the
intersection of the tangent through the steepest part
of the slope (determined by the maximum first
derivative point) with its baseline. The PWTT series
is the set of these consecutive measurements. The
IPWTT series corresponds to 1/PWTT. The IPWTT
series was also interpolated to achieve 1.5 SPS.
The RFW was decimated to 1.5 SPS in order to
have all the input signals sampled at the same rate.
The use of this sampling rate allows the comparison
of the obtained impulse responses to those of Perrott
and Cohen (1996).
The smoothness priors approach (Tarvainen et
al., 2001) was used to detrend the HR, IPWTT and
RFW. For that, the lambda value used was 50 that
makes the detrending to correspond to a high-pass
filter with a cut-off frequency of 0.0375 Hz.
The HR, RFW and the IPWTT series were then
normalized by their respective standard deviation.
2.4 The Model
Closed-loop systems have been proposed to model the
cardiovascular system neural control to take into
account the SBP and heart rate (HR) interactions
(Appel et al., 1989). Nevertheless, Takalo et al.
(2004) showed that the transfer functions obtained
from the open-loop model proposed by Perrott and
Cohen (1996) were not significantly different from
those obtained by the closed-loop model. In order to
assess the adequacy of the IPWTT and RFW as model
inputs, this work employs the open-loop model.
Briefly, the open-loop model is described by the
Eq. 1 where the usual ILV and SBP inputs are
replaced by RFW and IPWTT, respectively.
[
]
=−
∑
a
[
]
[ − ]
+
+
∑
b
[
j
]
RFW
[
n−j
]
+
(1)
+
∑
[]
[
−
]
+[]
where n, i, j and k are discrete time indexes; a
[
i
]
are
the autoregressive (AR) coefficients; b[j] and c[k]
are the moving average (MA) coefficients and e[n]
is the estimation error of the model. N, M and Q
define the order of the model. m and q stand for
delays between each input and the output.
Due to the non-causal coupling between the
breathing and the HR (RFW→HR) (Mullen et al.,
1997), m was made equal to -4.
The interactions of the SPB and HR are mediated
by their autonomic coupling (IPWTT→HR) and
also, by the mechanical effects of the HR on the SBP
(HR→IPWTT). To disentangle that, it is necessary
to impose causality (Mullen et al., 1997) that is
achieved by making q equal to 1.
The coefficients estimates are calculated using
the least square method. The multivariate model
order was determined by means of the
autoregressive moving average (ARMA) parameter
reduction method: APR (Perrot and Cohen, 1996).
Applying the Z transform to the Eq. 1, the
transfer functions between each input and the output
are given by:
,
(
)
=
()
()
=
∑
b(j)
z
1+
∑
a
(
i
)
z
(2)
,
(
)
=
()
()
=
∑
c(k)
z
1+
∑
a
(
i
)
z
(3)
From these equations, each impulse response
(RFW→HR and IPWTT→HR) can be obtained by
applying the inverse Z transform for RFW(z)=1 and
IPWTT(z)=1.
2.5 Statistical Analysis
The Student’s t-test was used to compare the power
of the LF and HF bands between the PSD curves
obtained from the measured (LF
measured
and
HF
measured
) HR and from the modelled (LF
model
and
HF
model
) HR. This was repeated for the different
postures and breathing patterns. A p-value below
BIOSIGNALS 2012 - International Conference on Bio-inspired Systems and Signal Processing
234
0.05 was chosen as threshold for statistical
significance.
3 RESULTS
From the data recorded during the broadband
respiratory protocol, the ARMA model order and its
coefficients were estimated for each volunteer.
With the estimated ARMA model parameters of
each subject, HR output series were generated from
the IPWTT and RFW series obtained for irregular
(broadband) and paced breathing patterns at the
supine and standing postures.
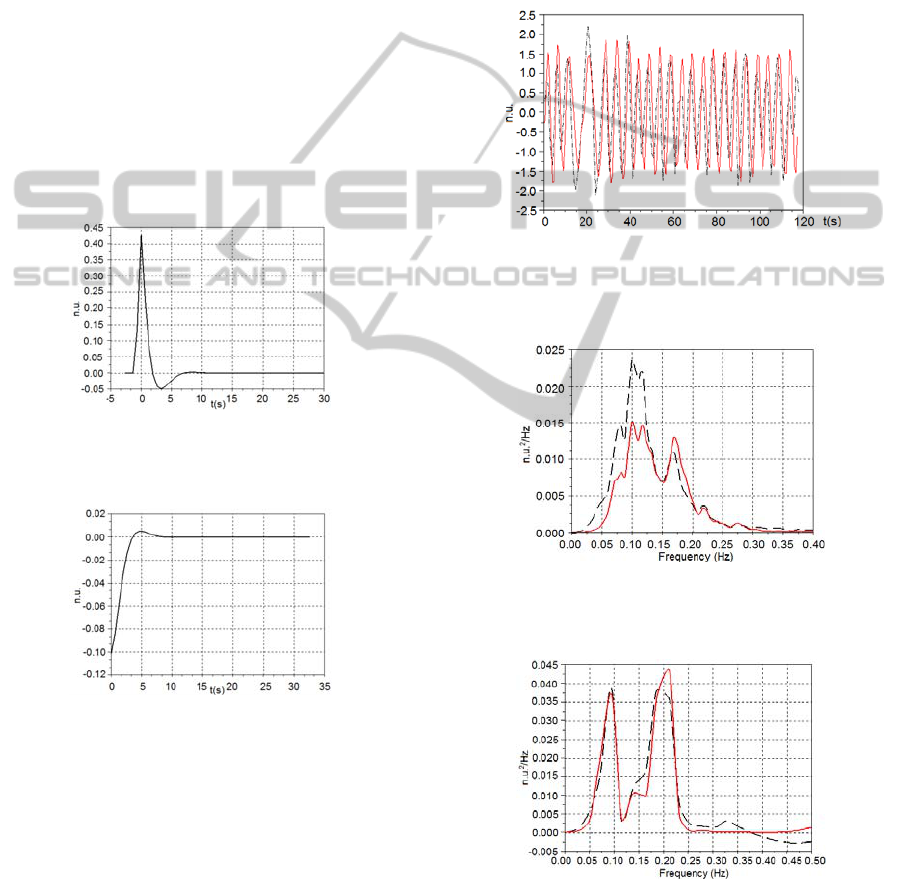
Figures 2 and 3 show the typical impulse
responses (RFW→HR and IPWTT→HR,
respectively) obtained from the ARMA model for a
subject at supine posture breathing according to the
broadband pattern.
Figure 2: Typical RFW→HR impulse response of the
ARMA model obtained from a subject at supine position,
breathing according to the broadband pattern.
Figure 3: Typical IPWTT→HR impulse response of the
ARMA model obtained from a subject at supine position,
breathing according to the broadband pattern.
The fitness of the models could be verified by
observing their responses to the RFW and IPWTT
series that were acquired from the same subjects
during the paced breathing. As illustrated by the
Figure 4, the models outputs were able to follow up
the measured HR, showing their suitability.
In order to compare the model output (HR
model
)
to the measured HR (HR
measured
) in the frequency
domain, each of these two series were segmented in
three non-overlapping 40s segments and Hamming
window was applied to all them. For each series, the
DFT of the three segments were averaged. Next, the
PSD curves of the HR
measured
and HR
model
obtained
from all five subjects were averaged. Figures 5 and 6
show the averaged PSD curves obtained from the
subjects at supine and standing postures,
respectively, breathing at irregular pace. These
averaged PSD curves were also obtained for the
subjects breathing at 12 breaths/min during supine
(Figures 7) and standing (Figures 8) positions.
Figure 4: Typical result of HR series generated by the
model (continuous red line) that follows up the HR
(dashed black line) measured from a subject at supine
posture breathing at 12 breaths/min.
Figure 5: Averaged PSD of the HR
measured
(dashed black
line) and the HR
model
(continuous red line) for all subjects
at supine posture, breathing at irregular pace.
Figure 6: Averaged PSD of the HR
measured
(dashed black
line) and the HR
model
(continuous red line) for all subjects
at standing posture, breathing at irregular pace.
Measurements of LF and HF power were carried
out in normalized units (Task Force, 1996).
NONINVASIVE CARDIOVASCULAR SYSTEM IDENTIFICATION USING PULSE WAVE TRANSIT TIME
235

Table 1 contains the HR power values within the
LF and HF bands that were obtained from the
averaged PSD curves of all subjects breathing at
irregular breathing pattern in the different postures.
Table 2 shows the same for the subjects breathing at
12 breaths/min.
The Student’s t-test does not show significant
differences between LF
measured
and LF
model
and neither
between HF
measured
and HF
model
for the two different
postures and for the two different breathing patterns.
Figure 7: Averaged PSD of the HR
measured
(dashed black
line) and HR
model
(continuous red line) for all subjects at
supine posture, breathing at 12 breaths/min.
Figure 8: Averaged PSD of the HR
measured
(dashed black
line) and the HR
model
(continuous red line) for all subjects
at standing posture, breathing at 12 breaths/min.
4 DISCUSSION
According to Payne et al. (2006), the variable
cardiac pre-ejection period constrains the use of the
IPWTT as a reliable estimate of the SBP; however,
these authors point out that it may be useful for
assessing the SBP variability.
When compared to non-invasive SBP
measurements carried out with an arterial tonometer,
the IPWTT has lower cost and does not offer risk of
interrupting the perfusion due to the application of
excessive pressure to the finger-cuff (Teng and
Zhang, 2006).
Using the IPWTT and RFW as inputs, the model
parameters were generated for each volunteer from
data recorded when they were breathing according to
an irregular pattern (Berger et al, 1989). The APR
method was used to define the model orders (Perrott
and Cohen, 1996).
Table 1: LF and HF powers (nu) measured from the
averaged PSD curves for subjects breathing at irregular
pace (Mean±SD).
LF
measured
HF
measured
LF
model
HF
model
Supine
70.42
±10.36
29.58
±10.36
58.74
±11.60
41.25
±11.60
Standing
84.71
±6.02
15.29
±6.02
73,24
±10.74
26.76
±10.74
Table 2: LF and HF powers (nu) measured from the
averaged PSD curves for subjects breathing at 12
breaths/min (Mean±SD).
LF
measured
HF
measured
LF
model
HF
model
Supine
46.8
±27.14
53.82
±27.14
27.59
±22.35
72.41
±22.35
Standing
66.46
±11.52
33.54
±11.52
60.00
±24.70
40.04
±24.70
As can be seen in Figure 4, the generated models
were able to follow the measured HR when the
subjects were breathing at a constant rate.
It is possible to note in the Figures 2 and 3 that
the model impulse responses are, respectively, very
similar to the ILV→HR and SBP→HR impulse
responses obtained, for instance, by Perrott and
Cohen (1996) and by Chen and Mukkamala (2008).
The averaged PSD obtained for the HR
measured
and HR
model
from the different volunteers breathing
at irregular pace (Figures 5 and 6) and at 12
breaths/min (Figures 7 and 8) presented similar
trends.
The statistics results do not point significant
differences between the LF powers and HF powers
calculated for the HR
measured
and HR
model
.
5 CONCLUSIONS
This work investigated the use of the IPWTT and
RFW as inputs to generate ARMA models of the
heart rate autonomic control.
The assessment of the presented results allows us
to conclude that the generated models are able to
follow up the HR of subjects not submitted to
nervous blockade.
It is much safer and easier to get these two series
to model the autonomic control during routine
clinical exams as alternatives to ILV and SPB.
Therefore, they can be recorded from a larger
BIOSIGNALS 2012 - International Conference on Bio-inspired Systems and Signal Processing
236

number of patients under different clinical
conditions, speeding up the investigation of
parameters obtained from the models that may be
useful to assist diagnosis.
Additional experiments using the RFW and
IPWTT series as inputs are going to be carried out
under sympathetic, vagal and double blockade to
evaluate the model output generated in these
scenarios. Furthermore, the effect of the IPWTT on
the causal analysis as proposed by Faes et al. (2006)
will be also investigated.
REFERENCES
Appel, M. L., Saul, J. P. and Cohen, R. J., (1989). Closed-
Loop identification of Cardiovascular Regulatory
Mechanisms. In Proceedings of the Computers in
Cardiology 1989, 3-8.
Basselli, G., Porta, A., Rimoldi, O., Pagani, M. and
Cerutti, S., (1997). Spectral Decomposition in
Multichannel Recordings Based on Multivariate
Parametric Identification. IEEE Transactions on
Biomedical Engineering: 44(11), 1092-1101.
Berger, R. D., Saul, J. P. and Cohen, R. J., (1989). IEEE
Transactions on Biomedical Engineering: 36(11),
1061-1065.
Berntson, G. G., Bigger Jr., J. T., Eckberg, D. L.,
Grossman, P., Kaufmann, P. G., Malik, M., Nagaraja,
H. N., Porges, S. W., Saul, J. P., Stone, P. H. and Van
Der Molen, M. W., (1997). Heart Rate Variability:
Origins, Methods, and Interpretative Caveats.
Psychophysiology: 34, 623-648.
Chen, X. and Mukkamala, R., (2008). Selective
Quantification of the Cardiac Sympathetic and
Parasympathetic Nervous Systems by Multisignal
Analysis of Cardiorespiratory Variability. American
Journal of Physiology - Heart and Circulatory
Physiology: 294, 362-371.
Chiu, Y. C., Arand, P. W., Shroff, S. G., Feldman, T. and
Carroll, J. D., (1991). Determination of pulse wave
velocities with computerized algorithms. Am Heart J.
121: 1460–1470.
Eckberg, D. L., (2003). The Human Respiratory Gate. The
Journal of Physiology: 548, 339-352.
Faes, L., Widesott, L., Del Greco, M., Antonili, R. and
Nollo, G., (2006). Causal Cross-Spectral Analysis of
Heart Rate and Blood Pressure Variability for
Describing the Impairment of the Cardiovascular
Control in Neurally Mediated Syncope. IEEE
Transactions on Biomedical Engineering: 53(1), 65-73.
Ghaffari, A., Golbayani, H. and Ghasemi, M., (2008). A
New Mathematical Based QRS Detector Using
Continuous Wavelet Transform. Computers and
Electrical Engineering: 34, 81-91.
Giassi Jr., P., Baggio, J. R. B., Moraes, R. and Oliveira,
M. G., (2011). Wireless Device for Noninvasive
Recordings of Cardio-Respiratory Signals. In
Proceedings of the International Conference on
Biomedical Electronics and Devices, 363-367.
Lass, J., Meigas, K., Karai, D., Kattai, R., Kaik, J. and
Rossmann, M., (2004). Continuous Blood Pressure
Monitoring During Exercise Using Pulse Wave
Transit Time Measurement. In Proceedings of the 26
th
Annual International Conference of the IEEE EMBS,
2239-2242.
Mullen, T. J., Appel, M. L., Mukkamala, R., Mathias, J.
M. and Cohen, R. J., (1997). System Identification of
closed-Loop Cardiovascular control: effects of Posture
and autonomic Blockade. American Journal of
Physiology:272(1), 448-461.
Pagani, M., Lombardi, F., Guzzetti, S., Furla, R.,
Pizzinelli, P., Sandrone, G., Malfatto, G., Dell’Orto, S.
and Piccaluga, E., (1986). Power Spectral Analysis of
Heart Rate and Arterial Pressure Variabilities as a
Marker of Sympatho-Vagal Interaction in Man and
Concious Dog. Circulation Research: 59, 178-193.
Payne, R. A., Symeonides, C.N., Webb, D. J. and
Maxwell, R.J., (2006). Pulse Transit time Measured
from ECG: an Unrealible Marker of beat-to-Beat
Blood Pressure. Journal of Apllied Physiology: 100,
136-141.
Perrott, M. H. and Cohen R. J., (1996). An Efficient
Approach to ARMA Modeling of Biological Systems
with Multiple Input and Delays. IEEE Transactions on
Biomedical Engineering: 43(1), 1-14.
Takalo, R., Saul, J. P. and Korhonen, I., (2004).
Comparison of Closed-loop and Open-loop Models in
the Assessment of cardiopulmonary and Baroreflex
Gains. Methods of Information in Medicine: 43, 296-
301.
Tarvainen, M. P., Ranta-aho, P. O. and Karjalainen, P. A.,
(2002). An Advanced Detrending Method with
Application to HRV Analysis. IEEE Transactions on
Biomedical Engineering: 49(2), 172-175.
Task Force of The European Society of Cardiology and
The North American Society of Pacing and
Electrophysiology, (1996). Heart Rate Variability.
Standards of Measurement, Physiological
Interpretation, and Clinical Use. European Heart
Journal: 17, 354-381.
Teng, X. F. and Zhang, Y. T., (2006). An Evaluation of a
PTT-Based Method for Noninvasive and Cuffles
Estimation of Arterial Blood Pressure. Proceedings of
the 26
th
Annual International Conference of the IEEE
EMBS, New York, USA.
Xiao, X., Mullen, T. J. and Mukkamala, R., (2005).
System Identification: A Multi-Signal Approach for
Probing Neural Cardiovascular Regulation.
Physiological Measurement: 26, 41-71.
NONINVASIVE CARDIOVASCULAR SYSTEM IDENTIFICATION USING PULSE WAVE TRANSIT TIME
237
