
OBJECT RECOGNITION IN PROBABILISTIC 3-D VOLUMETRIC
SCENES
Maria I. Restrepo
∗
, Brandon A. Mayer
†
and Joseph L. Mundy
‡
School of Engineering, Brown University, 182 Hope Street, Providence, RI, U.S.A.
Keywords:
3-d Object recognition, 3-d Data processing, Machine vision, Bayesian learning.
Abstract:
A new representation of 3-d object appearance from video sequences has been developed over the past several
years (Pollard and Mundy, 2007; Pollard, 2008; Crispell, 2010), which combines the ideas of background
modeling and volumetric multi-view reconstruction. In this representation, Gaussian mixture models for in-
tensity or color are stored in volumetric units. This 3-d probabilistic volume model, PVM, is learned from a
video sequence by an on-line Bayesian updating algorithm. To date, the PVM representation has been applied
to video image registration (Crispell et al., 2008), change detection (Pollard and Mundy, 2007) and classifica-
tion of changes as vehicles in 2-d only (Mundy and Ozcanli, 2009;
¨
Ozcanli and Mundy, 2010). In this paper,
the PVM is used to develop novel viewpoint-independent features of object appearance directly in 3-d. The
resulting description is then used in a bag-of-features classification algorithm to recognize buildings, houses,
parked cars, parked aircraft and parking lots in aerial scenes collected over Providence, Rhode Island, USA.
Two approaches to feature description are described and compared: 1) features derived from a PCA analysis
of model neighborhoods; and 2) features derived from the coefficients of a 3-d Taylor series expansion within
each neighborhood. It is shown that both feature types explain the data with similar accuracy. Finally, the
effectiveness of both feature types for recognition is compared for the different categories. Encouraging ex-
perimental results demonstrate the descriptive power of the PVM representation for object recognition tasks,
promising successful extension to more complex recognition systems.
1 INTRODUCTION AND PRIOR
WORK
A semantic description of 3-d scenes is essential to
many urban and surveillance applications. This pa-
per presents a new volumetric representation for the
description of 3-d scenes that captures the probabilis-
tic nature of 3-d reconstruction from multiple image
views and video sequences. A recognition approach is
described to provide semantic labels for aerial scenes
including such categories as houses, buildings, parked
cars, and parked aircraft. The labels are found by an
object classification algorithm based on features ex-
tracted directly from a 3-d representation of scene ap-
pearance. The resulting object-centered recognition
model combines the probability of surface appearance
and surface occupancy at densely sampled locations
in 3-d space, thus incorporating the ambiguity inher-
ent in surface reconstruction from imagery. To the
authors’ knowledge, this paper represents the first
——————————-
∗
aa
†
Ph.D. Student
‡
Professor of Engineering
attempt to base scene classification on a volumetric
probabilistic model that learns, in a dense manner, the
appearance and geometric information of 3-d scenes
from images.
In related work, many 3-d object recognition algo-
rithms have been developed in recent years to search
the rapidly growing databases of 3-d models (Pa-
padakis et al., 2010; Shapira et al., 2010; Drost et al.,
2010; Bariya and Nishino, 2010; Bronstein et al.,
2011). These recognition algorithms operate on mod-
els that are synthetically generated or obtained in a
controlled environment using 3-d scanners. Through-
out most of the object-retrieval literature, the domi-
nant representation of 3-d geometry is a mesh or point
cloud, where the intrinsic properties of the represen-
tation are used to describe shape models. However,
neither of these representations is able to express the
uncertainty and ambiguity of 3-d surfaces inherent in
reconstruction from aerial image sequences.
Other recent works have favored volumetric shape
180
I. Restrepo M., A. Mayer B. and L. Mundy J. (2012).
OBJECT RECOGNITION IN PROBABILISTIC 3-D VOLUMETRIC SCENES.
In Proceedings of the 1st International Conference on Pattern Recognition Applications and Methods, pages 180-190
DOI: 10.5220/0003776301800190
Copyright
c
SciTePress

descriptors to better cope with isometric deformations
(Raviv et al., 2010), and to improve segmentation of
models into parts and matching of parts from differ-
ent objects (Shapira et al., 2010). However, the volu-
metric cues of Raviv and Shapira are defined by an
enclosing boundary (represented by a mesh). The
probabilistic volume model, PVM, used in this work,
learns geometry and appearance in a general frame-
work that can handle changes in viewpoint, illumina-
tion and resolution, without regard to surface topol-
ogy. Therefore, this work addresses the problem of
categorizing static objects in scenes learned from im-
ages collected under unrestricted conditions, where
the only requirement is known camera calibration ma-
trices. It is worth pointing out that the volumetric rep-
resentation used in this work is different from a rep-
resentation obtained from a range scanner, not only
in that appearance information is stored in the vox-
els, but also in that surface geometry is estimated in
a probabilistic manner from images. The probabilis-
tic framework provides a way to deal with uncertain-
ties and ambiguities that make the problem of com-
puting exact 3-d structures based on 2-d images in
general ill-posed (e.g. multiple photo-consistent in-
stances, featureless surfaces, unmodeled appearance
variations, and sensor noise).
In another related body of work, image-based
recognition in realistic scenes is performed using
appearance-based techniques on 2-d image projec-
tions. Deformable part models are used (Fergus et al.,
2003; Felzenszwalb et al., 2008) to handle shape vari-
ations and to account for the random presence and ab-
sence of parts caused by occlusion, and variations in
viewpoint and illumination. Thomas et al. have ex-
tended these ideas to multi-view models, where shape
models are based on 2-d descriptors observed in mul-
tiple views, and single-view codebooks are learned
and interconnected (Thomas et al., 2006). Gupta et
al. (Gupta et al., 2009) learn 3-d models of scenes
by first recovering the geometry of the scene using
a robust structure from motion algorithm, and then
transferring 2-d appearance descriptors (SIFT) to the
3-d points. While the works just mentioned, combine
geometry and appearance information to model 3-d
scenes, appearance information is only available for a
sparse set of 3-d points. The recovered 3-d points cor-
respond to 3-d structures that, when projected onto the
2-d images yield salient and stable 2-d features. Con-
trary to the idea of reconstructing 3-d appearance and
geometry from a sparse set of 2-d features, the PVM
used in this work, models surface occupancy and ap-
pearance at every voxel in the scenes. A dense re-
construction of a scene’s appearance makes available
valuable view-independent characteristics of objects’
surfaces that are not captured by sparse 2-d feature
detectors.
In computer vision, local descriptors are widely
used in recognition systems developed for 2-d im-
ages. Through out the last several years, the vast
majority of the local descriptors are obtained using
derivative operators on image intensity, e.g. steerable
filters (Freeman and Adelson, 1991), HOG (Dalal and
Triggs, 2005) and SIFT (Lowe, 2004) . Inspired by
the success of local descriptors in feature-based 2-d
recognition, the work presented in this paper uses lo-
cal descriptors for 3-d recognition in volumetric prob-
abilistic models. In contrast to a mesh representation,
where derivatives are only approximately defined for
arbitrary topologies, the information stored at each
voxel (to be defined later), allows for a natural way
to perform dense differential operations. In this work,
derivatives are computed using 3-d operators that are
based on a second degree Taylor series approximation
of the volumetric appearance function to be defined in
a later section. The performance of the Taylor-based
features and features extracted from the PCA analy-
sis of the same volumetric feature domain, are com-
pared. It is shown that both features have comparable
descriptive power and recognition accuracy, provid-
ing an avenue to generalizing the methods that have
been used successfully in 2-d derivative-based recog-
nition systems to the 3-d probabilistic volume models
used in this work.
To date, the PVM has been been applied to video
image registration (Crispell et al., 2008), change de-
tection in images (Pollard and Mundy, 2007) and
classification of changes in satellite images as vehi-
cles (Mundy and Ozcanli, 2009;
¨
Ozcanli and Mundy,
2010). For the purpose of these applications, a
small number of probabilistic volume models are
needed. However, in order to perform multi-class ob-
ject recognition experiments it was necessary to train
a larger number of models. The aerial imagery was
collected in Providence, RI, USA, and used to learn
18 volumetric models. These models represent a vari-
ety of landscapes and contain large number of objects
per scene. Each scene model, composed of approxi-
mately 30 million voxels, covers an estimate ground
area of (500 × 500)m
2
. The areal video data, camera
matrices and other supplemental material are avail-
able on line
2
.
In summary, the contributions of the work pre-
sented in this paper are:
1. To be the first work to perform object catego-
rization task on probabilistic volume models that
learn geometry and appearance information ev-
2
http://vision.lems.brown.edu/project desc/Object-Rec-
ognition-in-Probabilistic-3D-Scenes
OBJECT RECOGNITION IN PROBABILISTIC 3-D VOLUMETRIC SCENES
181

(a)
I
I
X
R
X
C
S
V
X '
Voxel Volume!
Intesity!
P(I
X
|V=X’)!
(b)
octree cell
empty space
surface
leaf nodes contain the Gaussian mixture models
...
...
...
...
(c)
Figure 1: 1(a) and 1(b) PVM proposed by Pollard and Mundy (Pollard and Mundy, 2007; Pollard, 2008). 1(b) explains the
voxel notation, a pixel I
X
back projects into a ray of voxels R
X
, V is the unique voxel along R
X
that produces the intensity I
X
.
1(c) Octree subdivision of space proposed by Crispell (Crispell, 2010).
erywhere in space, and that are learned in unre-
stricted settings from images sequences.
2. To characterize for the first time the local, 3-d
information in the PVM. The result are novel,
view-invariant, volumetric features that describe
local neighborhoods of the probabilistic informa-
tion of 3-d surface geometry and appearance in
the scenes.
3. A demonstration of the descriptive power, through
rigorous analysis of function approximation and
object recognition experiments, of features based
on a Taylor series approximation, and PCA analy-
sis of the probabilistic information in the models.
Encouraging initial recognition results promise
successful extensions based on generalization
of 2-d features e.g. Harris corners (Harris and
Stephens, 1988), HOG (Dalal and Triggs, 2005),
SIFT (Lowe, 2004), and 3-d differential features
(Sipiran and Bustos, 2010; Raviv et al., 2010), to
the probabilistic models in question.
4. The creation of the largest database of probabilis-
tic volume models available today.
The rest of the paper is organized as follows: Sec-
tion 1.1 explains the probabilistic volume model used
to learn the 18 areal sites of the city of Providence
used in this work. Section 2 discusses two types of
features used to model local neighborhoods in the vol-
umetric scenes. Section 3 explains category learning
and object classification. Section 4 presents the exper-
imental results. Finally, conclusions and further work
are described in Sections 5 and 6.
1.1 Probabilistic Volume Model
Pollard and Mundy (2007) proposed a probabilistic
volume model that can represent the ambiguity and
uncertainty in 3-d models derived from multiple im-
age views. In Pollard’s model (Pollard and Mundy,
2007; Pollard, 2008), a region of three-dimensional
space is decomposed into a regular 3-d grid of cells,
called voxels (See Figure 1). A voxel stores two kinds
of state information: (i) the probability that the voxel
contains a surface element and (ii) a mixture of Gaus-
sians that models the surface appearance of the voxel
as learned from a sequence of images. The surface
probability is updated by incremental Bayesian learn-
ing (see Equation 1 below), where the probability of
a voxel X containing a surface element after N+1 im-
ages increases if the Gaussian mixture (see Equation 2
below) at that voxel explains the intensity observed in
the N+1 image better than any other voxel along the
projection ray. The resulting models look more like
volumetric models obtained from CT scans than mod-
els obtained from point clouds generated by range
scanners (see Figure 2).
P
N+1
(X ∈ S) = P
N
(X ∈ S)
p
N
(I
N+1
X
|X ∈ S)
p
N
(I
N+1
X
)
(1)
p(I) =
3
∑
k=1
w
k
W
1
q
2πσ
2
k
exp
−
(I−µ
k
)
2
2σ
2
k
(2)
In a fixed-grid voxel representation, most of the
voxels may correspond to empty areas of a scene,
making storage of large, high-resolution scenes pro-
hibitively expensive. Crispell (2010) proposed a con-
tinuously varying probabilistic scene model that gen-
eralizes the discrete model proposed by Pollard and
Mundy. Crispell’s model allows non-uniform sam-
pling of the volume leading to an octree representa-
tion that is more space-efficient and can handle finer
resolution required near 3-d surfaces, see Figure 1(c).
The octree representation (Crispell, 2010), makes
it feasible to store models of large urban areas. How-
ever, learning times of large scenes using the PVM
remained impractical until recently, when a GPU im-
plementation was developed by Miller et al. (2011).
ICPRAM 2012 - International Conference on Pattern Recognition Applications and Methods
182

Figure 2: From left to right (column by column): Camera path and 3-d points (only used for visualization purposes) obtained
using Bundler (Snavely and Seitz, 2006). Details of collected video frames. The learned expected appearance volumes, EVM.
Examples of bounding boxes around objects of interest (this figure is best seen in color).
Training times decrease by several orders of magni-
tudes, depending on available computing resources
and model complexity, see (Miller et al., 2011) for
performance comparisons evaluated on single core
CPU and OpenCL implementation on CPU and GPU.
With a GPU framework in place is now feasible to
think of multi-class object recognition tasks where
large number of objects are required for training.
2 VIEW INDEPENDENT 3-D
FEATURES
This section describes how the geometry and appear-
ance information at every voxel are used to compute
a voxel’s expected appearance. It then describes two
approaches used to characterize the local information
(i.e. expected appearances) in the volumetric scenes,
namely PCA features and Taylor features.
2.1 Expected Volume Model
Though the work by Pollard was designed to de-
tect changes in a new image, the occupancy and ap-
pearance information can be used to render synthetic
images of the expected scene appearance (Pollard,
2008). For every pixel in the image, its intensity
is the summation, across all voxels in its projection
ray, of the expected color of the voxel and the likeli-
hood of that voxel containing a surface element and it
not being occluded. Consider a pixel I
X
, which back
projects into a ray of voxels R
X
, if V is the unique
voxel along R
X
that causes the intensity value at the
pixel, then the expected intensity at I
X
is explained by
(3) and (4) (also see Figure 1(b)).
E(I
X
) =
∑
X
0
∈R
X
E(I
X
|V = X
0
)P(V = X
0
) (3)
=
∑
X
0
∈R
X
E(I
X
|V = X
0
)P(X
0
∈ S)P(X
0
is not occluded) (4)
E(I
X
|V = X
0
) represents the expected intensity,
given that voxel X
0
∈ R
X
produced the intensity seen
in the image. This quantity is obtained from the mix-
ture of Gaussians stored at voxel X
0
. P(X
0
∈ S) is
the probability of X
0
containing a surface element
and it is also stored at X
0
. P(X
0
is not occluded) is
defined as the probability that all voxels (along R
X
)
between X
0
and the camera contain empty space i.e.
P(X
0
is not occluded) =
∏
X
00
<X
0
(1 − P(X
00
∈ S)).
For every ray containing a particular voxel
X
0
, the quantity E(I
X
|V = X
0
)P(X
0
∈ S) remains
unchanged, and the only ray-dependent term is
P(X
0
is not occluded). When learning neighborhood
configurations in the PVM, only the ray-independent
information is taken into account. The information at
every voxel is combined into to the quantity in Equa-
tion (5) (see below), here referred to as a voxel’s ex-
pected appearance, and the volume of expected ap-
pearances, as the expectation volume model, EVM.
E(I
x
|V = X
0
)P(X
0
∈ S) (5)
2.2 PCA Features
One way to represent the volumetric model is by iden-
tifying local spatial configurations that account for
OBJECT RECOGNITION IN PROBABILISTIC 3-D VOLUMETRIC SCENES
183

most of the variation in the data. Principal Com-
ponent Analysis (PCA) is carried out to find the or-
thonormal basis that represents the volumetric sam-
ples in the best mean squared error sense. The prin-
cipal components are arranged in decreasing order of
variation as given by the eigenvalues of the sample
scatter matrix.
In order to perform PCA, feature vectors are ob-
tained by sampling locations on the scene according
to the octree structure, i.e. fine sampling in regions
near surfaces and sparse sampling of empty space.
At each sampled location, n
x
ˆ
l × n
y
ˆ
l × n
z
ˆ
l cubical re-
gions are extracted (centered at the sampled location),
where
ˆ
l is the length of the smallest voxel present in
the 3-d scene. The extracted regions are arranged into
vectors by traversing the space at a resolution of
ˆ
l, and
using a raster visitation schedule.
The scatter matrix S, of randomly sampled vec-
tors, is updated using a parallel scheme (Chan et al.,
1979) to speed up computation, and the principal
components are found by the eigenvalue decompo-
sition of S. In the PCA space, every neighborhood
(represented by a d-dimensional feature vector x) can
be exactly expressed as x =
¯
x +
∑
d
i=1
a
i
e
i
, where e
i
are principal axes associated with the d eigenval-
ues, and a
i
are the corresponding coefficients. A k-
dimensional (k < d) approximation of the neighbor-
hoods can be obtained by using the first k principal
components i.e.
˜
x =
¯
x +
∑
k
i=1
a
i
e
i
. Section 4 presents
a detailed analysis of the reconstruction error of lo-
cal neighborhoods, namely |x −
˜
x|
2
, as a function of
dimension and training set size. In the remainder of
this paper, the vector arrangement of projection coef-
ficients in the PCA space is referred as a PCA feature.
2.3 Taylor Features
Mathematically, the appearance function in the scene
can be approximated (locally) by its Taylor series ex-
pansion. The computation of derivatives in the ex-
pectation volume model, EVM, can be expressed as
a least square error minimization of the following en-
ergy function.
E =
ni
∑
i=−ni
n j
∑
j=−n j
nk
∑
k=−nk
V (i, j, k) −
˜
V (i, j, k)
2
(6)
Where
˜
V (i, j, k) is the Taylor series approxima-
tion of the expected 3-d appearance of a volume V
centered on the 3-d point (i, j, k). Using the second
degree Taylor expansion of V about (0, 0, 0), (6) be-
comes
E =
∑
x
V (x) −V
0
− x
T
G −
1
2!
x
T
Hx
2
(7)
Where V
0
, G, H are the zeroth derivative, the gra-
dient vector and the Hessian matrix of the volume
of expected 3-d appearance about the point (0, 0, 0),
respectively. The coefficients for 3-d derivative op-
erators can be found by minimizing (7) with re-
spect to the zeroth, first and second order deriva-
tives. The computed derivative operators are applied
algebraically to neighborhoods in the EVM. The re-
sponses to the 10 Taylor operators, which correspond
to the magnitude of the zeroth, first and second order
derivatives, are arranged into 10-dimensional vectors
and are referred to as Taylor features.
3 3-D OBJECT LEARNING AND
RECOGNITION
This section explains in detail the model used to learn
five object categories. It is important to keep in mind
that models are based on either Taylor features of
PCA features, but not both. The results obtained for
the two representations are presented in Section 4.
3.1 The Model: Bag of Features
Bag-of-features models have their origins in texture
recognition (Varma and Zisserman, 2009; Leung and
Malik, 1999) and bag-of-word representations for text
categorization (Joachims, 1997). Their application
to categorization of visual data is very popular in
the computer vision community (Sivic et al., 2005;
Csurka et al., 2004) and have produced impressive
results in benchmark databases (Zhang et al., 2007).
The independence assumptions inherent to bag-of-
features representation make learning models for few
object categories a simple task, assuming enough
training samples are available to learn the classifica-
tion space. In this paper, a bag-of-features represen-
tation is constructed for five categories as outlined in
the following subsections.
3.2 Learning a Visual Vocabulary with
k-means
In order to produce a finite dictionary of 3-d expected
appearance patterns, the scenes are represented by a
set of descriptors (Taylor or PCA) that are quantized
using k-means-type clustering. Two major limitations
of k-means clustering must be overcome: (i) the algo-
rithm does not determine the best number of means,
i.e k, and (ii) it converges to a local minimum that
may not represent the optimum placement of cluster
centers.
ICPRAM 2012 - International Conference on Pattern Recognition Applications and Methods
184

To address (i), there exist available algorithms to
automatically determine the number of clusters (Pel-
leg and Moore, 2000; Hamerly and Elkan, 2003).
However, in the experiments in this paper the algo-
rithm was run using various values of k. An op-
timal value was selected based on object classifica-
tion performance and running times. Disadvantage
(ii) requires careful attention because the success of
k-means depends substantially on the starting posi-
tions of the means. In the experiments, the train-
ing scenes are represented by millions of descriptors
(even if only a percentage of them are used), and ran-
dom sampling of k means, where k << 1 × 10
6
, may
not provide a good representation of the 3-d appear-
ance patterns.
The means are initialized using the algorithm pro-
posed by Bradley and Fayyad (1998), which has been
shown to perform well for large data sets (Maitra
et al., 2010). In the initialization algorithm (Bradley
and Fayyad, 1998), a random set of sub-samples of
the data is chosen and clustered via modified k-means.
The clustering solutions are then clustered using clas-
sical k-means, and the solution that minimizes the
sum of square distances between the points and the
centers is chosen as the initial set of means. In or-
der to keep computation time manageable, while still
choosing an appropriate number of sub-samples (10
being suggested in (Maitra et al., 2010; Bradley and
Fayyad, 1998)), an accelerated k-means algorithm
(Elkan, 2003) is used whenever the classical k-means
procedure is required.
The large number of volumetric training features
can only be practically processed using parallel com-
putation. While parallel clustering algorithms are
available (Judd et al., 1998), message passing be-
tween iterations could not be easily implemented for
the current framework. Therefore, an approximate k-
means method was selected, which is a modification
of the refinement algorithm by Bradley and Fayyad
(1998). The modified k-means algorithm is the fol-
lowing:
1. Sample an initial set of means, SP, as described above
2. Divide training samples into J blocks. Let CM =
/
0
3. Process each block in parallel as follows:
a. Let S
i
be the data in block J
i
b. CM
i
= AcceleratedKMeans(SP, S
i
, K)
4. CM =
S
j
i=0
CM
i
, FM =
/
0
5. Process each CM
i
in parallel as follows:
a. FM
i
= AcceleratedKMeans(CM
i
,CM, K)
6. FM = argmin
FM
i
Distortion(FM
i
,CM)
The minimization function, Distortion(FM
i
,CM),
computes the sum of square distances of each data
point to its nearest mean (for all J estimates). The set
of clusters with the smallest distortion value is cho-
sen as the final solution, FM. The proposed algorithm
does not seek to improve the complexity of the tradi-
tional k-means algorithm but to manage memory re-
quirements and allow parallel processing of large data
sets.
3.3 Learning and Classification
With a 3-d appearance vocabulary in place, individual
objects are represented by feature vectors that arise
from the quantization of the PCA or Taylor descrip-
tors present in that object. These feature vectors can
be used in supervised multi-class learning, where a
naive Bayes classifier is used for its simplicity and
speed. During learning, the classifier is passed train-
ing objects used to adjust the decision boundaries;
during classification, the class label with the maxi-
mum a posteriori probability is chosen to minimize
the probability of error.
Formally, let the objects of a particular category be
the set O
l
=
S
N
l
i=1
o
i
, where l is the class label and N
l
is
the number of objects with class label l. Then, the set
of all labeled objects is defined as O =
S
N
c
l=1
O
l
, where
N
c
is the number of categories. Let the vocabulary of
3-d expected appearance patterns be defined as V =
S
k
i=1
v
i
, where k is the number of cluster centers in
the vocabulary. From the quantization step a count is
obtained, c
i j
, of the number of times a cluster center,
v
i
, occurs in object o
j
. Using Bayes formula, the a
posteriori class probability is given by:
P(C
l
|o
i
) ∝ P(o
i
|C
l
)P(C
l
) (8)
The likelihood of an object is given by the product of
the likelihoods of the independent entries of the vo-
cabulary, P(v
j
|C
l
), which are estimated during learn-
ing. The full expression for the class posterior be-
comes:
P(C
l
|o
i
) ∝ P(C
l
)
k
∏
j=1
P(v
j
|C
l
)
c
ji
(9)
∝ P(C
l
)
k
∏
j=1
N
m
∑
m=1:o
m
∈O
l
c
jm
k
∑
n=1
N
m
∑
m=1:o
m
∈O
l
c
nm
c
ji
(10)
According to the Bayes decision rule, every ob-
ject is assigned the label of the class with the largest
a posteriori probability. In practice, log likelihoods
were computed to avoid underflow of floating point
computations.
OBJECT RECOGNITION IN PROBABILISTIC 3-D VOLUMETRIC SCENES
185
(a) (b) (c)
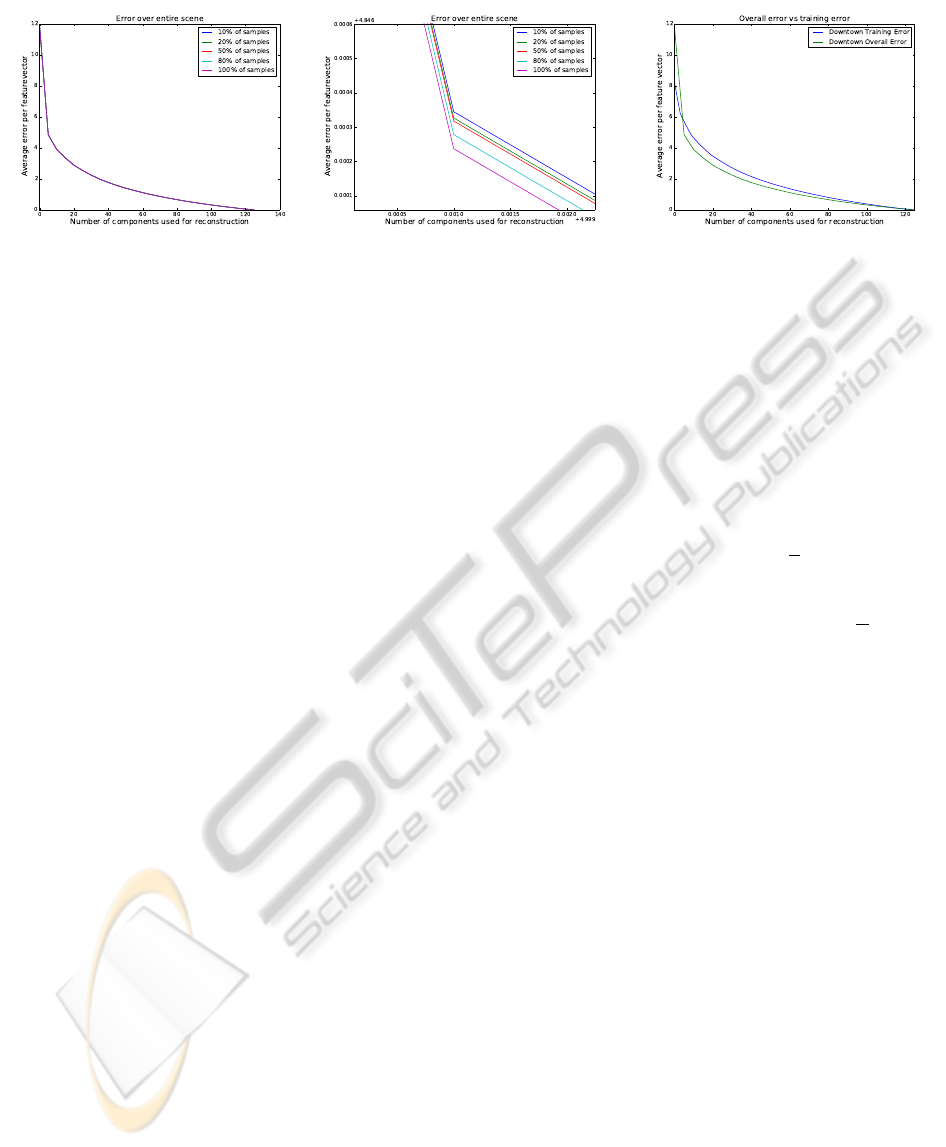
Figure 3: Analysis of reconstruction error. 3(a) Error as a function of the number of components used. The different curves
represent different proportion of samples used to perform PCA. 3(b) A zoomed-in detail of 3(a). 3(c) Comparison of errors
obtained over training neighborhoods vs. all available neighborhoods.
4 EXPERIMENTS AND RESULTS
The data collection and scene reconstruction pro-
cesses are now described, followed by comparisons
of scene data modeling accuracy based on either PCA
or Taylor features. The section concludes with multi-
class object recognition results, where objects from
8 scenes were classified among 5 categories; planes,
cars, houses, buildings, and parking lots. Training
samples consist of labeled objects from 10 scenes
(different from the ones used for testing). In order
to localize surface features through k-means, only
features centered at leaf-cells at the finest resolution
level of the octree were considered i.e. cells contain-
ing high occupancy probability
4.1 Data Collection and Scene
Formation
The aerial data used to build 18 different probabilis-
tic volume scenes was collected from a helicopter fly-
ing over Providence, RI, USA, and its surroundings.
An approximate resolution of 30 cm/pixel was ob-
tained in the imagery and translated to 30 cm/voxel
in the models. The camera matrices for all image se-
quences were obtained using Bundler (Snavely and
Seitz, 2006). The probabilistic volume models were
learned using a GPU implementation (Miller et al.,
2011). For multi-class object recognition, bounding
boxes around objects of interest were given a class
label. Ten scenes were used for training and eight
for testing. Figure 2 contains examples of aerial im-
ages collected for these experiments, the EVMs and
the bounding boxes used to label objects of interest.
4.2 Neighborhood Reconstruction
Error
Ideally, the difference between the original expected
appearance data and the data approximated using
PCA or a Taylor series expansion should be small.
The difference between the reconstructed data and the
original data was measured as the average square dif-
ference between neighborhoods, i.e.
1
N
∑
N
train
i=1
|x −
ˆ
x|
2
,
where x and
ˆ
x are the vector arrangement of the orig-
inal and the approximation neighborhoods, respec-
tively. For Taylor features,
ˆ
x = V
0
+ x
T
G +
1
2!
x
T
Hx.
For PCA features
ˆ
x =
¯
x +
∑
10
i=1
a
i
e
i
. In the experi-
ments, the size of the extracted neighborhoods was
5
ˆ
l ×5
ˆ
l ×5
ˆ
l,
ˆ
l being the length of the smallest voxel in
the model. The error was computed for the top scene
in Figure 2, here referred to as the Downtown scene.
Using all available neighborhoods to learn the
PCA basis is impractical; thus, a set of experiments
were performed to evaluate the reconstruction error
for different sizes of randomly chosen neighborhoods.
Figures 3(a) and 3(b) show the reconstruction error
for different sample sizes (as a percentage of the to-
tal number of neighborhoods). The error was basi-
cally identical for all computed fractions and 10%
was the fraction used for the remaining of the ex-
periments. Figure 3(c) compares the projection error
over the training samples and the overall projection
error (over all available neighborhoods). The curves
are very similar, indicating that the learned basis rep-
resents the training and testing data with compara-
ble accuracy. Finally, the reconstruction error for a
10-dimensional approximation in the PCA space was
compared to the reconstruction error achieved using a
2
nd
-degree Taylor approximation. The results in Ta-
ble 1 indicate that a 2
nd
-degree Taylor approximation
represents expected appearance of 3-d patterns with
only slight less accuracy than a PCA projection onto
a 10-dimensional space.
ICPRAM 2012 - International Conference on Pattern Recognition Applications and Methods
186

Table 1: Average approximation error over all 5x5x5 neigh-
borhoods. PCA and Taylor approximations are compared
for the Downtown scene.
Scene Name PCA Error Taylor Error
Downtown 3.88 4.05
4.3 3-d Object Recognition
This section presents multi-class object recognition
results. Five object categories were learned: planes,
cars, buildings, houses, and parking lots. Table 2
presents the number of objects in each category used
during training and classification.
Table 2: Number of objects in every category.
Planes Cars Houses Buildings Parking Lots
Train 18 54 61 24 27
Test 16 29 45 15 17
Two measurements were used to evaluate the clas-
sification performance: (i) classifier accuracy (i.e the
fraction of correctly classified objects), and (ii) the
confusion matrix. During classification experiments,
the number of clusters in the codebook was varied
from k = 2 to k = 100. Figure 4 presents classification
accuracy as a function of the number of clusters. For
both, Taylor-based features and PCA-based features,
the performance improves rapidly up to a 20-word
codebook, with little or no improvement for larger
vocabularies. Thus, for the remaining of the experi-
ments k was set to 20.
Figure 4: Classification Accuracy. The curves represent the
fraction of correctly classified objects as a function of the
number of clusters.
Figure 5 presents examples of class distributions
learned with PCA and Taylor codebooks of twenty
features. To facilitate interpretation, the volumetric
form of the vocabulary entries are arranged along the
x-axis. It is important to keep in mind that each voxel
(in the volumetric feature), contains its expected 3-
d appearance as defined by Eq. 5. The value of
expected 3-d appearance ranges from [0, 2] (and the
color used in the volumetric rendering from black to
white respectively). For empty space, the information
in the voxels is dominated by the occupancy proba-
bility, which takes values in the interval [0,1]; thus,
empty neighborhoods appear black. Appearance val-
ues, which are initially learned between [0,1], are off-
set to [1,2], to avoid confusing dark surfaces with
empty space. White voxels represent white surfaces
with a high occupancy probability; dark surfaces are
represented by gray voxels. For the planes cate-
gory, see Figures 5(a) and 5(c), empty neighborhoods,
white surface neighborhoods and neighborhoods con-
taining half white-surface space and half empty space
are the most common features. On the other hand, the
buildings category, see Figures 5(b) and 5(d), is rep-
resented by mid range neighborhoods corresponding
to dark surfaces and slowly changing derivatives.
Finally, the confusion matrices for a 20-keyword
vocabulary of PCA-based features and Taylor-based
features, are shown in Tables 6(a) and 6(b). Both
methods recognize planes, cars and parking lots with
high accuracy. Lower performance for buildings and
houses is expected, since a more discriminative model
is needed to successfully differentiate such similar
categories. The PCA-based representation is slightly
better at learning effective models for cars than the
Taylor based representation.
5 CONCLUSIONS
This paper presented a completely new representation
for object recognition models, where view-invariant
features were extracted directly from 3-d probabilis-
tic information. The representation was used to learn
and recognize objects from five different categories.
To the author’s knowledge, this work represents the
first attempt to apply this representation to the classi-
fication of aerial scenes or indeed any type of scene.
The performance of the proposed features, was rig-
orously tested through reconstruction accuracy and
object categorization experiments. The recognition
results are very encouraging with high accuracy on
labeling bounded regions containing objects of the
selected categories. The experiments show that dif-
ferential geometry features derived from appearance
lead to essentially the same recognition performance
as PCA. This suggests that additional features repre-
senting geometric relationships defined on differen-
tial geometry are likely to have good performance and
represent a basis for formally extending the feature
vocabulary.
OBJECT RECOGNITION IN PROBABILISTIC 3-D VOLUMETRIC SCENES
187

(a) Plane - PCA (b) Building - PCA
(c) Plane - Taylor (d) Building - Taylor
Figure 5: Class histograms for plane and building categories. The top row corresponds to class representations learned
with PCA-based features. The bottom row corresponds to those learned with Taylor-based features. The x-axis shows the
volumetric form of the 20 features; the y-axis, the probability of each feature. The most probable volumetric features for each
class are shown beside each histogram.
True
Class
Plane
House
Building
Car
Parking
Lot
Plane
House
Building
Car
Parking
Lot
0.86
0.02
0.00
0.03
0.00
0.00
0.67
0.27
0.00
0.12
0.00
0.31
0.67
0.00
0.00
0.00
0.00
0.07
0.93
0.00
0.14
0.00
0.00
0.03
0.88
(a) PCA
True
Class
Plane
House
Building
Car
Parking
Lot
Plane
House
Building
Car
Parking
Lot
0.86
0.02
0.00
0.03
0.00
0.00
0.64
0.27
0.00
0.12
0.00
0.33
0.67
0.00
0.00
0.00
0.00
0.07
0.86
0.00
0.14
0.00
0.00
0.10
0.88
(b) Taylor
Figure 6: Confusion matrix for a 20-keyword codebook of
PCA based features on the left and Taylor based features on
the right.
While there are many computational and storage
challenges faced when learning multiple object cate-
gories in large volumetric scenes, the work presented
in this paper makes an important contribution towards
true 3-d, view-independent object recognition. The
object categorization results demonstrate the descrip-
tive power of the PVM for 3-d object recognition and
open an avenue to more complex recognition systems
for dense, 3-d probabilistic scenes.
6 FURTHER WORK
The current feature representation will be extended to
incorporate features detected with differential opera-
tors that have been used successfully in 2-d featured-
based recognition systems and 3-d object retrieval al-
gorithms, e.g. 2-d and 3-d features based on the Har-
ris operator (Harris and Stephens, 1988; Sipiran and
Bustos, 2010), 3-d heat kernels based on the Laplace-
Beltrami operator (Raviv et al., 2010), SIFT features
(Lowe, 2004), HOG features (Dalal and Triggs, 2005)
and others. The occlusion, shadows and 3-d relief
present in the imagery collected for the experiments
presented in this work, pose great challenges to 2-d
multi-view recognition systems. However, in future
work, it will prove informative to compare 2-d multi-
view systems to the framework presented in this pa-
per.
The probabilistic scenes learned for this work
have known orientation and scale. In order to keep
feature-base representation of objects compact, future
work will explore representations for scale-invariant
and isometric features. Localization of objects is also
a desirable goal for future algorithms.
Finally, more advanced recognition models should
make full use of the geometric relations inherent
in the probabilistic volume model. Compositional
recognition models could represent a venue to learn
and share parts, allowing for object representations
that are efficient, discriminative and geometrically co-
herent.
ICPRAM 2012 - International Conference on Pattern Recognition Applications and Methods
188

REFERENCES
Bariya, P. and Nishino, K. (2010). Scale-Hierarchical 3D
Object Recognition in Cluttered Scenes. IEEE Con-
ference on Computer Vision and Pattern Recognition.
Bradley, P. S. and Fayyad, U. M. (1998). Refining Initial
Points for K-Means Clustering. In Proceedings of the
15th International Conference on Machine Learning.
Bronstein, A. M., Broinstein, M. M., Guibas, L. J., and Ovs-
janikov, M. (2011). Shape Google: Geometric Words
and Expressions for Invariant Shape Retrieval. ACM
Transactions on Graphics.
Chan, T. F., Golub, G. H., and LeVeque, R. J. (1979). Up-
dating Formulae and a Pairwise Algorithm for Com-
puting Sample Variances. Technical report, Depart-
ment of Computer Science. Stanford University.
Crispell, D., Mundy, J., and Taubin, G. (2008). Parallax-
Free Registration of Aerial Video. In BMVC.
Crispell, D. E. (2010). A Continuous Probabilistic Scene
Model for Aerial Imagery. PhD thesis, School of En-
gineering, Brown University.
Csurka, G., Dance, C. R., Fan, L., Willamowski, J., and
Bray, C. (2004). Visual categorization with bags of
keypoints. In In Workshop on Statistical Learning in
Computer Vision, ECCV.
Dalal, N. and Triggs, B. (2005). Histograms of oriented
gradients for human detection. In IEEE Conference
on Computer Vision and Pattern Recognition.
Drost, B., Ulrich, M., Navab, N., and Ilic, S. (2010). Model
Globally, Match Locally: Efficient and Robust 3D Ob-
ject Recognition. IEEE Conference on Computer Vi-
sion and Pattern Recognition.
Elkan, C. (2003). Using the triangle inequality to acceler-
ate k-means. In Proceedings of the Twentieth Interna-
tional Conference on Machine Learning.
Felzenszwalb, P., McAllester, D., and Ramanan, D. (2008).
A discriminatively trained, multiscale, deformable
part model. In IEEE Conference on Computer Vision
and Pattern Recognition.
Fergus, R., Perona, P., and Zisserman, A. (2003). Ob-
ject class recognition by unsupervised scale-invariant
learning. In IEEE Conference on Computer Vision and
Pattern Recognition.
Freeman, W. and Adelson, E. (1991). The design and use of
steerable filters. IEEE Transactions on Pattern Analy-
sis and Machine Intelligence.
Gupta, P., Arrabolu, S., Brown, M., and Savarese, S. (2009).
Video scene categorization by 3D hierarchical his-
togram matching. In International Conference on
Computer Vision.
Hamerly, G. and Elkan, C. (2003). Learning the k in k-
means. In Seventeenth annual conference on neural
information processing systems (NIPS).
Harris, C. and Stephens, M. (1988). A combined corner and
edge detector. Alvey vision conference.
Joachims, T. (1997). Text Categorization with Support Vec-
tor Machines: Learning with Many Relevant Features.
In ECML.
Judd, D., McKinley, P., and Jain, A. (1998). Large-scale
parallel data clustering. IEEE Transactions on Pattern
Analysis and Machine Intelligence.
Leung, T. and Malik, J. (1999). Recognizing surfaces us-
ing three-dimensional texton. In Proceedings of the
Seventh IEEE International Conference on Computer
Vision.
Lowe, D. G. (2004). Distinctive Image Features from Scale-
Invariant Keypoints. International Journal of Com-
puter Vision.
Maitra, R., Peterson, A. D., and Ghosh, A. P. (2010). A sys-
tematic evaluation of different methods for initializing
the K-means clustering algorithm. In IEEE Transac-
tions of Knowledge and Data Engineering.
Miller, A., Jain, V., and Mundy, J. (2011). Real-time Ren-
dering and Dynamic Updating of 3-d Volumetric Data.
In Proceedings of the Fourth Workshop on General
Purpose Processing on Graphics Processing Units.
Mundy, J. L. and Ozcanli, O. C. (2009). Uncertain geom-
etry: a new approach to modeling for recognition. In
2009 SPIE Defense, Security and Sensing Conference.
¨
Ozcanli, O. and Mundy, J. (2010). Vehicle Recognition as
Changes in Satellite Imagery. In International Con-
ference on Pattern Recognition.
Papadakis, P., Pratikakis, I., and Theoharis, T. (2010).
PANORAMA: A 3D Shape Descriptor Based on
Panoramic Views for Unsupervised 3D Object Re-
trieval. International Journal of Computer Vision.
Pelleg, D. and Moore, A. (2000). X-means: Extending K-
means with E cient Estimation of the Number of Clus-
ters. In International Conference on Machine Learn-
ing.
Pollard, T. (2008). Comprehensive 3-d Change Detection
Using Volumetric Appearance Modeling. PhD thesis,
Division of Applied Mathematics, Brown University.
Pollard, T. and Mundy, J. (2007). Change Detection in a 3-d
World. In IEEE Conference on Computer Vision and
Pattern Recognition.
Raviv, D., Bronstein, M. M., Bronstein, A. M., and Kim-
mel, R. (2010). Volumetric heat kernel signatures. In
3DOR ’10: Proceedings of the ACM workshop on 3D
object retrieval.
Shapira, L., Shalom, S., Shamir, A., Cohen-Or, D., and
Zhang, H. (2010). Contextual Part Analogies in 3D
Objects. International Journal of Computer Vision.
Sipiran, I. and Bustos, B. (2010). A Robust 3D Interest
Points Detector Based on Harris Operator. In Euro-
graphics Workshop on 3D Object Retrieval.
Sivic, J., Russell, B., Efros, A., Zisserman, A., and Free-
man, W. (2005). Discovering objects and their loca-
tion in images. In International Conference on Com-
puter Vision.
Snavely, N. and Seitz, S. (2006). Photo tourism: exploring
photo collections in 3D. ACM Transactions on Graph-
ics.
Thomas, A., Ferrar, V., Leibe, B., Tuytelaars, T., Schiel, B.,
and Van Gool, L. (2006). Towards Multi-View Object
Class Detection. In IEEE Conference on Computer
Vision and Pattern Recognition.
Varma, M. and Zisserman, A. (2009). A Statistical Ap-
proach to Material Classification Using Image Patch
Exemplars. IEEE Transactions on Pattern Analysis
and Machine Intelligence.
OBJECT RECOGNITION IN PROBABILISTIC 3-D VOLUMETRIC SCENES
189

Zhang, J., Marszalek, M., Lazebnik, S., and Schmid, C.
(2007). Local Features and Kernels for Classification
of Texture and Object Categories: A Comprehensive
Study. Int. J. Comput. Vision.
ICPRAM 2012 - International Conference on Pattern Recognition Applications and Methods
190
