
FEATURE VECTOR APPROXIMATION
BASED ON WAVELET NETWORK
Mouna Dammak, Mahmoud Mejdoub, Mourad Zaied and Chokri Ben Amar
Regim Research Group on Intelligent Machines, ENIS University, BP W, 3038 Sfax, Tunisia
Keywords:
Wavelet network, Approximation, Local feature, Bag of words.
Abstract:
Image classification is an important task in computer vision. In this paper, we propose a new image representa-
tion based on local feature vectors approximation by the wavelet networks. To extract an approximation of the
feature vectors space, a Wavelet Network algorithm based on fast Wavelet is suggested. Then, the K-nearest
neighbor (K-NN) classification algorithm is applied on the approximated feature vectors. The approximation
of the feature space ameliorates the feature vector classification accuracy.
1 INTRODUCTION
Visual descriptors for image categorization generally
consist of either global or local features. The for-
mer ones represent global information of images. On
the contrary, local descriptors (Piro et al., 2010; Tao
et al., 2010; Li and Allinson, 2008; Mejdoub et al.,
2008; Mejdoub et al., 2009; Mejdoub and BenAmar,
2011) extract information corresponding to locations
of a specific image that are relevant to characterize
the visual content. Indeed, these techniques are able
to emphasize local patterns, which images of the same
category are expected to share. Research suggests that
a regular dense sampling of descriptors can provide a
better representation (Lazebnik et al., 2006; Nowak
et al., 2006) than the “interest” points. The bag of
words (Csurka et al., 2004) representation can be con-
sidered as the practical proof of the effectiveness of
visual feature points. This approach is applied to im-
ages in (Csurka et al., 2004; Lazebnik et al., 2006)
to extract a histogram of words from the image. The
essential characteristic of this representation is that it
dismisses any kind of information associated to the
arrangement of words.
Analyzing a signal from its corresponding graph
does not give us access to all the information it con-
tains. It is often necessary to transform it, i.e., to give
it another representation which clearly shows its fea-
tures. Fourier (Fourier, 1822), suggests that all func-
tions must be able to express themselves in a simple
way as a sum of sinus. As an advanced alternative to
the classical Fourier analysis, wavelets (Cohen et al.,
2001) have been successfully used for signal approx-
imation. The fundamental idea behind wavelets is to
process data at different scales or resolutions. In such
a way, wavelets provide a time-scale presentation of
a sequence of input signal (Yan and Gao, 2009). The
wavelet transform applies a multi-resolution analysis
to decompose a signal into the low-frequency coeffi-
cients and the high-frequency coefficients. The for-
mer represent the original signal approximation and
the latter represent the detailed information of the
original signal.
Besides, the Wavelet Networks (WN) (Li et al.,
2003) is a powerful tool to approximate signals. In-
deed, it mixes the performances of the wavelet theory
in terms of localization and multi-resolution represen-
tation and the Neural Network in terms of classifica-
tion. The keypoint of the wavelet networks lies in the
optimization of network weights that permits to ex-
tract an approximation of the original signal. In (Je-
mai et al., 2011), the authors introduce a new training
method for WN to assess this algorithm in the field
of images classification directly from pixel value im-
ages. In (Ejbali et al., 2010), the authors advance a
new approach for the approximation of acoustic units
for the task of the speech recognition.
In this paper, we propose a novel image catego-
rization approach based on the approximation of lo-
cal features by Wavelet Networks. Firstly, we ex-
tract local features based on SIFT (Lowe, 1999) and
SURF (Bay et al., 2006) descriptors and we represent
them using the BOW model based on spatial pyramid.
Secondly, we approximate the histogram of words by
wavelet networks in an attempt to obtain greater rep-
resentation efficiency of the histogram of words. Fi-
394
Dammak M., Mejdoub M., Zaied M. and Ben Amar C..
FEATURE VECTOR APPROXIMATION BASED ON WAVELET NETWORK.
DOI: 10.5220/0003776803940399
In Proceedings of the 4th International Conference on Agents and Artificial Intelligence (ICAART-2012), pages 394-399
ISBN: 978-989-8425-95-9
Copyright
c
2012 SCITEPRESS (Science and Technology Publications, Lda.)

nally, k-NN algorithm is applied on the approximated
histogram of words for image categorization.
The rest of the paper is organized as follows:
Section 2 focuses on the theoretical concept of the
wavelet networks. Section 3 outlines the proposed ap-
proach of the extraction and the approximation of the
local descriptors. Some experimental results are pre-
sented in the final section with the aim to illustrate the
effectiveness of the proposed categorization method.
2 WAVELET NETWORK
The concept of wavelet networks was proposed firstly
by Zhang and Benveniste (Zhang and Benveniste,
1992). The basic idea of wavelet networks is to com-
bine the localization property of wavelet decomposi-
tion and the optimization property of neural networks
learning. The multilayered networks allow the rep-
resentation of a nonlinear function by training while
comparing their inputs and their outputs. This train-
ing is made while representing a nonlinear function
by a combination of activation functions. The ad-
missible wavelet is used as an activation one. They
reached the result that the wavelet networks preserve
the property of universal approximation of the RBF
networks.
Wavelet analysis gives a representation of signals that
simultaneously shows the location in time and fre-
quency, thereby facilitating the physical characteris-
tics identification of the signal source (Morlet et al.,
1982). This analysis uses a family of translate-dilated
functions ψ
a,b
constructed from a function ψ of
L
2
(ℜ), called mother wavelet ψ
a,b
(x) =
1
√
a
ψ
x−b
a
with a, b represent respectively the dilation and trans-
lation parameters. Discret Wavelet Transform DWT
is defined as a set of wavelets are generated by consid-
ering only a sampled value of a and b parameters. For
analyzing a signal containing a
j
0
points (1 ≤ j ≤ m, j
represents the scale parameter) we use only the family
wavelets: ψ
a
−m
0
x −nb
0
with n = 1 . . . a
m−j
0
:
w
j,n
= a
−
j
2
0
∑
x
f (x)ψ
a
−j
0
x −nb
0
(1)
For the particular case, when a
0
= 2 and b
0
= 1, the
sampling is called dyadic.
The multiresolution analysis consists on, firstly, a
scaling function φ (x) ∈L
2
(ℜ), which constitutes an
orthonormal basis by varying its position on a given
scale j. The functions of every scale generate an ap-
proximation of a given signal f to analyze. Secondly,
additional functions, i.e. wavelet functions, are then
used to encode the difference in information between
adjacent approximations (Meyer, 1990). If we have
a finished number N
w
of wavelets ψ
a,b
obtained from
the mother wavelet and a finished number N
s
of scales
φ
a,b
obtained from the mother scaling function φ, Eq.
2 will be considered as an approximation of the in-
verse transform:
f (x) '
N
w
∑
j=1
α
j
ψ
j
(x) +
N
s
∑
k=1
β
k
φ
k
(x) (2)
This equation establishes the idea of Wavelet Net-
works.
The model, introduced by Zhang et Benveniste
(Zhang and Benveniste, 1992), is composed of three
layers. Input of this is considered a set of parameters
t
j
that describe signal coordinate positions to analy-
sis. So the entries are not actual data but only val-
ues describing specific positions of the analyzed sig-
nal. The hidden layer contains a set of neurons, each
neuron composed of a translated and dilated wavelet.
The output layer contains one neuron which sums
the outputs of the hidden layer by weighted connec-
tions weights a
j
and d
j
that represent respectively the
wavelets and the scaling functions coefficients 1. Fig-
ure 1 displays the structure of wavelet network of the
second model.
2
22
2
a
bt
k
kk
k
a
bt
k
w
1
11
1
a
bt
)1( kit
i
),,,(
21 n
yyy
1
w
2
w
K : The number of neurons
T : Input positions values
W: Connections weights of Network
B: Values of translations
A : Values of dilatation
Y: Value of the approximation
Figure 1: The model of Wavelet Network architecture.
3 OVERVIEW OF THE
PROPOSED APPROACH
We suggest in this paper a solution of image clas-
sification based on local feature and approximation
vector by wavelet networks. The solution which we
present proceeds, at first, by local feature image rep-
resentation. Second, an image is represented based on
a BoW model. Third, the approximation by wavelet
networks is used on this image. In classification stage
(on-line), the same procedure is carried out to extract
the approximate test image signature. Finally, to de-
cide upon the image category, we search for the test
image the k-similar images in the training data and
we apply the majority vote. This search is based on
the computation of the distances between the approx-
imate feature vector of the test image and all the ap-
FEATURE VECTOR APPROXIMATION BASED ON WAVELET NETWORK
395

proximate feature vectors of the training images. The
pipeline of all these stages is illustrated in figure 2.
Plan
Category 1 Category n
…..
FEATURE EXTRACTION AND REPRESENTATION
…
.
Category ?
…
…..
…..
…..
…
.
…
.
Feature
extraction
Detection of
local regions
K-PPV
FEATURE EXTRACTION AND REPRESENTATION
…
.
.
Code book
…..
Bag of Words
and pyramid
spatial
…
Input
…..
Approximation
by WN
…..
mountains
Test
Training
Figure 2: Complete Framework of image classification by
BOW and WN.
3.1 Extraction of Local Features
In this paper, we focus on local feature vectors ex-
traction. Our system makes use of three types of low-
level features: SIFT features (Lowe, 1999), SIFT-
HSV (Bosch et al., 2008) features and SURF (Bay
et al., 2006) features. We use a dense sampling to
extract patches at a regular grid in the image, and at
multiple scales. Given the feature space, the visual
vocabulary is built through the clustering of low-level
feature vectors using k-means based on the acceler-
ated ELKAN (Elkan, 2003) algorithm for optimiza-
tion. The clusters define the visual vocabulary and
then the image is characterized with the number of
occurrences of each visual word. Similar to (Lazeb-
nik et al., 2006) we use a spatial pyramid of 1x1, 2x2,
and 4x4 regions in our experiments for all visual fea-
tures.
Figure 3: Hybrid descriptor.
The steps needed to calculate the signa-
ture of an image for a given local descriptor
(D ∈
{
SIFT, SURF
}
) are :
1. Extraction of local descriptors based on the de-
scriptor D.
2. Translation of each local descriptor in a histogram
of visual words using the technique of bag of
words on the descriptors obtained in step (1).
3. Division of the image into bands using the spatial
pyramid technique.
4. For each band obtained from the spatial pyramid.
extraction of a visual histogram of keywords by
combining visual keyword histograms obtained in
step (2).
5. Combining histograms obtained for each band to
derive a histogram H
D
associated with local de-
scriptor D.
6. Combining histograms obtained for SURF de-
scriptor and SIFT descriptor.
3.2 Wavelet Network
The Wavelet Network is used to approximate each lo-
cal feature vectors computed as indicated in the sec-
tion 3.1. We denote by V the local feature vector ex-
tracted from a given image database. To define the
Wavelet Network, we first take a family of n wavelets
Ψ = (ψ
1
, . . . , ψ
n
) with different parameters of scaling
and translation (generated by distributing the parame-
ters on a dyadic grid) that can be chosen arbitrarily at
this point. The architecture of the wavelet network is
exactly specified by the number of particular wavelets
required. In this work, we build the candidate hid-
den neurons representing a library of wavelets (scal-
ing functions), and then we select the hidden neurons
in order to form the optimal structures.
3.2.1 Wavelet Network Initialization
The G library of wavelet and scaling function candi-
dates to join the network are the results of a sampling
on a dyadic grid of the parameters of expansion and
translation. This family of functions is:
(
G =
n
ψ
a
−m
0
x −nb
0
, φ
a
−j
0
x −nb
0
o
with m ∈S
a
, n ∈ S
b(m)
)
(3)
In Eq.3, a
0
, b
0
> 0 are two scalar constants defin-
ing the discretization step sizes for dilation and trans-
lation. a
0
is typically dyadic. S
b
and S
a
are finite sets
related to the size of the data input domain D. The first
derivate from the wavelet beta (Amar et al., 2005) is
used as mother wavelet, given by equation 4:
B(x) =
x−x
0
x
c
−x
0
p
x−x
0
x
c
−x
0
q
i f x ∈ [x
0
, x
1
]
0 otherwise
wherep, q, x0, x1 ∈ R and x0 < x1
and x
c
=
px
1
+qx
0
p+q
(4)
We give below the used steps to initialize the WN:
Step 1: Start the learning by preparing a library of
candidate wavelets and scaling functions.
Step 2: Calculation of the weights corresponding to
all the functions of activation of the library.
ICAART 2012 - International Conference on Agents and Artificial Intelligence
396
Step 3: Impose a stop criterion; an error E between
the feature vector V and the exit of the network.
Step 4: Initialize the output network to
˜
V = 0.
3.2.2 Learning Wavelet Network
The training model is built according to the following
steps:
Step 1: Calculate the weights γ
l
α
l
ou β
l
respec-
tively associated with the wavelets and scales func-
tions, of the library already created in section 3.2.1.
Step 2: Calculate the contribution of all the functions
of activation in the library (γ
l
g
l
) for the rebuilding of
the feature vector V . V can be written :
V =
L
∑
l=1
γ
l
g
l
(5)
Step 3: Select the function g
k
of activation which pro-
vided the best approximation of the feature vector V .
Step 4: Recruit the best function with the hidden
layer of the wavelet network. The total approxima-
tion, which is the accumulation of all the approxima-
tions obtained with each iteration, is calculated by:
˜
V =
˜
V + γ
k
g
k
.
Step 5: Compute the difference between the original
signal and that approximated one is calculated. If the
error E, is reached, then it is the end of the phase of
training. If not, we move back to Step 3.
4 EXPERIMENTAL RESULTS
4.1 Presentation of the Datasets
We have carried out experiments on the WANG
database (Wang et al., 2001) which contains 1000 im-
ages. The database contains ten clusters representing
semantic generalized meaningful categories.Besides,
we have carried our experiments on the OT dataset
(Oliva and Torralba, 2001) that contains 2688 color
images , divided in 8 categories. For evaluation we
divide the images randomly into 500 training and
500 test images for wang dataset and 800 training
and 1688 test images for OT. Experiments were per-
formed on a personal computer with configurations:
Intel Core2 Duo (2 GHZ), 4GO. In our experiments,
image patches are extracted on regular grids at 4 dif-
ferent scales. SIFT, SIFT-HSV and SURF descrip-
tors are computed at every point of the regular grid.
The dense features are vector quantized by the bag of
words model with N-cluster = 120 for Wang database
and N-cluster = 300 for OT database. We tested the
performance of our proposed image retrieval method
taking into account the retrieval process accuracy. For
the accuracy evaluation, we use the precision.
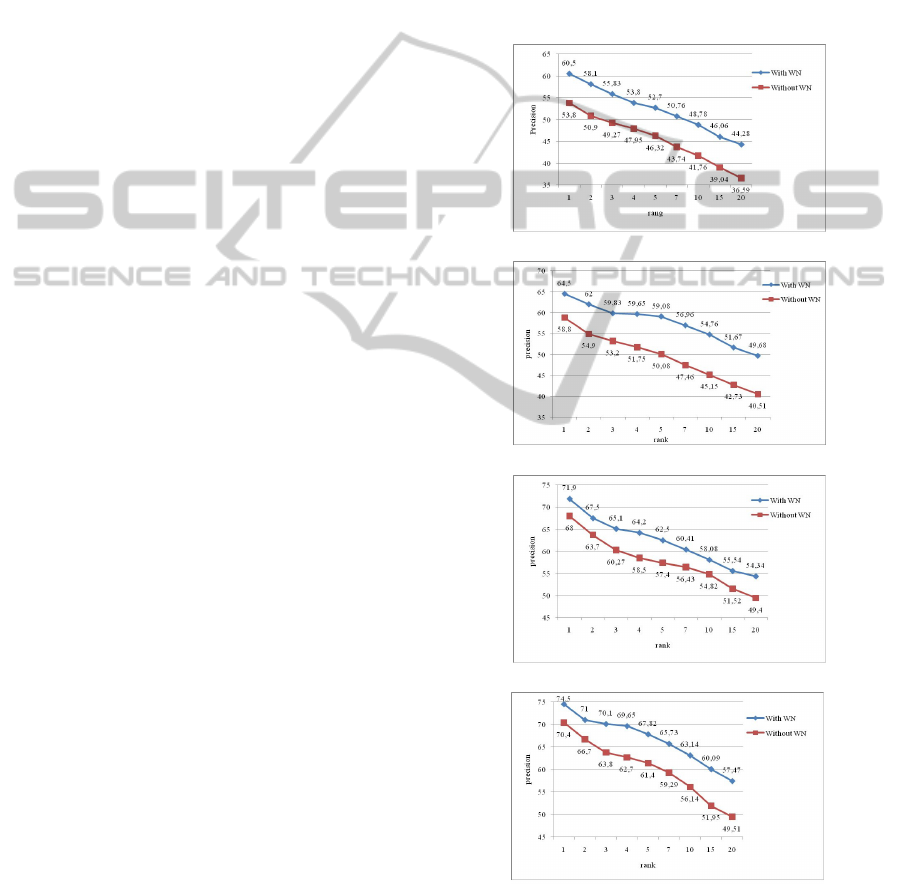
4.2 Impact of the Space Approximation
Feature
Several experiments are made using the Wang and OT
databases. We observe in Figure 5 and 6 that the im-
age signature approximated by WN for the various
types of descriptors (SIFT, SIFT-HSV, SURF and Hy-
brid) give a better performance in term of precision of
retrieval than the original signature (signature not ap-
proximated by WN).
(a) SIFT.
(b) SIFT-HSV.
(c) SURF.
(d) Hybrid.
Figure 4: Comparison between original and approximate
feature vectors (Wang).
FEATURE VECTOR APPROXIMATION BASED ON WAVELET NETWORK
397

(a) SIFT.
(b) SIFT-HSV.
(c) SURF.
(d) Hybrid.
Figure 5: Comparison between original and approximate
feature vectors (OT).
4.3 Comparison of the Proposed
Classifier to Popular Methods in the
Literature
We will now compare the results and using differ-
ent machine learning algorithms as Support Vector
Machines (SVMs), Hidden Markov Model (HMM),
K-Nearest Neighbor (KNN), or Universal Nearest
Neighbors rule (UNN) could be applied for catego-
rization.
The experimental results reported here see (1)
seem very promising and the proposed approach out-
Table 1: Comparison with some State-of-the-Art methods.
(a) Wang database.
Classification Model Classification rate
(Jemai et al., 2011) 71,2
(Jemai et al., 2010) 71,4
(Mouret et al., 2009) 70,60
Our approach 74,50
(b) OT database.
Classification Model Classification rate
(Piro et al., 2010)-KNN 73,8
(Piro et al., 2010)-UNN 75,70
(Oliva and Torralba, 2001) 83,70
(Horster et al., 2008) 79
Our approach 80,20
performs the other methods.
4.4 Comparison between Raw Pixels
and Feature Vectors Representation
In (Jemai et al., 2011), the authors reshape the size
of the image to 90*90 pixels. The wavelets network
is directly applied to the pixel values of image.Our
work allows on the one hand reducing the dimension
of the feature vector of the image, and on the other
hand generating a compact representation of the im-
age. And consequently, we obtained a faster comput-
ing time and a more precise categorization rate. Table
2 compares CPU-times spent to compute the different
stages of the learning algorithm for one image and
rate categorization.
Table 2: Classification rate and Time consumption for the
processing steps on Wang.
BWNN (Jemai
et al.,
2011)
Our ap-
proach
Time consumption
Training 20mn 0.1176s 0,010531s
Classification 2mn 0.0627s 0.038517s
Classification rate
Rate classi-
fication
60,2 71,4 74,5
5 CONCLUSIONS
A new indexing method was proposed in this paper.
This method is based on a combined local feature ex-
traction and approximated signal by Wavelet Network
is proposed. This method is applied to the image clas-
sification fields. Based on the experiment results, the
ICAART 2012 - International Conference on Agents and Artificial Intelligence
398

proposed approach exhibits high classification rates
and small computing times.
REFERENCES
Amar, C. B., Zaied, M., and Alimi, M. A. (2005). Beta
wavelets. synthesis and application to lossy image
compression. Advances in Engineering Software,
36:459–474.
Bay, H., Tuytelaars, T., and Gool, L. V. (2006). Surf:
Speeded up robust features. In 9th European Con-
ference on Computer Vision.
Bosch, A., Zisserman, A., and Munoz, X. (2008). Scene
classification using a hybrid generative/discriminative
approach. IEEE Transactions on Pattern Analysis and
Machine Intelligence, 30(4):712–727.
Cohen, A., Dahmen, W., Daubechies, I., and Devore,
R. (2001). Tree approximation and optimal encod-
ing. Applied and Computational Harmonic Analysis,
11(2):192–226.
Csurka, G., Dance, C. R., Fan, L., Willamowski, J., and
Bray, C. (2004). Visual categorization with bags of
keypoints. In Workshop on Statistical Learning in
Computer Vision, ECCV.
Ejbali, R., Zaied, M., and Amar, C. B. (2010). Wavelet net-
work for recognition system of arabic word. Interna-
tional Journal of Speech Technology, 13(3):163–174.
Elkan, C. (2003). Using the triangle inequality to accelerate
k-means. ICML, pages 147–153.
Fourier, J. B. J. (1822). Thorie analytique de la chaleur.
Horster, E., Greif, T., Lienhart, R., and Slaney, M. (2008).
Comparing local feature descriptors in plsa-based im-
age models. In DAGM-Symposium, pages 446–455.
Jemai, O., Zaied, M., Amar, C. B., and Alimi, M. A.
(2010). Fbwn: An architecture of fast beta wavelet
networks for image classification. In International
Joint Conference on Neural Networks (IJCNN), pages
1–8, Barcelona.
Jemai, O., Zaied, M., Amar, C. B., and Alimi, M. A. (2011).
Pyramidal hybrid approach: Wavelet network with ols
algorithm-based image classification. International
Journal of Wavelets, Multiresolution and Information
Processing (IJWMIP), 9(1):111–130.
Lazebnik, S., Schmid, C., and Ponce, J. (2006). Beyond
bags of features: Spatial pyramid matching for rec-
ognizing natural scene categories. In Proceedings of
the IEEE Conference on Computer Vision and Pattern
Recognition, volume 2, pages 2169–2178, New York.
Li, C., Liao, X., and Yu, J. (2003). Complex-valued wavelet
network. Journal of Computer and System Sciences,
67(3):623–632.
Li, J. and Allinson, N. M. (2008). A comprehensive review
of current local features for computer vision. Neuro-
computing, 71:1771–1787.
Lowe, D. (1999). Object recognition from local scale-
invariant features. In International Conference on
Computer Vision, pages 1150–1157, , Corfu, Greece.
Mejdoub, M. and BenAmar, C. (2011). Hierarchical cat-
egorization tree based on a combined unsupervised-
supervised classification. In Seventh International
Conference on Innovations in Information Technol-
ogy.
Mejdoub, M., Fonteles, L., BenAmar, C., and Antonini, M.
(2008). Fast indexing method for image retrieval using
tree-structured lattices. In Content based multimedia
indexing CBMI.
Mejdoub, M., Fonteles, L., BenAmar, C., and Antonini,
M. (2009). Embedded lattices tree: An efficient in-
dexing scheme for content based retrieval on image
databases. Journal of Visual Communication and Im-
age Representation, Elsevier.
Meyer, Y. (1990). Ondelettes et oprateurs I. Actual-
its Mathmatiques Current Mathematical Topics. Her-
mann, Paris.
Morlet, J., Arens, G., Fourgeau, E., and Giard, D. (1982).
Wave propagation and sampling theory. Geophysics,
47:203–236.
Mouret, M., Solnon, C., and Wolf, C. (2009). Classifica-
tion of images based on hidden markov models. In
IEEE Workshop on Content Based Multimedia Index-
ing, pages 169–174.
Nowak, E., Jurie, F., and Triggs, B. (2006). Sampling strate-
gies for bag-of-features image classification. In Euro-
pean Conference on Computer Vision. Springer.
Oliva, A. and Torralba, A. (2001). Modeling the shape
of the scene: A holistic representation of the spatial
envelope. International Journal of Computer Vision,
42(3):145–175.
Piro, P., R.Nock, Nielsen, F., and Barlaud, M. (2010).
Boosting k-nn for categorization of natural scenes.
CoRR.
Tao, Y., Skubic, M., Han, T., Xia, Y., and Chi, X. (2010).
Performance evaluation of sift-based descriptors for
object recognition. In Prooceeding of The Interna-
tional MultiConference of Engineers and Computer
Scientists.
Wang, J. Z., Li, J., and Wiederhold, G. (2001). Simplicity
: Semantics-sensitive integrated matching for picture
libraries. IEEE Transactions on Pattern Analysis and
Machine Intelligence, 23(9):947–963.
Yan, R. and Gao, R. (2009). Base wavelet selection for bear-
ing vibration signal analysis. International Journal of
Wavelets, Multi-resolution, and Information Process-
ing, 7(4):411–426.
Zhang, Q. and Benveniste, A. (1992). Wavelet networks.
IEEE Transactions on Neural Networks, 3(6):889–
898.
FEATURE VECTOR APPROXIMATION BASED ON WAVELET NETWORK
399
