
MONOCULAR EGOMOTION ESTIMATION BASED ON
IMAGE MATCHING
Diego Cheda, Daniel Ponsa and Antonio Manuel L´opez
Computer Vision Center, Universitat Aut`onoma de Barcelona, Edifici O, Campus UAB, 08193, Bellaterra, Barcelona, Spain
Keywords:
Advanced driver assistance systems, Egomotion estimation, Monocular camera system, Template tracking.
Abstract:
In this paper, we propose a novel method for computing the egomotion of a monocular camera mounted on a
vehicle based on the matching of distant regions in consecutive frames. Our approach takes advantage of the
fact that the image projection of a plane can provide information about the camera motion. Instead of tracking
points between frames, we track distant regions in the scene because they behave as an infinity plane. As a
consequence of tracking this infinity plane, we obtain an image geometric transformation (more precisely, an
infinity homography) relating two consecutive frames. This transformation is actually capturing the camera
rotation, since the effect produced by the translation can be neglected at long distances. Then, we can compute
the camera rotation as the result of the previously estimated infinity homography. After that, rotation can be
canceled from images, just leading to a translation explaining the motion between two frames. Experiments
on real image sequences show that our approach reaches higher accuracy w.r.t. state-of-the-art methods.
1 INTRODUCTION
The estimation of changes in the vehicle position and
orientation along time (i.e., its egomotion) is a key
component of many advanced driver assistance sys-
tems (ADAS) like adaptive cruise control, collision
avoidance, lane-departure warning, etc. Despite that
several sensors are available for obtaining egomotion
measurements (e.g., inertial sensors), many research
efforts tend toward the use of cameras due to their
ease of integration, low-cost and power consumption.
In that sense, different proposals exist for determin-
ing the camera pose based just on images, avoiding
the installation of additional sensors on the vehicle.
Our work concerns monocular egomotion estima-
tion using a camera mounted rigidly in a vehicle. Al-
though the problem ismore challenging, we have con-
sidered that monocular systems will be present in ve-
hicles solving other applications, and our aim is ex-
tending functionalities without adding more cost.
Regarding visual egomotion methods, in general,
they treat all image points in the same way w.r.t. their
distance from the camera. However, those points be-
longing to distant scene objects from the camera be-
have as lying on an infinity plane. The image pro-
jection of this plane is only affected by camera rota-
tion. Taking advantage of that, we propose to track
the image projection of distant regions to estimate the
camera rotation. Specifically, in the following, dis-
tant regions are the ones whose optical flow due to
camera translation between two consecutive frames is
smaller than one pixel. As a consequence of tracking
this plane, we obtain a transformation relating both
frames, which captures the camera rotation, since the
effect produced by the translation is assumed as neg-
ligible at long distances. Then, camera rotation is ex-
tracted from the computed transformation. Once ro-
tation is known, we register both frames, canceling its
effects and leading to a pure translation motion be-
tween frames. From this image flow, translation is
estimated by solving a linear equation system.
Our approach has several advantages w.r.t. most
general egomotion methods. First, we avoid the fea-
ture extraction and matching, which is valuable since
small errors in the estimated image flow usually bring
to large perturbations in the motion estimation. Sec-
ond, in contrast to most of the feature-based meth-
ods, we decouple rotation from translation estimation,
leading to accurate estimations because translation es-
timation errors do not affect the rotation computation.
Third, our method is not affected by ambiguities pro-
duced by camera motion (Ferm¨uller and Aloimonos,
1998), since distant regions are mainly affected just
by rotation. Finally, our method is also robust to out-
liers because errors in the distant regions segmenta-
tion have a low impact on the regions tracking.
425
Cheda D., Ponsa D. and López A. (2012).
MONOCULAR EGOMOTION ESTIMATION BASED ON IMAGE MATCHING.
In Proceedings of the 1st International Conference on Pattern Recognition Applications and Methods, pages 425-430
DOI: 10.5220/0003776904250430
Copyright
c
SciTePress

Obviously, the results of our algorithm would be
affected when acquired images do not show distant
regions due to obstructions in the field of view (e.g.,
a truck or a wall in front of the vehicle). These situa-
tions could be detected and properly treated.
The paper is organized as follows. In Sec. 2, we
review related works. Next, we introduce our ap-
proach based on tracking distant regions. Finally, we
describe and discuss the experimental results.
2 RELATED WORK
The egomotion problem concerns the estimation of
the 3D rigid motion of the camera along a sequence,
involving six degrees of freedom (DOF). The goal is
estimating a translation vector
˙
t and the angles ω
ω
ω of a
rotation matrix R from the image motion observed in
subsequent frames. In this paper,we develop a vision-
based method to egomotion estimation. Using a sin-
gle camera, DOF is reduced to five since translation
can be only recovered up to a scale factor (i.e., only
translation direction is estimated, while its magnitude
cannot be recovered due to lack of depth information).
In the following, we review the most important related
works.
Egomotion methods are classified as discrete or
differential (Cheda et al., 2010) depending on whether
they use point matches between views or optical flow,
respectively. In contrast to these methods, direct ones
compute egomotion without the need of matching be-
tween views (Zelnik-Manor and Irani, 2000).
In general, feature-based methods consider all
points in the similar way w.r.t. their depth in the scene.
However, some recent works try to take advantage of
the relation between image motion and scene depth.
Using a monocular camera, in (Burschka and Mair,
2008), a RANSAC process selects optical flow vec-
tors that can be explained only by a particular rotation.
Implicitly, this process tries to select image points lo-
cated at far distances from the camera. Then, using
the selected set of optical flow vectors, rotation is es-
timated by solving a linear equation system. Using
a stereo camera, in (Obdrzalek and Matas, 2010), a
voting strategy is used to egomotion estimation. Ro-
tation is estimated through a voting schema where a
vote weighted with the triangulated distance of each
point to the camera is assigned for each motion vec-
tor. Once rotation is computed, the rest of motion is
due to translation, which is also estimated by a vot-
ing strategy. In (Thanh et al., 2010), rotation and
translation are estimated using far/near features, re-
spectively. The point classification is done by check-
ing their disparity over seven views of the same scene
provided by a special omnidirectional sensor.
Another approach uses homographies to estimate
motion parameters when the corresponding points are
on a plane. In the ADAS context, some works try
to track points over a ground plane such that this
plane induces a homography relating two consecutive
frames (Liang and Pears, 2002; Wang et al., 2005;
Scaramuzza et al., 2010). To do that, a homogra-
phy over two frames is robustly estimated by selecting
points belonging to the ground plane. Inlier points are
used to compute the camera motion by decomposing
the estimated homography.
A disadvantage of using just points for egomotion
estimation is that valuable information for motion es-
timation is unexploited. For instance, distant regions
like sky, mountains, etc. are discarded because a few
points can be detected over nearly uniform and low-
textured surfaces. Then, distant regions are hard to
be tracked by using interesting points. In contrast to
the feature-based methods, direct methods avoid fea-
ture matching, and use only measurable information
from images (Zelnik-Manor and Irani, 2000; Com-
port et al., 2010). Most of these approaches require a
physical plane existing in the scene to obtain an accu-
rate estimation of the camera motion. However, if no
such planar surface exists, they cannot be applicable.
The work of (Comport et al., 2010) does not require a
region of interest, but it uses all image information by
performing a dense stereo matching between consec-
utive frames.
Our proposal is a novel method within this cat-
egory. Instead of requiring a real scene plane, we
extract camera motion information from distant re-
gions since they behave as an infinite plane. This
strategy allows us to effectively annihilate the rotation
between two consecutiveframes, leading to just trans-
lation explaining the remaining camera motion. The
basis of our proposal is the assumption that distant re-
gions can be automatically segmented from images,
which has been proved feasible in several application
domains (see Sec. 3.3). In the next section, we define
our approach.
3 PROPOSED METHOD
Now, we overview our method. First, we summarize
the coplanar relation between two frames. Then, we
describe our algorithm in the subsequent sections.
3.1 Transformation Relating Two Views
We consider the relation between two frames based on
the property that the projection of a plane into these
ICPRAM 2012 - International Conference on Pattern Recognition Applications and Methods
426

frames is related by a homography.
Let p = [p
x
, p
y
, p
z
]
T
and p
′
= [p
′
x
, p
′
y
, p
′
z
]
T
be the
coordinates of the same scene point, expressed in two
different cameras coordinates systems C and C
′
, re-
spectively. The projection of p and p
′
into the im-
age planes is q = Kp = [q
x
, q
y
, q
z
]
T
and q
′
= Kp
′
=
[q
′
x
, q
′
y
, q
′
z
]
T
, and K is a calibration matrix with a focal
length f and the principal point at the origin [0, 0].
C and C
′
are related by a rigid body motion
p
′
= Rp+ t , (1)
where t = [t
x
, t
y
, t
z
]
T
is a translation vector and, as-
suming that the camera rotation is small, R is a
rotation matrix parametrized by Euler angles ω
ω
ω =
[ω
x
, ω
y
, ω
z
]
T
(pitch, yaw and roll, respectively) and
approximated by (Adiv, 1985)
R =
1 −ω
z
ω
y
ω
z
1 −ω
x
−ω
y
ω
x
1
.
Furthermore, we assume that p lies on a plane Π,
which is defined by its normal vector n = [α, β, γ] as
n
d
Π
p = 1 , (2)
where n
T
is a unit vector in the direction of the plane
normal, and d
Π
is the distance to the plane from C.
Plugging (2) into (1), we obtain the expression
p
′
= Gp , (3)
where G= (R +
nt
d
Π
) is the homography induced by
Π in 3D. In 2D, the transformation between the cor-
responding image points can be written as q
′
= Hq,
where H is the homography between two views of Π
defined as
H = K
R+
nt
d
Π
K
−1
. (4)
Since t depends on the unknown depth d
Π
, it can
be computed only up to a scale factor. Notice that the
contribution of camera rotation R to the displacement
of an image point is independent of the depth. We
exploit this fact to camera rotation estimation.
In similar manipulation to (Zelnik-Manor and
Irani, 2000), due to H is computed up to a scale factor
q
′
x
q
′
y
=
1
H
3
q
H
1
q
H
2
q
,
where H
i
is the i
th
-row of H, and the image flow field
[ ˙q
x
, ˙q
y
]
T
= [q
′
x
− q
x
, q
′
y
− q
y
]
T
is
˙q
x
˙q
y
=
(H
1
− H
3
q
x
)q
H
3
q
(H
2
− H
3
q
y
)q
H
3
q
. (5)
If the camera rotations are small, which is the case
in the neighboring frames of a sequence taken by a
moving vehicle, we can assume that H
3
q is approx-
imately equal to 1, f is large enough, and the trans-
lation over Z-axis is small relative to the plane depth
(Zelnik-Manor and Irani, 2000).
Now, we assume that Π is located at infinity,
which is the case for distant regions. In this case,
from Eq. (3), we observe that if d
Π
tends to ∞, then
nt
d
Π
tends to 0, letting G = R. This means that H from
Eq. (4) does not depend on the translation between
views, only on the rotation and camera internal pa-
rameters. Thus, the transformation between the corre-
sponding image points can be rewritten as q
′
= H
∞
q,
where H
∞
is the infinite homography matrix between
the two views of Π
∞
defined as H
∞
= KRK
−1
.
Given H
∞
, and operating over Eq. (5), the image
flow describing the motion between frames becomes
˙
q = Qω
ω
ω , (6)
where Q only depends on q = [q
x
, q
y
, 1]
T
, with q
z
= 1
Q =
−
q
x
q
y
f
f +
q
2
x
f
−q
y
− f −
q
2
y
f
q
x
q
y
f
q
x
.
We use Eq. (6) as the base of our approach to
compute camera orientation. In the next section, we
overview our algorithm that takes advantage of this
motion’s particularity to estimate camera rotation by
tracking distant regions.
3.2 Algorithm Overview
Basically, given two consecutive frames I at instant t
and t + 1, the algorithm proceeds as follows:
1. Distant regions are detected in I
t+1
as we explain
in Sec. 3.3. The result of this step is a template T
containing the plane to be tracked.
2. T is aligned w.r.t. I
t
. Camera rotation parameters
are extracted based on Eq. (6) (see Sec. 3.4).
3. The rotation effect between I
t
and I
t+1
is can-
celed, leading to just a translation t explaining the
observed motion between both frames.
4. Finally, translation t is computed as in Sec. 3.5.
3.3 Distant Regions Segmentation
Traditionally, depth estimation has been addressed as
a 3D reconstruction problem, focusing on multi-view
methods (e.g., structure from motion). Nevertheless,
studies on human vision suggest that depth perception
MONOCULAR EGOMOTION ESTIMATION BASED ON IMAGE MATCHING
427

is also supported by monocular cues such as occlu-
sions, perspective, textures, etc. Recently, some pro-
posals on depth estimation from a single image have
been done (Saxena et al., 2009). However, for many
applications, obtaining exact depths of the scene may
not be necessary. In our case, only having informa-
tion about the proximity/distantness of some regions
can be enough for egomotion estimation. It is out
of scope of the paper to address this problem. How-
ever, a discrete depth map could be estimated by seg-
menting the distance space in two (or more) threshold
ranges. Using an appropriate set of discriminative vi-
sual features, a classifier could be trained for distin-
guishing close/distant regions according to a desired
distance threshold. This segmentation would allow us
to effectively distinguish the distant regions in an im-
age.
3.4 Distant Regions Matching
Once distant regions for the frame I
t+1
have been
computed, we have a template T corresponding to a
plane. Then, we align T w.r.t. I
t
using Lucas-Kanade
algorithm (Lucas and Kanade, 1981). This algorithm
iteratively minimizes the difference between T and I
t
under the following goal objective
∑
q
(I
t
(W (q, ω
ω
ω)) − T (q))
2
w.r.t. ω
ω
ω, where W (q, ω
ω
ω) = q +
˙
q = q + Qω
ω
ω from
Eq. (6). As the result of this process, we obtain the
rotation parameters ω
ω
ω to align T w.r.t. I
t
.
3.5 Translation Estimation
Once rotation angles ω
ω
ω are estimated by aligning T
w.r.t. I
t
, we can cancel the rotation effects. Without
rotation motion, the difference between both frames
I
t
and I
t+1
is due to the camera translation.
Assuming a plane with n = [0, 0, 1]
T
(i.e., the
plane is located over the camera principal axis), we
can compute translation by solving the following
equation system from Eq. (5)
˙
q =
f 0 −q
x
0 f −q
y
t .
To solve this system, we select matching points be-
tween I
t
and I
t+1
, belonging to close regions.
4 EXPERIMENTAL RESULTS
In this section, we test our approach on sequences
taken with a stereo camera mounted on a vehicle
driven through a city (Kitt et al., 2010)
1
. This se-
quence consists of more than 1400 frames, where
translations and rotations ground truth (GT) are pro-
vided by measurements of an INS sensor. Addition-
ally, we have taken advantage of a stereo depth map
available on the processed sequence to optimally seg-
ment distant regions. In that way, we quantify the best
performance that can be achieved with our proposal.
Distant regions are defined as those composed by pix-
els located beyond 70 meters (m), where the effect of
the vehicle translation on the optical flow is subpixel.
In the ADAS context, the dominant angle varia-
tion is on the pitch and yaw angles, due to the suspen-
sion system and the vehicle turning effects, respec-
tively. In normal driving situations, the roll can be
assumed as null. Then, Eq. (6) is reduced to two DOF.
Region matching between two consecutive frames
is done by a modified version of Lucas-Kanade algo-
rithm based on the public available Matlab code de-
scribed in (Baker and Matthews, 2004). The main
improvements w.r.t. that version are the inclusion of
a multi-resolution pyramidal schema that allows us
to consider different scales during template matching,
and the use of arbitrary shape templates.
We measure the accuracyof our approach by com-
puting the rotation estimation errors as in (Tian et al.,
1996). Mean rotation error is quantified by the dif-
ference angle between the true rotation ω
ω
ω
i
and the es-
timated rotation
¯
ω
ω
ω
i
, at frame i = 1, . . . , N. For this
purpose, R
i
and
¯
R
i
for both ω
ω
ω
i
and
¯
ω
ω
ω
i
are built. The
product between R
i
and
¯
R
i
is an identity matrix when
both are equal. Thus, the difference between both ma-
trices is defined as △R
i
= R
T
i
¯
R
i
. In Euler terms, △R
i
can be characterized by an axis unit vector and an an-
gle. This angle is used as the rotation error. Since
trace(R
i
) = 1+ 2cos(α
i
), then the angle is equal to
µ(△R
i
) = cos
−1
1
2
(trace(△R
i
) − 1)
.
Then, we compute the mean of rotation errors (MRE)
for the whole sequence, providing a scalar value for
ω
ω
ω, and simplifying the evaluation of the algorithms.
Trajectory errors are quantified by computing the
Euclidean distance between both the GT and esti-
mated trajectory as follows
e(q
i
, q
′
i
) =
q
(q
x
− q
′
x
)
2
+ (q
z
− q
′
z
)
2
,
where q
i
are the 2D coordinates of the GT trajectory
and q
′
i
are the coordinates of the estimated trajectory
on XZ plane. We compute the mean Euclidean dis-
tance (MED) averaging e(q
i
, q
′
i
) over all frames. We
do not include the displacement onY-axis because GT
1
http://www.rainsoft.de/software/
ICPRAM 2012 - International Conference on Pattern Recognition Applications and Methods
428
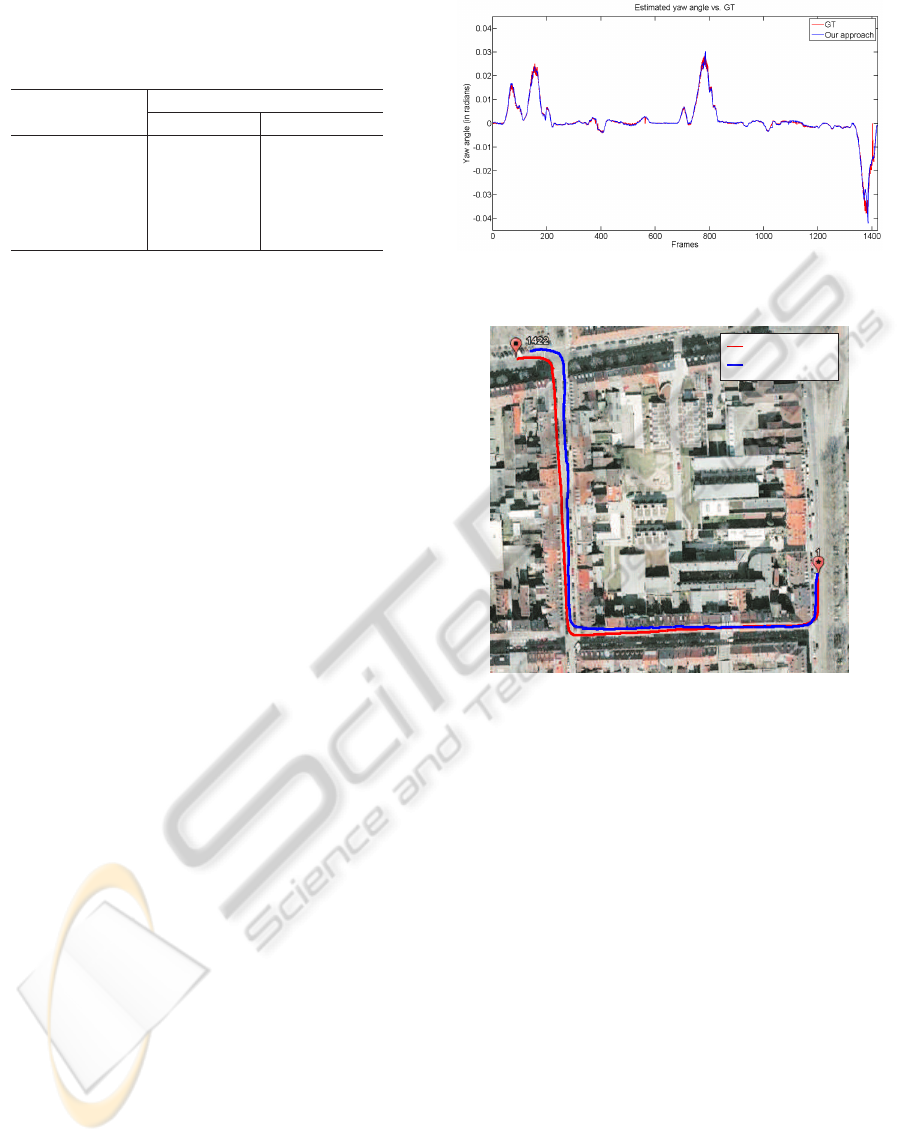
Table 1: Comparison between our approach and general and
distance-point-based egomotion methods. The mean rota-
tion error (in degrees) and the mean Euclidean distance er-
ror (in meters) are shown for each algorithm.
Algorithms
Error
MRE (in
◦
) MED (in m)
Our 0.052 4.93
5pts 0.094 10.70
Stereo 0.067 4.16
Burschka 0.108 7.32
Distant Points 0.147 4.38
data are unreliable in this coordinate (recognized by
their authors), and distort the comparison.
Next, we show the results obtained by our ap-
proach versus general and distant-based methods. Fi-
nally, we analyze the robustness of our approach
when distant regions are imprecisely segmented.
4.1 Comparison Against Other Methods
We compare our results against the ones obtained by
two general methods: 5pts algorithm (Nist´er, 2004)
and by a stereo algorithm proposed by (Kitt et al.,
2010); and we also compare our results against the
ones of two distant points-based methods: Burschka
et al. (Burschka and Mair, 2008) and distant-point al-
gorithms. The last algorithm, implemented by us, use
distant points instead of distant regions to egomotion
estimation. In this case, the camera rotation is com-
puted by solving a linear equation system over the op-
tical flow of points located at a distance over 70 m.
Results are shown in Tab. 1. The accuracy of our
method outperforms the other considered methods in
rotation estimation (MRE). This is because we take
advantage of valuable information for motion esti-
mation, which is unexploited by feature-based meth-
ods. For instance, we are considering regions located
at sky which are discarded by feature-based methods
since few points can be detected over such regions.
Figure 1 shows a comparison between our estimation
of yaw angle (in radians) against the GT provided by
the INS sensor. Our estimation is very close to GT.
Notice that the estimated yaw angle variation using
our method is smoother. We guess that this is because
we do a maximal use of the information available in
frames to estimate the camera rotation, which lead
to estimated parameters reflecting the behavior of the
real camera motion in the sequence, characterized by
a slow and smooth movement.
Regarding the estimated trajectory (MED), our
approach has a comparable performance to the stereo
and distant point algorithms, and outperforms both
5pts and Burschka et al. algorithms. The error per-
centage is 1.08 % of the total traveled distance, which
Figure 1: Comparison between estimated yaw angle versus
GT (in radians) on the sequence.
GT
Our approach
Figure 2: Comparison between estimated trajectory and GT.
is a good performance. Figure 2 shows the trajectory
described by our algorithm versus GT. Our result is
accurate w.r.t INS sensor measurements.
Naturally, as we stated in Sec. 1, the results of our
approach would be affected when most of the field of
view is obstructed. In these situations, the distant re-
gion segmenter does not provide enough information
to apply our method. Then, we can use another ego-
motion method to deal with such cases.
4.2 Robustness to Noisy Segmentation
We are based on stereo depth maps to segment the im-
age in close/far regions. However, segmentations as
described in Sec. 3.3 will present outliers due to clas-
sification errors. To test our algorithm under these
situations, we add different amounts of near regions
simulating the performance of a realistic segmenter.
Close regions are chosen randomly and used during
template matching as if they were distant ones. Ad-
ditionally, we remove (in the same proportion as we
add) distant regions from the considered template to
simulate misclassification. Table 2 shows the results
MONOCULAR EGOMOTION ESTIMATION BASED ON IMAGE MATCHING
429

Table 2: The mean rotation error (in degrees) is shown for
our approach under different amount of outliers.
Error
Outliers
10% 20% 30%
MRE (in
◦
) 0.0570 0.0613 0.0667
of this experiment. The performancedoes not degrade
significantly even under a large number of outliers.
5 CONCLUSIONS
In this work, we have proposed a direct monocular
egomotion method based on tracking distant regions.
These regions can be assumed as located at the infi-
nite plane, inducing an infinity homography relation
between two consecutive frames. By tracking that
plane, we are able to estimate the camera rotation.
Once rotation is computed, we cancel its effect on
the images, leaving the resulting motion due to cam-
era translation. This method is simple and performs a
sufficiently stable camera parameter’s estimation.
We successfully apply our algorithm to a sequence
taken from a vehicle driving in an urban scenario. Ro-
tations are accurately estimated, since distant regions
provide strong indicators of camera rotation. In com-
parison to the state-of-the-art methods, our approach
outperforms the considered methods. Moreover, from
the experimental results, we conclude that our method
is also robust to segmentation errors. Occasional mis-
takes can occur when acquired images do not show
distant regions due to obstructions in the field of view.
As future work, we plan to test the proposal using
a monocular segmentation algorithm to distinguish
between close/far regions from single images. These
segmentations will provide enough information about
depth to be used in our egomotion algorithm.
ACKNOWLEDGEMENTS
This work is supported by Spanish MICINN
projects TRA2011-29454-C03-01, TIN2011-29494-
C03-02, Consolider Ingenio 2010: MIPRCV
(CSD200700018), and Universitat Aut`onoma de
Barcelona.
REFERENCES
Adiv, G. (1985). Determining Three-Dimensional Motion
and Structure from Optical Flow Generated by Several
Moving Objects. IEEE Trans. Pattern Anal. Mach.
Intell., 7(4):384 –401.
Baker, S. and Matthews, I. (2004). Lucas-Kanade 20 Years
On: A Unifying Framework. Int. J. Comput. Vision,
56(1):221 – 255.
Burschka, D. and Mair, E. (2008). Direct Pose Estimation
with a Monocular Camera. In Int. Workshop Robot
Vision, pages 440–453.
Cheda, D., Ponsa, D., and L´opez, A. (2010). Camera Ego-
motion Estimation in the ADAS Context. In IEEE
Conf. Intell. Transp. Syst., pages 1415 –1420.
Comport, A., Malis, E., and Rives, P. (2010). Real-
time Quadrifocal Visual Odometry. Int. J. Rob. Res.,
29:245–266.
Ferm¨uller, C. and Aloimonos, Y. (1998). Ambiguity in
structure from motion: sphere versus plane. Interna-
tional Journal of Computer Vision, 28(2):137–154.
Kitt, B., Geiger, A., and Lategahn, H. (2010). Visual
Odometry based on Stereo Image Sequences with
RANSAC-based Outlier Rejection Scheme. In IEEE
Intell. Veh. Symp., pages 486 – 492.
Liang, B. and Pears, N. (2002). Visual Navigation Using
Planar Homographies. In IEEE Int. Conf. Rob. Au-
tom., volume 1, pages 205 – 210.
Lucas, B. and Kanade, T. (1981). An Iterative Image Reg-
istration Technique with an Application to Stereo Vi-
sion. In Int. Joint Conf. Artif. Intell., pages 674–679.
Nist´er, D. (2004). An Efficient Solution to the Five-Point
Relative Pose Problem. IEEE Trans. Pattern Anal.
Mach. Intell., 26(6):756–777.
Obdrzalek, S. and Matas, J. (2010). A Voting Strategy for
Visual Ego-motion from Stereo. In IEEE Intell. Veh.
Symp., pages 382 –387.
Saxena, A., Sun, M., and Ng, A. (2009). Make3D: Learning
3D Scene Structure from a Single Still Image. IEEE
Trans. Pattern Anal. Mach. Intell., 31(5):824–840.
Scaramuzza, D., Fraundorfer, F., and Pollefeys, M. (2010).
Closing the Loop in Appearance-Guided Omnidirec-
tional Visual Odometry by Using Vocabulary Trees.
Rob. Autom. Syst., 58:820–827.
Thanh, T., Kojima, Y., Nagahara, H., Sagawa, R.,
Mukaigawa, Y., Yachida, M., and Yagi, Y. (2010).
Real-Time Estimation of Fast Egomotion with Feature
Classification Using Compound Omnidirectional Vi-
sion Sensor. IEICE Trans. Inf. Syst., 93D(1):152–166.
Tian, T., Tomasi, C., and Heeger, D. J. (1996). Compar-
ison of Approaches to Egomotion Computation. In
IEEE Conf. Comput. Vision Pattern Recogn., pages
315–320.
Wang, H., Yuan, K., Zou, W., and Zhou, Q. (2005). Visual
Odometry Based on Locally Planar Ground Assump-
tion. In IEEE Int. Conf. Inf. Acquisition, pages 59–64.
Zelnik-Manor, L. and Irani, M. (2000). Multi-Frame Esti-
mation of Planar Motion. IEEE Trans. Pattern Anal.
Mach. Intell., 22:1105–1116.
ICPRAM 2012 - International Conference on Pattern Recognition Applications and Methods
430
